In English
Гравитационный 4-потенциал
Из проекта Викизнание
Гравитационный 4-потенциал представляет
собой четырёхмерную векторную функцию (4-вектор), посредством которой
определяются свойства гравитационного поля в лоренц-инвариантной
теории гравитации, [1] а также в ковариантной теории гравитации. [2]
В состав гравитационного 4-потенциала входят скалярный и векторный потенциалы
гравитационного поля. При калибровочном преобразовании потенциалы
гравитационного поля могут изменять свой вид, вследствие чего одному и тому же
гравитационному полю могут соответствовать не совпадающие друг с другом
4-потенциалы, отличающиеся разной зависимостью от координат и времени.
Оглавление
|
Определение
В
соответствии с метрической теорией
относительности, одни и те же физические явления могут регистрироваться и описываться не только с помощью электромагнитных, но и других волн, например,
гравитационных. В гравитационно- волновом представлении вместо скорости
света ![]() должна использоваться скорость гравитации
должна использоваться скорость гравитации ![]() . В этом
случае гравитационный 4-потенциал, как и любой 4-вектор, состоит из скалярной и
векторной частей, дающих в сумме 4 компоненты:
. В этом
случае гравитационный 4-потенциал, как и любой 4-вектор, состоит из скалярной и
векторной частей, дающих в сумме 4 компоненты:

Временной
компонентой 4-потенциала будет скалярный потенциал ![]() ,
делённый на
,
делённый на ![]() . Пространственную компоненту 4-потенциала представляет
векторный потенциал гравитационного поля
. Пространственную компоненту 4-потенциала представляет
векторный потенциал гравитационного поля
![]() , имеющий три компоненты.
, имеющий три компоненты.
Поскольку в реальных явлениях одновременно действует несколько полей, удобно для всех этих полей использовать электромагнитно-волновое представление, позволяющее сравнивать действие полей без пересчёта единиц измерения физических величин. В электромагнитно-волновом представлении скалярный и векторный потенциалы определяются так, чтобы гравитационный 4-потенциал имел следующий вид:
![]()
Определение
(1) 4-потенциала ![]() в ковариантном представлении
с нижним индексом оказывается предпочтительным по сравнению с контравариантным
представлением (с верхним индексом), так как это облегчает решение уравнений.
в ковариантном представлении
с нижним индексом оказывается предпочтительным по сравнению с контравариантным
представлением (с верхним индексом), так как это облегчает решение уравнений.
При переходе из одной системы отсчёта в другую 4-потенциал преобразуется в соответствии с аксиомами метрической теории относительности. В случае пространства Минковского специальной теории относительности преобразования 4-потенциала осуществляются из одной инерциальной системы отсчёта в другую с помощью преобразований Лоренца.
В
международной системе единиц СИ гравитационный 4-потенциал ![]() измеряется в
м/с, в системе физических единиц СГС – в см/с.
измеряется в
м/с, в системе физических единиц СГС – в см/с.
Связь с напряжённостью гравитационного поля и полем кручения
Через гравитационный 4-потенциал (1) определяется тензор гравитационного поля, для чего используется четырёхмерный ротор:
![]()
Антисимметричный
тензор ![]() содержит лишь 6 компонент, три из которых
связаны с вектором напряжённости
гравитационного поля
содержит лишь 6 компонент, три из которых
связаны с вектором напряжённости
гравитационного поля ![]() ,
а другие три компоненты – с вектором поля
кручения
,
а другие три компоненты – с вектором поля
кручения ![]() .
В декартовых координатах данные вектора получаются в следующем виде:
.
В декартовых координатах данные вектора получаются в следующем виде:
![]()
![]()
Из последнего соотношения видно, что поле кручения зависит только от векторного потенциала. В то же время вклад в напряжённость гравитационного поля делает не только градиент скалярного потенциала, но и скорость изменения во времени векторного потенциала.
Калибровка 4-потенциала
Наиболее удобной является калибровка, при которой 4-дивергенция
4-потенциала равна нулю:
![]()
В специальной теории
относительности ковариантная производная ![]() превращается в частную производную
превращается в частную производную ![]() .
Это позволяет с учётом (1) представить калибровочное условие в
явном виде так:
.
Это позволяет с учётом (1) представить калибровочное условие в
явном виде так:
![]()
В лоренц-инвариантной теории гравитации уравнения Хевисайда для
гравитационного поля представляются в четырёхмерной форме:
:
![]()
![]()
Можно показать, что условие калибровки 4-потенциала (3) вытекает
из определения тензора гравитационного поля (2) и уравнений поля (4) и (5).
Если применить к (5) частную производную ![]() ,
то её действие в первых двух членах в (5) на тензор
,
то её действие в первых двух членах в (5) на тензор ![]() можно
учесть с помощью соотношения (4). Для третьего члена в (5) получается
соотношение
можно
учесть с помощью соотношения (4). Для третьего члена в (5) получается
соотношение ![]() ,
где
,
где ![]() обозначает
четырёхмерный оператор Д’Аламбера :
обозначает
четырёхмерный оператор Д’Аламбера :
![]()
здесь применяется оператор Лапласа, в декартовых координатах
имеющий вид 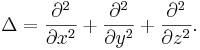
Заменяя ещё в (5) ![]() его
выражением согласно (2), из (5) как наиболее простое решение
получается волновое уравнение для 4-потенциала, источником для
которого служит массовый 4-ток
его
выражением согласно (2), из (5) как наиболее простое решение
получается волновое уравнение для 4-потенциала, источником для
которого служит массовый 4-ток ![]() : [3]
: [3]
![]()
где ![]() – гравитационная
постоянная.
– гравитационная
постоянная.
С другой стороны, если в (4) заменить ![]() его
выражением согласно (2), то получается снова волновое уравнение (6) для
4-потенциала, но только при выполнении условия калибровки 4-потенциала (3). Тем
самым можно считать, что в силу симметрии полей данная калибровка позволяет
упростить уравнения поля.
его
выражением согласно (2), то получается снова волновое уравнение (6) для
4-потенциала, но только при выполнении условия калибровки 4-потенциала (3). Тем
самым можно считать, что в силу симметрии полей данная калибровка позволяет
упростить уравнения поля.
Заметим, что если взять частную производную ![]() от
обеих частей в (4), то с учётом (2) левая часть будет равна нулю. Тогда из
равенства нулю правой части вытекает уравнение непрерывности для
массового 4-тока:
от
обеих частей в (4), то с учётом (2) левая часть будет равна нулю. Тогда из
равенства нулю правой части вытекает уравнение непрерывности для
массового 4-тока:
![]()
Если из гравитационного 4-потенциала ![]() вычесть
калибровочный 4-вектор вида
вычесть
калибровочный 4-вектор вида ![]() ,
зависящий от некоторой скалярной калибровочной функции
,
зависящий от некоторой скалярной калибровочной функции ![]() ,
то при условии, что функция
,
то при условии, что функция ![]() удовлетворяет
волновому уравнению
удовлетворяет
волновому уравнению
![]()
для нового 4-потенциала ![]() останется
в силе условие калибровки (3), а тензор гравитационного поля согласно (2) не
изменит свой вид. Таким образом, в лоренц-инвариантной теории гравитации и в
построенной на её основе ковариантной теории гравитации
проявляется калибровочная инвариантность.
останется
в силе условие калибровки (3), а тензор гравитационного поля согласно (2) не
изменит свой вид. Таким образом, в лоренц-инвариантной теории гравитации и в
построенной на её основе ковариантной теории гравитации
проявляется калибровочная инвариантность.
В ковариантной
теории гравитации уравнения Хевисайда (4) и (5) для гравитационного поля обобщаются
для искривлённого пространства-времени и записываются так: [2] [4] [5]
![]()
![]()
Волновое уравнение вместо (6) выглядит следующим образом:
![]()
В искривлённом пространстве-времени в данном уравнении происходит перемешивание
компонент векторов. В частности, скалярный потенциал гравитационного поля
становится функцией не только от плотности движущегося вещества ![]() ,
но и от плотности массового тока
,
но и от плотности массового тока ![]() ,
где
,
где ![]() –
скорость движения вещества.
–
скорость движения вещества.
Решение волнового уравнения для 4-потенциала
В специальной теории относительности коэффициенты
Кристоффеля ![]() равны нулю и тогда решение волнового уравнения
можно представить в следующем виде: [2]
равны нулю и тогда решение волнового уравнения
можно представить в следующем виде: [2]
![]()
где
гравитационный 4-потенциал ![]() в момент времени
в момент времени ![]() в точке пространства, определяемой
радиус-вектором
в точке пространства, определяемой
радиус-вектором ![]() ,
находится путём интегрирования по объёму, содержащему в себе массовый 4-ток
(4-вектор плотности тока массы)
,
находится путём интегрирования по объёму, содержащему в себе массовый 4-ток
(4-вектор плотности тока массы) ![]() . При
этом интегрирование по объёму осуществляется для более раннего момента
времени
. При
этом интегрирование по объёму осуществляется для более раннего момента
времени ![]() ,
где
,
где ![]() есть радиус-вектор, задающий расположение
массового 4-тока в ранний момент времени.
есть радиус-вектор, задающий расположение
массового 4-тока в ранний момент времени.
Из приведённого решения для временных компонент 4-векторов видно, что скалярный потенциал зависит от плотности вещества некоторой движущейся массы в ранний момент времени и от расстояния от этой массы до точки, где измеряется потенциал. В свою очередь, векторный потенциал зависит ещё от скорости движения массы в ранний момент времени. Наличие интеграла по объёму подразумевает, что для потенциалов гравитационного поля выполняется принцип суперпозиции, и для вычисления суммарного 4-потенциала следует учитывать все источники поля.
4-потенциал
собственного гравитационного поля одиночной твёрдой материальной точки может
быть получен по-другому – путём умножения скалярного гравитационного
потенциала ![]() вокруг этой точки, вычисленного в
сопутствующей этой точке системе отсчёта, на 4-скорость движения материальной
точки:
вокруг этой точки, вычисленного в
сопутствующей этой точке системе отсчёта, на 4-скорость движения материальной
точки:
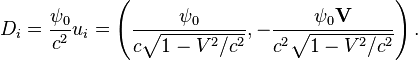
Для
наблюдателя, относительно которого движется материальная точка, согласно
преобразованиям Лоренца скалярный потенциал изменяется за счёт движения
точки: 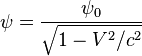 ,
а также появляется векторный потенциал, равный
,
а также появляется векторный потенциал, равный 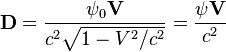 . Это даёт обычное определение
гравитационного 4–потенциала в виде
. Это даёт обычное определение
гравитационного 4–потенциала в виде
![]()
Действительно,
4-потенциал любого векторного поля для одной частицы, внутри которой
векторные потенциалы полей отсутствуют, может быть представлен так: [6] [7]
![]()
где ![]() для электромагнитного поля и
для электромагнитного поля и ![]() для остальных полей,
для остальных полей, ![]() и
и ![]() –
плотность массы и соответственно плотность заряда в сопутствующей системе
отсчёта,
–
плотность массы и соответственно плотность заряда в сопутствующей системе
отсчёта, ![]() –
плотность энергии поля частицы,
–
плотность энергии поля частицы, ![]() –
ковариантная 4-скорость.
–
ковариантная 4-скорость.
Для гравитационного поля получается ![]() ,
, ![]() ,
что приводит к формуле для 4-потенциала
,
что приводит к формуле для 4-потенциала ![]() .
.
В системе из множества материальных точек, составляющих материальные тела, для нахождения общего 4-потенциала следует суммировать 4-потенциалы всех материальных точек, с учётом различия их 4-скоростей и разного их расположения в пространстве. В результате суммарный векторный потенциал системы точек лишь косвенно отражает суммарный скалярный потенциал данной системы точек, в отличие от прямой связи между скалярным и векторным потенциалом отдельной материальной точки. В случае вычисления суммарного 4-потенциала массивного твёрдого тела, с учётом различных расстояний от частей тела до точки, где определяется 4-потенциал, получаются гравитационные потенциалы Лиенара-Вихерта. [8] [9]
Гравитационный 4-потенциал для релятивистской однородной системы вычислен в статье. [10]
Лагранжиан и действие
Гравитационный 4-потенциал входит в лагранжиан для вещества в гравитационном и электромагнитном поле, что позволяет записать соответствующую функцию действия: [11] [4]
![]()
![]()
где ![]() – функция Лагранжа или лагранжиан,
– функция Лагранжа или лагранжиан, ![]() –
дифференциал времени используемой системы отсчёта,
–
дифференциал времени используемой системы отсчёта, ![]() –
некоторый коэффициент,
–
некоторый коэффициент, ![]() –
скалярная кривизна,
–
скалярная кривизна, ![]() –
космологическая константа, характеризующая плотность энергии рассматриваемой
системы в целом, и потому являющаяся функцией системы,
–
космологическая константа, характеризующая плотность энергии рассматриваемой
системы в целом, и потому являющаяся функцией системы, ![]() –
скорость света, как мера скорости распространения электромагнитного и
гравитационного взаимодействий, электромагнитный 4-потенциал
–
скорость света, как мера скорости распространения электромагнитного и
гравитационного взаимодействий, электромагнитный 4-потенциал ![]() ,
где
,
где ![]() есть скалярный потенциал, а
есть скалярный потенциал, а ![]() является векторным потенциалом,
является векторным потенциалом, ![]() –
электрический 4-ток,
–
электрический 4-ток, ![]() –
электрическая постоянная,
–
электрическая постоянная, ![]() –
тензор электромагнитного поля,
–
тензор электромагнитного поля, ![]() – 4-потенциал поля ускорений,
– 4-потенциал поля ускорений, ![]() –
тензор ускорений,
–
тензор ускорений, ![]() и
и ![]() –
постоянные, подлежащие определению,
–
постоянные, подлежащие определению, ![]() –
4-потенциал поля давления,
–
4-потенциал поля давления, ![]() – тензор
поля давления,
– тензор
поля давления, ![]() – инвариантный 4-объём, выражаемый через
дифференциал временной координаты
– инвариантный 4-объём, выражаемый через
дифференциал временной координаты ![]() ,
через произведение
,
через произведение ![]() дифференциалов
пространственных координат, и через квадратный корень
дифференциалов
пространственных координат, и через квадратный корень ![]() из детерминанта
из детерминанта ![]() метрического тензора, взятого с отрицательным
знаком.
метрического тензора, взятого с отрицательным
знаком.
В
интеграле действия гравитационный 4-потенциал присутствует внутри
инварианта ![]() ,
а также в составе тензора гравитационного поля
,
а также в составе тензора гравитационного поля
![]() и его
инварианта
и его
инварианта ![]() . В первом случае 4-потенциал
задаёт функцию энергии связи вещества с полем, а во втором случае –
энергетическую функцию поля как самостоятельного объекта. Варьирование функции
действия приводит к определению тензора
энергии-импульса гравитационного поля, задаёт уравнения гравитационного
поля (7) и (8), уравнение движения вещества в поле и выражение для
гравитационной 4-силы.
. В первом случае 4-потенциал
задаёт функцию энергии связи вещества с полем, а во втором случае –
энергетическую функцию поля как самостоятельного объекта. Варьирование функции
действия приводит к определению тензора
энергии-импульса гравитационного поля, задаёт уравнения гравитационного
поля (7) и (8), уравнение движения вещества в поле и выражение для
гравитационной 4-силы.
Роль 4-потенциала в теории гравитации
В
классической механике вместо полного 4-потенциала используют его скалярную
компоненту в виде гравитационного потенциала. Это позволяет находить
потенциальную гравитационную энергию тел и уравнения их движения. Для
вычисления скалярного гравитационного потенциала применяется уравнение Пуассона
вида: ![]() , где
, где ![]() есть оператор Лапласа,
есть оператор Лапласа, ![]() – объёмная плотность распределения массы в
рассматриваемой точке. Однако получающиеся выражения для потенциала, сил и
энергий оказываются не лоренц-ковариантными, то есть возникает проблема при
пересчёте результатов из одной инерциальной системы отсчёта в другую.
– объёмная плотность распределения массы в
рассматриваемой точке. Однако получающиеся выражения для потенциала, сил и
энергий оказываются не лоренц-ковариантными, то есть возникает проблема при
пересчёте результатов из одной инерциальной системы отсчёта в другую.
Гравитационный
4-потенциал практически не рассматривается и в общей
теории относительности (ОТО). Это связано с тем, что в ОТО гравитационное
поле отождествляется с метрическим полем, причём в качестве гравитационных
потенциалов выступают компоненты метрического тензора, а вместо напряжённости
поля используются символы Кристоффеля. В слабом поле может быть установлена
связь между компонентой ![]() метрического тензора пространства-времени и
значением гравитационного скалярного потенциала классической механики:
метрического тензора пространства-времени и
значением гравитационного скалярного потенциала классической механики: ![]() , где
, где ![]() – скорость света. Векторный потенциал
гравитационного поля
– скорость света. Векторный потенциал
гравитационного поля ![]() ,
используемый в лоренц-инвариантной теории гравитации, также может быть выражен
через компоненты метрического тензора ОТО.
,
используемый в лоренц-инвариантной теории гравитации, также может быть выражен
через компоненты метрического тензора ОТО.
С другой
стороны, при аксиоматическом построении лоренц-инвариантной
теории гравитации (ЛИТГ) именно 4-потенциал
![]() представляет
гравитационное поле, тогда как в отношении вещества это делает массовый
4-ток
представляет
гравитационное поле, тогда как в отношении вещества это делает массовый
4-ток ![]() .
Пятая аксиома ЛИТГ утверждает, что даламбертиан от 4-потенциала равен 4-току с
соответствующим постоянным множителем. [2] Этого оказывается достаточным, чтобы вывести
все соотношения лоренц-инвариантной теории гравитации. Аксиоматика ЛИТГ
оказывается той же самой и для ковариантной
теории гравитации (КТГ), поскольку КТГ является обобщением ЛИТГ на
искривлённое пространство-время, в котором у метрического тензора появляется
зависимость от времени и координат.
.
Пятая аксиома ЛИТГ утверждает, что даламбертиан от 4-потенциала равен 4-току с
соответствующим постоянным множителем. [2] Этого оказывается достаточным, чтобы вывести
все соотношения лоренц-инвариантной теории гравитации. Аксиоматика ЛИТГ
оказывается той же самой и для ковариантной
теории гравитации (КТГ), поскольку КТГ является обобщением ЛИТГ на
искривлённое пространство-время, в котором у метрического тензора появляется
зависимость от времени и координат.
Гравитационный
4-потенциал, как и электромагнитный 4-потенциал, действуя на пробные тела,
оказывает влияние на скорость течения времени в этих телах. [12] Это
приводит к тому, что одинаковые процессы, протекающие в телах, находящихся в
разных 4-потенциалах, перестают совпадать по фазе. Для гравитационного фазового сдвига между двумя
одинаковыми частицами с массой ![]() и зарядом
и зарядом
![]() ,
одна из которых находится в некотором гравитационном (электромагнитном) поле,
получается:
,
одна из которых находится в некотором гравитационном (электромагнитном) поле,
получается:


здесь ![]() – постоянная
Дирака,
– постоянная
Дирака, ![]() – электромагнитный
4-потенциал,
– электромагнитный
4-потенциал, ![]() – 4-перемещение
частицы во времени и пространстве.
– 4-перемещение
частицы во времени и пространстве.
Последнее соотношение для сдвига фаз в электромагнитном поле подтверждается эффектом Ааронова-Бома.
С помощью гравитационного 4-потенциала вычисляется обобщённый 4-импульс, [13] являющийся частью 4-импульса физической системы из частиц и полей. [14]
Теорема энергии поля, имеющая тот же смысл для
полей, что и теорема вириала для частиц, применима к векторному гравитационному
полю в искривлённом пространстве-времени. В формулировке теоремы присутствует
гравитационный 4-потенциал: [15]
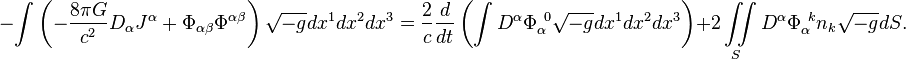
См. также
- Гравитационный потенциал
- Векторный потенциал гравитационного поля
- Электромагнитный потенциал
Ссылки
1.
Федосин С. Г. Физика и философия подобия от
преонов до метагалактик, Пермь: Стиль-МГ, 1999, ISBN
5-8131-0012-1. 544 стр., Табл.66, Ил.93, Библ. 377 назв.
2.
а б в г Федосин С.Г. Физические теории и бесконечная
вложенность материи, Пермь, 2009, 844 стр., Табл. 21, Ил.41,
Библ. 289 назв. ISBN
978-5-9901951-1-0.
3.
Федосин С.Г.
Современные проблемы физики, М: Эдиториал УРСС, 2002, ISBN
5-8360-0435-8. 192 стр., Ил.26, Библ. 50 назв.
4. а б Fedosin
S.G. About the cosmological constant, acceleration field, pressure field and
energy. Jordan
Journal of Physics. Vol. 9, No. 1, pp. 1-30 (2016). http://dx.doi.org/10.5281/zenodo.889304; статья на русском языке: О
космологической постоянной, поле ускорения, поле давления и об энергии.
5. Fedosin S.G. Lagrangian formalism in the theory of relativistic vector fields. International Journal of Modern Physics A, Vol. 40, No. 02, 2450163 (2025). https://doi.org/10.1142/S0217751X2450163. // Лагранжев формализм в теории релятивистских векторных полей.
6. Fedosin S.G. The procedure of finding the stress-energy tensor and vector field equations of any form. Advanced Studies in Theoretical Physics, Vol. 8, no. 18, pp. 771-779 (2014). http://dx.doi.org/10.12988/astp.2014.47101; статья на русском языке: Процедура для нахождения тензора энергии-импульса и уравнений векторного поля любого вида.
7. Fedosin S.G. Equations of
Motion in the Theory of Relativistic Vector Fields. International Letters of
Chemistry, Physics and Astronomy, Vol. 83, pp. 12-30 (2019). https://doi.org/10.18052/www.scipress.com/ILCPA.83.12. // Уравнения движения в
теории релятивистских векторных полей.
8. Fedosin S.G. Energy, Momentum, Mass and Velocity of a Moving Body. Preprints 2017, 2017040150. http://dx.doi.org/10.20944/preprints201704.0150.v1; статья на русском языке: Энергия, импульс, масса и скорость движущегося тела.
9. Fedosin
S.G. Energy, Momentum, Mass and Velocity of a Moving Body in the Light of
Gravitomagnetic Theory.
Canadian Journal of Physics, Vol. 92, No. 10, pp. 1074-1081 (2014). http://dx.doi.org/10.1139/cjp-2013-0683; статья на русском языке: Энергия,
импульс, масса и скорость движущегося тела в свете теории гравитомагнетизма.
10. Fedosin S.G. The Gravitational Field in the
Relativistic Uniform Model within the Framework of the Covariant Theory of
Gravitation. International Letters of Chemistry, Physics and Astronomy, Vol.
78, pp. 39-50 (2018). http://dx.doi.org/10.18052/www.scipress.com/ILCPA.78.39. // Гравитационное поле в релятивистской однородной модели в рамках ковариантной теории гравитации,
11. Fedosin S.G. The Principle of Least Action in Covariant Theory of Gravitation. Hadronic Journal, Vol. 35, No. 1, pp. 35-70 (2012). http://dx.doi.org/10.5281/zenodo.889804; статья на русском языке: Принцип наименьшего действия в ковариантной теории гравитации.
12. Fedosin S.G. The Hamiltonian in Covariant Theory of Gravitation. Advances in Natural Science, Vol.
5, No. 4, pp. 55-75 (2012). http://dx.doi.org/10.3968%2Fj.ans.1715787020120504.2023;
статья на русском языке: Гамильтониан в
ковариантной теории гравитации.
13. Fedosin S.G. Generalized Four-momentum for
Continuously Distributed Materials. Gazi University Journal of Science, Vol.
37, Issue 3, pp. 1509-1538 (2024). https://doi.org/10.35378/gujs.1231793. // Обобщённый 4-импульс для
непрерывно распределённого вещества,
14. Fedosin S.G. What should we understand by the
four-momentum of physical system? Physica Scripta, Vol. 99, No. 5,
055034 (2024). https://doi.org/10.1088/1402-4896/ad3b45.
// Что
мы должны понимать под 4-импульсом физической системы?
15.
Fedosin S.G. The Integral Theorem of the Field Energy. Gazi University Journal of
Science. Vol. 32, No. 2, pp. 686-703 (2019). http://dx.doi.org/10.5281/zenodo.3252783. // Интегральная
теорема энергии поля.