Hadronic
Journal, February 2012, Vol. 35, No. 1, P. 35 - 70.
УДК 53.02+
530.12:531.51 +531.314+531.422+537.8
Принцип наименьшего действия в ковариантной теории гравитации
Федосин Сергей Григорьевич
г. Пермь, Пермский край, Россия
e-mail intelli@list.ru
Путём вариации функционала действия находятся уравнения для вычисления
метрики, уравнения движения вещества, а также уравнения для гравитационного и
электромагнитного полей в ковариантной теории гравитации. В ковариантной форме
определяется тензор плотности энергии-импульса гравитационного поля, тензор
напряжённостей гравитационного поля и 4-ток плотности массы. Находится смысл
космологической постоянной и её связь с компонентами плотности энергии в функционале
действия. Полученные результаты указывают на справедливость принципа Маха, если
полагать гравитацию следствием воздействия на тела потоков гравитонов.
Обосновывается мысль о том, что метрика может быть полностью определена через
переменные, описывающие свойства полей.
Ключевые слова: действие; метрика; космологическая постоянная; тензор плотности
энергии-импульса гравитационного поля; уравнения движения; уравнения поля;
ковариантная теория гравитации.
The principle of least action in
covariant theory of gravitation
Sergey G. Fedosin
Perm, Perm Region, Russia
e-mail intelli@list.ru
The integral equations for
calculation of metric, equations of substance motion, as well as equations for
gravitational and electromagnetic fields in covariant theory of gravitation are
obtained by means of variation of action functional. In covariant form
stress-energy tensor of gravitational field, strength tensor of gravitational
field and 4-current of mass are determined. The meaning of the cosmological
constant and its relation to the components of energy density in action
functional are explained. The results obtained prove the validity of Mach's
principle, assuming that gravitation effects are due to the flows of gravitons.
The idea that metric can be entirely determined by variables describing fields’
properties is substantiated.
Keywords: action; metric; cosmological
constant; stress-energy tensor of gravitational field; equations of motion;
field equations; covariant theory of gravitation.
Ковариантная теория гравитации (КТГ) является одной из
альтернативных теорий гравитации по отношению к общей теории относительности.
Целью данной статьи является вывод уравнений КТГ из принципа наименьшего
действия. В качестве основы наших рассуждений мы будем использовать работы
Эйнштейна [1], Дирака [2], Паули [3], Фока [4], Ландау и Лифшица [5].
Далее будут применяться международная система единиц СИ,
базовые координаты в виде координат с контравариантными индексами 
, сигнатура метрики (+, –, –, –), метрический тензор 
. Наличие
в формулах повторяющихся индексов подразумевает суммирование по правилу Эйнштейна, то есть отдельное
суммирование по каждому повторяющемуся индексу.
Функция
действия
В случае непрерывно распределённой по всему объёму
пространства материи функция действия для вещества, находящегося в гравитационном
и электромагнитном полях, в ковариантной теории гравитации имеет вид:
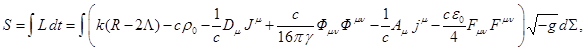
(1)
где 
– функция Лагранжа или
лагранжиан,
– дифференциал времени используемой системы отсчёта,
– некоторый
коэффициент,
– скалярная кривизна,
– некоторая константа,
характеризующая плотность энергии рассматриваемой системы в целом, и потому
являющаяся функцией системы,
– скорость света, как
мера скорости распространения электромагнитного и гравитационного
взаимодействий,
– плотность массы
вещества в системе отсчёта, в которой данное вещество покоится,
– 4-потенциал
гравитационного поля, описываемый через скалярный потенциал 
и
векторный потенциал
этого поля,
– 4-вектор плотности
массового тока,
– гравитационная
постоянная,
есть гравитационный
тензор (тензор напряжённостей гравитационного поля),
– определение
гравитационного тензора с контравариантными индексами с помощью метрического
тензора 
,
– 4-потенциал
электромагнитного поля, задаваемый с помощью скалярного потенциала 
и
векторного потенциала 
этого поля,
– 4-вектор плотности
электрического тока,
– электрическая
постоянная,
– электромагнитный
тензор (тензор напряжённостей электромагнитного поля),
– инвариантный
4-объём, выражаемый через дифференциал временной координаты 
, через произведение 
дифференциалов
пространственных координат, и через квадратный корень 
из детерминанта 
метрического тензора,
взятого с отрицательным знаком.
Символом 
обозначена
ковариантная производная по координатам (в данном случае по координатам 
). Аналогично 
есть оператор частной
производной по координатам или 4-градиент.
Под знаком интеграла в (1) находится функция Лагранжа 
, состоящая из шести членов. Первый член со скалярной
кривизной зависит от
метрического тензора и его производных по координатам. В КТГ метрика вводится
для того, чтобы учесть влияние фундаментальных полей (к которым относятся
электромагнитное и гравитационное поля) материальных тел на результаты
пространственно-временных измерений вблизи этих тел. Влияние полей на
результаты измерений проявляется в том, что под действием поля электромагнитные
волны отклоняются от прямолинейного движения, электромагнитные часы изменяют
свой ход, меняются и измеряемые расстояния. Данные эффекты можно описать путём
введения искривлённого пространства-времени с метрическим тензором 
вместо плоского
пространства Минковского с его единичным метрическим тензором 
. В КТГ гравитационное поле является самостоятельным
физическим полем, а метрический тензор имеет геометрический
смысл и носит вспомогательный характер, в отличие от общей теории
относительности, где метрическое поле полностью заменяет собой гравитационное
поле.
В КТГ второй член в (1) не просто связан с плотностью энергии
покоя вещества и его инерцией относительно действующих сил. Согласно [6],
[7], основная часть массы покоя (и
плотности покоящегося вещества) является следствием сильной гравитации и
электромагнитных взаимодействий, действующих на уровне элементарных частиц.
Только первый и второй члены в (1) связаны с микроскопическими фундаментальными
полями, тогда как остальные члены относятся к действию макроскопических
гравитационных и электромагнитных полей. Разделение на микроскопические и
макроскопические фундаментальные поля вытекает из теории бесконечной
вложенности материи, в которой на каждом основном уровне материи действует своё
собственное гравитационной поле. В результате обычная гравитация полагается
дальнодействующей компонентой сильной гравитации.
Третьим членом в (1) является инвариант относительно
различных преобразований координат вида 
, отражающий взаимодействие плотности массового тока 
произвольного элемента
вещества с гравитационным полем.
Согласно [8], четвёртый член в (1), связанный с энергией
поля, представляет собой инвариант гравитационного поля, не меняющий свой вид
при смене системы отсчёта. Пятый и шестой члены, для электромагнитного поля, по
своей структуре подобны третьему и четвёртому членам для гравитационного поля.
При этом 4-вектор плотности электрического тока 
может быть определён
через плотность заряда элемента вещества 
и 4-скорость: 
.
Следует сказать, что в КТГ 4-потенциалы 
и 
с ковариантными
индексами, и 4-токи 
и с контравариантными
индексами, были определены в [7] и [9] как исходные понятия при аксиоматическом
построении теории. Отсюда следует, например, что 4-вектор 
не может быть найден в
отсутствие информации о метрике в данной системе отсчёта.
Варьирование
инварианта кривизны
Для получения уравнений для метрики необходимо приравнять
нулю вариацию функцию действия для случая, когда в функции Лагранжа варьируется
метрический тензор . При этом на границах четырёхмерного объёма, по которому в
(1) происходит интегрирование, вариации метрического тензора должны быть равны
нулю. Для полной вариации действия следует записать:
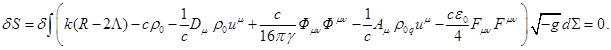
(2)
Найдём вариацию, связанную с первым членом в (2). Учитывая
определение скалярной кривизны через коэффициенты
Кристоффеля, имеем аналогично [2]:
, (3)
где 
, 
, 
.
Выражение 
может быть получено
путём дифференцирования по частям:
. (4)
Первые два члена в правой части (4) являются полными
производными (дивергенциями), и после их подстановки в (3) интегралы от
дивергенции по объёму согласно теореме Гаусса-Остроградского могут быть
заменены на интегралы по поверхности, окружающей объём, по которому происходит
интегрирование. Поскольку вариации метрического тензора на поверхности равны
нулю, они не будут вносить вклада в вариацию функции действия, так что в (4)
следует учитывать только два последних члена. Используем далее два соотношения:
, 
.
(5)
Подставляя их в последние два члена в (4) и переобозначая
некоторые индексы, по которым происходит суммирование, имеем:
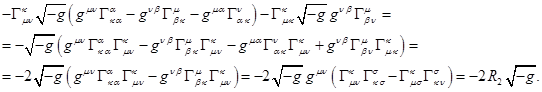
Вследствие этого вместо (3) можно записать:
. (6)
Первая вариация в (6) будет равна:
.
(7)
Используя соотношение:
,
дифференцирование по частям произведения двух функций, и применяя
второе соотношение в (5), для первой части (7) получим:
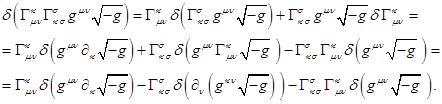(8)
Выражение для производной метрического тензора имеет вид: 
. После умножения на 
, взятия вариации и ещё одного умножения на 
получится:
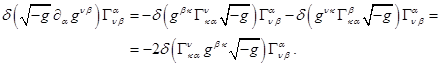
Преобразуем теперь вторую часть в (7), используя в нужных
местах замену индексов, операцию дифференцирования по частям, и предыдущее
выражение:
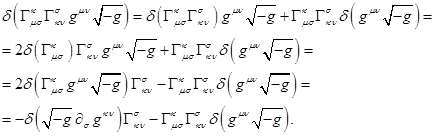(9)
Подстановка (8) и (9) в (7) даёт:
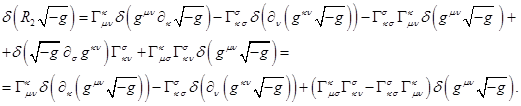
(10)
Преобразуем члены 
и 
в (10):
.
.
(11)
В выражениях (11) находятся дивергенции вида 
, которые после подстановки в (10) и далее в (6) будут
интегрироваться по объёму и превращаются в интегралы по поверхности, где
вариации равны нулю. С учётом этого, после подстановки (10) и (11) в (6)
получается:
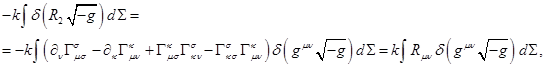(12)
где 
есть тензор Риччи.
Для вариаций метрического тензора 
и можно записать:
, 
.
(13)
Учитывая (13) в (12), находим:
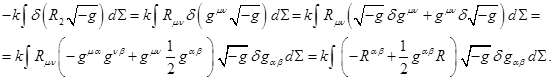
Учитывая этот результат и выражение для 
из (13), имеем:
. (14)
Варьирование
инварианта плотности массы
Второй член в (2) является инвариантом, связанным с 4-током
массы 
, поскольку можно записать:
.
(15)
4-вектор может быть определён
через 4-скорость 
, где 
есть 4-вектор
смещения, 
– дифференциал
собственного времени, следующим
образом: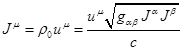 
, причём 
. Заметим, что в физике элементарных частиц пользуются не
значениями массы и скорости частиц, а их энергиями 
и импульсами 
как величинами, прямо
находимыми из экспериментов. Эти величины входят в 4-импульс частицы: 
, а инвариантная масса 
становится вторичным
понятием и находится из соотношения 
. Соответственно для вычисления скорости частиц в специальной
теории относительности применяется соотношение: 
.
Вариация действия для второго члена в (2) с учётом (15) имеет
вид:
. (16)
Определим вариацию в (16) с учётом (13):
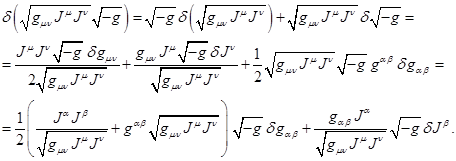(17)
В (17) содержится вариация 
, которая согласно [2], [4] может быть найдена с помощью
смещений 
, представляющих собой вариации координат, вследствие которых
возникает вариация массового 4-тока 
:
.
(18)
Выражение (18) было получено из того условия, что масса элемента
вещества при варьировании координат остаётся постоянной, несмотря на изменение
плотности вещества и его объёма. С учётом (15) и (18) последний член в (17)
можно преобразовать через 4-скорость 
:
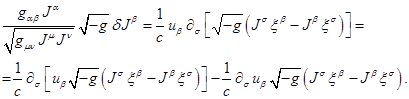
Член с полной дивергенцией при интегрировании по 4-объёму в
функции действия не будет давать никакого вклада. Оставшийся член в предыдущем
равенстве можно преобразовать дальше:
(19)
Здесь было использовано условие 
, поскольку оно следует из равенства 
, к которому применяется ковариантная производная 
.
Введём симметричный тензор плотности энергии-импульса
вещества:
.
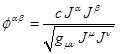(20)
Подставляя (20) в (17)
и используя (19) вместо последнего члена в (17), находим вариацию 
в (16):
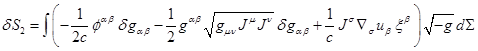. (21)
Варьирование
функции Лагранжа гравитационного поля и его источников
Действие макроскопического гравитационного поля проявляется в
третьем и четвёртом членах в (2), что даёт следующее:
, 
. (22)
Рассмотрим вначале вариацию для 
в (22), учитывая 
из (13), а также (18)
для 
:
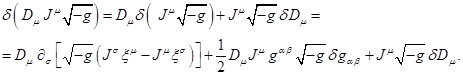
Преобразуем первый член:
.
Пренебрегая при вариации действия членом с полной
производной, рассмотрим следующее:
Подставляя полученные результаты в (22), находим:
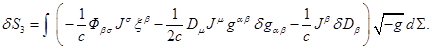(23)
Вариация для 
в (22) с учётом (13)
будет равна:
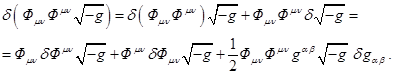(24)
Поскольку 
, тензор 
антисимметричен, то
используя 
из (13), находим:
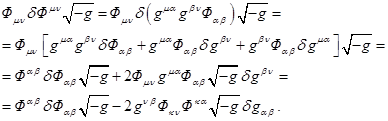
Подстановка этого выражения в (24) даёт:
(25)
Обозначим через 
тензор плотности
энергии-импульса гравитационного поля:
. (26)
Вспоминая, что 
, используя дифференцирование по частям, а также равенство,
справедливое для антисимметричного тензора:
, для члена 
в (25) имеем:
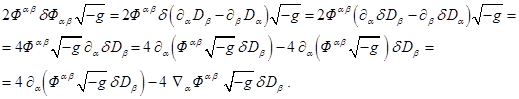
(27)
Член 
в последнем выражении
является дивергенцией и им можно будет пренебречь при вариации функции
действия. Подставляя (26) и (27) в (25), а результат в (22), находим:
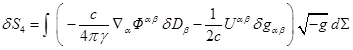. (28)
Варьирование
функции Лагранжа электромагнитного поля и его источников
Варьирование в (2) для электромагнитного поля производится
так же, как для гравитационного поля в предыдущем разделе. Для пятого и шестого
членов в (2) можно записать:
, 
. (29)
Заменяя в (22) 
на 
, 
на 
, 
на 
, вместо (23) находим:
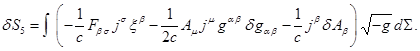(30)
При выводе (30) было использовано выражение для вариации
электромагнитного 4-тока, подобное (18):
.
(31)
Введём тензор плотности энергии-импульса электромагнитного
поля:
. (32)
С его помощью вариация 
аналогично (28) будет
равна:
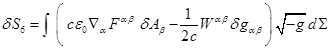. (33)
Уравнения
для метрики
Соберём вместе и подставим в (2) все члены из (14), (21), (23),
(28), (30) и (33), содержащие вариацию 
метрического тензора.
В силу произвольности вариации сумма всех этих членов должна быть равна нулю.
Это даёт следующее:
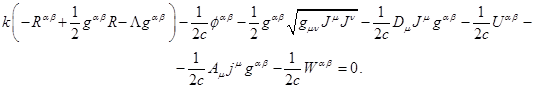
Перепишем данное
равенство при 
, где
– малый коэффициент
порядка единицы, как уравнение для определения метрического тензора 
через известные
источники энергии-импульса. При этом вместо 
введём новую
постоянную 
, согласно соотношению: 
. Так же как и , постоянная определяет свойства
рассматриваемой системы в целом. Это даёт:
(34)
В случае, когда
рассматривается такая большая система, как наша Вселенная, имеет особое название
– космологическая постоянная. Она оценивается величиной 
м–2 . Отсюда значение получается порядка 
Дж/м3 , имея размерность плотности энергии.
Для других систем,
которые также могут приблизительно рассматриваться как
системы с непрерывно распределённой по всему объёму пространства материей, постоянные
и будут иметь другие
значения.
Напомним, что (34)
получается при условии, что либо вариации координат 
и 4-потенциалов 
и 
в функции действия (2)
равны нулю, либо всегда равны нулю суммы всех членов, стоящих перед этими
вариациями. В первом случае (34) приобретает смысл уравнения для определения
метрики системы, в которой изначально заданы как движение заряженного и
гравитирующего вещества по заданным траекториям, так и значения откалиброванных
потенциалов поля (то есть в потенциалах определены входящие в них константы).
Во втором случае допускаются вариации координат (траекторий движения вещества)
и вариации потенциалов, вследствие их взаимного влияния друг на друга. Однако
предполагается, что каждый раз комбинации членов в функции действия, задающие
связь между веществом и полем, включая порождение поля веществом и силу
воздействия поля на вещество, оказываются таковы, что они обнуляются и никак не
влияют на функцию действия и на метрику. Можно также сказать, что во втором
случае произвольно заданы начальное распределение вещества в пространстве и его
начальная скорость, а также начальные значения потенциалов, и при этом законы
связи между последующим движением вещества и поля в силу каких-то причин
приводят к тому, что выполняется уравнение (34). Очевидно, что справедливость
второго случая требует дополнительного доказательства либо должна
постулироваться, тогда как для первого случая этого не требуется.
За пределами вещества,
где гравитационный и электромагнитный 4-токи 
и 
стремятся к нулю,
вклад в метрику согласно (34) вносят только тензор плотности
энергии-импульса гравитационного поля 
(26) и тензор
плотности энергии-импульса электромагнитного поля 
(32). Если же метрика
определяется внутри вещества, то вклад в метрику зависит от всех членов в (34).
Заметим, что в правой
части (34) присутствуют дополнительные члены, которые в работах по общей теории
относительности обычно не рассматриваются. В частности, в (34) включены
практически все инвариантные скалярные величины из функции действия (1),
включая и члены с произведениями 
и 
, вошедшие в состав тензоров
и 
соответственно. В общей теории относительности отсутствует
тензор плотности энергии-импульса гравитационного
поля 
в том виде, как его определили мы. Это вытекает из
того, что в общей теории относительности гравитационное поле сводится к
метрическому полю, когда компоненты 
метрического тензора
рассматриваются как потенциалы, описывающие гравитационное поле. В таком случае
в уравнении для метрики (34) наличие в правой части
означало бы, что гравитационное поле является источником самого себя. В
отсутствие материи это приводило бы к замкнутому кругу, когда метрическое
гравитационное поле порождает само себя, поле даёт метрику, а метрика даёт
поле. В отличие от этого, в ковариантной теории гравитации (КТГ) метрика есть
лишь вспомогательное геометрическое поле, возникающее под действием гравитации
и электромагнитного поля, взятых во всех своих формах на различных масштабных
уровнях материи.
В КТГ
используется метрическая теория относительности [7], сутью которой является
зависимость метрики не только от свойств движения рассматриваемой системы, но и
от вида пробных тел, которыми могут быть как частицы вещества, так и кванты
поля. Пробные тела необходимы для определения метрики системы в натуре, для
осуществления процедуры измерений масштабов и времени, и имеют разные свойства
благодаря различию в уравнениях движения. В результате коэффициент 
в (34) может
различаться для разных систем и должен находиться отдельно для полного
определения метрического тензора. В частности, 
находился в нескольких
ситуациях, например при расчётах отклонения пробных тел под действием
гравитации, и при вычислениях сдвига перигелия. Замечания о последних четырёх
членах в (34) и о члене
с постоянной будут сделаны далее в разделе «Тензоры энергии».
Уравнения
движения вещества и поля
Для получения уравнений
движения вещества необходимо в полной вариации действия (2) выбрать те члены, в
которых содержится вариация координат . Ввиду произвольности сумма всех таких
членов должна равняться нулю. Из суммы (21), (23) и (30) получается:
.
Учитывая, что 
, 
, и используя оператор производной по собственному времени [7]: 
, где 
обозначает
ковариантный дифференциал, 
есть собственное время,
последнее
равенство можно записать так:
, (35)
где 
– 4-ускорение с
ковариантным индексом, первый член в правой части есть плотность гравитационной
силы, а последний член задаёт электромагнитную силу Лоренца для плотности
заряда 
.
Согласно (35), вклад в
4-ускорение элемента вещества делает как гравитационное 4-ускорение 
, так и 4-ускорение в электромагнитном поле 
.
Физический смысл (35)
заключается в том, что оно определяет воздействие полей на вещество в условиях,
когда задан метрический тензор системы (это означает, что в функции действия 
), и заданы потенциалы поля (то есть в функции действия 
, 
).
Соотношение, связывающее
тензор гравитационного поля 
с его источником в
виде 4-вектора 
, вытекает из (23) и (28) как следствие вариации 
по гравитационному
4-потенциалу. С учётом антисимметричности тензора 
:
, или 
. (36)
Аналогичное соотношение
для электромагнитного поля с учётом выражений для вариации по электромагнитному
4-потенциалу в (30) и (33) имеет вид:
, или 
,
(37)
где 
– магнитная
постоянная.
Соотношения (36) и (37), как это видно из их получения из вариации
функции действия, справедливы в том случае, когда вариация координат вещества и
вариация метрики равны нулю, то есть 
, 
. Это означает, что если задано движение вещества и метрика
системы, то можно вычислить, как вещество порождает напряжённости поля.
Если учесть определение гравитационного
тензора: 
, и взять ковариантную
производную данного тензора с последующей циклической перестановкой индексов,
то следующее уравнение выполняется тождественно:
.
(38)
Другая запись (38) имеет
вид:
,
где 
есть символ
Леви-Чивиты или совершенно
антисимметричный единичный тензор.
Уравнение (38) задаёт
уравнения гравитационного поля без источников,
так что комплект уравнений (36) и (38) полностью определяет свойства гравитационного поля.
Для электромагнитного
поля имеем аналогично (38):
или 
.
(39)
Уравнения (37) и (39)
есть уравнения Максвелла, записанные в четырёхмерных обозначениях.
Равенство (36) можно
записать по-другому: 
. Если взять от обеих частей этого равенства контравариантную
производную 
, и применить соотношение 
, то вследствие симметрии и возможности менять порядок
дифференцирования в левой части равенства получится нуль. Это приводит к
уравнению непрерывности (сохранения массы), в котором накладывается
определённое условие на 4-скорость и плотность вещества:
.
Для сохранения
электрического заряда имеем аналогичное соотношение:
.
Если также задать какое-либо
условие для 4-вектора гравитационного потенциала 
, или для 4-вектора электромагнитного потенциала 
, то это позволяет получить определённые соотношения между
соответствующими скалярными и векторными потенциалами. Стандартным подходом
является калибровка Лоренца, что даёт следующие условия:
,
. (40)
Подставляя (40) в (36) и
в (37) с учётом того, что 
, 
, а выражение 
есть оператор
Д’Аламбера, приходим к волновым уравнениям для 4-потенциалов в Лоренцевой
калибровке:
, 
.
О
применимости уравнений движения в общем случае
Как мы упоминали выше, уравнение для определения метрики (34) точно справедливо для
случая, когда полностью задано движение вещества и заданы потенциалы поля.
Однако в большинстве случаев известны лишь начальное состояние движения и
начальные потенциалы, в последующие моменты времени движение вещества начинает
определяться полем и потому задаётся косвенно. Как использовать уравнение (34)
в этом случае и при каких условиях? Для ответа на этот вопрос будем считать,
что движение вещества и потенциалы поля на небольшом интервале времени после
начального момента остаются неизменными. Тогда можно из (34) найти метрический
тензор. Затем, полагая неизменность метрики и движения вещества на следующем,
втором интервале времени, с помощью (36) и (37) вычисляются производные
тензоров 
и 
по координатам. После
интегрирования этих производных находятся напряжённости поля, входящие в состав
этих тензоров. Так как теперь известны уточнённые с помощью метрики тензоры 
и 
, с их помощью на третьем интервале времени в уравнении
движения (35) оценивается ускорение вещества и его движение, и делается
корректировка движения. На четвёртом интервале времени можно использовать
данные по движению вещества из третьего интервала и по величине полей из
второго интервала для того, чтобы оценить изменённую метрику. Далее вычисления
повторяются в указанном порядке. Таким образом реальное движение вещества,
находящегося в гравитационном и электромагнитном полях, и метрика
пространства-времени могут быть приблизительно найдены путём определённой
итерационной процедуры, если использовать указанные выше уравнения для метрики,
движения вещества и поля.
Тензоры
энергии
Возвратимся теперь к
уравнению для метрики (34). Как известно, ковариантная производная левой части
(34) равна нулю, что является свойством находящегося там тензора
Гильберта-Эйнштейна. Следовательно, ковариантная производная правой части (34)
также должна быть равна нулю:
. (41)
С учётом определения
тензора энергии-импульса вещества (20), соотношений 
, 
, и используя оператор производной по собственному времени: , можно записать:
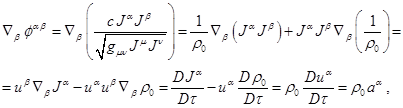(42)
где 
– 4-ускорение.
Найдём теперь
ковариантную производную тензора энергии-импульса гравитационного поля.
Учитывая, что метрический тензор при ковариантном дифференцировании ведёт себя
как константа, используя (36), получаем из (26):
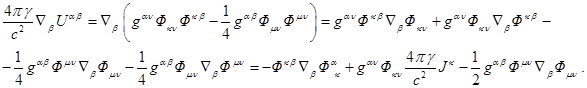
(43)
Применим (38) к
последнему члену в (43) при том условии, что тензор 
антисимметричен:
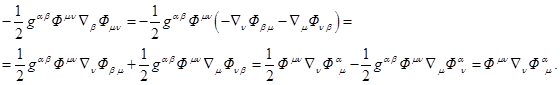
Подстановка этого в (43)
даёт связь между ковариантной производной от тензора энергии-импульса
гравитационного поля и 4-вектором плотности гравитационной силы:
.
(44)
Для ковариантной
производной от тензора энергии-импульса электромагнитного поля и 4-вектора
плотности электромагнитной силы (плотности силы Лоренца) с учётом (32) и (39)
получается аналогичное выражение:
.
(45)
Подставим (42), (44) и
(45) в (41):
.
(46)
Равенство нулю в (46)
вытекает из уравнения движения вещества в гравитационном и электромагнитном
полях (35). Следовательно, ковариантная производная оставшихся в (41) членов
тоже должна равняться нулю:
.
(47)
В скобках в (47) находится скалярная величина, в этом случае
ковариантная производная 
равна частной
производной 
(4-градиенту).
Соотношение (47) будет автоматически удовлетворено, если считать, что в нём в
скобках находится константа, которую можно положить равной нулю. Это даёт
соотношение:
. (48)
Выполнение равенства (48) необходимо для выполнения в (34) предельных
соотношений для тензоров на бесконечности, где нет ни вещества, ни полей. Как
указывается в [4], на бесконечности правая часть (34) с тензорами энергии
обнуляется, а пространство-время становится плоским, приводя к нулю и левую
часть с тензором Гильберта-Эйнштейна. С учётом (48) вид уравнений для метрики
упрощается до предела:
(49)
Используем (15) и раскроем в (48) скалярные произведения
4-векторов, учитывая, что 
, 
, 
, 
:
.
(50)
Здесь 
является 3-вектором,
входящим в состав 4-вектора скорости 
. В не искривлённом пространстве-времени справедлива
специальная теория относительности, в которой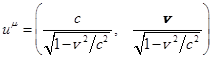 
, и тогда 
, 
, где 
есть скорость движения
вещества.
Отсюда видно, что 
даёт плотность энергии
вещества в гравитационном поле со скалярным потенциалом 
. Векторный потенциал 
гравитационного поля
также связан с энергией, но её величина 
может иметь разный
знак в зависимости от направления вектора , пропорционального скорости 
, и направления вектора . Такая же картина складывается и относительно плотности
электромагнитной энергии – она зависит от плотности заряда 
, скалярного электрического потенциала 
и векторного
потенциала 
электромагнитного
поля.
Предположим теперь, что в (50) каким-то образом выключены
макроскопические гравитационные и электромагнитные поля, и их потенциалы равны нулю.
В этом случае плотность вещества должна достичь некоторого значения 
, которое зависит только от микроскопических фундаментальных
полей, действующих на уровне элементарных частиц. Тогда будет 
и (50) можно
переписать следующим образом:
, (51)
где через 
и через 
мы обозначили
плотность энергии вещества в гравитационном и электромагнитном полях
соответственно.
Поскольку для вещества как
правило отрицательна (вследствие отрицательности гравитационного потенциала ), то из (51) следует, что плотность вещества 
в гравитационном поле
становится больше, чем плотность вещества в отсутствие поля
(когда вещество тела разделено на части и разнесено на бесконечность). Это же
самое можно сказать и о массе – в гравитационном поле она должна увеличиться за
счёт вклада гравитационной массы-энергии вещества в поле. Тем самым мы получили
результат, похожий на тот, который обосновывался нами ранее в [6] и [10], но в
отношении вклада массы-энергии самого поля в общую массу системы из вещества и
поля. Тогда мы нашли, что масса сферического тела растёт за счёт его поля, и
при неизменном объёме это означает увеличение эффективной плотности вещества.
Мы можем проинтегрировать (51) по объёму вещества сферического
незаряженного тела в статическом случае, когда тело неподвижно и не вращается.
Если вещество бесконечно медленно наслаивается на тело тонкими сферическими
оболочками с одной и той же плотностью
вещества , то можно считать, что в (49) 
, а также:
, 
,
,
где 
– наблюдаемая масса
тела при его радиусе 
,
– масса вещества тела
без учёта энергии гравитации,
– масса внутри
текущего радиуса 
, увеличивающегося от 0 до радиуса тела 
по мере роста массы.
В результате (51) превращается в равенство для масс:
,
(52)
где 
есть гравитационная
постоянная.
В (52) масса-энергия
тела увеличивается на модуль всей массы-энергии гравитационного поля. В
реальности при образовании космических объектов в гравитационном поле действует
теорема вириала, согласно которой приблизительно половина работы гравитационного
поля уходит из системы в виде излучения, а другая половина разогревает
вещество. Это уменьшает вдвое добавку к массе-энергии в (52).
Для основных объектов звёздного уровня материи вклад в (51)
плотности энергии вещества 
в электромагнитном
поле по сравнению с невелик. В частности,
для нейтронных звёзд гравитационная энергия равна 
Дж, здесь 
в приближении
однородной плотности вещества, 
– гравитационная
постоянная, 
кг и 
км – масса и радиус
типичной нейтронной звезды. Электромагнитная энергия достигает максимума у
магнитаров, на полюсе которых индукция магнитного поля может быть порядка 
Тл.
Поскольку плотность магнитной энергии определяется выражением 
,
то интеграл по всему объёму внутри звезды и за её пределами даёт величину
магнитной энергии около 
Дж, что значительно меньше модуля гравитационной
энергии.
Похожая ситуация наблюдается и на уровне элементарных частиц, где
согласно теории бесконечной вложенности материи [8] аналогом нейтронной звезды
является нуклон. Энергия протона в собственном поле сильной гравитации
оценивается по формуле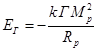 
, где 
и 
обозначают массу и
радиус протона, 
м3∙∙кг–1∙с–2 –
постоянная сильной гравитации, 
– элементарный заряд, 
– электрическая
постоянная, 
– масса электрона.
Выражение для электрической энергии протона для случая однородного
распределения заряда таково: 
.
Следовательно, для протона
отношение модуля энергии сильной гравитации к электрической энергии
равно отношению массы протона к массе электрона, то есть энергия сильной
гравитации преобладает.
Глобальное преобладание гравитационных сил над электромагнитными приводит
к возможности образования элементарных частиц, вещества, массивных тел и прочих
объектов, обнаруживаемых в космосе. Для наблюдаемой Вселенной космологическая
постоянная 
оценивается величиной 
м–2 , а постоянная 
достигает 
Дж/м3 . Мы считаем, что 
характеризует видимую
Вселенную в целом, задавая плотность энергии покоя всего распределённого в
космосе вещества без учёта энергии полей. Предположим далее, что потоки
гравитонов, задающие гравитационные поля, вырабатываются мельчайшими частицами
всего вещества, имеющегося во Вселенной. И чем больше вещества во Вселенной,
тем больше плотность этого вещества и больше плотность потоков гравитонов.
Тогда соотношение (50) подтверждает идею Эйнштейна о том, что «Инерция тела должна возрастать
по мере скопления весомых масс вблизи него» [11], являющуюся в свою очередь
развитием принципа Маха о влиянии удалённых масс на ускорение тел.
Напомним, что в обычной трактовке
космологическая постоянная считается пропорциональной плотности энергии вакуума, причём до сих пор точно неизвестно,
какие частицы или поля ответственны за эту энергию. Существуют также
предположения, что космологическая постоянная зависит от времени, от скалярной
кривизны пространства-времени (в 
гравитации) или от тензора энергии-импульса [12].
Оценим ещё величину скалярной
кривизны для нашей Вселенной.
Умножим (49) на 
и найдём с учётом того, что 
, 
, а для тензоров энергии-импульса (26) и (32) справедливы соотношения:
, 
. Используя выражение (20), находим:
.
Если предположить, что плотность
вещества 
, то кривизна с точностью до знака получается равной
космологической постоянной: 
.
В первом приближении наблюдаемую
Вселенную можно рассматривать как пространство-время постоянной отрицательной
кривизны, для которого должно быть 
. Отсюда радиус такого мира будет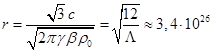 
м. С другой стороны,
если наблюдаемая Вселенная близка по своему состоянию к чёрной дыре
Шварцшильда, то радиус такой дыры должен быть:
.
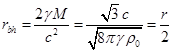В обоих случаях, при определении
кривизны в пространстве-времени, и при оценке радиуса чёрной дыры, в качестве
меры скорости движения и передачи информации используется скорость света.
Анализ
уравнения движения в отношении массы
Согласно (46) уравнение движения вещества в гравитационном и
электромагнитном полях имеет вид:
.
(53)
Рассмотрим (53) в пределе слабого поля, когда становится справедливой
специальная теория относительности, а ковариантная производная переходит в
4-градиент. В этом случае имеем:
,
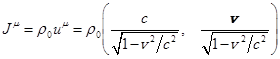и для скалярных компонент тензора энергии-импульса вещества (20) можно
записать:
, 
, (54)
где индекс 
, так что в декартовой системе отсчёта 
, 
, 
, и вектор 
есть 3-вектор
плотности потока механической энергии или релятивистский вектор Умова.
Гравитационный тензор 
определяется через
4-потенциал гравитационного поля 
, зависящий от скалярного потенциала
и векторного потенциала 
гравитационного поля.
Введём гравитационное ускорение 
и поле кручения 
следующим образом:
, 
.
С помощью величин 
и скалярные компоненты
тензора энергии-импульса гравитационного поля (26) представляются так:
,
, (55)
где 
обозначают компоненты
3-вектора плотности потока энергии гравитационного поля (вектора Хевисайда) 
.
Для тензора
энергии-импульса электромагнитного поля (32) в не намагниченном и в не
поляризованном веществе в пределе специальной теории относительности получается
аналогично:
,
, (56)
где 
обозначают компоненты
3-вектора плотности потока энергии электромагнитного поля (вектора
Пойнтинга) 
.
Подстановка (54), (55) и (56) в (53) при 
и при замене 
на 
для пространства
Минковского даёт выражение теоремы Пойнтинга:
, или 
. (57)
Величины 
, 
и 
задают плотности
энергии соответственно вещества, гравитационного и электромагнитного полей.
Проинтегрируем (57) по всему объёму пространства, занимаемого веществом и
полем. Будем рассматривать
квазистационарный случай, когда все потоки энергии замкнуты таким образом, что
интеграл по объёму от дивергенции в правой части (57) становится близким к
нулю. Это означает, что сумма потоков энергии, уходящая безвозвратно в
бесконечность, мала. Тогда с учётом (54), (55) и (56)
должно быть:
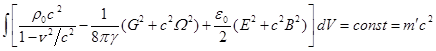, (58)
,
.
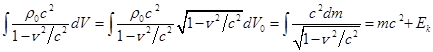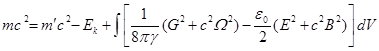Мы обозначили через 
массу вещества, когда
это вещество разнесено на бесконечность и находится там в покое. При этом все
поля 
, 
, 
и 
будут стремиться к
нулю. Из (58) видно, что масса вещества 
по отношению к массе
вещества 
увеличивается за счёт
вклада от полной массы-энергии гравитационного поля, и уменьшается за счёт
вклада от массы-энергии электромагнитного поля и кинетической энергии движения
вещества 
. Фактически (58) подтверждает соотношение (52) из
предыдущего раздела.
Дополнительные
замечания
На наш взгляд, уравнение
движения вещества (35) должно выглядеть несколько по-другому:
. (59)
В (59) плотность вещества
внесена под знак
полной производной по собственному времени. Это позволяет описать случаи, когда
плотность вещества меняется и тем самым создаётся дополнительное ускорение
элемента вещества. Между тем, уравнение (35) было получено из вариации координат,
описанных в [2]
и [4], при условии постоянства массы в ходе варьирования. Это привело к тому,
что (35) отличается от (59) так, что как будто 
и потому выносится за
знак полного дифференциала.
Интересно, что можно
подобрать тензор плотности энергии-импульса вещества такой, что его
ковариантная производная точно даёт скорость изменения 4-импульса вещества.
Этот тензор имеет необычный вид с точки зрения набора индексов, но формальное
ковариантное дифференцирование даёт нужный результат. Вместо (20) запишем: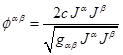
. Отсюда с учётом уравнения непрерывности 
имеем:
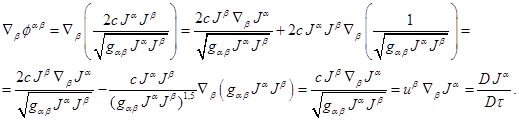
Фактически тензор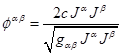 
мы находили в (17).
Причина того, что мы его не использовали так, как это описано здесь,
заключается в том, что вместо точного вида вариации 
как функции вариации
координат, при выводе уравнений движения использовалась упрощённая форма (18).
Это и приводит к (35), но не к (59).
Из вариации соотношения (48) вытекает, что полная вариация массового
4-тока 
связана с вариацией
метрического тензора 
, вариацией электромагнитного 4-тока 
и вариациями
4-потенциалов полей:
, (60)
.
Связь вариаций в (60) осуществляется через вариацию координат
, причём так, что масса элемента объёма при варьировании не
меняется. Однако можно представить случай, когда масса-энергия превращается в
энергию излучения, или плотность вещества меняется вследствие притока или
оттока массы. Тогда некоторые представленные в данной работе результаты будут
требовать соответствующего изменения.
Подставим теперь (48) в (2) и при равенствах 
, 
, получим:
.
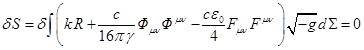После осуществления вариации в данном равенстве мы придём к
уравнениям для метрики (49), но без тензора
:
(61)
В (61) метрика получается такая, какая она должна быть за
пределами вещества, и эта метрика прямо зависит от величины имеющихся полей и
косвенно от распределения вещества, находящегося в этом поле.
В КТГ существует понятие геодезической линии, совпадающее с
выражением в общей теории относительности, но только для распространения
квантов поля. Уравнение движения (35) , с учётом того, что 
, можно записать так:
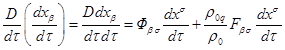. (62)
Для полевых квантов 
. Умножая (62) на 
, получаем равенство нулю правой части: 
. Разделив это на квадрат дифференциала временной координаты 
, отмеряющей время вдоль траектории кванта, и вспоминая
определение оператора производной по собственному времени, получаем уравнение
геодезической в ковариантных индексах:
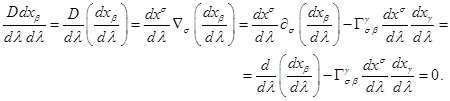(63)
Пока полевые кванты распространяются за пределами вещества в
некотором заданном поле (гравитационном и электромагнитном), их движение происходит
согласно уравнению движения (63), причём метрика пространства-времени
определяется из (61). Что может измениться, когда кванты поля проходят через
вещество? Если вещество разрежено и не взаимодействует с квантами, то кванты
движутся между частицами вещества. Тогда в принципе снова должно быть
справедливо уравнение для метрики (61) с той поправкой, что теперь надо
учитывать тензор плотности энергии-импульса поля сильной гравитации,
действующей на уровне элементарных частиц. Этот новый тензор должен выглядеть
как некоторая добавка к тензору плотности энергии-импульса 
обычной гравитации из
(26), с заменой постоянной гравитации 
на постоянную сильной
гравитации 
, и с некоторым множителем пропорциональности. Вместо того,
чтобы использовать этот новый тензор, на практике заменяют его тензором
плотности энергии-импульса вещества 
, и говорят, что «вещество изменяет метрику
пространства-времени внутри себя, и влияет на метрику за своими пределами».
Это приводит к уравнению для метрики в форме (49). Но
возможна и другая интерпретация – всегда лишь поле влияет на метрику, тогда как
роль вещества сводится только к созданию поля. В этом случае следует наложить
условие на свойства пробных тел, с помощью которых исследуется метрика и находятся
компоненты метрического тензора – эти пробные тела должны взаимодействовать с
веществом на расстоянии и только посредством полей, без механического контакта,
хаотически изменяющего характер движения.
Указанная интерпретация связи между веществом, полем и
метрикой затруднена в общей теории относительности (ОТО), в которой гравитация
прячется в тень геометрического метрического поля и теряет физическую сущность.
Метрическое гравитационное поле (метрика пространства-времени) зависят в ОТО от
вещества и электромагнитного поля и полностью определяется ими. Но каким
образом вещество физически изменяет метрическое поле даже вдали от себя? Каков
механизм связи между веществом и полем? Всё это остаётся загадкой.
В ковариантной теории гравитации в качестве основной идеи
генерации гравитационного поля рассматривается теория гравитации Фатио-Лесажа,
позволяющая одним и тем же способом описать сильную гравитацию на уровне
элементарных частиц и обычную макроскопическую гравитацию [13], а также и
электромагнитное взаимодействие тел [7]. Кванты гравитационного поля,
образуемые релятивистскими объектами на нижележащих уровнях материи
предположительно в виде электромагнитного излучения и нейтрино, становятся
гравитонами для объектов вышележащих уровней материи и дают для них
гравитационное взаимодействие. Градиенты плотности энергии потоков гравитонов
можно рассматривать как напряжённости гравитационного поля. Тогда
гравитационный потенциал есть разность между плотностью энергии потоков
гравитонов вблизи или внутри тел, и плотностью энергии потоков гравитонов на
бесконечности в отсутствие тел. Именно потоки гравитонов ответственны за
отклонение пробных частиц и квантов поля вблизи массивных тел. В такой картине
кванты поля нижележащих уровней материи порождают макроскопические поля и
формируют макроскопическую метрику, а вещество (рассматриваемое как
совокупность объектов различных уровней материи, отличающихся своими
характерными размерами и массами) взаимодействует с квантами поля и само
порождает их.
Список использованных источников
1.
Альберт
Эйнштейн и теория гравитации: Сборник статей / Под ред. Е.
Куранского. – М.: Мир, 1979. 592 с. С. 146–196.
2. Дирак П. А. М. Общая теория относительности: Пер. с англ./ Под. ред. Д. И. Блохинцева. – Пер. изд.: США, 1975. – М.: Атомиздат, 1978. – 64 с.
3. Паули В. Теория
относительности. Пер. с англ. – 2-е изд. / Под ред. В.Л. Гинзбурга
и В.П. Фролова. – М.: Наука, 1983. – 336 с.
4.
Фок
В.А. Теория пространства, времени и гравитации. 2-е издание. – М.: Физматгиз, 1961. –568 с.
5.
Ландау Л. Д.,
Лифшиц Е. М. Теория поля. – Издание 7-е,
исправленное. – М.: Наука, 1988. – 512 с. – («Теоретическая физика»,
том II).
6. Федосин С.Г. Энергия, импульс, масса и скорость движущегося тела. vixra.org, 12 июня 2011.
7. Федосин
С.Г. Физические
теории и бесконечная вложенность материи. Пермь, 2009, 842 стр., Табл. 21, Ил.41, Библ. 289
назв. ISBN 978-5-9901951-1-0.
8. Федосин
С.Г. Физика
и философия подобия от преонов до метагалактик.
Пермь, Стиль-МГ, 1999, 544 стр., Табл.66, Ил.93, Библ. 377 назв. ISBN
5-8131-0012-1.
9.
Федосин С.Г. Общая теория относительности,
метрическая теория относительности и ковариантная теория гравитации.
Аксиоматизация и критический анализ. vixra.org,
26 марта 2011.
10. Федосин С.Г. Принцип пропорциональности массы и
энергии: новая версия. vixra.org, 12 июля 2011 .
11. Einstein
A. The Meaning of Relativity, Princeton, 1955, Fifth Edition. p. 99–108.
12. Poplawski N. J. A Lagrangian
description of interacting energy. – arXiv:gr-qc/0608031v2 .
13. Fedosin S.G. Model of
Gravitational Interaction in the Concept of Gravitons.
Journal of Vectorial Relativity, Vol. 4, No. 1, March 2009, P.1–24.
Источник:
http://sergf.ru/pnd.htm