Hadronic
Journal, February 2012, Vol. 35, No. 1, P. 35 –
70.
The principle of least action in covariant theory of
gravitation
Sergey G. Fedosin
Perm, Perm Region, Russia
e-mail intelli@list.ru
The integral equations for
calculation of metric, equations of substance motion, as well as equations for
gravitational and electromagnetic fields in covariant theory of gravitation are
obtained by means of variation of action functional. In covariant form
stress-energy tensor of gravitational field, strength tensor of gravitational
field and 4-current of mass are determined. The meaning of the cosmological
constant and its relation to the components of energy density in action
functional are explained. The results obtained prove the validity of Mach's
principle, assuming that gravitation effects are due to the flows of gravitons.
The idea that metric can be entirely determined by variables describing fields’
properties is substantiated.
Keywords:
action;
metric; cosmological constant; stress-energy tensor of gravitational field;
equations of motion; field equations; covariant theory of gravitation.
PACS: 04.20.Fy,
04.40.-b, 11.10.Ef
Covariant theory of
gravitation (CTG) is one of the alternative gravitation theories in relation to
the general relativity theory. The purpose of this article is to derive
equations of CTG from the principle of least action. As the basis of our
discussion we will use works of Einstein [1], Dirac [2], Pauli [3], Fock [4],
Landau and Lifshitz [5].
We will use international
system of units, basic coordinates in the form of coordinates with
contravariant indices 
, metric signature (+, –, –, –),
metric tensor 
. The presence of repeated indices in
formulas implies Einstein summation convention, which is a separate summation
for each repeated index.
The action function
In the case of
continuously distributed throughout the volume of space matter, the action
function for the matter in gravitational and electromagnetic fields in
covariant theory of gravitation can be presented as follows:
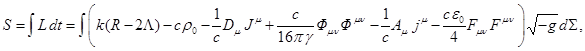
(1)
where 
– Lagrange function or Lagrangian,
– differential of time in the used reference
frame,
– certain coefficient,
– scalar curvature,
– a constant, which characterizes the energy
density of the system as a whole, and therefore is a function of the system,
– speed of light, as a measure of velocity of
electromagnetic and gravitational interactions propagation,
– density of substance mass in reference frame
in which the substance is at rest,
– 4-potential of gravitational field which is described
by scalar potential 
and vector potential 
of the field,
– 4-vector of mass current,
– gravitational constant,
– gravitational tensor (tensor of gravitational
field strength),
– determining the gravitational tensor with
contravariant indices by means of the metric tensor 
,
– 4-potential of electromagnetic field, set by
scalar potential 
and vector potential 
of the field,
– 4-vector of electric current density,
– electric constant,
– electromagnetic tensor (field
strength tensor),
– invariant 4-volume, expressed through
differential of time coordinate 
, through product of differentials of
spatial coordinates 
, and through the square root 
of determinant 
of metric tensor, taken with the negative
sign.
The symbol 
denotes covariant derivative with respect to
coordinates (in this case the coordinates 
). Similarly, 
is an operator of partial derivative with respect to
coordinates or 4-gradient.
The integrand in (1) is
Lagrangian function, consisting of six terms. The first term with the scalar
curvature depends on the metric tensor and its
derivatives with respect to coordinates. In covariant theory of gravitation
(CTG) metric is used to consider the impact of fundamental fields (which
include electromagnetic and gravitational fields) of material bodies on the
results of space-time measurements near the bodies. The field’s effect on
measurement results shows that under the field’s action electromagnetic waves
are deflected from rectilinear motion, electromagnetic clock changed its
course, and measured distances changed its value. These effects can be
described by introducing a curved space-time with metric tensor 
instead of flat Minkowski space with its
single metric tensor 
. In CTG gravitational field is an
independent physical field and the metric tensor has the geometric meaning and auxiliary
function, unlike general relativity where the metric field completely replaces
gravitational field.
In CTG second term in (1)
is not simply related to rest energy substance density and its inertia with
respect to the applied forces. According to [6], [7], the rest mass (and
substance density at rest) is a consequence of strong gravitation and
electromagnetic interactions operating at the level of elementary particles.
But the first and the second terms in (1) are associated with microscopic
fundamental fields, while other terms refer to action of macroscopic
gravitational and electromagnetic fields. The division to microscopic and
macroscopic fundamental fields follows from the theory of infinite nesting of
matter in which its own gravitational field operates at every main level of
matter. As a result, the usual gravitation is assumed as long-range component
of strong gravitation.
The third term in (1) 
is invariant with respect to different types
of coordinate transformations that reflect the interaction of mass current
density 
of arbitrary substance unit with gravitational
field.
According to [8], the
fourth term in (1) associated with energy field, is an invariant of
gravitational field which does not change its form by changing the reference
system. The fifth and sixth terms, for electromagnetic field, are similar in
structure to the third and fourth terms for gravitational field. And 4-vector
of electric current density 
can be determined by charge density 
of substance unit and 4-velocity: 
.
In CTG 4-potentials 
and 
with covariant indices, and 4-currents 
and with contravariant indices were determined in [7]
and [9] as initial concepts for construction of axiomatic theory. Hence we can
make a conclusion that, for example, 4-vector 
can not be found in absence of information
about metric in any frame of reference.
Variation of curvature invariant
To obtain equations for
metric the variation of action function for the case when in Lagrangian the
metric tensor is variable should be set to zero. At the same
time variation of metric tensor should be zero on the borders of
four-dimensional volume for which in (1) integration is performed. For full
variation of the action should be as follows:
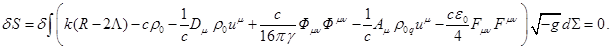
(2)
Let’s find the variation
associated with the first term in (2). Using definition of scalar curvature through Christoffel symbols, we
obtain the same as in [2]:
,
(3)
where 
,
,
.
The expression for 
can be obtained by means of differentiation by
parts:
.
(4)
The first two terms on the
right side of (4) are the total derivatives (divergence), and after
substituting them in (3), the integrals of the divergence over the volume
according to Gauss's theorem can be replaced by the integrals over the surface
surrounding the volume for which the integration takes place. Since variation
of metric tensor on the surface equals to zero, these terms will not contribute
to the variation of action function, so that in (4) only the last two terms
should be taken into account. Then we can use two relations:
, 
.
(5)
Substituting them in the
last two terms in (4) and renaming some of indices on which the summation takes
place, we obtain:
As a result, instead of
(3) we can write:
. (6)
The first variation in
(6) will equal to:
. (7)
Using the relation: 
, differentiation by parts, and using
the second relation in (5), for the first part (7) we obtain:
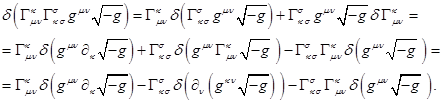(8)
The expression for derivative
of metric tensor has the form: 
. After multiplication by , taking variation and another
multiplication by 
we will obtain:
We now transform the
second part of (7), using replacing of indices, operation of differentiation by
parts, and the previous expression:
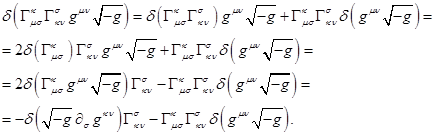(9)
Substitution of (8) and
(9) in (7) gives the following result:
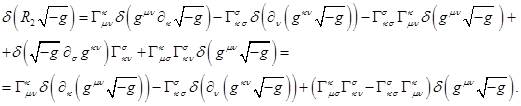
(10)
The terms 
and 
in (10) can be transformed:
.
.
(11)
In equations (11) there
are such divergences as 
, which, after substituting in (10)
and then into (6) will be integrated over 4-volume and transformed into
integrals over the surface, where variations are equal to zero. With this in
mind, after substituting (10) and (11) into (6) we obtain:
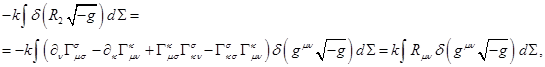(12)
where 
is Ricci tensor.
For variations of metric
tensor 
and 
we can write down:
, 
.
(13)
Using (13) in (12), we
obtain:
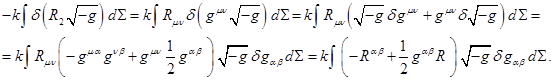
With this result and the
expression 
from (13), we obtain:
. (14)
Variation of invariant mass density
The second term in (2) is
an invariant associated with the 4-current of mass 
, so we can write down:
.
(15)
4-vector can be determined through 4-velosity 
, where 
is displacement 4-vector, 
– differential of proper time, as follows: 
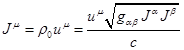, and 
.
In elementary particle
physics instead of the values of mass and velocity of particles their energies 
and momentums 
are used as the quantities directly found from
experiments. These quantities are part of 4-momentum of a particle: 
, and the invariant mass 
become a secondary concept, which may be found
from the relation 
. Accordingly, to calculate the
velocity of particles in special relativity theory is applied relation: 
.
The variation of the
second term in (2) with (15) has the following form:
. (16)
We determine the
variation in (16) with the help of (13):
(17)
In (17) variation 
is contained which according to [2], [4] can
be found using displacement 4-vector 
. The displacement 
is variation of coordinates, which gives
variation of mass 4-current 
:
. (18)
Equation (18) was
obtained based on the condition that mass of substance unit in variation of
coordinates remains constant despite the change in density and its volume. With
the help of (15) and (18) the last term in (17) can be transformed through
4-velosity 
:
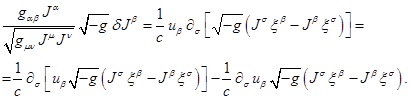
The term with complete
divergence in integration over 4-volume in the action function will not make
any contribution. The remaining term in the previous equation can be
transformed further:
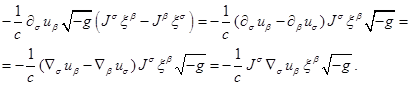(19)
Here the condition 
was used, since it follows from the equation 
, to which the covariant derivative 
is applied.
The symmetrical
stress-energy tensor of substance is:
.
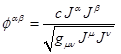(20)
Substituting (20) in (17)
and using (19) instead of the last term in (17), we obtain the variation 
in (16):
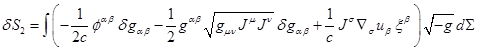. (21)
Variation of Lagrangian of gravitational field and its
sources
The effect of macroscopic
gravitational field is revealed in the third and fourth terms in (2), which
gives the following:
, 
.
(22)
We first consider
variation for 
in (22), using 
by (13) and then (18) for 
:
Transformation of the
first term:
.
Neglecting the term with
total derivative, we consider the following:
Substituting these
results into (22), we obtain:
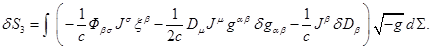(23)
Variation for 
in (22) with (13) is equal to:
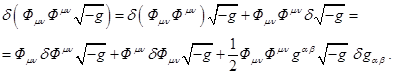(24)
Since 
, the tensor 
is antisymmetrical, then using 
by (13), we obtain:
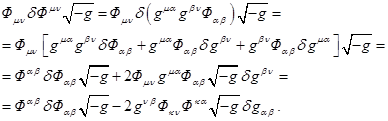
Substitution of this
expression into (24) gives the following result:
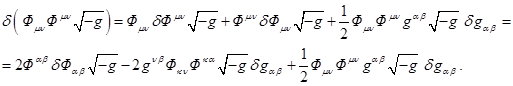(25)
We denote 
as the stress-energy tensor of gravitational
field:
.
(26)
Remembering that 
, using differentiation by parts, as
well as equality for an antisymmetrical tensor: 
, for the term 
in (25) we obtain:
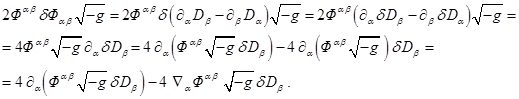
(27)
The term 
in the last expression is divergence and can be
neglected for variation of action function. Substituting (26) and (27) in (25),
and the result in (22), we obtain:
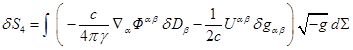. (28)
Variation of Lagrangian function of electromagnetic
field and its sources
Variation in (2) for
electromagnetic field is the same as for gravitational field in the previous
section. For the fifth and sixth terms in (2) we can write down:
, 
. (29)
Replacing in (22) 
with 
, 
with 
, 
with 
, instead of (23) we obtain:
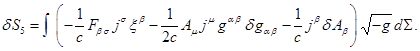(30)
In deriving (30) was used
the expression for variation of electromagnetic 4-current, similar to (18):
. (31)
The stress-energy tensor
of electromagnetic field is:
. (32)
With the help of this
tensor the variation 
will equal as in (28) to:
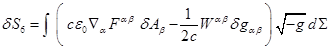. (33)
The equations for metric
Let us put together and
substitute in (2) all terms in (14), (21), (23), (28), (30) and (33) containing
the variation 
of metric tensor. Due to the arbitrariness of
the variation the sum of all these terms should equal to zero. The result is
the following:
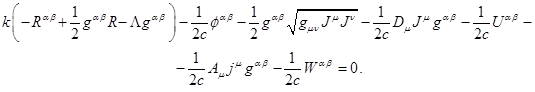
Let us rewrite this equation with 
, where 
– the
coefficient of order 1, as an equation for determining metric tensor 
with the
help of known sources of energy-momentum. Here, instead of 
, we introduce a new constant 
, according to the relation: 
. As well as , the constant determines
the properties of system as a whole. It has the following result:
(34)
In case when such a large system, like our universe is considered has a
special name – the cosmological constant. It is estimated as 
m–2. Hence the value is
of the order
J/m3,
having dimension of energy density.
For other systems, which can roughly be considered as systems with the
matter continuously distributed throughout the volume of space, the constants and can have
other values.
The equation (34) was obtained based on the condition that either the
variations of coordinates 
and
4-potentials 
and 
in
function of action (2) equal to zero, or the sums of all the terms with these
variations are always equal to zero. In the first case (34) is an equation for
the metric of a system, in which the motion of charged and gravitating
substance by the definite trajectories were originally determined and the
calibrated values of field potentials (that means, the constants appearing in
potentials were determined) were determined as well. In the second case
variations of coordinates (trajectories of substance) and variations of
potentials are allowed due to their mutual influence on each other. However, it
is assumed that each time the combinations of terms in function of action
defining the relationship between the substance and the field, including
generation of fields by substance and field influence on substance are of such
kind that they equal to zero and do not affect the function of action and the
metric. In the second case the initial distribution of substance in space and
its initial velocity and initial values of the potentials are arbitrarily, so
the laws of connection between the subsequent motion of substance and fields
due to some reasons lead to the equation (34). Obviously, the validity of the
second case requires additional evidence, or should be postulated, whereas in
the former case it is not required.
Outside the substance, where gravitational and electromagnetic
4-currents 
and tend to zero,
the contribution to the metric according to (34) is made only by the
stress-energy tensor of gravitational field 
(26) and
the stress-energy tensor of electromagnetic field 
(32). If
the metric is determined within the substance, the contribution to the metric
depends on all terms in (34).
We should note that the right side of (34) contains additional terms
that in general relativity theory usually are not considered. In particular,
(34) includes all invariant scalar values from the function (1), including
terms 
and
, which became components of the tensors 
and , respectively. In general relativity, there is
no stress-energy tensor of gravitational field in
the form in which we have determined it. This follows from the fact that in
general relativity, gravitational field reduces to the metric field, where the
components 
of metric
tensor are considered as potentials describing the gravitational field. In this
case, the presence of in the
right side of equation for the metric (34) would mean that gravitational field
is the source itself. In the absence of substance that would lead to a vicious
circle where a metric gravitational field generates itself, the field gives the
metric and the metric gives the field. As opposed to it, in covariant theory of
gravitation (CTG), the metric is only an auxiliary geometric field induced by
gravitation and electromagnetic field, taken in all their forms at different
scale levels of matter.
In CTG uses the metric theory of relativity [7], the
essence of which is dependence of metric on not only the properties of motion
of system, but also on the type of test bodies, which can be both substance
particles and quanta of field. Test bodies are needed to determine the metric
of system in nature, for measurement procedure of scale and time, and have
different properties due to the difference in equations of motion. As a result,
the coefficient 
in (34) may be different for different systems
and should be found separately for complete definition of metric tensor. In
particular, was found in several situations, such as
calculating deviation of test body’s motion under the action of gravitation,
and calculations of perihelion shift. Notes on the last four terms in (34) and
the term with constant will be made later in the section
"Tensors of energy".
The equations of motion of substance and field
To obtain the equations of motion of substance
it is necessary to select in the full variation of action (2) those
terms which contain variations of coordinates 
. Due to the arbitrariness of the sum of
all such terms should be equal to zero. From the sum of (21), (23) and (30) we
obtain:
.
Taking into account that 
, 
, and using the operator of
proper-time-derivative [7]: 
, where 
denotes
covariant differential, 
is proper
time, the last equation can be written as follows:
, (35)
where 
– 4-acceleration with covariant index, the first term on the right
is the density of gravitational force, and the last term sets electromagnetic
Lorentz force for charge density 
.
According to (35), the contribution to 4-acceleration of substance unit
makes the gravitational acceleration 
and
4-acceleration in electromagnetic field 
. The physical meaning of (35) consists in the
fact that it determines the impact on the substance of fields when the metric
tensor of the system (this means that 
in action
function), and field potentials (
, 
in action
function) are preset.
The relation connecting the tensor of gravitational field 
with its
source in the form of 4-vector 
, follows from (23) and (28) as the consequence
of variation for
gravitational 4-potential. Taking into account the antisymmetry of the tensor 
we
obtain:
,
or 
. (36)
A similar relation for electromagnetic field, from expressions for
variation 
of
electromagnetic 4-potential in (30) and (33) has the form:
,
or 
, (37)
where 
– vacuum permeability.
Equations (36) and (37), as it is evident after obtaining them from
variation of action function, are valid in case when the variation of
coordinates of substance and the variation of metric are equal to zero, that is
, 
. This means that if the motion of substance and metric
of system are preset, we can calculate how the substance generates the field
strengths.
If we consider the definition of
gravitational tensor: 
, and take the covariant derivative of the
tensor, followed by a cyclic permutation of indices, then the following
equation is performed identically:
. (38)
Another form of (38) is:
,
where 
is the
Levi-Civita symbol or totally antisymmetrical unit tensor.
Equation (38) sets the gravitational field equations without sources, so
that the set of equations (36) and (38) completely determines the properties of
the gravitational field.
For electromagnetic field we have the similar formula as in (38):
or 
. (39)
Equations (37) and (39) are the Maxwell equations, written in
four-dimensional notation.
Relation (36) can be written in another way: 
. If we take on both sides of this equation the
contravariant derivative 
, and use the definition 
, then due to the symmetry and changing of the
order of differentiation the left side will equal to zero. This leads to the
continuity equation (mass conservation), which imposes certain conditions on
4-velocity and the density of substance:
.
For conservation of the electric charge, we have a similar relation:
.
If we specify a condition for 4-vector of gravitational potential 
, or for 4-vector of electromagnetic potential 
, then it provides definite relation between
scalar and vector potentials. The standard approach is Lorenz gauge, which
gives the following conditions:
, 
. (40)
Substituting (40) into (36) and (37) and using 
, 
, while the expression 
is
D'Alembert operator, we obtain wave equations for 4-potentials in the Lorenz
gauge:
, 
.
About applicability of equations of motion in general
case
As we mentioned above, the
equation for the metric (34) is correct in case when the motion of substance
and field potentials are completely specified. However, in most cases only the
initial state of motion and initial potentials are known, later the motion of
substance is determined by field and is set indirectly. How the equation (34)
should be used in this case, and under what conditions? To answer this
question, we assume that the motion of substance and field potentials at a
short interval of time after initial time point remain unchanged. Then we can
find metric tensor from (34). After that, assuming immutability of metric and
the motion of substance in the second time interval, using (36) and (37) we can
calculate the derivatives of tensors 
and 
by coordinates. After integration of these
derivatives the field strengths can be found which are part of these tensors.
Since now correct tensors 
and 
are known, with the help of them on the third
time interval in the equation of motion (35) the acceleration of substance and
its motion can be estimated, and the motion can be adjusted. In the fourth time
interval the data about motion of substance from the third interval and about
fields from the second interval can be used in order to evaluate the change of
metric. Further calculations are repeated in the specified order. Thus the
actual motion of substance in gravitational and electromagnetic fields, and
space-time metric can be found approximately by an iterative procedure by means
of the above-mentioned equations for metric, motion of substance and fields.
Tensors of energy
Let’s return to the equation for metric (34). It is known that the
covariant derivative of left side of (34) is equal to zero, which is a
characteristic of the Hilbert-Einstein tensor located there. Consequently, the
covariant derivative of the right side of (34) must also equal to zero:
. (41)
Taking into account the definition of stress-energy tensor of substance (20), relations 
, 
, and using operator of the proper-time-derivative: 
, we can write down:
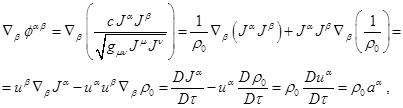(42)
where 
–
4-acceleration.
Now we find the covariant derivative of stress-energy tensor of
gravitational field. Since the metric tensor under covariant differentiation
acts as a constant, using (36), we obtain from (26):
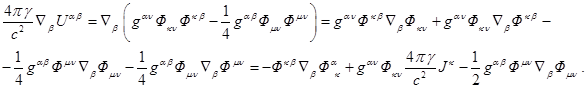
(43)
We apply (38) to the last term in (43), on condition that tensor 
is
antisymmetrical:
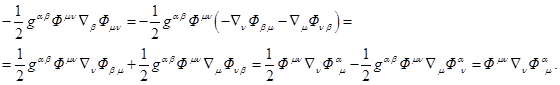
Substituting this into (43) we obtain the relation between the covariant
derivative of stress-energy tensor of gravitational field and 4-vector density
of gravitational force:
.
(44)
We obtain a similar expression for the covariant derivative of
stress-energy tensor of electromagnetic field and 4-vector density of
electromagnetic force (Lorentz force density) with (32) and (39):
.
(45)
Substituting (42), (44) and (45) into (41) we obtain:
. (46)
The zero right side of (46) follows from the equations of substance
motion in gravitational and electromagnetic fields (35). Consequently, the
covariant derivative for the remaining terms in (41) must also equal to zero:
. (47)
In brackets in (47) there
is a scalar quantity, in this case the covariant derivative 
is equal to partial derivative 
(that is 4-gradient). Relation (47) is
automatically satisfied if we assume that the constant in brackets is set equal
to zero. This gives the relation:
. (48)
Equality (48) is
necessary to perform in (34) the limit relations for tensors at infinity, where
there is neither substance nor fields. As it is indicated in [4], at infinity
the right side of (34) with energy tensors is equal to zero, and the space-time
becomes flat, bringing to zero the left side of Hilbert-Einstein tensor. Taking
into account (48) the equations for metric obtain the simplest form:
(49)
Let’s use (15) and reveal
in (48) the scalar product of 4-vectors, with the help of 
,
,
,
:
. (50)
Here 
is a 3-vector, which is part of 4-velocity 
. In uncurved space-time according to
special relativity theory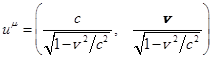 
, then 
, 
, where 
is the velocity of substance motion. This
shows that 
is the energy density for substance in gravitational
field with scalar potential 
. The vector potential 
of gravitational field is also associated with
energy, but its value 
can have different sign depending on the
direction of vector , which is proportional to speed 
, and the direction of vector 
. The same is true in respect of the
density of electromagnetic energy – it depends on the charge density 
, the scalar electric potential 
and vector potential 
of electromagnetic field.
Now suppose that in (50)
the macroscopic gravitational and electromagnetic fields are off and their
potentials are equal to zero. In this case, the density of substance must reach
a certain value 
, which depends only on fundamental
microscopic fields acting at the level of elementary particles. Then we will
obtain 
, and (50) can be rewritten as
follows:
,
(51)
where 
and 
denote the energy density of substance in
gravitational and electromagnetic fields, respectively.
As for substance is usually negative (due to the
negative gravitational potential ), then from (51) it follows that
density of substance 
in gravitational field becomes greater than
density of substance in the absence of field (when the substance of
a body is divided into parts and separated to infinity). The same thing can be
said about mass – in gravitational field it is expected to increase due to the
contribution of gravitational mass-energy of substance in the field. Thus we
have obtained the result similar to that which we have proved in [6] and [10],
but in relation to contribution of mass-energy of field to the total mass of
system of substance and field. Then we found that the mass of a spherical body
grows due to its field, and with constant volume, this means an increase in the
effective density of the substance.
We can integrate (51)
over the volume of substance of a spherical uncharged body in static position,
when the body is at rest and does not rotate. If the substance is infinitely
slowly superimposed on the body by parts in the form of thin spherical shells
with the same density of substance, we can assume that in (49) 
, as well as:
, 
,
,
where 
– the observed mass of the body with its
radius 
,
– the
mass of substance of the body without taking into account the energy of
gravitation,
– the mass inside the radius 
, increasing from 0 to the radius of
the body 
with increasing of mass.
As a result, (51) becomes
equality for the masses:
, (52)
where 
is gravitational constant.
In (52) the module of
mass-energy of gravitational field is added to the mass-energy of the body. In
reality, during the formation of space objects in gravitational field the
virial theorem applies according to which approximately half of gravitational
field energy leaves the system in the form of radiation, and the other half
heats the substance. This reduces by half the additive to mass-energy in (52).
For the main objects of
stellar level of matter the contribution to (51) of energy density of substance
in electromagnetic field is little in comparison to 
. In particular, for neutron stars,
gravitational energy is equal to 
J, here 
in approximation of uniform density of
substance, 
– gravitational constant, 
kg, 
km –
mass and radius of a typical neutron star. The electromagnetic energy reaches a
maximum in magnetars at magnetic pole of which the magnetic field can be about
T. Since magnetic energy density is given in
form 
, then the integral over the entire
volume inside the star and beyond it gives the magnitude of the magnetic energy
of about 
J, which is considerably less than the modulus
of gravitational energy.
The similar situation exists at the
level of elementary particles, where according to the theory of infinite
nesting of matter [8], an analog of a neutron star is a nucleon. The energy of
a proton in its own field of strong gravitation is estimated with the formula 
, where 
and 
denote
mass and radius of a proton, 
m3∙∙kg–1∙s–2
– strong gravitational constant, 
– elementary charge, 
– vacuum permittivity, 
– electron
mass. The expression for electric energy of a proton in the case of uniform
charge distribution is as follows: 
.
Consequently, for a proton the ratio
of module energy of strong gravitation to electrical energy is equal to the
ratio of a proton to an electron mass, and the energy of strong gravitation dominates.
The global dominance of gravitational
forces over electromagnetic forces leads to possibility of formation of
elementary particles of substance, massive bodies and other objects found in
space. For the observable universe cosmological constant 
is
estimated by
m–2,
and constant 
reaches 
J/m3. We consider that characterizes the visible universe as a whole,
setting the rest energy density of substance distributed in space, without
taking into account the energy fields. We further assume that gravitational
fields are a consequence of flows of gravitons, which are produced by tiny
particles of all the substance that exists in the universe. The more substance
is in the universe, the greater is the density of substance and the more is the
density of gravitons’ flows. Then relation (50) supports the Einstein’s idea
that the inertia of a body must increase near other gravitational masses [11],
which is in turn the development of Mach's principle of the impact of distant
masses to acceleration of bodies.
We should remind that in the usual
interpretation the cosmological constant is proportional to vacuum energy
density, and still it is not known exactly what particles or fields are
responsible for this energy. There are also suggestions that the cosmological
constant depends on the time, on the scalar curvature of space-time (in f(R)
gravity) or on the energy-momentum tensor [12].
We
will further evaluate the scalar curvature for our universe. To find we multiply (49) by 
and taking into
account the fact that 
, 
, while for
stress-energy tensors (26) and (32) there are equations: 
, 
. Using the
expression (20), we obtain:
.
If
we assume that the density of substance can be calculated as follows 
,
the
curvature of cosmological constant accurate to the sign equals to: 
. At the first
approximation the observed universe can be regarded as the space-time of
constant negative curvature, for which the equation is 
. Hence the
radius of such a world would be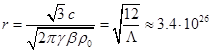 
m. On the other hand, if the observable
universe is close to the state of Schwarzschild’s black hole, its radius should
equal to: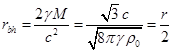 
.
In
both cases, in determination of space-time curvature, and in evaluating the
radius of the black hole, speed of light is used as a measure of speed
and means for measuring.
Analysis of equation of motion in relation to mass
According to (46) the equation of
substance motion in gravitational and electromagnetic fields has the form:
.
(53)
Let’s consider (53) in weak field
limit, where the special relativity theory is valid and the covariant
derivative becomes the 4-gradient. In this case we obtain:
,
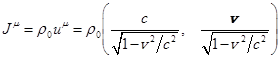and for the scalar components of
stress-energy tensor of substance (20) we can write down:
, 
, (54)
where the index 
, so that in the Cartesian coordinate
system 
,
, 
, and vector 
is 3-vector of mechanical energy flow density
or relativistic Umov’s vector.
The gravitational tensor 
is defined by the 4-potential 
of the gravitational field, which depends on
the scalar potential 
and vector potential 
of the gravitational field. We shall introduce
gravitational acceleration 
and torsion field 
(gravitomagnetic field) as follows:
, 
.
With the help of the quantities and 
the scalar
components of the stress-energy tensor of gravitational field (26) can be
represented as follows:
, 
, (55)
where
denotes the components of 3-vector
energy flow density of gravitational field (Heaviside vector)
.
For the stress-energy
tensor of electromagnetic field (32) in substance
which is not magnetized and not polarized in the limit of special relativity we
obtain similarly:
, 
, (56)
where 
denote the components of 3-vector of
electromagnetic energy flow density (Poynting vector) 
.
Substituting (54), (55) and (56) into
(53) for 
and for the replacement 
on 
in Minkowski space makes an expression of Poynting's
theorem:
,
or 
. (57)
The values 
, 
and 
set the
energy density of substance, gravitational and electromagnetic fields
respectively.
Let’s integrate (57) over the entire
volume of space occupied by substance and field. We shall consider the
quasi-stationary case, when all energy flows are closed so that the volume
integral of divergence of the right side of (57) becomes close to zero. This
means that the amount of energy flows, extending forever into infinity is
little. Then taking into account (54), (55) and (56) we should obtain:
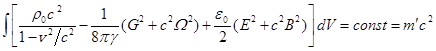, (58)
,
.
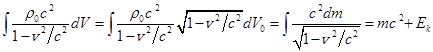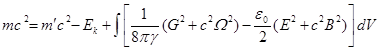We denoted by 
the mass
of substance when the substance is separated to infinity and is in rest there.
In this case all the fields 
, 
, 
and 
will tend
to zero. Equation (58) shows that the mass of substance 
in
relation to the mass of substance increases
due to the contribution of total mass-energy of gravitational field and
decreases due to the contribution of mass-energy of electromagnetic field and
the kinetic energy of motion of substance 
. Actually (58) confirms the relation (52) from
the previous section.
Additional notes
In our view, the equation of motion of substance (35) should look a
little differently:
. (59)
In (59) the substance density 
has been
included under the sign of total derivative with respect to proper time. This
allows us to describe cases where the substance density changes and thus
creates an additional acceleration of substance. Meanwhile, equation (35) was
obtained from the variation of coordinates described in [2] and [4], with
constant mass in the variation. This led to the fact that (35) differs from
(59), as in case 
, and therefore 
can be
outside of the total differential.
It is interesting that we can choose the stress-energy tensor of
substance so that its covariant derivative just gives the rate of change of
substance’s 4-current. This tensor has an unusual form in terms of indices, but
formal covariant derivative gives the correct result. Instead of (20) we shall
write down: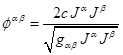 
. Taking into account the continuity equation 
we obtain:
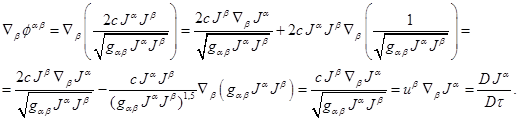
In fact, we have found
the tensor 
in (17).
The reason that we have
not used it as it is described here, is that instead of the exact form of
variation 
as the function of coordinate’s variations,
the simplified form (18) was used in derivation of motion equations. This leads
to (35), but not to (59).
From variation (48) it
follows that the total variation of mass 4-current 
is associated with variation of metric tensor 
, variation of electromagnetic
4-current 
and variations of 4-potentials:
, (60)
.
The relationship of variations in (60) is connected
through variation of coordinates 
in such a way that the mass of any local
volume does not change during variation. However, we can admit a situation when
the mass-energy is converted into radiation energy, or substance density
changes due to inflow or outflow of mass. Then, some results presented in this
paper will require a corresponding change.
Let’s now substitute (48)
into (2), and with equations 
,
,
we obtain:
.
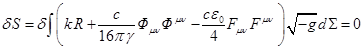After implementation of
variation in this equation we will obtain the equations for metric (49), but
without the tensor 
:
(61)
The metric obtained in (61) is as it should be outside
the substance, and this metric depends directly on the magnitude of existing
fields and indirectly on the distribution of substance in this field.
In CTG there is a concept
of geodesic line, which coincides with the expression of general relativity
theory, but only for field quanta. The equation of motion (35), taking into
account 
, can be written as:
. (62)
For field quanta we
obtain 
. Multiplying (62) by 
, we obtain the equality to zero of
the right side: 
. Dividing this by the square
differential of time coordinate 
, which measures time along the
trajectory of quantum, and recalling the definition of operator of proper-time-derivative, we obtain the geodesic equation in covariant indices:
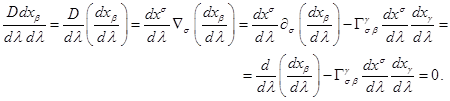(63)
While the field quanta are
distributed outside the substance in a given field (gravitational and
electromagnetic), their movement takes place in accordance with the equation of
motion (63), and the space-time metric is determined from (61). What can change
while the field quanta pass through the substance? If the substance is rare and
does not interact with quanta, the quanta move between the particles of
substance. Then in principle, equation (61) should be valid for the metric with
the amendment that it is now necessary to take into account the stress-energy
tensor of field of strong gravitation acting at the level of elementary
particles. This new tensor should look as a supplement to the stress-energy
tensor 
of normal gravitation (26), replacing the
constant of gravitation 
by the constant of strong gravitation 
, and with a factor of
proportionality. In practice instead of using this new tensor, it is replaced
by the stress-energy tensor of substance 
, and one say that "the
substance alters the space-time metric inside, and affects the metric beyond
its borders".
This leads to the
equation for the metric in the form of (49). But another interpretation is
possible – a field always affects the metric, whereas the role of substance is
reduced only to creation of field. In this case it is necessary to impose the
condition on the properties of test objects with the help of which we study
metric and find metric tensor components – these test bodies must interact with
the substance at a distance and only through the fields, without mechanical
contact randomly changing the movement.
The above interpretation
of relationship between substance, metric and field is difficult in general
relativity, in which gravitation is hiding in the shadow of geometrical metric
field and losing its physical essence. Metric gravitational field (metric of
space-time) in general relativity depends on the substance and electromagnetic
field and is fully determined by them. But how does the substance change
physically the metric field even if it is far away from it? What is the
relationship mechanism between the substance and the field? All this remains a
mystery.
In covariant theory of
gravitation the Fatio-Le Sage’s gravitation theory is considered as the basic
idea of generating gravitational field, which allows to describe in the same
way strong gravitation at the level of elementary particles and usual macroscopic
gravitation [13], as well as electromagnetic interaction between bodies [7].
Quanta of gravitation, which are formed by relativistic objects at the lower
levels of matter presumably in the form of electromagnetic radiation and
neutrinos, become gravitons for the objects of higher levels of matter and
create there gravitational interaction. The gradients of energy density of
gravitons’ flows may be considered as gravitational field strengths. Then the
gravitational potential is the difference between the energy density of
gravitons’ flows near or inside the bodies, and the energy density of
gravitons’ flows at infinity in the absence of bodies. These flows of gravitons
are responsible for deviation of test particles and field quanta near the massive
bodies. In this picture the field quanta of lower levels of matter generate
macroscopic fields and form macroscopic metric, and the substance (regarded as
an aggregation of objects from different levels of matter, distinguishing by
their characteristic sizes and masses) interacts with the field quanta and
generates them.
References
1.
A.
Einstein. Die Grundlage der
allgemeinen Relativitätstheorie, Annalen der Physik 354 (7), 769-822, 1916.
2. Dirac P.A.M. General theory of relativity. Florida State University.
John Wiley & Sons, Inc., New York - London • Sydney • Toronto, 1975.
3.
Pauli W. Theory of
Relativity. Pergamon Press, 1958.
4.
Fock V. A. (1964). "The Theory
of Space, Time and Gravitation". Macmillan.
5.
Landau L.D.,
Lifshitz E.M. (1975). The Classical Theory of
Fields. Vol. 2 (4th ed.). Butterworth-Heinemann.
ISBN 978-0-750-62768-9.
6. Fedosin S.G. Energy, Momentum, Mass and Velocity of Moving Body. vixra.org, 13 Jun 2011.
7.
Fedosin S.G. Fizicheskie teorii i beskonechnaia
vlozhennost’ materii. – Perm,
2009. – 844 p. ISBN 978-5-9901951-1-0.
8. Fedosin
S.G. Fizika i filosofiia podobiia: ot preonov do metagalaktik. – Perm, 1999.
– 544 p. Tabl.
66, Pic. 93, Ref. 377. ISBN 5-8131-0012-1.
9. Fedosin
S.G. The General Theory of Relativity, Metric Theory of Relativity and
Covariant Theory of Gravitation: Axiomatization and Critical Analysis.
vixra.org, 26 Mar 2011.
10.
Fedosin
S.G. The Principle of Proportionality of Mass and Energy: New Version. vixra.org, 13 Jul 2011.
11. Einstein
A. The Meaning of Relativity, Princeton, 1955, Fifth Edition. p. 99–108.
12. Poplawski N. J. A Lagrangian
description of interacting energy. – arXiv:gr-qc/0608031v2 .
13.
Fedosin
S.G. Model of
Gravitational Interaction in the Concept of Gravitons.
Journal of Vectorial Relativity, Vol. 4, No. 1, March 2009, P.1–24.
Source: http://sergf.ru/pnden.htm