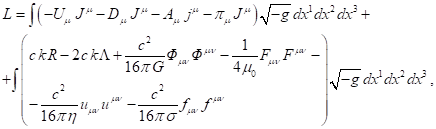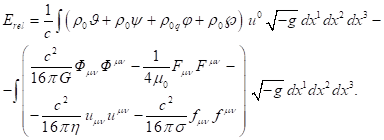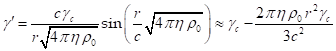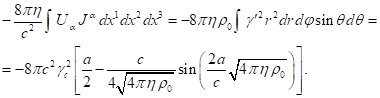GAZI UNIVERSITY JOURNAL OF SCIENCE, Vol.
32, Issue 2, pp. 686-703 (2019). http://dergipark.org.tr/gujs/issue/45480/435567
Интегральная теорема энергии поля
Федосин Сергей Григорьевич
ул. Свиязева 22-79, город Пермь, 614088, Пермский край, Россия
e-mail fedosin@hotmail.com
Ковариантным образом
выводится интегральная теорема энергии векторного поля, согласно которой при
определённых условиях потенциальная энергия поля системы по абсолютной величине
оказывается в два раза меньше кинетической энергии поля, связанной с 4-потенциалом
поля и 4-током частиц системы. Таким образом, интегральная теорема оказывается
аналогом теоремы вириала, но уже не в отношении частиц, а в отношении поля. С
помощью данной теоремы становится возможным обосновать тот факт, что
электростатическая энергия может быть вычислена двумя на первый взгляд никак не
связанными способами – либо через скалярный потенциал поля, либо через тензор
энергии-импульса поля. В замкнутых
системах формулировка теоремы упрощается для электромагнитного и
гравитационного полей, которые могут действовать на расстоянии вплоть до
бесконечности. В то же время для полей, локально действующих в веществе, таких
как поле ускорений и поле давления, в формулировке теоремы необходимо учитывать
дополнительный член с интегралом по поверхности системы. Проверка теоремы для
идеальной релятивистской однородной системы, содержащей не вращающиеся и
хаотически движущиеся частицы, показывает полное совпадение во всех значащих
членах, в том числе для электромагнитного и гравитационного полей, для поля
ускорений и для векторного поля давления.
Ключевые слова: векторное поле; интегральная теорема энергии;
релятивистская однородная система; поле ускорений; поле давления.
The integral
theorem of the field energy
Sergey G. Fedosin
PO
box 614088, Sviazeva
str. 22-79, Perm, Perm Krai, Russia
e-mail fedosin@hotmail.com
The integral
theorem of the vector field energy is derived in a covariant way, according to
which under certain conditions the potential energy of the system’s field turns
out to be half as large in the absolute value as the field’s kinetic energy
associated with the four-potential of the field and the four-current of the
system’s particles. Thus, the integral theorem turns out to be the analogue of
the virial theorem, but with respect to the field rather than to the particles.
Using this theorem, it becomes possible to substantiate the fact that
electrostatic energy can be calculated by two seemingly unrelated ways, either
through the scalar potential of the field or through the stress-energy tensor
of the field. In closed systems, the theorem formulation is simplified for the
electromagnetic and gravitational fields, which can act at a distance up to
infinity. At the same time for the fields acting locally in the matter, such as
the acceleration field and the pressure field, in the theorem formulation it is
necessary to take into account the additional term with integral taken over the
system’s surface. The proof of the theorem for an ideal relativistic uniform
system containing non-rotating and randomly moving particles shows full
coincidence in all significant terms, particularly for the electromagnetic and
gravitational fields, the acceleration field and the vector pressure field.
Keywords: vector field; integral theorem of
energy; relativistic uniform system; acceleration field; pressure field.
1. Введение
В классической механике частицы произвольной физической системы обладают как кинетической, так и потенциальной энергиями. При этом между кинетической и потенциальной энергиями существует связь, описываемая с помощью теоремы вириала. Кроме частиц, в каждой физической системе существуют либо внешние поля, генерируемые внешними источниками, либо внутренние поля, происходящие от самих частиц системы. Поля и частицы взаимодополнительны друг к другу и в совокупности представляют собой основное содержание физической системы. Таким образом, следует ожидать, что и для полей существует некоторая теорема, которая могла бы связать величины, эквивалентные кинетической и потенциальной энергиям.
Целью данной статьи как раз и является установление такой связи между энергиями полей в самом общем виде, пригодном в том числе и в искривлённом пространстве-времени. Хотя доказательство приводится в отношении электромагнитного поля, оно остаётся в силе для любых векторных полей, обладающих 4-потенциалами и соответствующими тензорами.
С целью проверки выведенной интегральной теоремы энергии поля мы применяем её к релятивистской однородной системе и показываем, как именно следует использовать данную теорему. При этом наш анализ будет касаться не только электромагнитного, но и векторного гравитационного поля, а также поля ускорений и векторного поля давления [1, 2]. В частности, применение интегральной теоремы энергии поля даёт возможность упростить вычисление гравитационной энергии системы, поскольку энергия поля, связанная с тензорным инвариантом, может быть заменена на энергию, связанную с 4-потенциалом гравитационного поля. Аналогично упрощается вычисление энергии и других полей.
В наших расчётах мы будем везде придерживаться сигнатуры метрики вида (+,–,–,–).
2. Интегральная теорема
энергии поля
Пусть в некоторой физической системе имеются заряженные частицы, движение
которых описывается зарядовым 4-током 
. В свою очередь, электромагнитное поле имеет 4-потенциал 
, при этом тензор электромагнитного поля 
определяется
соотношением:
. (1)
Символы 
и 
представляют собой
ковариантную производную и 4-градиент, соответственно. Уравнение
электромагнитного поля с источниками записывается стандартным образом:
, (2)
где 
есть магнитная
постоянная, и использована ковариантная производная 
с контравариантным
индексом.
Умножим тензор электромагнитного поля на 4-потенциал с
контравариантным индексом и возьмём от этого произведения ковариантную
производную таким образом, чтобы возник скалярный инвариант. Используем при
этом (2):
. (3)
Поменяем в (3) индексы 
и 
местами:
. (4)
Учтём теперь, что 
, 
, так как скалярные инварианты не зависят от перестановок
индексов. Вспоминая ещё, что тензор электромагнитного поля антисимметричен: 
, просуммируем соотношения (3) и (4) и используем (1):
. (5)
Тензорное произведение 
в (5) содержит свёртку
по индексу 
и потому эквивалентно
некоторому 4-вектору 
. Для произвольного 4-вектора справедливо следующее правило:
,
где 
есть определитель метрического
тензора 
.
Используем это правило в левой части (5) и затем проинтегрируем
(5) по инвариантному 4-объёму, заменяя при этом 
на 
:
. (6)
Тензор 
в (6) есть тензор
электромагнитного поля со смешанными индексами. Воспользуемся теперь теоремой о
дивергенции (Divergence theorem) и преобразуем левую часть в (6):
, (7)
где 
есть ортонормированный
дифференциал 
гиперповерхности,
окружающей физическую систему в четырёхмерном пространстве, 
есть четырёхмерный вектор
нормали, перпендикулярный гиперповерхности и направленный наружу.
Мы можем в (6) и в (7) не производить интегрирования по временной
координате 
и рассматривать
физическую систему в произвольный фиксированный момент времени. С этой целью
перепишем правые части (6) и (7):
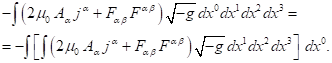(8)
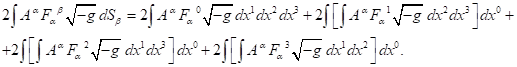(9)
Правые части в (8) и (9) равны друг другу как следствие (6).
Продифференцируем теперь их по переменной 
, где 
– скорость света, 
– координатное время, и
приравняем результаты друг другу:
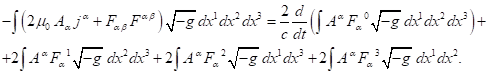
Последние три интеграла в правой части можно объединить в один
поверхностный интеграл по замкнутой двумерной поверхности 
, внутри которой
целиком должна помещаться вся система со всеми частицами и полями в ней. Всё
это даёт следующее:
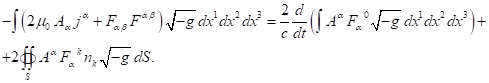(10)
В (10) трёхмерный единичный вектор 
, где 
, представляет собой вектор нормали к поверхности , направленный наружу.
Во многих практических случаях правая часть (10) обнуляется.
В частности, электромагнитное поле системы присутствует как внутри, так и
снаружи системы вплоть до бесконечности. Тогда последний интеграл в правой
части (10) есть поверхностный интеграл по поверхности бесконечно большого
радиуса. Но для замкнутой системы, в которой имеются только собственные поля
частиц системы, на бесконечности обнуляются как 4-потенциал 
, так и тензор электромагнитного поля , в силу калибровки потенциалов, напряжённости и магнитного
поля. Следовательно, для замкнутой системы данный интеграл в (10) равен нулю.
Если ещё равна нулю производная по времени внутри первого интеграла в правой
части (10), то для левой части будет справедливо соотношение:
. (11)
Величины внутри интеграла в (11) достаточно часто используются в
различных расчётах. Например, Лагранжиан для четырёх векторных полей, включая электромагнитное
поле, для сплошной среды имеет следующий вид [1]:
где 
– некоторый коэффициент, подлежащий
определению,
– скалярная кривизна,
– космологическая
постоянная,
– 4-вектор массового тока,
– плотность массы в сопутствующей частице
системе отсчёта,
– 4-скорость точечной
частицы, 
есть 4-смещение, а 
– интервал,
– 4-потенциал поля
ускорений, где 
и 
обозначают скалярный и векторный потенциалы,
соответственно,
– 4-потенциал гравитационного поля,
описываемый через скалярный потенциал 
и векторный потенциал 
этого поля,
– 4-потенциал поля
давления, состоящий из скалярного потенциала 
и векторного
потенциала 
,
– гравитационная
постоянная,
есть гравитационный
тензор,
– определение
гравитационного тензора с контравариантными индексами с помощью метрического тензора
,
– 4-потенциал электромагнитного поля,
задаваемый с помощью скалярного потенциала
и векторного потенциала 
этого поля,
– 4-вектор зарядового
тока,
– плотность заряда в сопутствующей частице системе отсчёта,
– тензор поля ускорений,
вычисляемый через ротор от 4-потенциала поля ускорений,
– коэффициент поля ускорений,
– тензор поля
давления,
– коэффициент поля давления.
В (12) гравитационное поле рассматривается как векторное поле в
рамках ковариантной теории гравитации. Если справедливо (11), то в (12)
член 
оказывается в два раза
меньше, чем член 
, и имеет противоположный знак.
В
качестве другого примера приведём выражение для релятивистской энергии
физической системы из частиц и четырёх векторных полей также в приближении
сплошной среды [1]:
(13)
Если в такой системе выполняется (11), то интеграл по бесконечному
объёму от величины 
в (13) можно будет
заменить на интеграл от величины 
по объёму, занимаемому
веществом. Это позволяет заметно упростить расчёт энергии системы.
Классическая теорема вириала для кинетической энергии 
частиц системы и
потенциальной энергии 
этих частиц записывается
так: 
. Сравнение (13) с (11) показывает, что для электромагнитного
поля в некоторых случаях выполняется количественно противоположное соотношение
вида 
. При этом
, 
,
так что 
играет роль
кинетической энергии поля при взаимодействии 4-потенциала 
с зарядовым 4-током 
частиц, а 
характеризует
потенциальную энергию, но не частиц, а поля.
3. Интегральная
теорема энергии для
других векторных полей
В
ковариантной теории гравитации [1], описание гравитационного поля происходит
таким же образом, как это делается для электромагнитного поля. Это означает
подобие уравнений обоих полей, и мы можем сразу записать интегральную теорему
энергии для гравитационного поля, заменив в (10) обозначения 4-тока, 4-потенциала
и тензора поля, а 
заменяя на 
:
Если
физическая система является замкнутой, то в (14) последний поверхностный
интеграл в правой части обнуляется как следствие калибровки поля на
бесконечности, где 4-потенциал 
и тензор
гравитационного поля 
системы должны быть
равны нулю.
Подобным образом мы можем поступить и с полем ускорений, и с векторным полем давления [2], для которых интегральная теорема энергии полей запишется следующим образом:
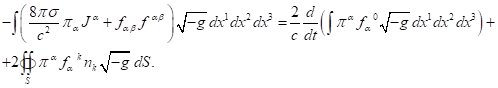(16)
Однако поле ускорений и поле давления существенно отличаются от электромагнитного и гравитационного полей тем, что действуют только в пределах вещества. Поэтому в (15) и в (16) поверхностные интегралы в правой части следует брать по внешней поверхности объёма, занимаемого веществом системы.
4. Применение интегральной
теоремы энергии в релятивистской
однородной системе
Релятивистская
однородная система является удобным объектом для тестирования многих физических
закономерностей. Так, в [3] мы исследовали теорему вириала и обнаружили отличие
от классического подхода благодаря учёту релятивистских поправок. В [4] мы
применили формулы, выведенные для релятивистской однородной системы, к планетам
и звёздам и нашли неплохое совпадение с результатами других авторов. При этом
мы предполагали, что вещество находится в хаотическом движении, частицы
вещества не имеют собственного вращения, а какие-либо направленные потоки
вещества отсутствуют. В результате в рассматриваемой системе исчезают как
глобальные векторные потенциалы всех полей, так и глобальные соленоидальные векторы
полей. Для электромагнитного поля это означает, например, что равны нулю как глобальный
векторный потенциал 
, так и магнитное поле 
. Более
тщательный анализ показывает, что каждая заряженная движущаяся типичная частица
имеет свой собственный небольшой по величине векторный потенциал 
, пропорциональный
мгновенной скорости движения частицы 
и собственному
скалярному электрическому потенциалу 
частицы, а также
собственное магнитное поле 
. Вклад от 
и 
в дальнейших расчётах
невелик из-за малой величины заряда у каждой из частиц, и им в первом
приближении можно пренебречь. Это же будет относиться и к соответствующим
величинам для гравитационного поля.
Рассмотрим теперь, как выполняется интегральная теорема энергии для электромагнитного поля в случае релятивистской однородной системы. Будем считать, что система является замкнутой, имеет сферическую форму и удерживается в равновесии под действием сил от гравитационного притяжения и сил отталкивания от электромагнитного поля и поля давления. Поле ускорений также вносит свой вклад в равновесие сил, поскольку при хаотическом движении внутри сферы частицы испытывают центростремительную силу от тангенциальной по отношению к радиусу сферы компоненты скорости частиц. Мы будем использовать приближение сплошной среды, так что промежутки между типичными частицами минимальны и можно считать, что объём сферы состоит из объёмов частиц.
С целью
упрощения дальнейших расчётов будем рассматривать ситуацию в рамках специальной
теории относительности, в которой 
.
Для замкнутой системы поверхностный интеграл в (10) обнуляется и для
электромагнитного поля остаётся
следующее:
Поскольку 
и мы в первом
приближении считаем, что в рассматриваемой системе 
, для вычисления 4-потенциала необходимо ещё знать распределение
в системе глобального электрического потенциала 
. Как было найдено в [5], электрический потенциал внутри
сферы зависит от синусоидальных функций:
(18)
В (18) 
– электрическая постоянная, 
– фактор
Лоренца частиц в центре сферы, 
– радиус сферы. Для зарядового 4-тока имеем: 
, при этом 4-скорость 
, где 
есть фактор Лоренца
для частиц, есть скорость частиц.
Зависимость 
от текущего радиуса 
следующая [6]:
С учётом этого для свёртки 4-векторов находим: 
. Теперь, используя (18) и (19), можно вычислить первый член
в левой части (17):
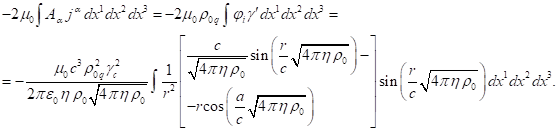
В сферических координатах 
, и этот интеграл будет равен:
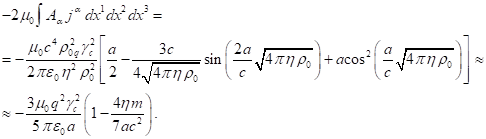
(20)
В (20) заряд 
есть
произведение инвариантной плотности заряда частиц 
на объём сферы, и
аналогично, масса 
есть
произведение инвариантной плотности массы частиц 
на объём сферы.
Величины и носят технический
характер и не равны соответственно полному заряду сферы 
и гравитационной массе
. В частности, согласно [5],
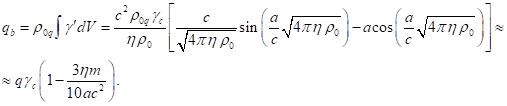
(21)
Напряжённость электрического поля внутри сферы с учётом (18) и
равенства нулю векторного потенциала, то есть 
, определяется по
формуле:
(22)
Аналогично, напряжённость электрического поля за пределами сферы
равна:
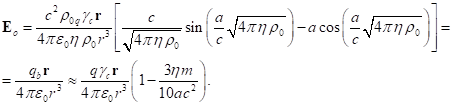(23)
В общем случае тензор электромагнитного поля 
содержит компоненты вектора напряжённости электрического
поля 
и вектора магнитного
поля 
. В рассматриваемой системе в среднем 
, при этом в декартовых пространственных координатах 
, 
, 
, остальные компоненты тензоров и 
мы полагаем равными
нулю. Следовательно, в данном случае 
. Интеграл по объёму внутри сферы от второго члена левой
части (17) с учётом (22) в сферических координатах будет равен:
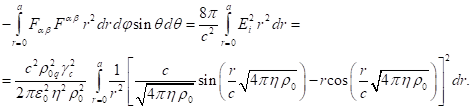
Данный интеграл следует брать по частям, внося 
под знак дифференциала
в виде 
. Это даёт следующее:
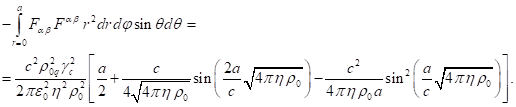(24)
Вычислим теперь интеграл по объёму за пределами сферы от второго члена левой части (17) с учётом (23) в сферических координатах:
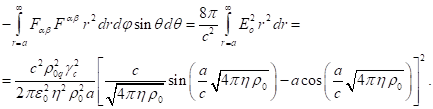(25)
Сумма (24) и (25) даёт интеграл по всему пространству:
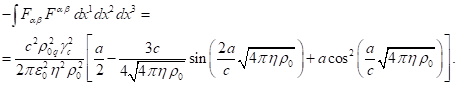
(26)
Если учесть тождество вида 
и подставить (20) и (26) в (17), то видно, что левая часть
(17) обнуляется. Следовательно, в данной физической системе должна равняться
нулю и правая часть (17):
. (27)
И это действительно так, поскольку пространственные компоненты
4-потенциала 
предполагаются равными
нулю, то есть 
. В то же время, временная компонента тензора
электромагнитного поля равна нулю ввиду антисимметричности тензора, 
. Следовательно, произведение 
и равенство (27)
выполняется.
Для гравитационного поля ситуация полностью аналогична электромагнитному
полю. Для замкнутой системы в рамках специальной теории относительности в (14) поверхностный
интеграл обнуляется и остаётся следующее:
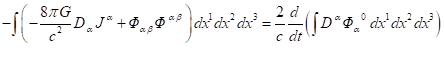. (28)
Поскольку в релятивистской однородной системе глобальный векторный
потенциал гравитационного поля равен нулю, 
, равны нулю как произведение
, так и правая часть (28). Что касается левой
части (28), то для её вычисления понадобятся глобальный скалярный
гравитационный потенциал 
внутри сферы, а также
напряжённости гравитационного поля внутри и снаружи сферы [5]:
.
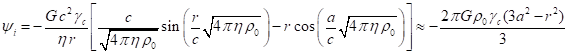(29)
(30)
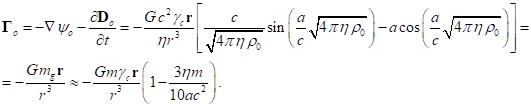
(31)
Произведение
получается в следующем
виде: 
. Учитывая далее (19) и (29), для первого члена в левой части
(28) находим:
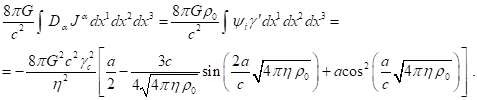(32)
Для второго члена в левой части (28) с учётом (30) и (31) имеем:
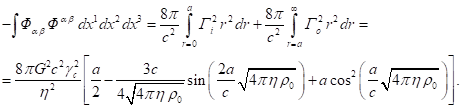(33)
Сумма (32) и (33) обращается в нуль в соответствии с (28), где
правая часть получается равной нулю.
Начнём с уточнения того, что в общем случае следует
подразумевать под 4-потенциалом поля ускорений некоторой физической системы. В
соответствии с [2], 4-потенциал любого векторного поля, векторный потенциал
которого равен нулю в собственной системе отсчёта, то есть в системе центра
импульсов, при прямолинейном движении в лабораторной системе отсчёта может быть
представлен по формуле:
, (34)
где 
для электромагнитного
поля и 
для остальных полей; 
есть инвариантная
плотность энергии взаимодействия, находимая через произведение 4-потенциала
поля на соответствующий 4-ток; 
есть 4-скорость с
ковариантным индексом, задающая движение центра импульсов физической системы в лабораторной системе
отсчёта.
В собственной системе отсчёта 
и векторный потенциал
как пространственная компонента 
согласно (34)
обнуляется. Однако некоторые физические системы, даже имея неподвижным свой
центр импульсов, обладают не только скалярным, но и векторным потенциалом поля в
пределах системы. Поэтому более общим выражением для
4-потенциала поля в лабораторной системе отсчёта будет следующее:
, (35)
где 
есть матрица,
связывающая координаты и время двух систем отсчёта, одна из которых является
лабораторной, а другая движется вместе с центром импульсов рассматриваемой
физической системой, так что в ней имеется 4-потенциал поля 
. В частном случае движения системы с постоянной скоростью представляет собой
матрицу преобразований Лоренца [7].
В качестве характерного примера рассмотрим
нейтронную звезду, состоящую в основном их нейтронов и некоторой доли протонов
и электронов. Как сама звезда, так и нуклоны имеют быстрое вращение и сильные
магнитные поля. Несмотря на отсутствие заряда, каждый нейтрон обладает сложной
внутренней электромагнитной структурой и магнитным моментом. Предположим, что
требуется моделировать звезду как релятивистскую однородную систему и задать
4-потенциал поля произвольного движущегося нуклона как типичной частицы. Для
этого придётся использовать формулу (35), так как в (34) предполагается
отсутствие векторного потенциала в системе центра импульсов нуклона.
Действительно, нуклон может не перемещаться в пространстве, но за счёт
собственного вращения и сложной внутренней структуры в нуклоне имеются
ненулевые векторные потенциалы практически всех полей.
С целью упрощения расчётов мы будем далее предполагать,
что рассматриваемая нами физическая система не имеет общего вращения, типичные
частицы системы движутся хаотически и также не имеют ни собственного вращения,
ни собственных векторных потенциалов в системах центра импульсов частиц. В этом
случае мы можем использовать более простую формулу (34) вместо (35).
У неподвижной сферы плотность энергии в объёме каждой
частицы 
, и для поля
ускорений при прямолинейном движении сферы в лабораторной системе отсчёта согласно
(34) 4-потенциал будет равен 
. Это означает, что если для наблюдателя внутри сферы с
частицами в рамках релятивистской однородной модели величина 
есть инвариантно
определённый фактор Лоренца как некоторая функция координат и времени, то для
наблюдателя в лабораторной системе отсчёта, в которой центр сферы имеет
4-скорость , 4-потенциал поля ускорений для
каждой точки внутри движущейся сферы будет равен 
.
В
идеальном случае, когда система частиц составляет абсолютно твёрдое тело и
частицы внутри системы неподвижны, должно быть 
, и тогда 4-потенциал поля ускорений совпадает с 4-скоростью центра
импульсов системы, 
. Материальная точка представляет собой миниатюрную
физическую систему, и если не вникать в структуру внутреннего движения её
вещества и рассматривать данную точку как твёрдое тело, то 4-потенциал поля ускорений такой точки будет равен
4-скорости её прямолинейного движения.
По определению 4-потенциал поля ускорений есть
4-вектор 
, где 
и 
обозначают
скалярный и векторный потенциалы, соответственно. С учётом (34) и соотношения 
получается, что в рассматриваемой нами релятивисткой
однородной системе в виде неподвижной сферы скалярный потенциала будет 
. Что касается глобального
векторного потенциала поля ускорений 
, то он равен нулю, ввиду хаотичности движения частиц
вещества. С другой стороны, внутри каждой типичной частицы всегда существует небольшой
по величине векторный потенциал 
поля ускорений, пропорциональный мгновенной
скорости движения частицы 
. Это несколько изменяет вид эффективно действующего
4-потенциала поля ускорений
внутри сферы.
Пусть произвольная типичная частица движется
внутри сферы, имея в рамках специальной теории относительности 4-скорость 
, где 
есть скорость частицы,
есть фактор Лоренца
частицы. Указанную частицу в свою очередь можно рассматривать как некоторую релятивистскую однородную систему, в
объёме которой хаотически движутся субчастицы с фактором Лоренца 
относительно центра
импульсов частицы. Тогда 4-потенциал
поля ускорений для этой движущейся частицы согласно (34) запишется в виде 
. Сравнение с выражением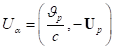 
даёт возможность
определить потенциалы поля ускорений внутри каждой движущейся частицы сферы: 
, 
. При этом получается, что 
, то есть движение субчастиц внутри частицы с фактором
Лоренца 
увеличивает скалярный
потенциал движущейся частицы до величины 
.
Ввиду малости локального векторного
потенциала 
, мы не будем использовать его в наших расчётах. В результате
для 4-потенциала поля ускорений внутри сферы можно записать:
. (36)
Это
означает, что мы не учитываем внутреннее движение субчастиц в отдельных частицах, считая, что 
, так что скалярный потенциал частиц будет равен 
и совпадает с
потенциалом поля ускорений внутри неподвижной сферы.
5.1 Расчёт
для поля ускорений
Учитывая,
что массовый 4-ток 
, а эффективный 4-потенциал поля ускорений внутри сферы задаётся
в (36), находим, что 
.
Теперь можно записать первую часть интеграла в левой части (15) и с учётом (19) провести интегрирование в сферических координатах:
Поскольку тензор ускорений определяется
выражением 
, то c учётом (36) тензорный инвариант получается в виде 
.
Напряжённость поля ускорений внутри сферы вычисляется
через скалярный и векторные потенциалы [2], и так как согласно (36) , 
, с учётом (19) имеем:
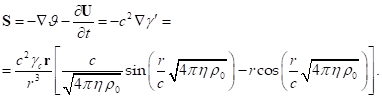(38)
Используя (38), будем вычислять следующий интеграл по объёму сферы:
Данный интеграл может быть вычислен аналогично (24) в сферических координатах:
(39)
Перейдём теперь к правой
части (15), для чего нужно вычислить произведение 
внутри сферы. Если
4-потенциал согласно (36) имеет компоненты 
, то временными компонентами тензора ускорений в декартовых
пространственных координатах являются 
, 
, 
, 
. Следовательно, 
, и первый интеграл правой части (15) равен нулю.
Радиальная компонента вектора 
определяется
выражением 
, где 
есть единичный вектор,
направленный вдоль радиуса. Для определения
удвоенного потока вектора 
будет достаточно умножить значение 
, вычисленное при 
, на удвоенную площадь сферы:
. (40)
Так как 4-потенциал поля ускорений внутри сферы согласно (36)
имеет компоненты 
, а ненулевые компоненты тензора ускорений в декартовых
пространственных координатах равны 
, 
, 
, то должно быть:
, 
.
С учётом (19) и (38), находим:
.
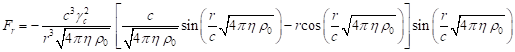При 
данное выражение даёт 
, и тогда вычисляется поверхностный интеграл (40):
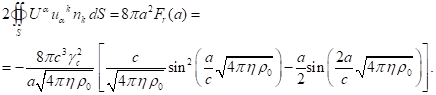
(41)
Подставляя (37), (39) и (41) в (15), убеждаемся, что теорема энергии для поля ускорений выполняется точно.
6. Поле давления
В рассматриваемой нами физической системе векторный потенциал
полагается
равным нулю и тогда 4-потенциал поля давления внутри сферы в приближении
специальной теории относительности запишется так:
. (42)
Скалярный потенциал поля давления был вычислен в [6]:
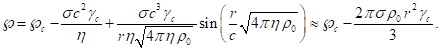(43)
Массовый 4-ток имеет следующий вид: , С учётом этого 
, и можно записать первый интеграл в левой части (16):
.
Подставляя сюда (43) и из (19), находим:
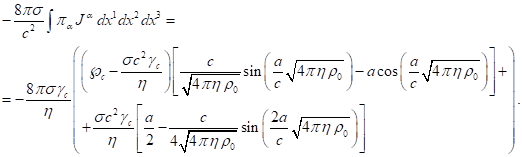
(44)
Так как мы приняли, что векторный потенциал поля давления в
рассматриваемой системе отсутствует, то будет равен нулю и соленоидальный
вектор 
поля
давления, вычисляемый как ротор векторного потенциала [2]. В таком случае
тензор поля давления 
будет зависеть только
от напряжённости поля 
, так что тензорный инвариант будет равен 
. Напряжённость поля давления определяется по формуле:
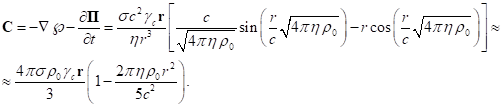(45)
Теперь можно записать второй интеграл в левой части (16) в сферических координатах:
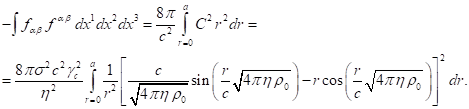
Данный интеграл вычисляется аналогично (24):
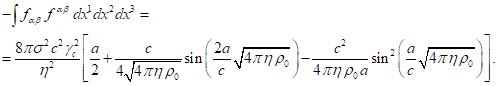(46)
В правой части (16) присутствует произведение 
, причём компоненты тензора поля давления следующие: 
, 
, 
, 
. Если учесть компоненты 4-потенциала 
согласно (42), то
видно, что 
.
Перейдём теперь к произведению 
в правой части (16), где
. Так как 4-потенциал содержит только
временную компоненту при индексе 
, выпишем все ненулевые компоненты 
: 
, 
, 
. Следовательно, произведение 
есть радиальный
вектор, направленный противоположно вектору напряжённости 
поля давления. То, что
является радиальным
вектором, позволяет сразу найти поверхностный интеграл в правой части (16). Для
вычисления этого интеграла необходимо положить в напряжённости поля (45) и в скалярном
потенциале 
(43), входящих в , умножить на вектор нормали 
, а результат умножить на площадь поверхности сферы:
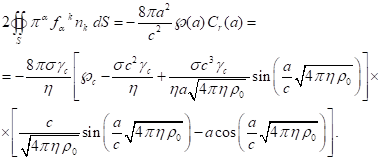(47)
Подставляя выражения из (44), (46) и (47) в (16), находим, что теорема энергии для поля давления выполняется, так как все члены в (16) полностью сокращаются друг с другом.
7. Заключение
На примере электромагнитного поля мы вывели
интегральную теорему энергии поля в соотношении (10). Кроме этого, мы ввели в
рассмотрение понятия кинетической энергии 
и потенциальной
энергии 
электромагнитного поля:
, 
. (48)
В (48) энергия 
связана с энергией
взаимодействия поля и частиц и
вычисляется через произведение 4-потенциала 
поля на зарядовый
4-ток 
частиц, а энергия 
выражается через
объёмный интеграл от тензорного инварианта 
электромагнитного поля. Из (10) и (48) следует
соотношение:
. (49)
Для замкнутой системы поверхностный
интеграл в правой части (49) обращается в нуль ввиду калибровки 4-потенциала 
и тензора
электромагнитного поля 
на бесконечности. В
релятивистской однородной системе обнуляется ещё произведение 
, и тогда (49) сводится к простому соотношению 
. Это соотношение для поля напоминает классическую теорему
вириала для частиц вида 
, где 
есть кинетическая энергия, 
– потенциальная энергия частиц. Соотношение часто используется в
электростатике, позволяя определить электрическую энергию системы двумя
различными способами – либо через плотность заряда и электрический потенциал,
либо через напряжённость, входящую в тензор электромагнитного поля. Однако доказательство
существования связи между энергиями (48) в общем случае при наличии
электрических токов и магнитных полей отсутствовало. Теперь мы видим, что такая
связь в (49) является следствием интегральной теоремы энергии поля.
В (14) мы представили интегральную теорему энергии для векторного
гравитационного поля в рамках ковариантной теории гравитации, а в (15) и в (16)
– интегральную теорему энергии для поля ускорений и поля давления,
соответственно. По аналогии с (48), для этих полей можно также ввести понятия
кинетической и потенциальной энергии поля. В частности, в [8] для замкнутых
статических однородных систем было найдено, что в них выполняется соотношение
вида 
для гравитационного
поля.
Для всех четырёх векторных полей в разделах 4, 5 и 6 мы показали путём прямого вычисления всех членов в формулировке интегральной теоремы энергии, как именно выполняется данная теорема в случае релятивистской однородной системы. Указанные расчёты доказывают, что интегральная теорема энергии поля выполняется точно, подтверждая справедливость теоремы.
Список использованных источников
1. Fedosin
S.G. About the cosmological constant, acceleration
field, pressure field and energy. Jordan Journal of
Physics. Vol. 9, No. 1, pp.
1-30 (2016). http://dx.doi.org/10.5281/zenodo.889304; О космологической постоянной, поле ускорения,
поле давления и об энергии.
2.
Fedosin S.G. The procedure of finding the stress-energy
tensor and vector field equations of any form. Advanced Studies in Theoretical
Physics. Vol. 8, pp. 771-779
(2014). doi: 10.12988/astp.2014.47101; Процедура для нахождения тензора
энергии-импульса и уравнений векторного поля любого вида.
3.
Fedosin S.G. The virial theorem and the kinetic energy of particles of a macroscopic
system in the general field concept. Continuum Mechanics
and Thermodynamics, Vol. 29, Issue 2, pp. 361-371 (2016). https://dx.doi.org/10.1007/s00161-016-0536-8; Теорема вириала и
кинетическая энергия частиц макроскопической системы в
концепции общего поля.
4. Fedosin
S.G. Estimation of the physical
parameters of planets and stars in the gravitational equilibrium model. Canadian
Journal of Physics, Vol. 94, No. 4, pp. 370-379 (2016). http://dx.doi.org/10.1139/cjp-2015-0593; Оценка физических параметров планет и звёзд в
модели гравитационного равновесия.
5. Fedosin
S.G. Relativistic Energy and Mass in the Weak Field
Limit. Jordan Journal of
Physics. Vol. 8, No. 1, pp.
1-16 (2015). http://dx.doi.org/10.5281/zenodo.889210; Релятивистская энергия и масса в пределе слабого
поля.
6. Fedosin
S.G. The Integral Energy-Momentum
4-Vector and Analysis of 4/3 Problem Based on the Pressure Field and
Acceleration Field.
American Journal of Modern Physics, Vol. 3, No. 4, pp. 152-167 (2014). doi: 10.11648/j.ajmp.20140304.12; Интегральный
4-вектор энергии-импульса и анализ проблемы 4/3 на основе поля давления и поля
ускорений.
7. Dennery P. and Krzywicki A. Mathematics for Physicists. Courier
Corporation. p. 138 (2012). ISBN 978-0-486-15712-2.
8.
Fedosin S.G. The
Gravitational Field in the Relativistic Uniform Model within the Framework of
the Covariant Theory of Gravitation. International Letters of Chemistry,
Physics and Astronomy, Vol. 78, pp. 39-50 (2018). http://dx.doi.org/10.18052/www.scipress.com/ILCPA.78.39. // Гравитационное поле в релятивистской однородной модели в
рамках ковариантной теории гравитации.
Источник: http://sergf.ru/tf.htm