In English

Jordan Journal of Physics. Vol. 8 (No. 1), pp. 1-16 (2015). http://journals.yu.edu.jo/jjp/Vol8No1Contents2015.html

Релятивистская энергия и масса в пределе слабого поля

Федосин Сергей Григорьевич

г. Пермь, Пермский край, Россия

E-mail: intelli@list.ru

В рамках ковариантной теории гравитации (КТГ) для системы с непрерывно распределённым веществом вычислена энергия с учётом вклада гравитационного и электромагнитного полей, и вклада поля давления и поля ускорений. Суммарная энергия всех полей оказывается равной нулю, а энергия системы формируется из энергии частиц, находящихся под действием указанных полей. Из выражения для энергии находится инертная M и гравитационная m_g массы системы. Эти массы сравниваются с массой m_b , получаемой путём интегрирования плотности по объёму, и с суммарной массой m’ частиц тела, разнесённых на бесконечность с целью обнуления энергии макроскопических фундаментальных полей. Для масс получено соотношение: m’ = M < m_b = m_g . Отсюда следует возможность безизлучательного идеального сферического коллапса, когда масса системы M не меняется в ходе коллапса. Кроме этого, масса системы оказывается меньше, чем гравитационная масса. В противоположность этому, в общей теории относительности (ОТО) соотношение для масс получается в другом виде: M = m_g < m_b < m’. В КТГ энергия электромагнитного поля уменьшает гравитационную массу, а в ОТО наоборот, увеличивает. С целью проверки полученных результатов предлагается провести эксперимент по измерению изменения гравитационной массы тела при увеличении его электрического заряда.

Ключевые слова: релятивистская энергия; масса; поле ускорений; поле давления; ковариантная теория гравитации.

Relativistic energy and mass in the weak field limit

Sergey G. Fedosin

PO box 614088, Sviazeva str. 22-79, Perm, Russia

E-mail: intelli@list.ru

Within the framework of the covariant theory of gravitation (CTG) the energy is calculated for a system with continuously distributed matter, taking into account the contribution of the gravitational and electromagnetic fields and the contribution of the pressure and acceleration fields. The total energy of all the fields is equal to zero, and the system’s energy is formed from the energy of the particles, which are under the influence of these fields. From the expression for the energy the inertial M and gravitational m_g masses of the system are found. These masses are compared with mass m_b, obtained by integrating the density over the volume, and with the total mass m’ of the body particles scattered to infinity in order to make the energy of macroscopic fundamental fields equal to zero. The ratio for the masses is obtained: m’ = M < m_b = m_g . From this the possibility of non-radiative ideal spherical collapse follows, when the system’s mass M does not change during the collapse. In addition, the mass of the system is less than the gravitational mass. In contrast, in the general theory of relativity (GTR) the ratio for masses is obtained in a different form: M = m_g < m_b < m’. In CTG the electromagnetic field energy reduces the gravitational mass and in GTR, on the contrary, increases. In order to verify the obtained results it is suggested to conduct an experiment on measuring the change of the gravitational mass of the body with increasing its electrical charge.

Keywords: relativistic energy; mass; acceleration field; pressure field; covariant theory of gravitation

1. Введение

Современные физические теории как правило описывают энергию, импульс и массу системы в четырёхмерном формализме и вводят в рассмотрение различные 4-векторы и 4-тензоры. С целью упрощения сравнения полученных выражений удобно перейти к пределу настолько слабого поля, что большинство формул можно будет без потери точности записать в том виде, какой они имеют в специальной теории относительности. В данной работе это будет сделано для ковариантной теории гравитации и общей теории относительности; особое внимание будет уделено тому смыслу, который приобретает масса в данных теориях.

2. Энергия и масса в ковариантной теории гравитации

Вычислим релятивистскую энергию для тела в виде сферы с однородной плотностью массы и заряда, движущейся со скоростью вдоль оси системы отсчёта . Рассматриваемое тело представляет собой множество одинаковых частиц, движущихся хаотически в разных направлениях и находящихся внутри указанной сферы радиуса . Будем считать, что все эти частицы удерживаются вместе силой гравитации. С целью упрощения предположим, что промежутки между частицами настолько малы, что интегрирование по объёму всех частиц эквивалентно тому, что мы интегрируем по объёму сферы. Сфера неподвижна в сопутствующей системе отсчёта , связанной с центром масс, а скорости частиц в равны и зависят от координат.

Гамильтониан для непрерывно распределённого вещества в ковариантной теории гравитации получается из лагранжиана с помощью преобразований Лежандра. Данный гамильтониан оказывается равен релятивистской энергии системы и имеет вид [1-2]:

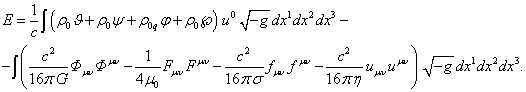(1)

Здесь – скорость света, – плотность массы произвольной точечной частицы в сопутствующей частице системе отсчёта , – скалярный потенциал поля ускорений, – скалярный потенциал гравитационного поля, – плотность заряда в системе отсчёта , – скалярный потенциал электромагнитного поля, – скалярный потенциал поля давления, обозначает временную компоненту 4-скорости частицы, включает в себя детерминант метрического тензора со знаком минус, есть элемент трёхмерного объёма в системе отсчёта , – гравитационная постоянная, – гравитационный тензор, – магнитная постоянная, – электромагнитный тензор, – тензор поля ускорений, – тензор поля давления, и – некоторые постоянные.

Для наших целей достаточно рассмотреть выражение для релятивистской энергии (1) в том случая, когда рассматриваемая сфера неподвижна в . Тогда все расчёты можно производить в системе отсчёта , связанной с центром масс системы. Предположим, что гравитационное поле мало и ковариантная теория гравитации переходит в лоренц-инвариантную теорию гравитации. В этом случае метрический тензор перестаёт зависеть от координат и превращается в метрический тензор пространства-времени Минковского , используемый в специальной теории относительности. Для случая неподвижной одиночной системы выражения для физических величин становятся такими:

, , , (2)

, , , .

где фактор Лоренца , – скорость частицы в , – напряжённость гравитационного поля, – вектор поля кручения, – напряжённость электрического поля, – индукция магнитного поля, – электрическая постоянная, – напряжённость поля давления, – соленоидальный вектор поля давления, – напряжённость поля ускорений, – соленоидальный вектор поля ускорений.

Подстановка выражений (2) в (1) даёт:

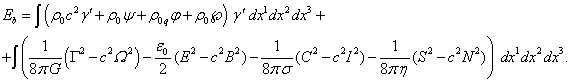(3)

Вычислим вначале первый интеграл в (3). Согласно [2], фактор Лоренца для частиц внутри неподвижной сферы является функцией текущего радиуса :

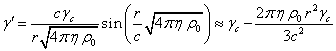, (4)

где есть фактор Лоренца для скоростей частиц в центре сферы, и ввиду малости аргумента синус может быть разложен до членов второго порядка.

Для первого члена в первом интеграле в (3) учётом (4) в сферических координатах можно записать:

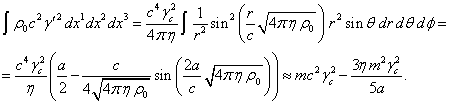(5)

В (5) масса есть произведение плотности массы частиц на объём неподвижной в системе отсчёта сферы. Происхождение множителя в (5) можно понять из следующего. Величина есть та плотность массы частиц в центре, которая видна в системе отсчёта . Тогда произведение даёт массу частиц в сфере для наблюдателя в в том случае, как если бы все частицы были в центре сферы. Очевидно, что . В (5) получается, что , то есть это суммарная энергия частиц, увеличенная за счёт внутреннего движения частиц, что учитывается фактором Лоренца . Второй член в (5) возникает из-за радиального градиента средних скоростей частиц внутри сферы и учитывает то, что не все частицы находятся в центре сферы.

Скалярный потенциал гравитационного поля в (3) внутри сферы согласно [2] равен:

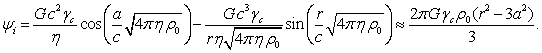(6)

Исходя из подобия гравитационного и электромагнитного полей, для электрического потенциала можно записать аналогично (6):

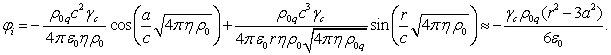
(7)

Скалярный потенциал поля давления внутри сферы равен:

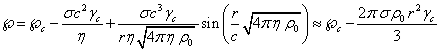, (8)

где обозначает потенциал поля давления в центре сферы.

Подставляя (6), (7) и (8) в (3), с учётом (4) находим:

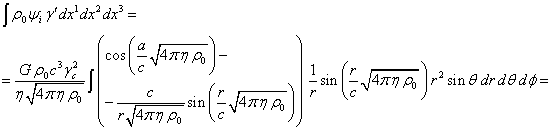
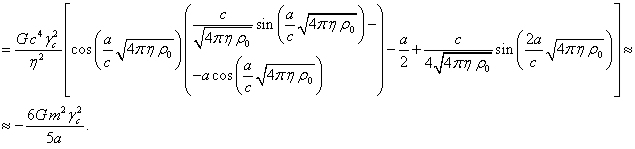(9)

(10)

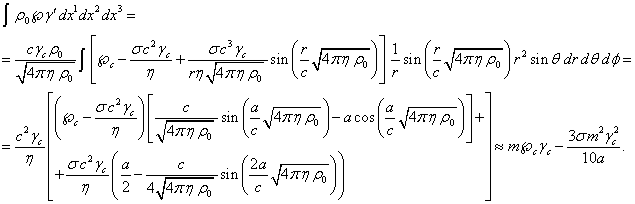
(11)

С учётом (5) и (9-11) первый интеграл в (3) будет равен:

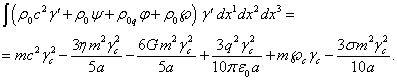(12)

Напряжённость гравитационного поля и поле кручения внутри сферы определяются формулами:

, , (13)

где есть векторный потенциал гравитационного поля.

Векторный потенциал каждой частицы направлен вдоль её скорости, и ввиду хаотичности направлений скоростей частиц суммарный векторный потенциал внутри и за пределами сферы будет равен нулю. Следовательно, будет равно нулю и поле кручения: . Подставляя в (13) скалярный потенциал (6) , находим напряжённость гравитационного поля:

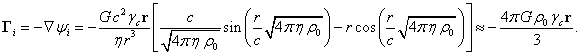
(14)

С учётом (14) и равенства для интеграла от первого члена во втором интеграле в (3) имеем:

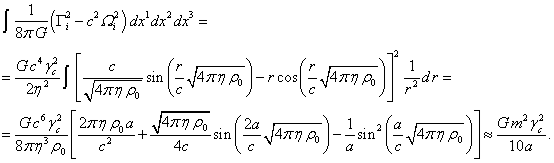(15)

Согласно [2], потенциал гравитационного поля за пределами сферы равен:

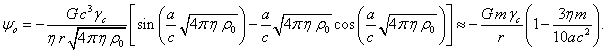
Отсюда следует, что гравитационной массой сферы является величина .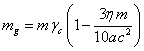

Используя (13), при находим напряжённость поля:

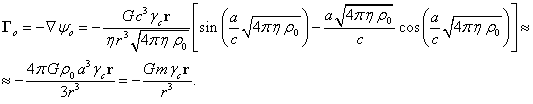
Подставляя в (3) с учётом равенства , находим для гравитационного поля за пределами сферы:

(16)

Сумма (15) и (16) равна:

. (17)

Вычисление для члена с электромагнитным полем в (3) производится аналогично и даёт следующее для однородно заряженных частиц внутри неподвижной сферы:

, (18)

где заряд есть произведение плотности заряда произвольной частицы в сопутствующей частице системе отсчёта на объём неподвижной сферы.

В пространстве Минковского 4-скорость неподвижной сферы равна , и исходя из определения общего 4-потенциала поля давления сферы , находим: , , где обозначает плотность внутри покоящейся сферы. При этом скалярный потенциал , плотность и давление внутри сферы оказываются функциями текущего радиуса внутри сферы, а равенство для векторного потенциала поля давления в данном случае вытекает из отсутствия упорядоченных движений частиц внутри сферы. С учётом этого и соотношения (8) для векторы и внутри сферы выражаются следующим образом:

, .

При однородной плотности массы вычисления для вектора напряжённости давления внутри сферы дают следующее:

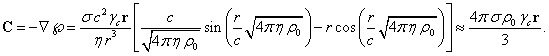
Используя это, подсчитаем интеграл для давления:

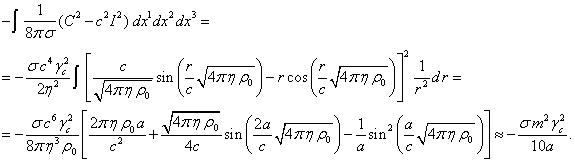
(19)

Нам осталось вычислить ещё один член во втором интеграле в (3). Компоненты векторов и для поля ускорения определяются так:

, ,

где скалярный потенциал и векторный потенциал входят в 4-потенциал поля ускорений , являющийся ковариантной 4-скоростью.

В пределе специальной теории относительности , где есть фактор Лоренца для скорости движения частицы.

В системе отсчёта скорости частиц внутри сферы равны и вместо следует использовать . Тогда потенциалы произвольной частицы будут , . Нам же нужны суммарные потенциалы поля ускорений внутри сферы, получающиеся за счёт непосредственного взаимодействия частиц друг с другом и за счёт действия полей. При хаотическом движении частиц скорости направлены в разные стороны и потому внутри сферы , а также . Однако суммарный фактор Лоренца частиц оказывается функцией текущего радиуса, и суммарный скалярный потенциал не равен нулю. С учётом (4) для это даёт следующее:

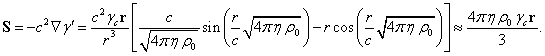
Вычисляем последний интеграл:

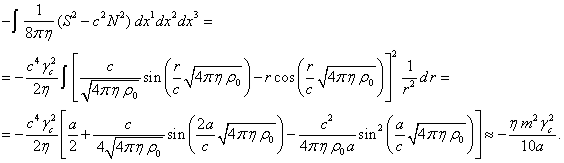
(20)

Подставляя (12), (17), (18), (19) и (20) в (3), находим релятивистскую энергию системы:

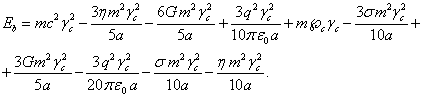(21)

В [2] были вычислены коэффициенты и для рассматриваемого нами случая:

. (22)

Если подставить (22) в (21), то видно, что энергии полей сокращаются полностью. Остаётся лишь энергия частиц в соответствующих полях:

. (23)

Соотношение (22) фиксирует определённую связь между полем давления, полем ускорений и гравитационным и электромагнитным полями. Эта связь согласно [2] выражается в том, что сохраняющийся интегральный 4-вектор, являющийся результатом интегрирования уравнения движения, оказывается равным нулю. При этом возникает условие (22), а также в рамках представленной модели объясняется проблема 4/3.

Оценим суммарную массу частиц в сфере, для чего с учётом (4) проинтегрируем плотность массы частиц в по объёму сферы:

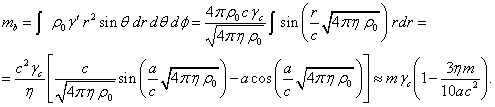(24)

Отсюда путём решения квадратного уравнения получаем: . Аналогичным образом можно связать заряд с зарядом сферы, который обнаруживает наблюдатель в : . Подставим это в (23) с учётом из (22):

. (25)

Выразим из (8) скалярный потенциал поля давления в центре через потенциал вблизи поверхности сферы и учтём соотношение :

. (26)

Аналогично, выразим из (4) через фактор Лоренца частиц вблизи поверхности сферы:

. (27)

Если учесть (27) и (22) в (24), можно уточнить связь между и :

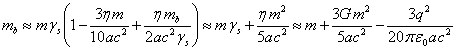. (28)

Подстановка (22), (26) и (27) в (25) даёт следующее:

. (29)

Из (29) видно, что когда ковариантная теория гравитации в пределе слабого поля переходит в Лоренц-инвариантную теорию гравитации, все поля в системе, включая поле ускорений, поле давления, электромагнитное и гравитационное поля, компенсируют друг друга таким образом, что релятивистская энергия зависит только от массы, от энергии гравитационного и электромагнитного полей, от энергии поверхностного давления и от скорости движения частиц на поверхности.

Скалярный потенциал поля давления вблизи поверхности сферы связан с давлением соотношением: , где и обозначают давление и плотность массы вблизи поверхности сферы. Используя соотношение , где есть средняя плотность по объёму сферы, находим: . Для тех массивных тел, где можно положить и пренебречь давлением на поверхности, (29) превращается в простое выражение:

. (30)

Выразим из (29) массу системы, состоящую из массы вещества и массы четырёх полей, связанных с данной системой:

. (31)

Масса одинакова и в покое и в движении и является инвариантной инертной массой системы. Выше из формулы для внешнего гравитационного потенциала было найдено, что гравитационной массой сферы является величина 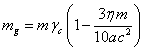. Сравнение с (24) показывает, что масса сферы в рамках принятых нами допущений равна гравитационной массе . Согласно (31), инертная масса системы по отношению к массе увеличивается на величину массы-энергии поверхностного давления, и на определённую долю от массы-энергии электромагнитного поля, но уменьшается за счёт такой же доли от массы-энергии гравитационного поля.

3. Соотношения между энергиями

Сравним между собой различные компоненты энергий, из которых складывается общая релятивистская энергия (29). Обозначим через , , и компоненты энергии электромагнитного и гравитационного поля, поля давления и поля ускорений, соответственно. В качестве единицы измерения энергии возьмём сумму компонент энергий электромагнитного и гравитационного поля из (17) и (18). С учётом (24), (19), (20) и (22) находим:

. (32)

, .

Согласно (32), компоненты энергий поля давления и поля ускорений в два раза меньше суммы компонент энергии гравитационного и электромагнитного поля и имеют другой знак. Это приводит к тому, что сумма компонент энергии полей в (21) обращается в нуль.

Рассмотрим теперь компоненты энергии частиц вещества, находящихся под действием полей. Обозначим эти компоненты в виде , , и , как компоненты энергии частиц в электромагнитном и гравитационном поле, в поле давления и в поле ускорений, соответственно. Согласно (9), (10), (11), (26), (5), (27) имеем:

, ,

,

, (33)

.

Теперь сложим компоненты энергий в (32) и (33) отдельно для каждого поля:

, ,

. (34)

Величина обозначает сумму компонент энергии гравитационного и электромагнитного поля, включая компоненты энергий для самих полей и для частиц в этих полях, определение дано в (32). Сумма всех компонент энергии в (34) даёт релятивистскую энергию системы (29):

. (35)

Если в (35) пренебречь произведением из-за малого давления на поверхности тела, и не учитывать энергию покоя , то остаётся величина энергии, равная: .

В классической механике, в которой энергия покоя не учитывается, сумма энергий гравитационного и электромагнитного поля для сферы с однородным распределением массы и заряда равна:

.

По теореме вириала считается, что внутренняя кинетическая энергия должна равняться половине модуля энергии полей: . Полная энергия складывается из энергии полей и внутренней энергии:

. (36)

Отсюда видно, что полная энергия классической механики совпадёт с релятивистской энергией (35), если в последней убрать энергию покоя и энергию давления на поверхности. Таким образом осуществляется переход ковариантной теории гравитации в классическую механику. Однако в классической механике не определено, каким образом внутреннее давление делает вклад в массу и энергию системы.

Уточним теперь, как в нашей модели реализуется теорема вириала, отдельно для энергий полей и для энергий частиц. У нас имеется энергия поля давления и энергия поля ускорений, и сумма этих энергий согласно (32) равна модулю суммы энергий гравитационного и электромагнитного полей. В результате сумма энергий полей равна нулю.

Для энергий частиц в полях складывается другая картина. Энергия частицы в поле в отсутствие векторного потенциала определяется произведением массы (заряда) на скалярный потенциал. Сумма энергий частиц в гравитационном и электромагнитном поле по (33) равна , энергия частиц в поле давления равна , а энергия частиц в поле ускорений равна . Из энергии частиц в поле давления можно выделить энергию , и из энергии частиц в поле ускорений также выделяется энергия . Но сумма этих энергий оказывается меньше в раз, чем модуль суммы энергий частиц в гравитационном и электромагнитном поле. В то же время избыток энергии частиц в гравитационном и электромагнитном поле, равный , компенсируется тем, что энергия гравитационной массы системы увеличивается от значения до .

4. Связь с космологической постоянной

В [1] было получено соотношение, связывающее космологическую постоянную с 4-потенциалами полей, входящих в лагранжиан:

. (37)

Раскроем произведения 4-векторов:

, ,

, ,

здесь – массовый 4-ток, – зарядовый (электромагнитный) 4-ток, , , и обозначают векторные потенциалы поля ускорений, гравитационного и электромагнитного полей и поля давления, соответственно, и мы используем приближение специальной теории относительности, в котором , где , – скорость движения произвольной частицы тела.

Рассмотрим ситуацию в системе отсчёта , которая неподвижна относительно рассматриваемого тела. В скорости частиц равны , и вместо следует использовать фактор Лоренца . В результате (37) можно переписать так:

. (38)

В соотношении (38) космологическая постоянная имеет своё собственное значение для каждой частицы тела. Мы намереваемся проинтегрировать (38) по объёму тела в виде неподвижной сферы, заполненной движущимися частицами настолько плотно, насколько это возможно, с однородной плотностью массы и заряда по объёму сферы. В отсутствие общего вращения или направленных потоков вещества скорости частиц направлены хаотически в разные стороны. Тогда в результате интегрирования (38) вклад от векторных произведений, содержащих , будет равен нулю, так как будут равны нулю суммарные векторные потенциалы , , и внутри сферы. Поэтому интеграл от (38) по объёму будет выглядеть следующим образом:

.

Величина по нашему мнению представляет плотность энергии каждой частицы, а интеграл от этой плотности по объёму даёт некоторую постоянную энергию , связанную со всеми частицами системы. В правой части равенства находится интеграл, который мы уже вычисляли в (12). С учётом этого можно записать:

. (39)

Если сравнить (39) с (21), то видно, что величина является составной частью релятивистской энергии системы, и обозначает сумму компонент энергии частиц, находящихся под действием полей. В энергии имеются ещё компоненты энергии, связанные с самими полями, но согласно (23) для случая сферического тела все эти компоненты сокращаются друг с другом. Следовательно, можно считать, что для сферы , а также .

В (39) масса есть некоторая неизменная масса, которая обозначает суммарную массу частиц тела без учёта вклада от массы-энергии макроскопических полей, связанных с этим телом. Если всё вещество тела разделить по частицам и разнести друг от друга на бесконечность, то для покоящегося там вещества исчезнут электромагнитные и гравитационные поля, связанные с взаимодействием этих частиц друг с другом. Не будет и внутреннего давления от воздействия частиц друг на друга. В этом случае с учётом (38), записанного для отдельной частицы, масса будет состоять из суммарной массы всех частиц с учётом энергии собственных полей частиц, энергии их внутреннего давления и внутренней кинетической энергии. Такую массу мы рассматривали в [4] как суммарную массу частей тела, разнесённых друг от друга и находящихся на бесконечности при нуле абсолютной температуры. На бесконечности будет , , и тогда масса системы переходит в массу .

Из (29-30) следует, что масса системы меньше массы тела: , причём масса тела равна гравитационной массе . Так как масса постоянна и связана с космологической постоянной, а , то получается, что гравитационная масса системы в (29) может изменяться, когда в системе происходит изменение энергии поля давления или энергии электромагнитного и гравитационного полей. Из (28) находим, что , причём находится посередине между и . В результате соотношение для масс получается следующим:

. (40)

5. Обсуждение результатов

5.1. Массы

Согласно (40) в слабом поле инертная масса системы в виде сферы с частицами, с учётом энергии полей, внутреннего давления и внутренней кинетической энергии может быть описана либо по формуле (29), либо через массу системы из (39). Равенство означает сохранение энергии системы независимо от того, находятся ли части системы на бесконечности и почти не взаимодействуют друг с другом, либо эти части пришли в тесное соприкосновение и образовали связанную систему. Такое возможно в случае идеального сферического коллапса, когда из системы не происходит излучения и выбросов вещества на любых стадиях коллапса либо скучивания вещества. Данный вопрос мы рассматривали в [2] в связи с проблемой энергии при сферическом коллапсе сверхновой. Там мы объясняли возможность малого излучения энергии посредством нейтрино на основе того, что почти вся работа сил гравитации при сжатии вещества может уйти на увеличение кинетической энергии движения вещества звезды и на энергию давления, а также на создание внутренних градиентов давления и скоростей частиц.

Ранее в [5] мы получали отличающееся от (40) выражение для масс: . Мы можем объяснить это различием принятой калибровки космологической постоянной – в данной работе мы используем формулы, получающиеся при калибровке согласно [1], которая отличается от калибровки в [5]. Кроме этого, сейчас мы используем для анализа другую физическую систему в виде сферы, которая состоит из множества движущихся внутри сферы частиц, связанных вместе силой гравитации. В такой системе неизбежно возникает различие между массами и , как следствие радиального градиента фактора Лоренца внутри сферы, и как следствие различия между плотностью частиц в системах отсчёта частиц и плотностью с точки зрения системы отсчёта , связанной с центром масс системы. Масса в (40) по своему смыслу носит технический характер, так как определяется лишь математически путём умножения плотности на объём сферы. Заметим, что плотность входит в лагранжиан системы через 4-вектор плотности гравитационного (массового) тока в виде . Плотность входит также в уравнение движения точечной частицы и в уравнения поля в [1].

Согласно (29) и (40), масса больше массы . Это означает, что гравитационная масса системы всегда больше инертной массы системы, на величину половины модуля гравитационной и электромагнитной энергии полей за вычетом массы-энергии поверхностного давления.

В силу (40) гравитационная масса получается также больше, чем масса частей системы, разнесённых на бесконечность. Мы можем объяснить это следующим образом. Как известно, для шара модуль потенциальной энергии гравитационного поля равен суммарной работе по переносу вещества из бесконечности на поверхность и внутрь шара. При этом предполагается, что шар получается путём постепенного роста за счёт наслоения сферических оболочек по мере переноса вещества. Но кроме переноса вещества из бесконечности внутрь тела, что приводит к росту модуля потенциальной энергии гравитационного поля тела, сила гравитации выполняет и другие действия – по увеличению кинетической энергии частиц внутри тела, по увеличению энергии давления частиц друг на друга, а также по созданию градиента давления и градиента кинетической энергии частиц внутри тела. Все эти виды работ сил тяготения по образованию тела увеличивают массу тела от до . Основной вклад в увеличение гравитационной массы делает появляющееся движение – на бесконечности частицы были неподвижны, а в составе тела частицы движутся со скоростями .

Если учесть теорему вириала, связывающую половину модуля гравитационной и электромагнитной энергии с внутренней энергией тела, то у нас получается, что половина работы гравитационного и электромагнитного полей по образованию тела трансформируется во внутреннюю энергию тела. Полная энергия тела согласно (36) отрицательна и с её помощью (35), (39) и (29) можно записать так:

. (41)

Так как равна половине суммы гравитационной и электрической энергии, то отсюда видно, что половина работы гравитационного и электромагнитного полей по образованию тела трансформируется в увеличение массы от до значения .

Из теоремы вириала следует приблизительное равенство между модулем полной энергии системы (36), внутренней энергией тела , и энергией связи, если её определить в (41) как разность между энергией покоя для массы , и энергией покоя начального состояния на бесконечности . Однако в обычной трактовке энергии связи это не так, так как энергия связи определяется как разность между суммарной энергией отдельных частей системы, и энергией системы, собранной из этих частей в единое целое. Это определение для энергии связи даёт в нашем случае соотношение: , то есть в случае идеального сферического коллапса энергия системы в начале и в конце процесса одинакова и энергия связи равна нулю. Несмотря на равенство нулю энергии связи, система не распадается из-за того, что массы всегда притягиваются. При этом полная энергия (36) системы остаётся отрицательной.

Инвариантная масса системы является мерой инерции системы в целом и мерой релятивистской энергии системы. Это значит, что ускорение системы под действием сил должно зависеть от массы . Масса может быть вычислена как интеграл от плотности по объёму сферы. Гравитационная масса равна и может быть определена с помощью гравитационных экспериментов вблизи тела по эффекту гравитационного влияния на пробные тела. Согласно (31), при бесконечно большом радиусе тела масса сферической системы становится равной гравитационной массе тела . Соотношение (31) можно рассматривать как квадратное уравнение для определения гравитационной массы в зависимости от радиуса тела , от его электрического заряда и от суммарной массы неподвижных частей этого тела , когда эти части неподвижны и бесконечно удалены друг от друга:

.

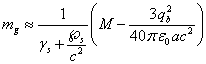5.2. Энергии и массы в общей теории относительности

В общей теории относительности (ОТО) масса системы считается меньше суммарной массы частей тела [6-7]. В ОТО имеется гравитационная масса системы с точки зрения удалённого наблюдателя, вычисляемая как объёмный интеграл от суммы , где – концентрация нуклонов вещества, – масса одного нуклона, – плотность массы внутренней энергии тела [8]. Рассматривается также инерциальная масса системы, вычисляемая через интеграл по объёму от времяподобной компоненты тензора энергии-импульса с последующим делением на квадрат скорости света, и приравниваемая к гравитационной массе на основе принципа эквивалентности. Соответственно для определения массы системы требуется знать либо не точно известную внутреннюю энергию тела, либо использовать тензор энергии-импульса, который однако принципиально не включает в себя энергию гравитационного поля. Последнее связано с тем, что в ОТО гравитационное поле понимается как метрическое поле, и описывается псевдотензором энергии-импульса. В результате вычисление релятивистской энергии и массы системы в ОТО оказывается существенно сложнее и сопряжено рядом оговорок. Например, для вычисления энергии требуется, чтобы координаты системы отсчёта на бесконечности переходили в координаты пространства Минковского.

Масса системы с учётом гравитационного и электромагнитного полей согласно [6] и [9] в ОТО в слабом поле в наших обозначениях в отношении массы, плотности и радиуса тела равна:

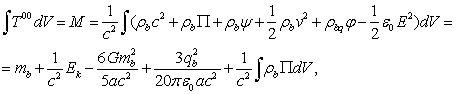(42)

где – тензор масс, превращающийся после умножения на квадрат скорости света в тензор энергии-импульса системы, масса тела , и есть плотность массы и заряда соответственно, – кинетическая энергия, – энергия давления на единицу массы, и рассматривается случай однородной плотности.

В [6] используется также инвариантная плотность массы , под которой понимается такая плотность массы, которая не меняется под действием давления или гравитационного поля. Предполагается, что именно такая инвариантная плотность входит в соотношение непрерывности в искривлённом пространстве-времени: , здесь – детерминант метрического тензора, есть 4-скорость. Заметим в этой связи, что в ковариантной теории гравитации соотношение непрерывности записывается не для , а для [1], причём может меняться и зависеть от любых факторов, включая давление и гравитационное поле.

В слабом поле для неподвижного тела в ОТО получают:

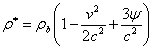. (43)

Предположим, что , как этого следует ожидать по теореме вириала. Если подставить (43) в (42), то получится соотношение: , так что масса системы больше, чем масса . После подстановки (43) в (42) для массы-энергии системы получится выражение, аналогичное представленным в [7] и [10] (в отличие от [6], в [10] есть инвариантная плотность, а обозначает плотность массы, соответствующую нашей плотности ).

Предположим, что масса системы в (42) согласно ОТО вычисляется точно и равна нашей массе системы в (31):

.

(44)

Из левой части (44) видно, что в ОТО гравитационная энергия входит в равенство с увеличенным весом по отношению к электромагнитной энергии, а в правой части обе энергии имеют одинаковый вес из-за подобия уравнений для полей. Это является следствием того, что в ОТО гравитационное поле заменяется эффектом от действия метрического поля метрического тензора. В результате метрика целиком содержит в себе гравитацию, а электромагнитное поле и давление остаются самостоятельными.

Если пренебречь вкладом в (44) и считать эту величину единицей, то с учётом выражения из (44) можно оценить энергию давления в ОТО:

.

В (42) масса системы в силу принципа эквивалентности полагается равной гравитационной массе. Это означает, что в ОТО заряженное тело увеличивает свою гравитационную массу. Исходя из изложенного, соотношение масс в ОТО следующее:

, (45)

где в первом приближении (здесь – число нуклонов в теле, – масса одного нуклона), ( – масса системы в виде тела и его полей, – внутренняя энергия в (36) ), масса равна гравитационной массе , масса определяется интегралом по объёму от инвариантной плотности (43), масса вычисляется интегрированием по объёму от плотности тела , а масса определена нами в (28) через и носит технический характер.

Если масса системы уменьшается от значения до , то возникает избыток энергии порядка . В ОТО коллапсирующая система обязана излучать эту энергию, так что идеальный сферический безизлучательный коллапс в ОТО невозможен [8].

Как видно, соотношение (45) для масс в ОТО существенно отличается от соотношения (40) для масс в ковариантной теории гравитации.

6. Заключение

Согласно (32) суммарная энергия гравитационного и электромагнитного полей в сумме с энергией поля ускорений и энергией поля давления внутри сферического тела равна нулю. При образовании тела происходит распределение энергий частиц тела в потенциалах всех четырёх полей. Это приводит к кинетической энергии движения частиц и к внутреннему давлению, к энергии частиц в гравитационном и электромагнитном поле.

Отличием нашего подхода от результатов ОТО оказывается то, что масса системы в ходе идеального сферического коллапса не меняется, . Действительно, если в начале идеального коллапса пространственная компонента суммарного 4-импульса падающих на центр масс частиц равна нулю ввиду сферической симметрии, то это же будет и в конце коллапса, так что масса-энергия, входящая во временную компоненту 4-импульса, может сохраняться. Однако гравитационная масса оказывается больше массы системы , так как меняется состояние частиц – они начинают двигаться внутри системы и оказывать давление друг на друга, кроме этого, частицы приобретают дополнительную энергию во внутренних полях.

Если в системе присутствует электромагнитное поле, то его действие в отношении массы противоположно действию гравитационного поля, то есть электромагнитное поле должно уменьшать гравитационную массу . Можно подсчитать, что если тело массой 1 кг и радиусом 1 метр зарядить до потенциала порядка 5 мегавольт, то это должно уменьшить гравитационную массу тела (без учёта массы добавленных зарядов) при взвешивании в поле тяжести на долю массы, что близко к современной точности измерения массы.

7. Список использованных источников

1. Федосин С.Г. О космологической постоянной, поле ускорения, поле давления и об энергии; Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy. vixra.org, 5 Mar 2014.

2. Fedosin S.G. The Integral Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based on the Pressure Field and Acceleration Field. American Journal of Modern Physics. Vol. 3, No. 4, 2014, pp. 152-167. doi: 10.11648/j.ajmp.20140304.12.

3. Fedosin S.G. 4/3 Problem for the Gravitational Field. Advances in Physics Theories and Applications, 2013, Vol. 23, P. 19 – 25.

4. Fedosin S.G. Energy, Momentum, Mass and Velocity of a Moving Body in the Light of Gravitomagnetic Theory. Canadian Journal of Physics, 2014, Vol. 92, no. 10, P. 1074 – 1081. http://dx.doi.org/10.1139/cjp-2013-0683.

5. Fedosin S.G. The Hamiltonian in Covariant Theory of Gravitation. Advances in Natural Science, 2012, Vol. 5, No. 4, P. 55 – 75.

6. Фок В.А. Теория пространства, времени и гравитации. 2-е издание. – М.: Физматгиз, 1961. – 568 с.

7. Papapetrou A. Equations of Motion in General Relativity. Proc. Phys. Soc. A, 64 (1951), P. 57.

8. Abhas Mitra. Why Gravitational Contraction Must be Accompanied by Emission of Radiation both in Newtonian and Einstein Gravity. Phys. Rev. D 74, 024010 (2006).

9. Ландау Л. Д., Лифшиц Е. М. Теория поля. – Издание 7-е, исправленное. – М.: Наука, 1988. – 512 с. – («Теоретическая физика», том II).

10. Chandrasekhar S. The Post-Newtonian Equations of Hydrodynamics in General Relativity. Ap. J. 142 (1965), P. 1488; Ap. J. 158 (1969), P. 45.

Источник: http://sergf.ru/re.htm

На научный сайт