In English

Jordan Journal of Physics. Vol. 9 (No. 1), pp. 1-30, (2016). http://journals.yu.edu.jo/jjp/Vol9No1Contents2016.html

О космологической постоянной, поле ускорения, поле давления и об энергии

Федосин Сергей Григорьевич

г. Пермь, Пермский край, Россия

E-mail: intelli@list.ru

Из условия однозначности релятивистской энергии осуществлена калибровка космологической постоянной. Это позволило получить соответствующее уравнение для метрики, определить обобщённый импульс, релятивистскую энергию, импульс и массу системы, а также выражения для кинетической и потенциальной энергий. Скалярная кривизна в произвольной точке системы получилась равной нулю, если в этой точке отсутствует вещество; для искривления пространства-времени достаточно наличия гравитационного или электромагнитного поля. С целью более точного описания движения системы в лагранжиан введены 4-потенциалы поля ускорений и поля давления, а также тензорные инварианты, определяющие плотность энергии этих полей. Структура используемого лагранжиана полностью симметрична по форме относительно 4-потенциалов гравитационного и электромагнитного поля, поля ускорений и поля давления. Тензоры энергии-импульса гравитационного поля, поля ускорений и поля давления получены в явном виде; каждый из них может быть выражен через соответствующий вектор напряжённости поля и дополнительный соленоидальный вектор. Дано описание уравнений поля ускорений и поля давления.

Ключевые слова: космологическая постоянная; 4-импульс; поле ускорений; поле давления; ковариантная теория гравитации.

About the cosmological constant, acceleration field, pressure field and energy

Sergey G. Fedosin

PO box 614088, Sviazeva str. 22-79, Perm, Russia

E-mail: intelli@list.ru

Based on the condition of relativistic energy uniqueness the calibration of the cosmological constant was performed. This allowed us to obtain the corresponding equation for the metric, to determine the generalized momentum, the relativistic energy, momentum and the mass of the system, as well as the expressions for the kinetic and potential energies. The scalar curvature at an arbitrary point of the system equaled zero, if the substance is absent at this point; the presence of a gravitational or electromagnetic field is enough for the space-time curvature. Four-potentials of the acceleration field and pressure field, as well as tensor invariants determining the energy density of these fields, were introduced into the Lagrangian in order to describe the system’s motion more precisely. The structure of the Lagrangian used is completely symmetrical in shape with respect to the 4-potentials of gravitational and electromagnetic fields and acceleration and pressure fields. The stress-energy tensors of the gravitational, acceleration and pressure fields are obtained in explicit form, each of them can be expressed through the corresponding field vector and additional solenoidal vector. A description of the equations of acceleration and pressure fields is provided.

Keywords: cosmological constant; 4-momentum; acceleration field; pressure field; covariant theory of gravitation.

PACS: 04.20.Fy, 04.40.-b, 11.10.Ef

1. Введение

Наиболее популярным применением космологической постоянной в общей теории относительности является то, что эта величина представляет собой проявление энергии вакуума [1-2]. Существует другой подход к интерпретации космологической постоянной, согласно которому эта величина представляет собой ту энергию, которой обладает любая уединённая частица в отсутствие внешних полей. В таком случае включение в лагранжиан кажется вполне уместным, поскольку лагранжиан состоит из таких компонент энергии, которые должны полностью описывать свойства любой системы, состоящей из частиц и полей.

Ранее в [3-4] мы применяли такую калибровку космологической постоянной, которая позволяла максимально упростить уравнение для нахождения метрики. Недостатком такого подхода было то, что релятивистская энергия системы определялась неоднозначно, поскольку в выражении для энергии присутствовала скалярная кривизна. В настоящей работе мы используем другую, универсальную калибровку космологической постоянной, пригодную для любой частицы и для системы частиц и полей. В результате энергия становится независимой как от скалярной кривизны, так и от космологической постоянной.

В общей теории относительности гравитационное поле как самостоятельный объект в лагранжиане отсутствует, а роль поля играет сама метрика. Известной проблемой, проистекающей из такого подхода, является то, что в общей теории относительности отсутствует тензор энергии-импульса гравитационного поля.

В отличие от этого в ковариантной теории гравитации используется лагранжиан, содержащий член с энергией частиц в гравитационном поле, и член с энергией гравитационного поля как такового. Тем самым гравитационное поле входит в лагранжиан таким же образом, что и электромагнитное поле. В таком случае метрика искривлённого пространства-времени используется для уточнения уравнений движения по сравнению со случаем такого слабого поля, который имеет своим пределом специальную теорию относительности. В пределе слабого поля используется упрощённая метрика, практически не зависящая от координат и времени. Этого оказывается достаточным во многих случаях, например, при описании движения планет. Однако в общем случае в сильных полях и при изучении тонких эффектов использование метрики становится необходимым.

Обратим внимание на то, что член с энергией частицы в лагранжиане может быть записан по-разному. В [5-6] этот член содержит инвариант , где является плотностью массы в сопутствующей системе отсчёта, есть 4-скорость. Соответствующая величина в [7] имеет вид . В [3] и [8] вместо этого используется произведение , где есть массовый 4-ток. В данной работе мы выбрали другую форму указанного инварианта – в виде . Причиной такого выбора является то, что мы полагаем массовый 4-ток наиболее полным представителем свойств частиц вещества, содержащим как плотность массы, так и 4-скорость. Массовый 4-ток можно рассматривать как 4-потенциал поля материи. Все остальные 4-векторы в лагранжиане являются 4-потенциалами соответствующих полей и записаны с ковариантным индексом. С помощью этих 4-потенциалов вычисляются тензорные инварианты, характеризующие в лагранжиане энергию соответствующего поля.

2. Действие и его вариации в принципе наименьшего действия

2.1. Функция действия

В качестве функции действия для непрерывно распределённой материи, находящейся в гравитационном и электромагнитном поле в произвольной системе отсчёта, используем следующее выражение:

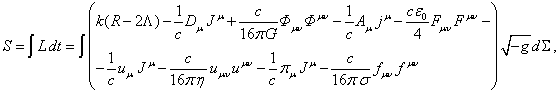
(1)

где – функция Лагранжа или лагранжиан,

– дифференциал координатного времени используемой системы отсчёта,

– некоторый коэффициент, подлежащий определению,

– скалярная кривизна,

– космологическая постоянная,

– 4-вектор гравитационного (массового) тока,

– плотность массы в сопутствующей частице системе отсчёта,

– 4-скорость точечной частицы, есть 4-смещение, а – интервал,

– скорость света, как мера скорости распространения электромагнитного и гравитационного взаимодействий,

– 4-потенциал гравитационного поля, описываемый через скалярный потенциал и векторный потенциал этого поля,

– гравитационная постоянная,

есть гравитационный тензор (тензор напряжённостей гравитационного поля),

– определение гравитационного тензора с контравариантными индексами с помощью метрического тензора ,

– 4-потенциал электромагнитного поля, задаваемый с помощью скалярного потенциала и векторного потенциала этого поля,

– 4-вектор электромагнитного (зарядового) тока,

– плотность заряда в сопутствующей частице системе отсчёта,

– электрическая постоянная,

– электромагнитный тензор (тензор напряжённостей электромагнитного поля),

– 4-скорость с ковариантным индексом, выражаемая через метрический тензор и 4-скорость с контравариантным индексом; удобно рассматривать локально усреднённую по системе частиц ковариантную 4-скорость как 4-потенциал поля ускорений , где и обозначают скалярный и векторный потенциалы, соответственно,

– тензор ускорений, вычисляемый через производные от 4-потенциала поля ускорений,

– некоторая функция координат и времени,

– 4-потенциал поля давления, состоящий из скалярного потенциала и векторного потенциала , – давление в сопутствующей частице системе отсчёта, отношение задаёт уравнение состояния вещества,

– тензор поля давления,

– некоторая функция координат и времени,

– инвариантный 4-объём, выражаемый через дифференциал временной координаты , через произведение дифференциалов пространственных координат, и через квадратный корень из детерминанта метрического тензора, взятого с отрицательным знаком.

Функция действия (1) состоит почти из тех же членов, что были рассмотрены в [3]. Различие заключается в том, что теперь член с плотностью энергии частиц мы заменяем на четыре члена, расположенные в конце (1). Естественно полагать, что каждый член входит в (1) относительно независимо от других членов, описывая состояние системы в том или ином отношении. Величина 4-потенцила множества элементов вещества или точечных частиц системы задаёт 4-поле скоростей системы, а произведение в (1) можно рассматривать как энергию взаимодействия массового тока с данным полем скоростей. Аналогично есть 4-потенциал гравитационного поля, а произведение определяет энергию взаимодействия массового тока с гравитационным полем. Электромагнитное поле задаётся 4-потенциалом , источником поля является электромагнитный ток , а произведение этих величин есть плотность энергии взаимодействия движущегося заряженного элемента вещества с электромагнитным полем. Инвариант гравитационного поля в виде тензорного произведения связан с энергией гравитационного поля и может быть не равен нулю даже за пределами тел. То же самое имеет место и для инварианта электромагнитного поля . Это следует из свойства дальнодействия указанных полей. Что касается поля скоростей , то это поле естественно применять для описания движения частиц вещества. Соответственно, поле ускорений в виде тензора , и энергия этого поля, связанная с инвариантом , относятся к ускоренному движению частиц и вычисляются для тех пространственных точек внутри объёма системы, где находится вещество.

Последние два члена в (1) связаны с давлением в веществе, причём произведение характеризует взаимодействие поля давления с массовым 4-током, а инвариант является частью тензора энергии-импульса поля давления.

Отметим ещё разницу 4-токов и – в массовый ток делают вклад все частицы системы, а в электромагнитный ток только заряженные частицы. Отсюда вытекает различие действия полей – гравитационное поле действует на любые частицы, а электромагнитное поле – только на заряженные частицы либо на вещество, в котором поле своим действием может в достаточной степени разделить заряды противоположного знака друг от друга. Поле скоростей , как и массовый ток , связано со всеми частицами системы. Поэтому произведение описывает ту часть энергии частиц, которая останется, если каким-либо образом «выключить» в рассматриваемой системе все макроскопические гравитационные и электромагнитные поля и убрать давление, не изменив при этом ни поле скоростей , ни массовый ток .

2. 2. Вариации функции действия

Будем варьировать функцию действия в (1) почленно, тогда общая вариация будет суммой вариаций отдельных членов. Всего в (1) внутри интеграла находятся 9 членов. Если величину считать константой (космологической постоянной), то согласно [7-9], вариация первого члена в функции действия (1) будет равна:

, (2)

где есть тензор Риччи,

– вариация метрического тензора.

Согласно [3] вариации членов 2 и 3 в функции действия следующие:

, (3)

, (4)

где представляет собой вариацию координат, вследствие которой возникает вариация массового 4-тока и вариация электромагнитного тока ,

– вариация 4-потенциала гравитационного поля,

и через обозначен тензор энергии-импульса гравитационного поля:

. (5)

Вариации членов 4 и 5 в функции действия согласно [6-7], [10] таковы:

, (6)

, (7)

где – вариация 4-потенциала электромагнитного поля,

и через обозначен тензор плотности энергии-импульса электромагнитного поля:

. (8)

Вариации остальных членов в функции действия (1) определяются в Приложениях A-D и имеют следующий вид:

, (9)

, (10)

где – вариация 4-потенциала поля ускорений,

и через обозначен тензор энергии-импульса поля ускорений:

. (11)

(12)

, (13)

где тензор энергии-импульса поля давления

. (14)

В вариации (10) с целью упрощения рассматривается тот частный случай, когда является константой, которая по определению не варьируется. По своему смыслу зависит от параметров рассматриваемой системы и потому может иметь разные значения. То же самое следует сказать и про .

3. Уравнения движения поля, частиц и метрики

В соответствии с принципом наименьшего действия, следует сложить все вариации отдельных членов функции действия и приравнять результат к нулю. Сумма вариаций (2), (3), (4), (6), (7), (9), (10), (12) и (13) даёт общую вариацию функции действия:

. (15)

3.1. Уравнения поля

При движении системы в пространстве-времени вариации , , , , и не обращаются в нуль, так как предполагается, что это может происходить лишь в начале и в конце процесса, когда точно фиксируются условия движения. Следовательно, должна обращаться в нуль сумма членов, стоящая перед каждой из этих вариаций. Например, вариация встречается лишь в согласно (6) и в из (7), тогда из (15) следует:

.

Отсюда получается уравнение электромагнитного поля с источниками поля:

или , (16)

где – магнитная постоянная.

Второе уравнение электромагнитного поля вытекает из определения электромагнитного тензора через электромагнитный 4-потенциал, и из свойства антисимметричности этого тензора:

или , (17)

где есть символ Леви-Чивиты или совершенно антисимметричный единичный тензор.

Вариация присутствует только в (3) и в (4), так что согласно (15) должно быть:

.

Из этого следует уравнение гравитационного поля с источниками:

или . (18)

Если учесть определение гравитационного тензора: , и взять ковариантную производную данного тензора с последующей циклической перестановкой индексов, то следующие уравнения выполняются тождественно:

или . (19)

Уравнение (19) без источников, и уравнение (18) с источниками задают полный комплект уравнений гравитационного поля в ковариантной теории гравитации.

Рассмотрим правило для разности вторых ковариантных производных в отношении ковариантной производной от электромагнитного 4-потенциала :

С учётом этого правила применение ковариантной производной к (16) и (18) даёт следующее:

.

.

Отсюда видно, что в искривлённом пространстве-времени тензоры поля и приводят к дивергенции соответствующих 4-токов. Смешанный тензор кривизны и тензор Риччи равны нулю лишь в пространстве Минковского. В этом случае ковариантные производные переходят в частные производные и получаются уравнения непрерывности электромагнитного и гравитационного 4-токов в специальной теории относительности:

, . (20)

Заметим, что с целью упрощения уравнений для 4-потенциалов полей используются выражения, называемые калибровочными условиями:

, . (21)

3.2. Уравнения поля ускорений

Вариация 4-потенциала имеется в (9) и в (10), поэтому согласно (15) должно быть:

.

, или . (22)

Если сравнить (18) и (22), то получается, что наличие 4-вектора массового тока не только приводит к появлению пространственно-временных градиентов гравитационного поля в рассматриваемой системе, но и в общем случае сопровождается изменениями во времени либо градиентами 4-скорости у частиц, составляющих данную систему. При этом ковариантные 4-скорости всего множества частиц образует поле скоростей , производные от которого задают поле ускорений и описываются тензором . В качестве примера системы, где это хорошо видно, можно взять вращающееся частично заряженное сжимающееся газово-пылевое облако, удерживаемое гравитацией. Упорядоченное поле ускорений возникает в облаке за счёт ускорения вращения и содержит центростремительное и тангенциальное ускорения.

Вследствие своего определения в виде 4-ротора от , для тензора ускорений справедливы следующие соотношения:

или . (23)

Как видно, структура уравнений (22) и (23) для поля ускорений подобна структуре уравнений для напряжённостей гравитационного и электромагнитного поля.

В локальной геодезической системе отсчёта производные от метрического тензора и тензор кривизны становятся равными нулю, ковариантная производная становится частной производной, а уравнения принимают наиболее простой вид. Перейдём в такую систему отсчёта и применим к (23) производную , а для первого и третьего членов используем замену с помощью (22):

.

Если применить определение к 4-даламбертиану , где есть оператор Д’Аламбера, то это даёт:

.

Сравнивая с предыдущим выражением, находим волновое уравнение для 4-потенциала :

.

С другой стороны, из (22) после опускания индексов у тензора ускорений имеем:

.

Сравнение этого равенства с выражением для приводит к следующему:

,

где является некоторой постоянной.

В произвольной системе отсчёта следует уточнить найденные выражения, так как в отличие от перестановок частных производных, при перестановке ковариантных производных от последовательности к последовательности возникают дополнительные члены. В частности, если использовать соотношение:

, (24)

то после подстановки в (22) выражения волновое уравнение можно записать так:

. (25)

В искривлённом пространстве оператор по разному действует на скаляры, 4-векторы и 4-тензоры, и как правило содержит тензор Риччи. Благодаря условию (24), в (25) тензор Риччи отсутствует, но остаются члены с символами Кристоффеля.

Соотношение (24) является калибровочным условием для 4-потенциала , подобным по смыслу калибровочным условиям (21) для электромагнитного и гравитационного 4-потенциалов. Как (24), так и (25) будут справедливы при условии, что .

В Приложении E будет показано, что тензор ускорений имеет в своём составе векторные компоненты и , из которых согласно (E6) можно построить 4-вектор ускорения частиц.

3.3. Уравнения поля давления

Для получения уравнений поля давления необходимо в (15) выбрать те члены, которые содержат вариацию . Эта вариация присутствует в (12) и в (13), что даёт следующее:

.

или . (26)

Из (26) следует, что массовый 4-ток генерирует в телах поле давления, описываемое тензором давлений . Для этого тензора справедливы те же самые соотношения, что и для тензоров других полей:

или . (27)

Из (26) следует волновое уравнение для 4-потенциала поля давления:

. (28)

Уравнение (28) будет справедливым при наличии условия калибровки 4-потенциала давления:

. (29)

Свойства поля давления описываются в Приложении F, где показывается, что тензор давления содержит две векторные компоненты и , которые определяют энергию и силу давления, а также поток энергии давления..

3.4. Уравнения движения частиц

Вариация , приводящая к уравнениям движения частиц, присутствует в (3), (6), (9) и (12). Для этой вариации из (15) следует:

,

.

Левую часть равенства можно преобразовать, учитывая выражение для 4-вектора плотности массового тока, и определение тензора ускорений :

. (30)

Мы использовали соотношение , вытекающее из равенства , а также оператор производной по собственному времени , где – символ 4-дифференциала в искривлённом пространстве-времени, – собственное время [11].

С учётом (30) уравнение движения приобретает вид:

. (31)

Отметим, что уравнения движения поля (16) – (19), поля ускорений (22) и (23), поля давления (26) и (27), и уравнение движения частиц (31) являются дифференциальными уравнениями, справедливыми в любом точечном объёме пространства-времени рассматриваемой системы. В частности, если в некотором точечном объёме плотность массы равна нулю, то все члены в (31) будут равны нулю.

Величина в левой части (31) есть 4-ускорение точечной частицы, причём дифференциал собственного времени связан с интервалом соотношением: , и выполняется соотношение: . Первые два члена в правой части (31) являются плотностями гравитационной и электромагнитной 4-сил, соответственно. Можно показать (смотри например, [3], [12]), что для 4-сил, действующих со стороны полей на частицу, имеются альтернативные выражения через тензоры энергии-импульса (5) и (8):

, . (32)

Подобно этому, левая часть (31) с учётом (30) выражается через тензор энергии-импульса поля ускорений (11):

. (33)

Для доказательства (33) следует раскрыть тензор с помощью определения (11), применить ковариантную производную к тензорным произведениям, а затем использовать уравнения (22) и (23). Из (33) видно, что 4-ускорение частицы может быть описано с помощью либо тензора ускорений либо тензора .

Для поля давления можно записать так же, как и для других полей:

. (34)

В (34) 4-сила давления связывается с ковариантной производной от тензора энергии-импульса поля давления.

Из (31) – (34) следует:

или . (35)

В пространстве Минковского , где , 4-дифферециалы переходят в обычные дифференциалы ,

, и уравнение движения (31) распадается на скалярное и векторное уравнения, причём в векторном уравнении содержится полная гравитационная сила с учётом поля кручения, электромагнитная сила Лоренца и сила давления:

, (36)

, (37)

где – скорость движения точечной частицы, – напряжённость гравитационного поля, – плотность заряда, – напряжённость электрического поля, – напряжённость поля давления, – вектор поля кручения, – индукция магнитного поля, – соленоидальный вектор поля давления.

Если за время плотность не меняется, её можно внести под знак производной. Тогда в левой части (36) появляется величина , где есть плотность релятивистской энергии.

Аналогично в левой части (37) появляется величина , где является плотностью массового 3-тока.

3.5. Уравнения для метрики

Рассмотрим вариации действия (2), (3), (4), (6), (7), (9), (10), (12) и (13), в которых содержится вариация . Сумма всех членов в (15) с вариацией должна равняться нулю:

.

(38)

Уравнение для метрики (38) позволяет определить метрический тензор по известным величинам, характеризующим вещество и поле. Если взять в данном уравнении ковариантную производную , то левая часть уравнения при условии обращается в нуль, и с учётом (35) остаётся следующее:

,

, (39)

где есть некоторая функция от времени и координат и скалярный инвариант относительно преобразований координат.

Если раскрыть скалярные произведения векторов с помощью выражений:

, , (40)

.

то (39) можно записать так:

. (41)

Если вещество и заряды системы разделить на малые части и разнести на бесконечность, то там потенциалы внешних полей обнуляются, так как межчастичное взаимодействие стремится к нулю, и при остаётся следующее:

. (42)

Следовательно, связано с собственными скалярными потенциалами частицы и , плотностью массы и давлением в частице, находящейся на бесконечности. Выражение (41) можно рассматривать как дифференциальный закон сохранения массы-энергии: чем больше скорость движения точечной частицы, чем больше потенциалы гравитационного поля и , потенциалы электромагнитного поля и , потенциалы поля давления и , тем сильнее отличается плотность массы от своего значения на бесконечности. Если, например, точечная частица попадает в гравитационное поле системы частиц с потенциалом , то изменение энергии частицы описывается членом . Согласно (41), такое изменение энергии может быть скомпенсировано изменением энергии покоя частицы за счёт изменения . Поскольку потенциал гравитационного поля всегда отрицателен, то плотность массы и давление внутри точечной частицы должны увеличиваться за счёт потенциала поля.

Такое возможно, если вспомнить, что вся процедура вывода уравнений движения частиц, поля и метрики из принципа наименьшего действия была основана на том, что масса и заряд элемента вещества при варьировании координат остаются постоянными, несмотря на изменение плотности заряда, плотности вещества и его объёма [7]. Если масса простейшей системы в виде точечной частицы и связанных с ней полей пропорциональна , то согласно (41) масса такой системы остаётся неизменной, несмотря на изменение полей, плотности массы и давления . Сохранение массы-энергии каждой частицы с учётом массы-энергии полей приводит к сохранению массы-энергии произвольной системы из множества частиц и окружающих их полей. Напомним, что в этой статье речь идёт о непрерывно распределённой материи, так что каждая точечная частица или элемент этой материи может иметь свою собственную плотность массы и своё значение .

Вернёмся теперь к (38) и возьмём свёртку тензоров путём умножения уравнения на , с учётом соотношения , затем разделим всё на 2:

. (43)

где – скалярная кривизна, и было учтено, что свёртки тензоров , , и равны нулю.

В случае если бы космологическая постоянная была известна, из (43) можно было бы найти скалярную кривизну .

С целью упрощения уравнения (38) в [3] и [4] была принята калибровка для , при которой, если дополнительно ещё учесть член с давлением , выполнялось равенство следующего вида:

. (44)

В калибровке (44) уравнение для метрики (38) при условии, что , где есть константа порядка единицы, приобретает следующий вид:

. (45)

Заметим, что если исключить из правой части (45) тензор энергии-импульса гравитационного поля , заменить тензор на тензор энергии-импульса вещества в виде , и пренебречь ещё тензором , то при получится типичное выражение уравнения для метрики, используемое в общей теории относительности:

. (46)

Уравнение для метрики (38) и выражение (39) должны выполняться в ковариантной теории гравитации при условии, что . Если в (39) убрать член , то получается выражение, пригодное для использования и в общей теории относительности. В этом случае, учитывая, что , вместо (39) находим:

. (47)

Если в (47) приравнять к нулю член с энергией частиц в электромагнитном поле (в случае, когда это поле равно нулю), то сумма плотности энергии покоя и энергии давления каждой незаряженной точечной частицы должна быть неизменной. Отсюда следует, что изменение давления должно сопровождаться изменением плотности массы. Если же в системе присутствует электромагнитное поле с 4-потенциалом , действующее на порождающие их 4-токи , то в общем случае должна быть обратная корреляция энергии покоя, энергии давления и энергии зарядов в электромагнитном поле.

Действительно, в общей теории относительности плотность массы задаёт плотность энергии покоя и метрику пространства-времени, которая олицетворяет гравитационное поле. В (47) энергия зарядов в электромагнитном поле задаётся членом , и плотность массы, а значит и метрика связаны с этой энергией при постоянной величине . С другой стороны, метрика находится из (46). Следовательно, появление электромагнитного поля влияет на метрику в двух соотношениях – в (47) меняется плотность массы и соответствующая ей метрика, а также в уравнении для метрики (46) меняется тензор энергии-импульса вещества , при этом вклад в метрику делает и тензор энергии-импульса электромагнитного поля .

Со всем этим связан известный парадокс общей теории относительности – электромагнитное поле влияет на плотность, на массу тел как источник гравитации, и на метрику, в то же время само гравитационное поле (то есть метрика) никак не влияет на электрические заряды тел, являющиеся источниками электромагнитного поля. Тем самым гравитационное и электромагнитное поля оказываются неравноценными друг другу, несмотря на подобие уравнений поля и одинаковый характер дальнодействия. Выше мы указывали ещё на то обстоятельство, что массовый 4-ток приводит к градиентам гравитационного поля, а добавка заряда к этому массовому току порождает дополнительный – электромагнитный (зарядовый) 4-ток и соответствующие градиенты электромагнитного поля, зависящие от знака заряда. Отсюда видно, что гравитационное поле выглядит как фундаментальное, базовое и неуничтожимое поле, а электромагнитное поле проявляется как некоторая надстройка и как следствие разделения зарядов в исходно нейтральном веществе.

Если считать справедливым (44), то из сравнения с (39) видно, что должно выполняться равенство: . Таким образом в случае, когда рассматривается как космологическая постоянная, можно с её помощью добиться упрощения уравнения для метрики (38) и привести его к форме (45). При этом соотношение (39) является симметричным в отношении вклада гравитационного и электромагнитного полей в плотность, несмотря на различие полей. Напомним, что в уравнении движения (31) оба поля также делают симметричный вклад в 4-ускорение точечного заряда.

Хотя калибровка для в виде (44) и кажется наиболее простой и упрощает некоторые уравнения, в разделе 7 будет показана необходимость и удобство другой калибровки.

4. Гамильтониан

В этом и следующем разделе мы опираемся на стандартный подход аналитической механики. В качестве координат удобно выбрать набор из декартовых координат: , , , .

Рассмотрим действие (1) и выразим из него лагранжиан:

(48)

Интегрирование в (48) осуществляется по бесконечному трёхмерному объёму пространства и по всем материальным частицам системы. Мы будем считать, что скалярная кривизна зависит от метрического тензора, а метрический тензор , тензоры полей , , , , плотность , плотность заряда и давление являются функциями от координат и не зависят от индивидуальных скоростей частиц. Тогда в общем виде лагранжиан (48) зависит от координат, а также от 4-потенциала давления и от 4-потенциалов гравитационного и электромагнитного полей и .

Разобьем первый интеграл в лагранжиане (48) на сумму частных интегралов, каждый из которых описывает состояние одной из множества частиц системы. Учтём ещё, что лагранжиан зависит от трёхмерных скоростей частиц , где задаёт номер частицы, причём скорость какой-либо частицы входит только в один соответствующий частный интеграл. Если через обозначить второй интеграл в (48) , связанный с энергиями полей внутри и за пределами физической системы и не зависящий от скоростей частиц, то для лагранжиана можно записать:

,

где есть частный лагранжиан произвольной частицы.

Введём теперь гамильтониан системы как функцию от обобщённых трёхмерных импульсов частиц: . Под обобщённым импульсом системы будем понимать сумму обобщённых импульсов всего множества частиц:

.

Для отыскания гамильтониана применяем преобразования Лежандра для системы частиц:

, (49)

при условии, что

. (50)

Равенство в (50) даёт определение обобщённого импульса , при этом видно, что для произвольной частицы её обобщённый импульс равен . С другой стороны, равенства позволяют выразить скорость произвольной частицы через её обобщённый импульс . Далее можно подставить эти скорости в (49) и определить только через .

Для того, чтобы найти в (50), в каждом частном лагранжиане следует выразить и через скорость и интервал :

, , (51)

при этом , и мы введём обозначение , где четырёхмерная величина не является настоящим 4-вектором. С учётом определения 4-потенциала поля ускорений , для каждой частицы имеем:

. (52)

В (48) элемент объёма системы в каждом частном интеграле можно выразить через элемент объёма в сопутствующей частице системе отсчёта следующим образом:

. (53)

Из этой формулы в пределе слабого поля в пространстве Минковского, когда , следует уменьшение объёма движущейся частицы по сравнению с объёмом покоящейся частицы. Учитывая, что , где есть собственное время в системе отсчёта частицы, из (53) вытекает равенство четырёхмерных объёмов в разных системах отсчёта:

.

Данное равенство отражает тот факт, что четырёхмерный объём является четырёхмерным инвариантом.

При указанных выше условиях (40), (51), (52) и (53) для лагранжиана (48) можно записать:

(54)

а также после частичного интегрирования по объёму:

(55)

где есть масса произвольной частицы, – заряд частицы. В (55) скалярные и векторные потенциалы полей усреднены по объёму частицы, то есть являются эффективными потенциалами в месте расположения частицы.

При операциях с 3-векторами удобно записывать вектора в виде компонент или проекций на пространственные оси системы координат, используя, например, вместо скорости величину , где . Тогда , , , а производную по скорости можно представить так: . Для гравитационного векторного потенциала имеем в частности: .

С учётом этого из (55) и (50) находим:

, . (56)

Отсюда для суммы скалярных произведений трёхмерных векторов находим путём суммирования по индексу :

. (57)

Из (49) с учётом (55) и (57) имеем:

(58)

В (58) гамильтониан содержит скалярную кривизну и космологическую постоянную . Как будет показано далее в разделе 6 об энергии, данный гамильтониан представляет собой релятивистскую энергию системы. Для завершения картины можно ещё выразить величину в (58) через обобщённый импульс . Такая процедура была описана нами в [4].

Для непрерывно распределённого вещества массы и заряды частиц в (58) можно выразить через соответствующие интегралы: , . Учитывая ещё (53), в которое можно подставить выражение , где обозначает временную компоненту 4-скорости произвольной частицы, из (58) находим:

(59)

Если в (58) выразить массы и заряды частиц через плотность массы и плотность заряда с точки зрения произвольной системы отсчёта , то (58) можно представить так:

(60)

Мы получили гамильтониан в произвольной системе отсчёта , причём в (59) используются плотности в сопутствующих частицам системах отсчёта, а в (60) – такие плотности частиц, какие они кажутся в .

5. Уравнения Гамильтона

Считая, что гамильтониан зависит обобщённых трёхмерных импульсов частиц : , а лагранжиан от трёхмерной скорости частиц : , где есть трёхмерный радиус-вектор частицы с номером , возьмём дифференциалы от и , а также дифференциалы от обеих сторон равенства (49):

(61)

(62)

. (63)

Подставляя (61) и (62) в (63), находим:

, , , ,

, , . (64)

Последнее равенство в (64) приводит к (50) и даёт выражение (56) для обобщённого импульса произвольной частицы системы в явном виде.

Применим теперь принцип наименьшего действия к лагранжиану вида , приравнивая вариацию действия к нулю при движении частицы от временной точки до временной точки .

(65)

В (65) предполагалось, что вариация по времени равна нулю: . Частные производные при вариациях , и приводят к уравнениям поля (16), (18) и (26). Если учесть определение скорости во втором члене внутри интеграла (65): , то для этого члена интеграл берётся по частям. Тогда для первого и второго членов в интеграле (65) имеем:

. (66)

При варьирования действия вариации равны нулю только в начале и в конце движения, то есть при и . Поэтому для равенства нулю вариации необходимо, чтобы скобка внутри интеграла (66) равнялась нулю. Это приводит к хорошо известным уравнениям движения Лагранжа:

. (67)

Согласно (64), , а также . Подставим это в (67):

. (68)

Уравнение (68) совместно с уравнением из (64)

представляют собой стандартные уравнения Гамильтона, описывающие движение произвольной частицы системы в гравитационном и электромагнитном полях и в поле давления. Согласно (68), скорость изменения обобщённого импульса частицы по координатному времени равна обобщённой силе, находимой как градиент по координатам частицы от релятивистской энергии системы, взятой с обратным знаком. Указанные уравнения широко применяются не только в общей теории относительности, но и в других областях теоретической физики. Мы проверяли эти уравнения в [4] в рамках ковариантной теории гравитации путём непосредственной подстановки гамильтониана.

6. Энергия системы

Рассмотрим замкнутую систему, находящуюся в состоянии некоторого стационарного движения. Примером может быть вращающийся вокруг собственного центра инерции заряженный шар, который совместно со своими гравитационными и электромагнитными полями и внутренним давлением образует рассматриваемую систему. В такой системе должна сохраняться энергия, как следствие отсутствия потерь энергии в окружающую среду, и с учётом однородности времени, то есть равнозначности моментов времени для состояния системы.

Лагранжиан системы с учётом энергии полей имеет вид (55). Благодаря стационарности движения можно считать, что в объёме системы метрический тензор , скалярная кривизна , 4-потенциалы полей , и давления не зависят от времени. Но поскольку любая точечная частица движется вместе с шаром, то изменяется её положение и скорость, задаваемые соответственно радиусом-вектором и скоростью . Мы можем считать, что лагранжиан системы не зависит явно от времени и является функцией вида: . Возьмём теперь производную по времени от лагранжиана, как это делается, например в [13], но не для одной, а для множества частиц, и применим (67):

.

Величина в скобках не зависит от времени и является постоянной. Отсюда следует определение релятивистской энергии как сохраняющейся величины для системы при стационарном движении:

. (69)

Учитывая (64) и (49), находим следующее:

. (70)

Получается, что релятивистская энергия может быть выражена в ковариантной форме, поскольку согласно (70) формула для энергии совпадает с формулой для гамильтониана в (49).

Для вычисления релятивистской энергии системы с непрерывно распределённым по объёму веществом удобно перейти от массы и заряда частицы к соответствующим плотностям внутри частицы. В согласии с (59) имеем:

(71)

С помощью выражения (71) можно найти инвариантную энергию системы, для чего следует перейти в систему отсчёта центра инерции и вычислить интеграл. Кроме этого, при известной скорости движения центра масс системы в произвольной системе отсчёта можно вычислить импульс системы в . Это можно уточнить следующим образом. Определим инвариантную массу системы с учётом массы-энергии полей соотношением: , где – скорость света, как мера скорости распространения электромагнитного и гравитационного взаимодействий. Если 4-перемещение в имеет вид: , то для 4-скорости движения системы в можно записать: . 4-вектор определяет 4-импульс, в котором содержится релятивистская энергия , и релятивистский импульс . Отсюда следует формула для определения импульса через энергию: , и соответственно для 4-импульса: .

В системе отсчёта , в которой система покоится, , , , и тогда , а также , то есть в 4-импульсе в системе отсчёта только временная компонента является ненулевой.

Если умножить 4-импульс на скорость света, получится 4-вектор вида , временной компонентой которого релятивистская энергия, равная по величине гамильтониану. Тем самым мы приходим к 4-вектору, который в [4] был назван 4-вектором гамильтониана.

7. Калибровка космологической константы и вытекающие следствия

Произведём преобразования и подставим (43) и (39) в (71):

(72)

Если выбрать условие для космологической константы в виде:

, (73)

то релятивистская энергия (72) определяется однозначно, так как исчезает зависимость от постоянных величин и :

(74)

Напомним, что величины и могут иметь свои собственные значения для каждой отдельной частицы материи. Но при условии (73) выражение для релятивистской энергии (74) становится универсальным для любой частицы, находящейся в произвольной системе из частиц и их полей.

Из (73) и (39) следует равенство:

. (75)

Чтобы оценить величину космологической постоянной , удобно разделить всё вещество системы на малые части, разнести их друг от друга на бесконечность и оставить там неподвижными. Тогда векторные потенциалы полей и давления обнуляются и остаётся соотношение: . Отсюда следует, что , так же как и в (42), связано с энергией покоя , с энергией давления и с собственной энергией полей рассматриваемой системы.

Если в некотором объёме нет частиц и плотность массы и плотность заряда равны нулю, то в этом объёме ещё остаётся релятивистская энергия внешних полей:

. (76)

Из (74) можно выразить энергию малого по размерам и массе покоящегося тела. Будем для упрощения считать, что тело не вращается как целое и внутри него движение вещества и зарядов отсутствует (идеальное твёрдое тело без собственного магнитного поля и поля кручения). При таких условиях координатное время системы становится приблизительно равным собственному времени тела: . Так как интервал , то мы получим: . Так как у любой части тела нет пространственных перемещений, можно записать:

, .

С учётом этого из (74) имеем:

(77)

В пределе слабого поля в (77) можно положить , . Тензорное произведение в отсутствие движения вещества внутри идеального твёрдого тела обращается в нуль. Используя (F5) и (F6), можно записать:

, , .

Кроме этого, в [4] было найдено, что в слабом поле для неподвижного тела в форме шара с однородной плотностью массы и заряда для собственных полей тела выполняются соотношения:

, ,

,

. (78)

Согласно (78), потенциальная энергия вещества шара в собственном гравитационном поле, связанная со скалярным потенциалом , в два раза больше, чем потенциальная энергия, связанная с напряжённостью поля . Это же справедливо и для электромагнитного поля с потенциалом и напряжённостью , как в случае однородного расположения зарядов в объёме шара, так и при расположении их только на поверхности. Подстановка (78) в (77) даёт в рамках специальной теории относительности инвариантную энергию системы в виде неподвижного твёрдого сферического тела с однородной плотностью массы и заряда с учётом энергии собственных потенциальных полей:

(79)

Данный расчёт очевидно не полон, так как в реальности внутри любого тела содержатся частицы, которые не могут быть неподвижными так же, как и само тело. Поэтому в (79) в дополнение к давлению и его градиенту внутри тела необходимо добавить ещё кинетическую энергию движения всех тех частиц, которые образуют тело.

7.1. Метрика

Подставляя (75) и (39) в (43), находим выражение для скалярной кривизны :

, (80)

причём , где есть константа порядка единицы.

Как видно, скалярная кривизна будет равна нулю во всём пространстве за пределами тела. Равенство не означает однако, что пространство-время плоское как в специальной теории относительности, поскольку кривизна пространства-времени определяется компонентами тензора кривизны Римана.

Подставим теперь (75) в уравнение для метрики (38):

(81)

что можно записать с помощью (39) ещё так:

. (82)

Если взять ковариантную производную от (82), то левая часть уравнения обратится в нуль в силу свойства находящегося здесь тензора Эйнштейна. Правая часть с учётом уравнения движения (35) и при условии, что метрический тензор при ковариантном дифференцировании ведёт себя как константа, а есть постоянная, также обращается в нуль.

В (81) можно использовать (80), чтобы заменить скалярную кривизну:

(83)

Если сложить (81) и (83) и результат разделить на 2, получится следующее уравнение для метрики:

, (84)

причём с учётом (80) , согласно (35) , а также как свойство тензора Эйнштейна.

В пустом пространстве тензор кривизны согласно (84) зависит только от тензоров энергии-импульса гравитационного и электромагнитного полей и , так что эти поля меняют кривизну пространства-времени за пределами тел. Обратим внимание на то, что в уравнении (84) отсутствует и космологическая постоянная и тензорные произведения типа . Это обстоятельство существенно облегчает нахождение компонент метрического тензора.

Если сравнить (84) с уравнением Эйнштейна (46), то обнаружатся два основных отличия – в правой части (84) присутствуют тензоры энергии-импульса , и , кроме этого, коэффициент перед скалярной кривизной в два раза меньше, чем в (46).

8. Компоненты энергии

В механике Ньютона известны соотношения для лагранжиана и полной энергии: , , где обозначает кинетическую энергию, зависящую только от скорости, а – потенциальную энергию системы, зависящую как от координат, так и от скорости. В релятивистской физике вместо отдельных скалярных функций и трёхмерных векторов используются 4-векторы и 4-тензоры, в которых скалярные функции и трёхмерные векторы объединяются в одно целое. Кроме этого, вместо отрицательной полной энергии используется обычно положительная релятивистская энергия . Если энергию мы уже определили в (74), то для лагранжиана (54) следует дополнительно сделать замену скалярной кривизны с помощью (80), и космологической константы с помощью (75). Это с учётом соотношения даёт следующее:

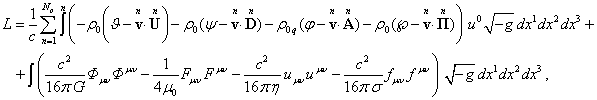
(85)

Вычисляя энергию , связанную с четырёхмерным движением, как полусумму релятивистской энергии (74) и лагранжиана (85), находим:

(86)

где индекс задаёт компоненты 3-вектора скорости частицы с номером .

Если в (57) заменить массы и заряды соответствующими интегралами в виде: , , и ещё преобразовать элементы объёма в виде , то получится соотношение: . Как видно, кинетическая энергия системы обращается в нуль только тогда, когда одновременно скорости движения всех частиц системы обращаются в нуль.

Определим потенциальную энергию как полуразность релятивистской энергии (74) и лагранжиана (85):

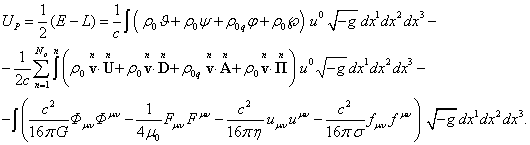
(87)

Для твёрдого тела в пределе специальной теории относительности, когда , , , , выражение для кинетической энергии (86) системы будет следующим:

(88)

Основная часть кинетической энергии пропорциональна квадрату скорости, при этом в данную часть энергии делают вклад векторные потенциалы всех полей, в том числе поле скоростей и поле давления.

Для потенциальной энергии (87) твёрдого тела в пределе специальной теории относительности тензорное произведение согласно (E8) стремится к нулю. Учтём ещё значения других тензорных произведений:

, , .

Это даёт:

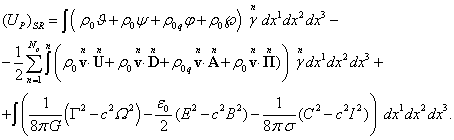
Потенциальная энергия зависит в том числе и от скорости. Если же для всех материальных точек системы, то остаётся потенциальная энергия системы с учётом энергии полей:

(89)

В отсутствие внешних полей и внутренних движений в неподвижной системе в (89) обнуляются ещё поля , , . В результате с учётом (78) потенциальная энергия становится равной релятивистской энергии (79) для неподвижного идеального твёрдого тела.

9. Выводы

Мы представили лагранжиан системы состоящим из одного члена для кривизны и из четырёх одинаковых по форме пар членов для каждого из четырёх полей – гравитационного и электромагнитного полей, поля ускорений и поля давления. В результате мы получили для каждого поля уравнения, совпадающие по форме друг с другом. Пространство-время так же представлено своим собственным тензорным метрическим полем . Массовый 4-ток взаимодействует с указанными полями, приобретая в этих полях энергию, при этом электромагнитное поле изменяет энергию электромагнитного 4-тока . Однако поля имеют и свою собственную энергию и импульс, которые содержатся в тензорах (5), (8), (11), (14), соответственно.

Из подобия уравнений для полей вытекает необходимость калибровки не только 4-потенциалов гравитационного и электромагнитного полей, но и 4-потенциалов поля ускорений и поля давления, а также массового 4-тока и электромагнитного 4-тока . С точки зрения физики смысл подобных калибровок заключается в том, что в качестве источника дивергенции вектора 3-скорости из малого объёма могут быть временные изменения энергии частицы в любых полях, имеющихся в данном объёме. Это может быть энергия частицы в поле скоростей, энергия в поле давления либо энергия в гравитационном или электромагнитном поле.

В отличие от стандартного подхода, мы не используем вообще какую-либо из множества известных форм тензора энергии-импульса вещества. Вместо этого энергия и импульс вещества описываются на основе поля ускорений, тензора поля ускорений и тензора энергии-импульса поля ускорений. Вклад давления в энергию и импульс системы соответственно описывается через поле давления с помощью тензора поля давления и тензора энергии-импульса поля давления. При этом поле ускорений и поле давления, так же как электромагнитное и гравитационное поля, рассматриваются как четырёхмерные векторные поля, имеющие свои собственные 4-потенциалы.

Представление гравитационного поля как векторного поля осуществляется в рамках ковариантной теории гравитации [3-4], в противоположность общей теории относительности, где гравитация описывается косвенно через геометрию пространства-времени и считается тензорным полем метрики. Преимуществом нашего подхода можно считать то, что энергия и импульс гравитационного поля в каждой точке определяются однозначно с помощью тензора энергии-импульса гравитационного поля. Между тем, в общей теории относительности вынуждены ограничиться только соответствующим псевдотензором, например псевдотензором энергии-импульса Ландау-Лифшица [13].

С целью однозначного определения релятивистской энергии частицы или элемента вещества мы применили специальную калибровку космологической постоянной, придав этой постоянной смысл энергии покоя частицы с «выключенными» внешними полями и воздействиями. Это привело к выражению для релятивистской энергии системы (74), и к уравнению для определения метрики (84), правая часть которого состоит из суммы четырёх тензоров энергии-импульса полей. В отсутствие космологической постоянной в лагранжиане (1) было бы невозможно провести указанную калибровку, энергия физической системы была бы неопределённой, и представленная теория осталась бы незавершённой. В нашем подходе космологическая постоянная отражает не плотность энергии пустого космического пространства или так называемую тёмную энергию, а скорее плотность энергии рассеянного в космосе вещества. При условии, что , где есть константа порядка единицы, из (75) следует, что . Подставляя сюда стандартную оценку космологической постоянной м^–2, находим соответствующую плотность вещества: кг/м. Данная плотность достаточно близка к плотности космического вещества, усреднённой по всему пространству.

Можно заметить, что наше выражение для релятивистской энергии и уравнение для метрики существенно отличаются от тех, которые получаются в общей теории относительности. Для энергии это следует из того, что вместо тензора энергии-импульса вещества мы используем тензоры энергии-импульса поля ускорений и поля давления, а гравитационное поле входит в энергию прямо, а не косвенно через метрику.

Возьмём теперь уравнение Эйнштейна для метрики с космологической постоянной из [14]. В общем случае в правой части этого уравнения содержится тензор энергии-импульса электромагнитного поля и тензор энергии-импульса вещества :

. (90)

Простейшей формой тензора энергии-импульса вещества без учёта давления является выражение через плотность вещества и 4-скорости: . Свёртка (90) с метрическим тензором даёт:

.

где .

После подстановки в (90) уравнение для метрики преобразуется так:

. (91)

Теперь уравнение (91) для метрики в общей теории относительности можно сравнить с нашим уравнением для метрики (84). Основное различие заключается в том, что в (84) все тензоры в правой части ведут себя одинаково и при свёртке с метрическим тензором обращаются в нуль. Но в (91) это не так – если для электромагнитного тензора энергии-импульса справедливо выражение , то для тензора энергии-импульса вещества соотношение не выполняется, так что в (91) необходим ещё член . В результате в общей теории относительности не только гравитационное поле представляется особым образом, через метрический тензор, отличаясь от способа введения электромагнитного поля в уравнение для метрики, но ещё и тензор энергии-импульса вещества не симметричен по отношению к метрике, в отличие от тензора энергии-импульса электромагнитного поля .

10. Список использованных источников

1. Misner, Charles W.; Kip. S. Thorne & John A. Wheeler (1973), Gravitation, W. H. Freeman, ISBN 0-7167-0344-0.

2. Poplawski N. J. A Lagrangian description of interacting energy. – arXiv:gr-qc/0608031v2 .

3. Fedosin S.G. The Principle of Least Action in Covariant Theory of Gravitation. Hadronic Journal, 2012, Vol. 35, No. 1, P. 35 – 70.

4. Fedosin S.G. The Hamiltonian in Covariant Theory of Gravitation. Advances in Natural Science, 2012, Vol. 5, No. 4, P. 55 – 75.

5. D. Hilbert, Die Grundlagen der Physik. (Erste Mitteilung), Göttinger Nachrichten, math.-phys. Kl., 1915, pp. 395-407.

6. Weyl H. – Raum-Zeit-Materie. – Берлин, 1918, 1-е изд.

7. Фок В.А. Теория пространства, времени и гравитации. 2-е издание. – М.: Физматгиз, 1961. – 568 с.

8. Дирак П. А. М. Общая теория относительности: Пер. с англ./ Под. ред. Д. И. Блохинцева. – Пер. изд.: США, 1975. – М.: Атомиздат, 1978. – 64 с.

9. Паули В. Теория относительности. Пер. с англ. – 2-е изд. / Под ред. В.Л. Гинзбурга и В.П. Фролова. – М.: Наука, 1983. – 336 с.

10. M. Born, Die träge Masse und das Relativitätsprinzip, Annalen der Physik, Vol. 333, No. 3, 1909, pp. 571-584.

11. Федосин С.Г. Физические теории и бесконечная вложенность материи. Пермь, 2009-2012, 858 стр., Табл. 21, Ил.41, Библ. 293 назв. ISBN 978-5-9901951-1-0.

12. Утияма Р. Теория относительности. М. Атомиздат, 1979. – 208 с.

13. Ландау Л. Д., Лифшиц Е. М. Теория поля. – Издание 7-е, исправленное. – М.: Наука, 1988. – 512 с. – (Теоретическая физика, том II).

14. Albert Einstein. Die Grundlage der allgemeinen Relativitätstheorie, Annalen der Physik, 1916, Vol. 354, No. 7, P. 769-822.

Приложение A. Варьирование шестого члена в функции действия

Необходимо найти вариацию для шестого члена в (1):

. (A1)

Нам понадобятся выражения для вариации метрического тензора и 4-вектора массового тока, которые можно найти, например, в [7], [9], [14]:

, . (A2)

. (A3)

С учётом (A2) и (A3) имеем:

(A4)

Преобразуем первый член в (A4) с помощью операции дифференцирования произведения функций по частям:

.

При вариации действия членом с дивергенцией можно пренебречь, оставшийся член можно преобразовать так:

Подставляя полученные результаты в (A4) и затем в (A1), находим:

.

Приложение B. Варьирование седьмого члена в функции действия

Вариация для седьмого члена в (1) для частного случая, когда является константой, с учётом (A2) будет равна:

,

(B1)

Поскольку , тензор антисимметричен, то используя выражение для из (A2), находим:

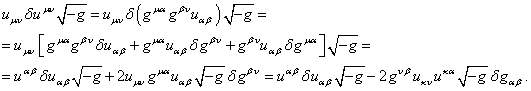
Подстановка этого выражения в (B1) даёт:

(B2)

Обозначим через тензор энергии-импульса поля ускорений:

. (B3)

Учитывая, что , используя дифференцирование по частям, а также равенство, справедливое для антисимметричного тензора:, для члена в (B2) имеем:

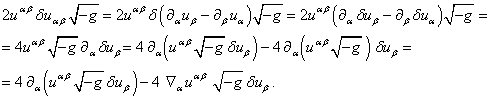
Член в последнем выражении является дивергенцией и им можно будет пренебречь при вариации функции действия.

Подставляя оставшийся член в (B2) и затем в (B1), и используя (B3), находим:

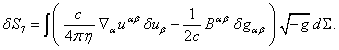
Приложение C. Варьирование восьмого члена в функции действия

Вариация действия для восьмого члена в (1) имеет вид:

.

Действуя так же, как в Приложении A, с учётом (A2) и (A3) находим:

.

При вариации действия член с дивергенцией является несущественным, второй член преобразуется дальше:

В результате вариация восьмого члена равна:

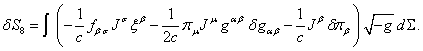
Приложение D. Варьирование девятого члена в функции действия

В том частном случае, когда является константой, для вариации девятого члена в (1) с учётом (A2) имеем:

,

(D1)

Делая замену и используя из (A2), преобразуем первый член равенства и затем подставляем в (D1):

.

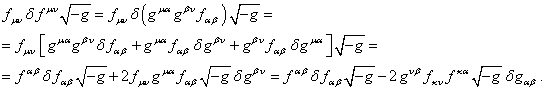
Обозначим через тензор энергии-импульса поля давления:

. (D2)

Преобразуем член , учитывая, что , используя дифференцирование по частям, а также равенство , справедливое для антисимметричного тензора:

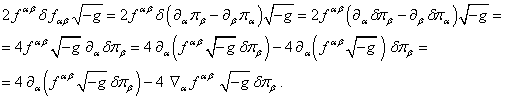
В последнем равенстве членом с дивергенцией можно пренебречь, так как он не даёт вклада в вариацию функции действия. Подставляя результаты в (D1), находим искомую вариацию:

.

Приложение E. Тензор ускорений и уравнения для поля ускорений

По определению, поле ускорений появляется как результат применения 4-ротора к 4-потенциалу:

.

Тензор антисимметричен и включает в себя различные компоненты ускорений. По своему построению этот тензор подобен гравитационному тензору и электромагнитному тензору , каждый из которых состоят из двух векторных компонент, зависящих от потенциалов поля и скоростей источников поля.

Для того, чтобы лучше понять физический смысл поля ускорений, введём следующие обозначения:

, , (E1)

где индексы образуют тройки неповторяющихся чисел вида 1,2,3 или 3,1,2 или 2,3,1; 3-векторы S и N можно расписать по компонентам: ; .

Тогда тензор можно представить следующим образом:

. (E2)

С целью упрощения наших дальнейших рассуждений рассмотрим случай плоского пространства-времени, то есть пространство Минковского или пространство-время специальной теории относительности. Роль метрического тензора при этом играет тензор , ненулевые компоненты которого , . Поднимем с его помощью индексы у тензора ускорений:

. (E3)

Раскроем 4-вектор массового тока: , где .

В уравнениях (22) и (23) можно заменить ковариантные производные на частные производные . Теперь с помощью векторов S и N эти уравнения можно представить следующим образом:

, , , . (E4)

Полученные в рамках специальной теории относительности уравнения (E4) для случая по своей форме аналогичны уравнениям Максвелла в электродинамике.

Если второе уравнение в (E4) умножить скалярно на S , а четвёртое уравнение умножить скалярно на – N и результаты сложить, получится следующее:

. (E5)

Уравнение (E5) содержит в себе теорему Пойнтинга в применении к полю ускорений. Смысл этого дифференциального уравнения в том, что если в системе совершается работа по ускорению частиц, то мощность этой работы связывается с дивергенцией потока поля ускорений и изменением во времени энергии, связанной с полем ускорений. Соотношение (E5) в общековариантном виде согласно (33) записывается так:

.

Подставим теперь (E2) в (30) и запишем скалярное и векторное соотношения для компонент 4-ускорения :

,

. (E6)

Компоненты 4-ускорения получаются из этих соотношений после сокращения на . Как видно, в пространственную компоненту 4-ускорения делают вклад оба вектора S и N, при этом вектор S имеет размерность обычного 3-ускорения, а размерность вектора N такая же, как у частоты.

Если учесть, что 4-потенциал поля ускорений для одной частицы можно рассматривать как ковариантную 4-скорость, то из (E1) в пространстве Минковского следует:

, . (E7)

Вектор S является напряжённостью поля ускорений, а вектор N – величиной, подобной по своему смыслу индукции магнитного поля в электродинамике или полю кручения в ковариантной теории гравитации (гравитомагнитному полю в общей теории относительности). При постоянной скорости векторы S и N обращаются в нуль. Если же существуют ненулевые временные производные или пространственные градиенты от скорости, то появляется поле ускорений с компонентами S и N, и тензор ускорений . При этом можно утверждать, что ненулевой тензор в инерциальной системе отсчёта приводит к соответствующим силам инерции, как к следствию любого ускорения тел относительно выбранной системы отсчёта.

Если тензоры из (E2) и (E3) подставить в (B3), то тем самым тензор энергии-импульса поля ускорений будет выражен через векторы S и N. В частности, для тензорного инварианта и временных компонент тензора имеем:

, , . (E8)

Компонента после интегрирования её по объёму в лоренцевой системе отсчёта определяет энергию поля ускорений в данном объёме, а вектор есть плотность потока энергии поля ускорений. Поэтому для вычисления потока энергии поля ускорений вектор K также необходимо проинтегрировать по объёму.

Приложение F. Тензор давления и уравнения для поля давления

Тензор давления строится путём антисимметричного дифференцирования 4-потенциала :

.

Введём следующие обозначения:

, , (F1)

где индексы образуют тройки неповторяющихся чисел вида 1,2,3 или 3,1,2 или 2,3,1; 3-векторы C и I в декартовых координатах имеют компоненты: ; .

В указанных обозначениях тензор можно представить по компонентам:

. (F2)

В пространстве Минковского метрический тензор не зависит от координат и времени и состоит из нулей и единиц. В таком пространстве компоненты тензора повторяют компоненты тензора , отличие только в знаках временных компонент:

. (F3)

Заменяя в уравнениях (26) и (27) ковариантные производные на частные производные , можно представить эти уравнения в виде четырёх уравнений для векторов C и I:

, , , . (F4)

Напомним, что полученные в рамках специальной теории относительности уравнения (F4) справедливы для случая . Аналогично (E5), получается уравнение локального сохранения энергии давления:

.

Это уравнение следует также из (34) и может быть записано с помощью тензора согласно (D2) так:

.

Тензорный инвариант и временные компоненты тензора выражаются с помощью (F2) и (F3) через векторы C и I:

, , . (F5)

Компонента тензора энергии-импульса давления определяет плотность энергии давления внутри тел, а вектор задаёт плотность потока энергии давления.

Оценим теперь величину при индексе . Согласно (31) эта величина определяет вклад поля давления в полную плотность силы, действующей на частицу. С учётом (F2) получается, что плотность силы давления имеет две компоненты:

.

Для сравнения, временная компонента есть плотность мощности силы давления, делённая на скорость света:

.

Вектор C имеет размерность ускорения, а вектор I имеет размерность частоты. Эти векторы с помощью (F1) и определения 4-потенциала поля давления в пространстве Минковского можно записать так:

, (F6)

,

где обозначает 4-скорость, – давление в сопутствующей частице системе отсчёта, есть фактор Лоренца и есть скорость движения частицы.

Вектор I по своим свойствам подобен вектору магнитной индукции, а вектор C аналогичен напряжённости электрического поля. Неподвижные частицы не создают вектор I, а для обнуления вектора C необходимо ещё, чтобы отношение не зависело от координат. В этом случае вклад поля давления в ускорение частиц будет отсутствовать.

Источник: http://sergf.ru/cc.htm

На научный сайт