Jordan Journal of Physics. Vol. 9 (No. 1), pp. 1-30,
(2016). http://journals.yu.edu.jo/jjp/Vol9No1Contents2016.html
About the cosmological constant,
acceleration field, pressure field and energy
Sergey G.
Fedosin
PO box 614088, Sviazeva str. 22-79,
Perm, Russia
E-mail: intelli@list.ru
Based on the condition
of relativistic energy uniqueness the calibration of the cosmological constant
was performed. This allowed us to obtain the corresponding equation for the
metric, to determine the generalized momentum,
the relativistic energy, momentum and the mass of the system, as well as
the expressions for the kinetic and potential energies. The scalar curvature at
an arbitrary point of the system equaled zero, if the substance is absent at
this point; the presence of a gravitational or electromagnetic field is enough
for the space-time curvature. Four-potentials of the acceleration field and
pressure field, as well as tensor invariants determining the energy density of
these fields, were introduced into the Lagrangian in order to describe the system’s
motion more precisely. The structure of the Lagrangian used is completely
symmetrical in form with respect to the 4-potentials of gravitational and
electromagnetic fields and acceleration and pressure fields. The stress-energy
tensors of the gravitational, acceleration and pressure fields are obtained in
explicit form, each of them can be expressed through the corresponding field
vector and additional solenoidal vector. A description of the equations of
acceleration and pressure fields is provided.
Keywords: cosmological constant;
4-momentum; acceleration field; pressure field; covariant theory of gravitation.
PACS: 04.20.Fy, 04.40.-b, 11.10.Ef
1. Introduction
The most popular application of the cosmological constant ![]() in the general theory of
relativity (GTR) is that this quantity represents the manifestation of the
vacuum energy [1-2]. There is another approach to the cosmological constant
interpretation, according to which this quantity represents the energy
possessed by any solitary particle in the absence of external fields. In this
case, including
in the general theory of
relativity (GTR) is that this quantity represents the manifestation of the
vacuum energy [1-2]. There is another approach to the cosmological constant
interpretation, according to which this quantity represents the energy
possessed by any solitary particle in the absence of external fields. In this
case, including ![]() into the Lagrangian seems quite
appropriate since the Lagrangian contains such energy components, which should
fully describe the properties of any system consisting of particles and fields.
into the Lagrangian seems quite
appropriate since the Lagrangian contains such energy components, which should
fully describe the properties of any system consisting of particles and fields.
Earlier in [3-4] we used such calibration of the cosmological constant,
which allowed us to maximally simplify the equation for the metric. The
disadvantage of this approach was that the relativistic energy of the system
could not be determined uniquely, since the expression for the energy included
the scalar curvature. In this paper we use another universal calibration of the
cosmological constant, which is suitable for any particle and system of
particles and fields. As a result, the energy is independent of both the scalar
curvature and the cosmological constant.
In GTR the gravitational field as a separate object is not included in
the Lagrangian, and the role of a field is played by the metric itself. A known
problem arising from such an approach is that in GTR there is no stress-energy
tensor of the gravitational field.
In contrast, in the covariant theory of gravitation the Lagrangian is
used containing the term with the energy of the particles in the gravitational
field and the term with the energy of the gravitational field as such. Thus,
the gravitational field is included in the Lagrangian in the same way as the
electromagnetic field. In this case, the metric of the curved spacetime is used
to specify the equations of motion as compared to the case of such a weak
field, the limit of which is the special theory of relativity. In the weak
field limit a simplified metric is used, which almost does not depend on the
coordinates and time. This is enough in many cases, for example, in case of
describing the motion of planets. However, generally, in case of strong fields
and for studying the subtle effects the use of metric becomes necessary.
We will note that the term with the particle energy in the Lagrangian
can be written in different ways. In [5-6] this term contains the invariant ![]() , where
, where ![]() is the mass
density in the co-moving reference frame,
is the mass
density in the co-moving reference frame, ![]() is 4-velocity. The corresponding
quantity in [7] has the form
is 4-velocity. The corresponding
quantity in [7] has the form ![]() . In [3] and [8] instead of it the product
. In [3] and [8] instead of it the product ![]() is used, where
is used, where ![]() is mass 4-current. In this
paper we have chosen another form of the mentioned invariant – in the form
is mass 4-current. In this
paper we have chosen another form of the mentioned invariant – in the form ![]() . The reason for this choice is the fact that we consider the mass
4-current
. The reason for this choice is the fact that we consider the mass
4-current ![]() to be the fullest representative of the
properties of substance particles containing both the mass density and the
4-velocity. The mass 4-current can be considered as the 4-potential of the
matter field. All the other 4-vectors in the Lagrangian are 4-potentials of the
respective fields and are written with covariant indices. With the help of
these 4-potentials tensor invariants are calculated which characterize the
energy of the respective field in the Lagrangian.
to be the fullest representative of the
properties of substance particles containing both the mass density and the
4-velocity. The mass 4-current can be considered as the 4-potential of the
matter field. All the other 4-vectors in the Lagrangian are 4-potentials of the
respective fields and are written with covariant indices. With the help of
these 4-potentials tensor invariants are calculated which characterize the
energy of the respective field in the Lagrangian.
2. Action and its variations in the principle of least action
2.1. The action function
We use the following expression as the action function for continuously
distributed matter in the gravitational and electromagnetic fields in an
arbitrary frame of reference:

(1)
where ![]() – the Lagrange function or Lagrangian,
– the Lagrange function or Lagrangian,
![]() – the differential
of the coordinate time of the used
reference frame,
– the differential
of the coordinate time of the used
reference frame,
![]() – a coefficient to be determined,
– a coefficient to be determined,
![]() – the scalar curvature,
– the scalar curvature,
![]() – the cosmological constant,
– the cosmological constant,
![]() – the 4-vector of gravitational (mass) current,
– the 4-vector of gravitational (mass) current,
![]() – the mass density in the reference frame
associated with the particle,
– the mass density in the reference frame
associated with the particle,
![]() – the 4-velocity of a point particle,
– the 4-velocity of a point particle, ![]() – 4-displacement,
– 4-displacement, ![]() – interval,
– interval,
![]() – the speed of light as a measure of the
propagation velocity of electromagnetic and gravitational interactions,
– the speed of light as a measure of the
propagation velocity of electromagnetic and gravitational interactions,
![]() – the 4-potential of the gravitational field, described by the scalar
potential
– the 4-potential of the gravitational field, described by the scalar
potential ![]() and the vector potential
and the vector potential ![]() of this field,
of this field,
![]() – the gravitational
constant,
– the gravitational
constant,
![]() – the gravitational tensor (the tensor of
gravitational field strengths),
– the gravitational tensor (the tensor of
gravitational field strengths),
![]() – definition of the gravitational tensor with
contravariant indices by means of the metric tensor
– definition of the gravitational tensor with
contravariant indices by means of the metric tensor ![]() ,
,
![]() – the 4-potential of the electromagnetic field, which is set by the
scalar potential
– the 4-potential of the electromagnetic field, which is set by the
scalar potential ![]() and the vector potential
and the vector potential ![]() of this field,
of this field,
![]() – the 4-vector of the electromagnetic (charge)
current,
– the 4-vector of the electromagnetic (charge)
current,
![]() – the charge density in the reference frame
associated with the particle,
– the charge density in the reference frame
associated with the particle,
![]() – the vacuum permittivity,
– the vacuum permittivity,
![]() – the electromagnetic tensor (the tensor of
electromagnetic field strengths),
– the electromagnetic tensor (the tensor of
electromagnetic field strengths),
![]() – the 4-velocity with a covariant index,
expressed through the metric tensor and the 4-velocity with a contravariant
index; it is convenient to consider the covariant 4-velocity locally
averaged over the particle system as the 4-potential of the acceleration field
– the 4-velocity with a covariant index,
expressed through the metric tensor and the 4-velocity with a contravariant
index; it is convenient to consider the covariant 4-velocity locally
averaged over the particle system as the 4-potential of the acceleration field ![]() , where
, where ![]() and
and ![]() denote the scalar and vector potentials,
respectively,
denote the scalar and vector potentials,
respectively,
![]() – the acceleration tensor calculated through
the derivatives of the four-potential of the acceleration field,
– the acceleration tensor calculated through
the derivatives of the four-potential of the acceleration field,
![]() – a function of coordinates and time,
– a function of coordinates and time,
![]() – the 4-potential of the pressure field,
consisting of the scalar potential
– the 4-potential of the pressure field,
consisting of the scalar potential ![]() and the vector potential
and the vector potential ![]() ,
, ![]() is the pressure in the reference
frame associated with the particle, the relation
is the pressure in the reference
frame associated with the particle, the relation ![]() specifies the equation of the substance state,
specifies the equation of the substance state,
![]() – the tensor of the pressure field,
– the tensor of the pressure field,
![]() – a function of coordinates and time,
– a function of coordinates and time,
![]() – the invariant 4-volume, expressed through
the differential of the time coordinate
– the invariant 4-volume, expressed through
the differential of the time coordinate ![]() , through the product
, through the product ![]() of differentials of the
spatial coordinates and through the square root
of differentials of the
spatial coordinates and through the square root ![]() of the determinant
of the determinant ![]() of the metric tensor, taken
with a negative sign.
of the metric tensor, taken
with a negative sign.
Action function (1) consists of almost the same terms as those which
were considered in [3]. The difference is that now we replace the term with the
energy density of particles with four terms located at the end of (1). It is
natural to assume that each term is included in (1) relatively independently of
the other terms, describing the state of the system in one way or another. The
value of the 4-potential ![]() of the set of matter units or
point particles of the system defines the 4-field of the system’s velocities,
and the product
of the set of matter units or
point particles of the system defines the 4-field of the system’s velocities,
and the product ![]() in
(1) can be regarded as the energy of interaction of the mass current
in
(1) can be regarded as the energy of interaction of the mass current ![]() with
the field of velocities.
with
the field of velocities.
Similarly, ![]() is the 4-potential of the gravitational field,
and the product
is the 4-potential of the gravitational field,
and the product ![]() defines the energy of interaction
of the mass current with the gravitational field. The electromagnetic field is
specified by the 4-potential
defines the energy of interaction
of the mass current with the gravitational field. The electromagnetic field is
specified by the 4-potential ![]() , the
source of the field is the electromagnetic current
, the
source of the field is the electromagnetic current ![]() , and the product of these quantities
, and the product of these quantities ![]() is the density of the energy of
interaction of a moving charged substance unit with the electromagnetic field.
The invariant of the gravitational field in the form of the tensor product
is the density of the energy of
interaction of a moving charged substance unit with the electromagnetic field.
The invariant of the gravitational field in the form of the tensor product ![]() is associated with the gravitational field
energy and cannot be equal to zero even outside bodies. The same holds for the
electromagnetic field invariant
is associated with the gravitational field
energy and cannot be equal to zero even outside bodies. The same holds for the
electromagnetic field invariant ![]() . This follows from the properties of long-range action of the specified
fields. As for the field of velocities
. This follows from the properties of long-range action of the specified
fields. As for the field of velocities ![]() , the field should be used to describe the motion of the substance
particles. Accordingly, the field of accelerations in the form of the tensor
, the field should be used to describe the motion of the substance
particles. Accordingly, the field of accelerations in the form of the tensor ![]() and the energy of this field
associated with the invariant
and the energy of this field
associated with the invariant ![]() refer to the accelerated motion
of particles and are calculated for those spatial points within the system’s
volume where the substance is located.
refer to the accelerated motion
of particles and are calculated for those spatial points within the system’s
volume where the substance is located.
The last two terms in (1) are associated with the pressure in the
substance, and the product ![]() characterizes the interaction
of the pressure field with the mass 4-current, and the invariant
characterizes the interaction
of the pressure field with the mass 4-current, and the invariant ![]() is part of the stress-energy
tensor of the pressure field.
is part of the stress-energy
tensor of the pressure field.
We will also note the difference of 4-currents ![]() and
and ![]() – all particles
of the system make contribution to the mass current
– all particles
of the system make contribution to the mass current ![]() , and only charged particles make contribution to the electromagnetic
current
, and only charged particles make contribution to the electromagnetic
current ![]() . This results in difference of the fields’ influence – the
gravitational field influences any particles and the electromagnetic field
influences only the charged particles or the substance, in which by the field
can sufficiently divide with its influence the charges of opposite signs from
each other. The field of velocities
. This results in difference of the fields’ influence – the
gravitational field influences any particles and the electromagnetic field
influences only the charged particles or the substance, in which by the field
can sufficiently divide with its influence the charges of opposite signs from
each other. The field of velocities ![]() , as well
as the mass current
, as well
as the mass current ![]() , are
associated with all the particles of the system. Therefore, the product
, are
associated with all the particles of the system. Therefore, the product ![]() describes that part of the
particles’ energy, which stays if we somehow "turn off " in the
system under consideration all the macroscopic gravitational and
electromagnetic fields and remove the pressure, without changing the field of
velocities
describes that part of the
particles’ energy, which stays if we somehow "turn off " in the
system under consideration all the macroscopic gravitational and
electromagnetic fields and remove the pressure, without changing the field of
velocities ![]() or the mass current
or the mass current ![]() .
.
2. 2. Variations
of the action function
We will vary the action function ![]() in (1) term by term, then the
total variation
in (1) term by term, then the
total variation ![]() will be
the sum of variations of individual terms. In total there are 9 terms inside
the integral in (1). If we consider the quantity
will be
the sum of variations of individual terms. In total there are 9 terms inside
the integral in (1). If we consider the quantity ![]() a constant
(a cosmological constant), then according to [7-9] the variation of the first
term in the action function (1) is equal to:
a constant
(a cosmological constant), then according to [7-9] the variation of the first
term in the action function (1) is equal to:
![]() , (2)
, (2)
where ![]() is the
Ricci tensor,
is the
Ricci tensor,
![]() is the
variation of the metric tensor.
is the
variation of the metric tensor.
According to [3] the variations of terms 2 and 3 in the action function
are as follows:
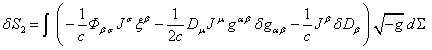 , (3)
, (3)
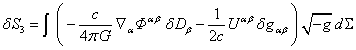 , (4)
, (4)
where ![]() is the variation of coordinates, which results in the variation of the
mass 4-current
is the variation of coordinates, which results in the variation of the
mass 4-current ![]() and in the
variation of the electromagnetic 4-current
and in the
variation of the electromagnetic 4-current ![]() ,
,
![]() is the variation of the 4-potential of the gravitational field,
is the variation of the 4-potential of the gravitational field,
and ![]() denotes the stress-energy tensor of the gravitational field:
denotes the stress-energy tensor of the gravitational field:
![]() . (5)
. (5)
Variations of terms 4 and 5 in the action function according to [6-7],
[10] are as follows:
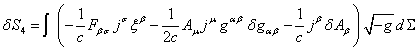 , (6)
, (6)
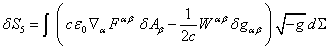 , (7)
, (7)
where ![]() is the variation of the 4-potential of the electromagnetic field,
is the variation of the 4-potential of the electromagnetic field,
and ![]() denotes the stress-energy tensor of the electromagnetic field:
denotes the stress-energy tensor of the electromagnetic field:
![]() . (8)
. (8)
Variations of the other terms in the action function (1) are defined in
Appendices A-D and have the following form:
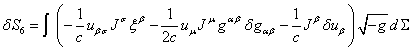 , (9)
, (9)
 , (10)
, (10)
where ![]() is the variation of the 4-potential
of the acceleration field,
is the variation of the 4-potential
of the acceleration field,
and ![]() denotes the stress-energy tensor of the field of accelerations:
denotes the stress-energy tensor of the field of accelerations:
![]() . (11)
. (11)
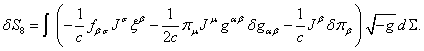 (12)
(12)
 , (13)
, (13)
where the stress-energy tensor of the pressure field:
![]() . (14)
. (14)
In variation (10) in order to simplify the special case is considered,
when ![]() is a
constant, which does not vary by definition. According to its meaning
is a
constant, which does not vary by definition. According to its meaning ![]() depends on the parameters of the system under consideration, and
therefore can have different values. The same should be said about
depends on the parameters of the system under consideration, and
therefore can have different values. The same should be said about ![]() .
.
3. The motion equations of the field,
particles and metric
According to the principle of least action, we should sum up all the
variations of the individual terms of the action function and equate the result
to zero. The sum of variations (2), (3), (4), (6), (7), (9), (10), (12) and
(13) gives the total variation of the action function:
![]() . (15)
. (15)
3.1. The field equations
When the system moves in spacetime, the variations ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() do not vanish, since it is supposed that it can occur only at the
beginning and the end of the process, when the conditions of motion are
precisely fixed. Consequently, the sum of the terms, which is located before
these variations, should vanish. For example, the variation
do not vanish, since it is supposed that it can occur only at the
beginning and the end of the process, when the conditions of motion are
precisely fixed. Consequently, the sum of the terms, which is located before
these variations, should vanish. For example, the variation ![]() occurs only in
occurs only in ![]() according to (6 ) and in
according to (6 ) and in ![]() from
(7), then from (15) it follows:
from
(7), then from (15) it follows:
![]() .
.
From this we obtain the equation of the electromagnetic field with the
field sources:
![]() or
or
![]() , (16)
, (16)
where ![]() is the vacuum permeability.
is the vacuum permeability.
The second equation of the electromagnetic field follows from the
definition of the electromagnetic tensor in terms of the electromagnetic
4-potential and from the antisymmetry properties of this tensor:
![]() or
or
![]() , (17)
, (17)
where ![]() is a Levi-Civita symbol or a completely antisymmetric
unit tensor.
is a Levi-Civita symbol or a completely antisymmetric
unit tensor.
The variation ![]() is present only in (3) and (4), so
that according to (15) we should obtain:
is present only in (3) and (4), so
that according to (15) we should obtain:
 .
.
The equation of gravitational field with the field sources follows from
this:
![]() or
or
![]() . (18)
. (18)
If we take into account the definition of the gravitational tensor: ![]() , and take the covariant derivative of this
tensor with subsequent cyclic interchange of the indices, the following
equations are solved identically:
, and take the covariant derivative of this
tensor with subsequent cyclic interchange of the indices, the following
equations are solved identically:
![]() or
or ![]() . (19)
. (19)
Equation (19) without the sources and equation (18) with the sources
define a complete set of gravitational field equations in the covariant theory
of gravitation.
Consider
now the rule for the difference of the second covariant derivatives with
respect to the covariant derivative of the electromagnetic 4-potential ![]() :
:
![]()
With the
rule in mind, the applying of the covariant derivative ![]() to (16) and (18) gives the following:
to (16) and (18) gives the following:
![]() .
.
![]() .
.
This shows
that field tensors ![]() and
and ![]() lead to the divergence of the corresponding
4-currents in a curved space-time. Mixed curvature tensor
lead to the divergence of the corresponding
4-currents in a curved space-time. Mixed curvature tensor ![]() and Ricci tensor
and Ricci tensor ![]() vanish only in Minkowski space. In this
case, the covariant derivatives become the partial derivatives and the
continuity equation for the gravitational and electromagnetic 4-currents in the
special theory of relativity are obtained:
vanish only in Minkowski space. In this
case, the covariant derivatives become the partial derivatives and the
continuity equation for the gravitational and electromagnetic 4-currents in the
special theory of relativity are obtained:
![]() ,
, ![]() . (20)
. (20)
We will note that in order to simplify the equations for the 4-potential of fields we
can use expressions which are called gauge conditions:
![]() ,
, ![]() . (21)
. (21)
3.2. The acceleration field equations
The variation of 4-potential
![]() is included in (9) and (10), therefore
according to (15) we should obtain:
is included in (9) and (10), therefore
according to (15) we should obtain:
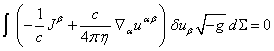 .
.
![]() , or
, or
![]() . (22)
. (22)
If we compare (18) and (22), it turns out that the presence of the
4-vector of mass current ![]() not only leads to occurrence
of space-time gradient of the gravitational field in the system under
consideration, but is generally accompanied by changes in time or by 4-velocity
gradients of the particles that constitute this system. Besides the covariant
4-velocities of the whole set of particles forms the velocity field
not only leads to occurrence
of space-time gradient of the gravitational field in the system under
consideration, but is generally accompanied by changes in time or by 4-velocity
gradients of the particles that constitute this system. Besides the covariant
4-velocities of the whole set of particles forms the velocity field ![]() , the
derivatives of which define the acceleration field and are described by the
tensor
, the
derivatives of which define the acceleration field and are described by the
tensor ![]() . As an example of a system, where it can be clearly observed, we can
take a rotating partially-charged collapsing gas-dust cloud, held by gravity.
An ordered acceleration field occurs in the cloud due to the rotational
acceleration and contains the centripetal and tangential acceleration.
. As an example of a system, where it can be clearly observed, we can
take a rotating partially-charged collapsing gas-dust cloud, held by gravity.
An ordered acceleration field occurs in the cloud due to the rotational
acceleration and contains the centripetal and tangential acceleration.
Due to its definition in the form of a 4-rotor of ![]() , the following relations hold for acceleration tensor
, the following relations hold for acceleration tensor ![]() :
:
![]() or
or ![]() .
(23)
.
(23)
As we can see, the structure of equations (22) and (23) for the
acceleration field is similar to the structure of equations for the strengths
of gravitational and electromagnetic fields.
In
the local geodetic reference frame the derivatives of the metric tensor and the
curvature tensor become equal to zero, the covariant derivative becomes a
partial derivative and the equations take the simplest form. We will go over to
this reference frame and apply the derivative ![]() to (23) and make substitution for
the first and third terms using (22):
to (23) and make substitution for
the first and third terms using (22):
![]()
![]() .
.
If we apply definition ![]() to
4-d’Alembertian
to
4-d’Alembertian ![]() , where
, where ![]() is
the d'Alembert operator, it will give:
is
the d'Alembert operator, it will give:
![]() .
.
Comparing with the previous expression, we find the wave equation for
the 4-potential ![]() :
:
![]() .
.
On the other hand, after lowering of the acceleration tensor indices we
have from (22):
![]() .
.
Comparing this equation with equation for ![]() leads to the expression:
leads to the expression:
![]() ,
,
where ![]() is some constant.
is some constant.
In
an arbitrary reference frame we should specify the obtained expressions, since
in contrast to permutations of partial derivatives, in case of permutation of
the covariant derivatives from the sequence ![]() to the sequence
to the sequence ![]() some additional terms appear. In particular, if we use the relation:
some additional terms appear. In particular, if we use the relation:
![]() ,
(24)
,
(24)
then
after substituting the expression ![]() in (22), the wave equation can be
written as follows:
in (22), the wave equation can be
written as follows:
![]() . (25)
. (25)
In
the curved space operator ![]() acts differently on scalars, 4-vectors and 4-tensors,
and usually it contains the Ricci tensor. Due to condition (24), the Ricci
tensor is absent in (25), but the terms with the Christoffel symbols remain.
acts differently on scalars, 4-vectors and 4-tensors,
and usually it contains the Ricci tensor. Due to condition (24), the Ricci
tensor is absent in (25), but the terms with the Christoffel symbols remain.
Equation (24) is a gauge condition for the 4-potential ![]() , which is similar by its meaning to gauge conditions (21) for the
electromagnetic and gravitational 4-potentials. Both (24) and (25) will hold on
condition that
, which is similar by its meaning to gauge conditions (21) for the
electromagnetic and gravitational 4-potentials. Both (24) and (25) will hold on
condition that ![]() .
.
In Appendix E it will be shown that the acceleration tensor ![]() includes the vector components
includes the vector components ![]() and
and ![]() , based on which, according to (E6), we can build a 4-vector of
particles’ acceleration.
, based on which, according to (E6), we can build a 4-vector of
particles’ acceleration.
3.3. The pressure field equations
To obtain the pressure field equations we need to choose in (15) those
terms which contain the variation ![]() . This variation is present in (12) and (13), which gives the following:
. This variation is present in (12) and (13), which gives the following:
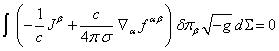 .
.
![]() or
or ![]() .
(26)
.
(26)
It follows from (26) that the mass 4-current generates the pressure
field in bodies, which can be described by the pressure tensor ![]() . The same relations hold for this tensor as for the tensors of other
fields:
. The same relations hold for this tensor as for the tensors of other
fields:
![]() or
or ![]() . (27)
. (27)
The wave equation for the 4-potential of the pressure field follows from
(26) and (27):
![]() .
(28)
.
(28)
Equations (26) and (28) will be consistent at the same time if there is
gauge condition of the pressure 4-potential:
![]() ,
(29)
,
(29)
where ![]() is some constant. As a rule,
these constants are chosen to be equal to zero.
is some constant. As a rule,
these constants are chosen to be equal to zero.
The properties of the pressure field are described in Appendix F, where
it is shown that the pressure tensor ![]() contains two vector components
contains two vector components ![]() and
and ![]() , which determine the energy and the pressure force, as well as the
pressure energy flux.
, which determine the energy and the pressure force, as well as the
pressure energy flux.
3.4. The equations of motion of particles
The variation ![]() that leads to the equations of
motion of the particles is present in (3), (6), (9) and (12). For this variation it follows from (15):
that leads to the equations of
motion of the particles is present in (3), (6), (9) and (12). For this variation it follows from (15):
![]() ,
,
![]() .
.
The left side of the equation can be transformed, considering the
expression ![]() for the 4-vector of mass current
density and the definition of the acceleration tensor
for the 4-vector of mass current
density and the definition of the acceleration tensor ![]() :
:
![]() . (30)
. (30)
We used the relation ![]() , which
follows from the equation
, which
follows from the equation ![]() , and the
operator of proper-time-derivative as operator of the derivative with respect
to the proper time
, and the
operator of proper-time-derivative as operator of the derivative with respect
to the proper time ![]() , where
, where ![]() is a symbol of 4-differential in
curved spacetime,
is a symbol of 4-differential in
curved spacetime, ![]() is the proper time [11]. Taking
into account (30) the equation of motion takes the form:
is the proper time [11]. Taking
into account (30) the equation of motion takes the form:
![]() . (31)
. (31)
We will note that the equations of field motion (16) – (19), of the acceleration
field (22) and (23), of the pressure field (26) and (27) and the equation of
the particles’ motion (31) are differential equations, which are valid at any
point volume of spacetime in the system under consideration. In particular, if
the mass density ![]() in some point volume is zero,
then all the terms in (31) will be zero.
in some point volume is zero,
then all the terms in (31) will be zero.
The quantity ![]() in the left side of (31) is the
4-acceleration of a point particle, while the proper time differential
in the left side of (31) is the
4-acceleration of a point particle, while the proper time differential ![]() is associated
with the interval by relation:
is associated
with the interval by relation: ![]() and the relation holds:
and the relation holds: ![]() . The first two terms in the right side of (31) are the densities of the
gravitational and electromagnetic 4-forces, respectively. It can be shown (see
for example [3], [12]) that for 4-forces, exerted by the field on the particle,
there are alternative expressions in terms of the stress-energy tensors (5) and
(8):
. The first two terms in the right side of (31) are the densities of the
gravitational and electromagnetic 4-forces, respectively. It can be shown (see
for example [3], [12]) that for 4-forces, exerted by the field on the particle,
there are alternative expressions in terms of the stress-energy tensors (5) and
(8):
![]() ,
, ![]() . (32)
. (32)
Similarly, the left side of (31) with regard to (30) is expressed in
terms of stress-energy tensor of the acceleration field (11):
![]() .
(33)
.
(33)
To prove (33) we should expand the tensor ![]() with the help of definition (11), apply the
covariant derivative
with the help of definition (11), apply the
covariant derivative ![]() to the tensor products and then use equations
(22) and (23). Equation (33) shows that the 4-acceleration of the particle can
be described by either the acceleration tensor
to the tensor products and then use equations
(22) and (23). Equation (33) shows that the 4-acceleration of the particle can
be described by either the acceleration tensor ![]() or the tensor
or the tensor ![]() .
.
For the pressure field we can write the same as for other fields:
![]() .
(34)
.
(34)
In (34) the pressure 4-force is associated with the covariant derivative
of the stress-energy tensor of the pressure field.
From (31) –
(34) it follows:
![]() or
or
![]() . (35)
. (35)
In Minkowski space ![]() , where
, where ![]() is present, 4-differetials
is present, 4-differetials ![]() become ordinary differentials
become ordinary differentials
![]() ,
, ![]() ,
,
and the motion equation (31) falls into the scalar and vector equations,
while the vector equation contains the total gravitational force with regard to
the torsion field, the electromagnetic Lorentz force and the pressure force:
![]() , (36)
, (36)
![]() , (37)
, (37)
where ![]() is the velocity of a point
particle,
is the velocity of a point
particle, ![]() is the gravitational field strength,
is the gravitational field strength, ![]() is the charge density,
is the charge density, ![]() is the electric field strength,
is the electric field strength, ![]() is the pressure field strength,
is the pressure field strength, ![]() is the torsion field vector,
is the torsion field vector, ![]() is the magnetic field induction,
is the magnetic field induction, ![]() is the solenoidal vector of the
pressure field.
is the solenoidal vector of the
pressure field.
If during the time ![]() the density
the density ![]() does not change, it can be
put under the derivative’s sign. Then in the left side of (36) the quantity
does not change, it can be
put under the derivative’s sign. Then in the left side of (36) the quantity ![]() appears, where
appears, where  is the relativistic energy density. Similarly,
in the left side of (37) the quantity
is the relativistic energy density. Similarly,
in the left side of (37) the quantity ![]() appears, where
appears, where ![]() is the mass 3-current
density.
is the mass 3-current
density.
3.5. The equations for
the metric
Let us consider action variations (2), (3), (4), (6), (7), (9), (10),
(12) and (13), which contain the variation ![]() . The sum of all the terms in (15) with the variation
. The sum of all the terms in (15) with the variation ![]() must be zero:
must be zero:
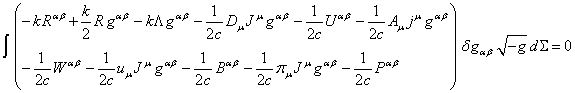 .
.
 (38)
(38)
The equation for the metric (38) allows us to determine the metric
tensor ![]() by the known quantities
characterizing the substance and field. If we take the covariant derivative
by the known quantities
characterizing the substance and field. If we take the covariant derivative ![]() in this
equation, the left side of the equation vanishes on condition
in this
equation, the left side of the equation vanishes on condition ![]() , and taking into account (35) we obtain the following:
, and taking into account (35) we obtain the following:
![]() ,
,
![]() , (39)
, (39)
where ![]() is a function of time and
coordinates and the scalar invariant with respect to coordinate
transformations.
is a function of time and
coordinates and the scalar invariant with respect to coordinate
transformations.
If we expand the scalar products of vectors using the expressions:
![]() ,
, ![]() , (40)
, (40)
![]() .
.
then (39) can be written as:
![]() . (41)
. (41)
If the system’s substance and charges are divided to small pieces and
scattered to infinity, then there the external field potentials become equal to
zero, since interparticle interaction tends to zero, and at ![]() we obtain the following:
we obtain the following:
![]() . (42)
. (42)
Consequently, ![]() is associated with the
particle’s proper scalar potentials
is associated with the
particle’s proper scalar potentials ![]() and
and ![]() , the mass density
, the mass density ![]() and the pressure
and the pressure ![]() in the particle located at
infinity. Expression (41) can be considered as the differential law of
conservation of mass-energy: the greater the velocity
in the particle located at
infinity. Expression (41) can be considered as the differential law of
conservation of mass-energy: the greater the velocity ![]() of a point particle is, and the
greater the gravitational field potentials
of a point particle is, and the
greater the gravitational field potentials ![]() and
and ![]() , the electromagnetic field potentials
, the electromagnetic field potentials ![]() and
and ![]() , the pressure field potentials
, the pressure field potentials ![]() and
and ![]() are, the more the mass density
are, the more the mass density ![]() differs from its value at
infinity. For example, if a point particle falls into the gravitational field
with the potential
differs from its value at
infinity. For example, if a point particle falls into the gravitational field
with the potential ![]() , then the change in the particle’s energy is described by the term
, then the change in the particle’s energy is described by the term ![]() . According to (41), such energy change can be compensated by the change
in the rest energy of the particle due to the change
. According to (41), such energy change can be compensated by the change
in the rest energy of the particle due to the change ![]() . Since the gravitational field potential
. Since the gravitational field potential ![]() is always negative, then the mass
density
is always negative, then the mass
density ![]() and the pressure inside the point
particle should increase due to the field potential.
and the pressure inside the point
particle should increase due to the field potential.
This is possible, if we remember that the whole procedure of deriving
the motion equations of particles, field and metric from the principle of least
action is based on the fact that the mass and charge of the substance unit at
varying of the coordinates remain constant, despite of the change in the charge
density, substance density and its volume [7]. If the mass of a simple system
in the form of a point particle and the fields associated with it is
proportional to ![]() , then according to (41) the mass of such a system remains unchanged,
despite of the change in the fields, mass density
, then according to (41) the mass of such a system remains unchanged,
despite of the change in the fields, mass density ![]() and pressure
and pressure ![]() . Conservation of the mass-energy of each particle with regard to the
mass-energy of the fields leads to conservation of the mass-energy of an
arbitrary system including a multitude of particles and the fields surrounding
them. We will remind that this article refers to the continuously distributed
matter, so that each point particle or a unit of this matter may have its own
mass density
. Conservation of the mass-energy of each particle with regard to the
mass-energy of the fields leads to conservation of the mass-energy of an
arbitrary system including a multitude of particles and the fields surrounding
them. We will remind that this article refers to the continuously distributed
matter, so that each point particle or a unit of this matter may have its own
mass density ![]() and its value
and its value ![]() .
.
We will now return to (38) and take the contraction of tensors by means
of multiplying the equation by ![]() , taking
into account the relation
, taking
into account the relation ![]() , and then dividing all by 2:
, and then dividing all by 2:
![]() . (43)
. (43)
where ![]() is the scalar curvature, and it was taken into
account that the contractions of tensors
is the scalar curvature, and it was taken into
account that the contractions of tensors ![]() ,
, ![]() ,
, ![]() and
and ![]() are equal to zero.
are equal to zero.
In case if the cosmological constant ![]() were known, based on (43) we could find the
scalar curvature
were known, based on (43) we could find the
scalar curvature ![]() .
.
In order to simplify the equation (38) in [3] and [4] we introduced the
gauge for ![]() , at which
the following equation would hold, if we additionally take into account the
term with the pressure
, at which
the following equation would hold, if we additionally take into account the
term with the pressure ![]() :
:
![]() . (44)
. (44)
In the gauge (44) the equation for the metric (38) takes the following
form, provided that ![]() , where
, where ![]() is a constant of order of unity:
is a constant of order of unity:
![]() . (45)
. (45)
We will note that if from the right side of (45) we exclude the
stress-energy tensor of the gravitational field ![]() , replace the tensor
, replace the tensor ![]() with the stress-energy tensor of the substance
in the form
with the stress-energy tensor of the substance
in the form ![]() , and also neglect the tensor
, and also neglect the tensor ![]() , then at
, then at ![]() we will obtain a typical equation for the
metric used in the general theory of relativity:
we will obtain a typical equation for the
metric used in the general theory of relativity:
![]() . (46)
. (46)
The equation for the metric (38) and the expression (39) must hold in
the covariant theory of gravitation, provided that ![]() . If in (39) we remove the term
. If in (39) we remove the term ![]() , then we will obtain an expression suitable for use in the general
theory of relativity. In this case, given that
, then we will obtain an expression suitable for use in the general
theory of relativity. In this case, given that ![]() , instead of (39) we obtain the following:
, instead of (39) we obtain the following:
![]() .
(47)
.
(47)
If in (47) we equate the term with the energy of particles in the
electromagnetic field (in the case when the field is zero) to zero, then the
sum of the rest energy density and the pressure energy of each uncharged point
particle must be unchanged. It follows that the pressure change must be
accompanied by a change in the mass density. If the system contains the
electromagnetic field with the 4-potential ![]() acting on the 4-currents
acting on the 4-currents ![]() generating them, then in the general case
there must be inverse correlation of the rest energy, pressure energy and the
energy of charges in the electromagnetic field.
generating them, then in the general case
there must be inverse correlation of the rest energy, pressure energy and the
energy of charges in the electromagnetic field.
Indeed, in the general theory of relativity the mass density determines
the rest energy density and spacetime metric, which represents the
gravitational field. In (47) the energy of charges in the electromagnetic field
is specified by the term ![]() , and the mass density and hence the metric are associated with this
energy at a constant
, and the mass density and hence the metric are associated with this
energy at a constant ![]() . On the other hand, the metric is obtained from (46). Therefore, the
occurrence of the electromagnetic field influences the metric in two relations
— in (47) the mass density and the corresponding metric change, as well as in
the equation for the metric (46) the stress-energy tensor of the substance
. On the other hand, the metric is obtained from (46). Therefore, the
occurrence of the electromagnetic field influences the metric in two relations
— in (47) the mass density and the corresponding metric change, as well as in
the equation for the metric (46) the stress-energy tensor of the substance ![]() changes, while the stress-energy
tensor of the electromagnetic field
changes, while the stress-energy
tensor of the electromagnetic field ![]() also makes contribution to the metric.
also makes contribution to the metric.
A well-known paradox of general theory of relativity is associated with
all of this — the electromagnetic field influences the density, the mass of the
bodies as the source of gravitation, and the metric, while the gravitational
field itself (i.e. metric) does not influence the electrical charges of the
bodies, which are the sources of the electromagnetic field. Thus the
gravitational and electromagnetic fields are unequal relative to each other,
despite the similarity of field equations and the same character of long-range
action. Above we pointed out at the fact that the mass 4-current leads to the
gravitational field gradients, and the addition of the charge to this mass
current generates additional electromagnetic (charge) 4-current and the
corresponding electromagnetic field gradients, depending on the sign of the
charge. From this we can see that the gravitational field looks like a
fundamental, basic and indestructible field and the electromagnetic field
manifests as some superstructure and the result of the charge separation in the
initially neutral substance.
If we consider (44) to be valid, then from comparison with (39) we see
that the equation ![]() must be satisfied. Thus, when
must be satisfied. Thus, when ![]() is considered as a cosmological constant, we
can use it to achieve simplification of the equation for the metric (38) and
bring it to the form of (45). At the same time the relation (39) is symmetrical
with respect to the contribution of the gravitational and electromagnetic
fields to the density, in spite of the difference in fields. We will remind
that in the equation of motion (31) both fields also make symmetrical
contributions to the 4-acceleration of a point charge.
is considered as a cosmological constant, we
can use it to achieve simplification of the equation for the metric (38) and
bring it to the form of (45). At the same time the relation (39) is symmetrical
with respect to the contribution of the gravitational and electromagnetic
fields to the density, in spite of the difference in fields. We will remind
that in the equation of motion (31) both fields also make symmetrical
contributions to the 4-acceleration of a point charge.
Although the gauge for ![]() in the form of (44) seems the simplest and
simplifies some of the equations, in Section 7 the necessity and convenience of
another gauge will be shown.
in the form of (44) seems the simplest and
simplifies some of the equations, in Section 7 the necessity and convenience of
another gauge will be shown.
4. Hamiltonian
In this and the next sections we rely on the standard approach of
analytical mechanics. As the coordinates it is convenient to choose a set of
Cartesian coordinates: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Let us consider action (1) and express the Lagrangian from it:
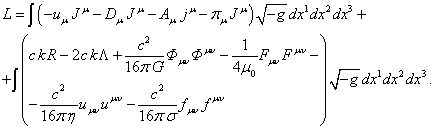 (48)
(48)
The integration in (48) is carried out over the infinite
three-dimensional volume of space and over all the material particles of the
system. We assume that the scalar curvature ![]() depends on the metric tensor, and
the metric tensor
depends on the metric tensor, and
the metric tensor ![]() , the field tensors
, the field tensors ![]() ,
, ![]() ,
, ![]() ,
, ![]() , the density
, the density ![]() , the charge density
, the charge density ![]() and the pressure
and the pressure ![]() are functions of the coordinates
are functions of the coordinates ![]() and do not depend on the particle
velocities. Then the Lagrangian in its general form (48) depends on the
coordinates, as well as on the 4-potential of pressure
and do not depend on the particle
velocities. Then the Lagrangian in its general form (48) depends on the
coordinates, as well as on the 4-potential of pressure ![]() and 4-potentials of the gravitational and
electromagnetic fields
and 4-potentials of the gravitational and
electromagnetic fields ![]() and
and ![]() .
.
We will
divide the first integral in the Lagrangian (48) to the sum of particular
integrals, each of which describes the state of one of the set ![]() of the system’s particles. We will take into
account also that the Lagrangian depends on the three-dimensional velocities of
the particles
of the system’s particles. We will take into
account also that the Lagrangian depends on the three-dimensional velocities of
the particles ![]() , where
, where ![]() specifies the particle’s number, while the
velocity of any particle is part of only one corresponding particular integral.
If we denote by
specifies the particle’s number, while the
velocity of any particle is part of only one corresponding particular integral.
If we denote by ![]() the second integral in (48), which is
associated with the energies of fields inside and outside the fixed physical
system and is independent of the particles’ velocities, then we can write for
the Lagrangian:
the second integral in (48), which is
associated with the energies of fields inside and outside the fixed physical
system and is independent of the particles’ velocities, then we can write for
the Lagrangian:
![]() ,
,
where ![]() is a particular Lagrangian of an arbitrary
particle.
is a particular Lagrangian of an arbitrary
particle.
We will
introduce now the Hamiltonian ![]() of the system as a function of generalized
three-dimensional momenta
of the system as a function of generalized
three-dimensional momenta ![]() of the particles:
of the particles: ![]() . Under the
system’s generalized momentum we mean the sum of the generalized momenta of the
whole set of particles:
. Under the
system’s generalized momentum we mean the sum of the generalized momenta of the
whole set of particles:
![]() .
.
To find the Hamiltonian we will apply the Legendre transformations to
the system of particles:
![]() , (49)
, (49)
provided that
 .
(50)
.
(50)
The equality
in (50) gives the definition of the generalized momentum ![]() , and we
can see that the generalized momentum of an arbitrary particle equals
, and we
can see that the generalized momentum of an arbitrary particle equals 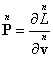 . On the
other hand, the equations
. On the
other hand, the equations 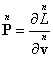 allow us to express the
velocity
allow us to express the
velocity ![]() of an arbitrary particle through its
generalized momentum
of an arbitrary particle through its
generalized momentum ![]() . Then we
can substitute these velocities in (49) and determine
. Then we
can substitute these velocities in (49) and determine ![]() only through
only through ![]() .
.
In order to find ![]() in (50), in each particular Lagrangian
in (50), in each particular Lagrangian ![]() we should express
we should express ![]() and
and ![]() in terms of the velocity
in terms of the velocity ![]() and interval
and interval ![]() :
:
![]() ,
, ![]() , (51)
, (51)
while ![]() and we introduce the notation
and we introduce the notation ![]() , where the four-dimensional quantity
, where the four-dimensional quantity ![]() is not a real 4-vector. With
regard to the definition of the 4-potential of the acceleration field
is not a real 4-vector. With
regard to the definition of the 4-potential of the acceleration field ![]() , for each
particle we obtain:
, for each
particle we obtain:
![]() .
(52)
.
(52)
In (48) the unit of volume of the system in any particular integral can
be expressed in terms of the unit of volume in the reference frame ![]() associated with the particle
in the following way:
associated with the particle
in the following way:
![]() . (53)
. (53)
From this
formula in the weak-field limit in Minkowski space, when ![]() , it
follows that the volume of a moving particle is decreased in comparison with
the volume of a particle at rest. Given that
, it
follows that the volume of a moving particle is decreased in comparison with
the volume of a particle at rest. Given that ![]() , where
, where ![]() is the proper time in the reference frame
is the proper time in the reference frame ![]() of the particle, the equality of 4-volumes in
different reference frames follows from (53):
of the particle, the equality of 4-volumes in
different reference frames follows from (53):
![]() .
.
This equation reflects the fact that the 4-volume is a 4-invariant.
Under the above conditions (40), (51), (52) and (53) can be written for
the Lagrangian (48) as follows:

(54)
as well as after partial volume integration:
 (55)
(55)
where ![]() is the mass of an arbitrary
particle,
is the mass of an arbitrary
particle, ![]() is the particle’s charge. In (55) the scalar
and vector field potentials are averaged over the particle’s volume, that means
they are the effective potentials at the location of the particle.
is the particle’s charge. In (55) the scalar
and vector field potentials are averaged over the particle’s volume, that means
they are the effective potentials at the location of the particle.
In operations with 3-vectors it is convenient to write vectors in the
form of components or projections on the spatial axes of the coordinate system
using, for example, instead of the velocity ![]() the quantity
the quantity ![]() , where
, where ![]() . Then
. Then ![]() ,
, ![]() ,
, ![]() and the velocity derivative can
be represented as:
and the velocity derivative can
be represented as: ![]() . For the gravitational vector potential in particular we obtain:
. For the gravitational vector potential in particular we obtain: ![]() .
.
With this in mind, from (55) and (50) we find:
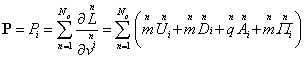 ,
, ![]() . (56)
. (56)
Based on this, we find for the sums of the scalar products of 3-vectors
by summing over the index ![]() :
:
![]() . (57)
. (57)
From (49) taking into account (55) and (57) we have:
 (58)
(58)
In (58) the Hamiltonian contains the scalar curvature ![]() and the cosmological constant
and the cosmological constant ![]() . As it will be shown in Section 6 about the energy, this Hamiltonian
represents the relativistic energy of the system. To make the picture complete
we could also express the quantity
. As it will be shown in Section 6 about the energy, this Hamiltonian
represents the relativistic energy of the system. To make the picture complete
we could also express the quantity ![]() in (58) through the generalized
momentum
in (58) through the generalized
momentum ![]() . We have described this procedure in [4].
. We have described this procedure in [4].
For continuously
distributed substance the masses and charges of the particles in (58) can be
expressed through the corresponding integrals: ![]() ,
, ![]() . Also
taking into account (53), in which we can substitute the expression
. Also
taking into account (53), in which we can substitute the expression ![]() , where
, where ![]() denotes the time component of the 4-velocity
of an arbitrary particle, from (58) we find:
denotes the time component of the 4-velocity
of an arbitrary particle, from (58) we find:
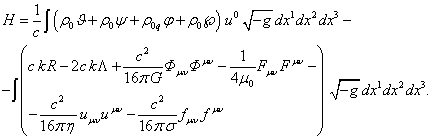 (59)
(59)
If in (58)
we express the masses and charges of the particles through the mass density ![]() and the charge density
and the charge density ![]() from the standpoint of the arbitrary reference frame
from the standpoint of the arbitrary reference frame ![]() , then (58)
can be represented as follows:
, then (58)
can be represented as follows:
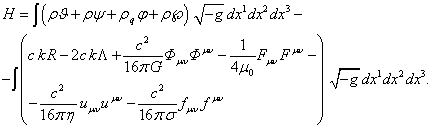 (60)
(60)
We obtained
the Hamiltonian in an arbitrary reference frame ![]() , while in
(59) the densities in reference frames associated with the particles are used
and in (60) such particle densities are used, as they seem to be in
, while in
(59) the densities in reference frames associated with the particles are used
and in (60) such particle densities are used, as they seem to be in ![]() .
.
5. Hamilton’s equations
Assuming
that the Hamiltonian depends on the generalized 3-momenta of particles ![]() :
: ![]() and the Lagrangian depends on 3-velocity of
particles
and the Lagrangian depends on 3-velocity of
particles ![]() :
: ![]() , where
, where ![]() is a three-dimensional radius-vector of
the particle with the number
is a three-dimensional radius-vector of
the particle with the number ![]() , we will
take differentials of
, we will
take differentials of ![]() and
and ![]() , as well
as the differentials of both sides of equation (49):
, as well
as the differentials of both sides of equation (49):
 (61)
(61)
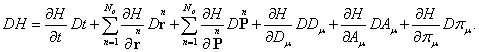 (62)
(62)
![]() . (63)
. (63)
Substituting (61) and (62) into (63), we find:
![]() ,
, 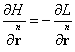 ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, 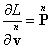 . (64)
. (64)
The last equation in (64) leads to (50) and gives the expression (56)
for the generalized momentum ![]() of an arbitrary particle of the
system in an explicit form.
of an arbitrary particle of the
system in an explicit form.
We will now apply the principle of least action to the Lagrangian in the
form ![]() , equating the action variation to zero, when the particle moves from
the time point
, equating the action variation to zero, when the particle moves from
the time point ![]() to the time point
to the time point ![]() .
.
 (65)
(65)
In (65) it was assumed that the time variation is equal to zero: ![]() . Partial derivatives with variations
. Partial derivatives with variations ![]() ,
, ![]() and
and ![]() lead to field equations (16),
(18) and (26). If we take into account the definition of velocity in the second
term in the integral (65):
lead to field equations (16),
(18) and (26). If we take into account the definition of velocity in the second
term in the integral (65): 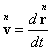 , then the integral for this term is taken by parts. Then for the first
and second terms in the integral (65) we have the following:
, then the integral for this term is taken by parts. Then for the first
and second terms in the integral (65) we have the following:
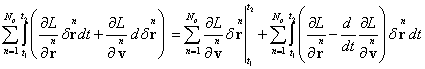 . (66)
. (66)
When varying the action, the variations ![]() are equal to zero only at the
beginning and at the end of the motion, that is when
are equal to zero only at the
beginning and at the end of the motion, that is when ![]() and
and ![]() . Therefore, for vanishing of the variation
. Therefore, for vanishing of the variation ![]() it is necessary that the quantity in brackets
inside the integral (66) would be equal to zero. This leads to the well-known
Lagrange equations of motion:
it is necessary that the quantity in brackets
inside the integral (66) would be equal to zero. This leads to the well-known
Lagrange equations of motion:
 .
(67)
.
(67)
According to (64) 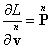 , as well
as
, as well
as 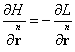 . Let us substitute this in (67):
. Let us substitute this in (67):
 .
(68)
.
(68)
Equation (68) together with equation ![]() from (64)
from (64)
represent the standard Hamiltonian equations describing the motion of an
arbitrary particle of the system in the gravitational and electromagnetic
fields and in the pressure field. According to (68), the rate of change of the
generalized momentum of the particle by the coordinate time is equal to the
generalized force, which is found as the gradient with respect to the
particle’s coordinates of the relativistic energy of the system taken with the
opposite sign. These equations are widely used not only in the general theory
of relativity, but also in other areas of theoretical physics. We have checked
these equations in [4] in the framework of the covariant theory of gravitation
by direct substitution of the Hamiltonian.
6. The system’s energy
We will consider a closed system which is in the state of some
stationary motion. An example would be a charged ball rotating around its
center of mass, which forms the system under consideration together with its
gravitational and electromagnetic fields and the internal pressure. In such a
system the energy should be conserved as a consequence of lack of energy losses
to the environment and taking into account the homogeneity of time, i.e. the
equivalence of the time points for the system’s state.
The system’s Lagrangian, taking into account the fields’ energy, has the
form of (55). Due to the stationary motion we can assume that within the
system’s volume the metric tensor ![]() , the scalar curvature
, the scalar curvature ![]() , the 4-potentials of the field
, the 4-potentials of the field ![]() ,
, ![]() and of the pressure
and of the pressure ![]() do not depend on time. But since
any point particle moves with the ball, then its location and velocity are
changed, being defined by the radius vector
do not depend on time. But since
any point particle moves with the ball, then its location and velocity are
changed, being defined by the radius vector ![]() and velocity
and velocity ![]() , respectively. We may assume that the Lagrangian of the system does not
depend explicitly on time and is a function of the form:
, respectively. We may assume that the Lagrangian of the system does not
depend explicitly on time and is a function of the form: ![]() . Now we will take the time derivative of the Lagrangian, as it is done
for example in [13], only not for one but for a set of particles, and will
apply (67):
. Now we will take the time derivative of the Lagrangian, as it is done
for example in [13], only not for one but for a set of particles, and will
apply (67):
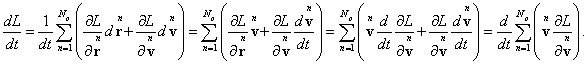
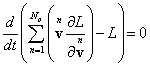 .
.
The quantity in the brackets is not time-dependent and is constant. This
gives the definition of relativistic energy as a conserved quantity for a
closed system at stationary motion:
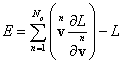 . (69)
. (69)
With regard to (64) and (49), we find the following:
![]() .
(70)
.
(70)
It turns out that the relativistic energy can be expressed in a
covariant form, since according to (70) the formula for the energy coincides
with the formula for the Hamiltonian in (49).
To calculate the relativistic energy of the system with the substance,
which is continuously distributed over the volume, it is convenient to pass
from the mass and charge of the particle to the corresponding densities inside
the particle. According to (59) we obtain:
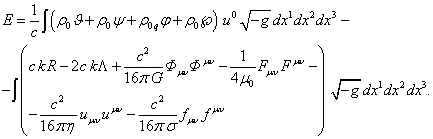 (71)
(71)
Using expression (71) we can find the invariant energy ![]() of the system, for which we
should use the frame of reference of the center of mass and calculate the
integral. In addition, at a known velocity
of the system, for which we
should use the frame of reference of the center of mass and calculate the
integral. In addition, at a known velocity ![]() of the center of mass of the
system in an arbitrary reference frame
of the center of mass of the
system in an arbitrary reference frame ![]() we can calculate the momentum of the system in
we can calculate the momentum of the system in
![]() . This can be clarified as follows. We will define the invariant mass of
the system taking into account the mass-energy of the fields using the
relation:
. This can be clarified as follows. We will define the invariant mass of
the system taking into account the mass-energy of the fields using the
relation: ![]() , where
, where ![]() is the speed of light as a measure of the
velocity of propagation of electromagnetic and gravitational interactions. If
the 4-displacement in
is the speed of light as a measure of the
velocity of propagation of electromagnetic and gravitational interactions. If
the 4-displacement in ![]() has the form:
has the form: ![]() , then for the 4-velocity of the system in
, then for the 4-velocity of the system in ![]() we can write:
we can write: ![]() . The 4-vector
. The 4-vector ![]() defines the 4-momentum, which
contains the relativistic energy
defines the 4-momentum, which
contains the relativistic energy ![]() and relativistic momentum
and relativistic momentum ![]() . This gives the formula for determining the momentum through the
energy:
. This gives the formula for determining the momentum through the
energy: ![]() , and,
correspondingly, for the 4-momentum:
, and,
correspondingly, for the 4-momentum: ![]() .
.
In the reference frame ![]() , in which
the system is at rest
, in which
the system is at rest ![]() ,
, ![]() ,
, ![]() , and then
, and then ![]() , and also
, and also ![]() , that is in the 4-momentum in the reference frame
, that is in the 4-momentum in the reference frame ![]() only the time component is
nonzero.
only the time component is
nonzero.
If we
multiply the 4-momentum by the speed of light, we will obtain the 4-vector of
the form ![]() , the time
component of which is the relativistic energy, equal in value to the
Hamiltonian. Thus we find the 4-vector, which in [4] was called the Hamiltonian
4-vector.
, the time
component of which is the relativistic energy, equal in value to the
Hamiltonian. Thus we find the 4-vector, which in [4] was called the Hamiltonian
4-vector.
7. The cosmological constant gauge and the resulting consequences
We will make transformations and substitute (43) and (39) in (71):
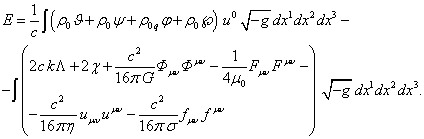 (72)
(72)
If we choose the condition for the cosmological constant in the form:
![]() ,
(73)
,
(73)
then the relativistic energy (72) is uniquely defined, since the
dependence on the constants ![]() and
and ![]() disappears:
disappears:
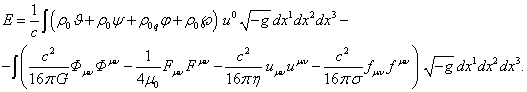 (74)
(74)
We will remind that the quantities ![]() and
and ![]() can have their own values for
each particle of matter. But on condition of (73) the expression for the
relativistic energy (74) becomes universal for any particle in an arbitrary
system of particles and their fields.
can have their own values for
each particle of matter. But on condition of (73) the expression for the
relativistic energy (74) becomes universal for any particle in an arbitrary
system of particles and their fields.
From (73) and (39) the equation follows:
![]() . (75)
. (75)
In order to estimate the value of the cosmological constant ![]() , it is convenient to divide all of the system’s substance into small
pieces, scatter them apart to infinity and leave there motionless. Then the
vector potentials of the fields and pressure become equal to zero and the
relation remains:
, it is convenient to divide all of the system’s substance into small
pieces, scatter them apart to infinity and leave there motionless. Then the
vector potentials of the fields and pressure become equal to zero and the
relation remains: ![]() . It follows that
. It follows that ![]() , just like
, just like ![]() in ( 42), is associated with the
rest energy, with the pressure energy and with the proper energy of the fields
of the system under consideration.
in ( 42), is associated with the
rest energy, with the pressure energy and with the proper energy of the fields
of the system under consideration.
If in some volume there are no particles and the mass density ![]() and the charge density
and the charge density ![]() are zero, then in this volume
there must remain the relativistic energy of the external fields:
are zero, then in this volume
there must remain the relativistic energy of the external fields:
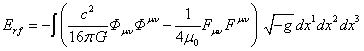 . (76)
. (76)
Based on (74) we can express the energy of a small body at rest. For
simplicity we will assume that the body does not rotate as a whole and there is no motion of the substance and
charges inside of it (an ideal solid body without the intrinsic magnetic field
and the torsion field). Under such conditions the coordinate time of the system
becomes approximately equal to the proper time of the body: ![]() . Since the interval
. Since the interval ![]() , then we obtain:
, then we obtain: ![]() . Since there are no spatial motion in any part of the body, we can
write:
. Since there are no spatial motion in any part of the body, we can
write:
![]() ,
, ![]() .
.
With this in mind we obtain from (74):
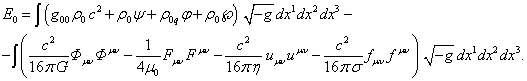 (77)
(77)
In the weak field limit in (77) we can use ![]() ,
, ![]() . The tensor product
. The tensor product ![]() in the absence of substance
motion inside the ideal solid body vanishes. Using (F5) and (F6) we can write:
in the absence of substance
motion inside the ideal solid body vanishes. Using (F5) and (F6) we can write:
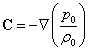 ,
, ![]() ,
,  .
.
Besides in [4] it was found that in the weak field for a motionless body
in the form of a ball with uniform density of mass and charge the following relations hold for the body’s
proper fields:
![]() ,
, ![]() ,
,
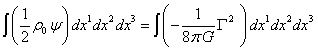 ,
,
![]() . (78)
. (78)
According to (78) the potential energy of the ball’s substance in the
proper gravitational field which is associated with the scalar potential ![]() is twice greater than the
potential energy associated with the field strength
is twice greater than the
potential energy associated with the field strength ![]() . The same is true for the electromagnetic field with the potential
. The same is true for the electromagnetic field with the potential ![]() and the strength
and the strength ![]() both in the case of uniform arrangement of
charges in the ball’s volume and in case of their location on the surface only.
Substituting (78) into (77) in the framework of the special theory of
relativity gives the invariant energy of the system in the form of a fixed
solid spherical body with uniform density of mass and charge, taking into
account the energy of their proper potential fields:
both in the case of uniform arrangement of
charges in the ball’s volume and in case of their location on the surface only.
Substituting (78) into (77) in the framework of the special theory of
relativity gives the invariant energy of the system in the form of a fixed
solid spherical body with uniform density of mass and charge, taking into
account the energy of their proper potential fields:
 (79)
(79)
This calculation is apparently not complete since in reality inside any body there are particles, which cannot be as motionless
as the body itself is. Therefore in (79), in addition to the pressure and its
gradient within the body it is necessary to add the kinetic energy of motion of
all the particles which constitute the body.
7.1. The metric
Substituting (75) and (39) into (43), we find the expression for the
scalar curvature ![]() :
:
![]() , (80)
, (80)
while ![]() , where
, where ![]() is a constant of the order of
unity.
is a constant of the order of
unity.
As it can be seen, the scalar curvature is zero in the whole space
outside the body. The equation ![]() does not mean however, that the
spacetime is flat as in the special theory of relativity, since the curvature
of spacetime is determined by the components of the Riemann curvature tensor.
does not mean however, that the
spacetime is flat as in the special theory of relativity, since the curvature
of spacetime is determined by the components of the Riemann curvature tensor.
We will now substitute (75) into the equation for the metric (38):
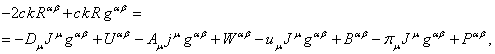 (81)
(81)
that also can be written using (39) as follows:
![]() . (82)
. (82)
If we take the covariant derivative of (82), the left side of the
equation vanishes due to the property of the Einstein tensor located there. The
right side, with regard to the equation of motion (35) and provided that the
metric tensor ![]() in covariant differentiation
behaves as a constant and
in covariant differentiation
behaves as a constant and ![]() is a constant, vanishes too.
is a constant, vanishes too.
In (81) we can use (80) to replace the scalar curvature:
![]()
(83)
If we sum up (81) and (83) and divide the result by 2 , we will obtain
the following equation for the metric:
![]() , (84)
, (84)
while with
regard to (80) ![]() , according
to (35)
, according
to (35) ![]() , and
, and ![]() as the property of the Einstein tensor.
as the property of the Einstein tensor.
In empty space according to (84) the curvature tensor ![]() depends only on the stress-energy
tensors of the gravitational and electromagnetic fields
depends only on the stress-energy
tensors of the gravitational and electromagnetic fields ![]() and
and ![]() , so these fields change the curvature of spacetime outside the bodies.
We will note that in equation (84) the cosmological constant
, so these fields change the curvature of spacetime outside the bodies.
We will note that in equation (84) the cosmological constant ![]() and the tensor
product of the type
and the tensor
product of the type ![]() are missing. This fact makes determination of
the metric tensor components much easier.
are missing. This fact makes determination of
the metric tensor components much easier.
If we compare (84) with the Einstein equation (46), then two major
differences will be found out — in the right side of (84 ) stress-energy
tensors ![]() ,
, ![]() and
and ![]() are present, and in addition the
coefficient in front of the scalar curvature
are present, and in addition the
coefficient in front of the scalar curvature ![]() is two times less than in (46).
is two times less than in (46).
8. Компоненты энергии
In Newtonian mechanics the relations for the Lagrangian and the total
energy are known: ![]() ,
, ![]() , where
, where ![]() denotes the kinetic energy, which
depends only on the velocity, and
denotes the kinetic energy, which
depends only on the velocity, and ![]() denotes the potential energy of the system,
depending both on the coordinates and the velocity. In relativistic physics
instead of individual scalar functions and three-dimensional vectors 4-vectors
and 4-tensors are used, in which the scalar functions and three-dimensional
vectors are combined into one whole. In addition, instead of the negative total
energy
denotes the potential energy of the system,
depending both on the coordinates and the velocity. In relativistic physics
instead of individual scalar functions and three-dimensional vectors 4-vectors
and 4-tensors are used, in which the scalar functions and three-dimensional
vectors are combined into one whole. In addition, instead of the negative total
energy ![]() the positive relativistic energy
the positive relativistic energy ![]() is usually used. While we
have already determined the energy
is usually used. While we
have already determined the energy ![]() in (74), then for the
Lagrangian (54) we should additionally replace the scalar curvature
in (74), then for the
Lagrangian (54) we should additionally replace the scalar curvature ![]() with the help of (80) and the
cosmological constant
with the help of (80) and the
cosmological constant ![]() with the help of (75). Taking
into account the relation
with the help of (75). Taking
into account the relation ![]() this will give the following:
this will give the following:
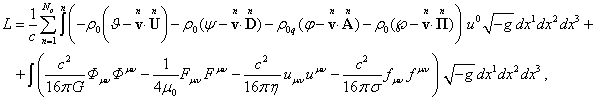
(85)
Calculating the energy ![]() , which is
associated with the four-dimensional motion, as a half-sum of the relativistic
energy (74) and the Lagrangian (85), we find:
, which is
associated with the four-dimensional motion, as a half-sum of the relativistic
energy (74) and the Lagrangian (85), we find:
![]() (86)
(86)
where the index ![]() defines the components of
3-velocity vector
defines the components of
3-velocity vector ![]() of the particle with the number
of the particle with the number ![]() .
.
If in (57)
we replace the masses ![]() and charges
and charges ![]() by the corresponding integrals in the form:
by the corresponding integrals in the form: ![]() ,
, ![]() , and
transform the volume units in the form
, and
transform the volume units in the form ![]() , then we
obtain the relation
, then we
obtain the relation ![]() . As we can
see the kinetic energy
. As we can
see the kinetic energy ![]() of the system in the reference frame of the
center of mass vanishes, only when the velocities
of the system in the reference frame of the
center of mass vanishes, only when the velocities ![]() of all the system’s particles at the same time
vanish.
of all the system’s particles at the same time
vanish.
We will determine the potential energy ![]() as a half-difference of the
relativistic energy (74) and the Lagrangian (85):
as a half-difference of the
relativistic energy (74) and the Lagrangian (85):

(87)
For a solid
body in the limit of the special theory of relativity, when ![]() ,
, ![]() ,
,  , the expression for the kinetic energy (86)
of the system is the following:
, the expression for the kinetic energy (86)
of the system is the following:
![]() (88)
(88)
The main part of the kinetic energy is proportional to the square of the
velocity, and vector potentials of all fields, including the velocity field and
pressure field, make contribution into this part of the energy.
For the
potential energy (87) of a solid body in the limit of special theory of
relativity the tensor product ![]() according to (E8) tends to zero. We will also
take into account the values of other tensor products:
according to (E8) tends to zero. We will also
take into account the values of other tensor products:
![]() ,
, ![]() ,
,
![]() .
.
It gives
the following:

The potential energy depends also on the velocity. If ![]() for all material particles of the system, then
the potential energy of the system remains, taking into account the field
energy:
for all material particles of the system, then
the potential energy of the system remains, taking into account the field
energy:
 (89)
(89)
In the absence of external fields and internal motions in the fixed
system in (89) the fields ![]() ,
, ![]() ,
, ![]() become equal to zero. As a result, with regard
to (78) the potential energy becomes equal to the relativistic energy (79) for
a fixed ideal solid body.
become equal to zero. As a result, with regard
to (78) the potential energy becomes equal to the relativistic energy (79) for
a fixed ideal solid body.
9. Conclusions
We have presented the
Lagrangian of the system as consisting of one term for the curvature and four
pairs of terms of identical form for each of the four fields: gravitational and
electromagnetic fields, acceleration
field and pressure field. As
a result, for each field we have obtained equations coinciding in form with
each other. The spacetime is also represented by its proper tensor metric field
![]() . The mass 4-current
. The mass 4-current ![]() interacts with the specified fields, gaining
energy in them, moreover the electromagnetic field
changes the energy of electromagnetic 4r-current
interacts with the specified fields, gaining
energy in them, moreover the electromagnetic field
changes the energy of electromagnetic 4r-current ![]() . However, the fields
also have their proper energy and momentum, which are part of the tensors
. However, the fields
also have their proper energy and momentum, which are part of the tensors ![]() (5),
(5), ![]() (8),
(8), ![]() (11),
(11), ![]() (14), respectively.
(14), respectively.
The similarity of field equations implies the necessity of gauge not
only of the 4- potentials of the gravitational and electromagnetic fields, but
also of the 4-potentials of the acceleration field and pressure field, as well
as of the mass 4-current ![]() and electromagnetic 4-current
and electromagnetic 4-current ![]() . From the standpoint of physics the meaning of such gauges is that the
source of divergence of the 3-velocity vector of small volume may be the time
changes in the particle’s energy in any fields which are present in the given
volume. This may be the particle’s energy in the velocity field, the energy in
the pressure field or the energy in the gravitational or electromagnetic
fields.
. From the standpoint of physics the meaning of such gauges is that the
source of divergence of the 3-velocity vector of small volume may be the time
changes in the particle’s energy in any fields which are present in the given
volume. This may be the particle’s energy in the velocity field, the energy in
the pressure field or the energy in the gravitational or electromagnetic
fields.
In contrast to the standard approach, we do not use
any of the variety of known forms of stress-energy tensors of matter. Instead,
the energy and momentum of the matter are described based on the acceleration
field, the acceleration field tensor and the stress-energy tensor of the
acceleration field. The contribution of pressure into the system’s energy and
momentum, respectively, is described through the pressure field with the help
of the pressure field tensor and the stress-energy tensor of the pressure field.
In this case, the acceleration field and the pressure field, as well as the
electromagnetic and gravitational fields are regarded as the 4-dimensional
vector fields with their own 4-potentials.
Representation of the gravitational field as a vector
field is performed within the covariant theory of gravitation [3-4], in
contrast to the general theory of relativity, where gravitation is described
indirectly through the spacetime geometry and is considered as a metric tensor
field. We consider as an advantage of
our approach the fact that the energy and momentum of the gravitational field
at each point are uniquely determined with the help of the stress-energy tensor
of the gravitational field. Whereas in the general theory of relativity we have
to restrict ourselves only to the corresponding pseudotensor, such as the
Landau-Lifshitz stress-energy pseudotensor [13].
In order to uniquely
identify the relativistic energy of a particle or a substance unit, we used a
special gauge of the cosmological constant, giving this constant the meaning of
the rest energy of the particle with “turned-off” external fields and influences.
This led to the expression for the relativistic energy of the system (74) and
to the equation for the metric (84), the right side of which is the sum of four
stress-energy tensors of the fields.
In the absence of the cosmological
constant in the Lagrangian (1) it would be impossible to perform the specified
calibration, the physical system’s energy would be uncertain, and the presented
theory would remain unfinished. In our approach, the cosmological constant does
not reflect the energy density of the empty cosmic space, or the so-called dark
energy, but rather the energy density of the matter scattered in space. Given
that ![]() ,
where
,
where ![]() is a constant of the order of unity, it follows from (75) that
is a constant of the order of unity, it follows from (75) that ![]() .
Substituting here the standard estimate
of the cosmological constant
.
Substituting here the standard estimate
of the cosmological constant ![]() m-2,
we find the corresponding mass density:
m-2,
we find the corresponding mass density: ![]() kg/m. This
density is sufficiently close to the density of cosmic matter, averaged over
the entire space.
kg/m. This
density is sufficiently close to the density of cosmic matter, averaged over
the entire space.
It can be noted that our expression
for the relativistic energy and the equation for the metric differ
substantially from those obtained in the general theory of relativity. For the
energy it follows from the fact that instead of the stress-energy tensor of
matter we use the stress-energy tensors of the acceleration field and the
pressure field, while the gravitational field is directly included in the
energy, and not indirectly through the metric.
Let us take the Einstein equation
for the metric with the cosmological constant from [14]. In the general case,
the right-hand side of this equation contains the stress-energy tensor of the
electromagnetic field ![]() and the stress-energy tensor of matter
and the stress-energy tensor of matter ![]() :
:
![]() .
(90)
.
(90)
The simplest form of the stress-energy tensor of
matter without taking into account the pressure is expression in terms of the
mass density and the four-velocity: ![]() . Contraction (90) with
the metric
tensor
. Contraction (90) with
the metric
tensor ![]() gives
the following:
gives
the following:
![]() .
.
where ![]() .
.
After substituting ![]() in
(90), the equation for the metric is transformed as follows:
in
(90), the equation for the metric is transformed as follows:
![]() .
(91)
.
(91)
Now equation for the metric (91) in the
general theory of relativity can be compared with our equation for the metric
(84). The main difference is that in (84) all the tensors on the right side act
the same way and in contraction with the metric tensor they vanish. But it is
not the case in (91) – if the expression ![]() is valid for the electromagnetic stress-energy
tensor, then for the stress-energy tensor of matter the relation
is valid for the electromagnetic stress-energy
tensor, then for the stress-energy tensor of matter the relation ![]() does not hold, so that in (91) one more term
does not hold, so that in (91) one more term ![]() is needed. As a result, in the general theory
of relativity not only the gravitational field is represented in a special way,
through the metric tensor, which differs from the method of introducing the
electromagnetic field into the equation for the metric, but also the
stress-energy tensor of matter
is needed. As a result, in the general theory
of relativity not only the gravitational field is represented in a special way,
through the metric tensor, which differs from the method of introducing the
electromagnetic field into the equation for the metric, but also the
stress-energy tensor of matter ![]() is not symmetric with respect to the metric,
in contrast to the stress-energy tensor of the electromagnetic field
is not symmetric with respect to the metric,
in contrast to the stress-energy tensor of the electromagnetic field ![]() .
.
10. References
1. C. W. Misner, K. S. Thorne, and J.
A. Wheeler, Gravitation (W. H.
Freeman, San Francisco, CA, 1973).
2.
N. J. Poplawski, A Lagrangian description of interacting energy. – arXiv:gr-qc/0608031v2.
3.
S.G.
Fedosin, The Principle of Least
Action in Covariant Theory of Gravitation. Hadronic
Journal, 2012, Vol. 35, No. 1, P. 35 – 70.
4.
S.G.
Fedosin, The Hamiltonian in
Covariant Theory of Gravitation. Advances in Natural
Science, 2012, Vol. 5, No. 4, P. 55 – 75.
5. D. Hilbert, Die Grundlagen der Physik. (Erste Mitteilung), Göttinger Nachrichten, math.-phys. Kl., 1915, pp. 395-407.
6. H. Weyl, Raum. Zeit. Materie. Vorlesungen über allgemeine Relativitätstheorie (J. Springer, Berlin, 1919).
7.
V. A. Fock, The
Theory of Space, Time and Gravitation (Pergamon Press, London, 1959).
8. P. A. M. Dirac, General Theory of
Relativity (John Wiley & Sons, New-York, 1975).
9. W. Pauli, Theory of Relativity
(Dover Publications, New York, 1981).
10.
M. Born,
Die träge Masse und das Relativitätsprinzip,
Annalen der Physik, Vol. 333,
No. 3, 1909, pp. 571-584.
11.
S. G. Fedosin, Fizicheskie teorii i beskonechnaia vlozhennost’ materii (Perm, 2009).
12.
Р. Утияма, Теория
относительности (М., Атомиздат, 1979).
13.
L.D. Landau and E.M. Lifshitz, The
Classical Theory of Fields (Vol. 2, 4th ed. Butterworth-Heinemann, 1975).
14. A. Einstein, Die Grundlage der allgemeinen Relativitätstheorie, Annalen der Physik, 1916, Vol. 354, No. 7, P. 769-822.
Appendix
A. Variation of the sixth term in the action function
We need to find the variation for the sixth term in
(1):
![]() . (A1)
. (A1)
We will need the expressions for variation of the
metric tensor and the 4-vector of the mass current, which can be found, for
example, in [7], [9], [14]:
![]() ,
, ![]() . (A2)
. (A2)
![]() . (A3)
. (A3)
In view of (A2) and (A3) we have the following:
 (A4)
(A4)
We will transform the first term in (A4) with the help
of functions’ product differentiation by parts:
![]() .
.
In action variation the term with the divergence can
be neglected, the remaining term can be transformed as follows:
![]()
Substituting these results in (A4) and then in (A1),
we find:
 .
.
Appendix
B. Variation of the seventh term in the action function
Variation for the seventh term in (1) for the special
case, when ![]() is a constant, taking into
account (A2) will be equal to:
is a constant, taking into
account (A2) will be equal to:
![]() ,
,
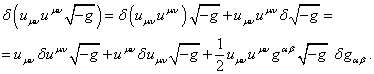 (B1)
(B1)
Since ![]() , the tensor
, the tensor ![]() is antisymmetric, then using
the expression for
is antisymmetric, then using
the expression for ![]() from
(A2), we find:
from
(A2), we find:
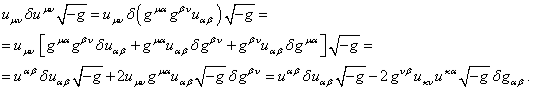
Substituting this expression in (B1) gives the
following:
![]() (B2)
(B2)
We will denote by ![]() the
stress-energy tensor of the acceleration field:
the
stress-energy tensor of the acceleration field:
![]() .
(B3)
.
(B3)
Given that ![]() , using differentiation by parts, as well as the equation which is valid
for the antisymmetric tensor:
, using differentiation by parts, as well as the equation which is valid
for the antisymmetric tensor: ![]() , for the term
, for the term ![]() in (B2) we obtain:
in (B2) we obtain:

The term ![]() in
the last expression is the divergence and it can be neglected in the variation
of the action function.
in
the last expression is the divergence and it can be neglected in the variation
of the action function.
Substituting the remaining term in (B2) and then in
(B1) and using (B3), we find:

Appendix
C. Variation of the eighth term in the action function
Action variation for the eighth term in (1) has the
form:
![]() .
.
Acting like in Appendix A, taking into account (A2)
and (A3) we find:

![]() .
.
In action variation the term with the divergence is
insignificant; the second term is transformed further:
![]()
As a result, the variation of the eighth term equals:

Appendix
D. Variation of the ninth term in the action function
In the special case when ![]() is a
constant, for the variation of the ninth term in (1), with regard to (A2), we
have:
is a
constant, for the variation of the ninth term in (1), with regard to (A2), we
have:
![]() ,
,
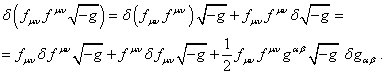 (D1)
(D1)
Replacing ![]() and
using
and
using ![]() in (A2), we transform the first
term of the equation and then substitute it in (D1):
in (A2), we transform the first
term of the equation and then substitute it in (D1):

![]() .
.
We will denote by ![]() the
stress-energy tensor of the pressure field:
the
stress-energy tensor of the pressure field:
![]() .
(D2)
.
(D2)
We will transform the term ![]() , given that
, given that ![]() , using differentiation by parts as well as equation
, using differentiation by parts as well as equation ![]() which is valid for the
antisymmetric tensor:
which is valid for the
antisymmetric tensor:
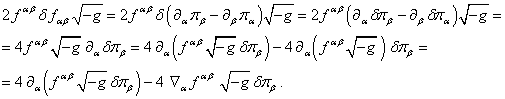
In the latter equation the term with the divergence
can be neglected, since it does not contribute to the variation of the action
function. Substituting the results in (D1), we find the required variation:
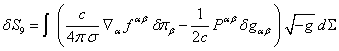 .
.
Appendix
E. Acceleration tensor and equations for the acceleration field
By definition, the acceleration field appears
as a result of applying the 4-rotor to the 4-potential:
![]() .
.
The tensor ![]() is antisymmetric and includes various
components of accelerations. By its structure this tensor is similar to the
gravitational tensor
is antisymmetric and includes various
components of accelerations. By its structure this tensor is similar to the
gravitational tensor ![]() and the electromagnetic tensor
and the electromagnetic tensor ![]() ,
each of which consists of two vector components depending on the field
potentials and the velocities of the field sources.
,
each of which consists of two vector components depending on the field
potentials and the velocities of the field sources.
In order to better understand the physical
meaning of the acceleration field, we will introduce the following notations:
![]() ,
, ![]() , (E1)
, (E1)
where the indices ![]() form triples of nonrecurring numbers of the form 1,2,3 or 3,1,2 or
2,3,1; 3-vectors
form triples of nonrecurring numbers of the form 1,2,3 or 3,1,2 or
2,3,1; 3-vectors ![]() and
and ![]() can be written by components:
can be written by components: ![]() ;
; ![]() .
.
Then the tensor ![]() can be represented as follows:
can be represented as follows:
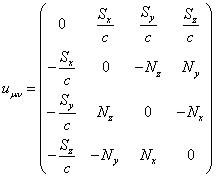 . (E2)
. (E2)
In order to simplify our further arguments, we
will consider the case of the flat spacetime, i.e. Minkowski space or the
spacetime of the special theory of relativity. The role of the metric tensor in
this case is played by the tensor ![]() , the non-zero
components of which are
, the non-zero
components of which are ![]() ,
, ![]() .
With its help we will raise the indices of the acceleration tensor:
.
With its help we will raise the indices of the acceleration tensor:
 . (E3)
. (E3)
We will expand the 4-vector of the mass
current: ![]() ,
where
,
where ![]() . In
equations (22) and (23) we can replace the covariant derivatives
. In
equations (22) and (23) we can replace the covariant derivatives ![]() with the partial derivatives
with the partial derivatives ![]() . Now
with the help of the vectors
. Now
with the help of the vectors ![]() and
and ![]() these equations can be presented as follows:
these equations can be presented as follows:
![]() ,
, ![]() ,
, ![]() ,
, ![]() . (E4)
. (E4)
The equations (E4) obtained in the framework of
the special theory of relativity for the case ![]() are similar by their form to Maxwell equations
in electrodynamics.
are similar by their form to Maxwell equations
in electrodynamics.
If we multiply scalarly the second equation in
(E4) by ![]() and multiply scalarly the fourth equation by
and multiply scalarly the fourth equation by ![]() and sum up the results, we will obtain the
following:
and sum up the results, we will obtain the
following:
![]() .
(E5)
.
(E5)
Equation (E5) contains the Poynting’s theorem
applied to the acceleration field. The meaning of this differential equation is
that if in a system the work is done to accelerate the particles, then the
power of this work is associated with the divergence of the acceleration
field’s flux and the change in time of the energy associated with the
acceleration field. The relation (E5) in a generally covariant form according
to (33) can be written as follows:
![]() .
.
We will now substitute (E2) in (30) and write
the scalar and vector relations for the components of the 4-acceleration ![]() :
:
![]() ,
,
![]() .
(E6)
.
(E6)
The components of the 4 -acceleration are
obtained from these relations after canceling ![]() . As we can
see both vectors
. As we can
see both vectors ![]() and
and ![]() make contribution to the space component
make contribution to the space component ![]() of the 4-acceleration, and the vector
of the 4-acceleration, and the vector ![]() has the dimension of an ordinary
3-acceleration, and the dimension of the vector
has the dimension of an ordinary
3-acceleration, and the dimension of the vector ![]() is the same as that of the frequency.
is the same as that of the frequency.
If we take into account that the 4-potential
of the acceleration field ![]() in the case of one particle can be regarded as the
covariant 4-velocity, then from (E1) in Minkowski space it follows:
in the case of one particle can be regarded as the
covariant 4-velocity, then from (E1) in Minkowski space it follows:
![]() ,
, ![]() . (E7)
. (E7)
The vector ![]() is the acceleration field strength and the
vector
is the acceleration field strength and the
vector ![]() is a quantity similar in its meaning to the
magnetic field induction in electrodynamics or to the torsion field in the
covariant theory of gravitation (the gravitomagnetic field in the general
theory of relativity). At the constant velocity
is a quantity similar in its meaning to the
magnetic field induction in electrodynamics or to the torsion field in the
covariant theory of gravitation (the gravitomagnetic field in the general
theory of relativity). At the constant velocity ![]() the vectors
the vectors ![]() and
and ![]() vanish. If there are nonzero time derivatives
or spatial gradients of the velocity, then the acceleration field with the
components
vanish. If there are nonzero time derivatives
or spatial gradients of the velocity, then the acceleration field with the
components ![]() and
and ![]() and the acceleration tensor
and the acceleration tensor ![]() appear. In this case it is possible to state that the nonzero tensor
appear. In this case it is possible to state that the nonzero tensor ![]() in the inertial reference frame leads to the
corresponding inertia forces as the consequence of any acceleration of bodies
relative to the chosen reference frame.
in the inertial reference frame leads to the
corresponding inertia forces as the consequence of any acceleration of bodies
relative to the chosen reference frame.
If we substitute the tensors from (E2) and (E3)
into (B3), then thus the stress-energy tensor of the acceleration field ![]() will be expressed through the vectors
will be expressed through the vectors ![]() and
and ![]() . In
particular, for the tensor invariant
. In
particular, for the tensor invariant ![]() and the time components of the tensor
and the time components of the tensor ![]() we have:
we have:
![]() ,
, ![]() ,
, ![]() . (E8)
. (E8)
The component ![]() after its integration over the volume in the
Lorentz reference frame determines the energy of the acceleration field in the
given volume, and the vector
after its integration over the volume in the
Lorentz reference frame determines the energy of the acceleration field in the
given volume, and the vector ![]() is the density of the energy flux of the acceleration
field. Therefore, to calculate the energy flux of the acceleration field the
vector
is the density of the energy flux of the acceleration
field. Therefore, to calculate the energy flux of the acceleration field the
vector ![]() also should be integrated over the volume.
also should be integrated over the volume.
Appendix F. The
pressure tensor and equations for the pressure field
The pressure tensor is built by antisymmetric
differentiation of the 4-potential ![]() :
:
![]() .
.
We will introduce the following notations:
![]() ,
, ![]() , (F1)
, (F1)
where the indices ![]() form triples of nonrecurring numbers of the
form 1,2,3 or 3,1,2 or 2,3,1; the 3-vectors
form triples of nonrecurring numbers of the
form 1,2,3 or 3,1,2 or 2,3,1; the 3-vectors ![]() and
and ![]() in the Cartesian coordinates have the components:
in the Cartesian coordinates have the components: ![]() ;
; ![]() .
.
In the specified notations the tensor ![]() can be represented by the components:
can be represented by the components:
 . (F2)
. (F2)
In Minkowski space the metric tensor does not depend
on the coordinates and time and consists of zeros and ones. In such space the
components of the tensor ![]() repeat the components of the tensor
repeat the components of the tensor ![]() and differ only in the signs of the time
components:
and differ only in the signs of the time
components:
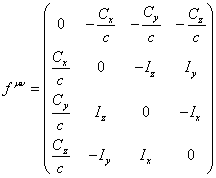 . (F3)
. (F3)
Substituting in equations (26) and (27) the
covariant derivatives ![]() with the partial derivatives
with the partial derivatives ![]() , we can
represent these equations in the form of four equations for the vectors
, we can
represent these equations in the form of four equations for the vectors ![]() and
and ![]() :
:
![]() ,
, ![]() ,
, ![]() ,
, ![]() . (F4)
. (F4)
We will remind that the equations (F4),
obtained in the framework of the special theory of relativity, are valid for
the case of ![]() . Similarly
to (E5), we obtain the equation of local pressure energy conservation:
. Similarly
to (E5), we obtain the equation of local pressure energy conservation:
![]() .
.
This equation also follows from equation (34)
and can be written with the help of the tensor ![]() according to (D2) as follows:
according to (D2) as follows:
![]() .
.
Tensor invariant ![]() and the time components of the tensor
and the time components of the tensor ![]() are expressed with the help of (F2) and (F3)
through the vectors
are expressed with the help of (F2) and (F3)
through the vectors ![]() and
and ![]() :
:
![]() ,
, ![]() ,
, ![]() . (F5)
. (F5)
The component ![]() of the stress-energy tensor of pressure
determines the pressure energy density inside the bodies, and the vector
of the stress-energy tensor of pressure
determines the pressure energy density inside the bodies, and the vector ![]() defines the density of the pressure energy
flux.
defines the density of the pressure energy
flux.
We will now estimate the quantity ![]() with the index
with the index ![]() . According to
(31), this quantity determines the contribution of the pressure field into the
total density of the force acting on the particle. In view of (F2) it turns out
that the density of the pressure force has two components:
. According to
(31), this quantity determines the contribution of the pressure field into the
total density of the force acting on the particle. In view of (F2) it turns out
that the density of the pressure force has two components:
![]() .
.
For comparison , the time component is the
density of the pressure force capacity divided by the speed of light:
![]() .
.
The vector ![]() has the dimension of acceleration and the
vector
has the dimension of acceleration and the
vector ![]() has the dimension of frequency. These vectors
with the help of (F1) and the definition of the 4-potential of the pressure
field
has the dimension of frequency. These vectors
with the help of (F1) and the definition of the 4-potential of the pressure
field ![]() in Minkowski space can be written as follows:
in Minkowski space can be written as follows:
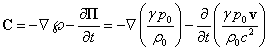 , (F6)
, (F6)
 ,
,
where ![]() denotes the 4-velocity,
denotes the 4-velocity, ![]() is the pressure in
the frame of reference associated with the particle,
is the pressure in
the frame of reference associated with the particle, ![]() is the Lorentz factor and
is the Lorentz factor and ![]() is the particle velocity.
is the particle velocity.
The vector ![]() according to its properties is similar to the
magnetic induction vector and the vector
according to its properties is similar to the
magnetic induction vector and the vector ![]() is similar to the electric field strength.
Motionless particles do not create the vector
is similar to the electric field strength.
Motionless particles do not create the vector ![]() and for the vanishing of the vector
and for the vanishing of the vector ![]() it is also necessary that the relation
it is also necessary that the relation ![]() would not depend on the coordinates. In this
case, the contribution of the pressure field into the acceleration of the
particles will be zero.
would not depend on the coordinates. In this
case, the contribution of the pressure field into the acceleration of the
particles will be zero.
Source:
http://sergf.ru/ccen.htm