In English

 

Canadian Journal of Physics, Vol. 94, No. 4, P. 370-379 (2016). http://dx.doi.org/10.1139/cjp-2015-0593

 

Оценка физических параметров планет и звёзд в модели гравитационного равновесия

 

Федосин Сергей Григорьевич

ул. Свиязева 22-79, город Пермь, 614088, Пермский край, Россия

e-mail intelli@list.ru

 

На основе теории поля рассматриваются уравнения движения вещества в гравитационном поле, поле ускорений, поле давления и в других полях. Это позволяет в рамках модели гравитационного равновесия вывести простые формулы, позволяющие делать оценки физических параметров космических тел. Коэффициент поля ускорений  и коэффициент поля давления  оказываются функцией состояния вещества, а их сумма близка по величине к постоянной гравитации . В представленной модели находятся зависимости внутренней температуры и давления от текущего радиуса. Вычисляются центральные температуры и давления для Земли и Солнца, для типичной нейтронной звезды и белого карлика. Находится тепловой поток и коэффициент теплопроводности вещества этих объектов, приводится формула для оценки энтропии. Все величины сравниваются с результатами расчётов в различных моделях космических тел. Обнаруженное хорошее согласие с этими данными подтверждает эффективность и универсальность предлагаемой модели как для оценки параметров планет и звёзд, так и для более точных расчётов физических величин.

Ключевые слова:  теория поля; поле ускорений; поле давления; гравитационное поле; модель гравитационного равновесия.

 

Estimation of the physical parameters of planets and stars in the gravitational equilibrium model

Sergey G. Fedosin

Sviazeva Str. 22-79, Perm, 614088, Perm region, Russian Federation

e-mail intelli@list.ru

 

The motion equations of matter in the gravitational field, acceleration field, pressure field and other fields are considered based on the field theory. This enables us to derive simple formulas in the framework of the gravitational equilibrium model, which allow us to estimate the physical parameters of cosmic bodies. The acceleration field coefficient  and the pressure field coefficient  are a function of the state of matter, and their sum is close in magnitude to the gravitational constant . In the presented model the dependence is found of the internal temperature and pressure on the current radius. The central temperatures and pressures are calculated for the Earth and the Sun, for a typical neutron star and a white dwarf. The heat flux and the thermal conductivity coefficient of the matter of these objects are found, and the formula for estimating the entropy is provided. All the quantities are compared with the calculation results in different models of cosmic bodies. The discovered good agreement with these data proves the effectiveness and universality of the proposed model for estimating the parameters of planets and stars and for more precise calculation of physical quantities.

Keywords: field theory; acceleration field; pressure field; gravitational field; gravitational equilibrium model.

PACS: 03.30.+p, 03.50.-s, 03.65.pm, 04.40.-b, 95.30.Sf

 

Résumé: Sur la base de la théorie des champs les équations du mouvement de la matière dans le champ gravitationnel, le champ de l'accélération, le champ de pression et dans autres champs sont considérées. Cela permet de dériver dans le domaine du modèle d'équilibre gravitationnel des formules simples qui permettent de faire des estimations des paramètres physiques des corps spatiaux. Le coefficient du champ de l'accélération  et le coefficient du champ de pression  sont une fonction de l'état de la matière, et leur somme est proche en amplitude à la constante gravitationnelle . Dans le présent modèle, les dépendances de temperature et pression intérieures du rayon actuel sont trouvées. Les températures centrales et les pressions sont calculées pour la Terre et le Soleil, pour une étoile à neutrons typique et une naine blanche. Le flux thermique et le coefficient de conductivité thermique de la matière de ces objets sont trouvés et une formule d'estimation de l'entropie est présentée. Toutes les quantités sont comparées avec les résultats des calculs en les différents modèles de corps spatiaux. Une bonne conformité trouvée avec les données confirme l'efficacité et l'universalité du modèle proposé pour estimer les paramètres des planètes et des étoiles, et pour les calculs plus précis de quantités physiques.

Les mots-clés: la théorie du champ, le champ d’accélération, le champ de pression, le champ gravitationnel, modèle d’équilibre gravitationnel.

 

1. Введение

Наиболее точные модели космических объектов включают в себя детальные числовые расчёты отдельных внутренних структур (твёрдое или жидкое ядро, оболочка, конвективная зона), с применением уравнений состояния различных фаз вещества и действующих полей. Для компактных объектов необходимым становится учёт квантовых и релятивистских эффектов.

Однако в арсенале физики имеются модели, позволяющие быстро оценить характерные параметры планет и звёзд, исходя лишь из таких наблюдаемых данных, как радиус, светимость, спектр, температура поверхности, гравитационное красное смещение, данные астросейсмологии и т.д. Известным примером является политропная модель, в которой давление газа связано с плотностью вещества политропой, при условии постоянства теплоёмкости вещества [1-3]. При политропном индексе  и  модель даёт правильный порядок величин центральной плотности, температуры, давления, потенциальной гравитационной энергии и ряда других величин.

Белые карлики представляют собой объекты, в которых электронный газ подвергается вырождению и осуществляет основной вклад в давление в веществе. Для нейтронных звёзд то же самое следует для нейтронного газа. Известен простой расчёт состояния вещества в белых карликах и в нейтронных звёздах, основанный на равенстве гравитационной энергии и квантовомеханической энергии, и дающий типичные значения масс и радиусов этих объектов. Более точный анализ приводит к пределу Чандрасекара [4-5] как наибольшей массе белого карлика, при превышении которой он превращается в нейтронную звезду.

В [6] структура компактных звёзд моделируется путём решения уравнения гидростатического равновесия и параметризации зависимости плотности вещества от радиуса. Это приводит к зависимости масс и радиусов объектов от центральной плотности и к зависимости давления от радиуса, выраженным через гамма функцию и гипергеометрическую функцию.

Естественными недостатками указанных подходов являются ограниченный диапазон применения или невысокая точность предсказаний физических величин и внутренней структуры объектов.

Далее мы представляем модель гравитационного равновесия, основанную на теории поля. С целью иллюстрации возможностей модели мы вычисляем некоторые физические величины ряда объектов и сравниваем их с результатами расчётов других авторов. Положительной стороной предлагаемого подхода является его универсальность, которая позволяет применять его для любых космических объектов. Кроме этого, модель даёт очень простые формулы для оценки параметров планет и звёзд при минимуме необходимых допущений.

 

2. Описание модели

В модели гравитационного равновесия предполагается, что соответствующий объект (планета, звезда) находится в состоянии, когда в нём завершились процессы обмена энергией между гравитационным полем и другими полями. С теоретической точки зрения все поля, действующие в космических объектах, можно рассматривать как компоненты единого общего поля [7]. Кроме гравитационного поля, являющегося основной компонентой, в общее поле могут делать вклад электромагнитное поле, поле давления, поле ускорений, поле диссипации, поле сильного взаимодействия, поле слабого взаимодействия, а также другие поля в веществе рассматриваемых объектов. В состоянии равновесия все поля становятся относительно самостоятельными, поскольку потоки энергии между полями и веществом в среднем стремятся к нулю. Из принципа наименьшего действия вытекает выражение для уравнений общего поля:

 

,                        ,                                 (1)

 

где  − тензор общего поля,

 − коэффициент общего поля,

 − символ Леви-Чивиты  или совершенно антисимметричный единичный тензор,

 – массовый 4-ток,

 – плотность массы в сопутствующей частице системе отсчёта,

 – 4-скорость точечной частицы,  – скорость света.

 

Поскольку тензор общего поля является суммой тензоров частных полей, то уравнения любого поля могут быть представлены в виде (1) после соответствующей замены тензора поля, постоянной этого поля и 4-тока. Характерной особенностью (1) является то, что уравнения общего поля и каждого частного поля имеют форму уравнений Максвелла для электромагнитного поля, записанных в ковариантном виде в искривлённом пространстве для неинерциальных систем отсчёта.

 

3. Поле ускорений и температура

Уравнения поля ускорений в согласии с (1) имеют следующий вид [8]:

 

,                        ,                                 (2)

 

где  − тензор поля ускорений,  − коэффициент поля ускорений.

 

Тензор  имеет в своём составе векторные компоненты  и , находимые по правилу:

 

,                 ,                     (3)

 

где индексы  образуют тройки неповторяющихся чисел вида 1,2,3 или 3,1,2 или 2,3,1; 3-векторы   и  можно расписать по компонентам: ;   .

 

С целью упрощения рассмотрим уравнения (2) в плоском пространстве Минковского, то есть в рамках специальной теории относительности. В этом случае (2) записываются как уравнения для напряжённости  и соленоидального вектора  поля ускорений:

 

,      ,      ,      .         (4)

 

С помощью векторов  и  можно построить 4-вектор ускорения, присущий частицам тела, движущимся со скоростью  и имеющим фактор Лоренца :

 

,

.                                 (5)

 

Гравитационно-связанное тело имеет как правило сферическую форму, так что 4-ускорение  с ковариантным индексом будет некоторой функцией координат. Векторы  и  позволяют также вычислить тензор энергии-импульса поля ускорений  и вектор , являющийся вектором плотности потока энергии-импульса поля ускорений.

Основной причиной того, что поле ускорений частиц вещества имеет свою плотность энергии, плотность потока энергии и напряжения поля, является сила гравитации. Под действием этой силы в космических телах формируются градиенты давления, температуры, плотности вещества и других величин. По мере приближения к центру тела растёт температура, соответственно средняя скорость движения частиц и величина 4-скорости. Для одной частицы 4-потенциалом поля ускорений является ковариантная 4-скорость  этой частицы. Однако в случае множества тесно взаимодействующих частиц это уже не так – в суммарном 4-потенциале поля ускорений системы   скалярный потенциал  и векторный потенциал  поля ускорений становятся независимыми друг от друга величинами как следствие разных правил суммирования вкладов скалярных и векторных величин разных частиц.

В [9] мы вычислили энергию и вектор плотности потока энергии-импульса  поля ускорений для множества одинаковых заряженных частиц, образующих гравитационно связанную систему в виде некоторой жидкости и заполняющих сферический объём. То же самое было сделано и для других полей, включая гравитационное и электромагнитное поля, а также поле давления. Это позволило оценить в первом приближении коэффициент поля ускорений через гравитационную постоянную , электрическую постоянную  и отношение  для рассматриваемых частиц:

 

.                                                      (6)

 

В статье [10] концепция поля ускорений позволила нам вычислить релятивистскую энергию системы частиц и гравитационную массу системы, а в [11] – вывести релятивистские уравнения Навье-Стокса для вязкого заряженного вещества с учётом поля давления и поля диссипации.

Поскольку в определении   тензор ускорений выражается через 4-потенциал поля ускорений, в уравнениях (2) можно перейти от тензора ускорений к 4-потенциалу . Это приводит к волновым уравнениям для потенциалов  и  поля ускорений [12]:

 

.            (7)

 

В (7)  представляет собой 4-потенциал поля ускорений, выраженный с контравариантным индексом с помощью метрического тензора , а  есть символы Кристоффеля, являющиеся функцией . Мы решали уравнение (7) в [9] для случая системы множества хаотически движущихся частиц без общего вращения, связанных друг с другом посредством гравитации и электромагнитного поля с учётом поля давления. В пространстве Минковского скалярная компонента (7) сводится к уравнению для фактора Лоренца, при этом получается следующее:

 

,           ,         ,                     (8)

 

где фактор Лоренца  

 

является функцией текущего радиуса  внутри сферы и усреднённым значением для множества частиц,  – средняя скорость частиц в системе отсчёта , связанной с центром инерции системы.

 

Решением (8) для случая однородной плотности является следующее выражение:

 

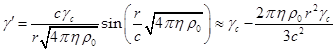,                            (9) 

 

где  есть фактор Лоренца для скоростей  частиц в центре сферы.

 

Из (9) путём взведения в квадрат приблизительно получаем:

 

,                                                    (10)

 

так что по мере увеличения текущего радиуса  внутри сферы при переходе от центра к периферии сферы скорость  частиц уменьшается.

 

Предполагая, что скорость  есть среднеквадратичная скорость частиц, и учитывая её связь с кинетической температурой в виде , где  – постоянная Больцмана, выражение (10) преобразуется в зависимость температуры от радиуса:

 

.                                    (11)

 

где  обозначает температуру в центре сферы,  есть масса одной частицы газа,  представляет собой массу внутри текущего радиуса .

 

Из (11) следует, что температура внутри космических тел в первом приближении спадает по параболе, завися от квадрата радиуса точки наблюдения. Полагая в (11), что при радиусе тела  масса тела становится равной , и пренебрегая температурой поверхности , находим формулу для температуры в центре тела:

 

.                                                           (12)

 

4. Поле давлений

4-потенциал поля давления для одной частицы находится путём умножения функции, зависящей от давления и плотности, на ковариантную 4-скорость [8-9], [12]:

 

,                                              (13)

 

где  и  обозначают давление и плотность в системе отсчёта  частицы, безразмерное отношение  пропорционально энергии давления частицы в расчёте на единицу массы частицы,  и  являются скалярным и векторным потенциалами поля давления.

 

Для системы частиц (13) можно также считать справедливым, но под   следует полагать не 4-скорость какой-либо конкретной частицы, а усреднённую 4-скорость по некоторому ансамблю частиц вблизи точки наблюдения.

Уравнения поля давления в согласии с (1) выглядят следующим образом:

 

,                      ,                            (14)

 

где  − тензор поля давления,  − коэффициент поля давления.

 

Тензор  представляет собой результат применения 4-ротора к 4-потенциалу :

 

,                                        (15)

 

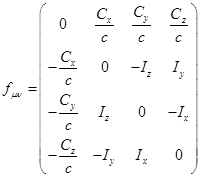.                                           (16)

 

 

 

 

при этом компонентами тензора оказываются компоненты вектора напряжённости   и соленоидального вектора  поля давления.

 

В пространстве Минковского уравнения поля давления (14) заметно упрощаются:

 

,      ,      ,      .         (17)

 

Знания векторов  и  достаточно, чтобы определить тензор энергии-импульса , вектор плотности потока энергии-импульса  поля давления и плотность силы давления в веществе.

Подстановка (15) в (14) даёт волновое уравнение для 4-потенциала поля давления:

 

.          (18)

 

В случае самогравитирующей системы частиц без вращения, занимающей сферический объём, уравнение (18) и его решение для скалярного потенциала с учётом (9) сводится к следующему:

 

.                                                     (19)

 

 

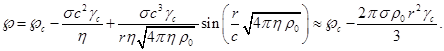
Поскольку имеется соотношение , при постоянной плотности решение (19) преобразуется в зависимость давления внутри системы:

 

.                                   (20)

 

В больших космических телах давление на поверхности при  достаточно мало и им в (20) можно пренебречь. Тогда для оценки давления в центре тела получается простая формула:

 

.                                                        (21)

 

5. Гравитационное поле и уравнение движения вещества

Уравнения гравитационного поля в ковариантной теории гравитации [13-16] по своему виду также соответствуют (1):

 

 ,                          ,                                   (22)

 

где  − тензор гравитационного поля, состоящий из компонент вектора напряжённости  и соленоидального вектора  поля кручения:

 

.

 

 

 

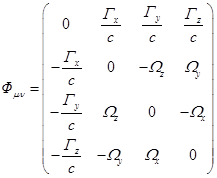Исходной точкой ковариантной теории гравитации является 4-потенциал гравитационного поля , описываемый через скалярный потенциал  и векторный потенциал  поля. 4-потенциал входит в лагранжиан и позволяет вывести уравнения гравитационного поля из принципа наименьшего действия, при этом тензор поля связан с 4-потенциалом: . Это равенство в векторных обозначениях может быть записано так:

 

,                    .                                           (23)

 

В пространстве Минковского плотность массы , плотность массового тока , массовый 4-ток , и уравнения (22) имеют следующий вид:

 

,      ,      ,      .

 

Если в (22) от тензора  перейти к 4-потенциалу , получится волновое уравнение:

 

.

 

В пространстве Минковского это уравнение распадается на два уравнения для потенциалов гравитационного поля:

 

,                   .                    (24)

 

Если система частиц не перемещается как целое в пространстве и не имеет общего вращения, то в ней векторный потенциал , поле кручения . Если ещё потенциал  не зависит от времени, то гравитационное поле становится статическим. В этом случае согласно [9] скалярный потенциал внутри тела при постоянной плотности вещества с учётом соотношения (9) определяется формулой:

 

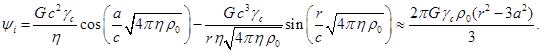   (25)

 

В концепции общего поля [7] уравнение движения вещества имеет вид:

 

.

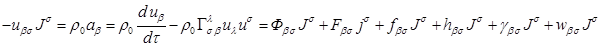(26)

 

где  есть 4-ускорение в искривлённом пространстве,

 – электромагнитный тензор,  – электромагнитный 4-ток,  – тензор поля диссипации,  – тензор поля сильного взаимодействия,  – тензор поля слабого взаимодействия.

 

Тензоры  и  важны в тех случаях, когда равновесие внутри космических тел поддерживается дополнительным давлением от термоядерных реакций или радиоактивного распада. Векторная компонента (26) с учётом (5) сводится к следующему:

 

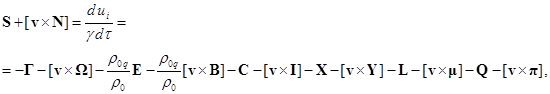    (27)

 

 

 

где векторы ,  и  обозначают напряжённости поля диссипации, поля сильного взаимодействия и поля слабого взаимодействия, соответственно, а векторы ,  и  являются соленоидальными векторами этих полей.

 

Если рассматривать уравнение движения в пространстве Минковского и учитывать только гравитацию, поле ускорений и поле давления, то в статическом случае можно положить , , а также . С учётом (23) и (25) имеем:

 

.                                   (28)

 

Напряжённость поля давления выражается формулой: , и если векторный потенциал , то с помощью (19) находим:

 

.                                      (29)

 

В соответствии с (3) и определением 4-потенциала поля ускорений в виде , напряжённость поля ускорений равна: .

Для не вращающегося тела равны нулю как векторный потенциал , так и соленоидальный вектор . В этом случае с помощью (8-9) находим внутри тела:

 

.                               (30) 

 

Подставляя ,  и  в (27) в отсутствие других полей, получаем равенство для напряжённостей полей и соотношение для коэффициентов полей:

 

,                               .                                  (31)

 

За пределами системы вблизи её границы можно считать, что , , имеется гравитационная сила, действующая на некоторую пробную частицу, но давление стремится к нулю ввиду малой плотности вещества. Тогда в (31) следует положить , и напряжённость гравитационного поля  будет задавать центростремительное ускорение для отдельных частиц, вращающихся вокруг системы. В нерелятивистском случае это можно записать так: . С учётом равенства  для кинетической температуры частиц вблизи поверхности системы должно быть:  

 

.                                                          (32)

 

Кинетическая температура  относится к кинетической энергии частиц при их вращении вокруг системы, и должна превышать среднюю температуру  газа из этих частиц, являющуюся мерой тепловой энергии газа вблизи системы.

Наилучшие условия для выполнения (32) должны быть в газовых облаках, например, в глобулах Бока, небольших тёмных космических облаках из газа и пыли. В [17] было найдено, что радиус типичной глобулы равен 0,35 парсек, масса 11 масс Солнца, а регистрируемая температура пыли в некоторых глобулах может достигать 26 К.

Полагая в (32)  равной атомной единице массы, для типичной глобулы находим температуру частиц на поверхности: К. Если в (11) положить , , , то с учётом равенства (6) для  температура в центре глобулы будет порядка 22 К, что достаточно близко к наблюдениям.

Использование (32) для Земли даёт кинетическую температуру  около 2500 К, а для Солнца – около 7,7 миллионов градусов. Такие температуры действительно наблюдаются – у Земли в ионосфере с тепловой температурой  более 2000 К, а у Солнца в короне, со средней температурой порядка 5 миллионов градусов. Благодаря действию гравитации Солнца частицы долговременно вращаются по орбитам вокруг звезды, почти не теряя свою энергию. Так решается известная проблема нагрева короны, согласно которой быстродвижущийся нагретый газ должен был бы быстро улетучиться, и корона должна была бы быстро охладиться из-за недостаточной скорости её нагрева из фотосферы. Очевидно, что при таком анализе проблемы не принимается во внимание, что частицы могут полностью удерживаться гравитационным полем Солнца и вращаться вокруг него. Кром этого, если частицы остаются всё время рядом с Солнцем, то они могут нагреваться длительное время за счёт солнечных вспышек и аналогичных явлений, достигая в конце концов наблюдаемой температуры в миллионы градусов. 

Однако мы должны ограничить действие формул (31) и (32) ввиду их неполноты, так как помимо движения частиц в твёрдых телах и в звёздной плазме основной вклад в давление делают силы межатомного взаимодействия, в том числе электромагнитные силы электрических зарядов и сильная гравитация как компонента сильного взаимодействия (в гравитационной модели сильного взаимодействия [14]). Эти силы могут заметно изменять ускорение частиц в уравнении движения (27).

Для идеально твёрдого тела движение частиц внутри тела отсутствует,  и из (31) с учётом (28) и соотношения  следует:

 

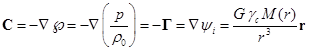.                              (33)

 

Между тем, при построении моделей космических объектов опираются обычно на так называемое гидростатическое уравнение равновесия, которое без поправок общей теории относительности имеет следующий вид:

 

.                                                    (34)

 

Мы видим, что (34) соответствует (33) с тем отличием, что в (33) плотность массы  входит под знак градиента вместе с давлением. При постоянной плотности оба выражения эквивалентны, но так как плотность обычно является функцией радиуса, выражения (33) и (34) в целом не совпадают. В случае заметного вращения объекта в (27) следует учитывать не равные нулю вектор поля кручения  и соленоидальный вектор  поля давления, и гидростатическое уравнение (34) становится ещё более неточным.

 

6. Случай неоднородной плотности

В [7] и [9] мы делали оценки температуры и давления в центре различных космических объектов по формулам (12) и (21) и получили достаточно хорошее совпадение с моделями звёзд, планет и газовых облаков. В данном разделе мы планируем увеличить точность наших расчётов.

В (11) и (20) плотность принималась постоянной величиной, хотя температура и давление меняются в больших пределах приблизительно по квадратичному закону. В общем случае при решении волновых уравнений (8) и (19) следует учитывать, что плотность также является некоторой функцией радиуса. Мы будем использовать далее следующую аппроксимацию:

 

.                                                    (35)

 

Подставим (35) в (8), где введём вспомогательную функцию  в виде , и выразим лапласиан как функцию текущего радиуса:

 

.                      (36)

 

Удобно искать решение этого дифференциального уравнения в виде ряда с постоянными коэффициентами:

 

.

 

Ограничивая ряд значением , после подстановки  в (36) и приведения подобных членов можно вычислить коэффициенты . Все эти коэффициенты получаются пропорциональными коэффициенту , причём . Обозначая , с учётом соотношения  находим приблизительную зависимость фактора Лоренца от текущего радиуса:

 

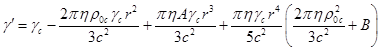.                     (37)

 

В (37) можно пренебречь членом  в скобке, который мал даже для нейтронных звёзд. В первом приближении имеем:

 

,           .

 

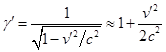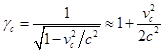Учитывая связь между скоростью частиц  и температурой , и переходя в (37) от факторов Лоренца к скоростям,  а затем к температуре, мы можем теперь уточнить (11) для зависимости температуры:

 

.                     (38)

 

С целью уточнения зависимости давления сделаем в (19) замену  и подставим туда (35) и (37):

 

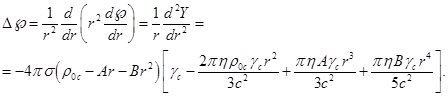             (39)

 

 

 

Ищем решение уравнения (39) в виде многочлена пятой степени с постоянными коэффициентами:

 

.

 

После подстановки  в (39) и приведения подобных членов видно, что , . Определяя другие коэффициенты, находим функцию  и затем скалярный потенциал  поля давления:

 

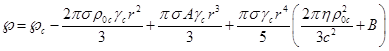.                   (40)

 

Членом  по сравнению с  в (40) можно пренебречь.

 

Как видно, коэффициенты  и  в зависимости (35) плотности от радиуса вносят дополнительный вклад в зависимости температуры (38) и потенциала поля давления (40) от текущего радиуса.

 

7. Оценки температуры и давления

Вычислим среднюю по объёму плотность массы, интегрируя (35) по радиусу от нуля до радиуса тела :

 

(41)

 

В (38) и в (40) положим  и подставим туда , выраженное из (41) через среднюю плотность . Используем ещё выражение для массы тела . Это позволяет оценить температуру поверхности  и потенциал поля давления на поверхности :

 

.                           (42)

 

.                                  (43)

 

В (43) мы можем считать, что скалярный потенциал  поля давления на поверхности космических тел близок к нулю по сравнению с потенциалом  в центре. Это даёт возможность вычислить , а также давление в центре:

 

.

 

В данном соотношении плотность в центре  можно выразить с помощью (41) через среднюю плотность, и использовать равенство :

 

(44)

 

Количество членов в (44) больше, чем в (21), что увеличивает точность расчётов. Рассмотрим теперь возможные значения коэффициентов поля давления и поля ускорений. Исходя из уравнения движения, в (31) было найдено соотношение . Если сравнивать давление в центре (21) и температуру в центре (12) при постоянной плотности , то получится:

 

.                                                      (45)

 

С другой стороны, стандартное выражение для давления с учётом давления от излучения имеет вид:

 

,                                                     (46)

 

где  есть постоянная плотности излучения,

 

 – количество нуклонов на одну частицу ионизированного газа, так что частицей газа в зависимости от его состояния может быть атом, ион, электрон и отдельный нуклон.

По определению: 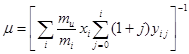, где  – массовая доля элемента с атомным номером ,   – масса ядра атома с номером  и атомной массой ,  – степень -кратной ионизации -го элемента, так что . В полностью ионизованном газе, состоящем из водорода, гелия и других элементов с , выражение для  становится следующим: , при этом , , .

 

Если не учитывать давление излучения, то из сравнения (45) и (46) следует равенство: . Учитывая соотношение , находим:

 

,                             .                               (47)

 

Для газа из нуклонов или из атомов водорода  и , ; для газа из полностью ионизированного водорода  и , ; для газа из полностью ионизированного гелия  и , ; для полностью ионизированного газа более тяжёлых химических элементов  и , .

Согласно модели Земли температура внутреннего ядра достигает 6000 К, а давление  Па [18]. Поскольку Земля существенно неоднородна, будем использовать данные для внешнего ядра Земли: радиус 3480 км, масса кг, температура на поверхности ядра порядка  К, а давление Па.

Из анализа зависимости вида (35) плотности от радиуса для ядра Земли можно оценить коэффициенты  кг/м4 и  при центральной плотности  кг/м3. С этими данными при условии , , и используя в качестве  атомную единицу массы, из (42) следует температура в центре ядра Земли порядка К. Очевидно, что вещество в центре Земли не является полностью ионизованным газом, а скорее представляет собой твёрдое кристаллическое вещество. Если принять температуру в центре равной 6000 К, из (42) можно оценить эффективное значение коэффициента поля ускорений: .

Для давления согласно (44) при условии  получается значение Па, а с учётом добавочного давления коры  давление в центре Земли должно быть Па. Это давление в 1,9 раз меньше давления в стандартной модели. Мы можем объяснить это среди прочего тем, что уравнения движения (33-34) для идеального твёрдого тела не совсем точные, поскольку не учитывают вклада поля ускорений в явной форме. В этих уравнениях предполагается равенство гравитационной силы и силы давления, что приводит к равенству ускорения нулю внутри тела и к соотношению . На самом же деле ускорение внутри тела отличается от нуля и вычисляется в (27) и (31) через поле ускорений, в результате согласно (47) .  

Для Земли в целом коэффициенты в (35) равны  кг/м4  и  кг/м5. Подставляя в (44) эти коэффициенты, находим давление в центре Земли: Па. Это давление ещё меньше, чем полученная выше оценка давления с помощью коэффициентов для ядра, что иллюстрирует эффект неоднородности внутри Земли.

Рассмотрим теперь нейтронную звезду с радиусом 12 км и массой , где  обозначает массу Солнца. В качестве оценки центральной плотности звезды возьмём значение  кг/м3, с уравнением состояния вещества согласно потенциалам AV18 + UIX в [19]. Используя зависимость плотности от радиуса из [20], можно оценить коэффициенты в (35):  кг/м4 ,  кг/м5. Пренебрегая температурой поверхности , при условии  из (42) получаем оценку температуры в самом центре нейтронной звезды: порядка К. Заметим, что согласно [21] вплоть до температуры К в веществе нейтронных звёзд могут существовать устойчивые атомные ядра.

Для давления в центре нейтронной звезды при условии из (44) получается значение   Па. Это можно сравнить с давлением ядерной материи  Па при плотности   кг/м3 согласно [22], и с давлением порядка  Па в [23], при этом в различных моделях нейтронных звёзд согласно [20] давление не превышает Па.

Гелиевый белый карлик при массе  должен иметь радиус м и центральную плотность  кг/м3 согласно [24]. Из (41) и из зависимости плотности от радиуса в [25] следуют коэффициенты в соотношении (35):  кг/м4 ,  кг/м5. С учётом этого из (42) при  находим температуру в центре белого карлика: К, а давление в центре согласно (44) равно Па.

В модели NASA в центре Солнца предполагается плотность вещества  кг/м3, давление около Па и температура К [26].

Поскольку звёзды главной последовательности гораздо больше по размерам, чем белые карлики и нейтронные звёзды, изменение плотности в зависимости (35) при переходе от ядра к поверхности звезды очень велико, и двух членов недостаточно для приемлемой точности. Перейдём поэтому от модели всего Солнца к модели его ядра, которое существенно более однородно. Радиус ядра оценивается величиной, в пять раз меньшей радиуса Солнца, масса ядра равна , давление на поверхности ядра не менее Па [27], а температура порядка К. При этом коэффициенты для ядра в (35) будут следующие:  кг/м4 ,  кг/м5. Согласно [28], для ядра Солнца , тогда из (47) следует , . Из (42) оцениваем температуру в центре ядра: К. Из (44) для давления получается Па. Это давление несколько меньше, чем в модели NASA, но следует учесть, что на ядро ещё оказывает давление кора Солнца. Если мы сложим давления  и , результат будет заметно ближе к .

 

8. Теплопроводность

Согласно модели звёздной эволюции, все звёзды главной последовательности со временем превращаются в белые карлики и нейтронные звёзды. Предполагается, что в компактных звёздах отсутствуют заметные источники внутренней энергии, связанные с превращениями ядер. В результате после своего образования белые карлики и нейтронные звёзды должны медленно остывать в течение многих миллиардов лет.

Температуры поверхности некоторых наблюдаемых горячих белых карликов достигают 150000 К, а у остывших белых карликов поверхность имеет температуру ниже 4000 К. Этим температурам соответствуют светимости соответственно  и  для карлика с типичной массой , причём для остывания до 4000 К требуется время порядка 12 миллиардов лет [29]. Для характеристики распространения тепла внутри звезды рассмотрим феноменологическое дифференциальное уравнение потока тепла, описывающее закон теплопроводности Фурье:

 

.                                                           (48)

 

В (48) вектор плотности потока энергии  пропорционален коэффициенту теплопроводности  и градиенту температуры.

В рассматриваемой нами модели гравитационного равновесия звезда или планета не могут остывать бесконечно. Действительно, распределение температуры (38) было выведено нами исходя из того, что гравитационному полю противодействуют поле ускорений и поле давления. Состояние равновесия должно выполняться в любой момент времени, в том числе и после того, как звезда остынет. Предположим, что наблюдаемые остывшие белые карлики находятся в таком состоянии, что в них осуществляется распределение температуры, близкое к равновесному распределению (38). Подставим зависимость температуры от радиуса (38) в (48) и найдём вектор :

 

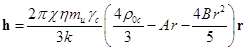.                                   (49)

 

Подставляя в (49) , , ,  кг/м3 и коэффициенты  и  для белого карлика из предыдущего раздела, получаем модуль вектора плотности потока энергии на поверхности: . Интеграл от вектора  по всей поверхности белого карлика должен равняться светимости звезды. Так как вектор  перпендикулярен поверхности звезды, то светимость равна: . С другой стороны, светимость белого карлика в устоявшемся режиме после длительного охлаждения предположительно равна . Из равенства  находим оценку теплопроводности вещества звезды: Вт/(м·К). Эта величина в основном характеризует теплопроводность верхней части коры и атмосферы белого карлика, при этом теплопроводности недр, коры и атмосферы звезды могут различаться во много раз из-за разницы температур и состояния вещества. Для сравнения, коэффициент теплопроводности алмаза с примесями при комнатной температуре имеет значение Вт/(м·К), а у очищенного алмаза коэффициент достигает Вт/(м·К) [30], что является одним из самых высоких экспериментальных значений для известных веществ.

Температура поверхности нейтронных звёзд может быть К и менее, что требует порядка  лет охлаждения [31]. Если использовать радиус звезды м, то соответствующая минимальная светимость будет  при постоянной Стефана-Больцмана ,  что близко к наблюдаемым светимостям некоторых звёзд [32].

Подстановка в (49) данных для нейтронной звезды при , , , центральной плотности  кг/м3 и коэффициентах  и  из раздела 7 даёт модуль вектора плотности потока энергии на поверхности: . Сравнение светимости  и  позволяет оценить коэффициент теплопроводности вещества звезды: Вт/(м·К). Данная оценка хорошо согласуется с результатами расчёта ионной теплопроводности в оболочке нейтронной звезды [33].

Применим (49) при  для Земли в целом, используя , центральную плотность  кг/м3 и соответствующие коэффициенты  кг/м4  и  кг/м5 из раздела 7. Плотность потока энергии на поверхности получается равной . Измерения теплового потока на суше и в океанах дают в среднем значение  Вт/м2 [34], что приводит к коэффициенту теплопроводности Вт/(м·К). Согласно [35], коэффициент теплопроводности в ядре Земли должен быть порядка 37 Вт/(м·К), соответствуя теплопроводности железа, на границе ядра и мантии   уменьшается до 16,4 Вт/(м·К) [36], а в оболочке теплопроводность должна быть почти на порядок меньше.

Найденное нами значение Вт/(м·К) больше, чем ожидается в оболочке Земли, что можно связать с неточностью определения плотности (35) через два коэффициента. Кроме этого, при расчёте мы не учли, что заметная часть тепловой энергии внутри Земли вырабатывается за счёт радиоактивного распада некоторых изотопов.

Если повторить все вычисления только для внешнего ядра Земли с его радиусом 3480 км, массой кг и предполагаемым общим тепловым потоком ядра 10,6 ТВт согласно [36], то при коэффициентах  кг/м4  и  кг/м5 получится более приемлемое значение для верхней части ядра: Вт/(м·К). Для улучшения результатов необходимо задавать плотность вещества в (35) с существенно большей точностью и учитывать все источники тепловой энергии. Это ещё более актуально для моделирования звёзд главной последовательности и Солнца.

 

9. Энтропия

Планеты и звёзды состоят из молекул, атомов, ионов, электронов, а в белых карликах и нейтронных звёздах в список основных частиц вещества добавляются атомные ядра и отдельные нуклоны. Для многокомпонентных систем удельная энтропия в расчёте на один нуклон вещества вычисляется суммированием по каждому виду частиц и с учётом энтропии излучения согласно [37] выглядит так:

 

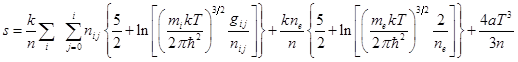,        (50)

 

где  – концентрация нуклонов,  – атомная единица массы,  – масса ядра атома с зарядовым числом  и массовым числом ,  – статистический вес иона -го химического элемента в -ом состоянии ионизации,  – концентрация ионов элемента  в -ом состоянии ионизации,  – массовая доля элемента с зарядовым числом ,  – степень - кратной ионизации -го элемента, так что ,  – постоянная Дирака,  – концентрация электронов в условиях электронейтральности.

 

Применим (50) для случая одноатомного нейтрального газа без учёта вклада от электронов:

 

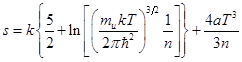.                                     (51)

 

Выражение (51) подойдёт для оценки удельной энтропии в только что образовавшейся нейтронной звезде, состоящей в основном из нейтронов с примесью протонов, электронов, а также атомных ядер в оболочке звезды. Если масса звезды , а радиус звезды м, то м–3. Подставляя в (51) температуру К в центре нейтронной звезды, найденную в разделе 7, получаем удельную энтропию в расчёте на один нуклон:  . Но в начальный момент энтропия существенно больше, так как при той же температуре радиус горячей звезды превышает  и плотность  меньше.

При данной температуре вклад энтропии от излучения в 31,5 раз меньше вклада от энтропии нуклонов. Величина удельной энтропии в равновесном состоянии должна быть меньше, чем , так как за счёт охлаждения температура в основном объёме звезды будет меньше, чем температура в центре К.

Оценку удельной энтропии можно сделать другим способом. Как было показано в [10], энергия поля ускорений как часть энергии хаотического движения частиц может быть выражена в следующем виде:

 

.

 

К этой энергии следует добавить энергию частиц за счёт их взаимодействия с 4-потенциалом поля ускорений. Для точного расчёта кинетической энергии частиц можно воспользоваться теоремой вириала либо определением кинетической энергии как разности между релятивистской энергией движущихся частиц и энергией их покоя. В обоих случаях для кинетической энергии получается следующее:

 

.

 

По определению приращение удельной энтропии выражается формулой: , где  – приращение полной энтропии,  – число нуклонов,  – приращение тепловой энергии при температуре . При образовании нейтронной звезды можно в первом приближении положить, что , а также . Тогда для удельной энтропии получается соотношение:

 

.                                                           (52)

 

Подставляя сюда  при  из (47) и центральную температуру К, находим , что меньше, чем . Однако этот результат подлежит дополнительному уточнению ввиду того, что звезда при переходе к равновесному радиусу теряет энергию вместе с улетающими нейтрино и быстро охлаждается, уменьшая свою энтропию.

Для сравнения, в [38] нашли, что у протонейтронной горячей звезды с массой , радиусом 55,75 км и температурой К удельная энтропия равна . Когда звезда достигает своего равновесного радиуса 11,15 км, её удельная энтропия при эффективной температуре вещества порядка  К становится равной  и затем непрерывно уменьшается за счёт последующего охлаждения.

Для планет и звёзд вычисление энтропии с помощью (50) требует знания количественного химического состава вещества. Если же использовать (52) для первичной оценки энтропии, необходимо знать массу, радиус и среднюю температуру. Для Юпитера удельная энтропия согласно (52) при  будет порядка , если в качестве  использовать значение температуры К, предполагаемое в центре Юпитера в современных моделях газовых гигантов. Данное значение удельной энтропии должно быть увеличено, поскольку в качестве  следует использовать меньшую по величине температуру, усреднённую по всему объёму. В частности, расчёты по стандартной методике дают  для планеты типа Юпитера [39].

 

10. Заключение

В представленной нами модели гравитационного равновесия важную роль играют поле ускорений и поле давления. Уравнения этих полей (2) и (14) позволяют вычислить напряжённости и соленоидальные векторы полей, дают возможность с помощью простых формул определить распределение температуры и давления внутри космических тел, вызванное действием гравитации. Уравнения (22) позволяют найти напряжённость гравитационного поля и соленоидальный вектор поля кручения в ковариантной теории гравитации. Знания напряжённостей и соленоидальных векторов полей достаточно для анализа уравнения движения вещества (26) и построения основы модели. В частности, из уравнения движения вытекает связь (31) между коэффициентами поля ускорений и поля давления, а в (47) эти коэффициенты выражаются через термодинамический параметр . Пользуясь значениями этих коэффициентов, мы определяем температуру и давление в центре различных объектов – в глобулах Бока, внутри Земли, Солнца, в белом карлике и в нейтронной звезде. Кроме этого, мы получаем оценки теплового потока и коэффициента теплопроводности, характеризующего тот или иной объект, а также оцениваем энтропию нейтронной звезды и газовой планеты. Анализ результатов показывает, что они хорошо согласуются с данными других авторов.

Исходя из значительно более высокой теплопроводности ядра и коры по сравнению с оболочкой, в ряде работ у типичной нейтронной звезды (а также у белого карлика) некоторые авторы предполагают существование почти изотермического ядра с малым градиентом температуры. В нашем подходе распределение температуры внутри звезды связано с зависимостью (37) для фактора Лоренца, при этом большая величина теплопроводности не играет существенной роли и не может приводить к изотермическому ядру. В свою очередь, зависимость (37) вытекает из волнового уравнения поля ускорений (7) и определяется только распределением плотности вещества и его движением.

С физической точки зрения, (37) и подобная зависимость для потенциала поля давления (40) связаны с распределением энергии между гравитационным полем, полем ускорений и полем давления. Результатом такого распределения энергии становится некоторое равновесное состояние и определённое распределение физических параметров в зависимости от текущего радиуса внутри рассматриваемого объекта. Если исходить из теории гравитации Лесажа, то непосредственным агентом, осуществляющим гравитационное сжатие и равновесный нагрев вещества космических объектов, являются потоки гравитонов. Плотность энергии, сечение взаимодействия поля гравитонов с нуклонным веществом и другие параметры могут быть вычислены исходя из того, что действие потоков гравитонов должно приводить к закону всемирного тяготения Ньютона [40-41].    

Универсальность модели гравитационного равновесия обеспечивается тем, что уравнения поля применимы к любым объектам независимо от состояния их вещества.  Некоторым ограничением является необходимость детального представления распределения плотности вещества для получения точных результатов, однако то же самое требуется и в любых других подходах, включая часто используемую политропную модель. Как правило для оценки распределения плотности вещества используются измерения скорости продольных и поперечных сейсмических волн, а также соответствие радиального распределения плотности массы общей массе тела и его моменту инерции.

Другим ограничением является использование в формуле (42) атомной единицы массы в качестве , что допустимо для водородного газа и однородной ядерной материи из нуклонов. Между тем, в ранее выведенных соотношениях (11) и (38)  имеет смысл массы одной частицы газа, которая может отличаться от атомной единицы массы. Так, в белых карликах существенный вклад в состояние вещества вносят электроны, релятивистские массы которых зависят от температуры. В звёздах и в планетах присутствуют как нейтральные, так и ионизированные атомы с массами порядка , где  – массовое число соответствующего химического изотопа. Вследствие сложного состава частиц в веществе, формулы (42) для температуры и (52) для удельной энтропии подлежат уточнению для каждого типа космических объектов. 

 

Список использованных источников

1.            J.H. Lane (1870). On the Theoretical Temperature of the Sun under the Hypothesis of a Gaseous Mass Maintaining its Volume by its Internal Heat and Depending on the Laws of Gases Known to Terrestrial Experiment. The American Journal of Science and Arts. 2 50: 57–74. http://dx.doi.org/10.2475/ajs.s2-50.148.57.

2.           Horedt, Georg P. (2004). Polytropes - Applications in Astrophysics and Related Fields. Dordrecht: Kluwer Academic Publishers. ISBN 978-1-4020-2350-7.

3.           L. Herrera, W. Barreto. Newtonian polytropes for anisotropic matter: General framework and applications. Phys. Rev. D 87, 087303 (2013). http://dx.doi.org/10.1103/PhysRevD.87.087303.

4.           Chandrasekhar S. The Maximum Mass of Ideal White Dwarfs. Astrophysical Journal, Vol. 74, P. 81 (07/1931). http://dx.doi.org/10.1086/143324.

5.           Яковлев Д.Г. Работа Я.И. Френкеля о силах сцепления и теория белых карликов (К 100-летию со дня рождения Я.И. Френкеля). Успехи физических наук. Т. 164. № 3-4. С. 653–656 (1994). https://dx.doi.org/10.3367%2FUFNr.0164.199406g.0653.

6.           Hilario Rodrigues. Modeling compact stars without numerical integration. European Journal of Physics. Vol. 34, P. 667 (2013). http://dx.doi.org/10.1088/0143-0807/34/3/667.

7.           Fedosin S.G. The concept of the general force vector field. vixra.org, 28 June 2014. // Концепция общего силового векторного поля.

8.           Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy. vixra.org, 5 Mar 2014. Accepted by Jordan Journal of Physics. // О космологической постоянной, поле ускорения, поле давления и об энергии.

9.           Fedosin S.G. The Integral Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based on the Pressure Field and Acceleration Field. American Journal of Modern Physics. Vol. 3, No. 4, 2014, pp. 152-167. http://dx.doi.org/10.11648/j.ajmp.20140304.12 . // Интегральный 4-вектор энергии-импульса и анализ проблемы 4/3 на основе поля давления и поля ускорений.

10.       Fedosin S.G. Relativistic Energy and Mass in the Weak Field Limit. Jordan Journal of Physics. Vol. 8 (No. 1), pp. 1-16, (2015). // Релятивистская энергия и масса в пределе слабого поля.

11.       Fedosin S.G. Four-Dimensional Equation of Motion for Viscous Compressible and Charged Fluid with Regard to the Acceleration Field, Pressure Field and Dissipation Field. International Journal of Thermodynamics. Vol. 18 (No. 1), pp. 13-24, 2015. http://dx.doi.org/10.5541/ijot.5000034003. // Четырёхмерное уравнение движения вязкого сжимаемого заряженного вещества с учётом поля ускорений, поля давления и поля диссипации.

12.       Fedosin S.G. The Procedure of Finding the Stress-Energy Tensor and Equations of Vector Field of Any Form. Advanced Studies in Theoretical Physics, Vol. 8, 2014, no. 18, 771 - 779. http://dx.doi.org/10.12988/astp.2014.47101. // Процедура для нахождения тензора энергии-импульса и уравнений векторного поля любого вида.

13.       Федосин С.Г. Физика и философия подобия от преонов до метагалактик. Пермь, Стиль-МГ, 1999, 544 стр., Табл.66, Ил.93, Библ. 377 назв. ISBN 5-8131-0012-1.

14.       Федосин С.Г. Физические теории и бесконечная вложенность материи. Пермь, 2009, 842 стр., Табл. 21, Ил.41, Библ. 289 назв. ISBN 978-5-9901951-1-0.

15.       Fedosin S.G. The Principle of Least Action in Covariant Theory of Gravitation. Hadronic Journal, 2012, Vol. 35, No. 1, P. 35 – 70. // Принцип наименьшего действия в ковариантной теории гравитации.

16.       Fedosin S.G. The Hamiltonian in Covariant Theory of Gravitation. Advances in Natural Science, 2012, Vol. 5, No. 4, P. 55 – 75. http://dx.doi.org/10.3968%2Fj.ans.1715787020120504.2023. // Гамильтониан в ковариантной теории гравитации.

17.       Clemens, Dan P.; Yun, Joao Lin; Meyer, Mark H. (March 1991), BOK globules and small molecular clouds – Deep IRAS photometry and 12CO spectroscopy, Astrophysical Journal Supplement 75: 877. http://dx.doi.org/10.1086/191552.

18.       Alfè, D.; Gillan, M. J.; Vocadlo, L.; Brodholt, J.; Price, G. D. (2002). The ab initio simulation of the Earth's core. Philosophical Transactions of the Royal Society. Vol. 360 (1795), P.1227–1244. http://dx.doi.org/10.1098/rsta.2002.0992.

19.       Akmal, A., & Pandharipande, V.R. (1997), Spin-isospin structure and pion condensation in nucleon matter. Phys. Rev. C, 56, 2261. http://dx.doi.org/10.1103/PhysRevC.56.2261.

20.       J. M. Lattimer and M. Prakash, Neutron Star Structure and the Equation of State. Astrophysical J. Vol. 550(1) P. 426-442 (2001). http://dx.doi.org/10.1086/319702.

21.       Lamb D.Q., Lattimer J. M., Pethick C.J., Ravenhall D.G. Hot dense matter and stellar collapse. Phys. Rev. Lett. Vol. 41, P. 1623-1626 (1978). http://dx.doi.org/10.1103/PhysRevLett.41.1623.

22.       Malone R., Johnson M. and Bethe H. Neutron star models with realistic high-density equations of state. Astrophysical J. (1975) Vol. 199, P. 741-748. http://dx.doi.org/10.1086/153746.

23.       F. J. Fattoyev and J. Piekarewicz. Relativistic models of the neutron-star matter equation of state. Phys. Rev. C 82, 025805 (2010). http://dx.doi.org/10.1103/PhysRevC.82.025805.

24.       M. Rotondo, J. A. Rueda, R. Ruffini and S.-S. Xue. Relativistic Feynman-Metropolis-Teller theory for white dwarfs in general relativity. Phys. Rev. D 84 084007 (2011). http://dx.doi.org/10.1103/PhysRevD.84.084007.

25.       M. I. Nouh, A. S. Saad , M. M. Elkhateeb and B. Korany. White Dwarf Stars as a Polytropic Gas Spheres. arXiv:1406.1482, 5 Jun 2014.

26.       Williams, D. R. (04 January 2016). Sun Fact Sheet. NASA.

27.       J. Christensen-Dalsgaard et al. (1996) The current state of solar modeling. Science, Vol. 272, P. 1286 – 1292. http://dx.doi.org/10.1126/science.272.5266.1286.

28.       Chaplin, W. J., Serenelli, A. M., Basu, S., Elsworth, Y., New, R., Verner, G. A. Solar heavy element abundance: constraints from frequency separation ratios of low-degree p modes. (2007), Astrophys. J. 670, 872–884. http://dx.doi.org/10.1086/522578.

29.       Brad M.S. Hansen, James Liebert. Cool White Dwarfs. Annu. Rev. Astro. Astrophys. (2003). 41: 465-515. http://dx.doi.org/10.1146/annurev.astro.41.081401.155117.

30.       Wei, Lanhua; Kuo, P. K.; Thomas, R. L.; Anthony, T. R.; Banholzer, W. F. (1993). Thermal conductivity of isotopically modified single crystal diamond. Physical Review Letters 70 (24): 3764–3767. https://dx.doi.org/10.1103%2FPhysRevLett.70.3764.

31.       M. V. Beznogov, D. G. Yakovlev. Statistical theory of thermal evolution of neutron stars. MNRAS 447, 1598 (2015). https://dx.doi.org/10.1093/mnras/stu2506.

32.       V.E. Zavlin. Theory of radiative transfer in neutron star atmospheres and its applications. In Neutron stars and pulsars, ed. W. Becker, Astronomy and Space Science Library. 357, 181 (2009). doi:10.1007/978-3-540-76965-1_9.

33.       A.I. Chugunov, P. Haensel. Thermal conductivity of ions in a neutron star envelope. MNRAS, 381 (2007), 1143-1153. https://dx.doi.org/10.1111/j.1365-2966.2007.12301.x .

34.       Davies, J. H., & Davies, D. R. (2010). Earth's surface heat flux. Solid Earth, 1(1), 5–24. http://dx.doi.org/10.5194/se-1-5-2010.

35.       Жарков В.Н. Внутреннее строение Земли и планет. М.: Наука, 1978. 198 с.

36.       Volker Haigis, Mathieu Salanne and Sandro Jahn. Thermal conductivity of MgO, MgSiO3 perovskite and post-perovskite in the Earth’s deep mantle. Earth and Planetary Science Letters, 355-356, 102-108 (2012). https://dx.doi.org/10.1016/j.epsl.2012.09.002.

37.       Ландау Л.Д., Лифшиц Е.М. Статистическая физика, Ч.1. М:. Наука, 1976.

38.       Marcio G. B. de Avellar, Rodrigo A. Souza and J. E. Horvath. Trends of stellar entropy along stellar evolution. RAA. 16, 21 (2016). doi:10.1088/1674–4527/16/2/021. http://www.raa-journal.org/raa/index.php/raa/article/viewFile/1837/2323, http://arxiv.org/abs/1509.05262 .

39.       G.-D. Marleau and A. Cumming. Constraining the initial entropy of directly-detected exoplanets. MNRAS, 2014, Vol. 437 (2), 1378-1399. http://dx.doi.org/10.1093/mnras/stt1967.

40.       Fedosin S.G. Model of Gravitational Interaction in the Concept of Gravitons. Journal of Vectorial Relativity, March 2009, Vol. 4, No. 1, P.1 – 24.

41.       Fedosin S.G. The graviton field as the source of mass and gravitational force in the modernized Le Sage’s model. Physical Science International Journal, 2015, Vol. 8, Issue 4, P. 1 – 18. doi: 10.9734/PSIJ/2015/22197. // Поле гравитонов как источник гравитационной силы и массы в модернизированной модели Лесажа.

 

Источник: http://sergf.ru/est.htm

На научный сайт