In English

International Journal of Thermodynamics. Vol. 18, No. 1, pp. 13-24 (2015). http://dx.doi.org/10.5541/ijot.5000034003

Четырёхмерное уравнение движения вязкого сжимаемого и заряженного вещества с учётом поля ускорений, поля давления и поля диссипации

Федосин Сергей Григорьевич

г. Пермь, Пермский край, Россия

E-mail: binbom@list.ru

Из принципа наименьшего действия выводится уравнение движения вязкого сжимаемого вещества. Эффект вязкости описывается 4-потенциалом поля диссипации энергии, тензором диссипации и тензором энергии-импульса диссипации. В пределе слабого поля показывается, что полученное уравнение эквивалентно уравнению Навье-Стокса. Даётся уравнение для мощности потерь кинетической энергии движения, интегрируется уравнение движения и определяется зависимость для модуля скорости. Представляется полный набор уравнений, достаточный для разрешения задачи о движении вязкого сжимаемого и заряженного вещества в гравитационном и электромагнитном поле.

Ключевые слова: уравнение Навье-Стокса; поле диссипации; поле ускорений; поле давления; вязкость.

Four-dimensional equation of motion for viscous compressible and charged fluid with regard to the acceleration field, pressure field and dissipation field

Sergey G. Fedosin

PO box 614088, Sviazeva str. 22-79, Perm, Russia

E-mail: intelli@list.ru

From the principle of least action the equation of motion for viscous compressible and charged fluid is derived. The viscosity effect is described by the 4-potential of the energy dissipation field, dissipation tensor and dissipation stress-energy tensor. In the weak field limit it is shown that the obtained equation is equivalent to the Navier-Stokes equation. The equation for the power of the kinetic energy loss is provided, the equation of motion is integrated, and the dependence of the velocity magnitude is determined. A complete set of equations is presented, which suffices to solve the problem of motion of viscous compressible and charged fluid in the gravitational and electromagnetic fields.

Keywords: Navier-Stokes equation; dissipation field; acceleration field; pressure field; viscosity.

1. Введение

С момента появления уравнений Навье-Стокса в 1827 году [1], [2], не прекращаются попытки вывести эти уравнения различными методами. Стокс [3] и Сен-Венан [4] при выводе этих уравнений основывались на том, что девиатор тензора нормальных и касательных напряжения линейно связан с трёхмерным тензором скоростей деформаций, а вещество является изотропным.

В книге [5] считается, что уравнения Навье-Стокса являются условиями экстремума некоторого функционала, и описывается метод поиска решения этих уравнений, который состоит в движении по градиенту к экстремуму этого функционала.

Один из вариантов четырёхмерного тензора энергии-импульса вязких напряжений в рамках специальной теории относительности можно найти в [6]. Дивергенция этого тензора даёт требуемые члены с вязкостью в уравнении Навье-Стокса. Феноменологический вывод этого тензора основан на предполагаемом условии возрастания энтропии в ходе рассеяния энергии. Как следствие, в сопутствующей системе отсчёта временные компоненты тензора, то есть плотность энергии диссипации и её поток, обнуляются. Следовательно, такой тензор не является универсальным тензором и не может служить, например, основой для определения метрики в присутствии вязкости.

В данной статье мы ставим своей целью представить в общем виде четырёхмерный тензор энергии-импульса диссипации энергии, описывающий в искривлённом пространстве-времени плотность энергии, поток энергии и напряжения, возникающие за счёт вязких напряжений. Данный тензор будет выводиться с помощью принципа наименьшего действия на основе ковариантного 4-потенциала поля диссипации. Затем мы применяем эти величины в уравнении движения вязкого сжимаемого вещества и путём выбора скалярного потенциала поля диссипации приходим к уравнению Навье-Стокса. При этом существенным элементом наших расчётов является применение волнового уравнения для потенциалов поля ускорений. В заключении мы представим полный набор уравнений, достаточных для описания движения вязкого вещества. С целью упрощения будем считать, что различные поля, существующие одновременно, не будет производить никаких индуцированных эффектов (токов) в связи друг с другом, и взаимодействие между полями отсутствует.

2. Функция действия

Исходной точкой наших расчётов является функция действия в следующем виде:

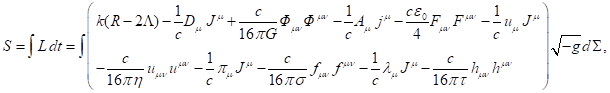
(1)

где – функция Лагранжа или лагранжиан,

– скалярная кривизна,

– космологическая постоянная,

– 4-вектор массового (гравитационного) тока,

– плотность массы в сопутствующей частице системе отсчёта,

– 4-скорость точечной частицы, – скорость света,

– 4-потенциал гравитационного поля, описываемый через скалярный потенциал и векторный потенциал этого поля,

– гравитационная постоянная,

– гравитационный тензор,

– 4-потенциал электромагнитного поля, задаваемый с помощью скалярного потенциала и векторного потенциала этого поля,

– 4-вектор электромагнитного (зарядового) тока,

– плотность заряда в сопутствующей частице системе отсчёта,

– электрическая постоянная,

– электромагнитный тензор,

– 4-скорость с ковариантным индексом, выражаемая через метрический тензор и 4-скорость с контравариантным индексом; ковариантная 4-скорость является 4-потенциалом поля ускорений , где и обозначают скалярный и векторный потенциалы, соответственно,

– тензор ускорений,

, и – некоторые функции координат и времени,

– 4-потенциал поля давления, состоящий из скалярного потенциала и векторного потенциала , – давление в сопутствующей частице системе отсчёта, отношение задаёт уравнение состояния вещества,

– тензор поля давления.

Указанные выше величины подробно описаны в [7]. В дополнение к ним мы вводим в рассмотрение 4-потенциал диссипации энергии в среде:

, (2)

где – функция диссипации, и – скалярный и векторный потенциалы диссипации, соответственно.

С помощью 4-потенциала мы строим тензор диссипации энергии:

. (3)

Коэффициенты , и мы в целях упрощения расчётов будем считать постоянными.

Член в (1) отражает тот факт, что энергия движения вещества может рассеиваться в окружающей среде и переходить во внутреннюю энергию вещества, при этом энергия системы не меняется. Последний член в (1) связан с энергией, накопленной системой благодаря действию диссипации энергии.

Способ построения 4-потенциала диссипации в (2) и тензора диссипации в (3) полностью идентичен тому, который был использован нами ранее в [7]. Поэтому мы не будем приводить здесь промежуточные результаты из [7] и сразу запишем уравнения движения вещества и поля, получающиеся как результат варьирования функции действия (1).

3. Уравнения поля

Уравнения электромагнитного поля имеют стандартный вид:

, , (4)

где – магнитная постоянная.

Уравнения гравитационного поля:

, . (5)

Уравнения поля ускорений:

, . (6)

Уравнения поля давления:

, . (7)

Уравнения поля диссипации:

, . (8)

Для того, чтобы получить уравнения (4-8), в функции действия (1) осуществляется варьирование по соответствующему 4-потенциалу.

Все указанные выше поля носят векторный характер. Каждое поле может быть описано двумя трёхмерными векторами, входящими в состав соответствующего тензора поля. Один из этих векторов является напряжённостью соответствующего поля, а другой соленоидальный вектор описывает завихрённость поля. Например, компоненты напряжённости электрического поля и индукции магнитного поля являются компонентами электромагнитного тензора . Гравитационный тензор состоит из компонент напряжённости гравитационного поля и поля кручения . Как видно из (4-8), постоянные , и имеют тот же смысл, что и постоянные и – все эти постоянные отражают связь между 4-током диссипирующего вещества и дивергенцией тензора соответствующего поля.

Суммарная сводка по обозначениям всех полей приведена в Приложении A. Свойства поля диссипации приведены в Приложении B.

4. Калибровка полей

С целью максимально упростить запись уравнений мы используем следующую калибровку полей:

, , (9)

, , .

В (9) калибровка каждого поля осуществляется путём приравнивания к нулю ковариантной производной соответствующего 4-потенциала. Так как 4-потенциалы состоят из скалярного и векторного потенциалов, то калибровка (9) связывает между собой скалярный и векторный потенциал каждого поля. В результате дивергенция векторного потенциала какого-либо поля из некоторого объёма сопровождается изменением во времени скалярного потенциала поля в этом объёме, и зависит ещё от тензорного произведения символов Кристоффеля и 4-потенциала, то есть от степени искривления пространства-времени.

5. Уравнения непрерывности

В уравнениях (4-8) дивергенции тензоров полей связываются со своими источниками, то есть с 4-токами. Тензоры полей задаются своими 4-потенциалами аналогично (3):

, , (10)

, .

Если подставить (3) и (10) в уравнения (4-8), и применить ко всем членам ковариантную производную , получатся следующие соотношения, содержащие тензор Риччи:

, , ,

, . (11)

В пределе специальной теории относительности тензор Риччи стремится к нулю, ковариантная производная превращается в 4-градиент, и тогда вместо (11) можно записать:

, . (12)

Соотношения (12) представляют собой обычные уравнения непрерывности зарядового и массового 4-токов в плоском пространстве-времени.

6. Уравнения движения

Вариация функции действия непосредственно приводит к уравнениям, описывающим движение элемента вещества под действием полей:

. (13)

Левую часть равенства можно преобразовать, учитывая выражение для 4-вектора плотности массового тока, и определение (10) для тензора ускорений :

.

(14)

В (14) обозначает 4-ускорение, и мы использовали оператор производной по собственному времени , где – символ 4-дифференциала в искривлённом пространстве-времени, – собственное время [8]. Если подставить (14) в (13), получается уравнение движения, в котором 4-ускорение выражается через тензоры полей и 4-токи:

. (15)

Вариация функции действия позволяет найти вид тензоров энергии-импульса всех полей, связанных с веществом:

, ,

, ,

. (16)

Одним из свойств этих тензоров является то, что их дивергенции наравне с тензорами поля задают плотности 4-сил, возникающих от действия на вещество соответствующего поля:

, ,

, ,

. (17)

В левой части соотношений (17) находится плотность соответствующей 4-силы, за исключением , которая с точностью до знака обозначает плотность 4-силы, действующей со стороны ускоренного вещества на остальные четыре поля.

Из (13-17) следует, что уравнение движения можно записать только через дивергенции тензоров энергии-импульса полей:

. (18)

Уравнение (18) мы интегрировали в [9] в пределе слабого поля (без учёта тензора энергии-импульса диссипации ), и это позволило нам объяснить известную проблему 4/3 неравенства массы-энергии полей в неподвижных и движущихся системах. Уравнение (18) будет использовано ещё в уравнении для метрики (21).

7. Энергия системы

В функции действия (1) содержится лагранжиан . Применяя к нему преобразования Лежандра для системы частиц, можно найти гамильтониан системы. Данный гамильтониан представляет собой релятивистскую энергию системы, записанную в произвольной системе отсчёта. Поскольку энергия оказывается зависящей от космологической постоянной , следует осуществить калибровку космологической постоянной с помощью соотношения:

. (19)

В результате для энергии системы можно записать:

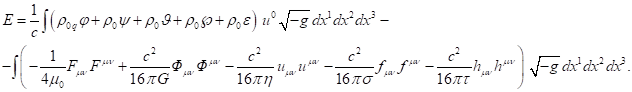
(20)

Энергия системы в виде множества тесно взаимодействующих частиц и связанных с ними полей в пределе слабого поля была вычислена нами в [10]. При этом было показано различие между массой системы и гравитационной массой, а также то, что масса-энергия собственного электромагнитного поля уменьшает гравитационную массу системы.

8. Уравнение для метрики

Согласно логике ковариантной теории гравитации [11] и метрической теории относительности [12], вклад в определение метрики в системе вносят тензоры энергии-импульса всех полей, включая гравитационное поле. Метрика является вторичной функцией, производной от действующих в системе полей, которые определяют все основные свойства системы. Уравнение для метрики получается в следующем виде:

. (21)

Если умножить (21) на метрический тензор и свернуть по всем индексам, правая и левая части уравнения обращаются в нуль. Это следует из свойств тензоров в (21). За пределами вещества с учётом калибровки скалярная кривизна получается равной нулю. Если учесть уравнение движения (18), ковариантная производная правой части (21) равна нулю. Ковариантная производная левой части (21) также равна нулю, поскольку как следствие калибровки космологической постоянной, а для тензора Эйнштейна справедливо равенство: .

9. Анализ уравнения движения

Из (14-15) следует связь между ковариантным 4-ускорением элемента вещества и плотностями действующих сил в искривлённом пространстве-времени:

.

Запишем это четырёхмерное уравнение отдельно для временной и пространственной компонент, учитывая, что

,

а также . Для поля диссипации будем использовать соотношения (B6) из Приложения B, где вместо в общем случае следует подставить . Выражения для других полей можно найти в [7]. Это даёт:

.

.

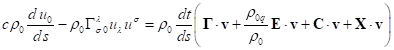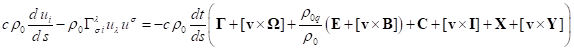Здесь , , и – векторы напряжённостей гравитационного и электромагнитного полей, поля давления и поля диссипации, соответственно. Обозначения , , и относятся к полю кручения, к магнитному полю, и к соленоидальным векторам поля давления и поля диссипации, соответственно.

После сокращения на множитель имеем:

. (22)

. (23)

В (23) сумма представляет собой вклад в общее ускорение от электромагнитной силы Лоренца, действующей на элемент вещества. Знак минус перед этой суммой получается потому, что есть пространственная компонента ковариантной 4-скорости, отличающаяся от обычной контравариантной пространственной компоненты множителем в виде метрического тензора. Аналогично, сумма есть ускорение от гравитационной силы Лоренца. Гравитационные и электромагнитные силы относятся к так называемым массовым силам, распределённым по всему тому объёму, где имеется масса и заряд вещества.

9.1. Уравнение движения в пространстве Минковского

С целью упрощения нашего анализа рассмотрим уравнения (22-23) в рамках специальной теории относительности. Сумма двух последних членов в (23) с учётом формул (B7) из Приложения B для и даёт следующее:

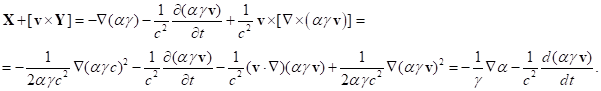
(24)

В (24) есть фактор Лоренца.

Для поля давления с учётом определения 4-потенциала в виде , тензора поля давления из (10), и определения векторов и по правилу:

, ,

находим выражение для векторов:

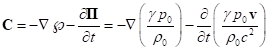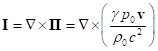, . (25)

С помощью (25) вычисляем сумму двух членов в (23):

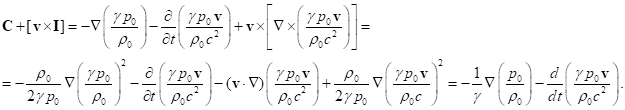
(26)

Подставляя (24) и (26) в (23), и учитывая, что в пространстве Минковского символы Кристоффеля равны нулю, а пространственная компонента 4-скорости равна , находим:

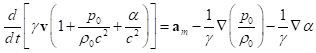. (27)

В (27) мы ввели обозначение для ускорения, возникающего от действия массовых сил:

.

До сих пор мы не определили функцию диссипации . В рассматриваемом приближении она связана со скалярным потенциалом поля диссипации соотношением: .

Будем считать, что

, (28)

то есть .

Это означает, что скалярный потенциал поля диссипации пропорционален как скорости движения рассматриваемого элемента вещества, так и пройденному им пути в окружающей среде. Вклад в делает также градиент дивергенции скорости с некоторым коэффициентом .

Коэффициент зависит от параметров трущихся слоёв вещества, в первом приближении он обратно пропорционален квадрату толщины слоёв. При этом коэффициент отражает свойства вещества и может быть различным у разных веществ. С учётом (28) уравнение (27) преобразуется так:

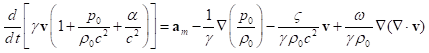. (29)

При наличии в (29) градиента 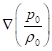от отношения давления к плотности массы, возникает ускорение, направленное против этого градиента. Член в (29), пропорциональный скорости , определяет ускорение торможения из-за действия вязкости среды. Поскольку торможение в (29) зависит не от абсолютной скорости движения, а от скорости движения одних слоёв вещества относительно других слоёв, скорость должна быть относительной скоростью. Воспользуемся свободой выбора системы отсчёта для того, чтобы от абсолютных скоростей перейти к относительным скоростям. Пусть система отсчёта является сопутствующей и движется в веществе вместе с контрольным объёмом малых размеров. Тогда в такой системе отсчёта скорость в (29) будет являться относительной скоростью: одни слои будут опережать, а другие отставать, и появятся вязкие силы.

Выпишем теперь уравнения для поля ускорений из [7]:

, , , . (30)

Вектор в (30) есть напряжённость поля ускорений, а вектор представляет собой соленоидальный вектор поля ускорений. 4-потенциал поля ускорений равен 4-скорости, взятой с ковариантным индексом. Тензор ускорений определяется в (10) как 4-ротор и содержит в себе векторы и :

, .

В пространстве Минковского от скалярного и векторного потенциалов поля ускорений можно перейти к компонентам 4-скорости и выразить через них векторы и :

, . (31)

Подставим (31) во второе уравнение в (30):

. (32)

Условие калибровки 4-потенциала поля ускорений (9) имеет вид: . В пространстве Минковского это соотношение упрощается:

, или . (33)

С учётом (33) преобразуем левую часть (32):

.

Подставляя это в (32), получаем волновое уравнение:

. (34)

Согласно (34), скорость движения вещества в системе должна подчиняться волновому уравнению, то есть скорость задаётся параметрами системы и непрерывно изменяется при переходе от одного контрольного объёма к другому.

Из (31) и первого уравнения в (30) с учётом (33) следует волновое уравнение для фактора Лоренца:

.

Мы можем выразить скорость из (34) и подставить в (29):

.

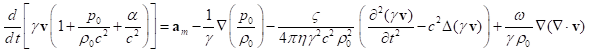(35)

Выясним физический смысл последнего члена в (35). Условие (33) калибровки 4-потенциала поля ускорений можно переписать следующим образом:

.

Отсюда при условии имеем:

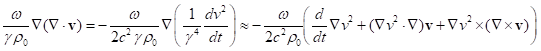. (36)

Величина есть градиент от половины квадрата скорости, то есть градиент кинетической энергии в расчёте на единицу массы. Эта величина пропорциональна ускорению, возникающему за счёт рассеяния кинетической энергии движения. Временная производная от приводит к скорости изменения ускорения. Другие члены в (36) также имеют размерность скорости изменения ускорения.

Таким образом в (35) учитывается вязкость не только за счёт скорости движения, но и за счёт скорости изменения ускорения движения вещества.

9.2. Сравнение с уравнением Навье-Стокса

Векторное уравнение Навье-Стокса в классическом виде применяется обычно для нерелятивистского описания движения жидкости и имеет следующий вид [6]:

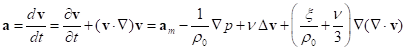, (37)

где и – ускорение и скорость произвольного точечного элемента жидкости, – плотность массы, – давление, – коэффициент кинематической вязкости, – коэффициент второй (объёмной) вязкости, – ускорение от действия массовых сил в жидкости, и предполагается, что коэффициенты и постоянны по объёму.

В (37) скорость зависит не только от времени, но и от координат движущегося элемента жидкости. Это позволяет разложить производную на сумму двух частных производных, по времени, , и по пространству, , соответственно, то есть применить материальную (субстанциональную) производную.

Сравнивая (35) и (37) для случая малых скоростей, когда стремится к единице, и при достаточно малом давлении и вязкости, получаем оценку коэффициента кинематической вязкости:

. (38)

Поскольку , где есть коэффициент динамической вязкости, то отсюда получается:

.

В данном соотношении зависит в основном от свойств вещества, а коэффициенты и зависят ещё от параметров рассматриваемой системы. Например, если исследуется течение жидкости между двумя близко расположенными пластинками, то коэффициент обратно пропорционален квадрату расстояния между пластинками.

Из равенства последних членов в (35) и (37) следуют соотношения:

, . (39)

Присутствие в (37) и подразумевает две причины появления скорости изменения ускорения – одна из них из-за изменения плотности вещества за счёт сопротивления среды, а другая из-за изменения импульса движущегося вещества в вязкой среде.

9.3. Мощность энергии

В пространстве Минковского временная компонента 4-скорости равна , символы Кристоффеля равны нулю, и (22) записывается так:

. (40)

К (40) можно также прийти, если в пространстве Минковского умножить уравнение движения (23) на скорость . Подставим в (40) вектор из (25), и вектор согласно (B7) из Приложения B:

.

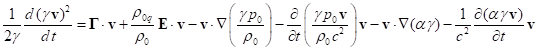Эквивалентное соотношение получится, если (29) умножить на скорость :

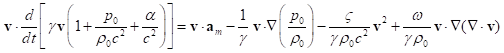. (41)

В левой части (41) стоит скорость изменения кинетической энергии на единицу плотности массы (с учётом вклада от давления и функции диссипации ), а в правой части находится мощность работы гравитационных и электромагнитных сил и мощность работы силы давления. Член с квадратом скорости в правой части (41) пропорционален самой кинетической энергии, а последний член описывает мощность энергии, преобразуемой при движении вещества в вязкой среде с эффектом сжатия вещества и изменения его плотности.

Ещё одно эквивалентное соотношение для мощности изменения энергии движущегося вещества будет при умножении скорости на уравнение (35). В этом случае в правой части (41) появляется лапласиан и вторая частная производная по времени. Если заменить коэффициенты и с помощью (38) и (39), получится следующее:

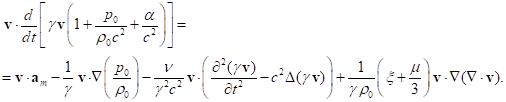(42)

9.4. Зависимость модуля скорости от времени

В этом разделе сделаем вывод о характере изменения кинетической энергии со временем. Для удобства будем рассматривать сопутствующую систему отсчёта, в которой скорости являются относительными скоростями движения слоёв вещества друг относительно друга. Если в (27) все члены умножить на и положить, что величина , то есть пренебречь вкладом от плотности энергии давления и функции диссипации по сравнению с плотностью энергии покоя, можно записать:

.

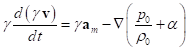Полагая, что , скорость , , после умножения на и интегрирования, с учётом (28) для , имеем:

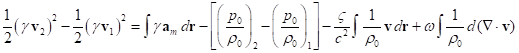. (43)

Согласно (43), кинетическая энергия меняется, когда над веществом осуществляется работа массовых сил, вещество переходит в состояние с другим отношением , в веществе происходит трение между слоями, а также не равна нулю дивергенция скорости.

В (43) возможны дальнейшие упрощения, если предположить, что на пути интегрирования подынтегральные выражения меняются незначительно и их можно вынести за знак интеграла. Используем ещё уравнение непрерывности в виде:

. (44)

Всё это с учётом (38-39) даёт:

.

(45)

В левой части (45) стоит изменение кинетической энергии в расчёте на единицу массы, происходящее за счёт изменения скорости от до . Кинетическая энергия увеличивается, если в правой части проекция ускорения массовых сил на вектор перемещения имеет положительный знак. При этом второй, третий и четвёртый члены в правой части имеют отрицательный знак. Это означает, что диссипация энергии движения пропорциональна росту давления на пути движения вещества, скорости и длине перемещения, а также увеличению плотности вещества, мешающего свободному движению.

Скалярное произведение , где обозначает время движения одного слоя относительно другого, не обращается в нуль при криволинейном или вращательном движении слоёв вещества или жидкости. Поэтому в движущемся веществе легко могут возникать вихри и зарождаться турбулентность. Этому способствует то, что члены в правой части (45) могут оказывать влияние друг на друга. Например, в зонах повышенного давления линии тока вещества искривляются, а температура меняет плотность в последнем члене в (45). Турбулентность можно характеризовать как способ перекачки энергии линейного движения вещества во вращательное движение различных масштабов.

Уравнение (45) можно переписать так, чтобы перенести в левую часть все члены, зависящие от скорости. Положив , где есть угол между скоростью и ускорением , находим квадратное уравнение для скорости как функции от времени и других параметров:

.

Константа в правой части задаёт начальное условие движения. Решение этого уравнения позволяет оценить изменение модуля скорости со временем.

10. Заключение

Для случая постоянных коэффициентов вязкости мы показали, что уравнение Навье-Стокса движения вязкой сжимаемой жидкости может быть выведено с помощью 4-потенциала поля диссипации энергии, тензора диссипации и тензора энергии-импульса диссипации. Вначале мы записали уравнения движения (15) в общем виде, затем выразили их в (22-23) через напряжённости гравитационного и электромагнитного полей, напряжённости поля давления и поля диссипации энергии. В 4-потенциал поля диссипации входят функция диссипации и связанный с ней скалярный потенциал поля диссипации. Значение может быть выбрано таким образом, что в уравнении (27) для ускорения движения вещества появляется зависимость от скорости движения этого вещества, связанная с вязкостью, когда торможение в веществе пропорционально относительной скорости его движения. Можно также учесть зависимость от скорости изменения ускорения со временем. Это даёт нам уравнение (29).

Затем мы анализировали волновое уравнение для поля скоростей (34) и выразили из него скорость, чтобы подставить в (29). Полученное уравнение (35) почти точно совпадает с уравнением Навье-Стокса (37). Одно различие состоит в том, что в ускорении от давления плотность массы в выражении 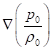находится у нас под знаком градиента, а в (37) вынесена из под знака градиента. Второе различие связано с тем, что в (35) у нас присутствует дополнительный член вида . Этот член пропорционален скорости изменения ускорения со временем и описывает те явления, в которых явления изменения свойств среды, влияющие на вязкость, происходят в заданном временном режиме.

Кроме этого, в (35) мы учли релятивистские поправки от фактора Лоренца , а также зависимость ускорения вещества от ускорения массы-энергии поля давления и поля диссипации (в квадратной скобке в левой части (35) ).

Направленная кинетическая энергия движения вещества в вязкой среде может рассеиваться в хаотические движения частиц окружающей среды и преобразовываться в тепло. Возможен и обратный процесс, когда нагревание среды приводит к изменению состояния движения вещества. В разделе 9.3. мы представили дифференциальные уравнения изменения кинетической энергии системы и преобразования её в другие виды энергии, включая и энергию поля диссипации. Эти уравнения не являются полностью самостоятельными, поскольку получаются путём скалярного умножения уравнения движения на скорость вещества.

Тензор энергии-импульса диссипации представлен нами в (16), а его инварианты даны в (B8) в Приложении B. В разделе 9.1. функция диссипации даётся формулой (28): .

Данная функция зависит от пройденного пути веществом относительно окружающего и тоже движущегося вещества, и может считаться функцией времени движения относительно той системы отсчёта, которая сопутствует в среднем движению вещества в данном малом контрольном объёме системы. С помощью известной величины по формулам (B7) можно вычислить векторы и , и следовательно, определить компоненты тензора . В частности, интеграл по объёму от компоненты этого тензора позволяет учесть всю ту энергию, которую движущееся вещество передало среде в виде энергии поля диссипации, а компоненты задают вектор как плотность потока энергии поля диссипации.

В рамках принятых допущений уравнение Навье-Стокса (37) сводится к уравнению (27), в котором ускорение зависит, помимо массовых сил, от суммы двух градиентов – от функции диссипации , и от величины .

Вид уравнения (27) таков, что это уравнение должно иметь гладкие решения, если нет разрывов в давлении или в функции диссипации . Если считать справедливым условие (28) и формулу (36), то градиент от также будет гладкой функцией.

Вместо того, чтобы от уравнения (27) переходить к уравнению (35), подобному уравнению Навье-Стокса (37), можно пойти другим путём. Дифференциальное уравнение (27) представляет собой уравнение для определения поля скоростей . В этом уравнении имеются как минимум ещё три неизвестные функции – поле давления , плотность массы , и функция диссипации . Следовательно, к (27) необходимо добавить не менее трёх уравнений, чтобы замкнуть систему уравнений и сделать её разрешимой в принципе. Одним из таких уравнений является уравнение непрерывности (12) в форме (44), связывающее плотность со скоростью. Для определения функции диссипации мы представили волновое уравнение (B10) в Приложении B. Распределение давления в системе может быть найдено из волнового уравнения (C4) в Приложении C.

В уравнении (27) присутствует ещё ускорение , возникающее от действия массовых сил. Это ускорение зависит от напряжённости гравитационного поля , поля кручения , напряжённости электрического поля , магнитного поля и плотности заряда :

.

Для каждой из этих величин имеются свои собственные уравнения, позволяющие их определить. Например, уравнения гравитационного поля (уравнения Хевисайда) могут быть представлены согласно [13] в следующем виде:

, , , . (46)

Уравнения (46) выводятся в [11] из принципа наименьшего действия и по своей форме подобны уравнениям Максвелла, с помощью которых вычисляют и . Наконец, плотность заряда может быть связана со скоростью уравнением непрерывности электрического заряда:

. (47)

Таким образом, набор уравнений (27), (44), (B10), (C4), (46), (47), в совокупности с уравнениями Максвелла, составляет полный набор, достаточный для решения задачи о движении вязкого сжимаемого и заряженного вещества в гравитационном и электромагнитном поле.

11. Список использованных источников

1. Navier C., Memoir sur Ies Iois du mouvement des fluids, Mem, de L' Ac. Royale de sc. de L' Institut de France, 1827, Vol. VI , 287-319.

2. Poisson S. D., Mémoire sur les équations générales de l'équilibre et du mouvement des corps solides élastique et des fluids. J. Ecole polytechn., 1831, Vol. 13, P. 1–174.

3. Stokes G.G., On the theories of the internal friction of fluids in motion and of the equilibrium and motion of elastic solids, Trans, of the Cambr. Philos. Society, т. VIII. 1844-1849, Vol. 8. P. 287–319.

4. Saint-Venant (Barre), A. J. C. Note à joindre au Mémoire sur la dynamique des fluides, présenté le 14 avril 1834 ; Comptes rendus, r. Acact. sci., 1843, Vol. 17, No 22, 1240-1243.

5. Khmelnik S. I. Navier-Stokes equations. On the existence and the search method for global solutions. 2010, ISBN 978-0-557-48083-8.

6. Ландау Л. Д., Лифшиц Е. М. Гидродинамика. – Издание 7-е, исправленное. – М.: Наука, 1988. – 731 с. – (Теоретическая физика, том VI).

7. Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy. vixra.org, 5 Mar 2014; О космологической постоянной, поле ускорения, поле давления и об энергии.

8. Федосин С.Г. Физические теории и бесконечная вложенность материи. Пермь, 2009-2012, 858 стр., Табл. 21, Ил.41, Библ. 293 назв. ISBN 978-5-9901951-1-0.

9. Fedosin S.G. The Integral Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based on the Pressure Field and Acceleration Field. American Journal of Modern Physics. Vol. 3, No. 4, 2014, pp. 152-167. doi: 10.11648/j.ajmp.20140304.12. // Интегральный 4-вектор энергии-импульса и анализ проблемы 4/3 на основе поля давления и поля ускорений.

10. Fedosin S.G. Relativistic Energy and Mass in the Weak Field Limit . vixra.org, 1 May 2014. Accepted by Jordan Journal of Physics; Релятивистская энергия и масса в пределе слабого поля .

11. Fedosin S.G. The Principle of Least Action in Covariant Theory of Gravitation. Hadronic Journal, 2012, Vol. 35, No. 1, P. 35 – 70. // Принцип наименьшего действия в ковариантной теории гравитации .

12. Fedosin S.G. The General Theory of Relativity, Metric Theory of Relativity and Covariant Theory of Gravitation. Axiomatization and Critical Analysis. International Journal of Theoretical and Applied Physics (IJTAP), ISSN: 2250-0634, Vol.4, No. I (2014), pp. 9-26. Общая теория относительности, метрическая теория относительности и ковариантная теория гравитации. Аксиоматизация и критический анализ .

13. Федосин С.Г. Физика и философия подобия от преонов до метагалактик. Пермь, Стиль-МГ, 1999, 544 стр., Табл.66, Ил.93, Библ. 377 назв. ISBN 5-8131-0012-1.

Приложение A. Обозначения полей

	Электромаг-нитное поле	Гравитацион-ное поле	Поле ускорений	Поле давления	Поле диссипа-ции
4-потенциал
Скалярный потенциал
Векторный потенциал
Напряжён-ность поля
Соленоидаль-ный вектор
Тензор поля
Тензор энергии-импульса
Вектор потока энергии-импульса

В данной таблице есть вектор Пойнтинга, – вектор Хевисайда.

Приложение B. Свойства поля диссипации

Компоненты антисимметричного тензора поля диссипации получаются из соотношения (3) с помощью (2). Введём следующие обозначения:

, , (B1)

где индексы образуют тройки неповторяющихся чисел вида 1,2,3 или 3,1,2 или 2,3,1; 3-векторы и можно расписать по компонентам: ; .

С данными обозначениями тензор можно представить следующим образом:

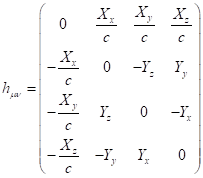. (B2)

Этот же тензор с контравариантными индексами равен: . В пространстве Минковского метрический тензор не зависит от координат, и в этом случае для тензора диссипации следует:

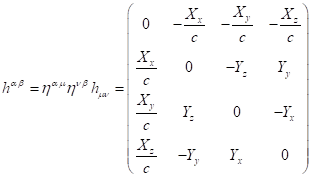. (B3)

Мы можем выразить уравнения поля диссипации (8) в пространстве Минковского через векторы и с помощью 4-вектора массового тока: , где . Заменяя в (8) ковариантные производные на частные производные , находим:

, , , . (B4)

Если второе уравнение в (B4) умножить скалярно на , а четвёртое уравнение умножить скалярно на и результаты сложить, получится следующее:

. (B5)

Уравнение (B5) содержит в себе теорему Пойнтинга в применении к полю диссипации. Смысл этого дифференциального уравнения в том, что если в системе осуществляется рассеяние энергии движения частиц вещества, то дивергенция потока поля диссипации связывается с изменением во времени энергии поля диссипации, и с мощностью плотности энергии рассеяния. Соотношение (B5) в общековариантном виде записывается как временная компонента уравнения (17):

.

Если подставить (B2) в (17), можно выразить скалярную и векторную компоненты плотности 4-силы поля диссипации:

, . (B6)

Вектор имеет размерность обычного 3-ускорения, а размерность вектора такая же, как у частоты.

Подставляя 4-потенциал поля диссипации (2) в определение (B1), в пространстве Минковского находим:

, . (B7)

Вектор является напряжённостью поля диссипации, а вектор – соленоидальным вектором поля диссипации. Оба вектора зависят от функции диссипации , которая в свою очередь зависит от координат и времени. В реальных жидкостях всегда существует внутреннее трение, , и вектора и также не равны нулю.

Мы можем подставить тензоры (B2) и (B3) в (16) и выразить тензор энергии-импульса поля диссипации через векторы и . Запишем здесь выражения для тензорного инварианта и временных компонент тензора :

, , . (B8)

Компонента определяет плотность энергии поля диссипации в данном объёме, а вектор задаёт плотность потока энергии поля диссипации.

Если подставить из (B7) в первое уравнение в (B4), и учесть калибровку 4-потенциала (9) в следующем виде:

, или , (B9)

получится волновое уравнение для скалярного потенциала:

, или . (B10)

Из (B7), (B9) и второго уравнения в (B4) следует волновое уравнение для векторного потенциала поля диссипации:

, или .

Приложение C. Уравнения поля давления

Четыре векторных уравнения для компонент поля давления в рамках специальной теории относительности были представлены в [7], как следствие вариации функции действия:

, , , . (C1)

Вектор напряжённости поля давления и соленоидальный вектор определяются через 4-потенциал поля давления по формулам:

, (C2)

.

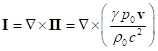Калибровка 4-потенициала согласно (9) в виде в пространстве Минковского превращается в выражение . Подставляя сюда выражение для 4-потенциала поля давления, имеем:

, или 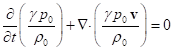. (C3)

Подставляя (C2) в первое уравнение в (C1) и используя (C3), получаем волновое уравнение для вычисления скалярного потенциала поля давления:

, или 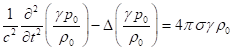. (C4)

Волновое уравнение для векторного потенциала поля давления следует из (C2), (C3) и второго уравнения в (C1):

, или .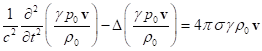

Источник: http://sergf.ru/fd.htm

На научный сайт