In English

International Journal of Theoretical and Applied Physics (IJTAP), ISSN: 2250-0634, Vol. 4, No. I (2014), pp. 9 – 26.

УДК 530.12:531.51+ 531.211

Общая теория относительности, метрическая теория относительности и ковариантная теория гравитации. Аксиоматизация и критический анализ

Федосин Сергей Григорьевич

г. Пермь, Пермский край, Россия

e-mail intelli@list.ru

Осуществлена аксиоматизация общей теории относительности (ОТО). Аксиомы ОТО сравниваются с аксиомами метрической теории относительности и ковариантной теории гравитации. Указывается на необходимость использования ковариантной формы полной производной по собственному времени от инвариантных величин, 4-векторов и тензоров. Даётся определение 4-вектора плотности силы в римановом пространстве-времени.

Ключевые слова: общая теория относительности; метрическая теория относительности; ковариантная теория гравитации; аксиоматизация.

The General Theory of Relativity, Metric Theory of Relativity and Covariant Theory of Gravitation. Axiomatization and Critical Analysis

Sergey G. Fedosin

Perm, Perm Region, Russia

e-mail intelli@list.ru

The axiomatization of general theory of relativity (GR) is done. The axioms of GR are compared with the axioms of the metric theory of relativity and the covariant theory of gravitation. The need to use the covariant form of the total derivative with respect to the proper time of the invariant quantities, the 4-vectors and tensors is indicated. The definition of the 4-vector of force density in Riemannian spacetime is deduced.

Keywords: general relativity; metric theory of relativity; covariant theory of gravitation; axiomatization.

Установление аксиоматических основ считается важным этапом развития любой современной физической теории. Это связано с тем, что из заданной полной системы взаимно независимых аксиом можно единственным и однозначным образом вывести всю теорию. Кроме этого, на основе аксиом легко определить область применимости теории и её отличие от альтернативных подходов.

Представленные в 1915 г. Альбертом Эйнштейном [1] и Давидом Гильбертом [2] уравнения общей теории относительности (ОТО) опирались на ряд принципов и эвристических аналогий, но не была аксиоматизированы. Имеющийся в ОТО математический аппарат давал возможность решать различные задачи, что позволило теории стать общепринятой моделью гравитации. Проблема с аксиоматизацией ОТО стала назревать уже в середине двадцатого века, когда выяснилось, что ОТО не может быть проквантована таким же образом, как например электромагнитная теория. В ОТО также не определён тензор гравитационного поля, что мешает назвать ОТО полноценной теорией гравитационного поля. Уравнения ОТО предсказывают сингулярности с бесконечной плотностью энергии, и чёрные дыры с такой величиной гравитации, что она должна удерживать внутри себя не только вещество, но даже и кванты света. Однако в рамках ОТО дать ответ о реальном существовании подобных экзотических объектов по всей видимости не представляется возможным.

Для теоретического обоснования ОТО обычно применяются следующие принципы:

1) Принцип эквивалентности в различных формах, в том числе:

1.1) Равенство инерционной и гравитационной масс.

1.2) Эквивалентность инерционного и гравитационного ускорений при описании явлений в бесконечно малой по размерам системе отсчёта пробной частицы.

1.3) Эквивалентность состояния свободного падения в любом гравитационном поле и движения по инерции в отсутствие гравитационного поля, при условии равенства мгновенных скоростей падения и скоростей движения по инерции.

1.4) Эквивалентность формы движения при одинаковых начальных условиях для любых незаряженных и невращающихся пробных частиц в гравитационном поле независимо от структуры и состава их вещества.

1.5) Эквивалентность протекания физических явлений для свободно падающего в гравитационном поле наблюдателя в системе его отсчёта, понимаемая как независимость формы явлений от скорости падения и местоположения в гравитационном поле.

1.6) Эквивалентность эффектов гравитации и деформации пространства-времени, описание гравитации через метрический тензор и его производные по координатам и времени.

2) Принцип движения по геодезическим, вытекающий из пунктов 1.1), 1.3) и 1.4).

3) Принцип искривления пространства-времени веществом, электромагнитным полем и другими негравитационными полями.

4) Принцип линейной связи между искривлением пространства и энергией-импульсом вещества и негравитационных полей (тензорное уравнение Эйнштейна-Гильберта для метрики).

5) Принцип определения силы и уравнения движения через ковариантную производную от тензора энергии-импульса.

6) Принцип соответствия: в слабом поле уравнения ОТО переходят в классическое уравнение тяготения Ньютона, а метрика пространства-времени – в метрику плоского пространства-времени Минковского.

7) Принцип ковариантности: физические величины и уравнения ОТО должны быть записаны в ковариантной форме, не зависящей от выбора системы отсчёта.

8) Принцип наименьшего действия: уравнения ОТО могут быть выведены в результате варьирования интеграла по четырёхмерному объёму от плотности функции Лагранжа.

Наиболее удобно измерять метрику в ОТО с помощью электромагнитных волн, путём определения отклонения лучей света и эффекта замедления времени электромагнитных часов, в зависимости от координат и времени. Отсюда находится метрический тензор, задающий гравитационное поле. Поэтому в ОТО полагают, что скорость изменения и распространения гравитации равна скорости света, с которой распространяется электромагнитная волна в данной точке пространства-времени. Скорость электромагнитной волны в гравитационном поле зависит от координат и времени и считается максимальной скоростью передачи взаимодействий. Метрический тензор в ОТО олицетворяет гравитационное поле, так что ковариантность метрического тензора относительно преобразований любых систем отсчёта задаёт ковариантность и гравитационного поля.

После появления в 2009 году метрической теории относительности (МТО) и ковариантной теории гравитации (КТГ), которые изначально аксиоматизированы [3], возникла необходимость провести аксиоматизацию ОТО с тем, чтобы сравнить физические основания данных теорий с единой точки зрения. Аксиоматизация ОТО может оказаться полезной и для сравнения с другими альтернативными теориями гравитации.

Анализ ОТО показывает, что она содержит в себе две тесно связанные компоненты. Первая из них является общей относительностью явлений в разных системах отсчёта. Эта часть теории позволяет связывать между собой результаты пространственно-временных измерений различных наблюдателей и пересчитывать физические величины из одной системы отсчёта в другую. Вторая часть ОТО есть теория гравитационного поля и его взаимодействия с веществом. Обе части ОТО могут быть полностью выведены из соответствующих систем аксиом [4]. Благодаря слиянию общей относительности и теории гравитации, в ОТО в данных системах аксиом имеется одна общая аксиома, описывающая связь метрики и материи в уравнении для вычисления метрики.

Удобство сравнения ОТО и КТГ связано с тем, что обе эти теории являются метрическими тензорными теориями гравитации. В отличие от ОТО, в КТГ в функции Лагранжа присутствуют дополнительные члены, прямо задающие гравитационное поле [5]. По своей форме эти члены подобны членам, определяющим электромагнитное поле. При этом в рассмотрение вводятся тензор напряжённостей и тензор энергии-импульса гравитационного поля. От функции Лагранжа возможен переход к функции Гамильтона в рамках КТГ [6].

Аксиомы общей относительности ОТО

1. Свойства пространства-времени, определяемые незаряженными и невзаимодействующими друг с другом пробными частицами и волнами, не зависят от типа используемых частиц и волн.

2. Характеристикой пространства-времени является симметричный метрический тензор , зависящий в общем случае от координат и времени. С помощью тензора вычисляются различные инварианты, связанные с 4-векторами и тензорами.

3. Квадрат интервала задаёт квадрат длины 4-вектора дифференциала координат, не зависящий от выбора системы отсчёта:

,

где символом обозначен полный дифференциал в искривлённом пространстве-времени.

Пространственно-временные измерения и фиксация метрических свойств осуществляются как правило с помощью электромагнитных волн, скорость которых считается равной скорости света для локальных наблюдателей и не зависит от скорости излучателей. Однако в глобальной координатной системе отсчёта скорость электромагнитных волн в общем случае зависит от координат и времени и уменьшается в области сильного поля. При этом для электромагнитных волн интервал всегда равен нулю: .

4. Физические свойства вещества и полей, кроме гравитационного поля, задаются соответствующими тензорами плотности энергии-импульса. Существует математическая функция от метрического тензора (например тензор Гильберта-Эйнштейна в левой части уравнения для метрики), пропорциональная суммарному тензору энергии-импульса вещества и поля в правой части:

, (1)

где − тензор Риччи, − скалярная кривизна, − гравитационная постоянная, − скорость света, − тензор плотности энергии-импульса вещества, − тензор плотности энергии-импульса электромагнитного поля и других негравитационных полей. С помощью данного уравнения осуществляется связь между геометрическими свойствами пространства-времени, с одной стороны, и физическими свойствами имеющегося вещества и негравитационного поля, с другой стороны.

5. Имеются дополнительные условия, с помощью которых задаётся необходимое для расчётов количество соотношений для сдвигов и поворотов сравниваемых систем отсчёта, скоростей их движения друг относительно друга, и учитывающие свойства симметрии систем отсчёта.

Для вывода преобразований, связывающих дифференциалы координат и времени двух любых систем отсчёта, используется условие равенства интервалов в аксиоме 3. Интервал является инвариантом, для вычисления которого в каждой системе отсчёта требуется знание метрического тензора, указанного в аксиоме 2. Кроме этого, согласно аксиоме 5 необходимы дополнительные соотношения и связи между этими системами отсчёта. Например, преобразования Лоренца для двух инерциальных систем отсчёта учитывают: расположение и взаимную ориентацию систем отсчёта; их скорости друг относительно друга; симметрию преобразований для осей, перпендикулярных скорости движения, включая одинаковую величину скорости света.

Принцип эквивалентности можно считать следствием независимости метрики от типа и свойств пробных частиц и волн, предполагаемой в аксиоме 1. Из аксиомы 4 следует, что переход от общей относительности ОТО к частной относительности специальной теории относительности должен сопровождаться устремлением к нулю плотности вещества и скоростей пробных частиц, а также и величин напряжённостей негравитационных полей, действующих на частицы. С учётом аксиомы 5 этого достаточно, чтобы получить все соотношения специальной теории относительности.

Выше мы представили систему аксиом общей относительности ОТО с нашей точки зрения. Существуют и другие попытки обосновать относительность в ОТО. В частности, статья [7] посвящена проблеме аксиоматического обоснования лоренцевой геометрии свободного падения и распространения света, которая проявляется в пространстве-времени общей теории относительности в совместимых конформных и проективных структурах на четырёхмерном многообразии.

Аксиомы гравитационного поля ОТО

1. Свойства гравитационного поля задаются скоростью распространения гравитационного воздействия, равной скорости света и зависящей в общем случае от координат и времени, а также невырожденным метрическим тензором второго ранга .

2. Гравитационное поле сводится к геометрическому искривлению (деформации) пространства-времени, вызываемого источниками вещества и любым негравитационным полем. Степень искривления пространства-времени фиксируется тензором кривизны Римана-Кристоффеля , являющимся функцией от и его производных первого и второго порядка по координатам и времени. Путём свёртки с метрическим тензором из тензора образуются тензор Риччи и скалярная кривизна .

3. Гравитационное ускорение сводится к градиентам от метрического тензора , то есть к скорости изменения компонент метрического тензора в пространстве и времени.

4. Свойства материи, определяемой как вещество и негравитационные поля, задаются тензором плотности энергии-импульса .

5. Связь между гравитационным (метрическим) полем, задаваемым метрическим тензором через кривизну пространства-времени, и материей, определяется уравнением Гильберта-Эйнштейна для метрики:

.

Из аксиомы 3 здесь может быть выведен принцип эквивалентности. Ковариантная производная, действующая на обе части уравнения для метрики в аксиоме 5, обращает их в нуль. Это фиксирует свойства тензора Гильберта-Эйнштейна, и одновременно задаёт уравнение движения вещества.

Сравнение теорий относительности

Аксиомы метрической теории относительности (МТО) имеют вид [3]:

1. Свойства используемого пространственно-временного многообразия в той или иной системе отсчёта зависят от свойств пробных тел или волн, с помощью которых осуществляются пространственно-временные измерения в данной системе отсчёта. Важнейшим свойством пробных тел или волн является скорость их распространения, поскольку она фигурирует в формулах как мера скорости других тел и запаздывания получения информации при дистанционных измерениях.

2. Геометрические свойства пространства-времени фиксируются соответствующим математическим объектом, являющимся функцией пространственно-временных координат системы отсчёта. Для широкого класса систем отсчёта подходящим математическим объектом является невырожденный четырёхмерный симметричный метрический тензор второго ранга , компонентами которого являются скалярные произведения единичных векторов осей координат выбранной системы отсчёта. Тензор позволяет находить любые инварианты, связанные с 4-векторами и тензорами.

3. Квадрат интервала между двумя близкими событиями, понимаемый как свёртка метрического тензора с произведением дифференциалов координат , является инвариантом, мерой собственного динамического времени движущейся частицы, и не зависит от выбора системы отсчёта:

.

Интервал для двух близких событий равен нулю, если эти события связаны с распространением пробных тел или волн, с помощью которых осуществляются пространственно-временные измерения и фиксация метрики.

4. Физические свойства любых полей, включая гравитационное поле, в той или иной системе отсчёта задаются соответствующими тензорами плотности энергии-импульса. Существует математическая функция от метрического тензора , находимая по определённым правилам, и пропорциональная суммарному тензору энергии-импульса полей, действующему в данной системе отсчёта. В простейшем случае такой функцией является тензор, находящийся в левой части уравнения для метрики [8]:

, (2)

где − постоянный коэффициент, зависящий от типа используемых пробных частиц или волн, определяемый путём сравнения с экспериментом либо с формулами классической физики в приближении слабого поля или малых скоростей, и мы считаем, что скорость гравитации равна скорости света,

− тензор плотности энергии-импульса поля ускорений, зависящий от тензора ускорений :

.

− тензор плотности энергии-импульса гравитационного поля. Этот тензор выражается через тензор гравитационного поля :

.

− тензор плотности энергии-импульса поля давления, находимый через тензор давления :

.

Здесь и являются некоторыми константами.

Уравнение (2) осуществляет связь между геометрическими свойствами используемого пространственно-временного многообразия, с одной стороны, и физическими свойствами действующих полей, с другой стороны. Ковариантная производная, действующая на обе части уравнения для метрики (2), обращает их в нуль. Это фиксирует свойства тензора в левой части (2), и одновременно задаёт уравнение движения вещества под действием полей.

5. Имеются дополнительные условия, с помощью которых задаётся необходимое для расчётов количество соотношений для сдвигов и поворотов сравниваемых систем отсчёта, скоростей их движения друг относительно друга, и учитывающие свойства симметрии систем отсчёта.

Из сравнения аксиом общей относительности ОТО с аксиомами метрической теории относительности вытекают особенности этих теорий, указанные в Таблице 1.

Таблица 1

Особенности теорий	Общая относительность ОТО	Метрическая теория относительности
Метрические свойства пространства-времени:	Не зависят от типа используемых пробных частиц и волн	Зависят от типа используемых пробных частиц и волн
Равенство нулю интервала:	Только для электромагнитных волн	Для любых пробных частиц и волн, с помощью которых производятся пространственно-временные измерения и фиксация метрики
Источники энергии-импульса, определяющие метрику:	Вещество и любые негравитационные поля	Любые поля, включая гравитационное поле
Принцип эквивалентности понимается как:	Эквивалентность явлений в двух системах отсчёта малого размера, одна из которых ускоряется гравитационной силой, а другая получает такое же ускорение под действием однородно распределённой негравитационной силы той же величины	Эквивалентность энергии-импульса: «В ускоренной системе отсчёта метрика локально зависит не от вида действующей силы, вызывающей данное ускорение, а от конфигурации этой силы в пространстве-времени системы отсчёта, определяемой тензором энергии-импульса»

Эквивалентность ускорения под действием силы тяжести и инерционного ускорения под действием однородно распределённой по объёму пробного тела негравитационной силы той же величины приводит к равенству гравитационной и инерционной масс. Однородность приложенной силы означает, что в системе малого размера все части системы ускоряются одинаково и относительные внутренние ускорения отсутствуют. В таком случае отдельные элементы пробного тела не оказывают давления друг на друга и ведут себя так же, как если бы пробное тело двигалось по инерции в отсутствие сил. Массы тел могут находиться взвешиванием по отношению к стандартной массе в гравитационном поле, причём массы оказываются пропорциональными действующим на них гравитационным силам. Отсюда вытекает независимость формы движения падающих тел от массы и состава этих тел. Поскольку в любой точке гравитационного поля падающее тело ведёт себя так же, как движущееся по инерции (но с изменением скорости движения), то предполагается, что в падающем теле осуществляется лоренц-ковариантность. Тогда такая лоренц-ковариантность должна быть в любой точке траектории падающего тела и не зависит от скорости движения, а падающий наблюдатель не должен внутренними опытами обнаруживать своё ускоряющееся движение. В итоге принцип эквивалентности приводит к отождествлению эффекта от поля гравитации массивного тела с эффектом деформации пространства-времени вокруг массивного тела. Таковы следствия принципа эквивалентности в ОТО.

В метрической теории относительности (МТО) вместо принципа эквивалентности сил рассматривают принцип эквивалентности энергии-импульса. Действительно, из уравнения (2) для метрики в МТО видно, что метрика полностью определяется источниками в виде тензоров плотности энергии-импульса полей, включая и само гравитационное поле [3]. Лишь энергия-импульс системы необходимы для определения как метрики, так и уравнения движения пробного тела. Если два различных взаимодействия имеют одну и ту же зависимость энергии-импульса, то как метрика, так и закон движения в обоих случаях совпадут. Уравнение ОТО для метрики (1) отличается от уравнения (2) для метрики МТО тем, что в правой части (2) присутствует тензор плотности энергии-импульса гравитационного поля . Вклад от этого тензора в слабых полях мал, и метрика МТО незначительно отличается от метрики ОТО. Однако в сильных гравитационных полях данным тензором пренебрегать уже нельзя, так как возникает значительное самодействие поля на источник поля. Другое отличие заключается в том, что в (2) отсутствует тензор энергии-импульса вещества и в МТО метрика зависит лишь тензоров энергии-импульса полей. В противоположность этому, в ОТО согласно (1) для определения метрики требуется тензор энергии-импульса вещества . Кроме этого, скалярная кривизна входит в (1) с множителем , а в соотношении МТО (2) скалярная кривизна имеет множитель . Это является следствием калибровки космологической постоянной и релятивистской энергии в ковариантной теории гравитации [8].

Сравнение теорий гравитационного поля

Аксиомы ковариантной теории гравитации (КТГ) в 4-мерном векторно-тензорном формализме имеют вид [3]:

1) Свойства гравитационного поля задаются скоростью распространения гравитационного воздействия , а также скалярным потенциалом и векторным потенциалом .

2) Потенциалы гравитационного поля можно объединить в 4-вектор гравитационного потенциала, записанный с нижним ковариантным индексом:

.

Скорость изменения потенциалов в пространстве-времени выбранной системы отсчёта задаётся тензором напряжённостей гравитационного поля, являющимся 4-ротором :

,

где обозначает ковариантную производную, – обычные 4-индексы, так что в случае декартовых координат , , , .

При соответствующем выборе потенциалов поля выполняется соотношение симметричности потенциалов:

. (3)

3) Свойства вещества задаются его плотностью в сопутствующей системе отсчёта и скоростью движения .

4) Величины и входят в 4-вектор плотности массового тока или плотности импульса, который в специальной теории относительности имеет следующий вид:

,

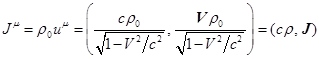где 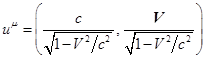– 4-скорость элемента вещества,

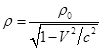– плотность движущегося вещества,

– 3-вектор плотности массового тока.

В римановом пространстве 4-скорость определяется выражением: , и .

5) Связь между гравитационным полем и веществом может быть выражена через взаимосвязь 4-вектора гравитационного потенциала и 4-вектора плотности массового тока , либо через связь между тензором и :

(4)

Особенности теории гравитационного поля в ОТО и в ковариантной теории гравитации, вытекающие из их аксиом, приведены в Таблице 2.

Таблица 2

Особенности теорий	Теория гравитационного поля ОТО	Ковариантная теория гравитации
Гравитационное поле есть:	Метрическое тензорное поле, характеризуемое тензором и его градиентами в виде коэффициентов (символов) Кристоффеля	Физическое векторное поле, характеризуемое 4-вектором потенциала и его градиентами в виде антисимметричного тензора напряжённостей гравитационного поля
Калибровка:	Свёртка метрического тензора в виде даёт символ Кронекера	4- потенциалы полей калибруются так, чтобы их дивергенции равнялись нулю
Скорость гравитационного поля равна:	Скорости света	Скорости распространения гравитации (порядка скорости света) [9]
Связь между гравитационным полем и веществом в случае отсутствия других полей:	Посредством тензорного уравнения Гильберта-Эйнштейна для метрики (1), связывающим функцию от метрического тензора и тензор плотности энергии-импульса вещества	Посредством уравнения (4) для потенциалов или напряжённостей гравитационного поля, и для 4-вектора плотности массового тока
Источники энергии-импульса, определяющие метрику:	Вещество и любые негравитационные поля	Любые поля, включая гравитационное поле

Несмотря на различие систем аксиом гравитационного поля в ОТО и в КТГ, можно показать, что уравнение движения ОТО является частным случаем уравнения движения КТГ. Как было найдено в [3], производная Лагранжа по собственному времени в самом общем случае может быть записана в виде оператора с помощью 4-скорости элемента вещества :

, (5)

где символом обозначен полный дифференциал в искривлённом пространстве-времени, а есть ковариантная производная.

Оператор (5) должен действовать только на четырёхмерные объекты в пространстве-времени, то есть на скаляры, 4-векторы и 4-тензоры. 4-скорость определяется через 4-вектор и инвариант собственного времени . Если же пытаться находить 4-скорость через координатную величину с помощью (5) в виде , то возникнет несоответствие, так как величина в римановом пространстве не является 4-вектором.

Согласно определению в КТГ, плотность силы есть полная скорость изменения 4-вектора плотности массового тока по собственному времени в римановом пространстве-времени:

, (6)

где – символ Кристоффеля.

С другой стороны, выражение для плотности силы, действующей на элемент вещества со стороны гравитационного и электромагнитного полей, а также поля давления, получается после взятия ковариантной производной в уравнении (2). Левая часть уравнения для метрики (2) обнуляется, а из правой части этого уравнения следует:

. (7)

где – тензор напряжённостей электромагнитного поля,

– 4-вектор плотности электромагнитного тока,

– плотность электрического заряда элемента вещества в системе его покоя.

Сравнение (6) и (7) даёт уравнение движения элемента вещества в КТГ под действием давления и гравитационной и электромагнитной сил:

. (8)

Уравнение (8) позволяет полностью учесть реактивную силу Мещерского [10], появляющуюся за счёт изменения плотности элемента вещества. Плотность вещества входит в состав 4-вектора плотности массового тока , от которого в (8) берётся производная по собственному времени, характеризующая силу реакции в механике тел с изменяющейся массой.

Для перехода к формуле для силы в ОТО в (8) следует сделать следующие упрощения: полагать равным нулю (в ОТО гравитационное поле есть метрическое поле, не обладающее свойством самодействия, в связи с чем гравитационное поле в правой части уравнения (1) как источник искривления пространства-времени отсутствует), и считать плотность массы постоянной по объёму пробной частицы и неизменной во времени. В ОТО также не используется тензор давления в том виде, как мы его определили.

Тогда величину в левой части (8) можно будет сократить, и от 4-вектора перейти к 4-вектору скорости :

. (9)

В простейшем случае рассматривается ситуация движения вещества в отсутствие электромагнитного поля: , или при отсутствии зарядов у частиц вещества, когда . Тогда правая часть уравнения движения (9) будет равна нулю и выполняется равенство , то есть 4-ускорение у свободно падающего тела в гравитационном поле отсутствует. С учётом соотношений для 4-скорости и для интервала в виде или , получается стандартное выражение уравнения движения ОТО для вещества в гравитационном поле:

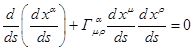. (10)

Для случая распространения света должно быть: . Следовательно, в (9) необходимо устремлять к нулю величину . После умножения в (9) на имеем:

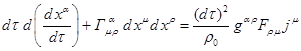. (11)

Для первого члена в левой части (11) можно записать:

.

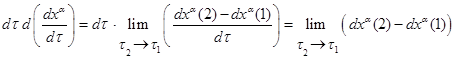Полагая теперь в (11) , получаем нулевую правую часть и приходим к следующему:

.

Выберем в качестве собственного времени для светового импульса временной параметр вдоль траектории, отмечающий местоположение импульса в пространстве, и разделим предыдущее равенство на квадрат дифференциала :

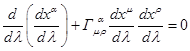. (12)

Уравнение (12) представляет собой стандартное уравнение движения для светового кванта в ОТО. Как было видно при выводе (10) и (12) из уравнения (8), уравнения движения ОТО для частиц и света являются следствием уравнения движения КТГ. В связи с этим снова встаёт вопрос о том, почему в пределах Солнечной системы обнаруживаются такие необъясняемые с помощью ОТО явления, как эффект «Пионера» [11] и flyby-эффект [12]? Одно из возможных объяснений имеется в работе [3], где подчёркивается различие уравнения движения (10) ОТО и уравнения движения (8) КТГ.

Таким образом, из системы аксиом для общей относительности ОТО, и системы аксиом для гравитационного поля выводятся все основные черты ОТО. При этом аксиомы ОТО даны в таком виде, который позволяет сравнить их с аксиомами ковариантной теории гравитации (КТГ) и метрической теории относительности (МТО). Как следствие этого оказывается [4], что общая относительность ОТО является частным случаем МТО. Что касается аксиом гравитационного поля, то в ОТО принцип геометризации гравитации и принцип эквивалентности приводят к концепции тензорного метрического поля как поля гравитации. В КТГ гравитационное поле характеризуется векторным полем 4-потенциала и построенным с его помощью тензорным антисимметричным полем напряжённостей гравитационного поля, состоящим из двух компонент – напряжённости гравитационного поля и поля кручения. Принцип определения гравитационного поля в КТГ аналогичен определению электромагнитного поля, вследствие чего гравитационное поле в КТГ считается не менее реальным, чем электромагнитное поле, вместе с которым относится к фундаментальным полям. Последнее означает, что электромагнитное и гравитационное поля существуют не только в области исследований, доступных современной науке, но согласно теории бесконечной вложенности материи действуют на разных уровнях материи. При этом гравитационное поле на уровне элементарных частиц приводит к сильной гравитации, а на макроуровне – к обычной гравитации [13].

Анализ принципа эквивалентности в ОТО показывает, что он справедлив только в бесконечно малых областях, в которых возможно приближение лоренц-ковариантности. Однако это приближение становится неточным в достаточно больших областях, где уже нельзя пренебречь искривлением пространства-времени. Например, если пробная частица массивна, то её собственное гравитационное поле должно учитываться в уравнении движения частицы во внешнем гравитационном поле. Это происходит потому, что метрика от двух взаимодействующих тел нелинейным образом зависит от значений метрики этих тел, взятых отдельно друг от друга. Поэтому ОТО, использующее в расчётах принцип эквивалентности и геометризации гравитационного поля, кажется лишь промежуточной теорией на пути построения более полной теории относительности и углублённой теории гравитационного поля, в полной мере учитывающей взаимодействие гравитационного поля с веществом и другими полями.

Список использованных источников

1. Einstein A. – Berl. Ber., 1915, S. 778, 779, 844.

2. Hilbert D. Grundlagen der Physik, 1 Mitt; Gott, Nachr., 1915, math.-nat. Kl., S. 395.

3. Федосин С.Г. Физические теории и бесконечная вложенность материи. Пермь, 2009, 842 стр., Табл. 21, Ил.41, Библ. 289 назв. ISBN 978-5-9901951-1-0.

4. Федосин С.Г. Комментарии к книге: Физические теории и бесконечная вложенность материи. Пермь, 2009, 842 стр., Табл. 21, Ил.41, Библ. 289 назв. ISBN 978-5-9901951-1-0.

5. Fedosin S.G. The Principle of Least Action in Covariant Theory of Gravitation. Hadronic Journal, February 2012, Vol. 35, No. 1, P. 35 – 70.

6. Fedosin S.G. The Hamiltonian in covariant theory of gravitation. Advances in Natural Science, 2012, Vol. 5, No. 4, P. 55 – 75.

7. Ehlers J., Pirani F. A. and Schild A. The geometry of free fall and light propagation. in: General Relativity. Papers honor of J. L. Synge, editor: L. O' Raifertaigh  (Oxford: Clarendon Press, 1972), pp. 63-82.

8. Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy. vixra.org, 5 Mar 2014.

9. Kopeikin S., Efroimsky M. and Kaplan G. Relativistic Celestial Mechanics in the Solar System, Wiley-VCH, 2011. XXXII, 860 Pages, 65 Fig., 6 Tab.

10. Мещерский И.В. Соч.: Работы по механике переменной массы, 2 изд., М., 1952.

11. Nieto, Michael Martin (2006), The quest to understand the Pioneer anomaly , EurophysicsNews, Vol. 37 (6), P. 30–34.

12. Anderson J.D., et. al. (7 March 2008), Anomalous Orbital-Energy Changes Observed during Spacecraft Flybys of Earth, Phys. Rev. Lett., Vol. 100 (9), 091102(1-4).

13. Fedosin S.G. Model of Gravitational Interaction in the Concept of Gravitons. Journal of Vectorial Relativity, Vol. 4, No. 1, March 2009, P.1–24.

Источник: http://sergf.ru/ax.htm

На научный сайт