In English

The Integral Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based on the Pressure Field and Acceleration Field.

American Journal of Modern Physics. Vol. 3, No. 4, 2014, pp. 152-167. doi: 10.11648/j.ajmp.20140304.12.

Интегральный 4-вектор энергии-импульса и анализ проблемы 4/3 на основе поля давления и поля ускорений

Федосин Сергей Григорьевич

г. Пермь, Пермский край, Россия

E-mail: intelli@list.ru

В результате интегрирования уравнений движения с учётом поля давления и поля ускорений находится интегральный 4-вектор энергии-импульса системы. Показывается, что этот вектор в ковариантной теории гравитации должен быть равным нулю. Это позволяет объяснить проблему 4/3 и проблему энергии нейтрино в идеальном сферическом коллапсе сверхновой. В то же время для описания состояния системы вместо интегрального 4-вектора необходимо использовать 4-вектор энергии-импульса, выводимый из лагранжиана. Описанный подход существенно отличается от результатов общей теории относительности, в которой интегральный 4-вектор служит 4-вектором энергии-импульса системы, а тензор энергии-импульса гравитационного поля заменяется соответствующим псевдотензором.

Ключевые слова: 4-вектор энергии-импульса; 4-вектор гамильтониана; проблема 4/3; поле ускорений; поле давления; ковариантная теория гравитации.

The Integral Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based on the Pressure Field and Acceleration Field

Sergey G. Fedosin

PO box 614088, Sviazeva str. 22-79, Perm, Russia

E-mail: intelli@list.ru

As a result of integration of the equations of motion with regard to the pressure field and acceleration field the system’s integral energy-momentum 4-vector is found. It is shown that this vector in the covariant theory of gravitation must be equal to zero. This allows us to explain the 4/3 problem and the problem of neutrino energy in an ideal spherical supernova collapse. At the same time, in order to describe the system’s state, instead of the integral 4-vector we must use the four-momentum, which is derived from the Lagrangian. The described approach differs substantially from the results of the general theory of relativity, in which the integral 4-vector serves as the system’s four--momentum, and the stress-energy tensor of the gravitational field is replaced by the corresponding pseudotensor.

Keywords: four-momentum; four-vector of Hamiltonian; 4/3 problem; field of accelerations; pressure field; covariant theory of gravitation.

1. Введение

Сущность проблемы 4/3 заключается в том, что масса-энергия, связанная с импульсом поля движущегося тела, в 4/3 больше, чем масса-энергия, связанная с энергией поля. Это существенно отличается от трактовки механической массы-энергии, когда масса-энергия покоя совпадает с массой-энергией импульса механического движения. Первоначально проблема 4/3 рассматривалась для электромагнитного поля электрона. В работах Томсона [1], Абрагама [2] и Пуанкаре [3] было сделано предположение о том, что в энергии электрона должны быть дополнительные виды энергии неэлектромагнитного происхождения. В частности, Пуанкаре вводил в рассмотрение скалярное поверхностное давление, которое не только должно было поддерживать целостность электрона, но и компенсировать избыточную массу-энергию в электромагнитном импульсе электрона. Ми [4] пытался решить эту проблему с помощью добавочных сил электрического происхождения. Беккер [5] показал, как неэлектромагнитные натяжения могут компенсировать излишнюю электромагнитную массу-энергию в импульсе тела. Для этого он к тензору энергии-импульса электромагнитного поля добавляет тензор энергии-импульса механических напряжений, записанный в общем виде, а затем совершает лоренцевское преобразование компонент тензора и находит суммарную энергию и импульс движущегося тела. Поскольку для покоящегося тела импульс равен нулю, то после лоренцевского преобразования в энергию и импульс дают вклад только компоненты энергии покоящегося тела (электрическая энергия плюс энергия механических напряжений). В результате для суммарной энергии и импульса тела с учётом напряжений соотношение для энергии и импульса остаётся по форме таким же, как и в специальной теории относительности для незаряженного тела.

В [6] проблема 4/3 описывается для заряженного тела путём учёта импульса массы-энергии отрицательного внутреннего давления, возникающего от сил взаимодействия между одноимёнными зарядами на поверхности (или в объёме) тела. В простейшем случае, когда давление внутри тела одинаково во всех точках, отрицательный импульс этого давления в 4 раза меньше положительного электромагнитного импульса. Данный вывод фактически повторяет вычисления Пуанкаре [3] с тем отличием, что Пуанкаре рассмотрел ещё и распределение давления внутри тела (электрона) как следствие лоренцевского сокращения. Краткий обзор по проблеме 4/3 можно найти в [7].

Заметим, что более общий подход требует одновременного учёта энергии-импульса не только электромагнитного, но и гравитационного поля, а также поля ускорений и поля давления движущегося тела. Как было показано в [8-10], проблема 4/3 существует и для гравитационного поля, причём для поля не только снаружи, но и внутри тела. Далее мы будем решать поставленную задачу в общем виде, при этом мы будем исходить из уравнения движения системы, записанного в четырёхмерном виде.

2. Интегрирование уравнения движения

В ковариантной теории гравитации уравнение движения системы в виде множества частиц и связанных с ними полей может быть записано в следующей форме [11]:

. (1)

Согласно (1), ковариантная производная от суммы четырёх тензоров энергии-импульса должна равняться нулю. Соотношение (1) является дифференциальной формой закона сохранения 4-импульса системы.

В (1) , , и обозначают тензоры энергии-импульса гравитационного поля, электромагнитного поля, поля давления и поля ускорений, соответственно. Эти тензоры получаются из принципа наименьшего действия и записываются так:

. (2)

. (3)

. (4)

. (5)

В (2) – скорость света, есть гравитационная постоянная, – метрический тензор, есть гравитационный тензор, – 4-потенциал гравитационного поля. В (3) – электрическая постоянная, есть электромагнитный тензор, – электромагнитный 4-потенциал. В (4) предполагается постоянной, зависящей от вида рассматриваемой системы, есть тензор поля давления, – 4-потенциал поля давления, обозначает 4-скорость рассматриваемой частицы относительно координатной системы отсчёта , – давление в сопутствующей частице системе отсчёта , – плотность частицы в . В (5) есть тензор ускорений, – ковариантная 4-скорость частиц и одновременно 4-потенциал поля ускорений, можно считать постоянной в ряде простейших случаев.

Указанные выше тензоры используются для нахождения метрики из уравнения:

,

где есть постоянный коэффициент.

Для того, чтобы проинтегрировать уравнение (1) по движущемуся 4-объёму, используем процедуру, применяемую в [12] и во многих других работах по теории гравитации, и позволяющую упростить интегрирование. Если ввести систему отсчёта, относительно которой элемент вещества в данный момент времени и в данной точке пространства движется так, что первые производные метрического тензора по координатам равны нулю, то в этой системе отсчёта символы Кристоффеля равны нулю. Тогда ковариантная производная становится равной обычной производной , являющейся 4-дивергенцией для суммы тензоров в (1) вследствие сворачивания по индексу . Такие системы отсчёта часто называют локально лоренцевыми. Согласно [13], превращение ковариантной производной в обычную производную возможно при выполнении условия гармоничности , приводящего к гармоническим координатам.

В лоренцевой системе отсчёта вместо (1) получается равенство , левую часть которого можно проинтегрировать по 4-объёму с учётом теоремы Гаусса:

,

где означает элемент некоторой бесконечной гиперповерхности, окружающей 4-объём, множитель в виде квадратного корня включает в себя детерминант метрического тензора, взятый со знаком минус. Данный множитель необходим для ковариантности элемента объёма в разных системах отсчёта.

Если взять проекцию данной гиперповерхности на гиперплоскость , то превращается в элемент трёхмерного объёма, и для сохраняющегося 4-вектора можно записать:

. (6)

Данное соотношение отражает тот факт, что поток 4-импульса системы через трёхмерную поверхность, окружающую 4-объём, остаётся неизменным, несмотря на обмен 4-импульсом между компонентами системы внутри этого объёма.

Интегрирование временных компонент тензоров энергии-импульса по бесконечному объёму является необходимым условием, поскольку только при этом возможен переход от этих тензорных компонент к сохраняющемуся 4-вектору .

3. Временная компонента 4-вектора

Соотношение (6) записано в отношении движения системы относительно лоренцевой системы отсчёта. Предположим, что имеется множество одинаковых частиц, образующих гравитационно связанную систему и заполняющих некоторый сферический объём. Пусть для всех частиц внутри сферы выполняется то условие, что они одновременно находятся в некоторой выбранной лоренцевой системе отсчёта, в которой может быть описано их движение. Тогда интегрирование в (6) может быть распространено на все частицы системы и на все поля, которые генерируют эти частицы.

Рассмотрим (6) в слабом поле в пределе плоского пространства-времени, когда можно считать, что . В этом случае временные компоненты тензоров можно выразить через соответствующие напряжённости полей, и для временной компоненты находим:

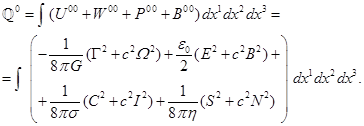. (7)

Вектор является напряжённостью поля ускорений, а вектор – величиной, подобной по своему смыслу индукции магнитного поля в электродинамике или полю кручения в ковариантной теории гравитации (гравитомагнитному полю в общей теории относительности).

Из компонент и строится тензор ускорений в (5). Вклад векторов и в интеграл (7) подсчитан в Приложении A и равен следующей величине:

. (8)

В (8) масса получается умножением плотности массы на объём покоящейся сферы радиуса , причём плотность есть плотность произвольной частицы из множества одинаковых частиц, взятой в системе отсчёта , сопутствующей движению частицы внутри сферы. Фактор Лоренца появляется в (8) из-за движения сферы с постоянной скоростью в системе отсчёта , в которой вычисляется . Величина есть фактор Лоренца для скоростей частиц в центре сферы.

Векторы и определяются соотношениями:

, ,

где индексы , и данные векторы являются компонентами тензора давления в (4).

Вклад этих векторов в интеграл (7) подсчитан в Приложении B:

. (9)

Через в (7) обозначена напряжённость гравитационного поля, есть поле кручения, – напряжённость электрического поля, – индукция магнитного поля. Энергия гравитационного поля вычислена нами в Приложении C:

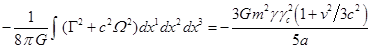. (10)

Ввиду подобия уравнений для гравитационного и электромагнитного полей в лоренц-инвариантной теории гравитации, для полной энергии электромагнитного поля движущейся сферы можно записать:

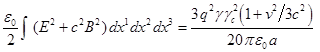, (11)

где есть заряд сферы, получаемый путём умножения плотности заряда частиц, находимой в сопутствующих им системах отсчёта , на объём сферы.

Следовательно,

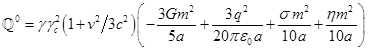. (12)

Третий член в скобке в (12) задаёт энергию поля давления, а четвёртый член связан с полем скоростей и его можно трактовать как кинетическую энергию движения частиц внутри сферы. Согласно теореме вириала, внутренняя кинетическая энергия тела должна равняться половине абсолютной величины потенциальной энергии гравитационного и электромагнитного полей. Отсюда следует условие, определяющее коэффициент в данной задаче:

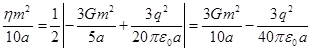, . (13)

Подставим (13) в (12):

.

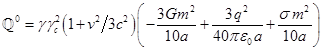Для того чтобы величина могла быть постоянной и не зависеть ни от времени, ни от скорости, должно выполняться условие:

. (14)

Выражение (14) определяет постоянную для поля давления внутри шара с однородным распределением массы и заряда. При выборе согласно (13) и (14) компонента становится равным нулю.

4. Пространственные компоненты 4-вектора

Рассмотрим теперь равенство (6) в пределе плоского пространства-времени для пространственно-подобной компоненты, когда индекс у 4-вектора , а становится равным единице:

. (15)

Подставим в (15) выражения тензорных компонент согласно [11]:

, (16)

где вектор Хевисайда задаёт плотность потока гравитационной энергии,

вектор Пойнтинга есть плотность потока электромагнитной энергии,

вектор задаёт плотность потока энергии поля давления,

вектор определяет плотность потока энергии поля ускорений.

Напряжённости гравитационного и электромагнитного поля и , поле кручения и индукция магнитного поля внутри и за пределами движущегося тела были определены в [9-10]. В Приложении C мы показали, что благодаря движению частиц внутри рассматриваемой сферы эти потенциалы и напряжённости гравитационного и электромагнитного поля должны быть умножены на фактор Лоренца ,

где обозначает скорость частиц в центре сферы. С учётом этого для сферы с радиусом суммарный интеграл от потоков гравитационной и электромагнитной энергий внутри и снаружи сферы будет равен:

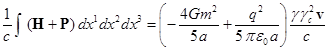. (17)

Интеграл от вектора по объёму выглядит следующим образом:

.

Величина этого интеграла определяется в Приложении D:

. (18)

Четвёртый интеграл вычисляется в Приложении E:

. (19)

Подставляя (17-19) в (16), находим:

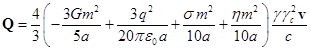. (20)

Для того, чтобы вектор был постоянным и не зависел от скорости, выражение в скобке должно равняться нулю. Заметим, что выражение в скобке в (20) совпадает с выражением в скобке в (12). Таким образом, мы снова приходим к соотношению (13) для и к соотношению (14) для в данной задаче.

В Приложении F даётся оценка коэффициентов в (13) и из (14), и делается их сравнение для ряда космических объектов.

5. Обсуждение

Выше в (12) и в (20) мы нашли выражение компонент 4-вектора для движения с постоянной скоростью сферы, наполненной движущимися в ней частицами. Данный 4-вектор получается интегрированием уравнения движения сферы. Если на сферу с частицами не действуют внешние силы, сфера движется с постоянной скоростью и интегральный 4-вектор должен быть постоянным. При условиях (13) и (14) можно считать, что 4-вектор равен нулю при любой скорости движения. Если же сфера ускоряется под действием силы, то нам следует ожидать появления некоторых новых соотношений между , , , , плотностями массы и заряда и тела, и между величинами внешних ускоряющих полей и давления. Эти соотношения при отсутствии ускорения должны переходить в соотношение, вытекающее из (12):

, (21)

а затем в соотношения (13) и (14). Тем самым мы хотим сказать, что 4-вектор может быть сделан равным нулю не только при движении с постоянной скоростью, но и при любом движении при соответствующем выборе физических величин, характеризующих рассматриваемое тело, и при учёте действующих на тело внешних полей и внешнего давления.

Соотношения (13) и (14) для коэффициентов и были получены для случая однородной плотности массы и заряда в объёме сферы. Пусть теперь плотность массы и заряда частиц увеличится в центре, при этом общая масса и заряд останутся прежними. Тогда в (21) перед квадратами массы и заряда появится один и тот же численный множитель, зависящий от степени неоднородности плотности. Но эти множители не изменят соотношения (21) и соотношений (13) и (14). Лишь в случае больших неоднородностей плотности следует ожидать какого-то изменения соотношений между , , , .

5.1. Проблема 4/3

Как известно, сутью проблемы 4/3 в теории гравитационного и электромагнитного полей является то, что импульс поля пропорционален не массе-энергии поля, а величине, в 4/3 больше. Тем самым кажется, что нарушается представление о стандартной связи массы, скорости и импульса для тел в специальной теории относительности. Однако на самом деле, если брать в учёт не только энергию и импульс гравитационного и электромагнитного полей, но и энергию и импульс давления внутри тела, то это позволяет решить проблему 4/3.

В частности, из (12) следует, что сумма гравитационной и электромагнитной энергии покоящейся сферы с частицами внутри неё равна . Если же сфера движется со скоростью , то эта энергия не только увеличивается за счёт лоренцевского фактора , но появляется ещё дополнительная энергия 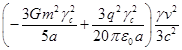, зависящая от квадрата скорости.

Однако в (12) присутствуют член от внутреннего поля давления и член от поля ускорений частиц внутри сферы, которые точно компенсируют гравитационную и электромагнитную энергии сферы при любой скорости движения.

Для того, чтобы получить импульсы, необходимо вектор в (16) и (20) разделить на скорость света . Это следует из взаимосвязи между векторами потока энергии и соответствующими импульсами. Например, плотность импульса электромагнитного поля . Тогда из (20) и (12) следует:

, (22)

где 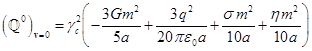обозначает компоненту при нулевой скорости движения сферы.

Если считать суммарной энергией гравитационного и электромагнитной полей, поля давления и поля ускорений покоящейся сферы, то отношение в (22) обозначает суммарную массу-энергию этих полей. Из (22) видно, что коэффициент перед скоростью есть суммарная масса-энергия полей в суммарном импульсе, которая в 4/3 раз больше, чем величина для покоящейся сферы. В этом и заключается проблема 4/3 . Решение же проблемы в том, что , так что энергия и импульс гравитационного и электромагнитной полей при движении системы компенсируются соответствующими энергиями и импульсами внутреннего давления и внутреннего поля ускорений, а для системы в покое компенсация осуществляется для энергий всех четырёх полей. Так идея Пуанкаре о внутренних натяжениях в движущемся теле реализуется с точки зрения нашей модели поля давления, кроме этого мы учитываем и поле ускорений.

По всей видимости, причиной проблемы 4/3 является двухкомпонентность рассматриваемых нами полей. И поле кручения (гравитомагнитное поле в общей теории относительности), и магнитная индукция являются самостоятельными компонентами поля и рассматриваются как релятивистские поправки к основным напряжённостям поля. В частности, появление магнитного поля при движении заряда не только приводит к необходимости учёта электромагнитного импульса, но и за счёт магнитной энергии увеличивает электромагнитную энергию движущегося заряда, добавляя к значению , где есть электромагнитная энергия системы в покое, величину 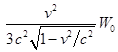, зависящую от скорости движения.

То же самое относится и к полю кручения.

Поле давления также является двухкомпонентным и имеет соленоидальную компоненту . При этом нельзя сказать, что компонента обусловлена какой-либо временной задержкой распространения напряжённости поля давления, так как обе компоненты поля давления действуют одновременно в одной и той же точке внутри частицы или тела. Точно также магнитная индукция не является простым следствием задержки распространения электрической напряжённости от источника поля до рассматриваемой точки, а представляет собой некоторую завихрённость электромагнитного поля, существующую отдельно и независимо от . Соленоидальная компонента поля ускорений в движущемся теле проявляется потому, что к внутренним скоростям частиц тела добавляется скорость движения тела как целого, при этом внутри тела существует радиальный градиент кинетической энергии частиц и соответствующий градиент модуля их скорости.

В нашей модели уравнения поля давления подобны уравнениям Максвелла, а тензор энергии-импульса поля давления аналогичен по своему строению тензорам энергии-импульса гравитационного и электромагнитного поля. То же самое относится и к полю ускорений с его тензором , как это описано в [11]. Векторная компонента поля давления, и компонента поля ускорений отражают завихрённость соответствующих полей. Компонента связана с вращательным ускорением частицы, а компонента задаёт давление от турбулентного движения частиц, когда они движутся в среде, аналогичной по свойствам жидкости.

Из изложенного следует, что лишь при учёте энергии и импульса поля ускорений и поля давления в лагранжиане, гамильтониане и в уравнении движения теория становится самосогласованной и даёт возможность описать проблему 4/3 во всех деталях.

5.2. Интегральный 4-вектор и идеальный сферический коллапс

Рассмотрим образование динамически равновесной космической системы в результате длительного процесса скучивания вещества из первоначального состояния с очень малой плотностью и практически нулевой энергией движения вещества и нулевой энергией взаимодействия посредством макроскопических полей. Основную работу по скучиванию вещества производит сила самогравитации системы, усиливающаяся по мере уменьшения размеров системы. Данной силе противостоит сила давления в веществе как следствие взаимодействия частиц друг с другом. В некотором равновесии обе силы выравниваются и система перестаёт изменять свои размеры.

Как правило, процесс скучивания вещества сопровождается выбросами вещества и излучением из системы. Особенно это имеет место при гравитационном коллапсе, когда система быстро уменьшает свой размер с большим выделением гравитационной энергии. Далее мы будем рассматривать идеальный сферический коллапс, отличающийся тем, что из баланса количества вещества, его энергии и импульса убраны все те компоненты, которые связаны с веществом и излучением, покидающим систему.

Другим словами, при идеальном сферическом коллапсе система переходит из одного состояния в другое без всяких потерь энергии и импульса в окружающую среду. В таком случае, вся работа гравитационного и электромагнитного поля при сжатии вещества должна преобразоваться в изменение энергии поля давления и энергии поля скоростей (кинетической энергии) частиц системы.

Вследствие того, что 4-импульс системы при идеальном коллапсе не изменяется, интегральный 4-вектор системы продолжает оставаться равным нулю. Тогда из (12), (13) и (14) следует, что при выполнении теоремы вириала половина работы гравитационного и электромагнитного полей при сжатии вещества переходит в энергию поля скоростей, а другая половина энергии переходит в энергию поля давления. В результате такого коллапса в веществе увеличиваются напряжения, а кинетическая энергия движения частиц возрастает. Идею о том, что энергия в веществе делится между потенциальной энергией давления и кинетической энергией, мы использовали в [14] для определения обобщённой температуры, учитывающей вклад в температуру не только кинетической, но и потенциальной энергии, приходящейся на одну частицу.

Интуитивно ясно, что механическая энергия системы распределяется между двумя крайними идеальными формами – с одной стороны в форме кинетической энергии идеального газа невзаимодействующих посредством поля частиц, и с другой стороны, в форме потенциальной энергии давления неподвижного вещества в идеальном твёрдом теле. Если применить теорему равнораспределения, то в среднем половина механической энергии системы должна быть кинетической, а другая половина – потенциальной энергией. В (21) выполняется именно такое распределение энергии, соответствуя также теореме вириала.

Указанная картина позволяет качественно объяснить, куда девается энергия идеального гравитационного коллапса в случае сверхновой с образованием нейтронной звезды. Одним из объяснений считается то, что до половины гравитационной энергии нейтронной звезды конвертируется в нейтринное излучение, а другая половина гравитационной энергии уходит на нагрев вещества звезды. Если же предположить, что гравитационная энергия делится в основном между нагревом вещества и энергией давления, то суммарное излучение нейтрино уже не обязано уносить с собой столь большую долю гравитационной энергии.

5.3. Сравнение с 4-вектором энергии-импульса системы

Как было показано выше, при постоянной скорости движения интегральный 4-вектор , содержащий компоненты энергии и импульса, обращается в нуль. Таким образом, этот 4-вектор, полученный путём интегрирования уравнения движения и являющийся сохраняющейся величиной, не может в нашем подходе служить 4-вектором энергии-импульса системы. В [11] из лагранжиана был получен гамильтониан , являющийся релятивистской энергией системы из частиц и полей, следующего вида:

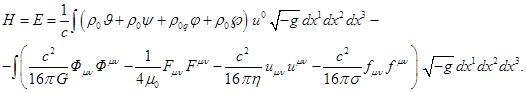(23)

В (23) частицы имеют плотность массы и плотность заряда , измеренные в сопутствующих им системах отсчёта . Энергия определена в произвольной системе отсчёта , 4-скорости частиц и временная компонента их 4-скорости измеряются относительно . Для элемента объёма в первом интеграле можно записать: , где обозначает элемент объёма, связанный с произвольной движущейся частицей. Тогда для энергии имеем:

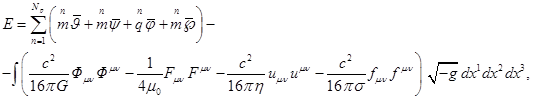
так что интеграл становится суммой по всем частицам, входящих в систему, и обозначают массу и заряд частицы с номером ; , , и обозначают усреднённые по объёму этой частицы скалярные потенциалы поля ускорений, гравитационного и электромагнитного полей и поля давления, соответственно, причём в учёт следует брать как собственные поля, так и поля от внешних источников.

Энергия системы может быть определена как временная компонента 4-вектора: , где есть 4-импульс системы, и обозначают импульс и скорость системы, соответственно. В статье [15] 4-вектор был назван 4-вектором гамильтониана. Если разделить на скорость света, то мы приходим к 4-импульсу системы, состоящей из частиц и связанных с ними полей:

. (24)

4-импульс и подобный ему 4-вектор описывают полностью физическое состояние системы и в стационарных условиях могут сохраняться относительно фиксированного координатного наблюдателя с его временем . В отличие от этого, 4-вектор задаёт связь лишь тех компонент энергии и импульса, которые входят в уравнение движения. При этом уравнение движения записывается таким образом, что в нём 4-ускорение, как производная от 4-скорости по собственному времени частицы, зависит от плотности действующих на частицу 4-сил. Поэтому различие между и можно связать с различием между собственным и координатным временами и с различием между собственным и координатным наблюдателями. Можно также сказать, что 4-вектор неизменен в лоренцевой системе отсчёта, а 4-вектор , будучи 4-вектором, является неизменным благодаря ковариантной форме записи во множестве систем отсчёта.

5.4. Сравнение с общей теорией относительности

В общей теории относительности (ОТО) интегральный 4-вектор приобретает особое значение – он считается 4-вектором энергии-импульса системы, смотри например [12-13]. При этом в отличие от подхода в ковариантной теории гравитации, вместо тензора энергии-импульса поля ускорений в соотношение (1) помещается тензор энергии-импульса вещества вида для пылевидной материи, или более сложный тензор, учитывающий давление и заменяющий тем самым наш тензор . Заметим, что ковариантная производная тензора приводит к 4-ускорению частицы:

, (25)

здесь было использовано уравнение непрерывности в виде , а также оператор производной по собственному времени , где – символ 4-дифференциала в искривлённом пространстве-времени, – собственное время [16].

Так как в ОТО гравитационное поле считается полем метрического тензора , то в соотношении (1) тензор энергии-импульса гравитационного поля с точки зрения ОТО присутствовать не может. Но роль тензора в ОТО играет псевдотензор энергии-импульса гравитационного поля , который ввиду своей не тензорной природы определяется различным образом и имеет различные формы. В [12] в рамках ОТО вместо (6) для 4-вектора энергии-импульса даётся другая формула:

. (26)

Выражение (26) отличается наличием множителя в виде детерминанта метрического тензора со знаком минус, обозначает временные компоненты тензора энергии-импульса вещества и электромагнитного поля, псевдотензор отражает вклад энергии-импульса гравитационного поля. Для того, чтобы (26) было справедливым, в ОТО необходимо дополнительное условие – на бесконечности координаты системы отсчёта должны переходить в координаты пространства-времени Минковского.

Соответственно, запись уравнения движения отличается от (1) и имеет вид:

. (27)

В нашем подходе для описания энергии-импульса вещества нет необходимости использования какого-либо специального тензора энергии-импульса вещества типа или аналогичного ему. Вместо этого мы используем тензор энергии-импульса поля ускорений , ковариантная производная от которого также даёт 4-ускорение точечной частицы аналогично (25):

. (28)

При этом, как было указано выше, 4-вектор энергии-импульса системы (24) мы получаем из лагранжиана, а не из уравнения движения, как это делается в ОТО согласно (26-27).

Рассмотрим ещё вопрос о законности использования в ОТО тензора в соотношении (25). Для этого уточним форму уравнения непрерывности в искривлённом пространстве-времени. Согласно [11], из уравнений электромагнитного поля следует:

, (29)

где – электромагнитный 4-ток, – магнитная постоянная, – электромагнитный тензор.

Ковариантная производная в (29) не обращается в нуль, поскольку не равно нулю тензорное произведение тензора Риччи на электромагнитный тензор. Лишь в плоском пространстве Минковского тензор Риччи обнуляется, ковариантная производная становится 4-градиентом, и из (29) получается стандартное уравнение непрерывности электромагнитного 4-тока в специальной теории относительности: .

Аналогичная картина в ковариантной теории гравитации складывается как для гравитационного поля, так и для поля давления и для поля ускорений – для всех этих полей получается выражение типа (29), с тем отличием, что вместо стоит массовый 4-ток . Например, для гравитационного поля получается:

Это означает, что в общем случае . Но в таком случае возникает вопрос – можно ли считать справедливым соотношение (25), связывающее дивергенцию тензора с 4-ускорением? Существенным элементом (25) является равенство , однако это равенство в ОТО лишь постулируется, но не доказывается, при этом данное равенство противоречит результатам ковариантной теории гравитации. В то же время замена тензора на тензор энергии-импульса поля ускорений в (28) приводит к ковариантному тензорному соотношению.

6. Список использованных источников

1. Thomson J J. On the electric and magnetic effects produced by the motion of electrified bodies. Philos. Mag. Ser. 5 11 (68) 229 (1881).

2. Abraham M. – Phys. Ztschr., 1904, Bd 5, S.576; Theorie d.Electrizität. – Leipzig, 1905, Bd 2, S. 205.

3. Poincaré H. Sur la dynamique de l’électron. – C. R. Acad Sci., Paris, 1905, v. 140, p. 1504.

4. Mie G. Grundlagen einer Theorie der Materie. – Ann. d. Phys., 1912, Bd 37, S. 511; 1912, Bd 39, S. 1; 1913, Bd 40, S. 1.

5. Becker R Theorie der Elektrizität Bd. II Elektronentheorie (Berlin: B.G. Teubner, 1933) [Беккер. Р. Теория электричества, Т-II, Электронная теория, Л.-М. Гостехиздат, 1941 г. ]

6. Морозов В Б К вопросу об электромагнитном импульсе заряженных тел УФН 181 389–392 (2011).

7. Rohrlich, F.. 1997 The dynamics of a charged sphere and the electron. Am. J. Phys. 65. 1051-1056.

8. Fedosin S.G. Mass, Momentum and Energy of Gravitational Field. Journal of Vectorial Relativity, Vol. 3, No. 3, September 2008, P. 30–35.

9. 5. Fedosin S.G. 4/3 Problem for the Gravitational Field. Advances in Physics Theories and Applications, 2013, Vol. 23, P. 19 – 25.

10. Fedosin S.G. Energy, Momentum, Mass and Velocity of a Moving Body in the Light of Gravitomagnetic Theory. Accepted by Canadian Journal of Physics.

11. Fedosin S.G. About the Cosmological Constant, Acceleration Field, Pressure Field and Energy. viXra:1403.0023, 5 March 2014.

12. Ландау Л. Д., Лифшиц Е. М. Теория поля. – Издание 7-е, исправленное. – М.: Наука, 1988. – 512 с. – («Теоретическая физика», том II).

13. Фок В.А. Теория пространства, времени и гравитации. 2-е издание. – М.: Физматгиз, 1961. – 568 с.

14. Федосин С.Г. Физика и философия подобия от преонов до метагалактик. Пермь, Стиль-МГ, 1999, 544 стр., Табл.66, Ил.93, Библ. 377 назв. ISBN 5-8131-0012-1.

15. Fedosin S.G. The Hamiltonian in Covariant Theory of Gravitation. Advances in Natural Science, 2012, Vol. 5, No. 4, P. 55 – 75.

16. Федосин С.Г. Физические теории и бесконечная вложенность материи. Пермь, 2009-2012, 858 стр., Табл. 21, Ил.41, Библ. 293 назв. ISBN 978-5-9901951-1-0.

17. Christensen-Dalsgaard et al. (1996) The current state of solar modeling. Science, Vol. 272, P. 1286 - 1292.

18. Alfè, D.; Gillan, M. J.; Vocadlo, L.; Brodholt, J.; Price, G. D. (2002). The ab initio simulation of the Earth's core. Philosophical Transactions of the Royal Society. Vol. 360 (1795), P.1227–1244.

19. Clemens, Dan P.; Yun, Joao Lin; Meyer, Mark H. (March 1991), BOK globules and small molecular clouds – Deep IRAS photometry and ¹²CO spectroscopy, Astrophysical Journal Supplement 75: 877.

20. J. M. Lattimer and M. Prakash, Neutron Star Structure and the Equation of State. Astrophysical J. Vol. 550(1) P. 426-442 (2001).

Приложение A

Согласно [11], уравнения для поля ускорений множества одинаковых частиц, полностью заполняющих неподвижную сферу, имеют следующий вид:

, , , , (A1)

где есть фактор Лоренца для движущихся внутри сферы частиц, – скорость частиц в системе отсчёта, связанной с данной сферой, – плотность массы произвольной частицы в сопутствующей ей системе отсчёта .

В приближении специальной теории относительности для векторов и поля ускорений можно записать:

, . (A2)

Здесь скалярный потенциал и векторный потенциал входят в 4-потенциал поля ускорений. Так как векторный потенциал каждой отдельной частицы направлен вдоль скорости частицы, то вследствие разнонаправленности векторов скорости у разных частиц суммарный векторный потенциал внутри неподвижной сферы будет равен нулю. Поэтому вектор будет зависеть только от суммарного скалярного потенциала внутри сферы: . Скалярный потенциал одной частицы , а нам необходимо найти суммарный скалярный потенциал . Предположим такое равновесное состояние, когда средняя скорость частиц является функцией от текущего радиуса, тогда и среднее значение будет функцией радиуса. Будем далее считать, что является усреднённым значением для частиц при каждом радиусе внутри сферы. Тогда подставляя в первое уравнение в (A1), приходим к уравнению Пуассона:

. (A3)

Удобно преобразовать это уравнение для путём перехода к сферическим координатам и учесть, что зависит только от радиуса. Тогда лапласиан в сферических координатах будет функцией только от радиуса . Дальнейшая замена на вспомогательную функцию в виде существенно упрощает решение, и в итоге содержит синус:

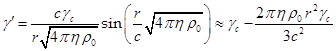, (A4)

где есть фактор Лоренца для скоростей частиц в центре сферы,

и ввиду малости аргумента синуса мы разложили синус до членов второго порядка.

4-потенциалом поля ускорения внутри сферы является ковариантная 4-скорость сферы, и поскольку сфера неподвижна в , 4-потенциал будет равен: .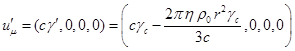

Компоненты векторов и определены в [11] формулами:

, . (A5)

Если 4-потенциал подставить в (A5), можно найти интегральные векторы и , происходящие от всех частиц внутри сферы.

Пусть теперь сфера движется в системе отсчёта с постоянной скоростью вдоль оси . В этом случае нам необходимо выразить 4-потенциал в системе отсчёта с помощью частного преобразования Лоренца. Для произвольного ковариантного вектора преобразование компонент имеет вид:

, , , ,

где есть фактор Лоренца для движения сферы.

Используем это правило для 4-потенциала поля ускорений:

. (A6)

Необходимо ещё заменить в выражении для координаты системы отсчёта на координаты системы отсчёта с помощью преобразований Лоренца:

, , , . (A7)

Подставляя в (A4), затем в (A6) и в (A5), вычисляем векторы и в системе отсчёта :

, , ,

, , . (A8)

Используем (A8) для вычисления интеграла с энергией поля ускорений в момент времени :

(A9)

Вследствие лоренцевского сокращения форма движущейся сферы изменяется и становится эллипсоидом Хевисайда с уравнением его поверхности при :

.

Если связать декартовые координаты со сферическими таким образом:

, , , (A10)

то внутри эллипсоида текущий радиус будет меняться от до , угол будет меняться от до , а угол от до . При этом элемент объёма как следствие преобразования от декартовых к сферическим координатам становится равным:

. (A11)

Подставляя (A10) и (A11) в интеграл (A9) и интегрируя, находим:

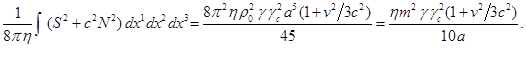
Приложение B

Согласно [11], дифференциальные уравнения поля давления для векторов и внутри неподвижной сферы в пространстве Минковского следующие:

, , , . (B1)

где ; – скорость движения произвольной частицы внутри сферы с точки зрения системы отсчёта , в которой сфера покоится.

Уравнения (B1) по форме совпадают с уравнениями Максвелла. Согласно определению 4-потенциала поля давления , для произвольной частицы компоненты 4-потенциала имеют вид:, , , и следовательно, векторный потенциал направлен вдоль скорости частицы.

Ввиду хаотичности движения частиц суммарный векторный потенциал внутри сферы будет равен нулю: . С учётом этого векторы и внутри сферы выражаются следующим образом:

, . (B2)

Подставляя в первое уравнение в (B1) вектор из (B2), получаем уравнение Пуассона:

.

С целью упрощения будем рассматривать случай постоянной плотности внутри сферы. Переходя к сферическим координатам, выражая соответствующим образом лапласиан, делая подстановку , где является функцией радиуса, приходим к дифференциальному уравнению:

.

Подставляя сюда соотношение (A4) для , находим, что частное решение неоднородного уравнения содержит синус. Добавляя решение однородного уравнения, находим и затем общее решение для скалярного потенциала поля давления внутри сферы:

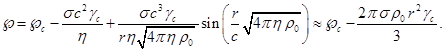(B3)

Согласно (B3), при постоянной плотности внутри сферы потенциал квадратичным образом должен зависеть от текущего радиуса , а в центре потенциал равен .

Снова обратимся к определению 4-потенциала поля давления: , где теперь и являются соответственно скалярным и векторным потенциалами поля давления внутри сферы как системы. Так как у нас , то для неподвижной сферы .

Совершим преобразование 4-потенциала в систему отсчёта , в которой сфера движется со скоростью вдоль оси . Действуя так же, как в Приложении A, находим:

. (B4)

Вектора и выражаются из 4-потенциала поля давления по формулам:

, . (B5)

Используя координаты (A7), подставляя в (B3), а затем в (B4), а (B4) в (B5), находим компоненты векторов напряжённостей поля давления в системе отсчёта :

, , ,

, , . (B6)

Теперь мы можем найти нужный нам интеграл при , когда центр сферы совпадает с началом системы отсчёта:

Подставляя сюда координаты (A10) и элемент объёма (A11), находим:

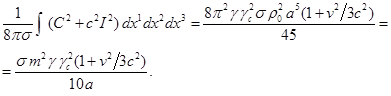
Приложение C

Согласно [14], уравнение для 4-потенциала гравитационного поля есть четырёхмерное волновое уравнение с даламбертианом:

, (C1)

где – 4-потенциал гравитационного поля, описываемый через скалярный потенциал и векторный потенциал этого поля,

– 4-вектор гравитационного (массового) тока.

Поскольку мы рассматриваем стационарное хаотическое движение одинаковых частиц внутри неподвижной сферы, потенциал внутри или снаружи сферы не будет зависеть от времени, а суммарный векторный потенциал повсюду будет равен нулю. В результате даламбертиан в (C1) превращается в лапласиан, и (C1) становится уравнением для внутреннего гравитационного скалярного потенциала:

. (C2)

В (C2) фактор Лоренца частиц , – скорость движения произвольной частицы внутри сферы, – плотность массы частицы, индекс отличает внутренний потенциал от внешнего потенциала, который генерирует сфера за своими пределами. Как потенциал , так и являются функциями текущего радиуса внутри сферы и не зависят от угловых переменных. Поэтому в сферических координатах в лапласиане достаточно взять лишь ту его часть, которая зависит от радиуса:

.

Если сделать замену переменных в виде , то уравнение переписывается так:

.

Подставим сюда значение из (A4), выраженное через синус:

.

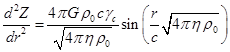Общее решение данного уравнения имеет вид:

.

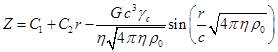Так как , и в центре при потенциал не может быть бесконечным, то коэффициент должен быть равен нулю. Отсюда потенциал внутри сферы будет равен:

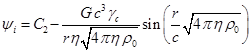. (C3)

Перейдём теперь к вычислению внешнего гравитационного потенциала неподвижной сферы, наполненной движущимися частицами. Вначале найдём напряжённость внешнего гравитационного поля сферы. Уравнения гравитационного поля в пределе специальной теории относительности согласно [14] приобретают следующий вид:

, , , . (C4)

Согласно (C4), частицы, движущиеся внутри сферы со скоростями , генерируют вокруг себя гравитационное поле с напряжённостью и полем кручения . Окружим сферу оболочкой сферической формы с произвольным радиусом и проинтегрируем первое уравнение в (C4) по объёму оболочки. При этом применим теорему Гаусса, заменяя интеграл от дивергенции на интеграл от вектора по поверхности оболочки. Ввиду симметрии сферы при постоянной плотности для модуля вектора за пределами сферы находим:

.

Вектор обозначает здесь единичный вектор нормали к поверхности оболочки, направленный наружу. Интегрирование по объёму оболочки сводится к интегрированию по объёму сферы, так как за пределами сферы . Подставляя сюда из (A4) в виде синуса и интегрируя, получим напряжённость поля за пределами сферы:

.

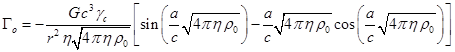Связь между напряжённостями гравитационного поля и 4-потенциалом следующая:

, . (C5)

Пространственные компоненты 4-потенциала являются компонентами векторного потенциала , который в данном случае равен нулю. Следовательно, компоненты вектора связаны только с временной компонентой 4-потенциала: . Это равенство в векторных обозначениях записывается так: . Отсюда с учётом выражения для следует, что:

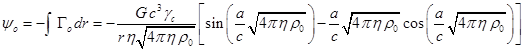. (C6)

.

На бесконечности этот потенциал становится равным нулю. На поверхности сферы потенциал (C6) должен совпасть с внутренним потенциалом в (C3). Положим и приравняем оба потенциала. Это позволяет определить коэффициент и уточнить внутренний потенциал :

,

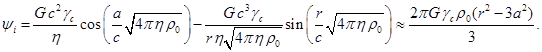(C7)

Для неподвижной сферы 4-потенциал гравитационного поля имеет вид: , где внутри сферы следует использовать потенциал (C7), а за пределами сферы – потенциал (C6). Если сфера движется с постоянной скоростью вдоль оси в системе отсчёта , 4-потенциал сферы в можно найти с помощью преобразований Лоренца. Действуя так же, как в Приложении A, находим:

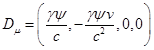. (C8)

Вычислим вначале напряжённости полей внутри сферы с точки зрения наблюдателя в системе отсчёта . Для этого наблюдателя движущаяся сфера в соответствии с преобразованиями Лоренца становится эллипсоидом Хевисайда. Так как координаты точек внутри сферы следует преобразовать в координаты системы отсчёта , то мы приходим к (A7) и к соотношению . Это соотношение следует подставить в (C7). После этого используем в (C8) с тем, чтобы посредством и (C5) вычислить напряжённости поля:

, , ,

, , . (C9)

Для внешнего поля с помощью (C6) находим аналогично:

, ,

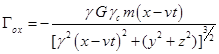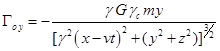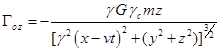, , (C10)

, .

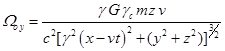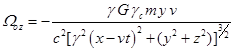Потенциалы и напряжённости гравитационного поля внутри и за пределами движущегося твёрдого тела мы вычисляли в [9]. В отличие от них, в (C9) и в (C10) появляется множитель , обязанный своим происхождением движению частиц внутри сферы.

Будем считать, что сфера с частицами движется с постоянной скоростью настолько долго, что собственное поле сферы внутри и снаружи стало стационарным и форма этого поля передвигается относительно наблюдателя с той же самой скоростью, что и сама сфера. Тогда для вычисления энергии сферы достаточно вычислить её в момент времени , когда сфера пересекает начало системы отсчёта. Вычислим гравитационную энергию внутри сферы с помощью (C9):

Подставляя сюда координаты (A10) и элемент объёма (A11), находим:

(C11)

Используем теперь (C10) для нахождения энергии движущейся сферы за её пределами при :

.

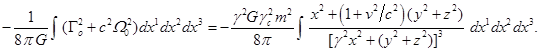
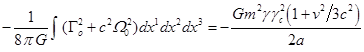Складывая полученное значение с (C11), находим полную гравитационную энергию:

.

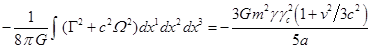Приложение D

Нам необходимо вычислить интеграл:

.

Подставим сюда векторы и согласно (B6) в Приложении B, и рассмотрим момент времени , когда центр сферы пересекает начало системы отсчёта. Из симметрии задачи видно, что интегральный поток энергии давления направлен параллельно скорости движения сферы, то есть параллельно оси . Следовательно, достаточно проинтегрировать ту компоненту векторного произведения , которая относится к оси . Это даёт следующее:

.

Переходя далее к сферическим координатам (A10) и элементу объёма в виде (A11) для эллипсоида Хевисайда как в Приложении A , находим:

.

Приложение E

Вычисляем интеграл по объёму от вектора плотности потока энергии поля ускорений:

.

Нам достаточно вычислить интеграл для момента времени , поскольку сфера движется с постоянной скоростью и интеграл в любой момент времени будет один и тот же. Используем векторы и согласно (A8) в Приложении A. Единственная ненулевая компонента потока энергии направлена вдоль оси и равна:

Интегрируя по объёму в координатах, связанных с эллипсоидом Хевисайда, как в Приложении A, находим:

Приложение F. Оценка коэффициентов и

Если величина является постоянной, то в каждой конкретной физической задаче она имеет своё собственное значение и является комбинацией фундаментальных физических постоянных и параметров рассматриваемой системы. Рассмотрим для примера достаточно большое газовое облако с постоянной плотностью , удерживаемое собственной силой гравитации, в рамках специальной теории относительности. Согласно (A4), решение уравнения для фактора Лоренца , где есть скорость движущихся внутри облака частиц, имеет вид:

,

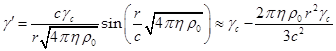где обозначает фактор Лоренца частиц, находящихся в центре облака.

Возведём в квадрат равенство для и приблизительно получим:

, (F1)

так что по мере увеличения текущего радиуса внутри облака при переходе от центра к периферии облака скорость частиц уменьшается.

Умножим равенство (F1) на , где есть масса одной частицы, и введём массу , находящуюся внутри сферы радиуса :

. (F2)

Если обозначить , то согласно (F2), разность кинетических энергий частицы в центре и на поверхности сферы определяется гравитационной энергией частицы на поверхности сферы, с точностью до коэффициента .

Предполагая справедливость газового закона и учитывая связь между температурой и кинетической энергией частиц в виде , где – постоянная Больцмана, выражение (F2) преобразуется в зависимость температуры от радиуса внутри однородного облака:

.

Применим это соотношение к космическим объектам. Для поверхности облака , масса , , и получается:

. (F3)

Во многих случаях поверхностная температура много меньше, чем температура в центре. Тогда левой частью в (F3) можно пренебречь. Согласно стандартной модели температура в центре Солнца оценивается величиной 15,7 миллионов Кельвин [17], и беря в качестве массу протона как ядра атома водорода, из (F3) находим , а также . В центре Земли температура достигает 6000 Кельвин [18], что даёт . Данные значения несколько меньше, чем согласно (13). По всей видимости, это связано с большой неоднородностью распределения вещества внутри Солнца и Земли. Кроме этого, внутри Солнца к энергии гравитации добавляется энергия от термоядерных реакций, а внутри Земли большая доля тепловой энергии получается от распадов радиоактивных элементов; всё это и изменяет значение . Оценка температуры в центре нейтронной звезды с массой кг и радиусом 12 км по (F3) даёт значение Кельвин.

Рассмотрим теперь глобулы Бока, небольшие тёмные космические облака из газа и пыли. В [19] было найдено, что радиус типичной глобулы равен 0,35 парсек, масса 11 масс Солнца, поверхностная температура пыли в глобуле порядка 26 Кельвин. Если эту температуру, массу и радиус подставить в (F3) и использовать значение согласно (13), то получится температура в центре типичной глобулы: Кельвин.

Если для суммарного 4-потенциала применить определение , где есть 4-скорость покоящейся сферы, то это позволяет связать суммарный скалярный потенциал поля давления внутри сферы с давлением: . Подставляя это в (B3), получаем приблизительную формулу для давления как функции от текущего радиуса:

Подставляя сюда и пренебрегая давлением на поверхности, оцениваем давление в центре при :

. (F4)

Для центра Солнца эта формула при условии согласно (14) даёт давление Па, что значительно меньше, чем давление Па в стандартной модели Солнца. Для Земли по формуле (F4) находим давление Па, тогда как в [18] для давления в центре Земли указывается значение Па. Для нейтронной звезды с массой кг и радиусом 12 км давление в центре по (F4) получается равным Па, а в различных моделях нейтронных звёзд согласно [20] давление не превышает Па. Полученные оценки в сравнении с теоретическими моделями для космических объектов показывают удовлетворительное согласие со значениями , за исключением оценки давления внутри Солнца.

Источник: http://sergf.ru/iv.htm

На научный сайт