На русском языке

The Integral Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based on the Pressure Field and Acceleration Field.

American Journal of Modern Physics. Vol. 3, No. 4, 2014, pp. 152-167. doi: 10.11648/j.ajmp.20140304.12.

The integral energy-momentum 4-vector and analysis of 4/3 problem based on the pressure field and acceleration field

Sergey G. Fedosin

PO box 614088, Sviazeva str. 22-79, Perm, Russia

E-mail: intelli@list.ru

As a result of integration of the equations of motion with regard to the pressure field and acceleration field the system’s integral energy-momentum 4-vector is found. It is shown that this vector in the covariant theory of gravitation must be equal to zero. This allows us to explain the 4/3 problem and the problem of neutrino energy in an ideal spherical supernova collapse. At the same time, in order to describe the system’s state, instead of the integral 4-vector we must use the four-momentum, which is derived from the Lagrangian. The described approach differs substantially from the results of the general theory of relativity, in which the integral 4-vector serves as the system’s four-momentum, and the stress-energy tensor of the gravitational field is replaced by the corresponding pseudotensor.

Keywords: four-momentum; four-vector of Hamiltonian; 4/3 problem; acceleration field; pressure field; covariant theory of gravitation.

1. Introduction

The essence of the 4/3 problem is that the mass-energy associated with the field momentum of the moving body is 4/3 times greater than the mass-energy associated with the field energy. This differs significantly from the treatment of mechanical mass-energy when the rest mass-energy coincides with the mass-energy of mechanical motion momentum. Initially 4/3 problem was considered for the electromagnetic field of the electron. In the works of Thomson [1], Abraham [2] and Poincaré [3], it was assumed that the electron energy should include additional types of energy of non-electromagnetic origin. In particular, Poincaré introduced the scalar surface pressure, which should not only maintain the integrity of the electron, but also compensate for the excess mass-energy in the electron’s electromagnetic momentum. Mie [4] tried to solve this problem with the help of additional forces of electrical origin. Becker [5] showed how non-electromagnetic tensions can compensate for the excess electromagnetic mass-energy in the body’s momentum. For this, he adds to the stress-energy tensor of the electromagnetic field the stress-energy tensor of mechanical stresses written in a general form, and then makes Lorentz transformation of the tensor components and finds the total energy and the momentum of the moving body. Since the momentum of body at rest is equal to zero, after Lorentz transformation only the energy components of the body at rest (the electric energy plus the energy of mechanical stresses) make contribution to the energy and momentum. As a result, for the total energy and momentum of the body with regard to the stresses the relation for the energy and momentum remains the same as in the special theory of relativity for an uncharged body.

In [6] the 4/3 problem is described for a charged body by taking into account the mass-energy momentum of the negative internal pressure, arising from the interaction forces between the like charges on the surface (or in the volume) of the body. In the simplest case, when the pressure inside the body is the same at all points, the negative momentum of this pressure is 4 times less than the positive electromagnetic momentum. This conclusion actually repeats the calculations of Poincare [3], the difference is that Poincare also considered the pressure distribution inside the body (electron) as the consequence of Lorentz contraction. A brief overview of the 4/3 problem can be found in [7].

We should note that a more general approach requires simultaneous consideration of energy-momentum of not only the electromagnetic but also gravitational field, as well as acceleration field and pressure field of the moving body. As it was shown in [8-10], the 4/3 problem also refers to the gravitational field – for the field not only outside but also inside the body. Next we will solve the posed problem in a general form, and we will proceed from the equation of the system’s motion, written in four-dimensional form.

2. Integration of the equation of motion

In the covariant theory of gravitation the equation of motion of the system in the form of a set of particles and associated fields can be written as follows [11]:

. (1)

According to (1), the covariant derivative of the sum of four stress-energy tensors must be equal to zero. Relation (1) is a differential form of the law of conservation of the system’s 4-momentum.

In (1) , , and denote the stress-energy tensors of the gravitational field, electromagnetic field, pressure field and acceleration field, respectively. These tensors are derived from the principle of least action and are written as follows:

. (2)

. (3)

. (4)

. (5)

In (2) is the speed of light, is the gravitational constant, is the metric tensor, is the gravitational tensor, is the 4-potential of the gravitational field. In (3) is the vacuum permittivity, is electromagnetic tensor, is the electromagnetic 4-potential. In (4) is assumed to be a constant, depending on the type of the system under consideration, is the tensor of the pressure field, is the 4-potential of the pressure field, denotes the 4-velocity of the particle relative to the reference frame under consideration , is the pressure in the reference frame associated with the particle, is the particle density in . In (5) is the acceleration tensor, is the covariant 4-velocity of the particles and at the same time the 4-potential of the acceleration field, can be considered constant in some simple cases.

The above mentioned tensors are used to find the metric from the equation:

,

where is a constant coefficient.

In order to integrate the equation (1) over the moving 4-volume, we will use the procedure which was used in [12] and in many other works on the theory of gravitation and which allows us to simplify integration. If we introduce a reference frame relative to which a matter unit at a given time and at a given point in space is moving in such a way that the first derivatives of the metric tensor by coordinates are equal to zero, then in this reference frame the Christoffel symbols are equal to zero. Then the covariant derivative becomes the ordinary derivative , which is the 4-divergence for the sum of tensors in (1) due to the contraction by index . Such reference frames are often called locally Lorentzian. According to [13] the transformation of the covariant derivative into the ordinary derivative is possible in case of satisfying the harmonicity condition which leads to harmonic coordinates.

In the Lorentz reference frame instead of (1) we have the equation , the left side of which can be integrated over a 4-volume, with regard to the Gauss theorem:

,

where denotes a unit of an infinite hypersurface surrounding the 4-volume, the factor in the form of the square root includes the determinant of the metric tensor, taken with a minus sign. This factor is required for the covariance of the volume unit in different reference frames.

If we take a projection of this hypersurface onto the hyperplane , then turns into a unit of three-dimensional volume, and for the conserved 4-vector we can be write:

. (6)

This relation reflects the fact that the flux of the system’s 4-momentum passing through the three-dimensional surface surrounding the 4-volume remains unchanged despite the exchange of the 4-momentum between the components of the system within this volume.

Integration of the time components of the stress-energy tensors over the infinite volume is a necessary condition, because only in this case the transition from these tensor components to the conserved 4-vector is possible.

3. The time component of the 4-vector

The equation (6) is written for the system’s motion relative to the Lorentz reference frame. We will assume that there is a set of identical particles that form a gravitationally bound system and fill some spherical volume. Suppose that for all particles inside the sphere the condition holds that they are at the same time located in some selected Lorentz reference frame, in which their motion can be described. Then integration in (6) can be extended to all particles of the system and to all of the fields generating these particles.

Let us consider (6) in a weak field in the limit of flat spacetime, when we can assume that . In this case the tensor’s time components can be expressed in terms of the corresponding field strengths, and for the time component we find:

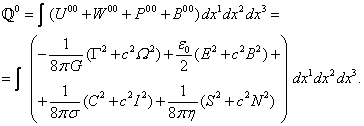. (7)

The vector is the acceleration field strength and the vector is a quantity similar in its meaning to the magnetic field induction in electrodynamics or to the torsion field in the covariant theory of gravitation (to the gravitomagnetic field in the general theory relativity).

Using the components and the acceleration tensor is constructed in (5). The contribution of the vectors and into the integral (7) is calculated in Appendix A and is equal to the following quantity:

. (8)

In (8) the mass is obtained by multiplying the mass density by the volume of a stationary sphere with the radius , while the density is the density of an arbitrary particle from the set of identical particles, taken in the reference frame associated with the motion of the particle inside the sphere. The Lorentz factor appears in (8) due to the motion of the sphere at a constant velocity in the reference frame , in which we calculate . The quantity is the Lorentz factor for the velocities of the particles in the center of the sphere.

The vectors and are given by relations:

, ,

where the indices , and these vectors are the components of the pressure tensor in (4).

The contribution of these vectors in the integral (7) is calculated in Appendix B:

. (9)

in (7) denotes the gravitational field strength, is the torsion field, is the electric field strength, is the magnetic field induction. We calculated the energy of the gravitational field in Appendix C:

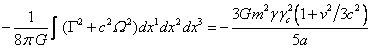. (10)

In view of similarity of equations for the gravitational and electromagnetic fields in the Lorentz - invariant theory of gravitation, for the total energy of the electromagnetic field of the moving sphere we can write:

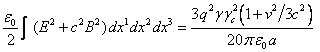, (11)

where is the charge of the sphere, which is obtained by multiplying the charge density of the particles, that was found in the co-moving reference frames, by the volume of the sphere .

Therefore,

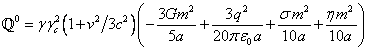. (12)

The third term in brackets in (12) specifies the energy of the pressure field, and the fourth term is associated with the velocity field and it can be treated as the kinetic energy of the particles’ motion inside the sphere. According to the virial theorem, the internal kinetic energy of the body should equal half the absolute value of the potential energy of the gravitational and electromagnetic fields. From this the condition follows, which determines the coefficient in this problem:

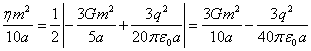, . (13)

Let us substitute (13) into (12):

.

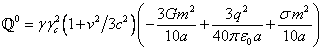To make the quantity constant and not dependent on either time or velocity the condition must be satisfied:

. (14)

Equation (14) defines the constant for the pressure field inside the ball with uniform distribution of mass and charge. Choosing according to (13) and (14), the component becomes zero.

4. The space components of the 4-vector

We will now consider the equation (6) in the limit of flat spacetime for the space-like component, when the index of the 4-vector , and becomes equal to unity:

. (15)

Let us substitute the expressions of tensor components according to [11] in (15):

, (16)

where the Heaviside vector specifies the density of the gravitational energy flux,

the Poynting vector is the density of the electromagnetic energy flux,

the vector specifies the density of the pressure field energy flux,

the vector specifies the density of the acceleration field energy flux.

The gravitational and electromagnetic field strengths and , the torsion field and the magnetic field induction inside and outside the moving body were determined in [9-10]. In Appendix C we showed that due to the motion of particles inside the sphere under consideration, these potentials and strengths of the gravitational and electromagnetic fields must be multiplied by the Lorentz factor , where denotes the velocity of particles in the center of the sphere.

With this in mind, for the sphere with the radius the total integral of the gravitational and electromagnetic energy fluxes inside and outside the sphere is equal to:

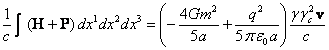. (17)

The integral of the vector over the volume is the following:

.

The value of this integral is determined in Appendix D:

. (18)

The fourth integral is calculated in Appendix E:

. (19)

Substituting (17-19) into (16) we find:

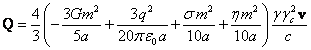. (20)

To make the vector constant and not dependent on the velocity, the expression in brackets must be zero. We should note that the expression in brackets in (20) coincides with the expression in brackets in (12). Thus, we again obtain equation (13) for and the equation (14) for in the given problem.

Appendix F provides evaluation of the coefficients in (13) and in (14) and their comparison for a number of space objects.

5. Discussion

Above, in (12) and (20) we found the expression of the 4-vector components for the motion at constant velocity of a sphere filled with particles which are moving inside it. This 4-vector is obtained by integrating the equation of the sphere’s motion. If no external forces act on the sphere with particles, this sphere is moving at a constant velocity and the integral 4-vector must be constant. Under the conditions (13) and (14) we can assume that the 4-vector is zero at any velocity. If the sphere is accelerated under action of a force, then we should expect to see some new ratios between , , , , the mass and charge densities and of the body, and between the quantities of the external accelerating fields and pressure. These ratios in the absence of acceleration must transform into the ratio, resulting from (12):

, (21)

and then to ratios (13) and (14). Thus we want to say that the 4-vector can be made equal to zero not only while moving at a constant velocity, but with any type motion in case of the appropriate choice of physical quantities characterizing the body under consideration and with regard to the external fields and external pressure acting on the body.

Equations (13) and (14) for the coefficients and were obtained for the case of the uniform mass and charge density in the volume of the sphere. Suppose now that the mass and charge density of the particles increases in the center, while the total mass and the charge remain the same. Then in (21) before the squared mass and charge the same numerical factor will appear, which depends on the degree of density nonuniformity. But these factors will not change relation (21) and relations (13) and (14). Only in case of large density nonuniformity we could expect some changes of ratios between , , , .

5.1. 4/3 problem

As we know, the essence of the 4/3 problem in the theory of gravitational and electromagnetic fields is that the field momentum is proportional not to the field’s mass-energy, but to the quantity which is 4/3 times greater. Thus it seems that the idea of standard ratio between mass, velocity and momentum of bodies in the special theory of relativity is not proved. However, actually if we take into account not only the energy and momentum of electromagnetic and gravitational fields, but also the energy and pressure momentum inside the body, it allows us to solve the 4/3 problem.

In particular, it follows from (12) that the sum of gravitational and electromagnetic energies of the stationary sphere with particles inside it is . If the sphere is moving at velocity , then this energy increases not only due to the Lorentz factor , but the additional energy 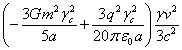emerges, which depends on the square of the velocity.

However, in (12) there is a term of the internal pressure field and a term of the field of particles’ acceleration inside the sphere, which exactly compensate the gravitational and electromagnetic energies of the sphere at any velocity.

In order to obtain the momenta, we need to divide the vector in (16) and (20) by the speed of light . This follows from the relationship between the energy flux vectors and the corresponding momenta. For example, the momentum density of the electromagnetic field . Then from (20) and (12) it follows:

, (22)

where 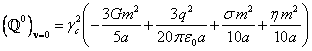denotes the component at zero velocity of the sphere.

If we assume to be the total energy of the gravitational and electromagnetic fields, the pressure field and acceleration field of the stationary sphere, then the ratio in (22) denotes the total mass-energy of these fields. From (22) we see that the coefficient before the velocity is the total mass-energy of the fields in the total momentum, which is 4/3 times greater than the quantity for the stationary sphere. This is the essence of the 4/3 problem. The solution of the problem is that , so that the energy and momentum of the gravitational and electromagnetic fields during the system’s motion are compensated with the corresponding energies and momenta of internal pressure and internal acceleration field, and for the system at rest the compensation takes place for the energies of all the four fields. Thus Poincare's idea of internal tensions in a moving body is realized from the standpoint of our pressure field model, in addition we take into account the acceleration field.

Apparently, the reason of the 4/3 problem is a two-component structure of the fields under consideration. Both the torsion field (the gravitomagnetic field in the general theory of relativity) and the magnetic induction are independent field components and are regarded as relativistic corrections to the main field strengths. In particular, emerging of the magnetic field during the charge’s motion not only leads to the need to take into account the electromagnetic momentum, but also due to the magnetic energy it increases the electromagnetic energy of the moving charge, adding to the quantity , where is the electromagnetic energy of the system at rest, the quantity 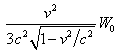, which depends on the velocity. The same applies to the torsion field.

The pressure field is also two-component and has a solenoidal component . In this case we cannot say that the component is due to time delay of the field intensity propagation of the pressure field, since both components of the pressure field are acting simultaneously in one and the same point inside the particle or body. Similarly, the magnetic induction is not a simple consequence of the delay of the electric intensity propagation from the field source to the point under consideration, but it represents some electromagnetic field vorticity that exists separately and independently from . The solenoidal component of the acceleration field in the moving body occurs because the velocity of the body as a whole is added to the internal velocity of the body particles, while inside the body there is a radial gradient of the kinetic energy of the particles and the corresponding gradient of the velocity’s magnitude.

In our model the pressure field equations are similar to Maxwell equations and the stress-energy tensor of the pressure field is similar in structure to the stress-energy tensors of the gravitational and electromagnetic fields. The same applies to the acceleration field with its tensor , as it was described in [11]. The vector component of the pressure field and the component of the acceleration field reflect the vorticity of the corresponding fields. The component is associated with the rotational acceleration of the particle, and the component specifies the pressure of the turbulent motion of particles as they move in the medium, which is similar by its properties to liquid.

From the stated above it follows that only with regard to the energy and momentum of the acceleration field and pressure field in the Lagrangian, Hamiltonian and in the motion equation, the theory becomes self-consistent and allows us to describe the 4/3 problem in detail.

5.2. The integral 4-vector and the ideal spherical collapse

Let us consider the formation of a dynamically equilibrium space system as a result of a long process of substance clustering from the initial state with very low density and almost zero energy of matter motion and zero energy of interaction by means of macroscopic fields. The basic work on substance clustering is produced by self-gravitational force of the system, which increases with decreasing of the system’s size. This force is opposed by the pressure force in the substance, which is a consequence of the interaction of particles with each other. In some equilibrium both forces are balanced and the system stops changing its sizes.

As a rule, the process of substance clustering is accompanied by matter ejection and radiation from the system. This happens especially during the gravitational collapse, when the system quickly reduces its size with large release of gravitational energy. Further we will consider an ideal spherical collapse, which is characterized by the fact that all the components, that are associated with the escaping matter and the emission from the system, are removed from the balance of the matter amount, its energy and momentum.

In other words, in case of the ideal spherical collapse the system turns from one state to another without any loss of energy and momentum to the environment. In this case, all the work of the gravitational and electromagnetic fields during the matter compression should be transformed into the change of the pressure field energy and the velocity field energy (the kinetic energy) of the system’s particles.

Due to the fact that the system’s 4-momentum in the ideal collapse does not change, the system’s integral 4-vector remains zero. Then from (12), (13) and (14) it follows that if the virial theorem is satisfied, half the work of the gravitational and electromagnetic fields during the matter compression turns into the velocity field energy and the other half of the energy turns into the pressure field energy. As a result of this collapse the pressure increases in the matter and the kinetic energy of the particles’s motion increases. In [14] we used the idea that the energy in the matter is divided between the potential pressure energy and the kinetic energy in order to determine the generalized temperature, taking into account the contribution made to the temperature not only by the kinetic but also by the potential energy per particle.

It is intuitively clear that the mechanical energy of the system is distributed between the two extreme ideal forms – on the one hand, in the form of the kinetic energy of the ideal gas of the particles non-interacting through the field, and on the other hand, in the form of the potential pressure energy of the motionless matter in the ideal solid body. If we apply the theorem of equipartition, then on the average half of the system’s mechanical energy must be kinetic and the other half must be the potential energy. In (21) such distribution of energy takes place, also complying with the virial theorem.

This picture allows us to qualitatively explain where the energy of the ideal gravitational collapse goes in case of supernova with formation of a neutron star. One explanation is that up to half of the gravitational energy of a neutron star is converted into neutrino emission, and the other half of the gravitational energy goes for heating the stellar matter. If we suggest that the gravitational energy is divided mainly between the matter heating and the pressure energy, then the total emission of neutrinos need not to take away such a large part of the gravitational energy.

5.3. Comparison with the four-momentum of the system

As it was shown above, at constant velocity the integral 4-vector , containing the energy and momentum components, vanishes. Thus in our approach this 4-vector, which is obtained by integrating the equation of motion and is a conserved quantity, cannot serve as the four-momentum of the system. In [11] from the Lagrangian we obtained the Hamiltonian , which is the relativistic energy of the system of particles and fields and has the following form:

(23)

In (23) the particles have the mass density and the charge density , measured in the reference frames associated with them. The energy is measured in the arbitrary reference frame , the 4-velocities of the particles and their time component of the 4-velocity are measured with respect to . For the volume unit in the first integral we can write: , where denotes the volume unit associated with any arbitrary moving particle. Then for the energy we have:

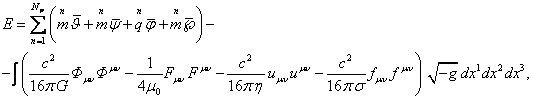
so that the integral becomes the sum for all particles in the system, and denote the mass and charge of the particle with the number ; , , and denote averaged with respect to particle’s volume scalar potentials of the acceleration field, gravitational and electromagnetic fields and pressure field, respectively, while both proper fields and fields from external sources should be taken into account.

The system’s energy can be determined as the time component of the 4-vector: , where is the system’s 4-momentum, and denote the system’s momentum and velocity, respectively. In [15] the 4-vector was referred to as the Hamiltonian 4-vector. If we divide by the speed of light, then we obtain the 4-momentum of the system consisting of particles and fields associated with them:

. (24)

The 4-momentum and the similar 4-vector fully describe the physical state of the system, and in stationary conditions can be conserved relative to the fixed coordinate observer with his time . In contrast, the 4-vector specifies relation only of those energy and momentum components, which are part of the equation of motion. In this case the equation of motion is written in such a form that the 4-acceleration in it, as a derivative of the 4-velocity with respect to the particle’s proper time, depends on the density of the 4-forces acting on the particle. Therefore, the difference between and can be attributed to the difference between the proper and coordinate time and the difference between the proper and coordinate observers. We can also say that the 4-vector is unchanged in the Lorentz reference frame, and the 4-vector , being a 4-vector, is unchanged due to the covariant notation in a variety of frames.

5.4. Comparison with the general theory of relativity

In the general theory of relativity (GTR) the integral 4-vector has special meaning – it is considered the energy-momentum of the system, for example, see [12-13]. Moreover, in contrast to the approach in the covariant theory of gravitation, in equation (1) instead of the stress-energy tensor of the acceleration field we must place the stress-energy tensor of matter in the form for dust-like matter or a more complex tensor, which takes into account the pressure and thereby replaces our tensor . We will note that the covariant derivative of the tensor leads to the particle’s 4-acceleration:

, (25)

here the continuity relation in the form is used, as well as the operator of proper-time-derivative , where is the symbol of 4-differential in the curved spacetime, is the proper time [16].

Since in GTR the gravitational field is considered the metric tensor field , then from the standpoint of GTR the stress-energy tensor of the gravitational field cannot be part of equation (1). But the role of the tensor in GTR is played by the stress-energy pseudotensor of the gravitational field , which, due to its non-tensor nature, is defined in different ways and has different forms. In [12] in the framework of GTR instead of (6) another formula is given for the integral 4-vector:

. (26)

Expression (26) is characterized by the presence of the factor in the form of the determinant of the metric tensor with a minus sign, denotes the time components of the stress-energy tensor of the matter and electromagnetic field, the pseudotensor reflects the contribution of the energy-momentum of the gravitational field. To make expression (26) valid, in GTR there should be an additional condition – at infinity the reference frame coordinates must transform into the coordinates of Minkowski spacetime.

Accordingly, the equation of motion is written in a different way than (1) and has the form:

. (27)

According to our approach, in order to describe the energy-momentum of the matter there is no need to use any special stress-energy tensor of matter such as or similar ones. Instead, we use the stress-energy tensor of acceleration field , the covariant derivative of which also gives the 4-acceleration of a point particle like in (25):

. (28)

And as it was indicated above, the four-momentum of the system (24) we obtain from the Lagrangian and not from the equations of motion, as it is done in GTR according to (26-27).

Let us consider the question of appropriateness of using in GTR the tensor in relation (25). To do this, we will define more precisely the form of the continuity equation in the curved spacetime. According to [12], the equations of the electromagnetic field imply the following:

, (29)

where is the electromagnetic 4-current, is the vacuum permeability, is the electromagnetic tensor.

The covariant derivative in (29) is not equal to zero, because the tensor product of the Ricci tensor and the electromagnetic tensor is not equal to zero. Only in the flat Minkowski space the Ricci tensor vanishes, the covariant derivative becomes the 4-gradient, and (29) gives the standard continuity equation of the electromagnetic 4-current in the special theory of relativity:.

A similar situation in the covariant theory of gravitation takes place both for the gravitational field, for the pressure field and the acceleration field – for all these fields we obtain the expression similar to (29), the difference is that instead of the mass 4-current is used. For example, for the gravitational field we obtain:

This means that in the general case . But in this case the question arises whether we can consider as valid relation (25), which links the divergence of tensor with 4-acceleration. The essential component of (25) is the equality , however in GTR this equality is only postulated, but not proved, and this equality contradicts the results of the covariant theory of gravitation. At the same time, substitution of the tensor with the stress-energy tensor of the acceleration field in (28) leads to the covariant tensor relation.

6. References

1. Thomson J J. On the electric and magnetic effects produced by the motion of electrified bodies. Philos. Mag. Ser. 5 11 (68) 229 (1881).

2. Abraham M. – Phys. Ztschr., 1904, Bd 5, S.576; Theorie d.Electrizität. – Leipzig, 1905, Bd 2, S. 205.

3. Poincaré H. Sur la dynamique de l’électron. – C. R. Acad Sci., Paris, 1905, v. 140, p. 1504.

4. Mie G. Grundlagen einer Theorie der Materie. – Ann. d. Phys., 1912, Bd 37, S. 511; 1912, Bd 39, S. 1; 1913, Bd 40, S. 1.

5. Becker R Theorie der Elektrizität Bd. II Elektronentheorie (Berlin: B.G. Teubner, 1933) [Беккер. Р. Теория электричества, Т-II, Электронная теория, Л.-М. Гостехиздат, 1941 г. ]

6. Морозов В. Б. К вопросу об электромагнитном импульсе заряженных тел. УФН, 181 389–392 (2011).

7. Rohrlich, F.. 1997 The dynamics of a charged sphere and the electron. Am. J. Phys. 65. 1051-1056.

8. Fedosin S.G. Mass, Momentum and Energy of Gravitational Field. Journal of Vectorial Relativity, Vol. 3, No. 3, 2008, P. 30–35.

9. 5. Fedosin S.G. 4/3 Problem for the Gravitational Field. Advances in Physics Theories and Applications, 2013, Vol. 23, P. 19 – 25.

10. Fedosin S.G. Energy, Momentum, Mass and Velocity of a Moving Body in the Light of Gravitomagnetic Theory. Accepted by Canadian Journal of Physics.

11. Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy . vixra.org, 5 Mar 2014.

12. L.D. Landau and E.M. Lifshitz, The Classical Theory of Fields (Vol. 2, 4th ed. Butterworth-Heinemann, 1975).

13. V. A. Fock, The Theory of Space, Time and Gravitation (Pergamon Press, London, 1959).

14. Fedosin S.G. Fizika i filosofiia podobiia ot preonov do metagalaktik, Perm, pages 544, 1999. ISBN 5-8131-0012-1.

15. Fedosin S.G. The Hamiltonian in Covariant Theory of Gravitation. Advances in Natural Science, 2012, Vol. 5, No. 4, P. 55 – 75.

16. Fedosin S.G. Fizicheskie teorii i beskonechnaia vlozhennost’ materii (Perm, 2009).

17. Christensen-Dalsgaard et al. (1996) The current state of solar modeling. Science, Vol. 272, P. 1286 - 1292.

18. Alfè, D.; Gillan, M. J.; Vocadlo, L.; Brodholt, J.; Price, G. D. (2002). The ab initio simulation of the Earth's core. Philosophical Transactions of the Royal Society. Vol. 360 (1795), P.1227–1244.

19. Clemens, Dan P.; Yun, Joao Lin; Meyer, Mark H. (March 1991), BOK globules and small molecular clouds – Deep IRAS photometry and ¹²CO spectroscopy, Astrophysical Journal Supplement 75: 877.

20. J. M. Lattimer and M. Prakash, Neutron Star Structure and the Equation of State. Astrophysical J. Vol. 550(1) P. 426-442 (2001).

Appendix A

According to [11], the equations for the acceleration field of a set of identical particles, completely filling the fixed sphere, are as follows:

, , , , (A1)

where is the Lorentz factor for the particles moving inside the sphere, is the velocity of particles in the reference frame associated with this sphere, is the mass density of an arbitrary particle in the reference frame associated with it.

In the approximation of the special theory of relativity for the vectors and of the acceleration field we can write:

, . (A2)

Here the scalar potential and the vector potential are included in the 4-potential of the acceleration field. Since the vector potential of each individual particle is directed along the particle velocity, then due to the different directions of the velocity vectors the total vector potential of different particles inside the fixed sphere is equal to zero. Therefore, the vector will depend only on the total scalar potential inside the sphere: . The scalar potential of a single particle is , and we need to find the total scalar potential . We will assume such an equilibrium condition when the average velocity of the particles is the function of the current radius, then the average value will be the function of the radius. We will further consider that is the average value for the particles at each radius inside the sphere. Then substituting in the first equation in (A1), we obtain the Poisson equation:

. (A3)

It is convenient to transform this equation for by moving to the spherical coordinates and to consider that depends only on the radius. Then the Laplacian in the spherical coordinates will be the function only of the radius . Further substitution with the auxiliary function in the form will significantly simplify the solution and as a result will contain the sine:

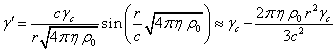, (A4)

where is the Lorentz factor for the velocities of the particles in the center of the sphere,

and due to the smallness of the sine argument we expanded the sinus to the second order terms.

The 4-potential of the acceleration field inside the sphere is the covariant 4-velocity of the sphere, and since the sphere is fixed in , the 4-potential will be equal to: .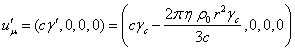

The components of vector and in [11] are given by the formulas:

, . (A5)

If we substitute the 4-potential in (A5), we can find the integral vectors and , arising from all the particles inside the sphere.

Let us suppose now that the sphere is moving in the reference frame at the constant velocity along the axis . In this case, we need to express the 4-potential in the reference frame with the help of the partial Lorentz transformation. For the arbitrary covariant vector the transformation of the components has the following form:

, , , ,

where is the Lorentz factor for the motion of the sphere.

We will use this rule for the 4-potential of the acceleration field:

. (A6)

We also need in the expression for to substitute the coordinates of the reference frame with the coordinates of the reference frame using the Lorentz transformations:

, , , . (A7)

Substituting in (A4), then in (A6) and in (A5), we calculate the vectors and in the reference frame :

, , ,

, , . (A8)

We use (A8) to calculate the integral with the energy of the acceleration field at the time point :

(A9)

As a result of the Lorentz contraction the shape of the moving sphere changes and becomes a Heaviside ellipsoid with the equation for its surface with :

.

If we connect the Cartesian coordinates with the spherical coordinates in the following way:

, , , (A10)

then inside the ellipsoid the current radius will vary from to , the angle will vary from to , and the angle will vary from to . In this case the volume unit as the consequence of transformation from the Cartesian coordinates to the spherical coordinates becomes equal to:

. (A11)

Substituting (A10) and (A11) into the integral (A9) and integrating, we obtain:

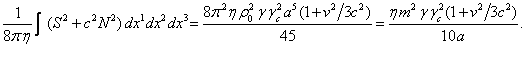
Appendix B

According to [11], the differential equations of the pressure field for the vectors and inside a stationary sphere in Minkowski space are as follows:

, , , . (B1)

where ; is the velocity of an arbitrary particle inside the sphere from the standpoint of the reference frame , in which the sphere is at rest.

Equations (B1) are identical by their form to Maxwell equations. By definition of the 4-potential of the pressure field , for an arbitrary particle the components of 4-potential have the form: , , and hence the vector potential is directed along the particle velocity. Due to the randomness of the particles’ motion the total vector potential inside the sphere is zero: . With this in mind, the vectors and inside the sphere are expressed as follows:

, . (B2)

Substituting the vector from (B2) in the first equation in (B1), we obtain the Poisson equation:

.

In order to simplify we will consider the case with the constant density inside the sphere. Passing to the spherical coordinates, expressing the Laplacian in the appropriate way, making the substitution , where is the function of the radius, we obtain the differential equation:

.

Substituting here relation (A4) for we find that the particular solution of the inhomogeneous equation contains sine. Adding the solution of the homogeneous equation, we find and then the general solution for the scalar potential of the pressure field inside the sphere:

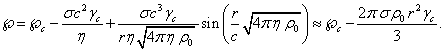(B3)

According to (B3), at constant density inside the sphere the potential must quadratically depend on the current radius , and in the center the potential equals .

Let us refer to the definition of the 4-potential of the pressure field: where now and are respectively the scalar and vector potentials of the pressure field inside the sphere as a system. Since we have , then for the fixed sphere we have .

We will perform transformation of the 4-potential in the reference frame , in which the sphere is moving at the velocity along the axis . Acting like in Appendix A, we find:

. (B4)

The vectors and are expressed from the 4-potential of the pressure field by the formulas:

, . (B5)

Using the coordinates (A7), substituting in (B3), then in (B4) and (B4) in (B5), we find the components of the pressure field strength vectors in the reference frame :

, , ,

, , . (B6)

Now we can find the required integral with , when the sphere’s center coincides with the origin of the reference frame:

Substituting here the coordinates (A10) and the volume unit (A11), we find:

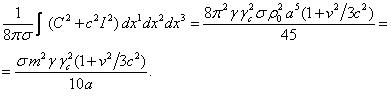
Appendix C

According to [14], the equation for the 4-potential of the gravitational field is a four-dimensional wave equation with d'Alembertian:

, (C1)

where is the 4-potential of the gravitational field, described by the scalar potential and the vector potential of this field,

is the 4-vector of the gravitational (mass) current.

Since we consider stationary random motion of identical particles inside a fixed sphere, the potential inside or outside the sphere will not depend on time, and the total vector potential will be zero everywhere. As a result, d'Alembertian in (C1) is transformed into the Laplacian, and (C1) becomes an equation for the internal gravitational scalar potential:

. (C2)

In (C2) the Lorentz factor of the particles , is the velocity of an arbitrary particle inside the sphere, is the mass density of the particle, the index distinguishes the internal potential from the external potential, which is generated by the sphere outside its limits. Both the potential and are functions of the current radius inside the sphere and do not depend on the angle variables. Therefore, in the spherical coordinates in the Laplacian it is sufficient to take only that part which depends on the radius:

.

If we make substitution of variables in the form , then the equation can be rewritten as follows:

.

We will substitute here the value from (A4), expressed in terms of the sine:

.

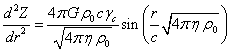The general solution of this equation has the form:

.

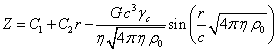Since , and in the center at the potential cannot be infinite, then the coefficient should be equal to zero. Hence the potential inside the sphere is equal to:

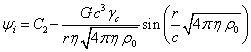. (C3)

We will now turn to calculating the external gravitational potential of the fixed sphere filled with moving particles. First we will find the external gravitational field strength of the sphere. The equations of the gravitational field in the limit of the special theory of relativity, according to [14], take the following form:

, , , . (C4)

According to (C4), the particles moving inside the sphere at velocities generate around themselves a gravitational field with the strength and the torsion field . We will surround the sphere with the shell of spherical shape with an arbitrary radius and integrate the first equation in (C4) over the shell volume. In this case we will apply the Gauss theorem, substituting the integral of the divergence with the integral of the vector over the surface of the shell. Due to the symmetry of the sphere at the constant density for the vector magnitude outside the sphere we find:

.

The vector here denotes to a normal unit vector to the shell surface, which is directed outward. Integration over the shell’s volume is reduced to integration over the sphere’s volume , since outside the sphere . Substituting here from (A4) in the form of sine and integrating, we obtain the field strength outside the sphere:

.

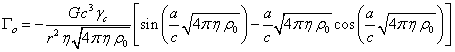The relation between the gravitational field strengths and the 4-potential is as follows:

, . (C5)

The space components of the 4-potential are the components of the vector potential , which in this case is equal to zero. Consequently, the components of the vector are associated only with the time component of the 4-potential: . This equation in vector notation is written as follows: . Hence taking into account the expression for it follows that:

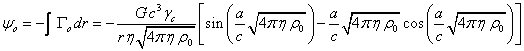. (C6)

.

At infinity, this potential becomes zero. On the sphere surface the potential (C6) must coincide with the internal potential in (C3). We will assume and equate both potentials. This allows us to determine the coefficient and to specify the internal potential :

,

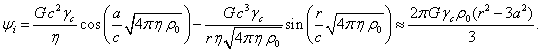(C7)

For the fixed sphere the 4-potential of the gravitational field has the form: , where the potential (C7) should be used inside the sphere and the potential (C6) – outside the sphere. If the sphere is moving at constant velocity along the axis in the reference frame , the 4-potential of the sphere in could be found using the Lorentz transformations. Acting like in Appendix A, we find:

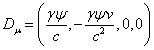. (C8)

First we will calculate the field strengths inside the sphere from the point of view of an observer in the reference frame . For this observer the moving sphere in accordance with Lorentz transformations becomes the Heaviside ellipsoid. Since the coordinates of the points inside the sphere should be transformed into the coordinates of the reference frame , we obtain (A7) and the relation . This relation should be substituted into (C7). After that we will use in (C8) in order to calculate the field strengths with the help of and (C5):

, , ,

, , . (C9)

For the external field using (C6) in a similar way we find:

, ,

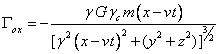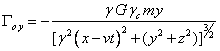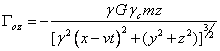, , (C10)

, .

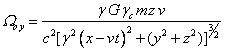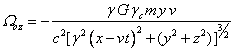We calculated the potentials and strengths of the gravitational field inside and outside the moving solid body in [9]. In contrast to them, the factor appears in (C9) and (C10), which owes its origin to the motion of particles inside the sphere.

We will assume that the sphere with the particles is moving at a constant velocity so long that its proper field inside and outside the sphere becomes stationary and the field’s shape is moving relative to the observer at the same velocity as the sphere itself. Then in order to calculate the sphere’s energy it is sufficient to calculate it at the time point , when the sphere crosses the origin of the reference frame. We will calculate the gravitational energy inside the sphere with the help of (C9):

Substituting here the coordinates (A10) and the volume unit (A11), we find:

(C11)

Now we will use (C10) to find the energy of the moving sphere outside its limits with :

.

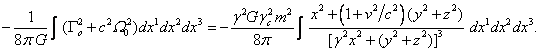
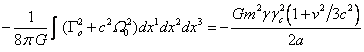Adding the obtained value to (C11), we find the total gravitational energy:

.

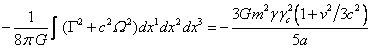Appendix D

We need to calculate the integral:

.

We will substitute here the vectors and according to (B6) in Appendix B, and consider the time point , when the center of the sphere crosses the origin of the reference frame. From the symmetry of the problem we see that the integral pressure energy flux is directed parallel to the velocity of the sphere, that is parallel to the axis . Therefore it suffices to integrate this component of the vector product , which refers to the axis . This gives the following:

.

Proceeding to the spherical coordinates (A10) and the volume unit in the form of (A11) for the Heaviside ellipsoid like in Appendix A, we find:

.

Appendix E

We will calculate the volume integral of the vector of the energy flux density of the acceleration field:

.

It is sufficient to calculate the integral for the time point , since the sphere is moving at the constant velocity and the integral at any given time point will be the same. We will use the vectors and according to (A8) in Appendix A. The only nonzero component of the energy flux is directed along the axis and is equal to:

Integrating over the volume in the coordinates, associated with the Heaviside ellipsoid, like in Appendix A, we find:

Appendix F. Estimation of the coefficients and

If the quantity is constant, then in each particular physical problem it has its own value and is a combination of the fundamental physical constants and parameters of the system under consideration. For example, let us consider a rather large gas cloud with the constant density held by its proper gravitational force in the framework of the special theory of relativity. According to (A4), the solution of the equation for the Lorentz factor , where is the velocity of the particles moving inside the cloud, has the form:

,

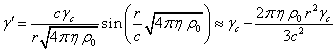where denotes the Lorentz factor of the particles at the center of the cloud.

We will square the equation for and approximately obtain the following:

, (F1)

so that as the current radius increases inside the cloud when moving from the center to the periphery of the cloud, the particles’ velocity decreases.

We will multiply equation (F1) by , where is the mass of one particle, and introduce the mass located inside the sphere with the radius :

. (F2)

If we denote , then according to (F2) the difference between the kinetic energies of the particle at the center and on the surface of the sphere is determined by the gravitational energy of the particle on the surface of the sphere, with accuracy up to the coefficient .

Assuming that the gas law is valid and taking into account the relationship between the temperature and the kinetic energy of the particles in the form , where is the Boltzmann constant, the expression (F2) is transformed into the dependence of the temperature on the radius inside the uniform cloud:

.

We will apply this relation to space objects. For the surface of the cloud , the mass is , , and we obtain:

. (F3)

In many cases the surface temperature is much lower than the temperature at the center. Then in the left side of (F3) can be neglected. According to the standard model, the temperature at the center of the Sun is estimated to be 15.7 million Kelvin [17], and taking as the mass of the proton as the nucleus of the hydrogen atom, from (F3) we find , and also . At the center of the Earth the temperature reaches 6000 Kelvin [18], which gives . These values are somewhat lower than according to (13). Apparently, this is due to the large heterogeneity of the substance distribution inside the Sun and the Earth. Besides, inside the Sun the energy from thermonuclear reactions is added to the gravitational energy, and inside the Earth a large proportion of heat energy is due to the decay of radioactive elements; all of this changes the value . Estimation of the temperature at the center of the neutron star with the mass kg and the radius 12 km according to (F3) gives the value Kelvin.

We will consider now the Bok globules - small dark cosmic clouds of gas and dust. In [19] it was found that the radius of a typical globule is 0.35 parsecs, the mass is 11 Solar masses, the surface dust temperature in the globule is about 26 Kelvin. If we substitute this temperature, mass and radius in (F3) and use the value according to (13), we will obtain the temperature at the center of a typical globule: Kelvin.

If for the total 4-potential we apply the definition , where is the 4-velocity of the stationary sphere, then it allows us to connect the total scalar potential of the pressure field inside the sphere with the pressure: . Substituting this in (B3), we obtain an approximate formula for the pressure as the function of the current radius:

Substituting here and neglecting the surface pressure, we estimate the pressure at the center with : 

. (F4)

For the center of the Sun this formula under the condition according to (14) gives the pressure Pa, which is substantially less than the pressure Pa in the standard model of the Sun. For the Earth, according to the formula (F4) we find the pressure Pa, whereas in [18] for the pressure at the center of the Earth the value Pa is indicated. For a neutron star with the mass kg and the radius 12 km the pressure at the center according to (F4) equals Pa, and in various models of neutron stars, according to [20], the pressure does not exceed Pa. The obtained estimates in comparison with theoretical models for space objects show satisfactory complying with the values , except for the estimate of the pressure inside the Sun.

Source: http://sergf.ru/iven.htm

Scientific site