Advances
in Natural Science, Vol. 5, No. 4, pp. 55-75 (2012). http://dx.doi.org/10.3968%2Fj.ans.1715787020120504.2023
УДК 53.01+531.314+
531.51 +537.8
Гамильтониан в ковариантной теории гравитации
Федосин Сергей Григорьевич
г. Пермь, Пермский край, Россия
e-mail intelli@list.ru
В рамках ковариантной теории гравитации записываются уравнения
Эйлера-Лагранжа и определяются уравнения движения с помощью функции Лагранжа,
для малой пробной частицы, и в случае непрерывно распределённого вещества. От
функции Лагранжа осуществляется переход к функции Гамильтона, которая
выражается через трёхмерный обобщённый импульс в явном виде, а также
определяется через 4-скорость, скалярные потенциалы и напряжённости
гравитационного и электромагнитного полей с учётом метрики. Даётся определение
четырёхмерной обобщённой скорости и описывается её применение в принципе
наименьшего действия и в гамильтониане. Делается предположение о существовании
4-вектора гамильтониана и рассматривается проблема массы тела. Для
характеристики свойства массы вводятся
три различные массы, одна из которых связана с энергией покоя, другая является
наблюдаемой массой, а третья масса определяется без учёта энергии
макроскопических полей. Показывается, что функция действия имеет физический
смысл как функция, описывающая изменение таких внутренних свойств, как скорость
течения собственного времени и скорость нарастания фазового угла периодических процессов.
Ключевые слова: уравнения Эйлера-Лагранжа; функция Лагранжа; функция Гамильтона;
обобщённый импульс; обобщённая 4-скорость; уравнения движения.
PACS: 03.30.+p,
04.20.Fy, 04.40.-b, 11.10.Ef
The Hamiltonian in covariant theory
of gravitation
Sergey G. Fedosin
Perm, Perm Region, Russia
e-mail intelli@list.ru
In the framework of covariant theory
of gravitation the Euler-Lagrange equations are written and equations of motion
are determined by using the Lagrange
function, in the case of small test particle and in the case of
continuously distributed matter. From the Lagrangian transition to the
Hamiltonian was done, which is expressed through three-dimensional generalized
momentum in explicit form, and also is defined by the 4-velocity, scalar
potentials and strengths of gravitational and electromagnetic fields, taking
into account the metric. The definition of generalized 4-velocity, and the
description of its application to the principle of least action and to
Hamiltonian is done. The existence of a 4-vector of the Hamiltonian is assumed
and the problem of mass is investigated. To characterize the properties of mass
we introduce three different masses, one of which is connected with the rest energy,
another is the observed mass, and the third mass is determined without the
energy of macroscopic fields. It is shown that the action function has the
physical meaning of the function describing the change of such intrinsic
properties as the rate of proper time and rate of rise of phase angle in
periodic processes.
Keywords: Euler-Lagrange equations; Lagrangian; Hamiltonian; generalized momentum;
generalized 4-velocity; equations of motion.
Введение
Существует несколько подходов для описания и построения любой
физической теории. В простейшем случае содержание теории сводится к нескольким
физическим законам и принципам, удовлетворяющим экспериментальным данным. Путём
их анализа и упрощения можно найти систему аксиом, на основе которых вся теория
может быть выведена аксиоматическим путём, как логическое следствие
первоначальных простейших предположений. В энергетическом подходе достаточно
знать всего лишь одну функцию с размерностью энергии, чтобы с её помощью найти
все уравнения теории. Примерами такой функции являются лагранжиан и
гамильтониан.
Теория ковариантной теории гравитации (КТГ) появилась в 2009
году [1], как следствие релятивистского обобщения лоренц-инвариантной теории
гравитации (ЛИТГ). Уравнения ЛИТГ по своей форме подобны уравнениям Максвелла и
могут быть выведены на основе аксиом [2]. Недавно вывод уравнений КТГ был
осуществлён из принципа наименьшего действия [3]. Исходя из формы полученного
лагранжиана, теперь становится возможным осуществить следующий шаг и перейти к
гамильтониану, соответствующему теории КТГ.
После краткого представления уравнений Эйлера-Лагранжа мы
применяем их для описания движения малой пробной частицы, а также для случая непрерывно
распределённого вещества. Затем мы находим гамильтониан в двух его формах,
через 4-скорость, и через обобщённый импульс, и подставляем гамильтониан в
уравнения Гамильтона с целью проверки уравнений движения. В конце данной работы
в рассмотрение вводится четырёхмерная обобщённая скорость, позволяющая
упростить выражения для лагранжиана и гамильтониана. От 4-вектора обобщённой
скорости делается переход к новому 4-вектору гамильтониана, задающему энергию и
импульс вещества в фундаментальных полях. Делается сравнение с лагранжевым
подходом, при котором энергия и импульс вычисляются через тензоры
энергии-импульса. С помощью формул для энергии анализируется проблема массы. В
последней части мы описываем функцию действия как функцию, имеющую
самостоятельное значение в физике – с её помощью можно определять эффекты
замедления времени, возникающие при изменении скорости движения тел или при
воздействии полей.
Принцип
наименьшего действия
В этом разделе запишем в применении к
ковариантной теории гравитации (КТГ) известные соотношения для функции
Лагранжа и принципа наименьшего действия. Согласно последнему, уравнения
движения вещества и поля могут быть найдены путём варьирования функции
действия 
. В координатах 
функция Лагранжа
зависит от координат 
, от 4-скорости движения вещества 
(где 
– скорость света, 
обозначает интервал
для движущегося элемента вещества), от 4-потенциала гравитационного поля 
и 4-потенциала
электромагнитного поля 
, а также от метрического тензора 
системы отсчёта. Если
перейти от и 
к трёхмерным
координатам, времени и скоростям, то для функции Лагранжа с этими переменными
можно записать: 
. Здесь величины 
, 
, 
являются компонентами
3-вектора координатной скорости 
. При движении по определённой траектории текущие координаты 
элемента вещества, и
скорости его движения 
будут функциями координатного времени 
. В общем случае 4-потенциалы и , в которых оказывается вещество, и метрический тензор , зависят от координат и времени. Если брать координаты
элемента вещества вдоль траектории движения как функции времени, то
величины , и на траектории также
можно считать функциями времени. Это позволяет рассматривать функцию Лагранжа 
как функцию от
времени, а интеграл 
между
пространственно-временными точками 1 и 2
– как некоторое число.
Теоретически под вариациями координат можно понимать малые по
величине функции времени, за счёт добавок которых изменяется форма траектории
движения вещества и соответственно меняется значение функции действия. Из принципа наименьшего действия
следует, что действие 
на истинной траектории
движения должно быть экстремальным (чаще всего имеет минимум).
Вариация функции действия по траектории, когда варьируются все
переменные, кроме времени, даёт следующее:
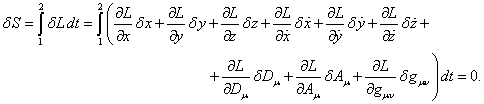
Член с вариацией скорости 
можно проинтегрировать
по частям:
.
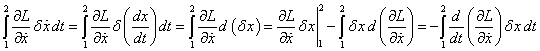Здесь было учтено, что вариация 
в начальной временной
точке 1 и в конечной временной точке 2 обращается в нуль согласно условию
варьирования траектории движения. Произведя интегрирование по частям ещё для
членов с 
и 
, для вариации действия получаем:
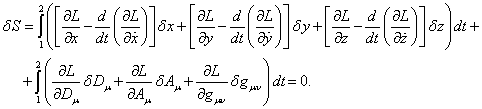(1)
Вариации , 
, 
, 
, 
и 
в (1) независимы друг
от друга и не равны нулю на истинной траектории, за исключением начальной и конечной
точек траектории. Отсюда вытекают уравнения Эйлера-Лагранжа:
, 
, 
.
(2)
, 
, 
. (3)
Напомним, что принцип
наименьшего действия применяется обычно к консервативным системам, для
которых точно заданы потенциальные функции, из которых могут быть найдены
действующие силы. Мы будем рассматривать физические системы с веществом и
фундаментальными полями, к которым относятся гравитационное и электромагнитное
поля. Эти системы являются консервативными, и для них может быть найден закон
сохранения энергии-импульса, имеющий один и тот же вид во всех системах отсчёта.
Если же система отсчёта фиксирована и не ускорена, то полная энергия и полный
импульс сохраняются по отдельности для каждого момента времени, при этом
возможен обмен энергией и импульсом между веществом и полем.
Функция
Лагранжа и уравнения движения
В случае непрерывно распределённого по всему объёму
пространства вещества, находящегося в гравитационном и электромагнитном полях,
используем функцию Лагранжа 
, которая в ковариантной теории гравитации (КТГ) имеет вид [3]:
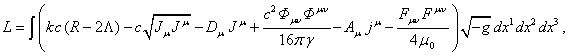
(4)
где 
– коэффициент
пропорциональности, 
– малый коэффициент
порядка единицы, зависящий от свойств системы отсчёта, 
– гравитационная
постоянная,
– скорость света, как
мера скорости распространения электромагнитного и гравитационного
взаимодействий,
– скалярная кривизна,
– постоянная величина для
рассматриваемой системы (в том случае, когда (4) применяется в космологии,
постоянная называется
космологическая постоянная),
– 4-потенциал
гравитационного поля, описываемый через скалярный потенциал 
и векторный потенциал 
этого поля,
– 4-вектор плотности
массового тока,
– плотность массы
вещества в системе отсчёта, в которой данное вещество покоится,
– 4-скорость рассматриваемого элемента вещества,
– гравитационный
тензор (тензор напряжённостей гравитационного поля),
– определение
гравитационного тензора с контравариантными индексами с помощью метрического
тензора 
,
– 4-потенциал
электромагнитного поля, задаваемый с помощью скалярного потенциала 
и векторного потенциала 
этого поля,
– 4-вектор плотности
электрического тока,
– плотность заряда
вещества в системе отсчёта, в которой заряд покоится,
– магнитная
постоянная,
– электромагнитный
тензор (тензор напряжённостей электромагнитного поля),
– квадратный
корень из детерминанта 
метрического тензора,
взятого с отрицательным знаком,
– произведение
дифференциалов пространственных координат, которое можно рассматривать как
пространственный координатный объём движущегося элемента вещества с точки
зрения используемой системы отсчёта.
Далее будут применяться международная система единиц СИ, базовые
координаты в виде координат с контравариантными индексами 
, сигнатура метрики (+, –, –, –), метрический тензор . Наличие
в формулах повторяющихся индексов подразумевает суммирование по правилу Эйнштейна, то есть отдельное
суммирование по каждому повторяющемуся индексу.
Символом 
будет обозначаться
ковариантная производная по координатам (в данном случае по координатам 
). Аналогично 
есть оператор частной
производной по координатам или 4-градиент.
Мы можем считать, что величины , , 
, 
, , 
, 
в месте расположения
элемента вещества являются функциями его координат 
, а также и функциями от координат и скоростей других
элементов вещества. Однако от 4-скорости движения самого элемента вещества
указанные величины в первом приближении не зависят. Это возможно в том случае,
когда элемент вещества настолько мал, что запаздыванием распространения его
собственного поля в пределах объёма элемента можно пренебречь даже при
релятивистских скоростях движения. Малость объёма, массы и заряда элемента
приводят к тому, что движение вещества этого элемента определяется только
градиентами внешних полей (в виде суперпозиции полей от всех внешних элементов
вещества), а сам элемент не вносит почти ничего в средний градиент поля внутри
себя. При указанных предположениях в (4) только 4-скорость 
, входящая в 
и в 
, будет зависеть от 3-скорости движения рассматриваемого элемента
вещества.
Если учесть, что тензор гравитационного поля зависит от
4-потенциала согласно определению 
, то соотношение из (3) для функции
Лагранжа (4) даёт:
, или 
. (5)
Аналогично получается и для соотношения из (3):
, или 
,
(6)
Соотношения (5) и (6) задают уравнения гравитационного и
электромагнитного поля соответственно, осуществляя связь между 4-потенциалами
поля и источниками поля в виде 4-токов массы и заряда. Согласно (5) и (6), чем
больше 4-токи, тем больше ковариантные производные от величин 
и 
(величины и есть 4-роторы
соответствующих 4-потенциалов поля).
Как было показано в [3], соотношение 
в (3) приводит к
следующему:
(7)
при условии, что:
. (8)
В уравнении для метрики (7) величина 
есть тензор Риччи, так
что левая часть (7) даёт тензор Гильберта-Эйнштейна. В правой части (7)
находится тензор энергии-импульса вещества 
, тензор энергии-импульса гравитационного поля 
, а также тензор энергии-импульса электромагнитного поля 
. Тензор выражается через
тензор гравитационного поля по формуле:
. (9)
Соотношение (8) утверждает, что существует связь между
космологической константой и величиной плотности
энергии 
вещества системы,
когда это вещество распылено на бесконечность и находится там неподвижно. В
этом случае 4-потенциалы и в (8) равны нулю. В
результате последующего взаимодействия вещество объединяется в некоторую меньшую
по размерам систему, при этом плотность вещества изменяется от 
до , и возникает потенциальная энергия взаимодействия между
веществом и полем за счёт 4-потенциалов поля.
При трактовке постоянной возможны два
подхода. В первом из них различие между и возникает лишь за счёт
макроскопических гравитационных и электромагнитных полей. Во втором случае
можно считать, что в 4-потенциалы поля и вносят вклад ещё
сильная гравитация и электромагнитные поля, действующие на уровне элементарных
частиц и изменяющие массу частиц [2]. В этом случае плотность должна состоять из
некоторой величины 
и добавок от
макроскопических и микроскопических полей, а масса становится характеристикой
тел, описывающей взаимодействие вещества с квантами поля – гравитонами и
электромагнитными квантами, действующими на всех уровнях материи [4]. Следует
отметить, что поскольку 4-потенциалы и поля определены с
точностью до калибровочного преобразования, с такой же точностью будет
определена и космологическая постоянная .
Обратимся теперь к соотношениям (2). Предварительно выделим в
функции Лагранжа (4) только те члены, которые прямо зависят и от координат и от
скоростей, и подставим соотношения 
и :
, (10)
.
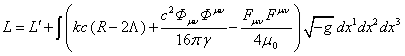Проинтегрируем (10) по трёхмерному объёму, полагая, что 
, и с учётом следующих соотношений [5]:
, 
, 
, (11)
где 
– детерминант
метрического тензора 
,
– дифференциал
собственного времени в той точке системы отсчёта, через которую проходит
элемент вещества,
– дифференциал
координатного времени используемой системы отсчёта,
– детерминант
трёхмерного метрического тензора 
, при этом
, 
, 
.
Инвариантом трёхмерного объёма является произведение 
, причём множитель 
обеспечивает переход
от движущегося координатного объёма к движущемуся местному
объёму с точки зрения местного наблюдателя в той точке пространства, через
которую в данный момент 
собственного
(местного) времени проходит элемент вещества. Это даёт в (10): 
, где 
есть дифференциал
движущегося местного объёма. Для движущегося элемента вещества 4-скорость 
, а также:
,
,
где 
есть дифференциал
объёма в сопутствующей элементу вещества системе отсчёта, 
– инвариантный движущийся
4-объём при условии, что .
Отсюда следуют выражения для плотности массы 
и плотности заряда 
движущегося вещества:
, 
,
где 
обозначает интервал
для движущегося элемента вещества, а 
есть интервал для
неподвижного наблюдателя, мимо которого движется вещество.
С учётом формул для 
и 
, 
в (10) будет равно:
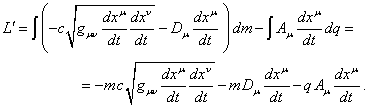(12)
В (12) 
и 
есть масса и заряд
малого элемента вещества, движущегося как целое с координатной скоростью 
, при этом данная скорость не является 4-вектором.
4-потенциалы и в результате
интегрирования по объёму рассматриваются как эффективные усреднённые по объёму
потенциалы, воздействующие на данный элемент вещества. В координатах 
величина 
, следовательно, произведение 
. Аналогично будет для электромагнитного потенциала: 
.
Заметим, что координатная скорость 
отличается от скорости
движения элемента вещества, фактически измеряемой местным наблюдателем. Это
связано с тем, что собственное время местного наблюдателя не совпадает с
координатным временем 
(координатное время является общим для
системы отсчёта в целом, а собственное время измеряется как
неподвижными электромагнитными часами в каждой конкретной точке системы
отсчёта, так и часами, связанными с движущимся веществом, и зависит от действия
на часы имеющихся гравитационных и электромагнитных полей в момент
измерения).
Трёхмерный векторный потенциал гравитационного поля имеет свои компоненты вдоль пространственных
осей системы координат: 
, так же для векторного потенциала электромагнитного поля
можно записать: 
.
С учётом этого для (12) имеем:
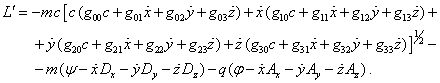(13)
В простейшем случае можно считать, что для произвольной
системы отсчёта скорости 
не зависят в явной
форме от координат 
, а зависят от времени; масса и заряд могут зависеть от 
и не зависят от ; скалярные потенциалы и , векторные потенциалы и 
, метрический тензор не зависят прямо от , но зависят от 
. Предположение о независимости в явной форме от
координат означает, что поле скоростей
является свободным, а не связанным векторным полем. Примером связанного поля
является поле скоростей в жидкости, протекающей в объёме, ограниченном
некоторой поверхностью. Вследствие взаимодействия жидкости с поверхностью и
частиц жидкости друг с другом возникает явная зависимость поля скоростей от
координат. Если же рассматривать квазисвободное движение непрерывно
распределённого вещества со слабым гравитационным и электромагнитным полями, то
скорости движения будут слабо зависеть от пространственных координат.
При этих условиях из (12) и (13) находим:
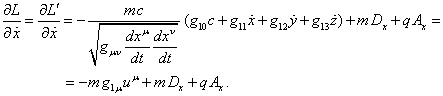(14)
В (14) было учтено, что 
, где есть интервал, а также
использовано соотношение 
. Заметим, что из определения 4-скорости и из определения интервала
вытекает стандартное
соотношение 
.
Полная производная по времени от (14) даёт:
. (15)
Первая пространственная компонента градиента от будет равна:
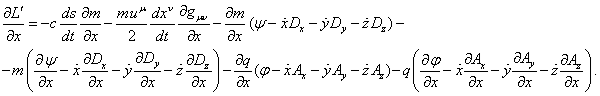
С учётом (10) должно быть:
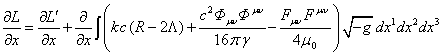. (16)
Уравнение Эйлера-Лагранжа
из (2) требует, чтобы
равенства (15) и (16) были равны друг к другу:
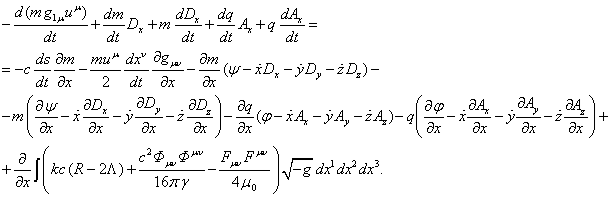(17)
Введём с помощью 3-вектора 
3-вектор обобщённого
импульса со следующими компонентами:
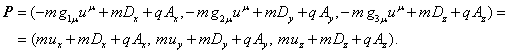(18)
С учётом (18) вместо (17) можно записать в 3-векторном виде:
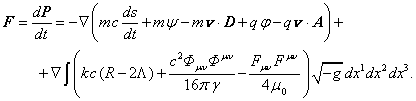(19)
Согласно (19), для непрерывно распределённого вещества
скорость изменения обобщённого импульса вещества и поля определяется
градиентами от следующих величин: от энергий элемента вещества в гравитационном
и электромагнитном полях, находимых через скорость движения 
и скалярные и
векторные потенциалы; от интеграла по объёму члена со скалярной кривизной
пространства-времени и инвариантов энергии гравитационного и электромагнитных
полей, находящихся в объёме элемента вещества, а также тех собственных полей,
которые генерируются данным веществом и взаимодействуют с ним. Обобщённая сила 
в (19) зависит также
от константы и от члена 
, связанных с релятивистской энергией массы .
Напомним, что при выводе (17) и (19) мы считали, что скорость
движения вещества не зависит от пространственных координат. В связи с этим в (17)
и (19) отсутствуют градиенты от компонент скорости, появляющиеся в случае поля
скоростей, каким-то образом связанного с точками пространства.
Случай
малой пробной частицы за пределами массивного заряженного тела
Уравнение движения (17) можно упростить, используя
операторное равенство: 
. Это даёт следующее:
, 
,
, 
.
Введём далее вектор напряжённости гравитационного поля 
и вектор интенсивности
поля кручения 
(гравитомагнитное
поле) по формулам:
, 
.
Можно убедиться, что эти определения величин и записаны в общековариантной
форме, поскольку данные величины с точностью до постоянного множителя
составляют компоненты гравитационного тензора 
. Аналогично определяется напряжённость электрического поля 
и индукция магнитного
поля 
:
, 
.
Поскольку 
, 
, то с учётом предыдущих равенств из (17) находим:
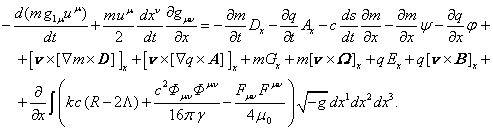(20)
Уравнение (20) есть уравнение движения элемента вещества в
направлении первой пространственной оси системы отсчёта, и соответствует
уравнению из (2). Для других
пространственных осей уравнения движения будут отличаться лишь заменой индексов
в производных и в компонентах векторов. Если ввести 3-вектор , то вместо (20) можно записать уравнение движения в
3-векторном виде:
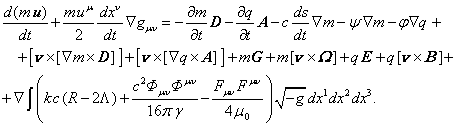(21)
3-вектор
в левой части (21) по
своему смыслу эквивалентен действию символов Кристоффеля, которые используются
в записи уравнения движения в римановом пространстве в четырёхмерных
обозначениях, как в общей теории относительности, так и в ковариантной теории
гравитации.
Поскольку мы рассматриваем малую пробную частицу за пределами
массивного заряженного тела, то вклад в кривизну и в постоянную делает только сама
пробная частица. Члены 
и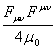 
в (21) связаны с
плотностью энергии гравитационного и электромагнитного полей соответственно.
Если пробная частица достаточно мала и имеет небольшую
плотность вещества и заряда, то основной вклад в плотность энергии полей в
объёме частицы будут вносить внешние поля от массивного заряженного тела. Кроме
этого, в (21) берётся градиент от интеграла по объёму, который в ряде случаев
может оказаться близким к нулю вследствие симметрии и однородности
распределения энергии полей внутри пробной частицы. Одним из таких случаев
является приблизительная пространственная однородность внешнего поля.
В пространстве Минковского 
, 
.
Если ещё предположить постоянство массы и заряда со временем,
нулевые градиенты массы, заряда, кривизны пространства и нулевые градиенты в распределении
энергии полей в пределах объёма частицы, то (21) приобретает вид уравнения
движения пробной частицы в гравитационном и электромагнитном полях в
лоренц-инвариантной теории гравитации [2]:
.
(22)
Левая часть (22) есть скорость изменения со временем
релятивистского импульса частицы, а в правой части стоит двухкомпонентная
гравитационная сила и подобная ей двухкомпонентная электромагнитная сила
Лоренца. Таким образом, из вариации действия (1) с функцией Лагранжа (4) в
рамках ковариантной теории гравитации (КТГ) можно получить уравнение движения
частицы (22), справедливое в специальной теории относительности (СТО). Это означает,
что уравнения КТГ и СТО связаны между собой принципом соответствия, когда при
устремлении кривизны пространства-времени к нулю уравнения КТГ переходят в
уравнения СТО.
В отличие от этого, уравнения общей теории относительности
(ОТО) не имеют такого прямого перехода в уравнения СТО. Действительно, в ОТО
функция Лагранжа отличается от (4) отсутствием гравитационных членов вида: 
. В результате в (21) нет соответствующих гравитационных
членов, остаётся лишь следующее:
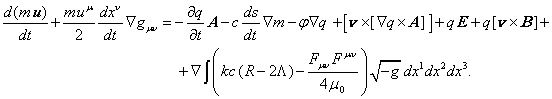(23)
Для того чтобы гравитация всё-таки проявилась в ОТО как
эффективная гравитационная сила в пределе слабого поля, в (23) осуществляют
разложение , появляющиеся члены переносят в правую часть и называют их
гравитационной силой. Различие позиций ОТО и КТГ связано с тем, что в ОТО гравитация
есть просто искривление пространства-времени (без указания причины такого
искривления), а в КТГ гравитация является реальной физической силой,
обосновываемой механизмом гравитации Фатио-Лесажа [6]. При этом скалярный
потенциал гравитационного поля в
КТГ считается характеристикой скалярного поля, связанного с потоками
гравитонов, и пропорционален разности между плотностью энергии потоков
гравитонов в той точке, где определяется потенциал, и плотностью энергии
потоков гравитонов на бесконечности. Градиенты плотности энергии потоков
гравитонов можно в этом случае рассматривать как напряжённости гравитационного
поля. В предположении, что часть гравитонов представляют собой мельчайшие
заряженные частицы, в [1] выводится схема возникновения электромагнитной силы и
электрического потенциала . Если известны скалярные потенциалы в неподвижной системе
отсчёта, то после пересчёта в движущуюся систему отсчёта появляются векторные
потенциалы гравитационного и электромагнитного полей, как следствие
запаздывания полевых воздействий из-за ограниченной скорости их
распространения. Таким образом можно понять, почему поля описываются
4-потенциалами 
и 
.
Связь между
функциями Гамильтона и Лагранжа
При описании принципа наименьшего действия мы записывали функцию Лагранжа в общем виде: 
, где величины 
, 
, 
являются компонентами
3-вектора координатной скорости 
движения элемента
вещества. Вариация функции действия приводит к уравнениям Эйлера-Лагранжа (2) и
(3) и требует вариации функции Лагранжа, которая имеет вид:
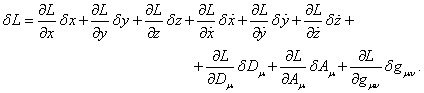(24)
Введём функцию Гамильтона 
, где величины 
являются компонентами
3-вектора так называемого сопряжённого обобщённого импульса 
(сопряжённого по
отношению к координатам 
). Функция Гамильтона в простейшем случае определяется
преобразованием Лежандра через компоненты сопряжённого импульса, компоненты
скорости элемента вещества и функцию Лагранжа:
.
(25)
При равенстве нулю вариации по времени, как это требуется для
функции Лагранжа в принципе наименьшего действия, для вариации функции
Гамильтона имеем:
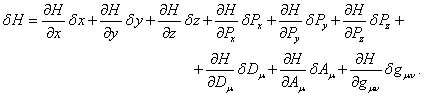(26)
При вариации (25) получается:
. (27)
Подстановка (24) и (26) в (27) даёт следующие соотношения:
, 
, 
,
(28)
, 
, 
,
(29)
, 
, 
, 
, 
, 
. (30)
Выражая 
через 
согласно (30), и
подставляя в (2), с учётом (28) имеем: 
. В общем случае можно записать:
.
(31)
Найдём компоненты обобщённого импульса из (30), учитывая, что
компоненты скоростей прямо входят в функцию
Лагранжа (4) только в трёх членах согласно (12) и (13), образующих часть
функции Лагранжа 
. Из (14) и аналогичных соотношений с помощью (30) для
обобщённого импульса получается то же самое, что и в (18):
, 
, (32)
, 
.
Скалярное произведение обобщённого импульса 
на скорость 
, с учётом соотношения 
, даёт:
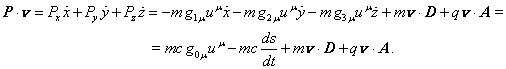(33)
Подстановка этого выражения в (25) с учётом (4), (10), (12),
(13) позволяет найти функцию Гамильтона для твёрдотельного движения элемента
вещества с массой и зарядом 
:
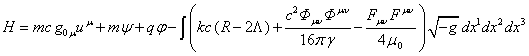. (34)
В механике функция Гамильтона как правило ассоциируется с
энергией тела (элемента вещества). Первый член в (34) связан с энергией покоя и
кинетической энергией вещества. Произведения 
и 
задают потенциальную энергию
массы и заряда в гравитационном и электромагнитном полях, связанную со
скалярными потенциалами. Интеграл по объёму в (34) определяет дополнительные
энергии, зависящие от кривизны пространства-времени 
, от постоянной 
, и от напряжённостей полей. Если объём вещества пробной
частицы мал, то интегралом по объёму в (34) можно пренебречь по сравнению с
первыми тремя членами. В этом случае энергия пробной частицы включает в себя
релятивистскую энергию движения и энергии частицы в потенциалах полей.
Если учесть формулы для 
и для 
, приведённые перед соотношением (12), то массу и заряд можно
выразить через интеграл по объёму от плотности массы и заряда:
, 
,
где 
– плотность вещества в
системе отсчёта, покоящейся относительно элемента вещества; 
– интервал; 
– плотность заряда в системе отсчёта, покоящейся относительно
элемента вещества.
С учётом этого функция Гамильтона для непрерывно
распределённого вещества будет иметь вид:
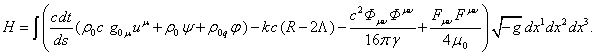
(35)
В пространстве Минковского справедливы соотношения:
,
,
,
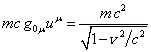где 
– напряжённость
гравитационного поля, 
– вектор интенсивности
поля кручения, 
– напряжённость
электрического поля, 
– индукция магнитного
поля, 
– электрическая
постоянная.
Подставим эти соотношения в (34) для случая малой пробной
частицы, когда можно пренебречь членом со скалярной кривизной :
.
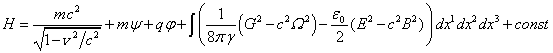(36)
Для внешних полей интегрирование в (36) производится по
объёму частицы, а для полей, генерируемых веществом данной частицы, интегрировать
следует по объёму и внутри, и снаружи частицы. Гамильтониан (36) как энергия
малой пробной частицы определён с точностью до константы, которая возникает от
интегрирования по объёму постоянной (о смысле данной
постоянной смотри наши рассуждения после соотношения (9) ). В пространстве
Минковского метрика не зависит от координат и времени, и потому член с
постоянной 
при вариации функции
Лагранжа исчезает и не даёт вклада в уравнения движения. Однако вследствие
определения функции Гамильтона (25), куда функция Лагранжа 
входит целиком,
постоянная проявляется в (36) как
дополнительная константа.
Выражение функции
Гамильтона через обобщённый импульс
В (34) и (35) функция Гамильтона выражается через 4-скорость 
, зависящую от 3-вектора скорости 
. Однако в каноническом виде функция
Гамильтона определяется через компоненты обобщённого импульса: 
. Выразим компоненты 3-скорости через компоненты обобщённого
импульса , для чего с учётом выражения 
перепишем (32) в
другом виде:
. (37)
.
(38)
. (39)
С учётом (32) введём следующие обозначения:
, 
,
, (40)
как компоненты некоторого 3-вектора, нормированные к единице
массы.
Нам понадобятся также следующие миноры:
– миноры матрицы
компонент метрического тензора 
, где 
;
– миноры
пространственной подматрицы компонент метрического тензора 
, где 
. В качестве примера миноров с учётом симметричности метрического
тензора 
можно записать:
, (41)
,
,
, 
, 
.
Мы будем также использовать следующие соотношения:
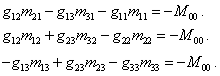(42)
, 
,
, 
,
, 
.
С данными обозначениями из (37), (38) и (39) следует:
. (43)
. (44)
. (45)
Разделив (44) и (45) на (43), можно выразить 
и 
через 
:
.
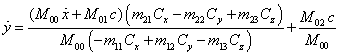(46)
.
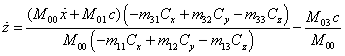(47)
Из (43) находим:
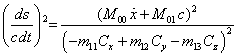. (48)
С другой стороны, 
, а для квадрата интервала 
. С учётом этого имеем:
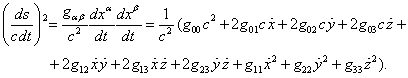(49)
Из равенств (48) и (49) вытекает:
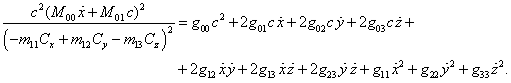(50)
Если подставить в (50) и 
из (46) и (47), то
получится квадратное уравнение для нахождения компоненты скорости . Однако это уравнение будет слишком громоздким для записи.
Уравнение (50) можно упростить введением новой переменной:
, 
. (51)
Используя в (50) соотношения (46), (47), (51), после
длительных вычислений находим:
.
(52)
где 
есть отрицательный по
величине детерминант метрического тензора :
,
и использовано сокращение:
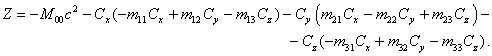(53)
Из (52) и (51) находим , а затем из (46) и (47) определяем и :
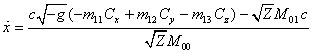, (54)
,
.
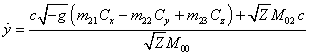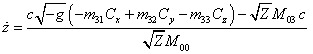Из (54) и (43) выводим величину 
:
.
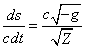(55)
Вычислим 
с учётом (54), (55) и
выражения 
:
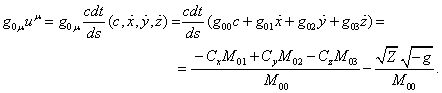(56)
В (56) с помощью введённых ранее в (40) обозначений 
, 
, 
можно перейти от 
, 
и 
к обобщённым импульсам
, 
и 
. После умножения (56) на 
результат будет:
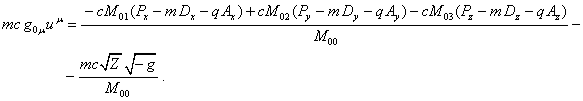
Подставим это в формулу для гамильтониана (34):
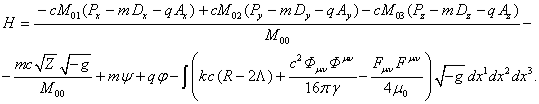
(57)
В пространстве Минковского, то есть в специальной теории
относительности, когда искривление пространства-времени отсутствует, 
, 
, 
, и с учётом выражений (53) для 
и (40) для , и , функция Гамильтона будет выражаться через 3-вектор
обобщённого импульса 
, через скалярные потенциалы 
, 
, и векторные потенциалы
, 
:
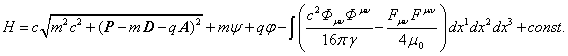
(57’)
В (57’) аналогично (36) в выражении для гамильтониана
появляется некоторая константа. При этом гравитационный тензор 
и электромагнитный
тензор 
являются
дифференциальными функциями от потенциалов полей в виде производных по
координатам и времени. Полученное
выражение (57’) для 
, но без учёта гравитационного поля, то есть без членов с
потенциалами и , и без учёта интеграла с тензорами и 
, можно найти, например, в [5].
Уравнения
Гамильтона согласно (30) и (31), с компонентами 3-вектора координатной скорости 
, и с компонентами 3-вектора
обобщённого импульса 
из (32), имеют вид:
, , 
, или 
.
(58)
.
(59)
Для того, чтобы убедиться в справедливости уравнений (58), следует
подставить в (57) значение 
из (53), причём
величины , и необходимо выразить
через
обобщённые импульсы , 
и с помощью (40). Если
затем от гамильтониана 
взять частные производные
согласно (58), получатся выражения (54) для компонент скоростей. Физический
смысл уравнения (59) заключается в том, что градиент гамильтониана как энергии
системы, взятый с обратным знаком, равен скорости изменения обобщённого
импульса со временем.
Запишем теперь (57) в четырёхмерном виде, для чего используем следующие
выражения:
, 
,
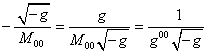(60)
, 
, 
.
Для первого члена в (57) это с учётом (32) даёт:
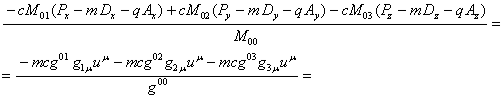
(61)
Сделаем далее
преобразования следующих вспомогательных величин с помощью равенств (41) и
(42):
.
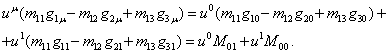
. (62)
Из (40) следует, что 
, 
, 
. Тогда с учётом (62) и равенства 
выражение (53) для можно преобразовать
так:
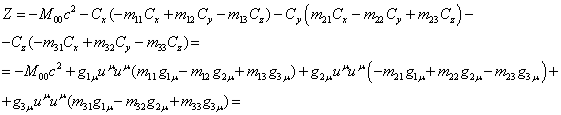
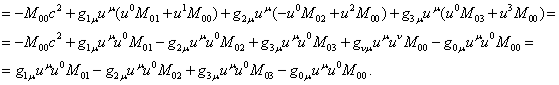
Используем
теперь (60):
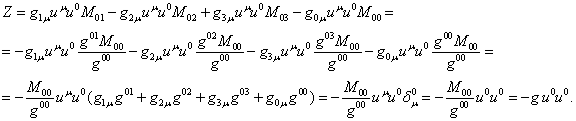
(63)
В (63) был
использован символ Кронекера 
. С учётом (63) для второго члена в (57) находим:
.
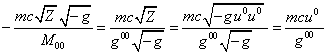Подставим это выражение и результат из (61) в (57):
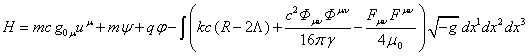. (64)
Гамильтониан (64) совпадает с выражением для гамильтониана (34). Таким
образом, мы сделали круг: вначале путём введения обобщённого импульса (32) был сделан
переход от (34) к гамильтониану в виде (57), а затем другим путём мы снова
вернулись к (34).
Чтобы проверить справедливость уравнений (59) для гамильтониана в форме
(64), найдём величину 
:
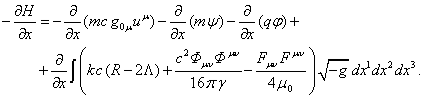
Из (59) следует:
Из последних двух равенств получается:
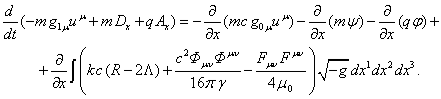(65)
В пространстве Минковского 
, 
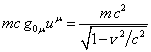. Если рассматривать ситуацию для малой пробной частицы за
пределами массивного заряженного тела и применить
соотношения:
, 
,
, 
,
, 
,
то при постоянной массе 
и заряде частицы, и при
условии, что скорость 
и скалярные
произведения 
и 
прямо не зависят от
координат, уравнение (65) переходит в (22) для компоненты импульса 
.
Четырёхмерная
обобщённая скорость
Введём 4-вектор обобщённой скорости с ковариантным индексом:
.
(66)
где 
– 4-потенциал гравитационного поля,
– 4-потенциал
электромагнитного поля.
Отношение 
в (66) есть отношение
плотностей заряда и массы элемента вещества в системе отсчёта, в которой
вещество покоится. Скаляр 
будет равен:
, (67)
где 
есть 4-вектор
плотности электрического тока.
С учётом этого можно переписать лагранжиан (4) в следующем виде:
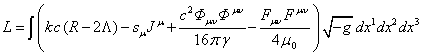, (68)
причём 
есть функция действия,
а 
– инвариантный 4-объём
при условии, что 
. С помощью (11) и последующих соотношений можно записать:
.
Таким образом, инвариантность 4-объёма 
относительно замены
координат выражается в инвариантности интервала 
движущегося элемента
вещества, а также в инвариантности трёхмерного объёма 
элемента вещества в
сопутствующей ему системе отсчёта.
Обозначим 
в (68) и найдём
вариацию 
, связанную с вариацией части функции действия 
:
, 
.
(69)
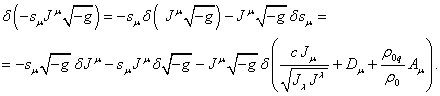(70)
Используем
следующие стандартные формулы:
, 
,
,
(71)
, 
,
где вариации 
, 
, 
взяты из [7], [8],
причём смещения 
представляют собой
вариации координат, вследствие которых возникает вариация массового 4-тока 
, вариация плотности вещества 
и вариация плотности
заряда .
Преобразуем
первый член в (70) с учётом (71):
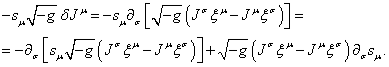
В этом
выражении член с полной дивергенцией при интегрировании по 4-объёму в функции
действия не будет давать никакого вклада. Оставшийся член преобразуется дальше:
,
где величина 
является ротором
4-вектора обобщённой скорости 
.
Преобразуем
выражение в третьем члене в (70):
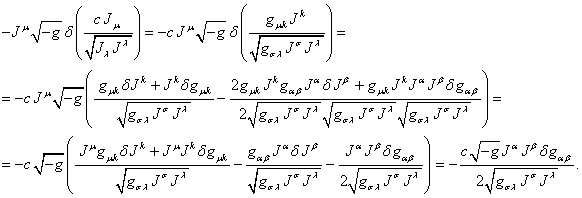
С помощью
(71) найдём вариацию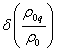 
:
.
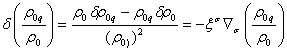Подстановка в
(70) и в (69) полученных выше выражений даёт:
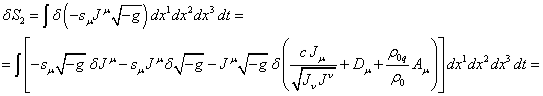
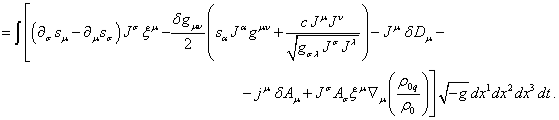
(72)
Обозначим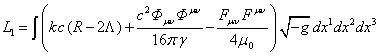 
в (68) и выпишем из
[3] вариацию 
, связанную с вариацией части функции действия 
. Это даёт следующее:
, 
.
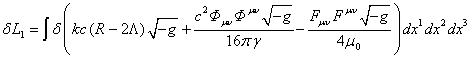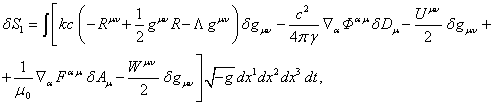(73)
где 
есть тензор энергии-импульса
гравитационного поля (9), а
тензор энергии-импульса электромагнитного поля 
имеет вид:
. (74)
В силу принципа наименьшего действия вариация действия должна быть равна
нулю:
. Подставим сюда (73) и (72), и приравняем к нулю все члены
внутри интегралов, стоящие перед вариациями 
, 
, 
,:
: 
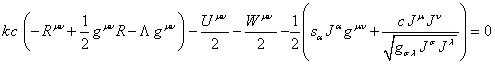, (75)
: 
,
: 
,
(76)
: 
.
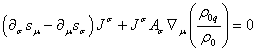(77)
Уравнения (76) эквивалентны уравнениям гравитационного (5) и
электромагнитного (6) полей. Первый член в уравнении (77) можно раскрыть с помощью
оператора производной по собственному времени 
согласно [1], и
определения 4-вектора обобщённой скорости (66):
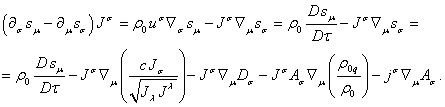
С учётом этого из (77) следует:
. (78)
Поскольку с
учётом (66):
,
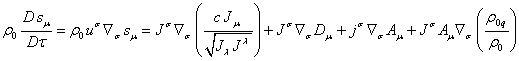то из
сравнения с (78) находим:
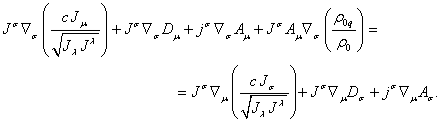(79)
Применим
следующие соотношения:
, 
,
, 
.
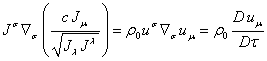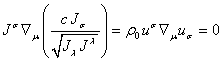Это даёт в
(79):
. (80)
Выше было
принято, что масса и заряд элемента вещества при варьировании не меняется. В
этом случае отношение плотностей будет неизменным,
ковариантная производная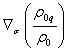 
равна нулю,
и (80)
превращается в уравнение движения вещества в гравитационном и электромагнитном
полях, принятое в ковариантной теории гравитации при данных условиях (смотри
уравнение (35) в [3]).
Рассмотрим
теперь уравнение для метрики (75). Если в нём выделить отдельно члены 
и 
, то при условии 
(75) разделится на два
уравнения:
,
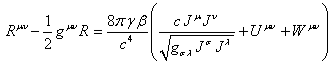(81)
. (82)
С учётом (67)
выражение (82) совпадает с (8). Что касается (81), то из сравнения с (7)
следует, что должно быть:
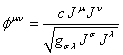. (83)
Соотношение
(82) можно рассматривать как калибровку космологической постоянной, при которой
становится возможным использовать уравнение (81) для нахождения метрики.
Напомним, что
вариации 
, , 
в (70), найденные в
[7], [8], определялись из условия постоянства массы и заряда элемента вещества
при варьировании. Это приводит к уравнению движения типа (80), в котором вместо
предполагаемой полной производной 
(это скорость
изменения 4-тока массы) фигурирует величина 
как произведение
плотности вещества на 4-ускорение.
Гамильтониан
и проблема массы
Гамильтониан
(64) можно представить в другом виде, если использовать обобщённую 4-скорость
(66). Если считать, что 
задаёт в (66)
отношение заряда к массе, и учитывая, что 
, для гамильтониана имеем:
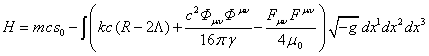. (84)
Отсюда следует,
что вклад в энергию элемента вещества с массой 
делают как временная
компонента 4-вектора обобщённой скорости с ковариантным индексом 
, так и энергии полей, находимые через интеграл по объёму
пространства. Кроме этого, величина энергии корректируется за счёт искривления
пространства-времени (член с кривизной 
) и определяется с точностью до постоянной (член с 
). Гамильтониан 
задаёт энергию таким
образом, что величина энергии в каждой системе отсчёта разная. Это относится и
к величине обобщённой 4-скорости элемента вещества, и к общему импульсу
вещества и поля. Так и должно быть, поскольку в теории относительности лишь
определённая комбинация энергии и импульса может быть инвариантной и
сохраняться в каждой системе отсчёта.
Гамильтониан
(84) выглядит так, что он должен быть временной компонентой некоторого
4-вектора энергии-импульса 
, записанного с нижним
(ковариантным) индексом. В таком случае временная компонента этого 4-вектора связана
с энергией, а пространственная компонента должна быть связана с импульсом
элемента вещества. Сделаем обозначение:
,
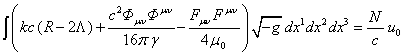(85)
где 
есть некоторый
инвариант, связанный с энергией полей и с поправками к энергии,
возникающими от кривизны 
и от постоянной 
,
– временная компонента
безразмерной 4-скорости 
, при этом 4-скорость является простейшим
4-вектором единичной длины.
При таком
определении интеграл (85) предполагается
равным временной компоненте некоторого 4-вектора. Тогда с учётом (66) имеем:
.
(86)
Выражение
(86) с учётом (85) совпадает с выражением для гамильтониана (34). Запишем
теперь 4-вектор гамильтониана в контравариантном виде:
.
(87)
Поскольку в
(87) присутствует 4-вектор обобщённой скорости 
, то 4-вектор гамильтониана содержит в себе 4-вектор
обобщённого импульса в виде 
. Временная компонента 4-вектора 
должна задавать
релятивистскую энергию 
, а пространственные компоненты – умноженный на скорость
света импульс 
. Это следует из общепринятого выражения 4-вектора
энергии-импульса свободной частицы без учёта действия на неё полей: 
. Этот вектор в плоском пространстве Минковского, то есть в
рамках специальной теории относительности, выражается так: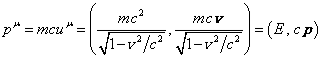 
.
Поля и
взаимодействия с другими частицами могут произвольно изменять величины и , но как только указанная частица снова становится свободной,
из инвариантности массы 
, скорости света и равенства 
следует известная
формула связи между массой, энергией и импульсом для частицы в релятивисткой
физике, справедливая в любой инерциальной системе отсчёта. По этой формуле
можно находить импульс частицы при известной энергии и массе покоя частицы, или
определить массу покоя и тип частицы по её импульсу и энергии.
По аналогии с
4-вектором энергии-импульса 
из компонент 4-вектора
(87) выводим:
. 
,
, 
.
(87’)
Для случая
вещества без прямого его взаимодействия с другим веществом (другими телами),
находящегося только лишь в собственных гравитационном и электромагнитном полях,
энергия и импульс элемента вещества при
постоянной массе и заряде не могут измениться, и должны равняться некоторой
константе для энергии, и постоянному вектору для импульса. Это можно
представить равенством 
, описывающим законы сохранения энергии и импульса замкнутой
системы.
Если в (85)
пренебречь членом с кривизной , определить равной нулю постоянную, необходимую
для калибровки энергии, и возникающую за счёт постоянной , то в пределе слабого поля, при переходе в специальную
теорию относительности, для энергии и импульса из (87’) получается:
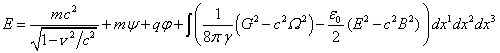. (88)
.
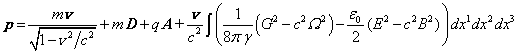Из (88)
видно, что член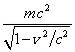 
играет роль
кинетической энергии, а остальные члены относятся к потенциальной энергии.
При этом в
потенциальную энергию включается энергия не только от напряжённостей поля, но и
энергия, связанная со скалярными потенциалами поля.
От элемента
вещества можно перейти к отдельно движущемуся телу, для прямолинейного движения
которого с постоянной скоростью в отсутствие внешних полей справедливы соотношения: 
, 
. В этом случае для импульса имеем:
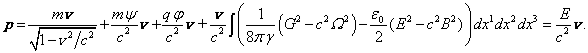
(89)
Здесь под
гравитационным скалярным потенциалом 
и под электромагнитным
скалярным потенциалом 
понимаются усреднённые
потенциалы внутри тела, возникающие от собственных полей. Чтобы найти массу
покоя тела с учётом полей, нужно записать отношение 
при 
. Используем (88) для определения массы покоя через интеграл
по объёму:
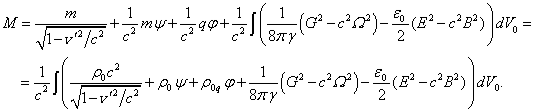
(90)
Масса
покоя 
тела отличается от массы его вещества 
за счёт вклада от энергии полей и энергии
внутреннего движения. Если тело в целом покоится, но его вещество находится в
некотором внутреннем движении со скоростью 
, то это вносит свой вклад в общую массу за
счёт кинетической энергии, а также за счёт возникающего гравитационного поля
кручения 
, и за счёт магнитного поля 
. При определении массы члены с
напряжённостями поля следует интегрировать по объёму как внутри, так и за
пределами тела.
Используем
теперь соотношение (8) и применим его к (90) в случае неподвижного и не
вращающегося твёрдого тела:
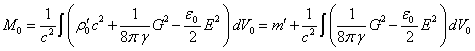, (91)
где 
есть постоянная плотность вещества, связанная с
космологической константой . Плотность получается при
исключении все полей в веществе. Например, если тело разделить на части и
разнести на бесконечность с нулевой скоростью, то поле обычной гравитации и
электромагнитное поле уже не будут делать большого вклада в плотность вещества
частей, а суммарная масса этих частей будет равна 
.
Согласно
(91), масса целого тела становится больше, чем суммарная масса его частей, за
счёт вклада гравитационной энергии с плотностью 
.
Одновременно
электрическая энергия тела уменьшает его массу. Данные выводы согласуются с
результатами, полученными другим путём [3], [4], [9]. В космических телах
гравитационная энергия как правило превышает электромагнитную энергию, поэтому
по мере перехода от малых тел к большим и при скучивании вещества масса тел
должна расти, в том числе и за счёт потенциальной энергии гравитации.
Заметим, что
вместо использования 4-вектора гамильтониана (87) для оценки энергии, импульса
и массы, может быть применён другой подход, основанный на интегрировании по
объёму временных компонент тензоров энергии-импульса вещества 
(83), гравитационного
поля 
(9), а также
электромагнитного поля 
(74). Из свойств левой
части уравнения для метрики (81) следует, что ковариантная производная правой
части равна нулю:
.
(92)
Это
соотношение эквивалентно уравнению
движения вещества в гравитационном и электромагнитном полях (80), в котором
считается, что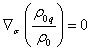 
.
Используем
далее процедуру, применяемую в [5] и во многих других работах по теории
гравитации, позволяющую упростить интегрирование (92) по 4-объёму. Если ввести
систему отсчёта, относительно которой элемент вещества в данный момент времени
движется так же, как он должен двигаться согласно специальной теории
относительности, то в этой системе отсчёта символы Кристоффеля 
и 
в (92) равны нулю.
Тогда ковариантная производная 
от тензора 
становится равной
обычной производной 
, являющейся 4-дивергенцией для тензора 
вследствие
сворачивания по индексу 
. Вместо (92) получается равенство 
, левую часть которого можно проинтегрировать по 4-объёму с
учётом теоремы Гаусса, причём в данном случае 
:
,
где 
означает элемент
некоторой бесконечной гиперповерхности, окружающей 4-объём. Проекция данной
гиперповерхности на гиперплоскость 
даёт элемент
трёхмерного объёма 
, и для 4-вектора энергии-импульса можно записать:
.
(93)
В отличие от
(87), выражение (93) не содержит энергии вещества в собственном поле, то есть
энергии, связанной со скалярными потенциалами и 
. Несмотря на это, для неподвижного однородного шара в
собственном гравитационном поле массы-энергии данного поля согласно (90) и (93)
совпадают. Это вытекает из следующего равенства:
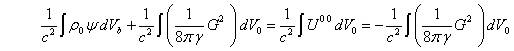, (94)
где 
есть дифференциал
объёма шара, 
– дифференциал объёма
пространства внутри и снаружи шара.
Согласно
(94), потенциальная энергия вещества шара в собственном гравитационном поле,
связанная со скалярным потенциалом, в два раза больше, чем потенциальная
энергия, связанная с напряжённостями поля. Это же справедливо и для
электромагнитного поля, как в случае однородного расположения зарядов в объёме
шара, так и при расположении их только на поверхности. Соотношение (94) по
своему смыслу напоминает теорему вириала для стационарной системы частиц,
связанной собственным гравитационным полем – в такой системе модуль полной
потенциальной энергии приблизительно равен удвоенной кинетической энергии всех
частиц.
Для
релятивисткой энергии вещества из (88) и соответственно из (93) также
получается равенство значений:
, 
.
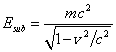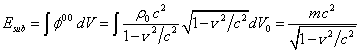Одним из аспектов
применения (93) является несовпадение масс-энергий поля движущегося тела,
находимых либо через напряжённости поля в потенциальной энергии, либо через
поток энергии и импульс поля (так называемая проблема 4/3). Попытка решения
этой проблемы была предпринята нами в [9] на основе учёта вклада массы-энергии
поля в общую массу тела. При этом с учётом (94) получается равенство импульса в
(89) и суммарного импульса вещества и поля, содержащегося в (93) в
пространственных компонентах 4-вектора 
.
Обратим
теперь внимание на соотношение масс элемента вещества, содержащихся в (90) и в
(91), для случая, когда вклад в массу от массы-энергии электромагнитного поля
по сравнению с массой-энергией гравитационного поля невелик. Если учесть (94),
то для масс покоящегося вещества должно выполняться соотношение: 
, где масса 
входит в энергию покоя 
; масса 
определяет общую массу вещества вместе с
полем; масса 
, как это следует из (8), есть масса вещества, рассеянного на
бесконечность, где все поля обнуляются. Какая же из этих масс определяет
собственные потенциалы и напряжённости гравитационного поля рассматриваемого
элемента вещества? По нашему мнению, наблюдаемой массой является масса ,
она должна задавать как инертные, так и гравитационные свойства массы. Эта
масса и должна входить в формулы для потенциала и напряжённости поля, и в
потенциальную энергию. Для однородного неподвижного шара можно тогда записать:
.
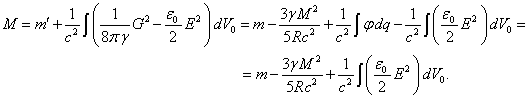
Поскольку
наблюдаемой массой является ,
то из последнего равенства определяется масса 
,
а затем из первого равенства может быть вычислена масса 
. Плотность массы вещества 
через 4-вектор
плотности массового тока 
входит в функцию
Лагранжа (4) для элемента вещества, а также включена в функцию Гамильтона (35).
При интегрировании по трёхмерному объёму члена 
в (35) возникает масса
,
а интегрирование по объёму члена 
приводит к появлению в
результате интегрирования массы 
.
Различие масс
и связано с тем, что при сложении элементов
вещества в единое тело 4-скорость 
полагается неизменной,
тогда как скалярный потенциал сам по себе является
функцией от массы (точнее говоря, при постоянной плотности вещества потенциал внутри тела зависит
от характерного размера тела, или от количества массы). Изменение потенциала при сложении элементов
вещества в единое тело в ходе интегрирования по объёму порождает вместо 
массу 
,
которая и используется для расчёта энергии поля.
Из
изложенного выше обнаруживается различие формы записи и одновременно взаимодополнительность
гамильтонова и лагранжевого подходов при нахождении массы, энергии и импульса
движущегося вещества.
Действие
как функция для определения эффекта замедления времени
С учётом (10)
и (12) запишем дифференциал функции действия для элемента вещества, имеющего
массу вещества и заряд 
:
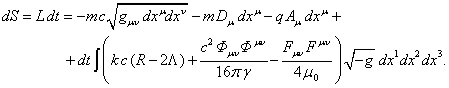(95)
Из (95)
видно, что действие является скалярной величиной. Кроме этого, дифференциал
действия можно разложить по дифференциалам интервала 
, 4-вектора сдвига 
, и координатного (мирового) времени 
, взятых с соответствующими множителями.
Обратимся
теперь к результатам, полученным в книге [1]. Там было показано, что в
выражении 
содержится
специфическая калибровочная функция гравитационного поля, которая равна 
, при условии 
. Аналогичная специфическая
калибровочная функция для электромагнитного поля равна 
. Напомним, что потенциалы фундаментального поля определяются
с точностью до производных по координатам и времени от произвольной
калибровочной функции. Если для гравитационного поля произвести замену
4-потенциалов следующим образом:
, (96)
где вводится
4-вектор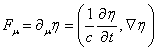 
, то напряжённости гравитационного поля и уравнения движения
вещества в поле не изменятся. Это же справедливо и для электромагнитного поля и
его специфической калибровочной функции 
. Калибровочное преобразование (96) в случае, когда выбрана
специфическая калибровочная функция в виде 
, фактически обнуляет имеющиеся в системе потенциалы
гравитационного поля. Хотя при этом кажется, что в системе ничего не
изменилось, это не так. На самом деле получается, что при сравнении двух
систем, в одной из которых произведено какое-либо калибровочное преобразование
за счёт изменения потенциалов, наблюдается разная скорость течения времени. Для
гравитационного и электромагнитного полей разность показаний часов в
приближении слабого поля описывается формулами:
, 
. (97)
При этом часы 2,
измеряющие время 
, являются контрольными, а часы 1 измеряют время 
и находятся под
воздействием дополнительных 4-потенциалов поля или 
. Временные точки 1 и 2 в пределах интегралов обозначают
начало и конец действия поля. Если есть только статическое гравитационное поле
с нулевым векторным потенциалом, то 
. Полагая тогда, что вначале все часы имели нулевые
показания, для разности показаний часов из (97) получим эффект гравитационного
замедления времени: 
.
От разности времени (97)
можно перейти к сдвигу фаз для однотипных процессов,
находящихся в разных точках поля. Для этого в (97) необходимо в знаменателях
заменить 
на величину
характерного момента импульса. В квантовой механике такой величиной является
постоянная Дирака 
(эта величина равна
постоянной Планка 
, делённой на 
), что позволяет учитывать соответствующий сдвиг фаз, обратно
пропорциональный этой постоянной:
, 
. (98)
Сдвиг фазы в (98),
получающийся за счёт электромагнитного 4-потенциала, подтверждается эффектом Ааронова-Бома.
Если разделить первую
часть в (95) на и взять интеграл,
то можно получить стандартный эффект замедления времени за счёт движения часов
со скоростью 
:
, (99)
здесь скорость 
часов измеряется
местным наблюдателем, находящимся в точке с временной компонентой метрики 
; движущиеся часы отмеряют время 
, а неподвижные часы – время 
местного наблюдателя,
выраженное через координатное время 
.
В (95) имеется ещё один,
последний член в виде интеграла, который по нашему мнению также должен влиять
на эффект замедления времени. Любое калибровочное преобразование 4-потенциалов
не затрагивает величину напряжённости полей, входящих в тензоры 
и 
. Энергия полей, связанных с элементом вещества с массой 
, зависит не только от абсолютной величины 4-потенциалов, но
и от скоростей их изменения в пространстве-времени, то есть от напряжённостей
полей. Каждая дополнительная энергия должна влиять на внутренние свойства
вещества, в том числе и на скорость течения собственного времени. Отсюда мы
выводим:
.
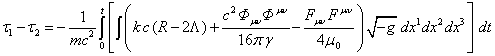Из изложенного следует,
что функция действия есть не только функция, с помощью которой из принципа
наименьшего действия находятся уравнения движения, через преобразования
Лежандра определяется гамильтониан, или составляется уравнение
Гамильтона-Якоби. Функция действия имеет и непосредственный физический смысл
как функция, описывающая изменение некоторых внутренних свойств физических тел.
К таким внутренним свойствам можно отнести скорость течения собственного времени,
и соответственно скорость нарастания
фазового угла периодических процессов в зависимости от времени.
Выделенность времени по отношению к пространственным размерам как характерное
свойство физических тел связано здесь с тем, что сдвиг времени при движении и в
фундаментальных полях является абсолютным эффектом, тогда как изменение
наблюдаемых размеров имеет только относительный характер.
Заключение
Исходя из принципа наименьшего действия и уравнений Эйлера-Лагранжа,
мы представили в (17) релятивистское уравнение движения элемента вещества в
фундаментальных полях (для движения вдоль оси 
декартовой системы отсчёта).
Это уравнение записано для случая, когда скорость зависит только от времени, и
может быть уточнено для общего случая путём введения в уравнение зависимости
скорости от пространственных координат. После определения обобщённого импульса
для вещества и поля получается векторное уравнение (19), выражающее зависимость
обобщённой силы от различных физических переменных для вещества в поле.
Различие позиций ковариантной теории гравитации (КТГ) и общей
теории относительности (ОТО) при описании движения малой пробной частицы во внешнем поле демонстрируется в
уравнениях (21) и (23). В слабых полях уравнение КТГ (21) точно переходит в
лоренц-ковариантное уравнение движения (22), используемое в специальной теории
относительности. В отличие от этого, для появления гравитационной силы в ОТО требуется не только приближение слабого поля, но и
предварительное вычисление градиентов метрического тензора. Так получается
потому, что в ОТО потенциалы гравитационного поля связаны с компонентами
метрического тензора и не являются самостоятельными величинами. Заметим также,
что в противоположность КТГ, в ОТО отсутствует однозначный предельный переход в
специальную теорию относительности, то есть в случай слабых полей, основанный
на принципе соответствия и законах сохранения физических величин типа энергии,
импульса и момента импульса [10].
Функция Гамильтона, выраженная через 4-скорость и
характеризующая энергию частицы (элемента вещества) массы 
, даётся соотношением (34). Для непрерывно распределённого
вещества функция Гамильтона определяется интегралом по 4-объёму в соотношении
(35). После упрощения этих выражений получается формула (36) для релятивистской
энергии частицы с учётом энергии полей в рамках специальной теории
относительности. Выражение для функции Гамильтона через обобщённые импульсы
приведено в (57), при этом соотношение (57’) задаёт
энергию частицы для плоского пространства Минковского.
В соотношении (66) мы ввели в теорию 4-вектор обобщённой скорости 
и записали с его
помощью лагранжиан (68). После применения принципа наименьшего действия к данному
лагранжиану получаются уравнения для гравитационного и электромагнитного полей
(76), уравнение движения вещества (80), а также уравнение для метрики (81) и
соотношение для космологической постоянной (82). Кроме этого, временная
компонента 4-вектора непосредственно входит
в гамильтониан (84), а произведение массы частицы на контравариантный 4-вектор 
задаёт 4-вектор
обобщённого импульса в виде . В результате гамильтониан
(84) оказывается временной компонентой некоторого 4-вектора с ковариантным
индексом 
, связанного с энергией и импульсом. Мы обозначили его как 4-вектор гамильтониана (4-энергия), в
контравариантном виде он определяется в (87) и согласно (87’) задаёт энергию и
импульс частицы через массу, заряд, 4-скорость, 4-потенциалы и напряжённости
полей. Альтернативное выражение энергии и импульса частицы через тензоры
энергии-импульса вещества и полей даётся в (93) в виде 4-вектора
энергии-импульса.
Масса частицы может быть определена из (87’), если вычислить
энергию в пределе нулевой
скорости движения и разделить эту энергию на квадрат скорости света. В
приближении слабого поля для массы неподвижного тела справедлива формула (90).
Из (91) – (94) следует соотношение для трёх масс, связанных с телом: 
, где масса 
входит в энергию покоя
; масса 
определяет
релятивистскую массу вещества тела вместе с собственными полями как меру
инерции и гравитационную массу; масса 
есть масса вещества,
рассеянного на бесконечность, где все поля обнуляются. При этом видно, что
выполняется соотношение: 
.
Из анализа дифференциала функции действия (95)
мы находим изменение скорости течения времени (97) в физических объектах за счёт
действия потенциалов гравитационных и электромагнитных полей. Для квантовых
объектов соответствующий сдвиг фазы выражается соотношениями (98). Движение
часов изменяет ход их времени согласно (99). В функцию действия входят также
напряжённости полей (через тензоры 
и 
), и мы считаем, что они, как и
каждая компонента функции действия, должны приводить к некоторому изменению
хода часов и фазы процессов. Вероятно, эта идея может быть подтверждена
экспериментально при измерении сдвига квантовомеханической фазы под действием
напряжённостей полей в тех случаях, когда напряжённости поля более изменяют
энергию самого поля, чем влияют на движение частиц.
Список использованных источников
1.
Федосин С.Г. Физические теории и бесконечная вложенность
материи. Пермь, 2009, 842 стр., Табл. 21, Ил.41, Библ. 289
назв. ISBN 978-5-9901951-1-0.
2. Федосин
С.Г. Физика
и философия подобия от преонов до метагалактик.
Пермь, Стиль-МГ, 1999, 544 стр., Табл.66, Ил.93, Библ. 377 назв. ISBN
5-8131-0012-1.
3.
Fedosin S.G.
The Principle
of Least Action in Covariant Theory of Gravitation. Hadronic Journal, February 2012, Vol. 35, No. 1, P. 35–70.
4.
Fedosin S.G. The Principle of Proportionality of Mass
and Energy: New Version. Caspian
Journal of Applied Sciences Research, 2012, Vol. 1, No. 13, P. 1–15.
5. Ландау Л. Д., Лифшиц Е. М. Теория поля. – Издание 7-е,
исправленное. – М.: Наука, 1988. – 512 с. – («Теоретическая физика», том II).
6. Fedosin S.G. Model of Gravitational Interaction in the Concept of
Gravitons. Journal of
Vectorial Relativity, Vol. 4, No. 1, March 2009, P.1–24.
7.
Дирак П. А. М. Общая теория относительности: Пер. с англ./ Под.
ред. Д. И. Блохинцева. – Пер. изд.: США, 1975. – М.: Атомиздат, 1978. – 64 с.
8.
Фок
В.А. Теория пространства, времени и гравитации. 2-е издание. – М.: Физматгиз, 1961. –568 с.
9. Fedosin S.G.
Energy,
Momentum, Mass and Velocity of a Moving Body.
vixra.org, 12 июня 2011.
10. Gorelik, Gennady. The Problem of Conservation
Laws and the Poincaré Quasigroup in General Relativity. In: Einstein studies in
Russia. Yuri Balashov, Vladimir Vizgin (eds.). Einstein Studies, Vol. 10.
Boston: Birkhäuser, ISBN 0-8176-4263-3, 2002, P. 17–43.
Источник:
http://sergf.ru/gam.htm