Advances in
Natural Science, Vol. 5, No. 4, pp. 55-75 (2012) . http://dx.doi.org/10.3968%2Fj.ans.1715787020120504.2023
The
Hamiltonian in covariant theory of gravitation
Sergey G. Fedosin
Perm, Perm Region, Russia
e-mail intelli@list.ru
In the framework of covariant theory of gravitation
the Euler-Lagrange equations are written and equations of motion are determined
by using the Lagrange function, in the
case of small test particle and in the case of continuously distributed matter.
From the Lagrangian transition to the Hamiltonian was done, which is expressed
through three-dimensional generalized momentum in explicit form, and also is
defined by the 4-velocity, scalar potentials and strengths of gravitational and
electromagnetic fields, taking into account the metric. The definition of
generalized 4-velocity, and the description of its application to the principle
of least action and to Hamiltonian is done. The existence of a 4-vector of the
Hamiltonian is assumed and the problem of mass is investigated. To characterize
the properties of mass we introduce three different masses, one of which is
connected with the rest energy, another is the observed mass, and the third
mass is determined without taking into account the energy of macroscopic fields.
It is shown that the action function has the physical meaning of the function
describing the change of such intrinsic properties as the rate of proper time
and rate of rise of phase angle in periodic processes.
Keywords: Euler-Lagrange equations; Lagrangian; Hamiltonian;
generalized momentum; generalized 4-velocity; equations of motion.
PACS: 03.30.+p, 04.20.Fy, 04.40.-b, 11.10.Ef
Introduction
There are
several approaches to describing and constructing any physical theory. In the
simplest case, the content of the theory is reduced to several physical laws
and principles that conform to the experimental data. By analyzing and
simplifying them, the system of axioms can be found, based on which the whole
theory can be derived by axiomatic method, as a logical consequence of the
initial simple assumptions. In the energy approach it is sufficient to know
only one function with the dimension of energy, in order to find all the
equations of the theory with the help of it. The examples of such functions are
Lagrangian and Hamiltonian.
The covariant
theory of gravitation (CTG) appeared in 2009 [1], as a consequence
of the relativistic generalization of the Lorentz-invariant theory of
gravitation (LITG). LITG equations are similar by their form to Maxwell's equations
and can be derived on the basis of axioms [2]. Recently derivation
of CTG equations was made based on the principle of least action [3].
Based on the resulting form of the Lagrangian now it is possible to make the
next step and go to the Hamiltonian corresponding to the CTG theory.
After a brief
presentation of the Euler-Lagrange equations we use them to describe the motion
of a small test particle, as well as in the case of continuously distributed
matter. Then we find the Hamiltonian in its two forms, with the help of
4-velocity and the generalized momentum, and substitute the Hamiltonian into
Hamilton equations to verify the motion equations. At the end of this paper we
introduce for consideration the four-dimensional generalized velocity to simplify
the expressions for the Lagrangian and Hamiltonian. The transition was done
from the 4-vector of the generalized velocity to a new 4-vector of the
Hamiltonian, specifying the energy and the momentum of substance in fundamental
fields. The comparison with the Lagrangian approach is made, in which the
energy and the momentum are calculated through energy-momentum tensors. The
problem of mass is analyzed with the help of formulas for the energy. In the
last part, we describe the action function as a function having an independent
meaning in physics – it can help to determine the effects of time dilation,
arising from the change of velocity of bodies’ motion or under the influence of
fields.
The principle of least action
In this section
we shall write down known relations for the Lagrange function and the principle
of least action for the covariant theory of gravitation (CTG). According to the
latter, the equations of motion of substance and fields can be found by varying
the action function 
. In
the coordinates 
the Lagrangian depends on the coordinates 
, on the
4-velocity of substance motion 
(where 
– the speed of light, 
indicates the interval for the moving
substance unit), on 4-potential 
of gravitational field and 4-potential 
of electromagnetic field and on metric tensor 
of the reference frame. If to move on from and 
to the three-dimensional coordinates, time and
velocity, then the Lagrangian function with these variables can be written in
the form:
. Here the
quantities 
, 
, 
are the components of 3-vector of coordinate
velocity 
. When
moving along a certain trajectory the current coordinates 
of a substance unit, and its velocities 
are functions of coordinate time 
. In general
4-potentials and , which act
on the substance, and the metric tensor depend on the coordinates and
time. If we take the coordinates of the substance along the trajectory as a
function of time, then , and at the trajectory can be considered as
functions of time too. This allows us to consider the Lagrange function as a
function of time, and the integral 
between the spacetime points 1 and 2 – as a
number. Theoretically, under variations of the coordinates we can understand
small in magnitude functions of time, due to adding of which the shape of
trajectory of the substance motion change, and respectively, change the value
of the action function. From the principle of least action it follows, that the
action 
on the true trajectory has to be extreme
(usually has a minimum).
Variation of
the action function along the trajectory, when all the variables are varying
except the time, gives the following:
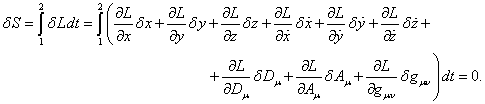
The term with
the variation of the velocity 
can be integrated by parts:
.
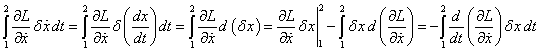It was
considered that the variation 
at the initial time point 1 and in the final
time point 2 is zero according to the condition of varying trajectory.
Integrating by parts also for terms with 
and 
, for the
variation of the action we obtain:
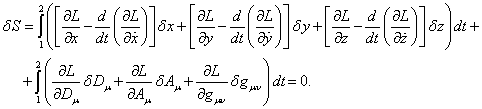(1)
Variations , 
, 
, 
, 
and 
in (1) are independent from each other and are
not equal to zero on the true path, except for the initial and final points of
the trajectory. From this we obtain the following Euler-Lagrange equations:
, 
, 
. (2)
, 
, 
. (3)
We shall remind
that the principle of least action is usually applied to conservative systems
for which precise potential functions are given, from which acting forces can
be found. We shall consider physical systems with substance and the fundamental
fields, which include the gravitational and electromagnetic fields. These
systems are conservative, and for them the law of conservation of
energy-momentum can be found, which has the same form in all frames of
reference. If the reference frame is fixed and is not accelerated, the total
energy and total momentum remain separately for each moment of time, with the
possible exchange of energy and momentum between substance and field.
Lagrange function and equations of motion
In the case of
continuously distributed substance throughout the entire volume of space in the
gravitational and electromagnetic fields, we shall use the Lagrangian function 
,
which in the covariant theory of gravitation (CTG) has the form [3]:
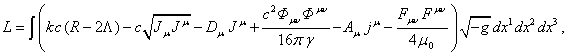
(4)
where 
– proportionality factor,
– low coefficient of order of unity that
depends on the properties of the reference frame,
– gravitational constant,
– speed of light, as the measure of velocity
of electromagnetic and gravitational interactions propagation,
– scalar curvature,
– constant for the system (in the case when
(4) is applied to cosmology, the constant 
is called the cosmological constant),
– 4-potential of gravitational field which is
described through scalar potential 
and vector potential 
of this field,
– 4-vector of mass current density,
– density of substance mass in reference frame
in which the substance is at rest,
– 4-velocity of the substance unit,
– gravitational tensor (gravitational field
strength tensor),
– definition of the gravitational tensor with
contravariant indices by means of the metric tensor 
,
– 4-potential of electromagnetic field, set by
scalar potential 
and vector potential 
of the field,
– 4-vector of electric current density,
– charge density of substance in reference
frame in which the charge is at rest,
– vacuum permeability,
– electromagnetic tensor (electromagnetic
field strength tensor),
– the square root of determinant 
of metric tensor, taken with the negative
sign,
– product of differentials of spatial
coordinates, which can be viewed as a spatial coordinate volume of the moving
substance unit in the used reference frame.
Further we
shall use international system of units, basic coordinates in the form of
coordinates with contravariant indices 
,
metric signature (+, –, –, –), metric tensor 
. The
presence of repeated indices in formulas implies Einstein summation convention,
which is a separate summation for each repeated index. The symbol 
denotes covariant derivative with respect to coordinates (in this case the
coordinates 
).
Similarly, 
is an operator of partial derivative with respect to coordinates, or 4-gradient.
We can assume
that the quantities 
, 
, 
, 
, , 
, 
in the location of the substance unit are
functions of its coordinates 
, as well as
the functions of the coordinates and velocities of other substance units.
However, the specified quantities in the first approximation are independent
from the 4-velocity of the substance unit. This is possible if the substance
unit is so small that the propagation delay of its own field within the volume
of the substance unit can be neglected even at relativistic speeds. The
smallness of the volume, mass and charge of the substance unit leads to the
fact that the motion of this substance unit is determined only by the gradients
of the external fields (in the form of superposition of fields from all the
external substance units), and the substance unit itself does not contribute to
the average gradient of the field inside the unit. With these assumptions in
(4) only 4-velosity 
, as a part
of 
and 
, will
depend on the 3-velocity of the substance unit.
If we consider
that the tensor of gravitational field depends on the 4-potential under the definition 
, then the
relation of (3) for the Lagrangian (4) provides:
, or 
. (5)
Similarly, we
obtain for the relation in (3):
, or
, (6)
The relations
(5) and (6) set the equations of gravitational and electromagnetic fields,
respectively, carrying out the connection between the 4-potentials of fields
and the sources of fields in the form of 4-currents of mass and charge. According
to (5) and (6), the larger 4-currents are, the higher are the covariant
derivatives of the variables 
and 
( and are 4-rotors of the 4-potentials of field).
As was shown in
[3], the relation in (3) leads to the following:
(7)
provided that:
. (8)
In the equation
for the metric (7) the quantity 
is Ricci tensor, so that the left side of (7)
gives the Hilbert-Einstein tensor. The right side of (7) contains the
stress-energy tensor of substance 
, the
stress-energy tensor of gravitational field 
, as well as
the stress-energy tensor of electromagnetic field 
. The tensor
is expressed through the tensor of
gravitational field by the formula:
. (9)
Equation (8)
states that there is a connection between the cosmological constant 
and energy density 
of the system’s substance when the substance
is dispersed to infinity and there it is still. In this case, the 4-potentials and in (8) are equal to zero. As a result of
further interaction the substance merges into a smaller size system, and the
substance density varies from 
to , and there is the potential energy of
interaction between the substance and the field due to the 4-potentials of the
field.
In the
interpretation of the constant two approaches are possible. In the first, the
difference between and arises only from the macroscopic gravitational
and electromagnetic fields. In the second case we can assume that to the
4-potentials of fields and the strong gravitation and electromagnetic
fields make contribution which act at the level of elementary particles and
alter the mass of the particles [2]. In this case, the density should be composed of a certain density 
and of additives from the macroscopic and
microscopic fields, and the mass of bodies is described as a characteristic
that defines the interaction of substance with field quanta – gravitons and
electromagnetic quanta, acting at all levels of matter [4]. It
should be noted that since the 4-potentials and of fields are defined up to gauge
transformation, the cosmological constant will be determined with the same precision.
Now we shall
turn to the relations (2). We shall preselect in the Lagrangian (4) only those
terms which directly depend on the coordinates and the velocities, and
substitute the relations 
and :
, (10)
.
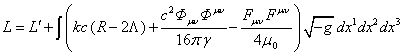We shall
integrate (10) for the three-dimensional volume, assuming that 
, taking
into account the following relations [5]:
, 
, 
, (11)
where 
– determinant of the metric tensor ,
– differential of the proper time at the point
of reference frame, through which the substance unit passes,
– differential of the coordinate time of the
used reference frame,
– determinant of the three-dimensional metric
tensor 
, with
components 
, 
, 
.
The invariant
of three-dimensional volume is the product 
, and
the factor 
provides transition from a moving coordinate
volume 
to moving local volume in terms of the local
observer at the point in space, through which at the moment 
of its proper (local) time the substance unit
passes. This gives in (10): 
, where 
is the differential of the moving local
volume. For the moving substance unit 4-velocity equals to 
, as well
as:
,
,
where 
is the differential of volume of substance
unit in the co-moving reference frame, 
– an invariant of moving 4-volume, provided .
This implies
the expression for the mass density 
and charge density 
of the moving substance:
, 
,
where 
denotes the interval for the moving substance
unit, and 
is an interval for a stationary observer, by
which the substance passes.
With the
formulas for 
and 
, 
in (10) will equal to:
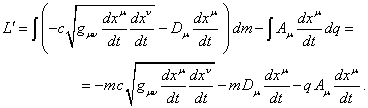(12)
In (12) 
and 
are the mass and the charge of a small
substance unit, moving as a whole with the coordinate velocity 
, and this
velocity is not a 4-vector. 4-potentials and in the result of integrating by volume are
considered to be effective averaged by volume potentials acting on the
substance unit. In the coordinates 
the quantity 
, hence the
product is 
. Similarly
for the electromagnetic potential is: 
.
We shall note
that the coordinate velocity 
is different from the velocity of the
substance unit, which is measured by the local observer. This is due to the
fact that the local observer's proper time does not coincide with the coordinate time 
(the coordinate time is common for the reference frame as a whole,
and the proper time is measured by stationary electromagnetic
clocks in each specific point of reference frame, or by the clock associated
with the moving substance, and depends on the actions on the clocks of existing
gravitational and electromagnetic fields at the time of measurement).
Three-dimensional
vector potential of gravitational field has its components along the spatial
axes of the coordinate system: 
, as well
for the vector potential of electromagnetic field it can be written down: 
.
Taking it into
account for (12) we have:
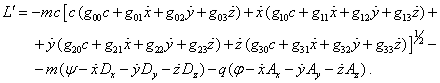(13)
In the simplest
case, we can assume that for an arbitrary reference frame the velocities 
do not depend explicitly on the coordinates 
, and are
time-dependent; the mass and the charge can be dependent on 
and independent on ; the scalar
potentials 
and 
, the vector
potentials 
and , the metric
tensor do not depend directly on , but depend
on . The
assumption of independence in an explicit form on the coordinates means that the velocity field is free, and not
the bound vector field. An example of the bound field is the velocity field in
the liquid flowing in the volume bounded by a surface. Due to the interaction
of the liquid with the surface and the liquid particles with each other there
is a clear dependence of the velocity field on the coordinates. If we consider
quasi-free motion of continuously distributed substance with weak gravitational
and electromagnetic fields, the velocity will depend weakly on the spatial
coordinates.
Under these
conditions from (12) and (13) we find:
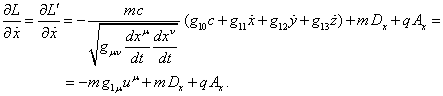(14)
In (14) it was
taken into account that 
, where
is the interval, and the relation 
was used. We shall note that from the
definition of 4-velocity and of the interval 
follows the standard relation 
.
The full time
derivative of (14) gives:
. (15)
The first
spatial component of the gradient from will be equal to:
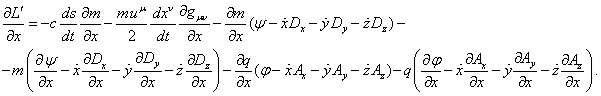
In view of (10)
we have:
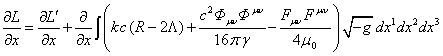. (16)
The
Euler-Lagrange equation 
from (2) requires that the equations (15) and
(16) should be equal to each other:
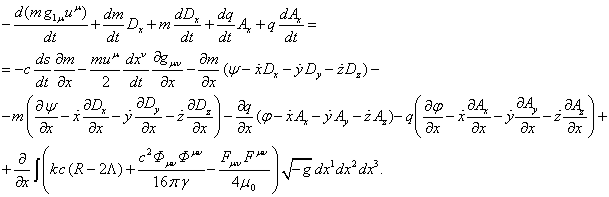(17)
With the help
of 3-vector 
we shall introduce the 3-vector of generalized
momentum with the following components:
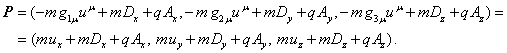(18)
In view of (18)
instead of (17) it can be written in the 3-vector form:
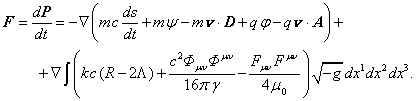(19)
According to
(19) for continuously distributed matter the rate of change of the generalized
momentum of substance and the field is determined by gradients from the
following quantities: the energy of the substance unit in gravitational and
electromagnetic fields that can be found through the velocity 
and the scalar and vector potentials; the
integral by volume of the term with scalar spacetime curvature; the integral by
volume of energy invariants of the gravitational and electromagnetic fields,
which are in the volume of the substance unit, as well as those of their proper
fields, which are generated by this substance and interact with it. Generalized
force 
in (19) also depends on the constant and the term 
associated with the relativistic energy of the
mass .
We shall remind
that deriving (17) and (19), we assumed that the velocity of the substance does
not depend on spatial coordinates. In this regard, in (17) and (19) there are
no gradients of the velocity components that appear in the case of the velocity
field in some way connected with the points in space.
The case of a small test particle outside a
massive charged body
The equation of
motion (17) can be simplified by using the operator equality: 
.
This gives the following:
, 
,
, 
.
Next, we shall
introduce the vector of gravitational acceleration strength 
and the vector of torsion field strength 
(gravitomagnetic field) according to the
formulas:
, 
.
It is seen that
these definitions of and are written in generally covariant form, since
these quantities with accuracy up to a constant factor, constitute the
components of the gravitational tensor 
. Similarly
the strength of the electric field 
and the induction of the magnetic field 
are defined:
, 
.
As far as 
, 
, then using the previous equations for (17) we
find:
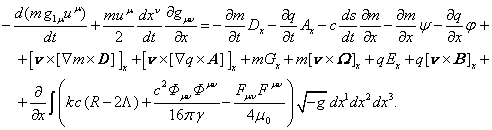(20)
Equation (20)
is the equation of motion of the substance unit in the direction of the first
spatial axis of the reference system, and it corresponds to the equation in (2). For other spatial axes the equations
of motion will differ only by replacing the indices in the derivatives and the
components of vectors. If we enter the 3-vector , then
instead of (20) we can write the equation of motion in 3-vector form:
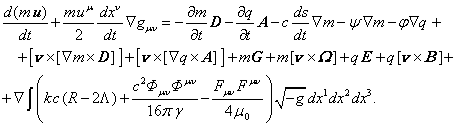(21)
3-vector 
in the left side of (21) is equivalent in its
meaning to action of Christoffel symbols, which are used to write the equations
of motion in Riemannian space in four-dimensional notation, both in the general
theory of relativity and in the covariant theory of gravitation.
Since we
consider a small test particle outside a massive charged body, then the
contribution to the curvature and the constant is made only by the test particle itself. The
terms 
and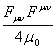 
in (21) are associated with the energy density
of gravitational and electromagnetic fields, respectively.
If the test
particle is small enough and has low density of mass and charge, then the main
contribution to the energy density of the fields in the volume of the particle
will be made by the external fields of the massive charged body. In addition,
in (21) the gradient of the integral over the volume is taken, which in some
cases can be close to zero due to symmetry and homogeneity of the distribution
of field energy within the test particle. One of such cases is the approximate
spatial homogeneity of the external field.
In Minkowski
space we have: 
, 
.
If we also
assume the constancy of the mass and charge with the time, zero gradients of
the mass, charge, curvature and zero gradients in the distribution of field
energy within the volume of the particle, then (21) takes the form of the
equations of motion of the test particle in gravitational and electromagnetic fields
in Lorentz-invariant theory of gravitation [2]:
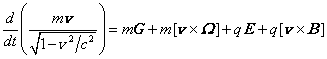. (22)
The left side
of (22) is the rate of change with the time of the relativistic particle
momentum, while in the right side there is the two-component gravitational
force and similar to it the two-component electromagnetic Lorentz force. Thus,
from the variation of action (1) with the Lagrangian (4) in the framework of
the covariant theory of gravitation (CTG), we can obtain the equation of motion
of a particle (22), which is valid in the special theory of relativity (SRT).
This means that the equations of CTG and SRT are linked by the correspondence principle,
when after the aspiration of the curvature of spacetime to zero the equations
of CTG turn into the equations of special relativity.
In contrast,
the equations of general relativity do not have such a direct transition to the
equations of special relativity. Indeed, in general relativity Lagrangian
differs from (4) by the absence of gravitational terms of the form:
. As
a result, in (21) there are no gravitational terms, only the following remains:
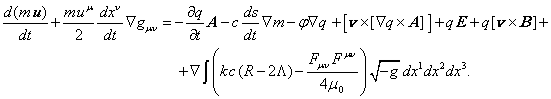(23)
In order that
gravitation could appear in general relativity as an effective force of
gravitation in the weak field limit, in (23) the decomposition of should be carried out, and the appearing terms
should be transferred to the right side are considered as a gravitational
force. The difference between the positions of the general relativity and CTG
is due to the fact that in general relativity gravitation is simply the
curvature of spacetime (without specifying the reasons for this curvature), and
in CTG gravitation is a real physical force which is substantiated by the
mechanism of Le Sage gravitation [6]. In this case the scalar
potential 
of the gravitational field in
CTG is the characteristic of scalar field associated with the flow of
gravitons, and is proportional to the difference between the energy density of
the graviton flux at the point where the potential is determined, and the energy
density of the graviton flux at infinity. The gradients of the energy density
of graviton flux in this case can be considered as gravitational field
strengths. In the assumption that some gravitons are tiny charged particles, in
[1] the scheme of appearance the electromagnetic force and the
electric potential is derived. If scalar potentials are known in
a fixed frame of reference, then after conversion into a moving frame of
reference vector potentials of gravitational 
and electromagnetic 
of fields appear, as a consequence of field
retardation effects due to the limited speed of their propagation. Thus we can
understand why the fields are described by 4-potentials 
and 
.
The relation between the Lagrange and
Hamilton functions
Describing the
principle of least action, we recorded the Lagrange function in the general
form: 
,
where the quantities 
, 
, 
are the components of 3-vector of coordinate
velocity 
of the substance unit motion. Variation of the
action function leads to the Euler-Lagrange equations (2) and (3) and requires
variation of the Lagrangian, which has the form:
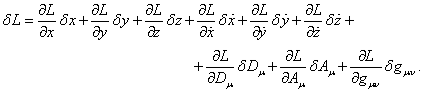(24)
We shall
introduce the Hamiltonian 
,
where the quantities 
are the components of the 3-vector of the
so-called conjugate generalized momentum 
(conjugate with respect to the coordinates 
). The
Hamiltonian in the simplest case is determined by the Legendre transformation
through the components of the conjugate momentum, the velocity components of
the substance unit and the Lagrange function:
.
(25)
With the
vanishing of the variation in time, as it is required for the Lagrange function
in the principle of least action, for the variation of the Hamiltonian we have:
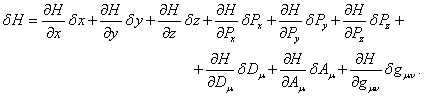(26)
The result of
the variation (25) is:
. (27)
Substituting
(24) and (26) in (27) gives the following relations:
, 
, 
, (28)
, 
, 
, (29)
, 
, 
, 
, 
, 
. (30)
After
determining 
through 
in accordance with (30), and substituting in
(2), taking into account (28) we have: 
. In
general, we can write down:
.
(31)
We shall find
the components of the generalized momentum from (30), given that the velocity
components are directly included in the Lagrangian (4)
according to (12) and (13) only in three terms, forming part of the Lagrangian 
. From (14)
and analogous relations with the help of (30) can be obtained for the generalized
momentum the same as in (18):
, 
, (32)
, 
.
The scalar
product of the generalized momentum 
and the velocity 
, taking
into account the relation 
, gives:
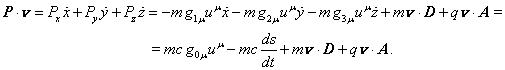(33)
Substituting
this expression into (25) in view of (4), (10), (12), (13) allows us to find
the Hamiltonian for the solid-state motion of the substance unit with the mass 
and the charge 
:
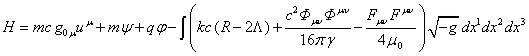. (34)
In mechanics
the Hamiltonian is usually associated with the energy of a body (a substance
unit). The first term in (34) is connected with the rest energy and kinetic
energy of substance. Products 
and 
give the potential energy of mass and charge
in the gravitational and electromagnetic fields associated with scalar
potentials. The volume integral in (34) defines the additional energies,
depending on the curvature of spacetime 
, the
constant 
, and the
field strengths. If the volume of the test particle is small, the volume
integral in (34) can be neglected compared to the first three terms. In this
case the energy of the test particle includes the relativistic energy of motion
and energy of the particle in field potentials.
If we consider
the formulas for 
and 
, given
before the relation (12), then the mass and the charge can be expressed in
terms of the volume integral of the density of mass and charge:
, 
,
where 
– the substance density in the reference frame
at rest relative to the substance unit;
– the interval;
– the charge density in the reference frame at
rest relative to the substance unit.
In view of this
the Hamiltonian for a continuously distributed matter would have the following
form:
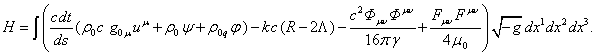
(35)
In Minkowski
space we have the following relations:
, 
,
,
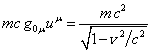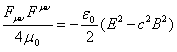where 
– the gravitational acceleration, 
– the vector of gravitational torsion field, 
– the electric field strength, 
– the magnetic induction, 
– the vacuum permittivity.
Substituting
these relations into (34) for the case of a small test particle, when one can
neglect the term with the scalar curvature 
:
.
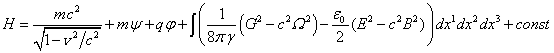(36)
For external
fields it is necessary in (36) to integrate over the volume of the particle,
and for the fields generated by the substance of the particle, it is necessary
to integrate over the volume both inside and outside the particle. The
Hamiltonian (36) as the energy of a small test particle is determined up to a
constant, which arises from integration over the volume of constant (for the meaning of this constant see our
discussion after relation (9)). In the Minkowski space metric does not depend
on the coordinates and time, and therefore the term with the constant 
in variation of Lagrangian disappears and does
not contribute to the equations of motion. However, due to the definition of
the Hamiltonian (25), where the Lagrange function 
is included as a whole, the constant appears in (36) as additional constant.
The expression of the Hamiltonian through the
generalized momentum
In (34) and
(35) the Hamiltonian is expressed through the 4-velocity 
,
depending on the 3-vector of velocity 
. However,
in the canonical form the Hamiltonian is defined by the components of
generalized momentum: 
. We express
the components of the 3-velocity through components of the generalized momentum
, for which,
taking into account the expressions 
, we rewrite
(32) in another form:
. (37)
. (38)
. (39)
In view of
(32), we introduce the following notation:
, 
,
,
(40)
as components
of a 3-vector, normalized to unit mass.
We also need
the following minors:
– minors of the matrix of the components of
the metric tensor 
, where 
;
– minors of the spatial submatrix of the
components of the metric tensor 
, where 
. As the
examples of such minors, taking into account the symmetry of the metric tensor we can write down:
, (41)
,
,
, 
, 
.
We shall also
use the following relations:
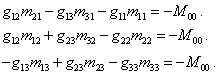(42)
, 
,
, 
,
, 
.
With these
notations from (37), (38) and (39) we have:
. (43)
. (44)
. (45)
Dividing (44)
and (45) by (43), 
and 
can be expressed by 
:
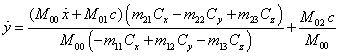. (46)
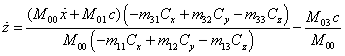. (47)
From (43) we
find:
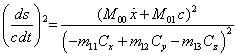. (48)
On the other
hand, 
, and
for the square of the interval 
. In view of
this, we have:
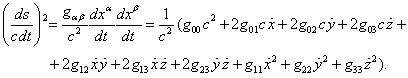(49)
From equations
(48) and (49) it follows:
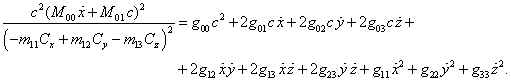(50)
If we
substitute 
and 
from (46) and (47) in (50), we obtain a
quadratic equation for the velocity component 
. However,
this equation is too cumbersome to write. Equation (50) can be simplified by
introducing a new variable:
, 
. (51)
Using in (50)
relations (46), (47) and (51), after lengthy calculations we find:
.
(52)
where is the determinant of the metric tensor , and 
is negative:
,
and the
following abbreviation is used:
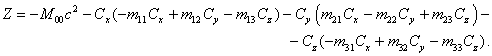(53)
From (52) and
(51) we find , and
then from (46) and (47) define 
and :
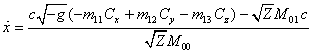, (54)
,
.
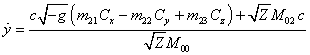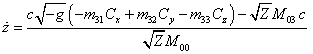From (54) and
(43) we derive the quantity 
:
.
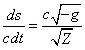(55)
We can
calculate 
using (54), (55) and the expression 
:
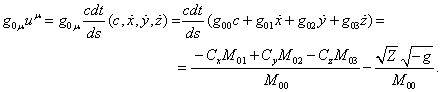(56)
In (56) using
the previously introduced in (40) notations 
, 
, 
, we can move from 
, 
and 
to the generalized momenta 
, 
and 
. After multiplying (56) by 
the result will be
equal to:
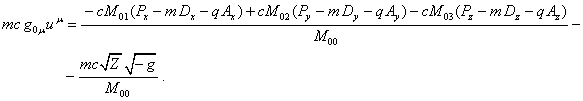
Let us
substitute this into the formula for the Hamiltonian (34):
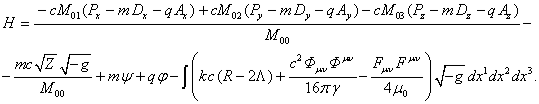
(57)
In Minkowski
space, i.e. in the special theory of relativity when the curvature of spacetime
is absent,
, 
, 
, and taking
into account the expressions (53) for 
and (40) for , and , the Hamiltonian will be expressed through the
3-vector of the generalized momentum 
, through
the scalar potentials 
, 
, and vector potentials 
, 
:
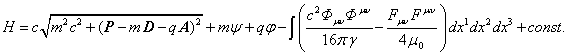
(57’)
Similarly to
(36) in the expression for the Hamiltonian (57’) there is some constant. In
this case the gravitational tensor 
and electromagnetic tensor 
are differential functions of the potentials
of fields in the form of derivatives of coordinates and time. The resulting
expression (57’) for 
, but
without taking into account the gravitational field, that is, without terms
with the potentials 
and , and
without taking into account the integral with the tensors and 
, we can
find in [5].
Hamilton's
equations according to (30) and (31), with the components of 3-vector
coordinate velocity 
, and
the components of 3-vector of the generalized momentum 
(32) have the following form:
, 
, 
, or
. (58)
.
(59)
In order to verify the validity of equations (58) the quantity 
of (53)
should be substituted into (57), and the quantities , and should be
expressed in terms of generalized momenta 
, and 
, using (40). If we then take the partial derivatives from the
Hamiltonian 
according to (58) we shall obtain expressions (54) for the components of
velocity. The physical meaning of equation (59) lies in the fact that the
gradient of the Hamiltonian as the energy of the system, taken with opposite
sign, is equal to the rate of change of the generalized momentum with time.
Now we shall write (57) in four-dimensional form, for which we shall use
the following expressions:
,
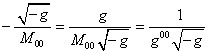, (60)
, 
, 
.
For the first term in (57) with the help of (32) it gives:
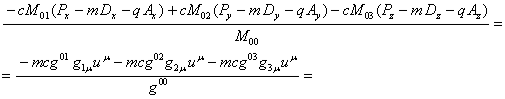
(61)
We shall make
further transformations of the following auxiliary quantities with the help of
(41) and (42):
.
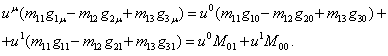
. (62)
From (40) it
follows that 
, 
, 
. Then,
using (62) and the equality 
the expression (53) for can be transformed as follows:
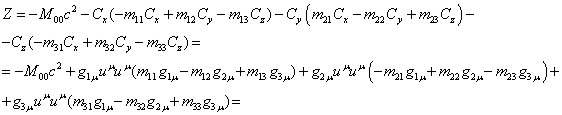
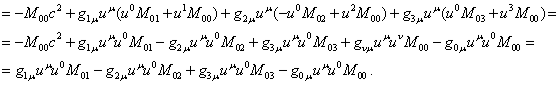
Now we shall
use (60):
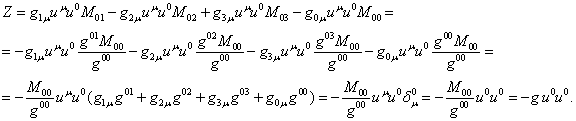
(63)
In (63) we used
Kronecker delta 
. In
view of (63) for the second term in (57) we find:
.
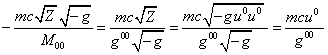We substitute this expression and the result from (61) into (57):
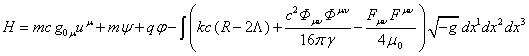. (64)
The Hamiltonian (64) coincides with the expression for the Hamiltonian
(34). Thus, we made a circle: first, by introducing the generalized momentum (32) we made
the transition from (34) to the Hamiltonian in the form of (57), and then by
other way, we got back to (34).
To check the validity of equations (59) for the Hamiltonian in the form
of (64), we find the quantity 
:
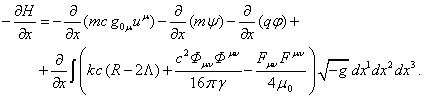
From (59) it follows:
From the last two equations we obtain:
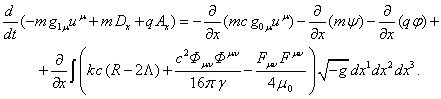(65)
In Minkowski space: 
, 
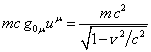. If we consider the situation for a small test
particle outside the massive charged body and apply the relations:
, 
,
, 
,
, 
,
then with constant mass and charge 
of the
particle, and assuming that the velocity 
and the
scalar products 
and 
do not
directly depend on the coordinates, the equation (65) turns into (22) for the
component of the momentum 
.
The four-dimensional generalized velocity
We shall introduce 4-vector of the generalized velocity with the
covariant index:
.
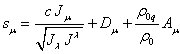(66)
where 
– 4-potential of gravitational field,
– 4-potential of electromagnetic field.
The ratio 
in (66) is the ratio of the densities of
charge and mass of the substance unit in the reference frame in which the
substance is at rest. The scalar 
will be equal to:
,
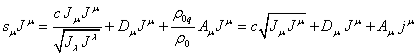(67)
where 
is the 4-vector of electric current density.
Taking it into account we can rewrite the Lagrangian (4) as follows:
,
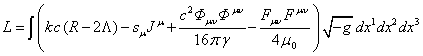(68)
and 
is the function of the action, and 
– an
invariant 4-volume, provided that 
. With the help of (11) and the subsequent
relations we can write down:
.
Thus, the invariance of the 4-volume 
with respect to the change of coordinates is expressed in the invariance
of the interval of the moving substance unit, and in the invariance of the
three-dimensional volume 
of the substance unit in the co-moving frame of reference.
We shall designate 
in (68) and
find the variation 
, associated with variation of part the action
function 
:
,
. (69)
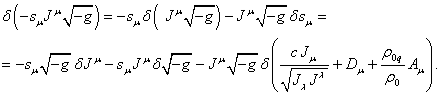(70)
We shall use
the following standard formulas:
, 
,
, (71)
, 
,
where the
variations 
, 
, 
are taken from [7-8], and
displacement 
are variations of the coordinates, due to of
which arise the variation of mass 4-current 
, the
variation of mass density 
and the variation of charge density 
.
We shall
transform the first term in (70) in view of (71):
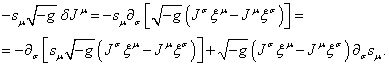
In this
expression the term with the total divergence in the integration over the
4-volume in the function of the action will not make any contribution. The
remaining term will be transformed further:
,
where the value
is the rotor of 4-vector of generalized
velocities 
.
We shall
transform the expression in the third term in (70):
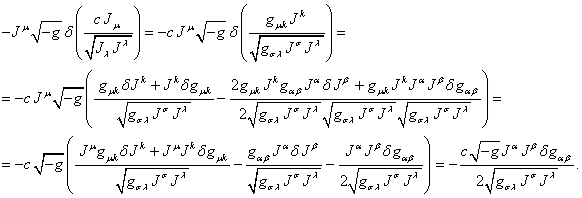
With the help
of (71) we shall find the variation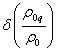 
:
.
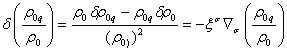Substitution in
(70) and (69) of the obtained above expressions gives:
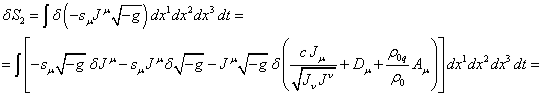
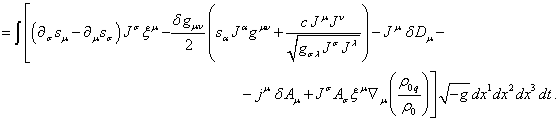
(72)
We shall designate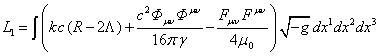 
in (68) and
take in [3] the variation 
, associated with the variation of the action
function 
. This gives the following:
, 
.
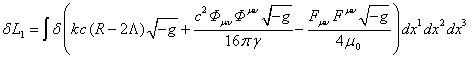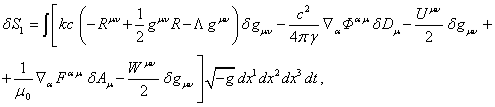(73)
where 
is the stress-energy tensor of gravitational
field (9), and the stress-energy tensor 
of electromagnetic field has the form:
. (74)
By the principle of least action, the variation of the action must be
equal to zero: 
. We shall substitute here (73) and (72), and equate
to zero all the terms inside the integrals, placed before the variations 
, 
, 
,
:
: 
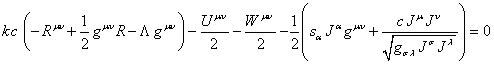, (75)
: 
, 
: 
, (76)
: 
.
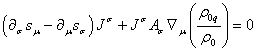(77)
Equations (76) are equivalent to the gravitational (5) and
electromagnetic (6) field equations. The first term in equation (77) can be
expanded by using the operator of proper-time-derivative 
according to [1], and the 4-vector of generalized velocity
(66):
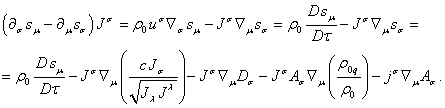
Taking into
account (77) it follows:
.
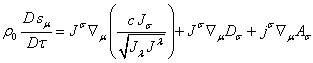(78)
As far as
according to (66):
,
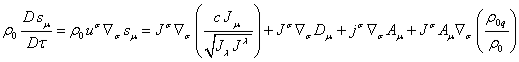so comparing
with (78) we find:
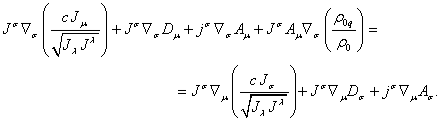(79)
We shall apply
the following relations:
, 
,
, 
.
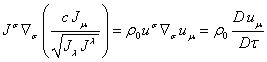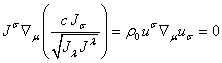This gives in
(79):
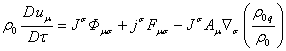. (80)
Above it was
assumed that the mass and the charge of substance unit in the variation does
not change. In this case, the density ratio will be unchanged, the covariant derivative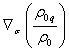 
is zero, and (80) turns into the equation of
motion of substance in gravitational and electromagnetic fields, taken in the
covariant theory of gravitation under these conditions (see the equation (35)
in [3] ).
Now we shall
consider the equation for the metric (75). If we separate out the terms 
and 
, then with
condition 
(75) is divided into two equations:
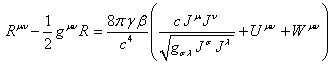, (81)
. (82)
In view of
(67), expression (82) coincides with (8). As for (81), from the comparison with
(7) it follows that it should equal to:
.
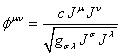(83)
Equation (82)
can be considered as the gauge of the cosmological constant, with which it is
possible to use equation (81) to find the metric.
We shall remind
that the variations , 
, 
in (70) found in [7-8], were
determined from the condition that the mass and charge of substance unit are
constants during variation. This leads to the equation of motion of the type (80),
in which instead of the proposed total derivative 
(the rate of change of mass 4-current) the
quantity 
appears as the product of the mass density and
the 4-acceleration.
The Hamiltonian and the problem of mass
The Hamiltonian
(64) can be represented in another form by using the generalized 4-velocity
(66). If we assume that 
sets in (66) the charge to the mass ratio, and
considering that 
, for the
Hamiltonian we have:
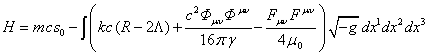. (84)
From here it
follows that the contribution to the energy of substance unit with mass 
is made by the timelike component of 4-vector
of generalized velocity with the covariant index 
, and the
energy of fields, found by the integral over the volume of space. In addition,
the amount of energy is corrected by the curvature of spacetime (the term with
curvature 
), and is
determined up to a constant (the term with 
).
Hamiltonian 
sets the energy in such a way that the energy
in each reference frame is different. This applies to the value of the
generalized 4-velocity of the substance unit, and the total momentum of the
substance and fields. So it should be, because in the theory of relativity only
a definite combination of energy and momentum can be maintained invariant and
preserved in each reference frame.
The Hamiltonian
(84) looks like it should be the timelike component of a 4-vector of
energy-momentum 
, written with a lower (covariant) index. In
this case, the timelike component of this 4-vector is associated with the
energy and the spatial component should be connected with the momentum of
substance unit. We shall make the notation:
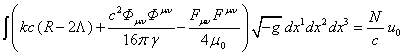, (85)
where 
is an invariant associated with the energy of
fields and with amendments to the energy arising from the curvature and from the constant ,
– the timelike component of the dimensionless
4-velocity 
, and the
4-velocity is a simplest 4-vector of unit length.
With this
definition, the integral (85) is assumed to be equal to the timelike component
of a 4-vector. Then, taking into account (66) we have:
.
(86)
Equation (86)
in view of (85) coincides with the expression for the Hamiltonian (34). Now we
shall write the 4-vector of the Hamiltonian in the contravariant form:
. (87)
As there is the
4-vector of generalized velocity 
in (87), the 4-vector of the Hamiltonian
contains the 4-vector of the generalized momentum in the form 
. The
timelike component of the 4-vector 
must specify the relativistic energy 
, and the
spatial components – multiplied by the speed of light momentum 
. This
follows from the conventional expression of the 4-vector energy-momentum of a
free particle without taking into account of the action of fields on it:
. This
vector in the flat Minkowski space, i.e., in the special theory of relativity,
is expressed as follows: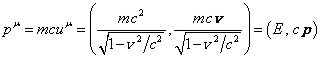 
. Fields and
interactions with other particles can vary quantities 
and 
, but when
the particle becomes free, from the invariance of the mass 
, the speed
of light and the equality 
should follow the well-known formula for the
relationship between mass, energy and momentum for a particle in relativistic
physics, valid in any inertial frame of reference. According to this formula,
one can find the momentum of the particle at certain energy and rest mass of
the particle, or determine the rest mass and the type of the particle by its
momentum and energy.
By analogy with
the 4-vector energy-momentum 
from the components of the 4-vector (87) we obtain:
. 
,
, 
.
(87’)
For the case of
substance without its direct interaction with another substance (other bodies),
located only in its own gravitational and electromagnetic fields, energy 
and momentum 
of the substance unit at constant mass and
charge can not change, and must be equal to some constant for the energy and
constant vector for the momentum. This can be represented by the equation 
, describing
the conservation laws of energy and momentum of a closed system.
If in (85) we
neglect the term with the curvature 
and determine the constant equal to zero
needed for the energy calibration, which arises due to the constant 
, then in
the weak field limit, at the transition to the special theory of relativity,
for the energy and the momentum in (87’) we obtain:
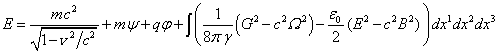. (88)
.
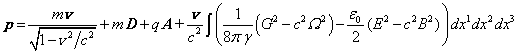From (88) it is
seen that the term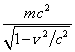 
plays the role of kinetic energy, and other
terms belong to the potential energy.
In this case
the potential energy includes not only the energy of the field strengths, but
also the energy associated with the scalar field potentials.
From the
substance unit we can proceed to a separate moving body, for which in case of
straight-line motion with constant velocity in the absence of external fields,
the relations 
, 
are valid. In this case for the momentum we
have:
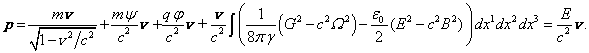
(89)
Here the
gravitational scalar potential 
and the electromagnetic scalar potential 
are understood as the averaged potentials
inside the body, arising from its own fields. To find the rest mass of the
body, taking into account the fields we should write the ratio 
with 
. We shall
use (88) to determine the rest mass with the help of volume integral:
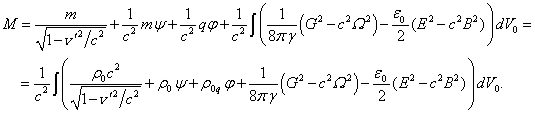
(90)
The rest mass 
of the body differs from the mass 
of its substance due to the contribution from
the field energies and energy of internal motion. If the body as a whole is at rest,
but its substance is in some internal motion with speed 
, it
contributes to the overall mass due to the kinetic energy, as well as due to
the emerging field of gravitational torsion 
, and due to
the magnetic field 
.
Determining the mass the terms with field strengths should be integrated over
volume both inside and outside the body.
Now we shall
use the relation (8) and apply it to (90) in case of stationary and not
rotating solid body:
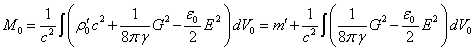, (91)
where 
is constant mass density associated with the cosmological
constant 
. The
density is obtained by excluding all the fields in the
substance. For example, if the body is divided into pieces and spread to
infinity with zero velocity, then the normal field of gravitation and the
electromagnetic field will not be making large contribution to the density of
the substance parts, and the total mass of these parts will be equal to 
.
According to
(91), the mass of the whole body becomes greater than the total mass of its parts,
due to the contribution of the gravitational energy with density 
.
Simultaneously, the electrical energy of the body reduces its mass. These
findings are consistent with results obtained by another way in [3], [4],
[9]. In the cosmic bodies the gravitational energy is generally higher
than the electromagnetic energy, so as we move from small to large bodies the
body mass should increase, as well due to the potential energy of gravitation.
We shall note
that instead of using the 4-vector of Hamiltonian (87) to estimate the energy,
momentum and mass, we can use another approach based on integration over volume
of the timelike components of the stress-energy tensors of substance 
(83), the gravitational field 
(9), as well as the electromagnetic field 
(74). From the properties of the left side of
the equation for the metric (81) it follows that the covariant derivative of
the right side is equal to zero:
. (92)
This equation
is equivalent to the equation of motion of substance in the gravitational and
electromagnetic fields (80), in which it is considered that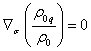 
.
Then we shall
use the procedure, which was used in [5] and many other works on the
theory of gravitation, to simplify the integration of (92) over 4-volume. If we
introduce a frame of reference relative to which the substance unit at a given
time is moving like it should move according to the special theory of
relativity, in this reference frame the Christoffel symbols 
and 
in (92) are equal to zero. Then the covariant
derivative 
of the tensor 
is equal to the ordinary derivative 
, which is
the 4-divergence of the tensor 
due to minimizing by the index 
. Instead of
(92) we obtain the equality
, the left
part of which can be integrated over the 4-volume, taking into account the
Gauss theorem, and in this case
:
,
where 
is the element of an infinite hypersurface
surrounding the 4-volume. The projection of this hypersurface at the hyperplane
gives a three-dimensional volume element 
, and for
the 4-vector energy-momentum we can write down:
. (93)
In contrast to
(87), the expression (93) does not contain the energy of substance in its
proper field, that is, the energy associated with scalar potentials 
and 
. Despite
this, for a stationary homogeneous ball in its proper gravitational field the
mass-energies of this field according to (90) and (93) coincide. This follows
from the next equation:
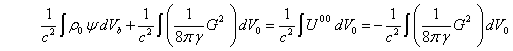, (94)
where 
is the differential of volume of the ball, 
– the differential of volume of space inside
and outside of the ball.
According to
(94), the potential energy of the ball in its proper gravitational field
associated with the scalar potential is two times greater than the potential
energy associated with the field strengths. The same is true for the
electromagnetic field, as in case of uniform arrangement of charges in the
volume of the ball, and at their location only on the surface. Equation (94) in
its meaning resembles the virial theorem for a stationary system of particles
bound by its proper gravitational field – in this system the absolute value of
the total potential energy is approximately equal to double kinetic energy of
all particles.
For the
relativistic energy of substance from (88), and respectively, from (93) we also
obtain the equality:
, 
.
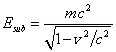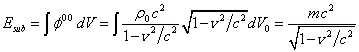One aspect of
the application (93) is the discrepancy between the mass-energy field of the
moving bodies that are found either through the field strengths in the
potential energy, or through the energy flux density and the momentum of the
field (the so-called problem of 4/3). An attempt to solve this problem was made
in [9] on the basis of the contribution of the field mass-energy
into the total body mass. At the same time taking into account (94) we obtain
the equality of the momentum in (89) and the total momentum of substance and
field contained in (93) in the spatial components of 4-vector 
.
We now turn our
attention to the mass ratio of the substance unit contained in (90) and (91),
for the case when the contribution to the mass of the mass-energy of the
electromagnetic field in comparison with the mass-energy of the gravitational
field is small. Taking into account (94), then for the masses of rest substance
the relation must be valid: 
,
where the mass 
is a part of the rest energy 
; the mass 
determines the total mass of substance
together with the field; the mass 
, as it
follows from (8), is the substance mass scattered to infinity, where all fields
are set to zero. Which of these masses determine proper potentials and
strengths of the gravitational field of the considered substance unit? In our
opinion, the observed mass is the mass , it must
specify both the inert and the gravitational properties of the mass. This mass
should be included in the formulas for the potential and field strength, and in
the potential energy. Then for a homogeneous stationary ball we can write down:
.
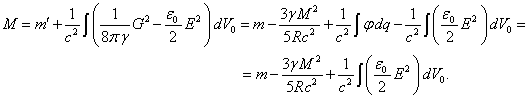
Since the
observed mass is 
,
then the mass 
can be determined from the last equation, and
then the mass can be calculated from the first equation. The
mass density of substance 
through the 4-vector of mass current density 
is included in the Lagrangian (4) for a
substance unit, and is also included in the Hamiltonian (35). In the
integration over three-dimensional volume of the term 
in (35), the mass 
appears, and the integration over the volume
of the term 
leads in the result of the integration to
appearing of the mass . The
difference between the masses and 
is due to the fact that at the addition of
substance units into a coherent body the 4-velocity 
is assumed constant, whereas the scalar
potential 
in itself is a function of mass (more
precisely, at the constant density of the substance the potential 
within the body depends on the characteristic
size of the body, or the amount of mass). Changing of the potential while the summation of the substance units
into a single body in the course of integration over volume instead of 
gives the mass 
, which is
used to calculate the energy of the field.
The stated
above reveals the difference of forms of writing, and complementarity of
Hamiltonian and Lagrangian approaches in finding the mass, energy and momentum
of the moving substance.
Action as the function to determine the
effect of time dilation
In view of (10)
and (12), we shall write the differential of the action function for a
substance unit with the mass 
and the charge 
:
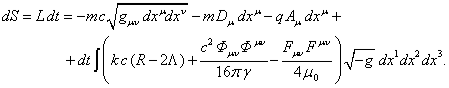(95)
From (95) it is
seen that the action is a scalar quantity. In addition, the differential of the
action can be decomposed by the differentials of the interval 
, the 4-vector of displacement 
, and the
coordinate (global) time 
, taken with
the relevant factors.
Now we shall
turn to the results obtained in [1]. It was shown there that the
expression 
contains a specific gauge function of
gravitational field, which equals to 
, provided 
. A similar
specific calibration function for electromagnetic field is equal to 
. We shall
remind that the fundamental field potentials are defined up to the coordinate
and time derivatives from an arbitrary gauge function. If we replace the
4-potentials for the gravitational field as follows:
,
(96)
where we
introduce the 4-vector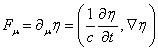 
,
then the strengths of the gravitational field and the equations of motion of
substance in the field will not change. The same is true for the
electromagnetic field and its specific gauge function 
. The gauge
transformation (96) in the case where the specific gauge function is selected
in the form 
, actually
clears the existing potentials of the gravitational field. Although it seems
that the system has not changed, it is not so. In fact, it turns out that when
comparing two systems, in one of which some gauge transformation is made by
changing the potentials, there are different rates of time flow. For
gravitational and electromagnetic fields the difference of a clock indications
in weak field approximation is described by the following formulas:
, 
. (97)
The clock 2,
which measures the time 
, is
check one and the clock 1 measures the time 
and is under the influence of additional
4-field potentials or 
. Time
points 1 and 2 within the integrals indicate the beginning and the end of the
field action. If there is only a static gravitational field with zero vector
potential, then 
. Assuming
then, that initially all the clocks had zero indication, for the difference in
the clocks’ indications from (97) we obtain the effect of gravitational time
dilation: 
.
From the time
difference (97) we can move to the phase shift for the same type of processes
in different points of the field. To do this, in (97) in the denominators it is
necessary to replace by the value of the characteristic angular
momentum. In quantum mechanics this value is the Dirac constant 
(this value is equal to Planck constant 
, divided by
), which
allows to take into account the appropriate phase shift which is inversely
proportional to this constant:
, 
. (98)
Phase shift in
(98), obtained due to the electromagnetic 4-potential 
, is
proved by the Aharonov-Bohm effect.
If we divide
the first part in (95) by 
and take the integral, we can obtain the
standard time dilation effect due to the clock motion with the speed 
:
, (99)
here the clock
speed is measured by the local observer at the point
with the timelike component of the metric 
; the moving clock measures time , and the
fixed clock – the time 
of the local observer, expressed by the
coordinate time 
.
In (95), there
is one more, the last term in the integral form, which in our opinion should
also influence the effect of time dilation. Any gauge transformation of
4-potentials does not affect the values of field strengths, which are part of
the tensors 
and 
. The energy
of fields associated with the substance mass 
, depends
not only on the absolute value of the 4-potentials, but also on the rates of
their changes in spacetime, that is, the field strengths. Each additional energy
must affect the intrinsic properties of substance, including the flow rate of
proper time. From this we deduce:
.
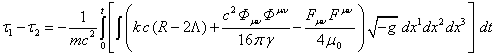From the stated
above it follows that the action is not only a function by which from the
principle of least action the equations of motion are obtained, through the
Legendre transformation the Hamiltonian, or the Hamilton-Jacobi equations are
defined. The action function has also a direct physical meaning as the function
describing the change in some intrinsic properties of physical bodies. These
include the intrinsic properties of the rate of the time flow, and consequently
the rate of increase of the phase angle of periodic processes depending on
time. The special role of time in relation to spatial size as a characteristic
property of physical bodies is due to the fact that the time shift during
motion and in the fundamental fields is an absolute effect, whereas the change
of the observed size is only relative.
Summary
Based on the
principle of least action and Euler-Lagrange equations, we presented in (17)
the relativistic equation of motion of a substance unit in fundamental fields
(for motion along the axis 
of the Cartesian reference frame). This
equation is written for the case when the velocity depends only on time, and
can be specified for the general case by introducing into the equation the
dependence of the velocity on the spatial coordinates. After determining the
generalized momentum for the substance and the field we obtain vector equation
(19), which expresses the dependence of the generalized force on different
physical variables for the substance in the field.
Difference in
positions of the covariant theory of gravitation (CTG) and the general theory
of relativity (GTR) describing the motion of a small test particle in an
external field is demonstrated in equations (21) and (23). In weak fields, the
equation of CTG (21) exactly transforms into the Lorentz-covariant equation of
motion (22) which is used in the special theory of relativity. In contrast, for
appearance of the gravitational force in GTR, not only the weak-field
approximation is required, but also preliminary calculation of the gradients of
the metric tensor. This is due to the fact that in GTR the gravitational field
potentials are related to the metric tensor components and are not independent
quantities. We shall note also that in contrast to CTG, in GTR there is no
definite limit transition into special theory of relativity, that is, into the
case of weak fields, based on the principle of conformity and conservation laws
for such quantities as energy, momentum and angular momentum [10].
Hamiltonian,
expressed through the 4-velocity and characterizing the energy of the particle
(substance unit) with mass 
, is
given by (34). For continuously distributed substance Hamiltonian is determined
by an integral over the 4-volume in relation (35). After simplification of these
expressions we obtain formula (36) for the relativistic energy of the particle
taking into account the energy of fields in the framework of the special theory
of relativity. The expression for Hamiltonian through generalized momenta is
given in (57), and relation (57’) sets the energy of the particle for flat
Minkowski space.
In relation
(66) we introduced into theory the 4-vector of generalized velocity 
and wrote with the help of it the Lagrangian
(68). After applying the principle of least action to this Lagrangian we obtain
equations for the gravitational and electromagnetic fields (76), the equation
of substance motion (80), and the equation for the metric (81) and the relation
for the cosmological constant (82). In addition, the timelike component of the
4-vector 
is directly included into Hamiltonian (84),
and the product of the particle mass and the contravariant 4-vector 
sets the 4-vector of the generalized momentum
in the form . As a
result, Hamiltonian (84) is the timelike component of a 4-vector with covariant
index 
associated with the energy and momentum. We
denoted it as a 4-vector of the Hamiltonian (4-energy), in contravariant form it
is determined in (87) and according to (87’) it sets the energy and momentum of
the particle through the mass, charge, 4-velocity, 4-potentials and field
strengths. The alternative expression of energy and momentum of the particle
through the energy-momentum tensors of substance and fields is given in (93) in
the form of a 4-vector of energy-momentum.
The mass of the
particle can be determined from (87’) by calculating the energy 
in the limit of zero velocity and dividing
this energy by the square of the light speed. In the weak-field approximation
formula (90) holds for the mass of a body at rest. The relation for three
masses associated with the body follows from (91) – (94): 
, where the
mass is part of the rest energy 
; the mass 
determines the relativistic mass of the body substance
with the proper fields as the measure of inertia and gravitational mass; the
mass 
is the mass of the substance scattered at infinity,
where all fields are zero.
In this case, we see that the relation holds: 
.
From the
analysis of the differential of action function (95) we find a change in the
rate of time (97) in physical objects
due to the action of potentials of the gravitational and electromagnetic
fields. For quantum objects the corresponding phase shift is expressed by
relations (98). The motion of clocks changes the rate of time according to
(99). The action function also includes the field strengths (through tensors 
and 
), and we
assume that they, as well as each component of the action function, should lead
to some change in the rate of clock and the phase of processes. Perhaps this
idea can be proved experimentally by measuring the quantum-mechanical phase
shift under the influence of field strengths in those cases when the field
strengths rather change the energy of the field than influence the motion of
particles.
References
[1] Fedosin, S.G. (2009). Fizicheskie teorii i
beskonechnaia vlozhennost’ materii. Perm: Fedosin.
[2] Fedosin, S.G. (1999). Fizika i filosofiia
podobiia: ot preonov do metagalaktik. Perm: Fedosin.
[3] Fedosin, S.G. (2012). The Principle of Least Action in Covariant
Theory of Gravitation. Hadronic Journal, 35(1),
35-70.
[4] Fedosin, S.G. (2012). The Principle of Proportionality of Mass and
Energy: New Version. Caspian Journal of Applied
Sciences Research, 1(13), 1-15.
[5] Landau, L.D., Lifshitz E.M. (1975). The
Classical Theory of Fields (Vol.
2, 4th ed.). Butterworth-Heinemann.
[6] Fedosin, S.G. (2009). Model
of Gravitational Interaction in the Concept of Gravitons. Journal of
Vectorial Relativity, 4(1), 1-24.
[7] Dirac, P.A.M. (1975). General theory of
relativity. New York: John Wiley & Sons.
[8] Fock, V. A. (1964). The Theory of Space, Time
and Gravitation. New York: Macmillan.
[9] Fedosin, S.G. (2011). Energy, Momentum, Mass and
Velocity of Moving Body. Retrieved from
http://vixra.org/abs/1106.0024.
[10] Gorelik, G. (2002) The Problem of
Conservation Laws and the Poincaré Quasigroup in General Relativity. In:
Einstein studies in Russia. Yuri Balashov, Vladimir Vizgin (eds.). Einstein Studies, 10, 17-43. Boston: Birkhäuser.
Source: http://sergf.ru/gamen.htm