Physical
Science International Journal, ISSN: 2348-0130, Vol. 8, Issue 4, P. 1-18
(2015). http://dx.doi.org/10.9734/PSIJ/2015/22197
Поле гравитонов как источник гравитационной силы и
массы в модернизированной модели Лесажа
Федосин Сергей Григорьевич
ул. Свиязева 22-79, город Пермь, 614088, Пермский край, Россия
e-mail intelli@list.ru
Выводится формула для гравитационной силы внутри сферического тела, а
также для ньютоновской силы притяжения между телами с точки зрения модели
гравитонов. Оцениваются параметры поля гравитонов, включая плотность его
энергии, поток энергии и сечение взаимодействия с веществом. Выводится
соотношение, из которого следует, что масса тела пропорциональна мощности
излучения энергии из тела от тех гравитонов, которые взаимодействовали с
веществом и передали телу свой импульс. На основе теории бесконечной
вложенности материи делается заключение о том, что гравитоны порождаются на
всех уровнях материи самыми плотными объектами типа нуклонов и нейтронных
звёзд.
Ключевые
слова: поле гравитонов;
гравитационная сила; источник массы; бесконечная вложенность материи.
The
graviton field as the source of mass and gravitational force in the modernized
Le Sage’s model
Sergey G. Fedosin
Sviazeva Str. 22-79, Perm, 614088, Perm region,
Russian Federation
e-mail intelli@list.ru
The formula for the
gravitational force inside a spherical body is derived, as well as for the
Newtonian force of attraction between bodies from the standpoint of the
gravitons’ model. The parameters of the graviton field are estimated, including
its energy density, energy flux and the cross section of interaction with
matter. The equation is derived, from which it follows that the body mass is
proportional to the power of radiation energy of the body from those of
gravitons that interacted with the matter and gave their momentum to the body.
The conclusion is made based on the theory of infinite nesting of matter that
gravitons are generated at all matter levels by the densest objects such as
nucleons and neutron stars.
Keywords: graviton field; gravitational force; origin of mass; infinite nesting of matter.
1. Введение
В модели Фатио-Лесажа гравитация возникает как следствие механического действия на тела потоков множества мельчайших частиц, падающих на тела со всех сторон [1-2]. В баллистической теории Ритца такие частицы не только падают на тела, но и вновь переизлучаются зарядами вещества тел, объясняя постоянство скорости света через неизменную скорость излучаемых зарядами частиц, и обосновывая электромагнитные и гравитационные силы [3].
В современной квантовой теории поля подобные частицы носят название
гравитоны. Они должны заполнять всё пространство и обладать достаточной
плотностью энергии и высокой проникающей способностью для того, чтобы давать
эффекты гравитации даже внутри больших космических тел. Важным преимуществом
модели с гравитонами является то, что модель позволяет дать наглядную
интерпретацию возникновению гравитационной силы и гравитационного ускорения
вблизи массивных тел. Большинство же других теорий, включая общую теорию
относительности [4], ковариантную теорию
гравитации [5] и другие тензорно-метрические теории,
скорее описывают гравитацию математически, чем представляют какой-либо механизм
её действия.
Предположим, что пространство заполнено полем
гравитонов подобно газу из релятивистски движущихся частиц, слабо
взаимодействующих друг с другом из-за большой скорости движения и своих малых
размеров. В каждой точке пространства можно найти такую систему отсчёта, в
которой потоки гравитонов являются изотропными. Для этого необходимо перейти в
систему центра импульсов гравитонов. В этом случае действие гравитонов со всех
сторон взаимно уравновешивается, система отсчёта наблюдателя становится
инерциальной и в ней будет справедлива расширенная специальная теория
относительности (РСТО) [6]. В РСТО выводятся все соотношения специальной теории
относительности (СТО). Отличие РСТО от СТО в том, что постулат о постоянстве
скорости света в СТО заменяется в РСТО на постулат о существовании изотропной
системы отсчёта такой, что в ней скорость света одинакова по всем направлениям.
Таким образом постоянство скорости света в инерциальных системах отсчёта
выводится как одно из следствий.
Если система отсчёта наблюдателя связана с
достаточно массивным телом, то она становится неинерциальной. Это выражается в
том, что вблизи тела поле гравитонов становится неоднородным, в нём появляются
градиенты потоков гравитонов. Как следствие, возникают гравитационные силы,
действующие на пробные тела со стороны нескомпенсированных потоков гравитонов.
Для большей наглядности, мы будем делать далее оценки всех основных величин,
характеризующих поле гравитонов и его взаимодействие с веществом.
2. Напряжённость поля внутри однородного шара
С целью упрощения потоки гравитонов можно характеризовать кубическим распределением в виде смешанной производной для направленного в одну сторону потока гравитонов:
![]() ,
(1)
,
(1)
где мощность флюенса ![]() обозначает количество
гравитонов, попавших за время
обозначает количество
гравитонов, попавших за время ![]() на перпендикулярную
потоку площадь
на перпендикулярную
потоку площадь ![]() одного из граней
некоторого куба, ограничивающего рассматриваемый объём.
одного из граней
некоторого куба, ограничивающего рассматриваемый объём.
Распределение (1) заменяет фактическое распределение потоков гравитонов в пространстве на идеализированное кубическое распределение, когда на данный кубический объём падает всего шесть потоков гравитонов, перпендикулярно граням куба.
В модернизированной модели Лесажа [7]
предполагается экспоненциальное изменение потока гравитонов веществом,
зависящее от самого потока, от длины пройденного в веществе пути ![]() , от концентрации частиц вещества
, от концентрации частиц вещества ![]() и от сечения
и от сечения ![]() взаимодействия
гравитонов с частицами вещества:
взаимодействия
гравитонов с частицами вещества:
![]() ,
, ![]() . (2)
. (2)
Соотношение (2) представляет собой закон Бугера–Ламберта–Бера, который связывает ослабление потока гравитонов со
свойствами вещества, через которое проходит поток. Если характеризовать
гравитоны как частицы с некоторым импульсом ![]() , движущиеся со скоростью света
, движущиеся со скоростью света ![]() и имеющие энергию
и имеющие энергию ![]() , то чем меньше гравитонов остаётся после прохождения пути
, то чем меньше гравитонов остаётся после прохождения пути ![]() в веществе, тем больше
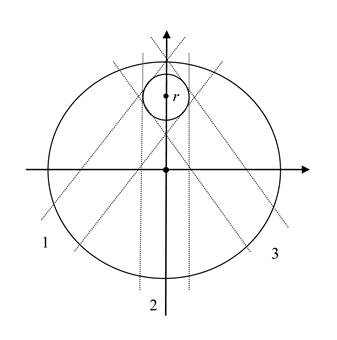
они передадут свой импульс этому веществу. На рисунке 1 показано сечение
однородного массивного шара радиуса
в веществе, тем больше
они передадут свой импульс этому веществу. На рисунке 1 показано сечение
однородного массивного шара радиуса ![]() , внутри которого находится небольшое пробное тело, также в
форме шара, с радиусом
, внутри которого находится небольшое пробное тело, также в
форме шара, с радиусом ![]() .
.
![]()
Потоки гравитонов идут по путям 1, 2 , 3 , а также по другим
путям, пересекая сечение малого шара, находящегося на расстоянии ![]() от центра большого
шара. Если заменить малый шар кубом таких же размеров, то при идеализированном
кубическом распределении достаточно рассмотреть вертикальные потоки вдоль пути
2. Потоки гравитонов через другие грани малого куба будут симметричны и не
влияют на гравитационную силу. Это значит, что при таком подходе мы будем не
прямо, а косвенно учитывать потоки по наклонным путям 1 и 3. Все эти потоки при
векторном сложении дают силу, действующую на малый шар и направленную к центру
большого шара, и добавляются к силе, вычисляемую на пути 2.
от центра большого
шара. Если заменить малый шар кубом таких же размеров, то при идеализированном
кубическом распределении достаточно рассмотреть вертикальные потоки вдоль пути
2. Потоки гравитонов через другие грани малого куба будут симметричны и не
влияют на гравитационную силу. Это значит, что при таком подходе мы будем не
прямо, а косвенно учитывать потоки по наклонным путям 1 и 3. Все эти потоки при
векторном сложении дают силу, действующую на малый шар и направленную к центру
большого шара, и добавляются к силе, вычисляемую на пути 2.
Пусть объём малого шара равен объёму некоторого куба. Тогда для объёма
куба с ребром ![]() , и для массы
, и для массы ![]() этого куба получаются
соотношения:
этого куба получаются
соотношения:
![]() ,
,
![]() , (3)
, (3)
где ![]() – концентрация
нуклонов в маленьком шаре,
– концентрация
нуклонов в маленьком шаре, ![]() – масса одного
нуклона.
– масса одного
нуклона.
Падающий сверху поток гравитонов проходит путь ![]() в большом шаре с
концентрацией нуклонов
в большом шаре с
концентрацией нуклонов ![]() в его веществе, и
достигает малого куба, которым мы заменили малый шар. Согласно (2) к этому
моменту мощность флюенса уменьшится до величины:
в его веществе, и
достигает малого куба, которым мы заменили малый шар. Согласно (2) к этому
моменту мощность флюенса уменьшится до величины:
![]() .
.
Далее поток проходит через малый куб с концентрацией нуклонов
![]() и снова уменьшается:
и снова уменьшается:
![]() .
.
Сила от этого потока гравитонов пропорциональна площади грани
малого куба и количеству гравитонов, передавших свой импульс в единицу времени
веществу куба:
![]() . (4)
. (4)
С нижней стороны большого шара поток гравитонов проходит вначале
путь ![]() до малого куба, а
затем проходит через этот куб:
до малого куба, а
затем проходит через этот куб:
![]() ,
, ![]() .
.
Сила, действующая на малый куб с этой стороны, равна:
![]() . (5)
. (5)
Суммарная сила есть разница сил (4) и (5):
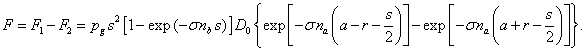
(6)
Как правило, показатели экспонент в (6) малы, поскольку мало
значение ![]() . В этом случае экспоненты можно разложить по малому
параметру по правилу:
. В этом случае экспоненты можно разложить по малому
параметру по правилу: ![]() . С учётом этого имеем:
. С учётом этого имеем:
![]() .
.
В данном выражении учтём, что плотность большого шара выражается
формулой: ![]() , и используем (3):
, и используем (3):
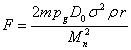 .
.
Мы приходим к тому, что сила ![]() действует на маленький
шар на рисунке 1, и направлена эта сила к центру большого шара. По определению,
напряжённость гравитационного поля есть отношение силы, действующей на пробное
тело, к массе пробного тела. Тогда вектор напряжённости гравитационного поля
внутри большого шара будет такой:
действует на маленький
шар на рисунке 1, и направлена эта сила к центру большого шара. По определению,
напряжённость гравитационного поля есть отношение силы, действующей на пробное
тело, к массе пробного тела. Тогда вектор напряжённости гравитационного поля
внутри большого шара будет такой:
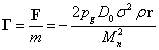 .
(7)
.
(7)
Знак минус в (7) связан с тем, что сила направлена противоположно
радиус-вектору ![]() .
.
В лоренц-инвариантной теории гравитации [8] вектор напряжённости гравитационного поля внутри однородного шара определяется формулой:
![]() .
(8)
.
(8)
Из сравнения (7) и (8) находим выражение гравитационной постоянной
через параметры поля гравитонов в приближении кубического распределения потоков
гравитонов:
![]() .
(9)
.
(9)
Гравитационная постоянная в (9) зависит от сечения ![]() взаимодействия гравитонов с нуклонами вещества, от среднего
импульса одного гравитона
взаимодействия гравитонов с нуклонами вещества, от среднего
импульса одного гравитона ![]() , от мощности флюенса гравитонов
, от мощности флюенса гравитонов ![]() и от массы нуклона
и от массы нуклона ![]() . Мы можем повторить все вычисления для случая, когда вместо
нуклонов характерными частицами вещества являются кварки. Тогда в (9) вместо
массы
. Мы можем повторить все вычисления для случая, когда вместо
нуклонов характерными частицами вещества являются кварки. Тогда в (9) вместо
массы ![]() появится некоторая
средняя кварковая масса, а сечение
появится некоторая
средняя кварковая масса, а сечение ![]() изменит свою
величину, поскольку сечение зависит от
вида взаимодействующих частиц.
изменит свою
величину, поскольку сечение зависит от
вида взаимодействующих частиц.
3. Напряжённость
гравитационного поля за пределами однородного шара
Из рисунка 1 видно, что формулы (7) и (9) в кубическом распределении получены без учёта действия потоков гравитонов, идущих по наклонным путям вида 1 и 3. Вклад этих потоков внутри шара фиксирован и зависит только от размеров шара. Поэтому если добавить вклад этих потоков, смысл формул (7) и (9) существенно не изменится, за исключением появления некоторых численных множителей порядка единицы.
Ситуация заметно меняется, когда пробное тело в виде малого шара находится за пределами большого массивного шара. В этом случае кубическое распределение потоков гравитонов в пространстве становится слишком грубым для описания этих потоков. Ведь в действительности потоки гравитонов направлены не только в шести взаимно перпендикулярных направлениях, но и в любых возможных направлениях. Перейдём поэтому к более точному на больших расстояниях сферическому распределению для потока следующего вида:
![]() . (10)
. (10)
В отличие от (1), для мощности флюенса (10) детектором гравитонов
выступает некоторая сферическая поверхность, внутрь которой за время ![]() из телесного угла
из телесного угла ![]() падает некоторое число
гравитонов
падает некоторое число
гравитонов ![]() . При этом телесный угол имеет начало в центре указанной
сферической поверхности и опирается на площадь элемента поверхности
. При этом телесный угол имеет начало в центре указанной
сферической поверхности и опирается на площадь элемента поверхности ![]() , так что считается, что гравитоны падают перпендикулярно
поверхности детектора. На самом же деле часть гравитонов будет падать на
, так что считается, что гравитоны падают перпендикулярно
поверхности детектора. На самом же деле часть гравитонов будет падать на ![]() под углами,
отличающимися от прямого угла, так что (10) является очередным приближением к
действительности.
под углами,
отличающимися от прямого угла, так что (10) является очередным приближением к
действительности.
Дальнейшие рассуждения с некоторыми изменениями повторяют выводы из [5] и [7]. На рисунке 2 показаны две массы, взаимодействие
которых можно оценить с помощью мощности флюенса
(10) для сферического распределения.
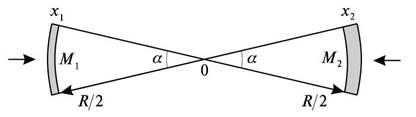
Подобно (2), можно считать, что в веществе
происходит экспоненциальное уменьшение количества гравитонов по мере того, как
поток гравитонов проходит в веществе
некоторый путь ![]() :
:
![]() .
(11)
.
(11)
Для масс притягивающихся друг к другу шаровых
сегментов можно записать:
![]() ,
, ![]() ,
, ![]() . (12)
. (12)
Детектор находится в точке ![]() посередине между двумя
сегментами. Для него каждый сегмент виден под одним и тем же телесным углом
посередине между двумя
сегментами. Для него каждый сегмент виден под одним и тем же телесным углом ![]() на расстоянии
на расстоянии ![]() , при этом поперечные площади сегментов одинаковы и равны
, при этом поперечные площади сегментов одинаковы и равны ![]() . Это означает, что прежде чем применять дальнейшие
рассуждения для двух больших тел, эти тела следует нарезать на сегменты и затем
вычислять суммарную гравитационную силу между всеми возможными парами сегментов
путём векторного суммирования отдельных сил.
. Это означает, что прежде чем применять дальнейшие
рассуждения для двух больших тел, эти тела следует нарезать на сегменты и затем
вычислять суммарную гравитационную силу между всеми возможными парами сегментов
путём векторного суммирования отдельных сил.
Уменьшение потока гравитонов с левой стороны после прохождения первого сегмента согласно (11) зависит от толщины этого сегмента и концентрации нуклонов:
![]() .
.
После этого поток гравитонов проходит через
второй сегмент с дополнительным уменьшением потока:
![]() .
.
Сила, действующая на второй сегмент слева, с
учётом (10) будет равна:
![]() .
.
Уменьшение потока гравитонов, проходящего
справа через второй сегмент, и сила с этой стороны равны соответственно:
![]() ,
, ![]() .
.
Для силы притяжения второго сегмента к первому находим:
![]() .
(13)
.
(13)
Эта сила симметрична относительно перемены сегментов местами, так что первый сегмент притягивается ко второму с такой же силой.
Показатели в экспонентах в (13) малы для всех космических объектов, кроме
нейтронных звёзд, где это уже не так. Раскладывая экспоненты в линейном
приближении по правилу: ![]() , с учётом (12) для силы получим:
, с учётом (12) для силы получим:
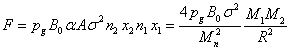 .
.
Согласно закону Ньютона, формула для модуля гравитационной силы между двумя телами имеет следующий вид:
![]() .
.
Сравнивая значения для сил, приходим к выражению для гравитационной постоянной через параметры поля гравитонов при идеализированном сферическом распределении потоков гравитонов:
![]() . (14)
. (14)
Из выражения для силы определяется напряжённость гравитационного поля одной массы в месте расположения второй массы:
![]() . (15)
. (15)
4. Параметры поля
гравитонов
Оценим плотность энергии для кубического распределения потоков гравитонов
в пространстве. Пусть есть куб с ребром ![]() , в который влетают гравитоны с шести сторон перпендикулярно
граням куба. Скорость гравитонов предполагается равной скорости света, так что
за время
, в который влетают гравитоны с шести сторон перпендикулярно
граням куба. Скорость гравитонов предполагается равной скорости света, так что
за время ![]() куб будет полностью
заполнен. С учётом распределения (1) количество гравитонов в кубе будет
равно:
куб будет полностью
заполнен. С учётом распределения (1) количество гравитонов в кубе будет
равно: ![]() . Если энергия одного гравитона равна
. Если энергия одного гравитона равна ![]() , то для плотности энергии поля гравитонов с помощью (9)
находим:
, то для плотности энергии поля гравитонов с помощью (9)
находим:
![]() . (16)
. (16)
Используем теперь сферическое распределение (10) для оценки плотности
энергии поля гравитонов. Пустая сфера радиуса ![]() может быть заполнена
гравитонами за время
может быть заполнена
гравитонами за время ![]() , если потоки гравитонов направлены радиально и укладываются
в полный телесный угол
, если потоки гравитонов направлены радиально и укладываются
в полный телесный угол ![]() . Число гравитонов внутри сферы будет равно
. Число гравитонов внутри сферы будет равно ![]() . Умножая это число на энергию одного гравитона и разделив на
объём сферы, можно найти плотность энергии. С учётом (14) и условия
. Умножая это число на энергию одного гравитона и разделив на
объём сферы, можно найти плотность энергии. С учётом (14) и условия ![]() , имеем:
, имеем:
![]() . (17)
. (17)
Плотность энергии (17) при сферическом распределении в 3/2 раза больше, чем при кубическом распределении (16), что подчёркивает приблизительность наших оценок из-за использования двух идеализированных распределений.
В (16) и (17) не определённой до сих пор величиной является сечение
взаимодействия гравитонов с веществом ![]() . В [9] для случая, когда
гравитоны взаимодействуют с электронами в атомах, приводится оценка сечения
. В [9] для случая, когда
гравитоны взаимодействуют с электронами в атомах, приводится оценка сечения ![]() , где
, где ![]() есть планковская
длина. В [10] для сечения даётся соотношение:
есть планковская
длина. В [10] для сечения даётся соотношение: ![]() м2, причём делается вывод, что сечение
взаимодействия мало зависит от типа частиц вещества. Все эти оценки основаны на
том, что энергия гравитонов выражается через постоянную Планка и длину волны
излучения. Но как будет показано далее, с точки зрения бесконечной вложенности
материи гравитоны возникают в основном не на уровне элементарных частиц и
атомов, а на более низких уровнях материи. А каждый уровень материи
характеризуется своей собственной постоянной, подобной постоянной Планка, но
отличающейся от неё по величине. Этот факт учитывается в [11], однако поскольку энергия гравитонов в виде фотонов
привязывается к планковским единицам путём приравнивания планковской длины к
длине волны фотонов, сечение взаимодействия этих фотонов с нуклонами получается
завышенным и равным
м2, причём делается вывод, что сечение
взаимодействия мало зависит от типа частиц вещества. Все эти оценки основаны на
том, что энергия гравитонов выражается через постоянную Планка и длину волны
излучения. Но как будет показано далее, с точки зрения бесконечной вложенности
материи гравитоны возникают в основном не на уровне элементарных частиц и
атомов, а на более низких уровнях материи. А каждый уровень материи
характеризуется своей собственной постоянной, подобной постоянной Планка, но
отличающейся от неё по величине. Этот факт учитывается в [11], однако поскольку энергия гравитонов в виде фотонов
привязывается к планковским единицам путём приравнивания планковской длины к
длине волны фотонов, сечение взаимодействия этих фотонов с нуклонами получается
завышенным и равным ![]() м2.
м2.
В связи с этим к определению сечения подойдём с другой стороны. В
качестве грубой оценки ![]() можно использовать
соотношение
можно использовать
соотношение ![]() для наиболее плотных
объектов с большой концентрацией частиц
для наиболее плотных
объектов с большой концентрацией частиц ![]() . Согласно (2), при этом условии поток гравитонов на пути до
центра звезды уменьшается в
. Согласно (2), при этом условии поток гравитонов на пути до
центра звезды уменьшается в ![]() раз и более, где
раз и более, где ![]() – основание
натурального логарифма.
– основание
натурального логарифма.
Для различных звёзд одинаковой массы произведение концентрации на радиус
звезды изменяется обратно пропорционально квадрату радиуса и достигает
максимума при уменьшении радиуса. Поэтому нейтронные звёзды как самые малые и
плотные известные объекты лучше всего пригодны для оценки ![]() из условия
из условия ![]() . Если бы звезда была однородным шаром радиуса 12 км и массы
1,35 массы Солнца, для неё было бы
. Если бы звезда была однородным шаром радиуса 12 км и массы
1,35 массы Солнца, для неё было бы ![]() м2 . В [7] было принято
значение
м2 . В [7] было принято
значение ![]() м2 для звезды радиусом 15 км, при этом получалось,
что максимально возможная скорость генерации энергии равнялась энергии покоя
звезды, освобождаемой за время пролёта гравитонами радиуса звезды. Если
применить такой же подход для звезды радиусом
м2 для звезды радиусом 15 км, при этом получалось,
что максимально возможная скорость генерации энергии равнялась энергии покоя
звезды, освобождаемой за время пролёта гравитонами радиуса звезды. Если
применить такой же подход для звезды радиусом ![]() км, то это даёт:
км, то это даёт:
![]() м2 , (18)
м2 , (18)
где ![]() для случая однородной
плотности.
для случая однородной
плотности.
Как следствие, для величины предельной силы притяжения между двумя
соприкасающимися массивными телами в [7] было
получено значение:
![]() ,
,
подразумевающее случай, когда потоки гравитонов полностью задерживаются этими телами.
В [5] рассматривалось притяжение двух
нейтронных звёзд при минимальном расстоянии между ними ![]() , при этом экспоненты в выражении для силы в (13) не
раскладывались по малому параметру, а учитывались полностью. Это привело к
тому, что сила притяжения между звёздами уменьшилась по сравнению с ньютоновской
силой
, при этом экспоненты в выражении для силы в (13) не
раскладывались по малому параметру, а учитывались полностью. Это привело к
тому, что сила притяжения между звёздами уменьшилась по сравнению с ньютоновской
силой ![]() и составила величину
порядка
и составила величину
порядка ![]() .
.
Другой способ оценки сечения ![]() взаимодействия
гравитонов с веществом заключается в
следующем. Если исходить из подобия уравнений Максвелла для электромагнитного
поля, и максвеллоподобных гравитационных уравнений в лоренц-инвариантной теории
гравитации [8], [12], то возникает соответствие между электрической постоянной
взаимодействия
гравитонов с веществом заключается в
следующем. Если исходить из подобия уравнений Максвелла для электромагнитного
поля, и максвеллоподобных гравитационных уравнений в лоренц-инвариантной теории
гравитации [8], [12], то возникает соответствие между электрической постоянной ![]() и гравитоэлектрической
постоянной вида
и гравитоэлектрической
постоянной вида ![]() . Кроме этого, магнитной постоянной
. Кроме этого, магнитной постоянной ![]() можно поставить в
соответствие гравитомагнитную постоянную вида
можно поставить в
соответствие гравитомагнитную постоянную вида ![]() , где
, где ![]() есть скорость
распространения гравитации. При распространении электромагнитной волны в
вакууме волновое сопротивление определяется отношением амплитуды напряжённости
электрического поля
есть скорость
распространения гравитации. При распространении электромагнитной волны в
вакууме волновое сопротивление определяется отношением амплитуды напряжённости
электрического поля ![]() к амплитуде
напряжённости магнитного поля
к амплитуде
напряжённости магнитного поля ![]() :
:
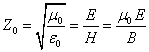 ,
,
где ![]() есть индукция
магнитного поля волны.
есть индукция
магнитного поля волны.
По аналогии с этим можно определить гравитационное волновое сопротивление
вакуума [13]. При условии, что скорость распространения гравитации ![]() равна скорости света,
имеем:
равна скорости света,
имеем:
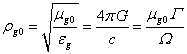 ,
,
где ![]() .
.
Гравитационное волновое сопротивление ![]() должно характеризовать
распространение гравитационных волн. Оно пропорционально отношению амплитуды
напряжённости гравитационного поля
должно характеризовать
распространение гравитационных волн. Оно пропорционально отношению амплитуды
напряжённости гравитационного поля ![]() к амплитуде
гравитационного поля кручения
к амплитуде
гравитационного поля кручения ![]() (последняя величина в
общей теории относительности называется гравитомагнитное поле). Предположим,
что гравитационный квант имеет характерный радиус вращения
(последняя величина в
общей теории относительности называется гравитомагнитное поле). Предположим,
что гравитационный квант имеет характерный радиус вращения ![]() как в поляризованном
по кругу фотоне. Для гравитационной силы Лоренца можно записать:
как в поляризованном
по кругу фотоне. Для гравитационной силы Лоренца можно записать:
![]() ,
, ![]() ,
,
где движущаяся со скоростью ![]() масса
масса ![]() вращается вокруг поля
кручения по окружности с радиусом
вращается вокруг поля
кручения по окружности с радиусом ![]() аналогично тому, как
вращается заряд, попавший в магнитное поле.
аналогично тому, как
вращается заряд, попавший в магнитное поле.
Амплитуду напряжённости гравитационного поля ![]() можно связать с
амплитудой гравитационного потенциала
можно связать с
амплитудой гравитационного потенциала ![]() стандартным
соотношением:
стандартным
соотношением: ![]() . Если подставить данные
. Если подставить данные ![]() и
и ![]() в выражение для
в выражение для ![]() при
при ![]() , а также при максимальной возможной величине амплитуды
потенциала
, а также при максимальной возможной величине амплитуды
потенциала ![]() , то получится
, то получится ![]() .
.
С другой стороны, массовый ток для случая вращения по окружности
определяется выражением: ![]() . Выражая отсюда
. Выражая отсюда ![]() , используя соотношения
, используя соотношения ![]() ,
, ![]() и
и ![]() , приходим к следующему:
, приходим к следующему:
![]() .
.
Отсюда следует, что гравитационное волновое сопротивление для волны можно
трактовать подобно гравитационному закону Ома, когда сопротивление прямо
пропорционально разности потенциалов и обратно пропорционально току.
Предположим теперь, что мы имеем некоторый сферический массивный объект с
массой ![]() и радиусом
и радиусом ![]() , модуль гравитационного потенциала на поверхности которого
достигает предельного значения, равного квадрату скорости света:
, модуль гравитационного потенциала на поверхности которого
достигает предельного значения, равного квадрату скорости света: ![]() , а также
, а также ![]() . Оценим ток массы поля гравитонов на этот объект с помощью
сферического распределения потоков гравитонов (10). Для этого умножим (10) на
полный телесный угол
. Оценим ток массы поля гравитонов на этот объект с помощью
сферического распределения потоков гравитонов (10). Для этого умножим (10) на
полный телесный угол ![]() , на площадь поверхности сферы
, на площадь поверхности сферы ![]() и на энергию одного
гравитона
и на энергию одного
гравитона![]() , а затем разделим на квадрат скорости света для перехода от
мощности потока энергии к току массы. Учитывая (17), находим:
, а затем разделим на квадрат скорости света для перехода от
мощности потока энергии к току массы. Учитывая (17), находим:
![]() .
.
Нашей идеей является то, что гравитационное волновое сопротивление служит
множителем пропорциональности между гравитационным потенциалом и током массы не
только в случае гравитационной волны, но и в случае потока массы ![]() поля гравитонов на
объект с предельно возможным потенциалом. Отсюда с учётом выражения для
поля гравитонов на
объект с предельно возможным потенциалом. Отсюда с учётом выражения для ![]() следует следующее:
следует следующее:
![]() ,
, ![]() ,
, ![]() .
.
В последнем выражении сделаем замену ![]() , полагая, что масса объекта
, полагая, что масса объекта ![]() та же самая, что и
масса
та же самая, что и
масса ![]() используемой нами
массы модели нейтронной звезды, равной 1,35 массы Солнца. Это даёт:
используемой нами
массы модели нейтронной звезды, равной 1,35 массы Солнца. Это даёт:
![]() м2 ,
м2 ,
что практически совпадает с оценкой в (18). Поэтому далее мы будем
использовать значение сечения ![]() взаимодействия
гравитонов с веществом из (18).
взаимодействия
гравитонов с веществом из (18).
Из (16) и (18) находим оценку плотности энергии поля гравитонов:
![]() Дж/м3 . (19)
Дж/м3 . (19)
Для сравнения, плотность модуля гравитационной энергии в объёме
рассматриваемой нами нейтронной звезды равна ![]() Дж/м3 , а плотность энергии покоя звезды равна
Дж/м3 , а плотность энергии покоя звезды равна ![]() Дж/м3 .
Дж/м3 .
Мощность флюенса энергии как мощность потока энергии поля гравитонов в
одном направлении можно найти путём умножения энергии одного гравитона ![]() на мощность флюенса
гравитонов
на мощность флюенса
гравитонов ![]() из кубического
распределения (1). С учетом (9) и (18-19) находим:
из кубического
распределения (1). С учетом (9) и (18-19) находим:
![]() Вт/м2
. (20)
Вт/м2
. (20)
Сечение ![]() взаимодействия
гравитонов с веществом в (18) настолько мало, что его можно сравнить лишь с
сечением взаимодействия нейтрино с энергией
взаимодействия
гравитонов с веществом в (18) настолько мало, что его можно сравнить лишь с
сечением взаимодействия нейтрино с энергией ![]() эВ. Особенностью нейтрино является то, что сечение их
взаимодействия с веществом зависит в основном от энергии нейтрино и от
концентрации нуклонов, а не от концентрации электронов.
эВ. Особенностью нейтрино является то, что сечение их
взаимодействия с веществом зависит в основном от энергии нейтрино и от
концентрации нуклонов, а не от концентрации электронов.
С другой стороны, если гравитоны представляют собой кванты
электромагнитного поля, то ![]() можно приравнять к
плотности энергии этого поля, выраженную через постоянную плотности излучения
можно приравнять к
плотности энергии этого поля, выраженную через постоянную плотности излучения ![]() и температуру
и температуру ![]() . Отсюда для температуры поля гравитонов в виде фотонов
находим:
. Отсюда для температуры поля гравитонов в виде фотонов
находим:
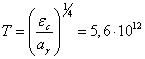 К.
(21)
К.
(21)
5. Бесконечная
вложенность материи
Согласуем теперь идею поля гравитонов с теорией бесконечной вложенности
материи [5], [8], [14], согласно которой во
Вселенной существуют различные и подобные друг другу уровни материи,
отличающиеся друг от друга своим расположением на масштабной оси. Два таких основных масштабных уровня материи, как уровни
атомов и звёзд, содержат объекты с предельной плотностью вещества. К ним
относятся нейтрон и протон, с одной стороны, и их звёздные аналоги, нейтронная
звезда и магнитар, с другой стороны. Другими аналогами считаются мюон и белый
карлик, атом водорода и магнитар с дисконом, где дискон представляет собой диск
возле нейтронной звезды, подобно электронному диску в атоме. Галактики
соответствуют мельчайшим пылинкам, в центре которых находится твёрдое вещество,
а снаружи толстая газообразная оболочка из различных атомов. Последняя аналогия
со временем становится всё более полной, так как звёзды в галактиках
эволюционируют и превращаются в нейтронные звёзды и белые карлики. В такой
картине магнитары возникают из нейтронных звёзд подобно тому, как протоны образуются
из нейтронов в бета-распаде.
Мы предполагаем, что чёрные дыры не существуют, так как им приписывается свойство поглощать материю и не выпускать ничего наружу. Но это противоречит тому, что поле гравитонов пронизывает все тела и создаёт тем самым гравитационные явления. Если чёрная дыра будет только поглощать энергию потоков гравитонов, она за самое малое время приобретёт гигантское количество массы-энергии и должна бесконечно расти в размерах, чего не наблюдается.
Для объектов, удерживаемых от распада гравитацией, мы в [15] нашли формулы для оценки температуры и давления в центре этих объектов:
![]() ,
,
![]() , (22)
, (22)
где ![]() – постоянная Больцмана,
– постоянная Больцмана,
![]() – масса протона, масса
объекта
– масса протона, масса
объекта ![]() заключена внутри сферы
радиуса
заключена внутри сферы
радиуса ![]() .
.
Из связи между давлением, концентрацией частиц и температурой в центре в
виде ![]() из (22) вытекает, что
плотность массы в центре
из (22) вытекает, что
плотность массы в центре ![]() приблизительно в 1,5
раза превышает среднюю плотность массы
приблизительно в 1,5
раза превышает среднюю плотность массы ![]() объекта:
объекта: ![]() .
.
Для нейтронной звезды радиуса 12 км и массы 1,35 массы Солнца из (22)
находим: температура ![]() К; давление
К; давление ![]() Па; плотность массы
Па; плотность массы ![]() кг/м3. Обратим внимание, что здесь температура
является не кинетической, а полной, обобщённой температурой. Если кинетическая
температура идеального газа определяется кинетической энергией его частиц, то
для нейтронной звезды обобщённая температура определяется отношением [8]:
кг/м3. Обратим внимание, что здесь температура
является не кинетической, а полной, обобщённой температурой. Если кинетическая
температура идеального газа определяется кинетической энергией его частиц, то
для нейтронной звезды обобщённая температура определяется отношением [8]: ![]() , где
, где ![]() – функция Лагранжа в
расчёте на одну частицу.
– функция Лагранжа в
расчёте на одну частицу.
Такое определение температуры позволяет учесть потенциальную энергию отталкивания нуклонов друг от друга, зависящую в гравитационной модели сильного взаимодействия от поля сильной гравитации и от кинетической энергии вращения нуклонов [5]. Движение нуклонов в звезде больше вращательное, чем поступательное, ввиду большой плотности вещества, и возникающее взаимное отталкивание нуклонов противостоит гравитационному давлению.
Оценим теперь температуру и давление для центра протона. Введём вначале
коэффициенты подобия как отношение соответствующих величин. Разделив массу
нейтронной звезды на массу протона, находим коэффициент подобия по массе: ![]() . Аналогично вычисляем коэффициент подобия по размерам как
отношение радиуса звезды к радиусу протона:
. Аналогично вычисляем коэффициент подобия по размерам как
отношение радиуса звезды к радиусу протона: ![]() , здесь было использовано значение
, здесь было использовано значение ![]() м в самосогласованной
модели протона [16].
м в самосогласованной
модели протона [16].
Коэффициент подобия по скоростям равняется отношению характерных
скоростей вещества внутри звезды и протона соответственно. Для звезды
характерная скорость ![]() вычисляется из равенства
энергий с точки зрения общего принципа эквивалентности массы и энергии,
обобщённого в отношении модуля полной энергии на любые космические объекты:
вычисляется из равенства
энергий с точки зрения общего принципа эквивалентности массы и энергии,
обобщённого в отношении модуля полной энергии на любые космические объекты:
![]() ,
,
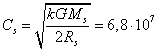 м/с.
м/с.
Аналогично этому для протона находим равенство характерной скорости его вещества и скорости света:
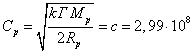 м/с, (23)
м/с, (23)
при этом ![]() м3·кг-1·с-2 есть постоянная сильной гравитации,
вычисляемая из равенства электрической и гравитационной сил в атоме водорода, и
согласно [16]
м3·кг-1·с-2 есть постоянная сильной гравитации,
вычисляемая из равенства электрической и гравитационной сил в атоме водорода, и
согласно [16] ![]() . Отсюда коэффициент подобия по скоростям будет равен:
. Отсюда коэффициент подобия по скоростям будет равен: ![]() .
.
Коэффициенты подобия позволяют использовать соотношения между подобными величинами разных объектов в соответствии с теорией размерностей физических величин. Например, обобщённая температура в центре протона с учётом (22) должна быть равна:
![]() ,
(24)
,
(24)
где ![]() обозначают массу
частицы (праона), причём праон относится к протону так же, как сам протон
относится к нейтронной звезде [17], а
обозначают массу
частицы (праона), причём праон относится к протону так же, как сам протон
относится к нейтронной звезде [17], а ![]() есть постоянная,
аналогичная постоянной Больцмана для праонного уровня материи.
есть постоянная,
аналогичная постоянной Больцмана для праонного уровня материи.
Из определения праона видно, что ![]() . Кроме этого, по теории размерностей для постоянной сильной
гравитации имеем:
. Кроме этого, по теории размерностей для постоянной сильной
гравитации имеем: ![]() .
.
Постоянная Больцмана имеет размерность Дж/К, и если температура не
подвергается преобразованию подобия, то по теории размерностей будет: ![]() . Подставляя всё это в (24), приходим к равенству обобщённых
температур внутри протона и нейтронной звезды:
. Подставляя всё это в (24), приходим к равенству обобщённых
температур внутри протона и нейтронной звезды:
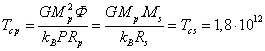 К. (25)
К. (25)
Для давления в центре протона аналогично (22) находим:
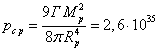 Па.
(26)
Па.
(26)
Мы получили, что давление в центре протона (26) более чем в 30 раз превышает давление в центре нейтронной звезды. Если учесть, что 1 Па = 1 Дж/м3 , то плотность энергии поля давления в центре протона приблизительно в три раза меньше по величине, чем плотность энергии поля гравитонов (19). Различие же плотности энергии от давления в центре нейтронной звезды и плотности энергии поля гравитонов (19) достигает 90 раз.
Кроме этого, у нас совпадают обобщённые температуры в центре протона и нейтронной звезды. Согласно (25) и (21), обобщённая температура в центре этих объектов в 3 раза меньше, чем температура поля гравитонов, рассматриваемого как фотонный газ. Мы можем связать это с тем, что гравитоны не полностью задерживаются веществом нейтронной звезды или протона, и поэтому не могут нагреть это вещество до своей собственной температуры.
С точки зрения теории подобия уровней материи следует ожидать, что на каждом уровне материи соотношение между плотностью энергии поля гравитонов и плотностью энергии поля давления в центре самого плотного объекта одно и то же. Поскольку характерная скорость вещества и давление в центре протона выше, чем аналогичные величины в нейтронной звезде, то и плотность энергии поля гравитонов сильной гравитации на уровне атомов должна быть соответственно больше. Отсюда вытекает зависимость эффективной плотности энергии поля гравитонов от уровня материи.
По нашему мнению, основными источниками поля гравитонов на некотором уровне материи являются излучения от самых плотных объектов более низких уровней материи. Например, ядро нейтронной звезды постоянно нагревается под действием падающих на него потоков гравитонов. Степень нагрева можно оценить по формуле (22), где даётся обобщённая температура. Кинетическая температура поверхности нейтронных звёзд определяется из наблюдений и имеет типичное значение порядка 106 К, а тепловая светимость редко превышает значение 1026 Дж/c [18].
Хотя кинетическая температура заметно меньше, чем обобщённая температура, ядро звезды нагрето достаточно для того, чтобы постоянно испускать потоки нейтрино, вылетающие из звезды и вливающиеся в окружающее поле гравитонов. В момент образования нейтронной звезды или при её преобразовании в магнитар с перестройкой конфигурации магнитного момента, возникают мощные и направленные магнитным полем (через связь общего магнитного поля и магнитных моментов нуклонов) потоки нейтрино, которые будут эффективно действовать и на более высоком уровне материи, чем звёздный уровень.
Нейтронные звёзды генерируют не только потоки нейтрино, но и приводят к
возникновению космических лучей, как это следует из изучения остатков
сверхновых. В [5] и [8] делается предположение о том,
что магнитары могут обладать положительным электрическим зарядом величиной до ![]() Кл, здесь
Кл, здесь ![]() – элементарный
электрический заряд, и используются коэффициенты подобия. Энергия протона на
поверхности заряженного магнитара будет достигать
– элементарный
электрический заряд, и используются коэффициенты подобия. Энергия протона на
поверхности заряженного магнитара будет достигать ![]() Дж или
Дж или ![]() эВ. Для сравнения, наибольшие значения регистрируемых энергий
космических лучей в расчёте на 1 нуклон оцениваются величиной порядка
эВ. Для сравнения, наибольшие значения регистрируемых энергий
космических лучей в расчёте на 1 нуклон оцениваются величиной порядка ![]() эВ, и такова же максимальная энергия регистрируемых фотонов и
нейтрино [19-20]. Если предположить, что космические
лучи ускоряются с поверхности дискона, окружающего магнитар, то для энергии
излучаемой частицы с одним элементарным зарядом можно записать:
эВ, и такова же максимальная энергия регистрируемых фотонов и
нейтрино [19-20]. Если предположить, что космические
лучи ускоряются с поверхности дискона, окружающего магнитар, то для энергии
излучаемой частицы с одним элементарным зарядом можно записать: ![]() Дж или
Дж или ![]() эВ, здесь
эВ, здесь ![]() м обозначает звёздный радиус Бора, причём
м обозначает звёздный радиус Бора, причём ![]() , где
, где ![]() – радиус Бора в атоме
водорода,
– радиус Бора в атоме
водорода, ![]() – коэффициент подобия
по размерам. Совпадение энергии
– коэффициент подобия
по размерам. Совпадение энергии ![]() с энергией
регистрируемых частиц говорит о том, что вероятным источником космических лучей
действительно могут быть магнитары с дисконами.
с энергией
регистрируемых частиц говорит о том, что вероятным источником космических лучей
действительно могут быть магнитары с дисконами.
В такой картине энергия поля гравитации перерабатывается нейтронными звёздами в различных механизмах в энергию частиц (нейтрино, протоны, фотоны), высокая энергия которых обеспечивает частицам большую проникающую способность. Перенося это на другие уровни материи, мы находим источник поля гравитонов – это излучения от самых плотных объектов, наподобие нуклонов и нейтронных звёзд, в том числе от объектов типа атомов. Наличие у магнитара постоянного электрического заряда позволяет ему генерировать космические лучи и различные частицы длительное время – по аналогии с практически вечным протоном. Таким образом, если каждый уровень материи обладает длительным временем существования, его будет достаточно для преобразования энергии поля гравитонов низших уровней материи в энергию гравитонов, которые будут действовать на более высоких уровнях материи.
Наличие в потоках гравитонов заряженных частиц позволяет объяснить
механизм притяжения и отталкивания между зарядами разных и противоположных
знаков [5], действующему подобно механизму
Фатио-Лесажа для силы гравитационного притяжения масс. Отсюда следует
одинаковая форма законов в силе Кулона для зарядов и в силе Ньютона для масс, и
подобие уравнений Максвелла с уравнениями гравитационного поля в
лоренц-инвариантной теории гравитации [8].
Коэффициенты подобия позволяют вычислить многие величины, характеризующие
различные уровни материи. Для примера в дополнение к постоянной Планка ![]() введём в рассмотрение
ещё две аналогичные постоянные. Одна из них, звёздная постоянная Планка,
рассчитывается с помощью коэффициентов подобия:
введём в рассмотрение
ещё две аналогичные постоянные. Одна из них, звёздная постоянная Планка,
рассчитывается с помощью коэффициентов подобия: ![]() Дж·с. Эта величина характеризует
вращение звёзд. Если предположить, что величина
Дж·с. Эта величина характеризует
вращение звёзд. Если предположить, что величина ![]() равняется моменту
импульса нейтронной звезды
равняется моменту
импульса нейтронной звезды ![]() , где
, где ![]() , то отсюда находится период вращения такой звезды:
, то отсюда находится период вращения такой звезды: ![]() с. Для сравнения, период вращения одного из самых быстрых
пульсаров PSR J1748-2446ad в 2,5 раза короче и составляет
с. Для сравнения, период вращения одного из самых быстрых
пульсаров PSR J1748-2446ad в 2,5 раза короче и составляет ![]() с. Аналогично, в квантовой механике для протона величина
с. Аналогично, в квантовой механике для протона величина ![]() принимается в качестве
величины спина этой частицы. В [16] радиус
протона равен
принимается в качестве
величины спина этой частицы. В [16] радиус
протона равен ![]() м, угловая скорость вращения
м, угловая скорость вращения ![]() рад/с при спине протона
рад/с при спине протона ![]() , а максимально возможная угловая
скорость достигает
, а максимально возможная угловая
скорость достигает ![]() рад/с.
рад/с.
В цепочке нейтронная звезда – протон объектом нижележащего уровня материи
является праон, для которого характерной планковской постоянной будет ![]() Дж·с. В связи с тем, что различным
уровням материи соответствуют различные постоянные Планка и различные энергии
излучения соответствующих квантов, на каждом уровне материи соотношение для
энергии электромагнитного кванта
Дж·с. В связи с тем, что различным
уровням материи соответствуют различные постоянные Планка и различные энергии
излучения соответствующих квантов, на каждом уровне материи соотношение для
энергии электромагнитного кванта ![]() должно содержать свою
собственную постоянную Планка. Так, на уровне праонов энергия кванта будет
должно содержать свою
собственную постоянную Планка. Так, на уровне праонов энергия кванта будет ![]() , где
, где ![]() есть частота кванта.
Следующим нижележащим уровнем материи является уровень граонов, причём граон относится к праону так же,
как сам праон относится к протону.
есть частота кванта.
Следующим нижележащим уровнем материи является уровень граонов, причём граон относится к праону так же,
как сам праон относится к протону.
Остановимся ещё на длине свободного пробега гравитонов. В космическом
пространстве согласно выводам Lambda-Cold Dark Model (![]() ) критическая плотность массы достигает величины
) критическая плотность массы достигает величины ![]() кг/м3 , если принять, что постоянная Хаббла
кг/м3 , если принять, что постоянная Хаббла ![]() равна 70 км/(с·Мпк) [21]. Физическая
плотность видимой барионной материи составляет при этом
равна 70 км/(с·Мпк) [21]. Физическая
плотность видимой барионной материи составляет при этом ![]() кг/м3 , что
даёт концентрацию
кг/м3 , что
даёт концентрацию ![]() нуклона на кубический
метр. Из соотношения
нуклона на кубический
метр. Из соотношения ![]() при данной концентрации
нуклонов и значении
при данной концентрации
нуклонов и значении ![]() согласно (18) находим
длину свободного пробега гравитонов:
согласно (18) находим
длину свободного пробега гравитонов: ![]() м. Эта величина на 23 порядка больше видимого размера
Вселенной, оцениваемого величиной 14 миллиардов парсек или
м. Эта величина на 23 порядка больше видимого размера
Вселенной, оцениваемого величиной 14 миллиардов парсек или ![]() м. Следовательно, гравитоны вполне могут достичь нашей
Вселенной издалека.
м. Следовательно, гравитоны вполне могут достичь нашей
Вселенной издалека.
С точки зрения подобия уровней материи совокупность всех звёзд в видимой
Вселенной соответствует чрезвычайно разреженному атомному газу. На первый
взгляд такой разреженный газ из звёзд, даже с учётом нижележащих уровней
материи, не может сам по себе создать ту плотность энергии поля гравитонов ![]() Дж/м3, которую мы нашли в (19). Но в отдалённых
областях космического пространства плотность вещества может оказаться намного
больше и достигнуть таких значений, что как раз способна генерировать
необходимую плотность энергии поля гравитонов, достигающих нашей Вселенной.
Дж/м3, которую мы нашли в (19). Но в отдалённых
областях космического пространства плотность вещества может оказаться намного
больше и достигнуть таких значений, что как раз способна генерировать
необходимую плотность энергии поля гравитонов, достигающих нашей Вселенной.
В [17] мы объяснили эффекты красного смещения спектров галактик и ослабления излучения от далёких сверхновых тем, что свет рассеивается на новых частицах. Указанные частицы являются нейтральными частицами типа мюонов, появившиеся естественным образом аналогично тому, как возникают белые карлики в ходе звёздной эволюции. Размеры новых частиц и их концентрация в космическом пространстве согласно теории бесконечной вложенности материи как раз таковы, что позволяют объяснить рассеяние света. Новые частицы объясняют также появление фонового излучения и эффекты, приписываемые тёмной материи. Если принять существование новых частиц, то отпадают важнейшие аргументы в пользу модели Большого взрыва. Мы уже не связаны временем 13,8 млрд. лет, как возрастом Вселенной. Если Вселенная существует больше, чем это время, то тогда гравитоны имеют возможность попасть в нашу Вселенную извне и осуществлять здесь своё действие.
6. Происхождение массы
Рассмотрим плотность энергии поля гравитонов внутри тела и рядом с ним.
Пусть имеется тело в виде куба с ребром ![]() . Количество гравитонов
. Количество гравитонов ![]() в единицу времени
через единичную площадку при движении гравитонов в веществе уменьшается по
формуле (2). За время
в единицу времени
через единичную площадку при движении гравитонов в веществе уменьшается по
формуле (2). За время ![]() шесть потоков
гравитонов с каждой из сторон пройдут куб насквозь через грани с площадью
шесть потоков
гравитонов с каждой из сторон пройдут куб насквозь через грани с площадью ![]() и изменятся до
величины:
и изменятся до
величины:
![]() ,
, ![]() ,
,
где ![]() есть число прошедших
через куб гравитонов.
есть число прошедших
через куб гравитонов.
Если бы гравитоны пролетали через такой же пустой объём, их количество на
выходе было бы ![]() . Следовательно, количество гравитонов, которые
взаимодействовали с веществом, составит:
. Следовательно, количество гравитонов, которые
взаимодействовали с веществом, составит:
![]() .
.
Предположим, что все эти гравитоны не просто передали веществу весь свой импульс и создали силу гравитации, но ещё и передали веществу всю свою энергию. Тогда для плотности этой энергии с учётом (16) имеем:
![]() .
(27)
.
(27)
Если нейтронная звезда имеет радиус 12 км и массу 1,35 массы Солнца, то
средняя концентрация нуклонов составит ![]() м-3 . Используя (18-19) и полагая
м-3 . Используя (18-19) и полагая ![]() , находим
, находим ![]() , а также
, а также ![]() Дж/м3 . Таким
образом, если бы взаимодействующие с веществом гравитоны передавали бы ему не
только импульс, но и свою энергию, плотность такой энергии достигла бы огромной
величины
Дж/м3 . Таким
образом, если бы взаимодействующие с веществом гравитоны передавали бы ему не
только импульс, но и свою энергию, плотность такой энергии достигла бы огромной
величины ![]() за малое время
за малое время ![]() с . Так как мы не можем представить себе, чтобы нейтронная
звезда могла накапливать столь большие количества энергии, мы должны полагать,
что хотя гравитоны передают веществу звезды свой импульс, но практически вся их
энергия должна переизлучаться обратно. Если умножить
с . Так как мы не можем представить себе, чтобы нейтронная
звезда могла накапливать столь большие количества энергии, мы должны полагать,
что хотя гравитоны передают веществу звезды свой импульс, но практически вся их
энергия должна переизлучаться обратно. Если умножить ![]() в (27) на объём звезды
и разделить на время
в (27) на объём звезды
и разделить на время ![]() , получим оценку гравитонной светимости звезды как мощности
потока энергии гравитонов, взаимодействующих с веществом звезды:
, получим оценку гравитонной светимости звезды как мощности
потока энергии гравитонов, взаимодействующих с веществом звезды: ![]() Вт.
Вт.
В природе немало процессов, когда падающая на тела энергия почти полностью отражается или рассевается, не нагревая эти тела. Одним из примеров является зеркало, принимающее на себя импульс фотонов и отражающее их обратно с той же энергией. Другим примером является нагрев планет Солнцем – как бы ни излучало Солнце, вся энергия света, упавшего на поверхность планет, излучается в конце концов обратно в космос. Но чем ближе планета к Солнцу, тем больше поток энергии падает на неё и тем больше температура поверхности планеты и её атмосферы. Поскольку поле гравитонов везде одинаково, то где бы ни было тело, температура внутри тела, возникающая как следствие переработки энергии потоков гравитонов, будет неизменна, если не меняются параметры тела. По-видимому, температура от потоков гравитонов не превышает той максимальной температуры, которая соответствует теореме вириала, связывающей внутреннюю (тепловую) энергию массивного тела и его гравитационную энергию.
Вычислим из (27) гравитонную светимость тела в виде куба, умножая ![]() на объём
на объём ![]() и деля на время
и деля на время ![]() . Выражая концентрацию нуклонов через массу, с учётом (16)
имеем:
. Выражая концентрацию нуклонов через массу, с учётом (16)
имеем:
![]() ,
, ![]() . (28)
. (28)
Из (28) следует, что гравитонная светимость тела ![]() , понимаемая как светимость тех потоков гравитонов, которые
взаимодействовали с веществом и передали ему свой импульс, пропорциональна
массе тела
, понимаемая как светимость тех потоков гравитонов, которые
взаимодействовали с веществом и передали ему свой импульс, пропорциональна
массе тела ![]() . Это означает, что масса, как мера инерции тела, может быть
выражена через параметры потоков гравитонов, взаимодействующих с телом. Чем
больше гравитонов передают свой импульс телу в единицу времени, тем больше
масса и инерция тела, тем больше требуется сила для ускорения тела.
. Это означает, что масса, как мера инерции тела, может быть
выражена через параметры потоков гравитонов, взаимодействующих с телом. Чем
больше гравитонов передают свой импульс телу в единицу времени, тем больше
масса и инерция тела, тем больше требуется сила для ускорения тела.
В (28) присутствует произведение ![]() , равное количеству нуклонов в рассматриваемом теле. Тогда
гравитонная светимость в расчёте на один нуклон с учётом (16) будет равна:
, равное количеству нуклонов в рассматриваемом теле. Тогда
гравитонная светимость в расчёте на один нуклон с учётом (16) будет равна:
![]() Вт.
(29)
Вт.
(29)
Отношение светимости ![]() к средней энергии
гравитона
к средней энергии
гравитона ![]() даёт количество
гравитонов, которые в единицу времени взаимодействуют с одним нуклоном вещества
и передают ему свой импульс. Согласно (29), это количество гравитонов равно
произведению
даёт количество
гравитонов, которые в единицу времени взаимодействуют с одним нуклоном вещества
и передают ему свой импульс. Согласно (29), это количество гравитонов равно
произведению ![]() , причём сечение
, причём сечение ![]() характеризует
эффективную площадь взаимодействия нуклона с гравитонами, а коэффициент 6
связан с шестью сторонами кубического распределения потоков гравитонов
характеризует
эффективную площадь взаимодействия нуклона с гравитонами, а коэффициент 6
связан с шестью сторонами кубического распределения потоков гравитонов ![]() в (2).
в (2).
Мы можем ещё подставить в (28) значение ![]() из (18):
из (18):
![]() .
.
Из этого соотношения видно, что гравитонная светимость пропорциональна и
почти равна энергии покоя тела, извлекаемой из тела за время ![]() прохождения
гравитонами радиуса тела. С одной стороны это является следствием определения
сечения
прохождения
гравитонами радиуса тела. С одной стороны это является следствием определения
сечения ![]() взаимодействия
гравитонов с веществом в (18). С другой
стороны, действие сильной гравитации на уровне атомов приводит к тому, что
нуклоны имеют характерную скорость своего вещества, равную скорости света. При
этом согласно (23) полная энергия нуклона, приблизительно оцениваемая как
половина его энергии в поле сильной гравитации, равна по модулю энергии покоя в
виде произведения массы на квадрат скорости света. В атомных реакциях с
нуклонами выделяется часть энергии покоя, и на основании вышеизложенного
имеются все основания полагать, что эта энергия обязана своим происхождением
энергии поля гравитонов, действующем на атомном уровне материи.
взаимодействия
гравитонов с веществом в (18). С другой
стороны, действие сильной гравитации на уровне атомов приводит к тому, что
нуклоны имеют характерную скорость своего вещества, равную скорости света. При
этом согласно (23) полная энергия нуклона, приблизительно оцениваемая как
половина его энергии в поле сильной гравитации, равна по модулю энергии покоя в
виде произведения массы на квадрат скорости света. В атомных реакциях с
нуклонами выделяется часть энергии покоя, и на основании вышеизложенного
имеются все основания полагать, что эта энергия обязана своим происхождением
энергии поля гравитонов, действующем на атомном уровне материи.
7. Заключение
Выражения для напряжённостей гравитационного поля внутри шара (8) и за его пределами (15), полученные в модели гравитонов, хорошо согласуются со значениями напряжённостей поля в лоренц-инвариантной теории гравитации. От напряжённостей поля нетрудно перейти к скалярным потенциалам гравитационного поля, поскольку напряжённость с точностью до знака определяется как градиент потенциала. Скалярный потенциал поля с точностью до константы интегрирования находится через контурный интеграл от напряжённости поля, взятый по некоторому пути. При этом потенциал задаёт энергию единичной массы в гравитационном поле, что видно из того, что напряжённость в контурном интеграле является гравитационной силой в расчёте на единицу массы.
До тех пор, пока плотность вещества меньше плотности вещества нейтронных
звёзд, для формул напряжённостей и потенциалов поля будет справедлив принцип
суперпозиции, по которому напряжённость или потенциал системы частиц равны
сумме соответствующих величин отдельных частиц. Как было показано в [22], применение принципа суперпозиции и метода
запаздывающих потенциалов к системе точечных частиц внутри сферы приводит к
формулам, согласно которым гравитационный потенциал системы выглядит так, как
будто он возникает от одной частицы с массой, равной сумме масс частиц системы,
расположенной в центре системы. Далее полученные формулы преобразуются с
помощью преобразований Лоренца согласно лоренц-инвариантной теории гравитации.
Как только гравитационный скалярный потенциал становится известным, с
помощью специальной процедуры [23] в рамках
ковариантной теории гравитации можно найти 4-потенциал, тензор энергии-импульса
гравитационного поля, уравнения гравитационного поля, гравитационную силу, а
также вклад гравитационного поля в уравнение для определения метрики. Это
означает, что теория гравитационного поля как в плоском пространстве
Минковского, так и в искривлённом пространстве-времени, полностью
обосновывается на субстанциональном уровне, через поле гравитонов. При этом
зависимость метрики от потенциала гравитационного поля позволяет учесть влияние
неоднородного поля гравитонов на результаты пространственно-временных
экспериментов, проводимых как правило на основе использования электромагнитных
волн и приборов.
Мы можем применить также аксиоматический подход к общей теории относительности, описанный в [24], для получения уравнения движения и других уравнений. Ньютоновская теория гравитации является одной из основ общей теории относительности, поскольку метрика, находимая из уравнений Эйнштейна, калибруется в пределе слабого гравитационного поля и приводит к классическому закону всемирного тяготения.
Ковариантная теория гравитации и общая
теория относительности являются метрическими теориями. Если в ковариантной теории гравитации гравитация является реальной фундаментальной силой, то в общей теории относительности гравитация заменяется действием метрического поля. В
обеих теориях метрика должна описать некоторые явления, такие как
гравитационное замедление времени и гравитационное красное смещение, которые
появляются как поправки к результатам Ньютоновской теории гравитации.
В (19) мы сделали оценку плотности энергии поля гравитонов, в (18)
представили сечение взаимодействия гравитонов с веществом, в (20) оценили
мощность потока энергии поля гравитонов в одном направлении, в (21) привели
температуру ![]() К поля гравитонов в виде фотонов. Обобщённая температура в
центре типичной нейтронной звезды и протона по всей видимости оказывается ниже
температуры поля гравитонов, как следствие того, что эти объекты не полностью
задерживают потоки гравитонов. На основе принципов теории бесконечной
вложенности материи в качестве источников поля гравитонов предлагаются самые
плотные объекты на каждом уровне материи – нейтронные звёзды и магнитары,
нуклоны и атомы, праоны как компоненты, составляющие нуклоны, и т.д. Указанные
объекты излучают нейтрино, фотоны, высокоэнергичные космические лучи, которые
могут давать свой вклад в поле гравитонов, причём на всех уровнях материи.
К поля гравитонов в виде фотонов. Обобщённая температура в
центре типичной нейтронной звезды и протона по всей видимости оказывается ниже
температуры поля гравитонов, как следствие того, что эти объекты не полностью
задерживают потоки гравитонов. На основе принципов теории бесконечной
вложенности материи в качестве источников поля гравитонов предлагаются самые
плотные объекты на каждом уровне материи – нейтронные звёзды и магнитары,
нуклоны и атомы, праоны как компоненты, составляющие нуклоны, и т.д. Указанные
объекты излучают нейтрино, фотоны, высокоэнергичные космические лучи, которые
могут давать свой вклад в поле гравитонов, причём на всех уровнях материи.
Для сравнения, недавние эксперименты
на релятивистском ионном коллайдере в Брукхэвене
показали [25], что вещество нуклонов может нагреваться в столкновениях до ![]() К. Вещество при этом ведёт
себя подобно жидкости с очень малой вязкостью, а его температура не превышает температуры поля
гравитонов.
К. Вещество при этом ведёт
себя подобно жидкости с очень малой вязкостью, а его температура не превышает температуры поля
гравитонов.
В теории бесконечной вложенности материи мы имеем последовательность уровней материи: уровень граонов – уровень праонов – уровень нуклонов – уровень нейтронных звёзд, и т.д. как в сторону уменьшения, так и в сторону увеличения с точки зрения массы основного объекта на том или ином уровне материи. Каждому уровню материи присуща своя собственная гравитация и своя собственная постоянная, аналогичная по своему смыслу постоянной Планка. Обычная гравитация наиболее сильно проявляется на уровне планет и звёзд, и мы предполагаем, что гравитонами для обычной гравитации являются частицы праонного уровня материи, находящегося на два уровня ниже уровня звёзд, и получившие свою энергию в релятивистских процессах вблизи нуклонов. На уровне нуклонов действует сильная гравитация, и рассуждая по аналогии, гравитонами для сильной гравитации должны быть частицы граонного уровня материи, получившие свою энергию в процессах вблизи праонов. Гравитонами могут быть как нейтральные частицы типа нейтрино и фотонов, так и релятивистские заряженные частицы, подобные по своим свойствам космическим лучам. Эффективной массой для всех этих частиц является их релятивистская масса-энергия с учётом большого по величине фактора Лоренца. В частности, гравитонами могут быть праоны, ускоренные сильными полями вблизи нуклонов практически до скорости света. Как составная часть поля гравитонов, такие релятивистские праоны могут участвовать в создании обычной гравитации согласно модели Лесажа и придавать массу телам на макроуровне. При этом сами праоны имеют свою собственную массу покоя, возникающую от действия на них гравитонов низших уровней материи. Релятивистские праоны при взаимодействии с полями и веществом могут порождать высокоэнергичные фотоны, которые также могут служить в качестве частиц поля гравитонов. Энергия обычных фотонов пропорциональна их частоте и постоянной Планка. Но для частиц, принадлежащих разным уровням материи, значение постоянной Планка согласно бесконечной вложенности материи существенно различается – чем ниже уровень материи, тем меньше соответствующая постоянная Планка, и тем меньше энергии фотонов на этом уровне энергии. В результате поле гравитонов представляет собой многокомпонентную систему из частиц, фотонов и нейтрино, энергии которых привязаны к каждому из бесконечного множества уровней материи.
В формуле (28) мы выразили массу тела через светимость тех потоков гравитонов, которые взаимодействовали с веществом тела и передали ему свой импульс. Масса тела при постоянном объёме пропорциональна концентрации нуклонов, и аналогично количество взаимодействий гравитонов с нуклонами увеличивается с ростом концентрации нуклонов. Таким образом, инерция тела как сопротивление приложенной силе, и гравитационная масса тела порождаются действием поля гравитонов на данное тело. Как следует из принципа относительности, при постоянной скорости движения действие потоков гравитонов с разных сторон уравновешивается, но при ускорении тела это уже не так. При ускорении тела необходимо приложить силу и совершить работу по переводу тела из состояния с одной скоростью в состояние с некоторой другой скоростью. Эта работа совершается против действия потоков гравитонов и приводит к понятию массы как меры инерции тела, пропорциональной приложенной силе и обратно пропорциональной возникающему ускорению. При этом основной вклад в инерцию тел вносит поле гравитонов на уровне атомов, где действует сильная гравитация.
Отметим ещё различие в том, как понимается концепция поля гравитонов. В нашем подходе поле гравитонов является источником силы гравитации, существует как необходимое дополнение к материи в виде элементарных частиц и сложенных из них тел, порождает эти тела в процессах гравитационного скучивания рассеянного вещества, и порождается само через излучение от самых плотных объектов типа граонов, праонов, нуклонов и нейтронных звёзд.
В отличие от этого, в квантовой теории гравитации понятие поля гравитонов
предельно сужается до такого поля гравитонов, на которое может быть разложена
какая-либо гравитационная волна. Таким гравитонам приписывается, по аналогии с
электромагнитной волной и фотонами, зависимость энергии гравитона от постоянной
Планка ![]() и от частоты
гравитационной волны
и от частоты
гравитационной волны ![]() . На наш взгляд, такой подход может оказаться ошибочным,
особенно если учесть, что основная часть гравитонов может порождаться не на
уровне атомов, а на более низком уровне материи, где постоянная Планка должна
быть заменена на другую аналогичную постоянную. С другой стороны, рассмотрение
элементарного процесса излучения в водородном атоме показывает [5], что вместе с электромагнитным квантом при
переходе электрона с некоторого уровня энергии на более низкий уровень, из
атома происходит квадрупольное излучение гравитационного кванта с энергией
. На наш взгляд, такой подход может оказаться ошибочным,
особенно если учесть, что основная часть гравитонов может порождаться не на
уровне атомов, а на более низком уровне материи, где постоянная Планка должна
быть заменена на другую аналогичную постоянную. С другой стороны, рассмотрение
элементарного процесса излучения в водородном атоме показывает [5], что вместе с электромагнитным квантом при
переходе электрона с некоторого уровня энергии на более низкий уровень, из
атома происходит квадрупольное излучение гравитационного кванта с энергией ![]() , зависящей не только от постоянной Планка, но и от скорости
движения
, зависящей не только от постоянной Планка, но и от скорости
движения ![]() электрона и отношения
массы электрона к массе протона
электрона и отношения
массы электрона к массе протона ![]() . Отсюда следует различие процессов излучения
электромагнитных и гравитационных квантов на атомном уровне, а также различие
процессов поглощения этих квантов.
. Отсюда следует различие процессов излучения
электромагнитных и гравитационных квантов на атомном уровне, а также различие
процессов поглощения этих квантов.
В общей теории относительности два тела, вращающиеся друг возле друга, излучают квадрупольную гравитационную волну. С точки зрения ковариантной теории гравитации [5], каждое тело излучает в основном дипольным образом, но в суммарном излучении от системы дипольные компоненты сокращаются и остаётся лишь квадрупольная компонента. Гравитационная волна уносит из системы энергию и момент импульса. Это происходит потому, что при вращении у тел имеется меняющееся со временем центростремительное ускорение и тела производят работу против потоков гравитонов, когда уменьшают свой момент импульса. Как правило, энергия гравитационной волны приравнивается к изменению полной энергии системы в виде двух тел. Очевидно, что такая гравитационная волна есть лишь рябь на том поле гравитонов, которое участвует в образовании гравитационной силы между телами системы. Соответственно, гравитоны такой волны, если их выделять искусственно как порции гравитационной энергии с помощью постоянной Планка, могут не иметь ничего общего с теми реальными гравитонами, которые создают поле гравитонов в нашей модели.
8. Список использованных источников
1. Fatio de Duillier, N. (1701), Die wiederaufgefundene
Abhandlung von Fatio de Duillier: De la cause de la Pesanteur, in
Bopp, Karl, "Drei Untersuchungen
zur Geschichte der Mathematik", Schriften der Straßburger
Wissenschaftlichen Gesellschaft in Heidelberg (Berlin & Leipzig, published 1929) 10:
19–66.
2. Georges-Louis
Le Sage (1756), "Letter à une académicien de Dijon..", ercure
de France: 153–171.
3. Ritz
W. Recherches critiques sur l'Électrodynamique
générale // Ann. de chim.
et phys., 13, 1908.
4. C. W. Misner, K. S. Thorne, and J.
A. Wheeler, Gravitation (W. H.
Freeman, San Francisco, CA, 1973).
5.
Федосин С.Г. Физические теории и бесконечная вложенность
материи. Пермь,
2009, 842 стр., Табл. 21, Ил.41, Библ. 289 назв. ISBN 978-5-9901951-1-0.
6.
Федосин
С.Г. Современные проблемы физики. В поисках
новых принципов, М: Эдиториал УРСС, 2002, 192 стр., Ил.26, Библ. 50 назв. ISBN 5-8360-0435-8.
7. Fedosin S.G. Model of Gravitational Interaction
in the Concept of Gravitons. Journal of Vectorial
Relativity, 2009, Vol. 4, No. 1, P.1–24; Модель гравитационного взаимодействия в концепции гравитонов.
8.
Федосин С.Г. Физика и философия подобия
от преонов до метагалактик. Пермь, Стиль-МГ, 1999, 544 стр., Табл.66, Ил.93,
Библ. 377 назв. ISBN 5-8131-0012-1.
9. Rothman, T.; Boughn, S. (2006). Can Gravitons be Detected? Foundations of
Physics 36 (12):
1801–1825. doi:10.1007%2Fs10701-006-9081-9 .
10.Freeman Dyson. Is a Graviton Detectable? Poincare Prize Lecture,
International Congress of Mathematical Physics, Aalborg, Denmark, August 6,
2012.
11.Maurizio Michelini.
A Flux of Micro Quanta Explains Relativistic Mechanics
and the Gravitational Interaction. Apeiron. 2007, Vol. 14, No 2, P. 65-94.
12.Fedosin S.G. Electromagnetic and Gravitational Pictures of the World. Apeiron,
2007, Vol. 14, No. 4, P. 385 – 413; Электромагнитная и гравитационная
картины мира.
13.Kiefer, C.; Weber, C. On the interaction of mesoscopic quantum systems with
gravity. Annalen der Physik, 2005, Vol. 14, Issue 4, Pages 253 – 278.
14.Fedosin
S.G. Scale Dimension as the Fifth
Dimension of Spacetime. Turkish Journal of
Physics, 2012, Vol. 36, No 3, P. 461 – 464. http://dx.doi.org/10.3906/fiz-1110-20. Масштабное измерение как пятое измерение
пространства-времени.
15.Fedosin S.G. The Integral Energy-Momentum
4-Vector and Analysis of 4/3 Problem Based on the Pressure Field and
Acceleration Field.
American Journal of Modern Physics. Vol. 3, No. 4, 2014, pp.
152-167. http://dx.doi.org/10.11648/j.ajmp.20140304.12 ; Интегральный
4-вектор энергии-импульса и анализ проблемы 4/3 на основе поля давления и поля
ускорений.
16.Fedosin
S.G. The radius of the proton in the self-consistent model. Hadronic Journal, 2012, Vol.
35, No. 4, P. 349 – 363; Радиус
протона в самосогласованной модели.
17.Fedosin S.G. Cosmic Red Shift, Microwave Background, and New Particles. Galilean Electrodynamics,
2012, Vol. 23, Special Issues No. 1, P. 3 – 13; Красное
смещение и космическое микроволновое фоновое излучение как следствие
взаимодействия фотонов с новыми частицами.
18.Alexander Y. Potekhin,
Andrea De Luca and Jose A. Pons. Neutron Stars – Thermal Emitters. arXiv:1409.7666. Accepted by Space
Science Reviews.
19.Piotr Homola.
Ultra-high energy photon studies with the Pierre Auger Observatory. Proceedings
of the 31st International Cosmic Ray Conference, Lod´z, Poland, 2009.
20.Javier Tiffenberg.
Limits on the diffuse flux of ultra high energy neutrinos set using the Pierre
Auger Observatory. Proceedings of the 31st International Cosmic Ray Conference,
Lod´z, Poland,
2009.
21.Hinshaw,
G.F., et.al. Nine-Year Wilkinson Microwave
Anisotropy Probe (WMAP) Observations: Cosmological Parameter Results. ApJS., 2013, Vol. 208, 19H.
22.Fedosin S.G. 4/3 Problem for the Gravitational Field. Advances in Physics Theories and
Applications, 2013, Vol. 23, P. 19 – 25; Проблема 4/3 для гравитационного поля.
23.Fedosin S.G. The Procedure of
Finding the Stress-Energy Tensor and Equations of Vector Field of Any Form. Advanced
Studies in Theoretical Physics, Vol. 8, 2014, no. 18, 771 - 779. http://dx.doi.org/10.12988/astp.2014.47101; Процедура для нахождения тензора энергии-импульса и уравнений векторного поля любого вида.
24.Fedosin S.G. The General Theory of
Relativity, Metric Theory of Relativity and Covariant Theory of Gravitation:
Axiomatization and Critical Analysis. International
Journal of Theoretical and Applied Physics (IJTAP), 2014, Vol. 4, No. 1, P. 9 – 26.
25.'Perfect' Liquid Hot Enough to be
Quark Soup.
Brookhaven National Laboratory News, 2010.
Источник: http://sergf.ru/fg.htm
