In English

Journal of Vectorial Relativity, 2009, Vol. 4, No 1, 1 - 24.

 

МОДЕЛЬ ГРАВИТАЦИОННОГО ВЗАИМОДЕЙСТВИЯ В КОНЦЕПЦИИ ГРАВИТОНОВ

 

С.Г. Федосин

 

intelli@list.ru

 

С помощью представления о гравитонах выводится закон Ньютона для притяжения тел. Получено выражение для гравитационной постоянной через поток импульса гравитонов и коэффициент поглощения. Вычислены значения коэффициента поглощения и мощности энергии потоков гравитонов в пространстве. Показано, каким образом при движении с постоянной скоростью выполняется закон инерции.

 

Ключевые слова: Гравитация; Сила; Экранирование; Инерция

 

PACS: 04.90.+E ; 14.80.-J ; 95.30 Sf ;

 

Одной из самых старых идей относительно природы гравитации является кинетическая теория Фатио – Ле Сажа [1], в которой механическое воздействие частиц (гравитонов) обеспечивает влечение тел друг к другу. Гравитация не только ответственна за притяжение тел, но и в существенной мере обеспечивает целостность и устойчивость самих тел. Стандартными возражениями против теории Фатио – Ле Сажа являются её неспособность точного предсказания относительно возможного гравитационного экранирования, природы и свойств потоков гравитонов, объяснения свободного движения тел по инерции, возможного теплового эффекта от действия гравитонов, вклада гравитационного поля в массу тел.

В работе [2] в качестве гравитонов были приняты космические кванты как составные части фотонов. Анализ взаимодействия этих квантов с веществом на основе эффекта Комптона позволяет вывести формулы для массы тел, инерции и гравитационного взаимодействия. Предлагаемая далее модель гравитационного взаимодействия по-своему решает указанные проблемы, при этом в качестве гравитонов предполагаются не только фотоны, но также нейтрино и релятивистские частицы, подобные космическим лучам.

 

Закон обратных квадратов

Вывод формулы Ньютона для силы гравитационного притяжения двух тел будем осуществлять на основе подхода, изложенного в [3]. Обозначим через  величину, равную числу гравитонов , влетающих снаружи в единицу времени  в единичный телесный угол  и тем самым имеющих компоненту импульса внутрь этого угла:

 

.

 

Величина  есть поток гравитонов, движущихся из бесконечности внутрь единичного телесного угла. Будем считать, что изменение количества гравитонов в единицу времени в слое вещества с плотностью  и толщиной  пропорционально числу влетающих гравитонов:

 

,                           ,                           (1)

 

где  – коэффициент поглощения,

 – половина характерного поперечного размера слоя вещества.

 

Соотношение (1) отражает зависимость между падающим на слой вещества, и выходящим из него количеством гравитонов с точки зрения передачи импульса от гравитонов веществу.  Возьмём теперь два отдельных тела на расстоянии  друг от друга,  причём плотности их вещества могут быть различными. Невзирая на разные плотности будем считать, что тела одинаковы в том смысле, что для них коэффициент поглощения  один и тот же. 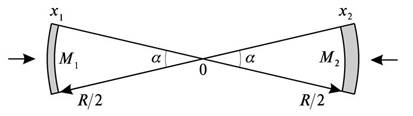В этих телах выберем круглые поверхностные площадки с радиусом, равным величине , и соединим их так, как на рисунке 1. Тогда очень малый телесный угол  будет удовлетворять условию равенства площадей:

 

.                                                        (2)

 

Телесный угол вырезает в рассматриваемых телах объёмы, близкие к шаровым сегментам, с массами  и  соответственно. Массы сегментов  и  зависят от толщины , , и плотностей , , соответственно.

 

454

 

 

Покажем вначале, что в данной конфигурации притяжение сегментов под действием гравитонов подчиняется закону Ньютона. Тем самым мы докажем, что и для обоих тел  в целом закон притяжения будет справедлив. Это следует из произвольности выбора площадок на поверхности этих тел и возможности векторного суммирования сил между всеми возможными парами элементов вещества в силу принципа суперпозиции.  

Из рисунка 1 видно, что массы сегментов равны:

 

,                        ,                               (3)

 

причём значения масс могут быть выбраны бесконечно малыми при подходящем выборе значения . Соответственно, бесконечно малым будет и телесный угол .

Действующая сила есть импульс, переданный веществу гравитонами в единицу времени:

 

,                                                           (4) 

 

где  – импульс одного гравитона,

 – изменение потока гравитонов.

 

Рассмотрим распространение потока гравитонов с левой стороны на рисунке 1, вначале сквозь элемент вещества с массой , затем в пространстве между массами и , и наконец через элемент вещества с массой .

Сила, действующая с левой стороны на  с учётом (4) и (1) равна:

 

   (5)

 

В (5) экспонента была разложена до членов второго порядка. В общем случае расстояние  может быть настолько большим, что нужно учитывать ослабление потока гравитонов при их распространении в пространстве от  до . Для оценки такого ослабления используем формулу типа (1):

 

,                                           (6)

 

где – интенсивность потока гравитонов, прошедших с левой стороны через элемент вещества с массой ,

– интенсивность потока гравитонов, достигших с левой стороны элемента с массой ,

– плотность вещества между  и .

 

Сила с левой стороны на  аналогично (5) равна:

 

 

С учётом выражения (6) и величины , для силы  находим:

 

             (7)

 

Для потока гравитонов справа аналогично (5) и (7)  имеем:

 

 

 

Сила тяготения, действующая на элемент массы  со стороны массы , равна:

 

                  (8)

 

 

 

На элемент массы  со стороны массы  действует сила, равная:

 

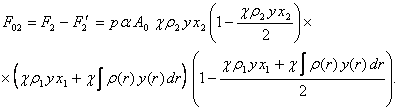                 (9)

 

 

 

Вспомним, что в общем случае гравитационные массы подразделяют на пассивные и активные. Под пассивной массой тела понимают такую массу, которая характеризует тело при его ускорении в заданном гравитационном поле (например, при взвешивании). Соответственно, активная масса тела ответственна за создание вокруг этого тела гравитационного поля.

Сравнение (8) и (9) показывает, что силы  и  не равны друг другу из-за наличия дополнительных сил от источников массы, находящихся между телами. Неэквивалентность вхождения плотностей вещества ,  в (8) и (9) кроме этого означает, что пассивная и активная гравитационная массы тел различаются между собой. При этом, активная масса превышает пассивную массу за счёт ослабления потоков гравитонов в пространстве между взаимодействующими телами. Можно также сказать, что наличие гравитирующей среды вблизи тела эффективно увеличивает его пассивную массу до значения активной гравитационной массы.

Более точное равенство сил между элементами масс  и  осуществляется в том случае, когда расстояние между массами относительно невелико, малы плотность промежуточного вещества  и характерный поперечный размер . Тогда изменением потоков гравитонов в пространстве между массами можно пренебречь.

Для оценки коэффициента поглощения  в веществе будем считать, что член  в (8) и (9) незначителен и его можно не учитывать. После подстановки (3) с учётом (2) для силы тяготения между элементами вещества  и  получаем:

 

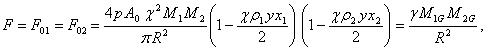      (10)

 

здесь через и  обозначены гравитационные массы элементов вещества, ответственные за силу гравитации. В отличие от них массы  и  вычисляются через измеряемые плотности вещества и объёмы элементов вещества согласно (3). Из (10) находим:

 

,                            ,                     (11)

 

где индекс  различает массы  и . В (11) видно, что гравитационная постоянная  определяется постоянными величинами – средним импульсом одного гравитона, потоком гравитонов, падающим в единицу времени из единичного телесного угла, и квадратом коэффициента поглощения гравитонов в веществе, составленного из нуклонов. Очевидно, что в ходе эволюции Вселенной и при перемещении тел в пространстве может меняться средний импульс гравитонов и плотность их потоков, что будет влиять на эффективное значение гравитационной постоянной. Изменения состава и качества вещества через коэффициент поглощения  также вносят свой вклад в действующие гравитационные силы.

 

Коэффициент поглощения и экранирование

С целью определения коэффициента  будем использовать формулу для гравитационной массы в общей теории относительности (для холодного вещества без учёта энергии давления):

 

,                                               (12)

 

где  и   – радиус и масса тела,

– скорость распространения возмущений поля,

 в приближении однородной плотности вещества.

 

Учтём предварительно, что формула (12) справедлива для тела в виде шара, а массы в (11) согласно рисунку 1 сосредоточены приблизительно в цилиндрической форме. Если в шар вписать цилиндр с высотой, равной основанию цилиндра, то объём шара будет превышать объём цилиндра в  раз. Такое же отношение будет и для масс. При этом высота цилиндра будет больше радиуса шара, так что . Вводя в (12) коэффициент  и сравнивая (11) и (12), получаем:

 

,                        .                 (13)

 

В (13) масса тела  в форме шара была выражена через плотность вещества и объём. Подставляя константы и значение  ,  оценим величину коэффициента поглощения:

 

 м/кг,                                                   (14)

 

если  равняется скорости света.

 

По своему смыслу  отражает свойство ослабления потоков гравитонов при их прохождении в веществе с точки зрения передачи импульса веществу. Оценку длины пробега гравитонов внутри тел, когда они теряют возможность передавать свой импульс, можно сделать на основании условия  для экспоненты в (1). Нейтронные звёзды обладают плотностью вещества порядка 2∙1017 кг/м3. В качестве значения  можно взять диаметр нейтронной звезды. Тогда на пути потока гравитонов необходимо поставить не менее 3 нейтронных звёзд, чтобы заметно уменьшить величину потока. Проникающая способность гравитонов получается настолько большой, что гравитоны можно сравнить лишь с нейтрино с энергией порядка 100 эВ.

Сравним (8), (9) с выражением для силы из [4], которая описывает возможный эффект гравитационного экранирования:

 

.                                        (15)

 

В (15) предполагается, что наличие вещества между телами каким-то образом уменьшает силу их притяжения.

Если поместить дополнительное вещество вблизи тела с массой , то согласно (9) увеличится сила, действующая на массу . Увеличение силы произойдёт так, как будто просто увеличивается гравитационная масса . В этом случае гравитационное экранирование не наблюдается, так как общая сила действия на массу  растёт путём сложения сил.

В противоположной ситуации дополнительное вещество с плотностью распределено снаружи двух тел со всех сторон так, что это в итоге приводит к изменению произведения  для потока гравитонов в единице телесного угла. На тела будет действовать, с учётом формулы типа (6), поток гравитонов:

 

.

 

Заменяя в (10)  на , с учётом (11) получим:

 

 ,                                    (16)

 

Из (16) следует, что если происходит экранировка внешним веществом, то эффективная сила притяжения между телами уменьшается. В отличие от силы (15), предполагаемой в [4], эффект экранировки согласно (16) зависит не только от толщины слоя экранирующего вещества, но и от площади слоя через величину .

 

Сильные поля

Рассмотрим соотношения для гравитационных сил (5) – (9) при больших плотностях вещества, когда уже нельзя без ошибки раскладывать экспоненты в ряды. В частности, для силы  без учёта гравитирующей среды между телами из (8) получаем:

 

.

 

Допустим, что плотности вещества настолько велики, что экспонентами в этом выражении можно пренебречь. С учётом (2) для , (11) для , правой части (13) для , для максимальной силы имеем:

 

.

 

Обозначая , при ранее использованном условии  получается выражение: , а также  (при  для двух массивных соприкасающихся тел).

 

С точностью до множителя порядка единицы мы находим, что гравитационный потенциал на поверхности массивного тела не может превысить величины .

Другой случай получается для нашей Метагалактики с наблюдаемой плотностью её вещества в пределах 10−27 – 10−26 кг/м3. Если подставлять вместо  и  размеры Метагалактики порядка 10 Гпк, то экспоненты в силах также становятся малыми. Получается, что и для Метагалактики гравитационный потенциал не может превысить . По всей видимости, гравитация, создаваемая источниками внутри самой Метагалактики, не способна превратить Метагалактику в чёрную дыру.

 

Движение энергии

Под действием пронизывающих все тела потоков гравитонов возникает гравитационная сила. Очевидно, что многие другие кажущиеся нам постоянными величины у стационарных тел – ускорение свободного падения, энергия поля, энергия покоя частиц и т.д. – могут быть следствием динамических процессов.

Найдём из (11) и (13) выражение для максимальной энергетической силы потока гравитонов, или мощности энергии на единицу телесного угла в данном направлении:

 

Вт/ср ,                                   (17)

 

если  равняется скорости света.

 

Мы можем приблизительно подсчитать эффективную плотность энергии гравитонов в пространстве для случая, если бы эта энергия направлялась со всего пространства только в одну точку. Из полного телесного угла  стерадиан за одну секунду внутрь шара может пройти энергия величиной . За это же время энергия может покинуть шар, если радиус шара будет равен по величине скорости света. Объём такого шара по величине равен . Разделив энергию  на объём шара, находим эффективную плотность энергии гравитонов:

 

 Дж/м3.

 

Величина  весьма велика, она во много раз превышает достижимую в настоящее время плотность энергии в коротких импульсах мощных лазеров (порядка 3·1013 Дж/м3). Плотность энергии  задаёт не всю пространственную плотность энергии потоков гравитонов, а только ту часть, которая может попасть в заданную точку со всех сторон за единицу времени, для гипотетического случая однонаправленного движения энергии.

Оценим теперь максимальную мощность генерации энергии в материальных телах. Из (17) и (1) для ситуации на рисунке 1 имеем:

 

.

 

Используя (3) в виде , выражая массу цилиндра  через  массу шара , уменьшенную в   раз, используя условие  (– радиус шара)   и условие  для полного телесного угла, получим с учётом (13) и (17):

 

.                                      (18)

 

Согласно (18) с точностью до множителя порядка единицы, максимальная мощность генерации энергии равна энергии покоя тела, излучаемой за время прохождения гравитонами радиуса тела: . Отсюда следует, что энергия покоя тел может создаваться и поддерживаться именно гравитацией.

Действительно, через каждое тело проходит поток гравитонов с определённой энергией и температурой. В стационарном случае энергии падающего и исходящего потоков одинаковы, но температура исходящего из тела потока гравитонов должна быть меньше из-за произошедшего взаимодействия с частицами тела. В результате тела получают негэнтропию извне, которая компенсируется выработкой соответствующей энтропии. Энергия, связанная с энтропией тела, реализуется в виде напряжений внутри тела под действием гравитационных сил. Кроме этого, возникают напряжённости поля и за пределами тела. Для гравитационно-связанных тел основной вклад в энтропию делает потенциальная энергия гравитационного поля. Эта энергия связана с телом и может частично перейти в энергию движения только в случае разбаланса между силой гравитации и внутреннего давления. В гипотетическом случае полной изоляции тела от внешней гравитации тело будет переходить в состояние равновесия с увеличением объёма вплоть до распыления вещества. Энтропия при этом будет расти, а гравитационная энергия будет переходить в кинетическую энергию вещества и излучения.

Энергия, связанная с энтропией, достаточно близка к энергии гравитационного поля (в сумме с энергией давления). По сути, эта энергия ответственна за уменьшение массы согласно (12). Чем более тело становится плотным при неизменной массе, тем более сильно происходит взаимодействие гравитонов с веществом. Это приводит к увеличению модуля гравитационной энергии тела, и к увеличению модуля энтропии и напряжений в теле. Само существование потенциальной гравитационной энергии и напряжений в телах есть следствие передачи энергии-импульса гравитонов веществу и преобразования энтропии гравитонов. Энергия потоков гравитонов определяет энергию покоя тел и наблюдаемую массу этих тел, аналогично гравитационная энергия делает свой вклад в изменение массы тела от значения  до значения  в (12).

С качественной точки зрения (18) можно понять ещё из следующих рассуждений. Известно, что в сверхновых излучается большое количество энергии в виде нейтрино, фотонов и быстрых частиц. На начальной стадии коллапса вещества сверхновой, при фоторасщеплении ядер железа и захвате электронов протонами и ядрами, в импульсе длительностью порядка 10 мс излучаются электронные нейтрино . Доля этого импульса в общем балансе нейтринного излучения сверхновой составляет около 5 %. После коллапса вещества образующаяся нейтронная звезда начинает охлаждаться, при этом идут реакции с электронами и позитронами с образованием нейтрино и антинейтрино: , где индекс , различает электронные, мюонные и лептонные нейтрино (антинейтрино). Типичные энергии возникающих нейтрино МэВ, основной их поток излучается в течение 4 секунд. Исходя из результатов измерений количества зафиксированных нейтринных событий, различные оценки энергии сверхновой SN 1987A дают для излучения антинейтрино   значение Дж. Эту энергию следует увеличить, учитывая излучение и других видов нейтрино и антинейтрино. Оценка модуля гравитационной энергии нейтронной звезды даёт: Дж (при массе типичной звезды , где  – масса Солнца, и радиусе звезды км). В [10] можно найти оценку массы вещества, превращающейся в нейтрино и в гравитационные волны – порядка . Получается, что при образовании нейтронной звезды энергия излучаемых нейтрино сравнима с полной гравитационной энергией звезды.

Прежде, чем вещество войдёт в состав нейтронной звезды, оно должно пройти несколько стадий своей трансформации. Вначале разрежённое водородное облако сгущается под действием гравитационных сил, и возникает звезда, в которой начинаются термоядерные реакции. После длительного пребывания на главной последовательности и выгорания термоядерного топлива, в звезде образуется железное ядро. Это ядро коллапсирует в нейтронную звезду после превышения предела массы, допустимого для такого ядра. Перейдём теперь от звёзд к элементарным частицам. В [3] было показано, как исходя из подобия между нуклонами и нейтронными звёздами ввести понятие о сильной гравитации, скрепляющей вещество элементарных частиц. Если нуклоны образуются по той же схеме, что и нейтронные звёзды, то при образовании каждого нуклона также излучается множество мельчайших частиц. Мы можем считать, что по крайней мере часть этих частиц выполняют роль гравитонов.  Эти частицы должны быть подобны по своим свойствам нейтрино и антинейтрино, излучаемым при образовании нейтронных звёзд. Суммарная энергия всех таких гравитонов, возникающих при образовании одного нуклона из мельчайшего разрежённого вещества, должна быть близка к энергии гравитационной связи вещества данного нуклона и к энергии покоя нуклона.  Таким образом, если средняя концентрация вещества в нашей Метагалактике равна 1 нуклон/м3, то соответствующая энергия покоя вещества в 1 м3 будет около Дж, здесь  – масса протона. Предполагаемая нами плотность энергии гравитонов от нуклонов получается того же порядка, что и плотность энергии покоя вещества, то есть  Дж/м3.

Найдём связь между плотностью энергии гравитонов  и величиной  из (17). Пусть имеется сфера радиуса . Время движения гравитонов от центра сферы наружу не превышает значения  . Величина  может быть найдена путём умножения плотности энергии  на объём сферы, и последующего деления на величину полного телесного угла и на время : . Подставляя сюда  из (17) и Дж/м3, можно оценить радиус сферы: м или около 17 Гпк. Эта величина превышает расстояния до самых далёких наблюдаемых галактик и близка к размерам Метагалактики. Следовательно, потоки гравитонов, рождённые нуклонным веществом Метагалактики и пронизывающие её, могли бы быть причиной, порождающей гравитацию макроскопических тел.

Несмотря на относительно небольшое значение плотности энергии гравитонов , происходящей от нуклонов, мощность энергии гравитонов на единицу телесного угла в данном направлении  согласно (17), и эффективная плотность энергии гравитонов  оказываются достаточно большими. Различие между  и  можно представить следующим образом. Если взять произвольную точку , то вклады в поток энергии гравитонов, приходящий в данную точку из единичного телесного угла, делают различные области пространства, находящиеся на разных расстояниях от  внутри данного телесного угла.  Чем дальше от точки  находится излучающая гравитоны область пространства, тем раньше должно быть произведено излучение для того, чтобы оно просуммировалось в  с потоками гравитонов от других областей. Таким образом, эффект накопления мощности потока энергии гравитации может возникнуть за счёт больших размеров Метагалактики. При этом следует полагать, что Метагалактика не находится в стационарном состоянии, а количество её нуклонного вещества увеличивается со временем за счёт образования новых нуклонов из мельчайших частиц рассеянного вещества.

Кроме нейтрино, вклад в гравитацию могут делать световое электромагнитное излучение и космические лучи низших масштабных уровней материи. Действительно, обычные и нейтронные звёзды постоянно излучают фотоны и быстрые частицы, и это же самое происходит на уровне нуклонов. Теперь можно уточнить смысл соотношения (18) следующим образом: Сильная гравитация порождает вещество в виде нуклонов и создаёт потоки гравитонов, электромагнитных квантов и быстрых частиц; полная энергия нуклонов связана с сильной гравитацией, а полная энергия нейтронных звёзд – с обычной гравитацией; гравитоны, световые кванты и быстрые частицы не могут сжать вещество плотнее такого состояния, при котором энергия гравитационной связи вещества превышала бы энергию покоя вещества.

Тепловой нагрев в массивных телах обычно связывают с выделением энергии в процессах гравитационной дифференциации вещества, с наличием распадающихся радиоактивных элементов, с протеканием ядерных реакций синтеза. В космических телах других значимых внутренних источников тепла не обнаруживается. Следовательно, действие гравитонов в стационарных телах не приводит к существенному дополнительному тепловому электромагнитному излучению от тел или тепловому движению вещества. Следует предположить, что потоки энергии гравитонов внутри тел преобразуются в основном так, что снова переходят в энергии потоков гравитонов. Тогда действие гравитонов сводится скорее не к постоянному увеличению внутренней энергии тела или к его нагреву, а к передаче импульса как к источнику давления и гравитационных напряжений в теле. Для иллюстрации этого приведём пример упругого отталкивания маленькой частицы от большого тела. В результате взаимодействия частица почти не изменит своей энергии, но передаст большому телу свой удвоенный импульс. Если множество подобных частиц будет взаимодействовать с телом изотропным образом, то тело будет неподвижным, но окажется под постоянным давлением от потоков падающих частиц.

Поскольку гравитоны взаимодействуют с веществом не полностью упруго, то в определённых реакциях, например в реакциях слабого взаимодействия, выделяется какая-то доля энергии. Это значит, что вещество гравитационно-связанных тел может иметь стабильный источник нагрева за счёт действия гравитонов. Следует предположить, что выделяемая при образовании гравитационно-связанных тел тепловая энергия на один нуклон не превышает потенциальной энергии гравитационной связи в расчёте на один нуклон (это однозначно следует из теоремы вириала и совершении работы гравитацией при сжатии вещества и уменьшении его объёма). В (18) и далее в (18') показывается, что скорость генерации гравитационной энергии в телах зависит от свойств и скорости потоков гравитонов. Гравитационная энергия становится величиной, характеризующей динамический процесс взаимодействия гравитонов с веществом. Отсюда и внутренняя тепловая энергия космических объектов будет некоторой функцией от действия потоков гравитонов, с тем отличием, что вещество в стационарных объектах хотя и подвергается гравитационному давлению, но находится почти в неизменном объёме. Заметим, что вычисленные на основе теоремы вириала средние внутренние температуры космических тел (Земли и Солнца) согласно [3] действительно близки к их настоящим средним температурам.

 

Закон инерции

Попытаемся найти объяснение тому факту, что при движении с постоянной скоростью тела не тормозятся гравитонами, а продолжают движение по инерции. Рассмотрим для примера формулу для гравитационной силы (5). В ней содержится множитель , получающийся в таком виде согласно (17) и (13).

 

Данный множитель включает в себя скорость , которую мы полагаем постоянной в инерциальных системах отсчёта. В (5) имеются ещё произведения величин типа . При движении тел с постоянной скоростью их поперечный размер не меняется, а видимый продольный размер согласно теории относительности испытывает лоренцевое сокращение. Одновременно увеличивается видимая плотность вещества вследствие лоренцевого сокращения объёма тела.  Если считать  поперечным размером,  а  – продольным размером, то при движении тела вдоль  величина  остаётся прежней. Возможным источником отклонения от закона инерции может быть зависимость от скорости величины коэффициента , находящегося в выражении .

 

Таким образом, в (5) почти все члены остаются неизменными и гравитационные силы не зависят от скорости движения с точностью по крайней мере до второго порядка по массе, когда становится необходимым учитывать вклад энергии поля в гравитационную массу. В таком же приближении можно считать точной и специальную теорию относительности, поскольку она включает в себя принцип относительности движения.

Мы можем применить полученный результат к движению планет вокруг Солнца. Пусть планета перемещается относительно системы отсчёта, в которой потоки гравитонов изотропны. Если скорость планеты изменяется медленно, то не возникает и различия в силе давления гравитонов спереди и сзади по отношению к направлению скорости. В качестве оценки в [3] был сделан расчёт силы торможения и соответствующего дипольного излучения гравитационных волн для Юпитера, возникающих за счёт центростремительного ускорения в направлении Солнца. Для времени жизни Юпитера на круговой орбите была получена величина лет. Как видно, для планет сила торможения мала и почти не влияет на их движение.

 

Альтернативный вывод формулы Ньютона

Как видно из приведённых выше расчётов, в (1) и в последующих соотношениях находятся величины  и . Оказывается, что есть возможность получить формулу Ньютона для тяготения тел с помощью других физических величин. Обозначим через  поток гравитонов, пересекающих в единицу времени единичную площадку  из единичного телесного угла :

 

.

 

Будем далее обозначать формулы номерами со штрихом, если они подобны по смыслу тем формулам, которые были приведены ранее. Пусть на рисунке 1 величина  соответствует площади шаровых сегментов, а под углом  будем подразумевать единичный угол . Тогда вместо (2) имеем:

 

.                                                  (2')

 

Можно предположить, что изменение потока гравитонов вследствие затухания в слое вещества толщиной  пропорционально концентрации  рассеивающих частиц (которыми могут быть нуклоны или атомы) и первоначальному потоку гравитонов:

 

,                ,                           (1')

 

где  – некоторый коэффициент, имеющий смысл эффективного сечения рассеяния гравитонов в веществе.

 

Для массы сегментов на рисунке 1 вместо (3) имеем:

 

,                ,                            (3')

 

здесь  – масса одного нуклона,

величины  и  задают концентрации нуклонов в массах  и .

 

Действующая сила, как импульс в единицу времени от потока поглощённых гравитонов, будет равна:

 

,                                                   (4') 

 

где  – импульс одного гравитона.

 

Сила с левой стороны на массу  на рисунке 1 с учётом (4') и (1') равна:

 

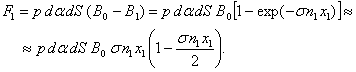                 (5')

 

Изменение потока гравитонов при их распространении в пространстве между массами  и  можно определить следующей формулой:

 

,                                           (6')

 

где – поток гравитонов, прошедших с левой стороны через элемент вещества с массой ,

– потока гравитонов, достигших с левой стороны элемента с массой ,

– концентрация вещества между  и  как функция координаты .

 

Сила с левой стороны на  аналогично (5') равна:

 

 

 

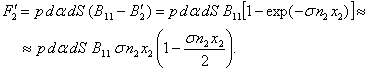
Подставляя сюда (6') и затем , для силы  находим:

 

.           (7')

 

Для потока гравитонов справа аналогично (5') и (7')  имеем:

 

 

.

 

Сила тяготения, действующая на элемент массы  со стороны массы , равна:

 

                             (8')

 

 

 

На элемент массы  со стороны массы  действует сила, равная:

 

                             (9')

 

 

 

Для упрощения будем считать, что сечение  взаимодействия гравитонов с нуклонной формой вещества одинаково для обеих масс  и  . Из (8') и (9') видно, что силы  и  не равны друг другу из-за наличия дополнительных сил от источников массы, находящихся между телами.

Пусть теперь взаимодействующие массы  и  находятся в вакууме и концентрация вещества  между ними равна нулю.  Тогда для силы тяготения между элементами вещества  и , с учётом (3') и (2') получаем:

 

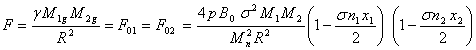,      (10')

 

здесь через  и  обозначены эффективные массы элементов вещества, участвующие в гравитации. Из (10') находим:

 

,              ,                         (11')

 

где индекс  различает массы  и .

 

Согласно (11'), гравитационная постоянная  определяется постоянными величинами – средним импульсом  одного гравитона, потоком гравитонов , падающим в единицу времени из единичного телесного угла на единичную площадку, квадратом эффективного сечения  поглощения гравитонов в нуклонном веществе, массой  одного нуклона.

Максимальное значение  можно оценить из условия  для экспоненты в (1'). Вследствие высокой плотности вещества у нейтронных звёзд концентрация  нуклонов в них достигает  м–3. Если в качестве длины пути  гравитонов в веществе нейтронных звёзд взять утроенный диаметр звезды, то есть величину порядка 90 км, то найдём сечение взаимодействия гравитонов с веществом: м2. Это сечение очень мало и сравнимо лишь с сечением для нейтрино с энергией порядка 100 эВ. С другой стороны, если законы для изменения потоков гравитонов  (1) и (1') подобны, то соответствующие члены внутри экспонент можно приравнять друг другу: . Для нейтронной звезды , и при  (где  – радиус нейтронной звезды)  для сечения с учётом (14) находим:  м2.

Основные выводы относительно эффекта гравитационного экранирования, полученные выше, остаются в силе. Если например, возле массы  добавлять вещество, то сила, действующая на массу , увеличится также, как будто просто растёт масса . Если же масса вещества растёт за пределами  и , то вместо (16) будет:

 

.                                    (16')

 

 

Соотношение (16') близко по смыслу к (15). Оно означает, что если в отсутствие внешнего вещества массы  и  двигаются друг к другу под действием гравитационного притяжения, то при наличии достаточного количества внешнего вещества оно может затормозить движение  и  друг к другу за счёт уменьшения эффективной силы между  и .

В сильных гравитационных полях, если не раскладывать экспоненты в ряды в (5') – (9'), выражения для сил будут несколько другими. Например, для силы  из (8') получаем:

 

.

 

При очень больших концентрациях вещества  и  у двух взаимодействующих масс, например у двух одинаковых близких нейтронных звёзд, вклад от экспонент становится относительно невелик и его можно в первом приближении не учитывать. В этом случае с учётом (2') и (11') для максимальной силы находим:

 

,       а также по закону Ньютона  ,

 

где – масса нейтронной звезды,  – расстояние между центрами звёзд.

 

Отсюда следует, что . Но отношение массы нейтронной звезды к массе нуклона есть коэффициент подобия  по массе между звёздным и нуклонным уровнями материи согласно [3]. Если мы возьмём в качестве  сечение нейтронной звезды и разделим его на величину сечения взаимодействия гравитонов с веществом м2, то у нас действительно получится величина, близкая к .

С другой стороны, под силой  мы можем понимать и силу максимального гравитационного взаимодействия двух нуклонов. В этом случае , где  – радиус нуклона, . Для силы получаем:

 

,

 

 

где  – постоянная сильной гравитации. Согласно [3], постоянная  может быть найдена из условия равенства гравитационной и электрической силы между протоном и электроном на радиусе Бора в атоме водорода. Она определяется выражением м3∙кг –1∙с–2, где  и – заряд и масса электрона, – масса протона, – электрическая постоянная. В то же время, как показано в [3], с помощью постоянной  вычисляется полная энергия нуклона, равная его энергии покоя.

Из выражения для силы  следует, что должно быть . Подставляя сюда гравитационную постоянную , радиус нуклона порядка м, сечение м2, находим значение, достаточно близкое к . Заметим, что сила  между двумя нуклонами весьма велика.

 

В [3] показывается, что эта сила в атомных ядрах может быть уравновешена электромагнитными силами и силой от поля кручения сильной гравитации нуклонов (смотри ещё формулы (19) и далее).

С помощью (11') можно оценить мощность потока энергии гравитонов через единичную площадку из единицы телесного угла:

 

Вт/(ср·м2) ,                               (17')

 

если  считать равной скорости света.

 

Разделив (17') на скорость  и умножив на полный телесный угол , найдём максимально возможный импульс за единицу времени, доставляемый гравитонами на единицу площади. Эта величина приблизительно равна максимальному гравитационному давлению от гравитонов: Па. Кроме этого, , где  есть плотность энергии потоков гравитонов, усреднённая по пространству и по всем направлениям. Соответственно,  во много раз больше, чем эффективная плотность энергии  Дж/м3, доставляемая потоками гравитонов в заданную точку в единицу времени для модельного случая однонаправленного движения энергии.

В обычных моделях нейтронных звёзд давление в веществе на порядок меньше, чем , вероятно потому, что значительная часть гравитонов проходит сквозь них без взаимодействия с передачей импульса силы. Но в нуклонах плотность вещества и его давление как раз на порядок величины превышают соответствующие величины для нейтронных звёзд. Тогда давления  от гравитонов могло бы быть достаточно для поддержания целостности нуклонов. С другой стороны, если гравитоны как нейтрино, фотоны и релятивистские частицы порождаются лишь нуклонами, их энергии будет недостаточно для гравитационной связи вещества нуклонов. Отсюда следует вывод о необходимости существования гравитонов более глубоких уровней материи, с ещё большей плотностью энергии.

Исходя из сечения взаимодействия гравитонов с веществом предположим, что гравитонами являются в частности нейтрино с энергией  эВ Дж. Отсюда можно найти импульс , с помощью которого из (17')  определяется поток гравитонов с–1ср–1м–2 .

 

Найдём теперь мощность генерации энергии в гравитационно связанных телах. С помощью (1') из (17') находим:

 

.

 

Воспользуемся (3') в виде , условием  для полного телесного угла, а также раскроем   с помощью (17'). Наконец, для звёзд при  используем полученное выше условие , делая замену , где  – радиус звезды. Это даёт следующее:

 

.                (18')

 

 

Из (18′) следует, что мощность генерации гравитационной энергии в обычных телах приблизительно равна гравитационной энергии тела, излучаемой за время прохождения гравитонами радиуса тела: . Гравитационная энергия связи нуклонов в поле сильной гравитации по порядку величины равна их энергии покоя, поэтому (18′) в применении для нуклонов (с заменой  на )  совпадает по смыслу с (18) для максимальной энергии гравитации.

 

Сила инерции

Как известно, при ускорении все тела оказывают сопротивление, которое называют силой инерции. Пусть тело постоянной массы ускоряется прямолинейно некоторой силой . Если в данный момент скорость тела , то для изменения полной энергии тела можно записать:

 

,  где .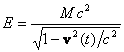

 

 

Дифференцируя энергию по времени, выразим силу через ускорение:

 

.

 

Перед ускорением  стоит так называемая продольная масса.

 

Полученная сила согласно третьему закону Ньютона о равенстве сил действия и противодействия по величине должна равняться силе инерции. Что же является причиной силы инерции, почему тела сопротивляются изменению своей скорости? Исходя из изложенного выше, причиной сил инерции должно быть действие потоков гравитонов. Во-первых, гравитоны ответственны за гравитационную энергию, а на уровне нуклонов и за энергию покоя тел. Следовательно,  изменение энергии в результате изменения движения тел должно быть связано с гравитонами.  Во-вторых, при постоянной скорости движения сила инерции не наблюдается, но проявляется при ускорении тел. Следовательно, при ускорении происходит выполнение работы над телом, одновременно тело  производит работу против потоков гравитонов. Можно считать, что независимо от вида работы, произведённой над телом, эта работа произведена в отношении потоков гравитонов, проходящих через тело.

 

Относительность движения

Рассмотрим ситуацию, когда два тела с массами  и  находятся на одной прямой вдоль вертикальной оси  и синхронно движутся с постоянной скоростью в горизонтальном направлении вдоль оси  системы отсчёта К. Пусть в системе отсчёта , в которой оба тела покоятся, оси  параллельны осям  системы отсчёта К. В  между телами имеется притяжение за счёт взаимного экранирования потоков гравитонов. А как будет происходить гравитационное взаимодействие при одновременном движении этих тел с точки зрения неподвижного наблюдателя в К?

Во-первых, для расчёта сил следует помнить о запаздывании гравитационного воздействия за счёт ограниченной скорости распространения гравитации. В рассматриваемом случае должно выполняться условие равенства времени: пока масса  проходит путь  со скоростью , поток гравитонов от массы  движется в сторону массы  со скоростью . Это можно выразить так: , где  – расстояние между массами.

 

Во-вторых, наблюдателю в системе отсчёта К кажется, что поскольку гравитоны от массы  движутся, как бы догоняя массу , их импульс направлен не строго вдоль оси . Тогда как будто бы должна возникать сила, в итоге тормозящая движение  вдоль оси . Это же самое можно сказать и в отношении торможения массы . Однако направление силы между  и  не должно изменяться в системе отсчёта , поскольку массы движутся с постоянной скоростью на неизменном расстоянии друг от друга.

Чтобы избежать противоречия, следует считать, что если массы  и  движутся со скоростью , то поток гравитонов,   взаимодействующий с этими массами, также имеет компоненту скорости, равную  и направленную вдоль оси . Общая скорость этих гравитонов в системе отсчёта К должна быть равна , поэтому скорость гравитонов вдоль оси  должна быть меньше  и равна . Следовательно, . Используем теперь для преобразования скоростей гравитонов в разных системах отсчёта векторную формулу сложения скоростей из теории относительности:

 

,

 

 

 

здесь – скорость любого объекта в системе отсчёта,

– скорость данного объекта в системе отсчёта К ,

– скорость движения системы отсчёта  относительно К,

.

 

У нас , , , . Из формулы сложения скоростей получаем: , .

 

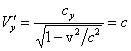С точки зрения второго наблюдателя, находящегося на движущейся массе , падающий на неё поток гравитонов от массы  направлен только вдоль оси . Следовательно, торможения масс вдоль осей  и  не будет. Для случая параллельного движения двух масс  и  вдоль оси  из расчёта в [3] для модуля гравитационной силы в системах отсчёта  и К вытекает следующее: ,  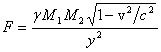  где – расстояние между массами вдоль оси .

 

При этом для наблюдателя в системе отсчёта К сила  между массами уменьшается по мере увеличения скорости  движения масс. Это соответствует тому, что эффективная скорость гравитонов вдоль оси  для движущихся масс также уменьшается: .

 

Гравитоны и теория относительности

Выше была показана относительность движения с учётом того, что скорости преобразуются согласно формуле сложения скоростей из теории относительности. В специальной теории относительности рассматривают запаздывание гравитационного влияния уже не просто от движущейся точечной массы, а от конечного по размерам тела. Именно это вносит такую поправку в потенциал гравитационного поля, которая в итоге приводит к преобразованиям координат Лоренца. При этом у гравитационной силы между двумя движущимися телами, вычисленной через градиент потенциала, возникает недостаток силы. Если данный недостаток силы компенсируется в электромагнетизме через магнитную силу, то в гравитации  вводится дополнительная сила от кручения.  В лоренц-инвариантной теории гравитации (ЛИТГ) уравнения для напряжённостей поля имеют вид [3], [5]:

 

             

(19)

,   ,

 

где векторы   и  – напряжённость гравитационного поля (гравитационное ускорение) и кручение соответственно,

– вектор плотности потока массы,

 – скорость распространения гравитации.

 

Гравитационная  сила, действующая на массу , определяется  выражением:   , где – скорость движения массы.

Векторы   и     можно выразить с помощью скалярного  и векторного  потенциалов гравитационного поля:

 

                                                        (20)

 

Из потенциалов поля можно составить 4-вектор потенциала :

 

.

 

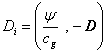Используем ещё 4-вектор плотности импульса:

 

 

 

 

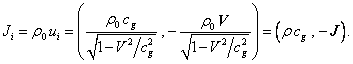
Из (19) и (20) вытекает, что действие четырёхмерного даламбертиана на 4-вектор потенциала даёт вектор, пропорциональный 4-вектору :

 

□2                                                   (21)

 

 

Уравнение (21) есть волновое уравнение для потенциалов. Следует сказать, что если двигаться из общей теории относительности (ОТО) в сторону слабых гравитационных полей путём разложения уравнений для метрики до первого порядка, то как раз получаются уравнения ЛИТГ (19). Это показано, например, в [6] и [7],  когда искали эффект экранирования гравитационного поля. Таким образом, концепция гравитонов согласуется с ЛИТГ, а гравитационные силы не требуют своего обоснования через общую теорию относительности. В таком случае, какую роль играет ОТО в связи с гравитацией с точки зрения ЛИТГ?

Специальная теория относительности выявила зависимость явлений и результатов пространственно-временных измерений от скорости движения систем отсчёта, взятой по отношению к скорости света. ОТО делает следующий шаг – она учитывает то, что масса-энергия вещества и имеющихся в пространстве полей воздействует на ход времени и значения измеряемых длин. Подобное влияние сопровождается изменением скорости электромагнитных волн (света), используемых в том числе в измерительных приборах.

В ЛИТГ гравитационное поле является самостоятельным физическим полем. Поэтому для правильного использования ОТО (или соответствующей метрической теории) нужно предварительно взять тензор энергии-импульса гравитационного поля, ковариантным образом определённый в ЛИТГ. После этого, зная все компоненты тензоров энергии-импульса материи, электромагнитного и гравитационного полей, можно подставлять их в уравнения для метрики.

Полученное решение в виде компонент для метрического тензора, сшитое на границах между веществом и пустым пространством, где присутствует только поле,  задаёт степень отличия метрики рассматриваемой неинерциальной системы от инерциальной системы отсчёта. Метрическое поле, состоящее из компонент метрического тензора и зависящее от времени и координат точки, где оно определяется, будет производным и суммарным эффектом от имеющейся плотности вещества, давления в нём, состояния движения этого вещества (скорости, ускорения), а также от имеющихся гравитационных и электромагнитных полей и других возможных величин энергии-импульса.

Расчёты, произведённые в работе [3] в отношении вклада энергии гравитационного поля в метрику, показали, что добавка имеет величину второго порядка и содержит члены с четвёртой степенью скорости распространения поля. Растущая точность гравитационных экспериментов вероятно позволит в ближайшем будущем проверить наличие указанных поправок. В описанном подходе метрическое поле уже не может считаться полем гравитации. Одновременно решается известная проблема с ковариантностью тензора энергии гравитационного поля в ОТО, поскольку этот тензор в ковариантном виде присутствует в ЛИТГ.

 

Заключение

С учётом вышеизложенного складывается следующая картина: потоки гравитонов со всех сторон проходят через тела почти без потери своего суммарного импульса. Вследствие эффекта взаимного экранирования и взаимодействия гравитонов с веществом все тела испытывают притяжение друг к другу. Взаимодействие гравитонов с веществом происходит так, что тела постоянно получают и отдают энергию, равную энергии их гравитационной связи. В статическом случае ситуация напоминает явление почти идеального отражения света зеркалом, когда на зеркало оказывается давление от излучения, но энергия передаётся зеркалу лишь в малой степени. Точно также на все тела действует гравитационное давление, но гравитация не приводит к существенному нагреву тел.

По нашему мнению, гравитонами являются очень мелкие многочисленные частицы, движущиеся со световыми скоростями и имеющие свойства, подобные нейтрино небольших энергий. Тогда цельность всех материальных объектов является следствием баланса сил гравитации и внутренних сил от давления (движения) частиц, составляющих эти объекты. Из пропорциональности сил тяготения массе тел следует, что гравитационная масса отражает способность тела получать от гравитонов импульс силы. Согласно общей теории относительности, масса определяется не только количеством частиц в теле, но и характером их взаимодействия или общей (суммарной) энергией. Если гравитоны более или менее равномерно распределены в пространстве и являются характерным свойством материи, то это позволяет связать глобальное и локальное, инертные и гравитационные массы в несколько переделанном принципе Маха: «Ускорения тел при взаимодействиях определяются не только самими телами (их массами), но и свойствами окружающей их среды».

В предположении, что гравитонами  являются мельчайшие релятивистские частицы, можно сделать определённые выводы с помощью теории бесконечной вложенности материи [8]. На каждом уровне материи, будь то нуклонное вещество или уровень звёзд, наиболее плотными и гравитационно-связанными объектами вырабатываются в различных процессах соответствующие потоки гравитонов. Тогда в мире существует целый спектр гравитонов различного уровня энергий и плотности, делающих свой вклад в гравитацию. Как было показано выше, в создании потоков гравитонов участвует практически весь объём Метагалактики.

Допустим, что обычная гравитация в какой-то степени порождается релятивистскими частицами от нуклонной формы вещества. Рассуждая по индукции, следует допустить, что и сами нуклоны возникают под действием подобных частиц от более глубокого уровня материи. Кроме этого видно, что потоки нейтрино или гравитонов высшего уровня состоят из потоков нейтрино и гравитонов низшего уровня материи. Действительно, нейтринный импульс от нейтронной звезды при какой-либо трансформации её вещества есть суммарный поток нейтрино и антинейтрино от нуклонов звезды. Поскольку при движении вниз по масштабным уровням материи растёт плотность энергии соответствующих объектов, то аналогично должна расти плотность энергии гравитонов и сила гравитации.

Мы можем оценить плотность энергии потоков гравитонов для метагалактического уровня материи, который так же превышает звёздный уровень материи, как звёздный уровень превышает атомный уровень. В соответствии с теорией подобия, отношение плотностей энергии связано с коэффициентами подобия: , где  есть коэффициент подобия по скоростям,  – коэффициент подобия по размерам согласно [3]. Подставляя сюда Дж/м3, , , находим Дж/м3. Поскольку гравитация на некотором уровне материи вызывается потоками гравитонов низшего уровня материи, то следует сопоставить  с плотностями энергии возможных источников гравитонов, существующих на звёздном уровне материи. Хорошо известными источниками являются микроволновое фоновое излучение с плотностью энергии порядка 4,18·10–14 Дж/м3, световое излучение звёзд с плотностью энергии около 8·10–13 Дж/м3, и космические лучи, дающие приблизительно 1,3·10–13 Дж/м3. Таким образом, гравитонами для метагалактического уровня материи могут оказаться имеющиеся в космосе потоки фотонов, нейтрино и релятивистских частиц, большей частью высокоэнергетичных протонов. Отсюда следует, что обычная гравитация на уровне планет и звёзд имеет источники гравитонов, принадлежащие более низкому уровню материи, чем нуклонно-атомный уровень.   

Естественным было бы называть изотропной такую систему отсчёта, в которой все потоки гравитонов распределены в пространстве изотропно, одинаково по всем направлениям. В такой системе отсчёта, при условии бесконечной малости массы системы, потоки гравитонов становятся также однородными, одинаковыми во всех точках системы отсчёта. Тогда гравитационное ускорение в системе в любом направлении стремится к нулю, а изотропная система отсчёта становится инерциальной. В силу закона инерции инерциальными будут и такие системы отсчёта, которые движутся с постоянной скоростью относительно изотропной системы отсчёта. Однако изотропная система отсчёта не задаёт абсолютное пространство по Ньютону, поскольку в космическом пространстве потоки гравитонов не могут быть однородными, и в каждой точке имеется своя изотропная система отсчёта.

Существование изотропной системы отсчёта является одной из аксиом в расширенной специальной теории относительности (РСТО), представленной в [9]. Как оказывается, формулы специальной теории относительности могут быть выведены из двух основных постулатов – из принципа относительности и существования изотропной системы отсчёта. Одним из результатов РСТО стал принцип постоянства скорости света в инерциальных системах отсчёта. Этот принцип раньше не мог  быть доказан и считался аксиомой теории относительности. 

С точки зрения концепции гравитонов можно определить различие между пассивной и активной гравитационными массами, которые отличаются также от массы, находимой из измерений через плотность и объём. Анализ предсказываемого эффекта гравитационного экранирования теоретически подтверждается для случая, когда тела экранированы веществом извне.

 

 

Литература

                               

1.       Теория гравитации Лесажа на сайте энциклопедии «Традиция»; на сайте http://en.wikipedia.org/wiki/Le_Sage's_theory_of_gravitation .

2.       Maurizio Michelini. The Physical Reality Underlying the Relativistic Mechanics and the Gravitational Interaction. – arXiv: physics/0607136 v1, 14 Jul 2006.

3.       Федосин С.Г. Физика и философия подобия от преонов до метагалактик. – Пермь: Стиль-МГ, 1999 – 544 с.

4.       Q. Majorana // Philos. Mag., 1920, Vol. 39, P.488.

5.       Fedosin S.G. Electromagnetic and Gravitational Pictures of the World. // Apeiron, Vol. 14, No. 4, P.385-413, 2007.

6.       M. Agop, C. Gh. Buzea and B. Ciobanu. On Gravitational Shielding in Electromagnetic Fields. – arXiv: physics / 9911011 v1, 10 Nov 1999.

7.       R.P. Lano. Gravitational Meissner Effect. – arXiv: hep-th/9603077 v1, 12 Mar 1996.

8.       Теория бесконечной вложенности материи. // на сайте  http://en.wikiversity.org/wiki/Infinite_Hierarchical_Nesting_of_Matter .

9.       Федосин С.Г. Современные проблемы физики. В поисках новых принципов. – М.: Эдиториал УРСС, 2002 – 192 с.

10.       Reisenegger Andreas. Neutron stars and their magnetic fields. – arXiv: astro-ph / 0802.2227v1, 15 Feb 2008.

 

 

MODEL OF GRAVITATIONAL INTERACTION IN THE CONCEPT OF THE GRAVITONS

 

 The law of Newton for the attraction of bodies is derived with the help of the concept of gravitons. The expression for the gravitational constant is obtained through the momentum of gravitons and the absorption coefficient. Calculations of the values of the coefficient of absorption and of the energy power of flows of gravitons in the space were made. It is shown that during the movement with constant speed the law of inertia is acting.

 

Источник: http://sergf.ru/mg.htm

На научный сайт