Journal of Vectorial Relativity, 2009, Vol. 4, No 1, 1
- 24.
Model of Gravitational
Interaction
in the Concept of Gravitons
S G Fedosin1
ABSTRACT: The law of Newton for the attraction of
bodies is derived with the help of the concept of gravitons. The expression for the gravitational constant is
obtained through the momentum of gravitons and the absorption coefficient.
Calculations of the values of the coefficient of absorption and of the energy
power of flows of gravitons in the space were made. It is shown that during the
movement with constant speed the law of inertia is acting.
KEYWORDS: Gravitation, Force,
Shielding, Inertia.
1 Perm State
University, Russia, intelli@list.ru
INDEX
I. Introduction
II. The inverse-square law
III. The absorption coefficient and
gravitational shielding
IV. Strong fields
V. The motion of energy
VI. Law of inertia
VII. Alternative derivation of
VIII. The inertial force
IX. The relativity of motion
X. Gravitons and the relativity theory
XI. Conclusion
REFERENCES
I.
INTRODUCTION
One of the oldest ideas, concerning the nature of gravity, is the
kinetic theory of Le-Sage [1], in which the mechanical action of particles
(gravitons) causes the attraction of bodies to each other. Gravity is not only responsible for the attraction of
bodies, but also essentially ensures integrity and stability of bodies
themselves. The standard objections against the theory of Le-Sage are: 1) its
inability of precise prediction concerning the possible gravitational
shielding, 2) the nature and the properties of the flows of gravitons, 3)
explanation of the free movement of bodies by inertia, 4) the possible thermal
effect from the gravitons’ action, 5) contribution of the gravitational field
to the mass of bodies.
We should notice, that in [2] gravitons were accepted as cosmic quanta,
the components of photons. The analysis of interaction of these quanta with the
substance on the basis of Compton effect allows deducing formulas for the mass
of bodies, inertia and gravitational interaction. The model of gravitational
interaction suggested below in its own way solves the problems in the concept
of gravitons, but as gravitons involves not only the
photons, but also neutrinos and relativistic particles, similar to cosmic rays.
II. THE
INVERSE-SQUARE LAW
We will derive the formula of 
the quantity,
equal to the number of gravitons 
, which fly from the outside per time unit 
into the
unit solid angle 
and thus have the component of momentum inside this angle:
.
According to the definition, is the graviton flux,
which must be connected to the gravitational constant 
. We will consider that the change in the quantity of gravitons per time
unit in the substance layer with the density 
and the thickness 
is
proportional to the number of incoming gravitons:
,
, (1)
Where, 
– the absorption coefficient,
– half of the characteristic transverse dimension
of the substance layer.
Relation (1) reflects the dependence
between the quantity of gravitons falling to the substance layer and outgoing
from it from the point of view of the transfer of momentum from the gravitons
to the substance. We shall take now two separate bodies at the distance 
from each other, the
densities of their substance can be different. Despite
of different density we shall consider, that the bodies are identical in the
sense that their absorption coefficient is the
same. In these bodies we should
select round surface areas with the radius, equal to , and we should connect them as it is shown in
figure 1. Then the small solid angle 
will meet the condition of
the equality of the areas:
. (2)
The solid angle cuts out in the bodies in question the volumes, close to
the ball segments, with the masses 
and 
respectively. The masses of segments
and depend on the thickness
, 
, and the
densities 
, 
, respectively.
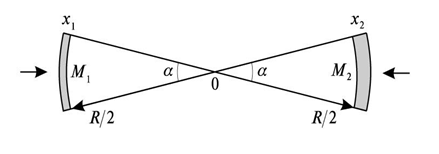
Fig.1. Masses
and in the
form of ball segments with different thickness and the density of the
substances, located at the distance 
from each
other.
We should show first that in this configuration the attraction of
segments under the action of gravitons is due
to the Newton's law. We will prove thus that the law of attraction will be
valid for the both bodies on the whole. It follows from the arbitrariness of
selection of the areas on the surface of these bodies and the possibility of
the vector summing up of forces between all the possible pairs of the substance
units.
It is evident from figure 1 that the masses of the segments are equal
to:
, 
, (3)
Where, the masses can be selected infinitely small with the suitable
selection of . Accordingly, infinitely small will be the
solid angle .
The acting force is the momentum, transmitted to the substance by
gravitons per time unit:
,
(4)
Where, 
– the momentum of one
graviton.
We should examine the propagation of the flow of gravitons from the left
side in figure 1, first through the substance unit with the mass 
, then in the space between the masses and 
, and finally through the substance unit with
the mass .
The force acting on from the
left side, taking into account (4) and (1) is equal to:
(5)
In (5) the exponent was expanded to the terms of the second order. In
the general case the distance can be so large that it is
necessary to consider weakening of the flow of gravitons with their propagation
in the space from to . For evaluating this weakening a formula (1) of
the following type is used:
, (6)
Where,
– the intensity of the flow of gravitons, which passed from the left side
through the substance unit with the mass ,
– the intensity of the flow of gravitons, which reached from the left side
the substance unit with the mass ,
– the substance density between and .
The force acting on from the
left side similarly to (5) is equal to:
Taking into account the same considerations for obtaining (5), (6) and
the quantity 
, for the force 
we find:
(7)
For the flow of gravitons on the right side similarly to (5) and (7) we have:
The gravity force, which acts on the mass from the
side of mass , is equal to:
(8)
The force which acts on the mass from the side of mass , is equal to:
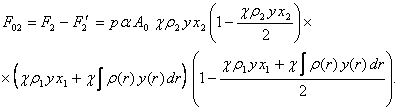(9)
Let us remember that in the general case the gravitational masses are
subdivided into the passive and the active. By passive mass of the body is
understood such mass, which characterizes the body with its acceleration in the
specified gravitational field (for example, with the weighing). Accordingly,
the active mass of the body is responsible for creation of
gravitational field around this body.
Comparison of (8) and (9) shows that the forces 
and 
are not equal to each other
because of the presence of additional forces from the sources of mass, which
are located between the bodies. Besides, the nonequivalence of the entry of the
substance densities 
, 
in (8)
and (9) means that the passive and the active gravitational masses of bodies
differ from each other. In
this case, the effective active mass exceeds the passive mass due to weakening
of the flows of gravitons in the space between the interacting bodies. It is
also possible to say that the presence of the gravitating medium near the body
effectively increases its passive mass to the value of the effective active
gravitational mass.
The more precise equality of forces between the masses and is
achieved when the distance between the masses is relatively small, the density of the intermediate substance and the
characteristic transverse dimension 
are
small. Then the change of the flows of gravitons in the space between the
masses can be disregarded.
For evaluating the absorption coefficient in the substance we will
consider that the term 
in (8)
and (9) is insignificant and it is possible to disregard it. After substitution (3), taking into account (2), we
obtain for the gravity force between the elements of substance and the following:
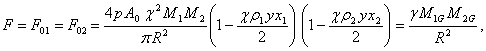(10)
Here, by 
and 
the
gravitational masses are designated, which are responsible for the force of
gravity. Unlike them the masses and are calculated
through the measured densities of substance and the volumes according to (3).
We find from (10):
, 
, (11)
Where,
the index 
distinguishes the masses and . It is evident in (11) that the gravitational
constant is determined by constants – the mean momentum of a graviton, the flow of
gravitons, which falls per time unit from the unit solid angle, and by the
squared coefficient of absorption of gravitons in the substance, consisting of
nucleons. It is obvious that in the course of evolution of the Universe and
with the displacement of bodies in the space the mean momentum of gravitons and
the density of their flows can change, what will influence the effective value
of the gravitational constant. Changes in the
composition and quality of substances through the absorption factor also
contributed to the existing gravitational forces.
III. THE ABSORPTION COEFFICIENT
AND GRAVITATIONAL SHIELDING
In order to determine the coefficient we will use the formula for
the gravitational mass in the general relativity theory (for the cold substance
without considering the pressure energy):
, (12)
Where,
and
– the radius and the mass of the body,
– the speed of field propagation,
in the approximation of the
uniform substance density.
We should consider preliminarily that the formula (12) is valid for the
body in the form of a sphere, and the masses in (11) according to figure 1 are
concentrated approximately in the cylindrical form. If in the sphere we
inscribe a cylinder with the height equal to the cylinder’s base, then the
volume of the sphere will exceed the cylinder’s volume
times. The same relation
there will be also for the masses. In this case the height of the cylinder will
be more than the radius of the sphere, so that 
. Introducing in (12) the coefficient 
and comparing (11) and
(12), we obtain:
, 
. (13)
In (13) the mass of the body in the
form of sphere was expressed through the substance density and the volume.
Substituting the constants and the value 
, we should estimate the value of the absorption
coefficient:
m/kg , (14)
If is equal to the speed of light.
According to its meaning reflects the weakening of
gravitons flows during their passing in the substance from the point of view of
the transfer of the momentum to the substance. The estimation of the length of
the free path of gravitons inside the bodies, when they lose their ability to
transfer their momentum, can be made on the basis of condition 
for the
exponential term in (1). Neutron stars possess the substance density about 2∙1017 kg/m3. As the value it is
possible to take the diameter of a neutron star. Then in the path of gravitons
it is necessary to place not less than 3 neutron stars in order to noticeably
decrease the extent of the flow. The penetrating power of gravitons is so large
that the gravitons can be compared only to the neutrino with energy of about
100 eV.
We should compare (8), (9) with the expression for the force from [4],
which describes the possible effect of the gravitational shielding:
. (15)
It is assumed in (15) that the presence of the substance between the
bodies decreases the force of their attraction by some means.
If we place additional substance near the body with the mass , then according to (9) the force, which acts on
the mass will
increase. Increase in the force will occur in the manner simply as if it is the
gravitational mass that
increases. In this case the gravitational shielding is not observed, since the
general effective force of the influence on the mass grows by means of
composition of forces.
In the opposite situation the additional substance with the density is
distributed outside the two bodies from all the sides so that as the result it
leads to a change of the product 
for the flow of gravitons per
unit of the solid angle. On bodies will operate, in view of the formula of type
(6), the flow of gravitons:
.
Replacing
in (10) 
on 
, in view of (11) we shall receive:
,
(16)
From (16) follows that if shielding occurs because of external
substance, then effective force of an attraction between bodies decreases.
Unlike the force (15) prospective in [4], effect of gravitational shielding
according to (16) depends not only on thickness of a layer of shielding
substance, but also from the area of a layer through size 
.
IV. STRONG
FIELDS
We should consider relations for gravitational force (5) – (9) with high substance densities, when it is
already impossible without error to expand the exponents into series. In
particular, for the force from (8)
we obtain:
.
We should assume that substance densities are so great that the
exponents in this expression can be disregarded. Taking into account (2) for , (11) for 
, (13) for, and (16) we have:
.
Designating
, the expression 
is
obtained with the previously used condition 
. Also we have 
with
condition 
, for maximum interaction of two massive bodies.
We
find with the accuracy to the coefficient of about 1 that the gravitational
potential on the surface of the massive body cannot exceed 
.
Another
case is obtained for our Metagalaxy with the observed density of its substance
in the limits of 10−27 – 10−26
kg/m3. If we substitute the dimensions of the Metagalaxy
about 10 Gpc for and 
, then the exponents in the forces also become
small. It turns out that for the Metagalaxy the gravitational potential cannot
exceed too. In
all likelihood, the gravity, created by the sources inside the Metagalaxy
itself, is not able to convert the Metagalaxy into the black hole.
V. THE MOTION
OF ENERGY
Under the action of graviton flows penetrating all bodies the
gravitational force appears. It is obvious that many other values in stationary
bodies which seem constant to us – the
gravitational acceleration, the energy of the field, the rest energy of
particles, etc. – they can be the consequence of dynamic processes.
We should find, with the help of (11) for and (13)
for, the expression for the maximum energy force of
the flow of gravitons, or of energy power per unit of solid angle in the given
direction:
W/st, (17)
If is equal to the speed of light.
We can approximately calculate the effective energy density of gravitons
in space. From the full solid angle 
steradian per second inside a sphere can pass the energy with the value 
. During this time, energy can leave
the sphere, if the radius of the sphere will be equal to the value of light speed. The volume of such sphere is equal to 
. By dividing the amount of energy on volume of the sphere, we find the effective energy density of gravitons:
J/m3.
We shall estimate now the maximum power of the energy generation in the
material bodies. From (17) and (1) for the situation in figure 1 we have:
.
Using (3) in the form of 
, expressing the mass of the cylinder 
through the mass of sphere , reduced in times,
using the condition 
(
–
the radius of the sphere) and the condition for the complete solid
angle, taking into account (13) and (17) we will obtain:
. (18)
According to (18) with an accuracy to the coefficient of about 1, the
maximum power of the energy generation is equal to the rest energy of the body,
radiated during the time when the gravitons pass the radius of the body: 
. Hence
it follows that the rest energy of bodies is created and is supported exactly
by gravity.
Actually, the flow of gravitons with the specific energy and the
temperature passes through each body. In the stationary case the energy of
incident and outgoing flows are equal, but the temperature of the flow of
gravitons outgoing from the body must be less because of the previous
interaction with the particles of the body. As the result the bodies obtain the
negentropy from the outside, which is compensated by the production of the
corresponding entropy. The energy, connected with the entropy of the body, is
realized in the form of stresses inside the body which appear under the action
of gravitational forces. Besides, the field strengths appear outside the body.
For the gravitationally-bound bodies the basic contribution to the entropy is
made by the potential energy of the gravitational field. This energy is
connected with the body and can partially pass into kinetic energy only in the
case of the imbalance between the force of gravity and the internal pressure.
In the hypothetical case of the complete isolation of the body from the
external gravity, the body will be converted to the state of equilibrium with
an increase in the volume up to the dispersion of substance. The entropy in
this case will increase, and the gravitational energy will pass into the
kinetic energy of substance and emission.
The energy, connected with the entropy, is close enough to the energy of
gravitational field (summed with the pressure energy). As a matter of fact,
this energy is responsible for the decrease of the mass according to (12). The
denser the body with the constant mass becomes, the stronger the interaction of
gravitons with the substance is. This leads to the increase of the module of
gravitational energy of the body, and to the increase of the module of entropy
and stresses in the body. The existence of potential gravitational energy and
stresses in the bodies itself is the consequence of the transfer of the
energy-momentum of gravitons to the substance and the conversion of the entropy
of gravitons. The energy of the flows of gravitons determines the rest energy of
the bodies and the observed mass of these bodies, similarly the gravitational
energy contributes to a change in the mass of the body from to 
in
(12).
From the qualitative standpoint (18) can be understood from the
following discourses. It is known, that in supernova a large amount of energy
is radiated in the form of neutrinos. At the initial stage of collapse of the
supernova substance and photodisintegration of iron nuclei and seizure of
electrons by protons and nuclei, in the impulse with duration about 10 ms
electron neutrinos 
are radiated. The share of this impulse in the
general balance of neutrino radiation of the supernova equals approximately 5
%. After the collapse of the substance, a neutron star which has been formed is
getting cool. At the same time the reactions with electrons and positrons are
taking place and neutrinos and antineutrinos are generated, for example in
reaction: 
, where the index 
differentiates electronic, muonic and 
leptonic neutrinos
(antineutrinos). Typical energies of the neutrinos which are formed 
MeV, their main stream is radiated during the
first 4 sec. Based on the results of the measurements of the number of neutrino
events fixed, different evaluations of energy of supernova SN 1987A give for
the radiation of the antineutrino 
the value 
J. This energy should be
increased, taking into account the radiation of other types of neutrinos and
antineutrinos. The evaluation of gravitational energy of neutron star equals: 
J (with the mass of a typical star
, where 
– the mass of the Sun, and the radius of the
star 
km). In [10] it is possible to
find an estimation of mass of the substance turning in neutrinos and in
gravitational waves – approximately 
. It turns out, that in formation
of a neutron star the energy of the neutrinos being radiated can be compared to
the full gravitational energy of the star.
Before the substance is included in the neutron star composition, it
should come through different stages of transformation. First the low density
hydrogen cloud gets condensed under the influence of gravitational forces, and
a star is formed in which thermonuclear reaction take place. After long stay in
the main sequence and burning-out of the thermonuclear fuel, the iron nucleus
is formed in the star. This nucleus collapses in a neutron star after the
increase of the mass limit, admissible for such nucleus. We should move from
stars to elementary particles. In [3] it was shown, how we can introduce a
concept of strong gravitation which binds the substance of the elementary
particles based on the analogy of nucleons and neutron stars. If nucleons are
formed based on the similar scheme as the neutron stars, then in forming of
each nucleon a large amount of particles of small size is also radiated. We can assume that at least some of these particles
serve as the gravitons. These
particles should be similar by their qualities to neutrinos and antineutrinos
radiated while neutron stars are formed. The total energy of all gravitons, which appear when one nucleon is
formed from smallest rarified substance, must be close to the gravitational
binding energy of the substance of this nucleon and to the rest energy of the
nucleon. Thus, if the average concentration of the substance in our Metagalaxy
equals 1 nucleon/m3, then the corresponding energy of the substance
in 1 m3 at rest will equal approximately 
J, where 
– is the mass of a proton. The density of the
energy of gravitons from
nucleons prospective by us is of the same level as the density of the energy of
substance at rest, that means 
J/m3.
We should find now the relation between the density of the gravitons energy 
and the value 
from (17). We will assume that there is a
sphere of a radius . The time of gravitons motion
from the centre of the sphere outside does not exceed 
. The value can be obtained by means of multiplication of
the density of energy to the sphere's volume, and the following
division to the value of the full solid angle and the time : 
. If we will insert from (17) and J/m3, it will be
possible to evaluate the radius of the sphere: 
m or about 17 Gpc. This value
exceeds the distance to the most remote galaxies and is close to the size of
Metagalaxy. Thus the streams of gravitons which are born by the nucleon substance of the
Metagalaxy and are penetrating it can be the reason of generating gravitation
of macroscopic bodies.
In spite of the relatively small value of the energy
density of gravitons originating
from nucleons, the value of the graviton's energy capacity to a unit of a
solid angle in the direction according to (17), and the effective energy density of gravitons 
are
sufficiently large. Distinction between and can be presented as follows. If we take some
point 
, then the cоntributions to the stream of gravitons energy, which come to this point from a single solid
angle, create different spheres of space, which are located at different
distances from within the given solid angle. The farther from
the sphere of space radiating gravitons is located, the earlier the
radiation should be produced so that it could be summed up in the point with the streams of gravitons from other spheres. Thus, the effect of accumulation of
the capacity of gravitation energy stream can arise due to large size of the Metagalaxy. It is assumed that Metagalaxy is not in a stationary state, and
the quantity
of nucleon matter increases with time due to the formation of new nucleons from
the smallest particles of substance.
In addition to the neutrino, electromagnetic
radiation and cosmic rays of the lowest scale levels of a matter can do the contribution to
gravitation. Indeed, usual and neutron stars constantly radiate photons and fast
particles, and the same thing suppose to be at the level of nucleons. Now we can specify the
meaning of the relation (18) in the following way: Strong gravitation produces
substance in the form of nucleons and creates the streams of gravitons, electromagnetic quanta and fast
particles; the full energy of nucleons is
connected with strong gravitation, and the full energy of neutron stars – with
common gravitation; gravitons can not press
the substance denser to the condition when the gravitational binding energy of
the substance would exceed the energy of the substance at rest.
The thermal heating in the massive
bodies is usually connected with the release of energy in the processes of the
gravitational differentiation of the substance, with the presence of the
decomposed radioactive elements, with the nuclear reactions of synthesis. In
cosmic bodies there are no other important internal sources of heat.
Consequently, the action of gravitons in the stationary bodies does not lead to
the essential additional thermal electromagnetic radiation from the bodies or
the thermal motion of substance. We should assume that the energy flows of
gravitons inside the bodies in general are converted so that they pass again in the energy of the flows of gravitons.
Then the action of gravitons is reduced not to the constant increase in the
internal energy of the body or to its heating, but rather to the transfer of
momentum as to the source of pressure and gravitational stresses in the body.
Nevertheless gravitons if we consider
them particles of the certain level of the matter, interact with substance, and
in reactions for example of weak interaction energy is allocated. It means,
that the gravitationally-connected bodies can have a stable source of heating
of their substance. It is possible to
assume, that allocated thermal energy per one nucleon does not exceed potential
energy of gravitational binding calculated per one nucleon. The internal
temperatures of cosmic bodies (the Earth and the Sun) calculated on the basis of
it according to [3] are really close to their present average temperatures.
VI. LAW OF
INERTIA
Let us try to find the explanation to that fact that during the motion
with the constant speed the bodies are not decelerated by gravitons, but
continue inertial motion. We shall consider for example the formula for
gravitational force (5). It contains the term 
, which is obtained in this form according to
(16) and (13).
This term includes the speed , which we assume to be constant in the inertial
reference systems. In (5) there are other products of values of the type 
, where is substance density, and are transverse and
longitudinal sizes of the body. During the motion of bodies with the constant
speed along the value
remains
the same in all inertial reference systems according to the relativity theory.
The dependence of the coefficient on the
speed, which is located in the expression 
, can be the possible source of deviation from
the law of inertia.
Thus, in (5) almost all the terms remain constant and the gravitational
forces do not depend on the speed of motion with the accuracy at least to the
second order by the mass, when it is necessary to consider the contribution of
field’s energy to the gravitational mass. In the same approximation it is
possible to consider the special relativity theory also precise, since it
includes the law of relativity of motion.
VII. ALTERNATIVE DERIVATION OF
As can be seen from the above calculations in (1) and in subsequent
relationships there are values and . It turns out that it
is possible to obtain 
the flow
of gravitons which cross per time unit the unit area 
from a
unit solid angle :
.
We
should designate the next formulae by numbers with a stroke, if they are
similar by meaning with the formulae, which were mentioned earlier. We should
assume that on the picture 1 the value corresponds to the area of spherical segments,
and the angle we will
understand as a unit angle .Then instead of (2) we will have:
.
(2')
We
can assume that changing of the gravitons’ flow because of attenuation in the
substance layer with width is proportional to concentration 
of dispersing particles (which can be nucleons
or atoms) and to the primary gravitons’ flow:
,
, (1')
Where,
– a certain
coefficient, which has the meaning of effective cross-section of the dispersion
of gravitons in substance.
For
the segments’ mass on picture 1 we have instead of (3):
,
,
(3')
Where
– the
mass of a nucleon,
and 
- the
values that assign concentration of nucleons in masses and .
The
effective force as the momentum per time unit from the flow of absorbed
gravitons will equal:
, (4')
Where,
– the momentum of one
graviton.
The
force from the left side to mass on
picture 1 taking into account (4') and (1') equals:
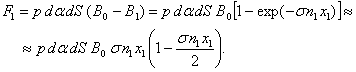(5')
Changing of gravitons’ flow during their
propagation in space between masses and we can
obtain with the formula:
, (6')
Where, 
– gravitons’ flow, which have come from the
left side through substance unit with mass ,
– gravitons’ flow,
which reached from the left side the mass ,
– substance’s
concentration between and 
as the
function of the coordinate 
.
The
force from the left side at similarly to (5') equals:
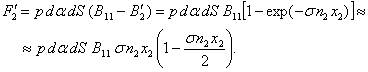
If we substitute here with (6') and then use , for the force we obtain:
. (7')
For the gravitons’ flow from the left side similarly to (5') and (7') we
obtain:
.
The gravitation force which influences the mass from the
side of , equals:
(8')
The mass from the
side of mass is
influenced by the force, which is equal to:
(9')
To make it simpler we can assume, that section of the interaction of gravitons with nucleon
form of substance is equal for masses and . From (8')
and (9') we see, that forces and are not equal because of additional forces
from the sources of mass which are between the bodies.
We
can assume, that interacting masses and are
situated in vacuum and concentration of substance between
them equals to 0. Then for the
gravitation force between and taking into account (3') and (2'), we obtain:
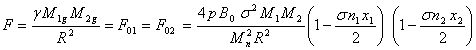, (10')
Here
through 
and 
effective
masses are designated, which are involved in gravitation. From (10') we obtain:
,
, (11')
Where
index differentiates masses and .
According
to (11'), gravitational constant is
determined by constant values – the momentum of one
graviton, gravitons’ flow 
, which falls per time unit from unit solid
angle to unit area, square effective cross-section of
graviton absorption in nucleon substance, mass of one
nucleon.
The maximum value can be estimated from the condition 
for the exponents of (1'). As a result of the high substance density of
neutron stars the concentration of
nucleons in them reaches 
m–3.
If we take a triple diameter of the stars as the length of the gravitons’ path , that means a value about 
m2. This section is very small and
can be compared to section for neutrino with energy about 100 eV. On the other hand, if the laws for change of flows of gravitons (1)
and (1') are
similar, then
the corresponding members inside the exponents can be equated to one another:
. For a neutron star
, and when 
(where 
– the radius of the neutron star) for section in view of (14) is found: 
m2.
The
main conclusions about the effect of gravitational shielding, which were
obtained above remain valid. If we add for example substance near mass , then the force which influences mass , will increase in the same way as mass increases. If substance’s mass increases
beyond the limits and , then instead of (16) we will have:
. (16')
Equation
(16') is close by its meaning to (15). It means that if in the absence of
external substance masses and will move
towards each other under influence of gravitational attraction, then with
enough quantity of external substance it can decelerate the motion of and towards
each other because of decrease of the effective force between and .
In
strong gravitational field if we would not expand the exponents into series in
(5') – (9'), the expression for the forces will be different. For example for
the force from (8')
we obtain:
.
With
high concentration of substance and for two
interacting masses, for example for two identical close neutron stars
contribution from exponents becomes rather small and it can be not taken into
account as first approximation. In this case, taking into account (2') and
(11') for the maximum force we obtain:
, and 
,
Where
– the mass of neutron star,
– the
distance between star’s centers.
It
follows that 
. But relation of the mass of neutron star to
the nucleon’s mass is the similarity coefficient 
in mass between star and nucleon levels of matter according to [3]. If
we take as 
the
section of a neutron star and divide it by the value of the section of
gravitons’ interaction with substance m2, then we will obtain the value
close to 
.
On
the other hand as force 
we can
understand the force of maximum gravitational interaction of two nucleons. In
this case 
, where 
– nucleon’s radius, 
. For the force we obtain:
,
Where
– the
constant of strong gravitation.
According
to [3], the constant can be
obtained from the condition of equality of gravitational and electrical forces
between a proton and an electron at the Bohr radius in hydrogen atom. It is
determined by the expression 
m3∙kg –1∙s–2,
where 
and 
– electron’s charge and mass, – proton’s mass, 
– vacuum permittivity.
At the same time, as it is shown in [3], with the help of the constant the full
energy of nucleon can be calculated, which is equal to its energy at rest.
From
the expression for the force it
follows that it should be 
. Substituting here the value of gravitational
constant , nucleon’s radius about 
m, section m2, we obtain the value close to . We should notice that the force between two
nucleons is rather big. In [3] it is shown, that the force in atomic nuclei can
be balanced by electromagnetic forces and by the force from strong
gravitational torsion field 
(see (19)
and after it).
With
the help of (11') we can evaluate the capacity of the flow of gravitons’ energy
through unit area from unit solid angle:
W/(st·m2), (17')
When
is taken
equal to light speed.
If
we divide (17') by speed and
multiply it by the full solid angle 
, we will obtain the maximum possible energy in
volume unit, which is delivered by graviton’s to this volume. This value equals
the maximum gravitational pressure from gravitons: 
from
gravitons could be almost enough for maintaining the integrity of nucleons. On
the other hand, if gravitons like neutrino, photons
and relativistic particles are generated by nucleons, their energy would
not be enough for gravitational binding of the nucleon’s substance. Hence the conclusion
about necessity of existence gravitons of
deeper levels of matter, with even greater density of energy from here follows.
Based
on the section of graviton’s interaction with the substance we can assume that
gravitons are for example neutrino with energy 
eV 
J. Then we can obtain the momentum , and with its help the flow of gravitons 
s–1st–1m–2 is
determined from (17').
We
should find now the capacity of energy generation in gravitationally bound
bodies. With the help of (1') from (17') we have:
.
We
should use (3') in the form 
, with condition 
for the
full solid angle, and also disclose 
with the
help (17'). Finally, for the stars with 
we should
use the condition obtained above , substituting 
, where – the
star’s radius. The result is the following:
. (18')
From
(18′) it follows that the capacity of generation of gravitational energy in
bodies is approximately equal to gravitational energy of the body, which is
radiated during the time of gravitons’ passing the radius of the body: 
. Gravitational energy of the nucleons’ binding
is almost equal to its energy at rest, that is why (18′) applied to nucleons
(substituting by ) coincides with (18) for maximum gravitation
energy.
VIII. THE INERTIAL
FORCE
As it is known, during acceleration all bodies have resistance, which is
called the inertial force. Let the body of the constant mass be accelerated
rectilinearly by a certain force 
. If at the given moment the velocity of the
body is 
, then for changing of the energy of the body it
is possible to write down:
, where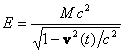 
.
Differentiating energy by the time, we should express the force through
the acceleration:
.
Before the acceleration 
there is
the so-called longitudinal mass.
The obtained force must be equal to the inertial force according to the
third Newton's law about the equality of the action and reaction forces.
However, what is the reason of the inertial force, why do bodies resist a
change in their velocity? Based on what was stated earlier, the action of the
flows of gravitons must be the reason of the inertial forces. Firstly, the gravitons are responsible for the gravitational
energy and the rest energy of the bodies at the nucleon level, and consequently
the change in energy as the result of the change in bodies’ motion must be
connected with gravitons.
Secondly, with the constant speed of motion the inertial force is not
observed, but it appears with the acceleration of bodies. Consequently, with
the acceleration the work towards the body is done, simultaneously the body
does work against the flows of gravitons. It is possible to consider that
regardless of the form of the work done to the body, this work is done to the
flows of gravitons, passing through the body.
IX. THE
RELATIVITY OF MOTION
We
should consider the situation, when two bodies with mass and are located on a straight
line along the vertical axis 
, and are moving with the constant speed in
horizontal direction along the axis 
of the
reference system К. We will assume that in the reference system 
, where the both bodies are at rest, the axes 
are
parallel to the axes 
of the
reference system К. In there is
attraction between the bodies due to the mutual shielding of gravitons’ flows.
But how will gravitational interaction proceed during the simultaneous motion
of these bodies from the point of view of a motionless observer in К?
Firstly, for calculation of the forces the concept of the delay of
gravitational effect due to the limited speed of gravity propagation should be
used. In the case in question, the condition of equality of the time must be
met: as the mass passes the way 
with the speed 
, the flow of gravitons from the mass is moving towards the mass with the speed . This can be expressed in the following way: 
, where – the distance between the masses. Secondly, for
an observer in К it seems that since the gravitons from the mass are
moving, as if overtaking the mass , their momentum is not directed strictly along
the axis . Then a force should appear, which would
decelerate the motion of along the
axis . The same can be said about deceleration of the
mass . However, the direction of force between and must not change in the
reference system , since the masses are moving with the constant
speed at the constant distance from each other.
In order to avoid the contradiction, we should consider that if the
masses and , move with the speed , the flow of gravitons interacting with the
masses has the component of speed, also equal to and
directed along the axis . The combined speed of gravitons in the
reference system К must equal , therefore the speed of gravitons along the
axis must be
less than and must
equal 
. Consequently, 
. For transformation of gravitons’ speed in
different reference systems we should use vector formula of speed summation
from relativity theory:
,
Here,
– the speed of any object in the reference
system ,
– the speed of the given object in the reference
system К ,
– the speed of moving of reference system along К,
.
We obtain 
, 
, 
, 
. From the speed summation formula we obtain: 
, 
.
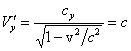From the point of view of the second observer, who is located at the
moving mass , the flow of gravitons which falls on it from
the mass is
directed along the axis 
only.
Therefore, there will be no deceleration of masses along the axes and 
. In case of parallel motion of two masses and along the
axis it
follows from the calculation [3] for the gravitation force‘s module in
reference systems and К: 
, 
,
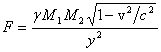where – the distance between the masses along the axis
. At the same time for an observer in the
reference system К the force 
between
the masses is reducing as the speed of
masses’ motion is increasing. It conforms to the fact that the effective speed
of gravitons along the axis for the
moving masses is also reducing: 
.
X. GRAVITONS
AND THE RELATIVITY THEORY
Above the relativity of motion was shown, where speed is transformed
according to the formula of speed summation in the relativity theory. In the
special relativity theory we should consider the retardation of gravitational
influence not simply from a moving mass point, but from the body which is
limited by its size. This makes such a correction into the potential of
gravitational field, which in the result leads to the Lorentz transformation of
coordinates. In this case the gravitational force between two moving bodies,
calculated through the potential gradient, has deficiency in force. If
analogous deficiency in electric force is compensated by the magnetic force, as
it occurs in electromagnetism, then in gravitation an additional force from the
torsion should be introduced.
In the Lorentz-invariant Theory of Gravitation (LITG) the equations for
the field strengths have the form [3], [5]:
(19)
,
,
Where the vectors 
and
– the strength
of the gravitational field (gravitational acceleration) and the torsion
respectively,
– the vector of the density of the mass flow,
– the speed of gravitation propagation.
The gravitational force, which acts on the mass 
, is determined by the expression: 
, where – the velocity of the motion of mass.
The vectors and
can be
expressed with the help of the scalar 
and the
vector 
potentials of the gravitational field:
(20)
With the potentials of the field it is possible to compose the 4-vector
of the potential 
:
.
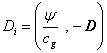We should also use 4-vector of the momentum density:
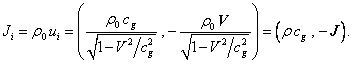
It follows from (19) and (20) that the action of four-dimensional d'Alembertian
on the 4-vector of the potential gives the vector, proportional to the 4-vector
:
□2
(21)
Equation
(21) is a wave equation for the potentials. We should say that if we move from
the General Theory of Relativity (GTR) to weak gravitational fields by
expanding the equations for the metric to the first order, then exactly the
equations of LITG (19) are obtained. This is shown, for example, in [6] and
[7], when the shielding effect of the gravitational field was searched for.
Thus, the concept of gravitons will be conform to LITG, and gravitational
forces do not require their substantiation through GTR. In this case, what role
does GTR play in respect of the gravity from the point of view LITG?
The special relativity theory revealed the dependence of phenomena and
the results of time-spatial measurements on the speed of the motion of
reference systems, taken with respect to the speed of light. GTR makes the
following step – it takes into account the fact that the mass-energy of the
substance and the fields existing in the space influences the course of time
and the measured lengths. Such influence is accompanied by a change in the
speed of the electromagnetic waves (of the light), used as well in the
measuring instruments.
In LITG gravitational field is an independent physical field. Therefore
for the correct use of GTR (or the corresponding metric theory) it is necessary
preliminarily to take the tensor of the energy-momentum of gravitational field,
determined in LITG by covariant means. After
this, knowing all the components of the tensors of the energy-momentum of matter,
electromagnetic and gravitational fields, it is possible to substitute them in
the equations for the metric.
The obtained solution in the form of components for the metric tensor,
cross-linked on the boundaries between the substance and the empty space, where
only the field is present, determines the degree of difference in the metric of
the noninertial system in question from the inertial reference system. The metric field, which consists of the components
of metric tensor and which depends on the time and the coordinates of the
point, where it is determined, will be derived as summary effect from the
existing density of substance, pressure in it, the state of the motion of this
substance (speed, acceleration), and also from the existing gravitational and
electromagnetic fields and other possible sources of energy-momentum.
The calculations, made in the book [3] with respect to the contribution
of energy of gravitational field to the metric, showed that the additive has a
second-order value and contains terms with the fourth power of the speed of
field propagation. The growing accuracy of gravitational experiments will
probably make it possible in the near future to verify the presence of the
corrections indicated. In the described approach the metric field can no longer
be considered the field of gravitation. At the same time the known problem with
covariance of the tensor of energy of gravitational field in GTR is solved, as
this tensor is present in the covariant form in LITG.
XI. CONCLUSION
Taking into account what was stated above the following picture appears: the flows of gravitons from all sides penetrate the
bodies almost without the loss of their total momentum. As the result of the
effect of mutual shielding and interaction of gravitons with the substance all
bodies have attraction to each other. Interaction of gravitons with the
substance occurs in the way that the bodies are constantly obtaining and
returning the energy, equal to their binding gravitational energy. In the static case, the situation reminds the phenomenon of almost perfect mirror reflection of
light when the mirror is under pressure from the radiation, but the energy is
transferred to the mirror only in a small degree. Similarly,
all bodies have a gravitational pressure, but gravitation does not lead to
significant heating of these bodies s.
In our opinion, gravitons are numerous particles of a very small size,
which move with the speed close to the speed
of light and which are similar to low energy neutrinos. Then the integrity of
all material objects is the consequence of the balance of forces of gravity and
internal forces from the pressure (motion) of the particles, which compose
these objects. From the proportionality of gravity forces to the mass of bodies
it follows that the gravitational mass reflects the
ability of the body to obtain impulse of force from the gravitons. According to
General Theory of Relativity, the mass is determined not only by the quantity
of particles in the body, but also by the nature of their interaction or by
full (summary) energy. If the gravitons are more or less evenly distributed in
the space and are the characteristic property of matter, then this makes it
possible to connect the global and the local, inert and gravitational masses in
the somewhat altered Mach principle: “The accelerations of bodies during
interactions are determined not only by the bodies themselves (their masses),
but also by the properties of their environment”.
In assumption that gravitons are the smallest relativistic particles, we can make conclusions with the help of the theory of infinite hierarchical nesting of matter [8].
At every level of matter either nucleon or star level the most dense and
gravitationally bound objects generate in different processes their own flows
of gravitons. Then there is a whole range of gravitons of different energy and
density levels which contribute to gravitation. As it has been shown
above, all volume of the Metagalaxy participates in creation of flows of gravitons. We
can assume that common gravitation is generated by relativistic particles
from nucleon form of substance. Reasoning by induction we should assume that
the nucleons appear under influence of relativistic
particles of deeper level of matter. Besides
we see that flows of neutrino or gravitons of higher levels of matter consist
of flows of neutrino and gravitons of lower levels of matter. Actually,
neutrino impulse of a neutron star in any of
transformations of its substance is combined flow of neutrino and antineutrino
from star’s nucleons. As during the motion downward by scale levels of matter
the density of energy of the corresponding objects increases, then similarly
the density of gravitons’ energy and the force of gravitation must also
increase.
We
can estimate density of energy of flows gravitons for the metagalactic level of
matter which as exceeds the star level of matter as the star level exceeds the
nuclear level. According to the theory of similarity, the ratio of energy
density is connected with factors of similarity: 
, where
is the factor of similarity
in the speeds, 
– the factor of similarity in the sizes according to [3]. Substituting
here 
J/m3, 
, , we find 
J/m3. As gravitation at some level of matter is caused by gravitons flows of
lowest level of matter it is necessary to compare 
to
density of energy of possible sources of gravitons, existing at the star level
matter.
Well-known sources are the microwave background radiation with the
energy density of order 4.18·10–14 J/m3, light radiation of stars
with the energy density of about 8·10–13 J/m3, and cosmic rays, providing approximately 1.3·10–13
J/m3. Thus, the gravitons for
metagalactic level of matter may be flows of photons,
neutrinos and relativistic particles, mostly protons of high energy. From here
follows, that usual gravitation at the level of planets and stars has sources
of gravitons, belonging lower level, than nucleon-atomic level of matter.
It
would be natural to call isotropic such reference system where all flows of
gravitons are distributed isotropically in space evenly in all directions. In
such reference system on condition of infinite smallness of the system’s mass,
the gravitons’ flows become homogeneous, equal in all points of the reference
system. Then the gravitational acceleration in the system tends to zero, and
the isotropic reference system becomes inertial. Due to the inertia law such
systems which move with the constant speed in relation to the isotropic
reference system will be inertial too. But the isotropic reference system does
not preset the absolute space according to
The
existence of an isotropic reference system is one of the axioms in the extended
special relativity theory (ESRT), presented in [9]. As it appears, the formulas
of the special relativity theory can be derived from two main postulates – the
relativity principle and the existence of isotropic reference system. One of
the results of ESRT was the principle of light speed constancy in inertial
reference systems. This principle could not be proven earlier and was
considered to be an axiom of the relativity theory.
From the point of view of the concept of gravitons it is possible to
determine the difference between the passive and the active gravitational
masses, which differ also from the mass, determined from the measurements
through the density and the volume. The analysis of the predicted effect of
gravitational shielding proves to be true for the case, when the substance
screens the bodies from the outside.
REFERENCES
1.
Le Sage's theory of
gravitation. http://en.wikipedia.org/wiki/Le_Sage's_theory_of_gravitation .
2.
Maurizio Michelini. The Physical Reality Underlying the
Relativistic Mechanics and the Gravitational Interaction. –
arXiv: physics/0607136 v1, 14 Jul 2006.
3.
S.G. Fedosin, Fizika i filosofiia podobiia ot preonov
do metagalaktik, Style-Mg, Perm. (1999) 544 pp. ISBN
5-8131-0012-1.
4.
Q. Majorana // Philos. Mag., 1920, Vol. 39, P.488.
5.
S.G. Fedosin. Electromagnetic
and Gravitational Pictures of the World. // Apeiron, Vol. 14, No. 4, P. 385-413, 2007.
6.
M. Agop, C. Gh. Buzea and B. Ciobanu. On Gravitational Shielding in
Electromagnetic Fields. – arXiv: physics / 9911011 v1, 10 Nov 1999.
7.
R.P. Lano. Gravitational Meissner Effect. –
arXiv: hep-th/9603077 v1, 12 Mar 1996.
8.
Infinite Hierarchical Nesting of Matter. http://en.wikiversity.org/wiki/Infinite_Hierarchical_Nesting_of_Matter
.
9.
S.G. Fedosin, Sovremennye problemy fiziki: v
poiskakh novykh printsipov, Editorial URSS, Moscow. (2002) 192 pp. ISBN
5-8360-0435-8.
10.
Reisenegger Andreas. Neutron stars and their magnetic fields. –
arXiv: astro-ph / 0802.2227v1, 15 Feb 2008.
Source:
http://sergf.ru/mgen.htm