Turkish Journal of Physics, 2012,
Vol. 36, No 3, P. 461 – 464.
УДК 51-7+514.114+531-4
МАСШТАБНОЕ ИЗМЕРЕНИЕ КАК ПЯТОЕ ИЗМЕРЕНИЕ ПРОСТРАНСТВА-ВРЕМЕНИ
Федосин Сергей Григорьевич
г. Пермь, Пермский край, Россия
e-mail intelli@list.ru
Масштабное измерение, открытое в теории бесконечной вложенности материи,
рассматривается с точки зрения физической реализации хорошо изученных
четырёхмерных и n-мерных геометрических объектов. Добавление к четырёхмерному пространству
Минковского масштабного измерения означает необходимость использования
пятимерного пространства-времени.
Ключевые слова: масштабное измерение; многомерное пространство; теория бесконечной
вложенности материи.
SCALE DIMENSION AS THE FIFTH
DIMENSION OF SPACETIME
Sergey G. Fedosin
Perm, Perm Region, Russia
e-mail intelli@list.ru
The scale dimension discovered in the
theory of infinite nesting of matter is studied from the perspective of
physical implementation of well-studied four-and n-dimensional geometric
objects. Adding the scale dimension to Minkowski four-dimensional space means
the necessity to use the five-dimensional spacetime.
Keywords: scale
dimension; multi-dimensional space;
theory of infinite nesting of matter.
Интенсивно развиваемая в
последнее время теория бесконечной вложенности материи, изучающая всю иерархию
космических систем, столкнулась с необходимостью введения в обиход науки
масштабного измерения. Целью данной статьи является анализ свойств нового
измерения и его связи с геометрической теорией n-мерных пространств.
Количество базовых измерений в физике определяется по числу степеней
свободы или независимых величин, задающих местоположение физического тела или
его элементов, рассматриваемых как точки, в заданной системе отсчёта. При этом
количество измерений или степеней свободы задаёт размерность используемого
пространства-времени. Добавляя масштабное измерение к четырёхмерному
пространству-времени, мы получаем пятимерное многообразие, включающее в себя
обычное пространство-время. Согласно порядку исторического осмысления это можно
записать в виде (3+1+1)-пространства, где на первом месте отражены
пространственные измерения, а затем измерения времени и масштаба. С точки
зрения геометрии удобно считать оси всех измерений перпендикулярными друг
другу.
В отличие от геометрии, в
физике имеют дело не с математическими точками, а с конкретными материальными
объектами. Бесконечное деление этих объектов на части не приводит к появлению
математических точек; вместо этого возникают новые объекты уменьшенных размеров.
Хотя эти объекты кажутся нам всё более похожими на точки, они содержат в себе
бесконечно большое количество носителей вещества и мельчайших полевых квантов. Если движение внутрь материальных
объектов рассматривать как движение вдоль масштабной оси размеров, то данная
ось оказывается особым измерением пространства.
При перемещении вдоль
масштабной оси происходит переход между масштабными уровнями материи, причём
объекты низших уровней входят в состав объектов более высоких уровней материи.
В результате масштабное измерение можно представлять как измерение,
характеризующее степень сложности космических систем, в смысле их композиции из
систем низшего порядка.
Теория бесконечной
вложенности материи и идея масштабного измерения приобрели свой современный вид
благодаря трудам Роберта Олдершоу [1] (самоподобная космологическая модель),
Сергея Сухоноса [2-3] (масштабное
подобие космических систем) и Сергея Федосина [4-5] (подобие уровней материи).
Пространственные
соотношения воспринимаются наблюдателем через формы предметов и их конфигурации
друг относительно друга, а временные соотношения определяются как изменения
форм и конфигураций, угловые и линейные сдвиги. Благодаря тому, что объекты на
разных уровнях материи развиваются и изменяются относительно независимо друг от
друга, а скорости процессов, характерные размеры и массы объектов значительно
различаются, масштабное измерение рассматривается как новое измерение
пространства-времени. При этом формы и конфигурации многих трёхмерных объектов
на разных уровнях материи похожи и во многом подобны друг другу. Это
фиксируется соотношениями подобия для различных физических величин и SPФ-симметрией, утверждающей подобие физических законов на
разных уровнях материи [4].
В той области исследований, в которой используются масштабные
преобразования и пространственные измерения, масштабное измерение может
изучаться геометрическими методами и тем самым входит в предмет геометрии. В четырёхмерном пространстве-времени
в качестве четвёртого измерения берётся обычно не само время t, а произведение ct ,
где c – скорость света (поскольку для
точных пространственно-временных измерений повсеместно используют
электромагнитные волны). Сечение такого пространства, перпендикулярное временной
оси в некоторой временной точке, задаёт гиперплоскость в виде трёхмерного
геометрического пространства в данный момент времени. Если в трёхмерном
пространстве наблюдается движение предмета с переходами будущих наступающих
событий через точку настоящего в прошлое, то в четырёхмерном
пространстве-времени движение от момента времени 1 до момента времени 2
проявляется как растущий в размерах от точки 1 до точки 2 след, связанный с
предметом. Возможность наблюдения такого следа в системе координат означает,
что движение может быть описано в виде некоторого набора трёхмерных образов
предмета в разные моменты времени.
При введении масштабного
измерения учитывается, что на разных уровнях материи скорости течения времени,
рассматриваемые как скорости типичных процессов с подобными объектами,
отличаются друг от друга. Однако можно ввести общее координатное время,
основанное например на периодических процессах в
электромагнитной волне. В этом случае гиперплоскости, перпендикулярные
масштабной оси, будут определять единое четырёхмерное пространство-время на
различных уровнях материи. По аналогии с четырёхмерным пространством-временем
Минковского, теперь можно ввести пятимерную систему отсчёта и для каждого
мирового события записать его вектор в виде: 
, где 
есть трёхмерный
радиус-вектор, 
− координата
вдоль масштабной оси.
Масштабное измерение
позволяет понять и обосновать возможность существования реальных четырёхмерных
тел в пятимерном пространстве-времени. Для построения подобных тел можно
использовать метод индукции, рассуждая следующим образом:
– одно ребро есть отрезок
линии, ограниченный двумя точками (вершинами);
– три ребра на плоскости
дают треугольник с тремя вершинами, в виде одной грани;
– шесть рёбер с четырьмя
вершинами в трёхмерном пространстве дают тетраэдр (треугольную пирамиду) с
четырьмя гранями;
– десять рёбер с пятью
вершинами, с десятью гранями и с пятью тетраэдрами в четырёхмерном пространстве
представляют объект под названием симплекс.
Для n-мерного тетраэдра или симплекса при увеличении
размерности пространства n на единицу
увеличивается количество вершин, причём количество вершин равно k = n + 1. Каждое
ребро есть связь двух произвольных точек тетраэдра, так что количество рёбер
зависит от количества вершин по формуле для сочетаний по два из k вершин. Для определения количества граней n-мерного тетраэдра в виде
треугольников необходимо находить сочетания по три из k вершин. В общем случае формула для r
сочетаний из k элементов выражается
через факториалы и имеет вид:
.
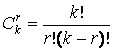(1)
Формула (1) позволяет находить количество рёбер, граней,
многогранников порядка r в составе n-мерного тетраэдра.
Для n-мерного куба (гиперкуба) можно считать, что у него
количество вершин зависит от размерности пространства n по формуле: 
, где размерность
точечного пространства равна нулю, у линейного пространства размерность 1, у
плоского пространства размерность 2, и т.д. Следовательно, тессеракт (тетракуб)
как гиперкуб в четырёхмерном пространстве должен иметь 16 вершин, а также
согласно (1) 120 рёбер. Если из этого количества убрать внутренние рёбра между
вершинами разных граней, а также лежащие в плоскостях граней диагональные
рёбра, то останутся только внешние 32 ребра, отвечающие за выпуклость
тессеракта как геометрической фигуры. Кроме этого тессеракт обладает 8
внешними трёхмерными гранями-кубами и 24 внешними двумерными гранями-квадратами, ограничивающими его в четырёхмерном
пространстве. Общим названием n-мерных тел является политоп (polytope), для четырёхмерных
тел принят термин полихорон (polychoron), тогда как для
трёхмерных тел используется термин многогранник (polyhedron), а для
двумерных тел – многоугольник (polygon).
В пространстве n измерений можно строить самые различные
фигуры, находить их свойства, включая n-мерные углы, площади и объёмы. В частности, объём n-мерной сферы
выражается через её радиус R и гамма-функцию
по формуле [6]:
.
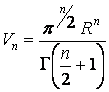Данная формула была
известна уже в 19 веке в трудах швейцарского математика Людвига Шлефли [7].
В настоящее время раздел
математики, изучающий геометрические объекты в пространстве n измерений, разработан настолько хорошо, что все
возможные объекты разбиты на классы по свойствам симметрии [8]. Существуют
интернет-ресурсы, наглядно показывающие проекции многомерных тел на плоскость
либо на трёхмерное пространство [9-10],
находимые путём компьютерного моделирования.
С математической точки
зрения, любое пространство меньшей размерности, входящее в состав пространства
более высокой размерности, является гиперплоскостью, на которую можно
спроектировать точки n-мерного тела. Если
ориентировать симплекс или тессеракт строго вдоль четвёртого пространственного
измерения, то в каждой точке трёхмерной гиперплоскости, перпендикулярной оси
четвёртого измерения, обнаружится тетраэдр либо соответственно куб. Точно так
же, если рассекать тетраэдр или куб перпендикулярно их основаниям, то на
плоскости сечения (двумерной гиперплоскости) будет треугольник, размер которого
зависит от точки сечения, либо квадрат. При прохождении четырёхмерного
тела через трёхмерное пространство можно было бы ожидать внезапных появлений и
исчезновений проекций этого тела, изменения их размеров. Поскольку в
повседневной жизни подобные примеры обычно не встречаются, то видно, что
четвёртое пространственное измерение прямо себя не обнаруживает.
Из изложенного следует,
что масштабная ось, открытая в иерархии космических систем, является физическим
воплощением четвёртого пространственного измерения [11]. Некоторый набор трёхмерных объектов на разных уровнях
материи представляет собой четырёхмерное тело, ориентированное вдоль масштабной
оси, так что каждое сечение этой оси представляет собой трёхмерную
гиперплоскость, на которой могут быть соответствующие трёхмерные объекты.
В отличие от
математической идеализации, объекты некоторой природной системы ввиду
ограниченности их общего числа расположены на масштабной оси не с одинаковой
вероятностью, а неоднородно, группируясь в отдельные уровни материи. Кроме
этого, на разных уровнях меняются и физические свойства вещества объектов, что
в геометрии обычно не учитывается. На тех уровнях материи, где преобладают гравитационные
силы, доминируют космические объекты сферической формы.
Любой ряд объектов,
состоящий из сферических галактик, шаровых звёздных скоплений, отдельных звёзд,
планет, нуклонов и т.д. образует определённое единое четырёхмерное сферическое
тело, протянувшееся вдоль масштабной оси как вдоль четвёртой пространственной
координаты. Данное четырёхмерное тело обнаруживается не через его проекции как
результат его прохождения через наш трёхмерный мир, а в противоположной
ситуации, когда наблюдатель сам движется относительно этого тела и изучает его
составные элементы на различных гиперплоскостях. Таким образом, масштабное
измерение подтверждает возможность реального существования четырёхмерных
геометрических объектов в природе. Это даёт возможность применения математических
методов n-мерных пространств
для изучения составных физических объектов различных масштабных уровней
материи.
Список использованных источников
1.
Oldershaw Robert L. Self-Similar
Cosmological Model: Introduction and Empirical Tests // International Journal of Theoretical Physics . – 1989. – Vol. 28 . – No. 6.
– P. 669-694. http://www.amherst.edu/~rlolders/OBS.HTM .
2.
Сухонос С.И. Взгляд издали // Знание-сила. – 1981.
– № 9. – С. 31-33.
3.
Сухонос С. И. Масштабная гармония Вселенной. – М.: Новый
центр. – 2002. – 312 с. ISBN
5-89117-096-5. http://www.trinitas.ru/rus/002/a0209004.htm .
4.
Федосин С.Г. Физика и философия подобия от преонов до
метагалактик. – Пермь: Стиль-МГ, 1999. – 544 с. ISBN 5-8131-0012-1.
5.
Федосин С.Г. Физические теории и бесконечная вложенность материи. – Пермь,
2009. – 844 с. ISBN 978-5-9901951-1-0. http://sergf.ru/kn.htm .
6.
Араманович И.Г., Гутер Р.С., Люстерник Л.А.
Математический анализ. Дифференцирование и интегрирование. – М.: ГИФМЛ, 1961. – 309
c.
7.
Schläfli, Ludwig (1901) [1852], Graf, J. H., ed. (in German), Theorie der vielfachen
Kontinuität, Republished by Cornell
University Library historical math monographs 2010, Zürich, Basel: Georg &
Co., ISBN 978-1-4297-0481-6.
8.
Coxeter
H. S. M. Regular
Polytopes. – 3-rd ed. – NY: Dover
Publications, 1973. –
321 p.
ISBN 0-486-61480-8.
9. Многомерность пространства (видео). Комментарии от имени математика Людвига Шлефли [Электронный ресурс]. – Режим доступа: http://dimensions-math.org/ (дата обращения 02.01.2011).
10.
Newbold Mark. HyperSpace Polytope Slicer [Электронный ресурс]. – Режим доступа: http://dogfeathers.com/java/hyperslice.html (дата обращения 30.12.2010).
11.
Wikiversity, Scale dimension. – http://en.wikiversity.org/wiki/Scale_dimension
.
Источник:
http://sergf.ru/mi5.htm