Advanced Studies in Theoretical Physics, Vol. 8, 2014, no. 18, 771 - 779. http://dx.doi.org/10.12988/astp.2014.47101
Процедура для нахождения тензора энергии-импульса и уравнений
векторного поля любого вида
Федосин Сергей Григорьевич
ул. Свиязева 22-79, город Пермь, 614088, Пермский край, Россия
e-mail intelli@list.ru
Описывается способ, позволяющий ввести в лагранжиан члены,
характеризующие произвольное векторное поле системы. В результате применения
принципа наименьшего действия становится возможным найти все основные
характеристики этого поля, включая его энергию и импульс, силу взаимодействия с
веществом, уравнения поля.
Ключевые слова: 4-потенциал;
поле давления; поле ускорений; уравнения
поля.
The procedure of finding the
stress-energy tensor and equations of vector field of any form
Sergey G. Fedosin
Sviazeva Str. 22-79, Perm, 614088, Perm region,
Russian Federation
e-mail intelli@list.ru
A method allowing us to introduce into the Lagrangian
the terms, which characterize an arbitrary vector field of a system, is
described. As a result of applying the principle of least action it becomes
possible to find all the main characteristics of this field, including its
energy and momentum, field equations, force of interaction
with the matter.
Keywords: four-potential; pressure field; acceleration field; field
equations.
1.
Введение
Концепция поля широко применяется не только в теории гравитации, но и в других физических теориях. Далее мы будем рассматривать свойства векторных полей в четырёхмерном пространстве.
Основной характеристикой электромагнитного векторного поля
является 4-потенциал 
, где 
есть скорость света, 
и 
обозначают скалярный и
векторный потенциалы, соответственно. Если в системе множество частиц, каждая
из которых генерирует свои собственные потенциалы, то потенциалы и системы частиц в основном зависят от общих параметров
системы – от размеров системы, полного заряда и т.д. При этом потенциалы
системы получаются по принципу суперпозиции потенциалов всех частиц. С помощью
4-потенциала можно определить все основные характеристики электромагнитного
поля системы.
Таким образом, прежде чем находить 4-потенциал системы, нужно
определить 4-потенциал отдельной частицы. Это можно сделать следующим образом:
инвариантный скалярный потенциал 
частицы разделить на квадрат
скорости света, чтобы получить необходимую размерность, и умножить на
ковариантную 4-скорость:
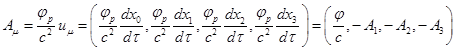. (1)
Потенциал считается
инвариантным, если он измерен в системе отсчёта 
, жёстко связанной с частицей. В (1) видно, как связан со скалярным
потенциалом 
и тремя компонентами
векторного потенциала 
частицы в произвольной
системе отсчёта 
, в которой частица имеет 4-скорость 
(здесь 
есть 4-перемещение с
ковариантным индексом, 
– собственное время
частицы). Для того, чтобы найти 4-потенциал системы, необходимо
проинтегрировать (1) по всем частицам системы.
2. Поле давления
Обратимся теперь к полю давления, свойства которого необходимо знать при вычислении метрики внутри материальных тел, а также для определения уравнения движения и состояния вещества. Существующие определения поля давления и его энергии-импульса выводят путём обобщения формул классической механики. Например, в общей теории относительности (ОТО) для идеальной жидкости используется следующий тензор давления [1]:
.
(2)
В (2) давление 
представляет собой
скалярное поле.
Характеристикой материи в ОТО считается тензор 
, а суммарный тензор энергии-импульса материи с давлением и плотностью 
равен: 
.
Зададимся теперь вопросом, можно ли считать поле давления не просто скалярным, а четырёхмерным векторным полем? По определению, векторное поле описывается в каждой точке некоторым вектором. Для непрерывно распределённого вещества частицы настолько близки друг к другу, что постоянно взаимодействуют между собой. В этом случае можно считать, что направление вектора давления одной частицы на другую параллельно вектору скорости частицы. Если для частиц задано векторное поле скоростей, то векторное поле давления можно рассматривать как следствие поля скоростей.
С другой стороны, давление даже в отсутствие движения частиц, когда оно выглядит как скалярное поле, вносит свой вклад в массу-энергию частиц. Поскольку давление имеет смысл и как скаляр, и как трёхмерный вектор, должен существовать 4-вектор, где давление входит и в скалярную, и в векторную компоненты. Такой 4-вектор естественно называть 4-потенциалом поля давления.
Определим 4-потенциал поля давления подобно (1):
, (3)
где 
и 
обозначают давление и
плотность в системе отсчёта частицы, безразмерное
отношение 
пропорционально
энергии давления частицы в расчёте на единицу массы частицы, 
и 
являются скалярным и
векторным потенциалами поля давления.
Применяя
далее 4-ротор, находим антисимметричный тензор давления 
, состоящий из шести компонент, принадлежащих двум векторам 
, 
:
. (4)
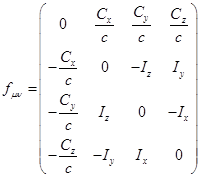. (5)
Теперь с помощью (4) можно построить тензорный инвариант 
, где 
подлежит определению.
Уравнения поля давления получаются из принципа наименьшего действия, при этом в
лагранжиан следует подставить сумму: 
, где 
есть массовый 4-ток.
Для сравнения, все свойства электромагнитного поля получаются варьированием
подобной суммы: 
, где 
есть электромагнитный
ток, 
– электрическая
постоянная, 
– электромагнитный
тензор.
Одним из итогов варьирования лагранжиана является тензор
энергии-импульса поля давления [2]:
. (6)
Данный тензор вместе с тензорами других полей входит в правую
часть уравнения для определения метрики, а левая
часть этого уравнения содержит тензор Риччи и скалярную кривизну. С помощью
тензора (4) или тензора (6) определяется плотность 4-силы в уравнении движения
вещества, возникающая за счёт давления:
.
Находятся также уравнения поля давления:
, 
,
(7)
где 
есть символ
Леви-Чивиты.
Уравнения (7) в пределе специальной теории относительности с
учётом (5) выглядят так же, как уравнения Максвелла:
, 
, 
, 
. (8)
Здесь 
есть фактор Лоренца, 
– скорость движения точечной частицы вещества.
Если в первое уравнение в (7) подставить (4) в виде: 
, то получится:
.
При условии калибровки 4-потенциала в виде 
в левой части равенства
будет 
, где 
обозначает тензор Риччи
со смешанными индексами. С другой стороны, 4-даламбертиан, действующий на
4-вектор 
, определяется в общем случае так:
В результате члены с тензором Риччи сокращаются, и остаётся
следующее:
. (9)
Уравнение (9) представляет собой волновое уравнение для
4-потенциала поля давления, позволяющее найти распределение давления внутри
массивных тел. В частности, для сферических тел с приблизительно постоянной
плотностью давление падает от центра тела к его поверхности из-за наличия в
формуле для давления отрицательного члена, пропорционального квадрату текущего
радиуса. Из (9) можно получить оценку давления в центре массивного тела:
,
(10)
где 
, 
–
гравитационная постоянная, 
и 
обозначают массу и
радиус тела.
3. Поле
ускорений
Изложенное выше описывает порядок получения тензора
энергии-импульса и уравнений векторного поля любого вида. В частности,
описанная процедура была применена в [2] также для того, чтобы найти
ковариантным способом тензор энергии-импульса вещества. В качестве 4-потенциала
поля ускорений была использована ковариантная 4-скорость без дополнительных
множителей:
,
где 
и 
обозначают скалярный и
векторный потенциалы, соответственно.
Тензор поля ускорений определяется выражениями:
. (11)
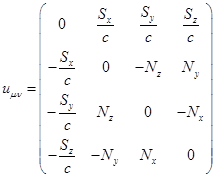, (12)
где векторы 
и 
задают ускорения
частицы.
Вклад поля ускорений в лагранжиан определяется суммой: 
, где 
подлежит определению. В
результате варьирования появляется тензор энергии-импульса поля ускорений:
. (13)
4-ускорение в уравнении движения малой частицы непрерывно распределённого вещества находится либо через тензор (11), либо через тензор (13):
.
Как и любое векторное поле, поле ускорений
определяется соответствующими уравнениями:
, 
.
Эти уравнения в специальной теории
относительности являются уравнениями для векторов 
и 
из (12):
, 
, 
, 
. (14)
Тензоры энергии-импульса поля давления 
(6) и поля ускорений 
(13) построены
ковариантным образом из 4-потенциалов и в ковариантной теории гравитации
заменяют собой тензор 
в (2) и тензор 
, соответственно.
Аналогично (9) получается волновое уравнение для поля скоростей внутри тел:
(15)
Решение данного уравнения даёт возможность вычислить скорости движения частиц внутри сферического тела как функцию от текущего радиуса. Кинетическая энергия частиц зависит от их скорости и задаёт кинетическую температуру. Следовательно, становится возможным найти и распределение равновесной температуры внутри массивных тел. В частности, для температуры в центре можно приблизительно записать:
.
(16)
где 
, 
– масса типичной
частицы тела, как правило это масса атома водорода, 
– постоянная
Больцмана.
4. Заключение
Несмотря на то, что формулы (10) и (16) были найдены в предположении однородной плотности, они неплохо выполняются для газовых облаков, планет и звёзд. Хорошее совпадение было найдено для глобул Бока, Земли и нейтронной звезды, а также для температуры внутри Солнца [3]. Различие возникает лишь для давления внутри Солнца, где оно получается в 58 раз меньше, чем в стандартной модели. Вероятно, это связано с тем, что внутри Солнца протекают термоядерные реакции, увеличивающие давление.
Мы считаем, что в массивных телах, удерживаемых в равновесии силой гравитации, имеются радиальные градиенты потенциала силы тяжести, давления, кинетической энергии частиц и других величин. Эти градиенты являются необходимыми элементами, обеспечивающими устойчивость системы при заданном состоянии вещества. Если предположить справедливость механизма гравитации в теории Лесажа [4], то при равновесии температура недр массивного космического тела не может упасть ниже значения, которое находится из теоремы вириала. Несмотря на постоянное излучение с поверхности тела, необходимый приток энергии осуществляется падающими на тело гравитонами. В модели Лесажа проникающие сквозь вещество потоки гравитонов не только создают гравитационную силу тяжести, но и оставляют часть своей энергии внутри тела, нагревая его.
Таким образом мы представили процедуру, согласно которой необходимо вначале определить скалярный потенциал произвольного векторного поля, присущий одной частице. После этого путём стандартных действий выводятся все характеристики данного поля, включая уравнения поля, его тензор энергии-импульса и вид силы, действующей со стороны поля на частицы.
Обратим внимание на то, что 4-потенциал поля выражается как ковариантный 4-вектор, а энергия вещества в этом поле зависит от произведения 4-потенциала на массовый (электромагнитный) 4-ток, взятый с контравариантным индексом. Тензор поля имеет дважды ковариантные индексы как следствие 4-ротора, действующего на 4-потенциал. Для того, чтобы найти этот же тензор с контравариантными индексами, необходим метрический тензор. Свёртка тензора поля самого с собой даёт тензорный инвариант, необходимый в лагранжиане для операции варьирования и выражения связи между веществом, метрикой и полем в соответствующих уравнениях. Ещё одной особенностью описанного подхода является то, что уравнения поля вида (8) и (14) по своей форме аналогичны уравнениям Максвелла.
Ранее описанный подход был использован в [5], [6], [7] для нахождения 4-потенциала
гравитационного поля, его тензора энергии-импульса, гравитационной 4-силы и
уравнений поля в рамках ковариантной теории гравитации (КТГ).
В КТГ поле гравитации отделяется от
метрического поля, гравитация становится самостоятельным полем, обладающим
собственной энергией, импульсом и действием в виде гравитационной силы. В
результате метрика оказывается необходимой лишь для описания отклонений
результатов гравитационных экспериментов от их вида в специальной теории
относительности. Необходимой частью лагранжиана КТГ является постоянная 
, называемая космологической постоянной. С помощью этой
постоянной осуществляется калибровка гамильтониана таким образом, чтобы энергия
системы могла быть определена однозначно.
5. Список использованных источников
1.
C. W. Misner, K. S. Thorne, and J. A. Wheeler, Gravitation
(W. H. Freeman, San Francisco, CA, 1973).
2.
Fedosin S.G. About
the cosmological constant, acceleration field, pressure field and energy. vixra.org, 5 Mar 2014;
О космологической постоянной, поле ускорения, поле давления и об энергии.
3. Fedosin
S.G. The Integral Energy-Momentum
4-Vector and Analysis of 4/3 Problem Based on the Pressure Field and
Acceleration Field.
American Journal of Modern Physics. Vol. 3, No. 4, 2014, pp. 152-167. doi: 10.11648/j.ajmp.20140304.12;
Интегральный 4-вектор энергии-импульса
и анализ проблемы 4/3 на основе поля давления и поля ускорений.
4. Fedosin S.G. Model of Gravitational Interaction in the Concept of Gravitons. Journal of Vectorial Relativity, 2009, Vol.
4, No. 1, P.1–24; статья на русском языке: Модель гравитационного взаимодействия в концепции
гравитонов.
5. Fedosin S.G. The Principle of Least Action in Covariant Theory of Gravitation. Hadronic Journal, 2012, Vol. 35, No. 1,
P. 35–70; статья на русском языке: Принцип наименьшего действия в ковариантной
теории гравитации.
6.
Федосин С.Г. Физические
теории и бесконечная вложенность материи. Пермь, 2009, 842 стр., Табл.
21, Ил.41, Библ. 289 назв. ISBN 978-5-9901951-1-0.
7.
Федосин С.Г. Физика и
философия подобия от преонов до метагалактик. Пермь, Стиль-МГ, 1999, 544 стр.,
Табл.66, Ил.93, Библ. 377 назв. ISBN 5-8131-0012-1.
Источник: http://sergf.ru/pf.htm