Advanced
Studies in Theoretical Physics, Vol. 8, 2014, no. 18, 771 - 779.
http://dx.doi.org/10.12988/astp.2014.47101
The procedure of finding the
stress-energy tensor and equations of vector field of any form
Sergey G. Fedosin
Sviazeva Str. 22-79, Perm, 614088, Perm region, Russian
Federation
e-mail intelli@list.ru
A method allowing us to
introduce into the Lagrangian the terms, which characterize an arbitrary vector
field of a system, is described. As a result of applying the principle of least
action it becomes possible to find all the main characteristics of this field,
including its energy and momentum, field equations, force of interaction
with the matter.
Keywords: four-potential; pressure field; acceleration field; field equations.
1. Introduction
The field concept is widely
used not only in the gravitation theory but also in other physical theories.
Further we will consider the properties of vector fields in four-dimensional
space.
The main characteristic
of the electromagnetic vector field is the 4-potential 
, where 
is the speed of light, 
and 
denote the scalar and vector potentials,
respectively. If the system contains a set of particles, each of which
generates its own potential, then the potentials and of the system of particles depend mainly on
the general system parameters – the dimensions of the system, the total charge,
etc. Besides the system’s potentials correspond to the superposition principle
the potentials of all the particles. We can determine all the main
characteristics of the system’s electromagnetic field with the help of the
4-potential.
Thus before we find the
4- potential of the system, we need to determine the 4-potential of a single
particle. This can be done as follows: the invariant scalar potential 
of the particle should be divided by the square
of the speed of light to get the necessary dimension, and then multiply it by
the covariant 4-velocity:
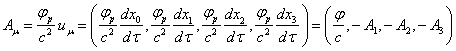. (1)
The potential is considered to be invariant, if it is
determined in the reference frame 
, which is rigidly
associated with the particle . We can see in (1), that is associated with the scalar potential 
and the three components of the vector
potential 
of a particle in an arbitrary reference frame 
, in which the particle
has a 4-velocity 
(where 
is a 4-displacement with the covariant index, 
is the proper time of the particle). In order
to find the 4-potential of the system, it is necessary to integrate (1) over
all of the system’s particles.
2. Pressure field
We will turn now to the
pressure field, the properties of which must be taken into account in
calculating the metric inside the material bodies, as well as in determining
the equation of motion and of the state of matter. The existing definitions of
the pressure field and its energy-momentum are derived by means of
generalization of the formulas of classical mechanics. For example, in the
general theory of relativity (GTR) the following pressure tensor [1] is used
for ideal liquid:
.
(2)
In (2) the pressure 
represents a scalar field.
The tensor 
is considered to be the matter characteristic
in GTR, and the total stress-energy tensor of the matter with pressure and density 
is equal to: 
.
Now we will answer the
question whether we can consider the pressure field not just scalar but a
four-dimensional vector field? By definition, a vector field at each point is described
by a certain vector. In continuously distributed matter the particles are so
close to each other, that they constantly interact
with each other. In this case, we can assume that the direction of the vector
of one particle’s pressure on another is parallel to the vector of particle
velocity. If a vector field of velocity is specified for the particles, then
the vector field of pressure can be considered as the consequence of the
velocity field.
On the other hand, the
pressure, even in the absence of particles’ motion when it looks like a scalar
field, makes its contribution to the mass-energy of the particles. Since the
pressure has meaning both of a scalar and of a three-dimensional vector, there
must be a 4-vector, where the pressure is part of the scalar and vector
components. It is natural to call such a 4-vector a 4-potential of the pressure
field.
We will determine the
4-potential of the pressure field similarly to (1):
,
(3)
where 
and 
denote the pressure and density in the
reference frame of the particle, the dimensionless ratio 
is proportional to the pressure energy of the
particle per particle’s unit mass, 
and 
are the scalar and vector potentials of the
pressure field.
Then applying the 4-rotor we find the antisymmetric
pressure tensor 
, consisting of six
components, belonging to two vectors 
, 
:
. (4)
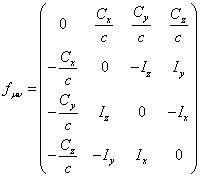. (5)
Now, using (4) we can
construct a tensor invariant 
, where 
should be determined. The pressure field
equations are obtained from the principle of least action, while the sum should
be substituted into the Lagrangian: 
, where 
is the mass 4-current. For comparison, all the
properties of the electromagnetic field are obtained by varying a similar sum: 
, where 
is the electromagnetic current, 
is the vacuum permittivity, 
is the electromagnetic tensor.
One of the results of
the Lagrangian variation is the stress-energy tensor of the pressure field [2]:
. (6)
This tensor with other
fields’ tensors is part of the right side of the equation for determining the metric,
and the left side of this equation contains the Ricci tensor and scalar
curvature. With the help of tensor (4) or tensor (6) we can determine the
density of 4-force in the equation of matter motion that arises due to the
pressure:
.
We also find the
pressure field equations:
, 
, (7)
where 
is the Levi-Civita symbol.
Equations (7) in the
limit of the special theory of relativity with regard to (5) look like Maxwell
equations:
, 
, 
, 
. (8)
Here 
is the Lorentz factor, 
is the velocity of a point particle of matter.
If we substitute (4) in
the first equation in (7) in the form: 
, we obtain:
.
In case if 4-potential
gauge 
in the left side of the equation we have 
, where 
denotes the Ricci tensor with mixed indices.
On the other hand, 4-d'Alembertian acting on the 4-vector 
is determined in the general case as follows:
As a result the terms
with the Ricci tensor are canceled and we have the following:
. (9)
Equation (9) represents
the wave equation for the 4-potential of the pressure field, which allows us to
find the pressure distribution inside the massive bodies. In particular, for
spherical bodies with approximately constant density the pressure decreases
from the body center to its surface, due to the presence of the negative term
in the formula for the pressure, which is proportional to the square of the
current radius. From (9) we can estimate the pressure at the center of the
massive body:
,
(10)
where 
, 
is the gravitational
constant, 
and 
denote the body mass and radius.
3. Acceleration field
The foregoing describes
the procedure of obtaining the stress-energy tensor and the vector field equations
of any kind. In particular, the above-mentioned procedure was also applied in
[2] in order to find the stress-energy tensor of matter in a covariant way. As
the 4-potential of the acceleration field the covariant 4- velocity was used
without additional factors:
,
where 
and 
denote the scalar and
vector potentials, respectively.
The tensor of the
acceleration field is given by:
. (11)
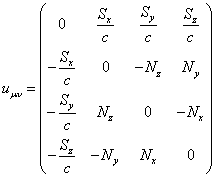, (12)
where the vectors 
and 
define the particle’s accelerations.
The contribution of the
acceleration field into the Lagrangian is given by the
sum: 
, where 
is to be determined. The
stress-energy tensor of the acceleration field appears as a result of
variation:
. (13)
The 4-acceleration in
the equation of motion of a small particle of continuously distributed matter
is found either with the help of tensor (11) or tensor (13):
.
Like any vector field,
the acceleration field is given by the corresponding equations:
, 
.
These equations in the
special theory of relativity are the equations for the vectors 
and 
from (12):
, 
, 
, 
. (14)
The stress-energy tensors
of the pressure field 
(6) and the
acceleration field 
(13) are constructed in
a covariant way using the 4-potentials and in the covariant theory of
gravitation they substitute the tensor 
in (2) and the tensor , respectively.
Similarly to (9) we
obtain the wave equation for the velocity field inside the bodies:
(15)
The solution of this
equation allows us to calculate the velocity of the particles’ motion inside
the spherical body as a function of the current radius. The kinetic energy of
the particles depends on their velocity and specifies the kinetic temperature.
Consequently, it becomes possible to find the equilibrium temperature
distribution inside the massive bodies. In particular, for the temperature at
the center we can approximately write the following:
.
(16)
where 
, 
denote the mass of a typical body particle,
usually it is the mass of a hydrogen atom, 
is the Boltzmann constant.
4. Conclusion
Despite the fact that
the formulas (10) and (16) were found in the assumption of uniform density,
they are well satisfied for gas clouds, planets and stars. Good agreement is
observed for Bok globules, the Earth and neutron star, as well as for the
temperature inside the Sun [3]. The difference occurs only for the pressure
inside the Sun, where it is 58 times less than in the standard model. This is
probably due to the fact that thermonuclear reactions take place inside the
Sun, which increase the pressure.
We believe that the
massive bodies, held in equilibrium by gravitation force, contain radial
gradients of the potentials of gravitation, pressure, particles’ kinetic energy
and other quantities. These gradients are the essential components that ensure
the system’s stability at a given matter state. If we assume the validity of
the gravitation mechanism in Le Sage’s theory [4], then at equilibrium the
temperature of the interior of a massive cosmic body cannot fall below the
value that is obtained from the virial theorem. Despite the constant emission
from the surface of the body, the necessary energy inflow is ensured by
gravitons falling on the body. In Le Sage’s model the graviton fluxes
penetrating the matter not only create the gravitational force, but also leave
some part of their energy inside the body, warming it.
Thus, we have introduced
a procedure, according to which it is necessary first to determine the scalar
potential of an arbitrary vector field, inherent in a single particle. After
that by means of standard methods all the characteristics of this field are
derived, including the field equations, its stress-energy tensor and the type
of the force, exerted by the field on the particles.
We must note that the
4-potential of the field is expressed as a covariant 4-vector, and the matter
energy in this field depends on the product of the 4-potential and the mass (electromagnetic)
4-current, taken with the contravariant index. The field tensor has doubly
covariant indices as the consequence of the 4-curl acting on the 4-potential.
In order to find this tensor with contravariant indices the metric tensor is
required. Contraction of the field tensor with itself gives the tensor
invariant, which is required in the Lagrangian to carry out variation and to
express relationship between the matter, metric and field in the appropriate
equations. Another peculiarity of this approach is that the field equations (8)
and (14) are similar in form to Maxwell equations.
The previously
described approach was used in [5], [6], [7] to find also the
4-potential of the gravitational field, its stress-energy tensor, gravitational
4-force and field equations in the framework of the Covariant Theory of
Gravitation (CTG).
In CTG the gravitational
field is divided from the metric field, gravitation becomes an independent
field with its own energy, momentum and action in the form of gravitational
force. As a result, the metric is only necessary to describe deviations of the
results of gravitational experiments from their form in the special theory of
relativity. The essential part of the Lagrangian in CTG is the constant 
,
which is called cosmological constant. With the help of this constant the
Hamiltonian gauge is performed so that the system’s energy could be determined
unambiguously.
5.
References
1. C. W. Misner, K. S. Thorne, and J. A. Wheeler, Gravitation (W. H. Freeman, San
Francisco, CA, 1973).
2. Fedosin S.G. About the cosmological constant,
acceleration field, pressure field and energy. vixra.org, 5 Mar
2014.
3. Fedosin S.G. The integral energy-momentum 4-vector
and analysis of 4/3 problem based on the pressure field and acceleration field. American Journal of
Modern Physics. Vol. 3, No. 4, 2014, pp. 152-167. doi: 10.11648/j.ajmp.20140304.12.
4. Fedosin S.G. Model of Gravitational Interaction in the Concept of Gravitons. Journal of Vectorial
Relativity, 2009, Vol. 4, No. 1, P.1–24.
5. Fedosin
S.G. The Principle of Least
Action in Covariant Theory of Gravitation. Hadronic Journal,
2012, Vol. 35, No. 1, P. 35–70.
6. Fedosin S.G. Fizicheskie teorii
i beskonechnaia vlozhennost’ materii. (Perm, 2009). ISBN
978-5-9901951-1-0.
7. Fedosin S.G. Fizika i
filosofiia podobiia ot preonov
do metagalaktik. (Perm, 1999). ISBN
5-8131-0012-1.
Source:
http://sergf.ru/pfen.htm