In English

Apeiron, 2007, Vol. 14, No. 4, P. 385 – 413

 

ЭЛЕКТРОМАГНИТНАЯ И ГРАВИТАЦИОННАЯ КАРТИНЫ МИРА

 

С.Г. Федосин

 

intelli@list.ru

 

Сделан обзор теории электромагнитного поля совместно со специальной и общей теорией относительности. Представлена аналогичная теория гравитации, обладающая свойством лоренц-инвариантности в собственном представлении, в котором информация переносится со скоростью распространения гравитационного поля. Произведено обобщение указанной теории гравитации на неинерциальные системы отсчёта с помощью математического аппарата общей относительности. Это позволяет избавиться от некоторых недостатков стандартной общей теории относительности и расширить её возможности. Показана возможность взаимодополнительного описания физических явлений благодаря одновременному использованию теорий гравитационного и электромагнитного полей.

 

Ключевые слова: Электромагнетизм; Гравитация; Теория относительности

 

PACS: 03.30.+p ; 03.50.-z ; 03.50.Kk ; 04.20.Cv ; 04.90.+e ; 

 

Существенной чертой теории относительности является то, что результаты физических измерений оказываются зависящими от применяемой техники и процедуры измерений. Например, в [1] указывается на различие результатов, возникающее как следствие различных применяемых волновых представлений. Здесь имеется в виду, что в качестве переносчика информации в средствах измерений времени и расстояний кроме электромагнитной волны могут быть взяты и другие волны. Это приводит к изменению теории относительности, хотя вид большинства формул остаётся прежним.

В связи с этим мы вначале опишем формализм, применяемый в классической теории электромагнитного поля и в теории относительности. Затем с той же степенью подробности представим лоренц-инвариантную теорию гравитации. Её вид в инерциальных и неинерциальных системах отсчёта зависит от используемого волнового представления, в котором основную роль играют гравитационные волны. В заключение будет сделано сравнение стандартной общей теории относительности и лоренц-инвариантной теории гравитации в неинерциальных системах отсчёта. Одним из выводов оказывается то, что тензор энергии-импульса гравитационного поля должен присутствовать в качестве одного из источников для определения метрики. Другой вывод касается сущности общей теории относительности как  таковой. В классическом подходе она представляется как теория гравитации. В новом подходе общая относительность предназначается для описания явлений в условиях, когда распространяющиеся волны, переносящие информацию о геометрии пространства-времени, подвергаются искажающему воздействию со стороны имеющихся полей.

 

Относительность и электромагнетизм

Теория электромагнитного поля по праву является одной из самых плодотворных физических теорий современности. Специальная теория относительности (СТО) появилась как следствие того, что уравнения движения и взаимодействия тел должны соответствовать преобразованиям электромагнитных сил в разных системах отсчёта. Для немагнитного вещества в отсутствие электрической поляризации дифференциальные уравнения Максвелла для напряжённостей электромагнитного поля имеют следующий стандартный вид:

 

                       

(1)

,                 ,

 

где  – вектор напряжённости электрического поля,

 – вектор магнитной индукции,

 – электрическая постоянная,

 – плотность зарядов элемента вещества,

 – скорость распространения электромагнитного поля (скорость света),

– вектор плотности тока зарядов, зависящий от скорости движенияэлемента вещества.

 

Выражение для электромагнитной силы, действующей на точечный заряд : . Для плотности силы, действующей на элемент вещества, сила имеет вид: .

Через величины  и  определяются плотность энергии, плотность потока энергии (в виде вектора Пойнтинга), а также плотность импульса электромагнитного поля:

 

,             ,           .                (2)

 

Для случая прямолинейного распространения излучения в вакууме для напряжённостей поля в плоской электромагнитной волне выполняется соотношение , причём напряжённости поля перпендикулярны друг другу и к направлению распространения волны.

Тогда из (2) следует, что . Если подобная плоская волна падает на поверхность тела, то она будет оказывать давление  на поверхность:  , где  – коэффициент отражения.

Из (1) следует, что напряжённости поля могут быть выражены через скалярный  и векторный  потенциалы электромагнитного поля:

 

,                           .                                (3)

 

Если связать между собой потенциалы поля  калибровочным условием  , то при подстановке (3) в (1) получаются известные волновые уравнения для потенциалов:

 

,                   .                 (4)

 

Согласно (4) электромагнитные волны в виде колебаний потенциалов в пространстве-времени возможны даже в отсутствие зарядов и токов (свободные волны). Наличие ненулевых потенциалов в волне означает, что в волне есть периодические колебания напряжённостей поля (это вытекает из (3) ), а значит волны переносят энергию и импульс согласно (2). Впрочем, волновые уравнения для векторов напряжённости поля получаются и непосредственно из (1):

 

,                   . 

 

 

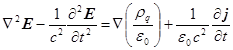Решение уравнений Максвелла (1) сводится к решению уравнений (4), далее по известным потенциалам находятся напряжённости поля из (3). Общее решение для потенциалов в (4) имеет интегральный вид:

 

,                    ,

 

потенциалы в произвольной точке 1 в момент времени  определяются путём интегрирования вкладов от элементов объёмов . В элементах объёма следует брать плотность заряда и токи в более ранний момент времени, равный , где  – расстояние между элементом объёма и точкой 1 в ранний момент времени. Таким образом учитывается то, что электромагнитное воздействие имеет ограниченную скорость своего распространения .

Если имеется движущееся заряженное малое тело с зарядом , то для потенциалов получается решение Льенара-Вихерта:

 

,                   ,

 

причём расстояние  между зарядом и точкой 1 и скорость  движения заряда следует подставлять в ранний момент времени .  Пусть заряд движется только поступательно с постоянной скоростью  вдоль оси . Тогда  , а также . Если выразить  и  через , то для потенциалов можно найти:

 

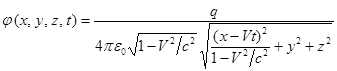,                     (5)

 

 

,       а также ещё:      .

 

В собственной системе отсчёта , в которой заряд покоится, скорость , и из (3) и (5) получается закон Кулона:

 

,              ,                (6)

 

,                           .

 

Сравнение (5) и (6) показывает, как должны трансформироваться координаты между системой отсчёта  (движущейся вместе с зарядом) и неподвижной системой отсчёта  для того, чтобы запись выражения для потенциала осталась неизменной:

 

,               ,              .                         (7)

 

 

Соотношения (7) есть частные преобразования Лоренца в СТО для пространственных координат. Характерной особенностью СТО является то, что в ней измерения координат и времени производятся с помощью инвариантной величины – скорости света, одинаковой во всех инерциальных системах отсчёта. В дополнение к (7) необходимо добавить преобразование времени:

 

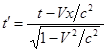.                                                     (8)

 

 

Выражение (8) можно получить, например, из (7), после применения принципа относительности. Если  движется относительно  вдоль оси , то и наоборот,  движется относительно, но уже со скоростью  против оси . Тогда должно быть:

 

,                  ,                .                  (9)

 

 

Комбинируя (7) и (9), приходим к (8). Преобразования координат и времени имеют вид (7) и (8) вследствие ограниченности скорости света. Это приводит к разному ходу времени и неодинаковости размеров, наблюдаемых у движущихся тел при разных скоростях.

Оказывается, что уравнения электромагнетизма не будут менять свой вид, если при переходе из одной в другую инерциальную систему отсчёта используются преобразования Лоренца типа (7) и (8) для всех физических величин, а не только для координат и времени. Соответственно говорят, что электродинамика инвариантна относительно преобразований Лоренца.

 

Электродинамика в четырёхмерном мире Минковского

Из (7) и (8) видно, что координаты и время преобразуются одновременно. В СТО соответствующие друг другу временные и пространственные величины, взятые как некоторые скаляры и обычные 3-векторы, составляют вместе 4-вектор либо входят в состав 4-тензоров. Для любых четырёхмерных величин (векторов и тензоров) вводится единый закон преобразования из одной инерциальной системы отсчёта в другую. В частности, если событие описывается 4-вектором положения точки в 4-пространстве Минковского , то частное преобразование Лоренца (7) и (8) может быть записано так:

 

,

 

где     .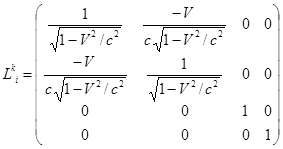

 

 

 

 

Тензорная величина  позволяет делать преобразования 4-векторов. Для преобразования компонент тензора второго ранга требуется дважды использовать , что даёт формулу следующего вида:  . В общем случае необходимо использовать  столько раз, сколько у преобразуемого тензора имеется неповторяющихся индексов.

Приведём теперь наиболее типичные 4-величины в электродинамике. 4-вектор плотности тока определяется как произведение плотности заряда , взятой в системе покоя, на 4-скорость:

 

.                   (10)

 

 

4-вектор потенциала связывает скалярный и векторный потенциалы:

 

.                                                    (11)

 

Четырёхмерный оператор градиента  определяется как ковариантный вектор:

 

.

 

 

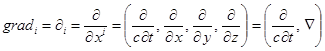В СТО переход от контравариантного к ковариантному вектору и наоборот осуществляется простой заменой знака у пространственных координат, так что например .

 

4-дивергенция вектора определяется как скалярное произведение оператора градиента на 4-вектор. В частности имеем:

 

,                    ,

 

что соответствует закону сохранения электрического заряда и калибровочному условию для потенциалов поля соответственно.

 

Скалярный 4-оператор даламбертиан получается как скалярное произведение операторов 4-градиента:

 

□2.

 

Нетрудно проверить, что следующее уравнение эквивалентно волновым уравнениям (4) для потенциалов:

 

□2.

 

Из 4-потенциала можно построить антисимметричный тензор электромагнитного поля по формуле: . С помощью (3) находим для немагнитного вещества в отсутствие электрической поляризации:

 

.

 

 

 

 

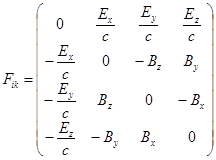Тензор  выражается через координаты вектора электрического поля  и вектора магнитной индукции  . Поэтому уравнения поля (1) могут быть выражены через  в следующем виде:

 

,                    .

 

Поскольку  и  составляют компоненты тензора , то их лоренцевские преобразования осуществляются не по векторному, а по тензорному закону. На основе тензора  можно построить тензор энергии-импульса электромагнитного поля:

 

,                           (12)

 

где  – метрический тензор. Тензор можно расписать по компонентам:

 

 

 

 

 

 

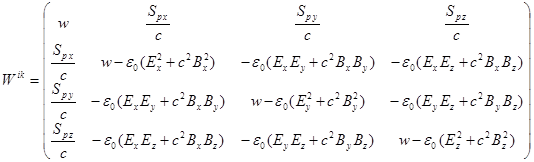
Видно, что в состав тензора входят компоненты напряжённостей полей, а также плотность энергии  и компоненты вектора потока энергии  согласно (2).

Связь между веществом и полем заключается в том, что на вещество в поле действуют силы и в веществе возникают напряжения и давления. Приведём тензор плотности энергии-импульса вещества  для сжимаемой жидкости или непрерывно распределённого вещества без учёта сдвиговой вязкости:

 

,                                   (13)

 

где  и  – давление и плотность вещества в покое,

 –  4-скорость элементов объёма,

 – функция сжатия, определённая в [2].

 

 

Предположим, что в некоторой области пространства есть вещество, электромагнитное поле, а также имеются какие-то дополнительные силы, вносящие свой вклад в давление  в тензоре . Тогда 4-дивергенция суммы тензоров энергии-импульса вещества и поля должна равняться нулю для каждого элемента объёма:

 

.                                                 (14)

 

Равенство (14) эквивалентно тому, что всегда осуществляется суммарный баланс притока и оттока энергии и импульса между веществом, полем и сторонними силами. Перенесём величину  в (14) в правую часть равенства, что даёт: . Мы считаем, что  есть скорость изменения 4-импульса вещества и сторонних сил, причём  пропорционально скорости изменения их энергии в единице объёма. В то же время  вектор есть вектор плотности 4-силы, действующей со стороны электромагнитного поля. Компоненты  таковы:

 

,  пропорционально мощности работы поля в единице объёма,  .

 

Таким образом, (14) есть уравнения движения вещества и электромагнитного поля при наличии дополнительных сил, создающих давление.

Отметим ещё раз, что согласно СТО любые физические результаты решающим образом зависят от самой процедуры пространственно-временных измерений. Под интервалом  между двумя событиями понимается модуль разности двух 4-векторов, отмечающих эти два события:

 

,

 

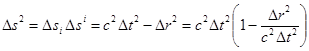.                      (15)

 

Пусть событиями 1 и 2 являются присутствие некоторого тела в близких друг к другу точках 1 и 2 в моменты  и , причём тело движется между точками 1 и 2 со средней скоростью . Тогда в (15) можно положить, что , . В СТО модуль 4-вектора и скорость света не зависят от выбора системы отсчёта, отсюда инвариантами для инерциальных систем являются как интервал , так и собственное время движущегося тела  . Другими словами, в разных системах отсчёта скорости тела  и отмечаемое время , соответствующее , будут разными, но вычисляемое значение  остаётся неизменным.

При пространственно-временных измерениях с помощью света всегда получается равенство нулю интервала между любыми измеряемыми точками. Свет (и любые частицы, движущиеся со скоростью света) в СТО являются универсальными переносчиками информации об измеряемых предметах. Любые физические величины являются или могут быть функциями координат в пространстве-времени. Поэтому вся физика становится в зависимость от процедуры измерений координат и времени. В имеющихся средствах измерений (начиная от человеческого глаза и заканчивая лазерами и атомными часами) используются электромагнитные явления или делается калибровка на основе электромагнитных волн. Принимается, что любая правильная физическая теория обязана быть совместимой с принципами СТО, в первую очередь с принципом относительности и с измеримостью явлений с помощью света. Тем самым можно констатировать, что в настоящее время  парадигма физики и научное мировоззрение целиком построены на электромагнитной картине мира.

 

Общая относительность

В общей теории относительности (ОТО) основными уравнениями являются уравнения Гильберта-Эйнштейна для нахождения коэффициентов метрического тензора . Данный тензор позволяет описывать явления в пространстве-времени, искривлённом под действием энергии-импульса вещества и полей. В левой части уравнений для метрики стоят геометрические тензорные величины, связанные с тензором  и его производными первого и второго порядка по координатам пространства-времени. В правой части уравнений стоят тензоры плотности энергии-импульса вещества и поля, то есть физические тензорные величины. Из равенства левой и правых частей уравнений, при определённом множителе пропорциональности, следует, что искривление пространства-времени прямо пропорционально тензорам энергии-импульса в этом пространстве-времени.

Исторически сложилось так, что уравнения Гильберта-Эйнштейна всегда решались только для тензоров вещества и электромагнитного поля. Найденные компоненты метрики фактически считалась потенциалами гравитационного поля, имеющего тензорный вид. Такое положение проистекало из того, что проявления гравитационного поля трактовали геометрическим образом, как искривление пространства-времени.

Уравнения для метрики в простейшем случае имеют вид:

 

,                                   (16)

 

где  – тензор Риччи,

– скалярная кривизна.

 

Ковариантная производная от левой части (16) равна нулю вследствие симметрии относительно тензора . Равенство нулю ковариантной производной от правой части (16) обеспечивается свойствами тензоров энергии-импульса и следует из соотношения, аналогичного (14). Скорость света в множителе пропорциональности в (16) соответствует тому факту, что в тензорах  и  также присутствует скорость света. При этом в случае слабого поля уравнения (16) переходят в волновые уравнения для тех поправок к метрике, которые отличают метрику искривлённого пространства-времени от плоского пространства-времени Минковского. Отсюда делается вывод, что колебания метрики, как эквивалент колебаний гравитации, распространяются также со скоростью света.

Очевидно, что равенство скорости распространения гравитации и скорости света в ОТО есть не свойство гравитации самой по себе, а следствие построения теоретического аппарата ОТО на основе электромагнитной парадигмы.

 

Лоренц-инвариантная теория гравитации

Необычность сведения физической гравитационной силы к свойствам пространства-времени, вытекающая из ОТО непредставимость гравитационной энергии в виде настоящего тензора, затруднения при квантовании гравитационного поля в рамках ОТО породили многочисленные попытки построения отличающихся от ОТО теорий гравитации. Опишем здесь одну из альтернатив ОТО, лоренц-инвариантную теорию гравитации (ЛИТГ) согласно [2]. Сущностью ЛИТГ является то, что сила гравитации признаётся настоящей физической силой. При этом скорость распространения гравитационного воздействия  не обязательно равна скорости света .

Уравнения гравитационного поля в ЛИТГ таковы:

 

                  

(17)

,            ,

 

где  – вектор напряжённости гравитационного поля или гравитационное ускорение,

 – вектор напряжённости кручения гравитационного поля или просто кручение,

 – гравитационная постоянная,

 – плотность массы вещества,

– вектор плотности тока массы, зависящий от скорости движенияэлемента массы.

 

Гравитационная  сила зависит от  напряжённостей поля и от массы  частицы, на которую действует сила:    . Соответственно, для плотности силы имеем: .   

Плотность энергии, векторы плотности потока энергии и плотности импульса гравитационного поля равны:

 

,   ,               .                (18)

 

Для плоской гравитационной волны в вакууме ,   ,    .

 

Напряжённости гравитационного поля выражаются через скалярный  и векторный  потенциалы:

 

,                       .                          (19)

 

Из (19) и (17) следуют волновые уравнения для потенциалов гравитационного поля:

 

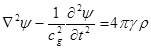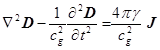,                  ,               (20)

 

при условии калибровки .

 

Уравнения (20) предсказывают свободно распространяющиеся гравитационные волны, которые могут иметь векторный характер и дипольное происхождение. В отличие от этого в ОТО гравитационное поле считается тензорным, порождаясь в простейшем случае квадрупольным образом. Сравним данную ситуацию с положением в электродинамике. Излучение системы зарядов обычно рассчитывают как сумму дипольного электрического, дипольного магнитного, квадрупольного электрического и последующих мультипольных излучений. В замкнутой нейтральной системе, состоящей из частиц с одинаковым отношением заряда к массе, дипольные и магнитные излучения исчезают, остаётся только квадрупольный член и высшие мультиполи. Возьмём теперь замкнутую гравитационно связанную систему, наподобие двух нейтронных звёзд, обращающихся друг возле друга. Для них также суммарное дипольное излучение стремится к нулю, однако квадрупольное излучение нулю не равно. В данном частном случае результаты ЛИТГ и ОТО совпадают.

Решение Льенара-Вихерта уравнений (20) для потенциалов движущейся точечной частицы с массой  получается таким:

 

,                           ,

 

потенциалы в произвольной точке 1 в момент времени  зависят от расстояния  между частицей и точкой 1, и от скорости  движения частицы. При этом  и  следует вычислять в более ранний момент времени . Выражая все физические величины в ранний момент времени через величины в данный момент времени , для равномерного движения со скоростью  получаем формулу аналогично (5):

 

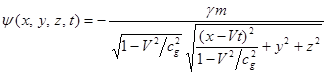,                        (21)

 

 

,           а также :     .

 

Введём собственную систему отсчёта , привязанную к  частице. В  скорость , и из (21) и (19) приходим к закону Ньютона:

 

,                ,                (22)

 

,                         .

 

За пределами вращающейся сферы кручение можно выразить через момент импульса  сферы с помощью дипольной формулы:

 

.

 

Благодаря данной  вращающаяся сфера дополнительно к силе Ньютона воздействует на тела, если эти тела имеют какую-то скорость относительно центра сферы.

Из (21) и (22) видно, что для лоренц-инвариантности потенциала в системах отсчёта  и  необходимо, чтобы координаты и время преобразовывались следующим образом:

 

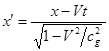,                 ,                  .                        (23)

 

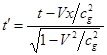.                                                (24)

 

 

Соотношения (23), (24) есть частные преобразования Лоренца для случая, когда вся информация о длинах и времени  в разных инерциальных системах определяется с помощью измерений событий по времени прихода гравитационных волн. Предположим, что мы научились детектировать гравитационные волны, создавать приёмники и передатчики гравитационных сигналов, а также измерительные приборы на их основе. Тогда при условии, что  в инерциальных системах отсчёта, мы приходим к специальной теории относительности в рамках ЛИТГ. Отличие гравитационной СТО от электромагнитной заключается тогда в замене скорости света на скорость , основные соотношения СТО остаются теми же самими.

Последовательное рассмотрение гравитационной СТО приводит к формуле для энергии покоя тел в виде: . Между тем в обычной СТО энергия покоя тела вычисляется так: . Какая же из этих формул верная? По всей видимости, верны обе формулы, но каждая верна только в рамках своего, гравитационного или электромагнитного представления. Для доказательства справедливости выражения  можно рассмотреть условный распад гравитационно-связанного тела массы  под воздействием двух встречно направленных гравитационно-волновых квантов энергии. Для покоящегося тела суммарная энергия падающих на тело квантов равна .  Если это же тело движется с постоянной скоростью  вдоль линии распространения квантов, то суммарная энергия квантов с точки зрения системы отсчёта тела изменится вследствие эффекта Допплера. Так как скорость квантов равна , то она будет присутствовать в формуле для сдвига частоты колебаний этих квантов. Отсюда энергия квантов будет равна 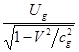. Приравнивая разность энергий квантов кинетической энергии тела: 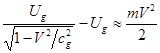, приходим к формуле для энергии покоя тела: .

 

При образовании из множества частиц единого гравитационно-связанного тела из него выделяется энергия, равная по модулю энергии связи этих частиц между собой. Если исходить из теоремы вириала, половина гравитационной энергии тела расходуется на нагрев составляющих тело частиц, а другая половина энергии уносится из тела гравитационным излучением. Мы можем считать, что энергия покоя тел как энергия связи есть энергия частиц тела в поле сильной гравитации, а излучение энергии связи осуществляется в основном электромагнитным способом. Нагретое тело активно излучает электромагнитные волны и в дальнейшем остывает. Таким образом, энергия гравитации при выполнении работы по скучиванию вещества частично перерабатывается в электромагнитную форму энергии. Из приблизительного равенства энергии покоя, энергии связи и излучённой энергии в силу теоремы вириала вытекает равенство , а значит и равенство . Это указывает на большую вероятность равенства скоростей распространения гравитационных и электромагнитных полей.

 

 

 

ЛИТГ в четырёхмерном мире Минковского

Лоренц-инвариантность ЛИТГ достигается, если все физические величины записывать в инвариантном виде относительно гравитационной  СТО и во всех формулах использовать скорость распространения гравитации . В частности, 4-вектор положения имеет вид: . Для преобразования 4-векторов и тензоров из одной инерциальной системы отсчёта в другую при движении систем отсчёта вдоль оси  можно ввести величину тензорного типа :

 

,

 

 

 

 

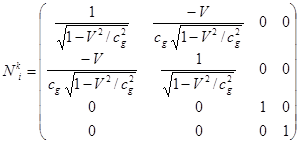так что, например, .

 

В уравнения гравитационного поля входят 4-вектор плотности массового тока:

 

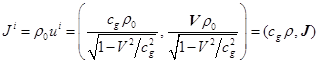,                    (25)

 

где  – плотность массы в системе покоя,

 

и 4-вектор потенциала:

 

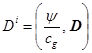.                                                   (26)

 

 

Уравнения поля (20) для потенциалов приобретают следующий вид:

 

□2.

 

Тензор гравитационного поля может быть найден по формуле: . Он выражается через компоненты вектора гравитационного ускорения  и вектора кручения  :

 

.

 

 

 

 

 

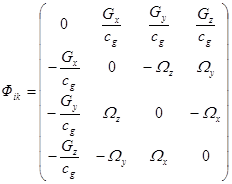С помощью тензора  можно по-другому записать уравнения поля (17):

 

,                    .

 

Тензор энергии-импульса гравитационного поля:

 

,                            (27)

 

причём различие знаков перед тензором  и тензором  в (12) определяется тем, что массы притягиваются друг к другу, а электрические заряды одного знака отталкиваются друг от друга.

Компоненты тензора  включают в себя плотность энергии   и компоненты вектора плотности потока энергии :

 

.

 

 

 

 

 

 

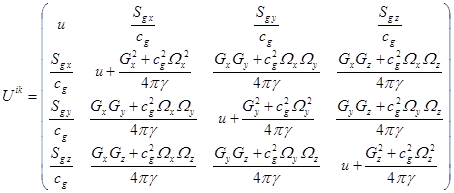Аналогично (14) запишем взаимосвязь тензоров энергии-импульса для вещества, находящегося в гравитационном поле:

 

.                                                 (28)

 

Соотношение (28) выражает собой уравнения движения вещества в поле. В (28) в левой части находится тензор  для сжимаемой жидкости или непрерывно распределённого вещества согласно определения (13). Заметим, что в данном случае 4-скорости в этом тензоре выражаются не через скорость света, а через скорость . Производная от тензора  есть изменение импульса вещества и сторонних сил в единицу времени. В правой части (28) стоит гравитационная 4-сила:

 

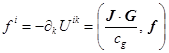,             где .

 

Исходя из вышеизложенного, ЛИТГ является полностью совместимой с гравитационной СТО. Другими словами, гравитационные явления будут инвариантны в разных инерциальных системах отсчёта, если в качестве переносчика информации используется само гравитационное поле, имеющее скорость . Таким образом мы приходим к тому, что возможно построить гравитационную картину мира. Различие гравитационной и электромагнитной картин мира вытекает из различия скоростей переноса информации  и .

 

 

ЛИТГ и общая относительность

Предположим для начала, что имеется только вещество и гравитационное поле, описываемые тензорами  и  соответственно. Мы вновь хотим использовать уравнения Гильберта-Эйнштейна для нахождения компонент метрического тензора . Общей идеей здесь как и в ОТО является то, что искривление пространства-времени прямо пропорционально тензорам энергии-импульса в этом пространстве-времени.

Уравнения для метрики подобны (16):

 

,                                     (29)

 

разница лишь в использовании скорости  и в замене тензора  на тензор .

 

Однако теперь уже нет смысла трактовать компоненты метрического тензора в искривлённом пространстве-времени как потенциалы тензорного гравитационного поля. Действительно, ЛИТГ позволяет определить все характеристики гравитационного поля ковариантным образом уже в рамках гравитационной СТО. В результате получающаяся из (29) метрика просто показывает степень искривления пространства-времени по отношению к плоскому пространству-времени Минковского. Метрика, как ей и положено быть, становится чисто геометрическим параметром. Колебания метрики в (29) происходят со скоростью распространения гравитации . Решение уравнений (29) для определения метрики внутри и за пределами покоящегося массивного шара было осуществлено в [2]. Вклад в метрику от энергии-импульса собственного гравитационного поля массивного тела вносит поправку второго порядка по отношению к виду решения Шварцшильда в ОТО. Очевидно, что метрика может изменяться и в отсутствие вещества, под действием внешних электромагнитных и гравитационных волн, свободно распространяющихся  в пространстве. Эти волны переносят энергию и импульс, и потому влияют на распространение света, если мы с его помощью определяем метрику и метрическое поле.

 

Заключение

Наличие тензора энергии-импульса  в (29) приводит к тому, что любое гравитационное поле, внешнее или внутреннее, стационарное или свободное, вносит свой вклад в метрику, в дополнение к энергии-импульсу движущегося или покоящегося вещества. А что можно сказать относительно вклада электромагнитного поля в метрику с точки зрения ЛИТГ? Данный вопрос требует более тщательного рассмотрения. Мы ограничимся здесь тем возможным случаем, когда скорости распространения гравитации и электромагнитных воздействий  и  равны друг другу, отражая тем самым две стороны одного общего явления. Тогда тензор энергии-импульса электромагнитного поля  можно просто добавить к тензорам  и  в правой части уравнений для метрики (29). Сумма компонент , , и , как плотности соответствующих энергий, будет равна сумме энергии покоя вещества, кинетической энергии массы-энергии от перепадов сил давления, энергии расталкивания зарядов и токов от электрического и магнитного полей, а также отрицательной энергии гравитационного поля. Такой порядок суммирования энергий вполне соответствует тому, что интегральная гравитационная масса складывается из всех видов энергии вещества и поля и ответственна за искривление пространства-времени.

Напомним, что ещё Эйнштейн отмечал существенную асимметрию между полем гравитации и другими полями в ОТО. Поскольку каждое поле имеет энергию и импульс, оно имеет массу и потому делает вклад в гравитацию. Гравитация порождается любым полем и в этом смысле неразрывна от других полей. Но возникновение гравитации в ОТО допускается и без других полей, при этом гравитация не обязана порождать другие поля или как-то влиять на них.

В ЛИТГ добавка тензора энергии-импульса электромагнитного поля  в уравнения (29) приводит к симметричному вхождению гравитации и электромагнетизма в решения для метрики. Каждое поле делает свой собственный вклад в метрику, поля уравниваются по своей значимости как источники для определения метрики. Если в ОТО гравитация как результат искривления пространства-времени не поддаётся квантованию, то в ЛИТГ возможна такая же процедура квантования гравитации, как и в электромагнетизме.

Добавка в (29) и использование трёх тензоров существенно обогащает и изменяет содержание ЛИТГ по сравнению с ОТО. Общая относительность в ЛИТГ предстаёт как способ описания физических явлений в условиях, когда любые массы, энергии и импульсы материи влияют на распространение электромагнитных и гравитационных волн. Волны являются основным источником информации о событиях и явлениях. Учёт метрики позволяет восстановить точную информацию о ходе часов, измеряемых размерах и физических величинах в неинерциальных системах отсчёта. Тем самым преодолевается искажение явлений, вносимое самой материей в наш способ физических наблюдений.

В ОТО ничто не мешает существовать таким экстремальным объектам, как чёрные дыры. Ведь гравитационное поле в ОТО является просто следствием искривления пространства-времени, на которое не накладывается никаких ограничивающих условий. Однако чёрные дыры как проявления сингулярностей пространства-времени означают, что в них не применимы полевые уравнения и известные нам законы природы. Если ОТО допускает существование подобных объектов и не может описать их, это говорит либо о недостатке самой ОТО как полной физической теории либо о противоречивости ОТО. В ЛИТГ не только вещество, но и само гравитационное поле определяет метрику. При этом естественным образом появляется граничное условие. Оно вытекает из того, что степень предельного скучивания вещества определяется взаимодействием гравитационных и электромагнитных сил с веществом. В свою очередь эти силы порождаются самой материей на более низких по масштабам уровнях, начиная с масштабов элементарных частиц и переходя к ещё более глубоким структурным уровням устройства вещества. В этом случае гравитация не может быть бесконечно большой.

Предположим, что гравитация и электромагнетизм есть следствие излучений от множества мельчайших частиц материи. На уровне звёзд характерным примером подобных процессов является коллапс нейтронной звезды, когда из звезды излучаются сферические гравитационные волны, потоки нейтрино, электромагнитное излучение, происходят выбросы вещества с релятивистскими скоростями. Тогда следует ожидать, что силы возможного гравитационного и электромагнитного действий на вещество ограничены по своей величине самой природой, причём на всех уровнях материи. Рассуждая по индукции, чёрные дыры должны либо существовать, либо не существовать одновременно на всех масштабных уровнях. При этом существование чёрных дыр вступает  в противоречие с их свойствами поглощения частиц и излучений. Если чёрные дыры всё поглощают и ничего не выпускают из себя, то в конце концов они должны поглотить всю материю на низлежащих масштабных уровнях. Но в таком случае пропадает тот источник, который может питать гравитацию, которую мы наблюдаем на нашем уровне материи. Имеется также ряд наблюдательных данных, противоречащих существованию чёрных дыр. Например, прародителем нейтронной звезды CXO J164710.2-455216 является очень массивная звезда, имеющая массу около 40 масс Солнца [3]. Ранее считалось, что столь массивные звёзды обязательно порождают чёрные дыры в конце своей эволюции.

Следует заметить, что необходимость присутствия тензора гравитационного поля в правой части уравнений (16) можно обосновать даже в рамках ОТО. Для этого достаточно принять следующее утверждение: Так как в ОТО метрика оказывается в сущности функцией потенциалов гравитационного и электромагнитного полей и внешних дополнительных сил (это хорошо видно в пределе слабого поля), то добавка тензора гравитационного поля в уравнения Гильберта-Эйнштейна для метрики эквивалентна самодействию гравитационного поля через метрику. Эффект самодействия вообще следует считать законом природы, так что можно постулировать следующее: если объект создаёт какое-либо изменение вокруг себя, то это изменение неизбежно воздействует на сам объект. Следовательно, если материя создаёт в ОТО метрическое поле как эквивалент гравитационного поля, то и само это гравитационное поле должно как-то действовать на материю, в свою очередь изменяя метрическое поле. Можно сказать и по другому – для достижения самосогласованности метрического поля в ОТО необходимо учесть его вклад также и через сам источник метрического поля в виде соответствующего тензора.

Повторим ещё раз, что ОТО является не теорией гравитационного поля, а теорией метрического поля. Известно, что в СТО становится возможным преобразование координат, физических величин наподобие скоростей, сил, потенциалов и т.д., а также уравнений движения тел из одной инерциальной системы в другую. При этом ускорению подвергаются только исследуемые тела, сами же инерциальные системы отсчёта вместе с их наблюдателями по определению двигаются без ускорения, то есть с постоянной скоростью. Основной задачей ОТО является преобразование координат и физических величин между любыми системами отсчёта, в том числе и неинерциальными, при наличии ускорения самих систем отсчёта. В таком случае СТО является частным случаем ОТО, когда ускорение используемых систем отсчёта равно нулю. Для правильного рассмотрения гравитационных сил в инерциальных системах отсчёта необходимо, чтобы гравитация действовала только между исследуемыми телами, и не ускоряла сами системы отсчёта. Для этого необходимо локальные системы отсчёта помещать в дополнительное внешнее гравитационное поле, противоположное исследуемому гравитационному полю. Тогда локальный наблюдатель вместе с приборами отсчёта времени и расстояний будет находиться в инерциальной системе отсчёта. Таким образом, потенциалы симметричного относительно радиуса гравитационного поля массивной сферы могут быть измеренными в инерциальных системах отсчёта во всех точках сферы. Далее с помощью преобразований Лоренца для 4-вектора потенциала (26) нетрудно найти потенциалы поля в любой другой инерциальной системе отсчёта. Таким образом, становится возможным рассматривать гравитационные явления уже в рамках СТО, с помощью уравнений ЛИТГ (17). Как показано выше, уравнения гравитационного поля можно записать и в тензорном виде через тензор . Это означает, что гравитация и без ОТО может быть представлена в ковариантном тензорном виде, в том числе в неинерциальных системах отсчёта с любой метрикой. Далее с помощью ОТО при известных начальных распределениях энергии-импульса материи можно находить метрику в каждой системе отсчёта и последующее движение материи. Для каждой системы отсчёта получается своя метрика и своя картина явлений, что позволяет находить корреляции между одними и теми же событиями в разных системах отсчёта. 

Теперь мы возвращаемся к заголовку данной статьи. Вначале мы показали возможность существования двух подобных лоренц-инвариантных теорий – электромагнетизма и гравитации. Каждой из этих теорий можно поставить в соответствие свою частную теорию относительности, зависящую либо от скорости света, либо соответственно от скорости распространения гравитации. Из электромагнитного подхода выросла общая теория относительности (ОТО), в то время как из гравитационного подхода получилась вначале лоренц-инвариантная теория гравитации (ЛИТГ), а затем обобщение ЛИТГ на относительность в неинерциальных системах отсчёта подобно ОТО. Единая форма уравнений для электромагнетизма и гравитации, симметричность их присутствия в рамках ЛИТГ и общей теории относительности как источников для нахождения метрики означают возможность построения более общей теории поля. Из изложенного видно, что при условии  единое гравиэлектромагнитное поле получается простым суммированием соответствующих физических величин в уравнениях. Таким образом мы приходим к альтернативности и взаимодополнительности электромагнитной и гравитационной картин мира.

 

 

Литература

 

1.       Федосин С.Г. Современные проблемы физики. В поисках новых принципов. – М.: Эдиториал УРСС, 2002 – 192 с.

2.       Федосин С.Г. Физика и философия подобия от преонов до метагалактик. – Пермь: Стиль-МГ, 1999 – 544 с.

3.       M. P. Muno at al. A Neutron Star with a Massive Progenitor in Westerlund 1. – arXiv: astro-ph /0509408 v3, 26 Jan 2006// на сайте http://arxiv.org/abs/astro-ph/0509408 .

 

 

ELECTROMAGNETIC AND GRAVITATIONAL PICTURES OF THE WORLD

 

The review of the theory of electromagnetic field together with the special and general theories of relativity has been made. The similar theory of gravitation has been presented which has the property of Lorentz-invariancy in own representation in which the information is transferred with speed of propagation of a gravitational field. Generalization of the specified gravitation theory on noninertial reference systems has been made with the help of the mathematical apparatus of the general relativity. It allows to avoid some drawbacks of the standard general relativity theory and to expand its possibilities. The possibility of complementary descriptions of the physical phenomena with the help of simultaneous use of theories of gravitational and electromagnetic fields has been shown.

 

Источник: http://sergf.ru/egp.htm

На научный сайт