На русском языке
Apeiron, 2007, Vol. 14, No. 4,
P. 385 – 413
Electromagnetic and Gravitational Pictures of
the World
Sergey G. Fedosin
Perm State University, Russia
E-mail: intelli@list.ru
The
review of the theory of electromagnetic field together with the special and
general theories of relativity has been made. The similar theory of gravitation
has been presented which has the property of Lorentz-invariancy in its own
representation in which the information is transferred at the speed of
propagation of the gravitational field. Generalization of the specified
gravitation theory on noninertial reference systems has been made with the help
of the mathematical apparatus of the general relativity. It allows to avoid
some drawbacks of the standard general relativity theory and to expand its applicability.
The possibility of complementary descriptions of the physical phenomena with
the help of simultaneous use of the theories of gravitational and
electromagnetic fields has been shown.
Keywords: electromagnetism,
gravitation, relativity theory
1. Introduction
The essential feature of the relativity theory is that
the results of physical measurements depend on the technique used and the
procedure of measurements. For example, in [1] the difference in results
obtained is shown, which arises as the consequence of various wave
representations used. Here it means that as the carrier of the information in terms
of time and distances measurements not only electromagnetic wave but other
waves can be used as well. It results in the change of the relativity theory,
though most formulas remain the same.
Therefore in the beginning we shall describe the
formalism used in the classical theory of the electromagnetic field and in the
relativity theory. Then we shall thoroughly consider the Lorentz-invariant
theory of gravitation. Its form in inertial and noninertial reference systems
depends on the wave representation used in which the basic role is played by
gravitational waves. In conclusion the comparison of the standard general
relativity theory and the Lorentz-invariant theory of gravitation in
noninertial reference systems will be made. One of conclusions is that the
energy-momentum tensor of gravitational field should be present as one of the
sources for definition of the metrics. Another conclusion concerns the essence
of the general relativity theory as such. In the classical approach it is
represented as the theory of gravitation. Whereas in the new approach the
general relativity is intended for the description of the phenomena for the
conditions when the extending waves carrying the information on geometry of
space-time, are exposed to a certain deforming effect of the existing fields.
2. Relativity and electromagnetism
The theory of electromagnetic field is rightfully considered
to be one of the most fruitful physical theories today. The Special Theory of Relativity
(STR) has appeared as the consequence of the fact that the equations of
movement and interaction of bodies should correspond to transformations of
electromagnetic forces in different reference systems. For nonmagnetic
substance in the absence of electric polarization the differential Maxwell equations
for strengths of electromagnetic field have the following standard form:
(1)
, 
,
where E – the vector of strength of electric field,
B – the vector of magnetic induction,
– the electric
constant,
– the density of
charge of the substance unit,
c – the speed of propagation of electromagnetic field (speed of light),
– the vector of current density, dependent on the velocity 
of movement of the substances
unit.
The expression for the
electromagnetic force acting on the point charge q: 
. For density of the force acting on the substance unit, the
force has the form: 
.
Through E and B, the density of energy, the density of the energy flux (the Poynting vector), and also the density of the momentum of electromagnetic field are determined:
, 
, 
. (2)
For the case of rectilinear
distribution of radiation in vacuum for strengths of the field in a flat
electromagnetic wave the relation 
is carried out, and strengths
of the field are perpendicular to each other and to the direction of
distribution of the wave. Then from (2) it follows, that 
. If the similar flat wave falls on the surface of a body it
will cause the pressure p upon the
surface: 
, where 
– the factor of
reflection.
From (1) it follows, that the strengths of field
can be expressed through the scalar 
and the vector A
potentials of electromagnetic field:
, 
. (3)
If we connect with one another the
potentials of field using the gauge condition 
, then substituting
(3) in (1) we will obtain the well known wave equations for potentials:
, 
. (4)
According to (4) the electromagnetic waves as fluctuations of potentials in space-time are possible even in the absence of charges and currents (free waves). The presence of nonzero potentials in the wave means, that in the wave there are periodic fluctuations of strengths of the field (it follows from (3)), so the waves transfer energy and momentum according to (2). However, the wave equations for the vectors of field strengths can be obtained directly from (1):
,
.
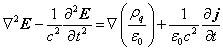The solution of the Maxwell equations (1) is reduced to the solution of the equations (4), then with the known potentials the strengths of the field from (3) are found. The common solution for potentials in (4) has integral form:
,
,
the potentials at any point 1 at
the moment of time t are determined
by integration of contributions from the elements of volumes 
. In the elements of volume it is necessary to take the
density of charge and currents at an earlier moment of time equal 
, where 
– the distance between
the element of volume and point 1 at the early moment of time. Thus it is taken
into account that electromagnetic influence has the limited speed of distribution
c.
If there is a small charged moving body with the charge q, the Liénard-Wiechert solution for potentials is:
,
,
and the distance 
between the charge and
point 1 and the speed 
of movement of the
charge should be substituted at the early moment of time 
. Assuming that the charge goes only forward with constant
speed 
along the axis 
, 
, and also 
, expressing 
and through 
, then for the potentials it is possible to find:
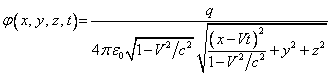, (5)
, and also: 
.
In the reference system 
in which the charge is
at rest, the speed 
, and from (3) and (5) we obtain the Coulomb law:
, 
, (6)
, 
.
Comparison of (5) and (6) shows,
how the coordinates should be transformed between the reference system (moving together with the
charge) and the motionless reference system K
so that the expression for the potential remains unchanged:
, 
, 
. (7)
Relations (7) are specific Lorentz transformations of the STR for spatial coordinates. The characteristic feature of the STR is that measurements of coordinates and time in it are made with the help of invariant – the speed of light, identical in all inertial reference systems. In addition to (7) it is necessary to use transformation of time:
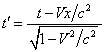. (8)
Expression (8) can be obtained, for
example, from (7), after using of the principle of relativity. If moves in K along the axis then on the contrary, K moves relative to , but with the speed opposite to the axis . Then it should be in the following way:
, 
, 
. (9)
Combining (7) and (9), we come to (8). Transformations of coordinates and time have forms (7) and (8) due to the limited speed of light. It results in different rate of time and difference in the sizes, which should be in moving bodies at different speeds.
It appears, that the equations of electromagnetism will not change its form if during transition from one inertial reference system into another the transformations of Lorentz of the type (7) and (8) for all physical functions are used, and not only for coordinates and time. According to this we can say, that electrodynamics is covariant regarding Lorentz transformations.
3. Electrodynamics in the four-dimensional world of Minkowski
From (7) and (8) it is evident, that coordinates and
time will be transformed simultaneously. In STR corresponding time-like and spatial functions taken as some scalars and
common 3-vectors, make together a 4-vector or are part of 4-tensors. For any
four-dimensional vectors and tensors the uniform law of transformation from one
inertial reference system in another is introduced. In particular, if the event
is described by 4-vector of position of a point in Minkowski 4-space: 
, then Lorentz transformation (7) and (8) can be written down
in the following way:
,
where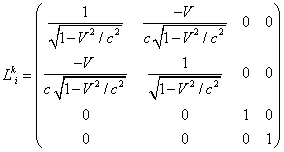 
.
The tensorial value 
allows making
transformations of 4-vectors. For transformation of the component of a second
rank tensor 
, should be used twice,
that gives the formula of the following kind: 
. Generally it is necessary to use as many times, as many
non-repeating indexes the transformed tensor has.
Consider the most common 4-variables in electrodynamics.
The 4-vector of current density is determined as the product of the density of
the charge 
taken in system at
rest, and 4-velocity:
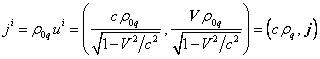. (10)
The 4-vector of potential connects scalar and vector potentials:
. (11)
The four-dimensional gradient’s operator is determined as a covariant vector:
.
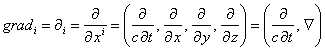In STR transition from
contravariant to covariant vector and vice versa is carried out by simple
change of the sign for spatial coordinates, for example 
. 4-divergence of the vector is determined as scalar product
of the gradient’s operator and the 4-vector. In particular we have:
, 
,
that corresponds to the law of conservation of electric charge and to the gauge condition for potentials of the field accordingly.
The scalar d'Alembertian 4-operator is obtained as
scalar product of the 4-gradient operators:
□2
.
It is easy to check, that the following equation is equivalent to the wave equations (4) for potentials:
□2
.
It is possible to construct an
antisymmetric tensor of electromagnetic field with the help of 4-potential by
the formula: 
. With the help of (3) we find for non-magnetic substance in
absence of electric polarization:
.
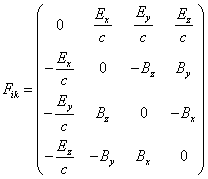The tensor 
is expressed through
the coordinates of the vector of electric field E and the vector of
magnetic induction B. Therefore the equations of field (1) can be expressed
through in the following way:
, 
.
As E and B
are components of the tensor their Lorentz's
transformations are carried out not according to vector, but to tensorial law.
On the basis of the tensor it is possible to
construct the energy-momentum tensor of electromagnetic field:
, (12)
where 
– the metric tensor.
It is possible to expand the tensor 
to components:
It is evident, that the structure
of the tensor includes the components of field strengths, and also the density
of energy w and the components of the
vector of energy flux 
according to (2).
Connection between the substance and the field is that
forces act on the substance in the field and in the substance stress and
pressure appear. We shall take the energy-momentum tensor of the substance 
for compressed liquid
or continuously distributed substance without taking into account the shift
viscosity:
, (13)
where 
and 
– the pressure and the
density of substance at rest,
– 4-velosity of substance
unit,
– the function
determined in [2].
Assuming that if in some area of
space there is substance, electromagnetic field, as well as some additional
forces contributing to the pressure in the tensor , then 4-divergence of the sum of the energy-momentum tensors
of substance and the field should equal zero for each element of volume:
. (14)
Equality (14) is equivalent to the
fact that the total balance of inflow and outflow of energy and momentum
between the substance, the field and extraneous forces is always carried out.
We shall transfer 
in (14) to the right
part of the equality, that gives: 
. It is easy to check, that 
here is the speed of
change of 4-momentum of the substance and extraneous forces, and 
is proportional to the
speed of change of their energy in a unit of volume. At the same time the
vector 
is the 4-vector of force density acting from the
electromagnetic field. The components of 
are the following:
, 
is proportional to the
capacities of the field’s work in a unit of volume, and 
.
Thus, (14) are equations of motion of the substance and the electromagnetic field in the presence of the additional forces creating pressure.
Remember that according to STR any physical results
depend considerably on the procedure of space-time measurements. The interval 
between two events is
understood as the module of difference of two 4-vectors marking these two events:
,
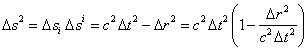. (15)
Suppose events 1 and 2 are the
presence of some body at close to each other points 1 and 2 at the time moments
and 
, and the body goes between points 1 and 2 at average speed . Then in (15) it is possible to assume, that 
, 
. In STR the magnitude of 4-vector and the speed of light do
not depend on the choice of reference system, from this the invariants for inertial
systems are both the interval 
, and the proper time of the moving body 
. In other words, in different reference systems the speeds
of the body and the recorded time 
corresponding to 
, will be different, but the
calculated value remains the same.
In space-time measurements with the help of light the interval between any measuring points always equals zero. Light (and any particles moving with the speed of light) in STR are universal carriers of the information about measured subjects. Any physical values are or can be functions of coordinates in space-time. Therefore the whole physics becomes depending on procedure of measurements of coordinates and time. In available means of measurements (from a human eye and to lasers and atomic clock) the electromagnetic phenomena are used or calibration is done on the basis of electromagnetic waves. It is accepted, that any correct physical theory must be compatible with principles of STR, first of all with the relativity principle and with measurability of the phenomena with the help of light. Thus it is possible to state, that now the paradigm of physics and scientific outlook are based entirely on the electromagnetic picture of the world.
4. General relativity
In the General Theory of the
Relativity (GTR) the basic equations are the equations of Hilbert-Einstein for
finding the components of the metric tensor 
. The given tensor is used to describe the phenomena in
space-time distorted under action of energy-momentum of substance and fields.
In the left part of the equations for the metrics there are geometrical
tensorial values connected to the tensor and its derivatives of
the first and second order by coordinates of space-time. In the right part of
the equations there are tensors of density of the energy-momentum of substance
and the field, that are physical tensorial values. From the equality of the left
and the right parts of the equations, with a certain multiplier of
proportionality, it follows, that the curvature of space-time is in direct
proportion to energy-momentum tensors in this space-time.
Historically it has developed so, that the equations of Hilbert-Einstein have always been solved only for tensors of substance and electromagnetic field. The found components of the metrics actually have been viewed as potentials of the gravitational field having a tensorial form. This resulted from the fact that features of gravitational field have been treated in terms of geometry as a space-time curvature.
The equations for the metrics in the simple case are the following:
, (16)
where 
– Ricci tensor,
– scalar curvature.
The covariant derivative from the
left part (16) is equal to zero due to symmetry of the tensor . The zero value of the covariant derivative from the right
part (16) is due to the properties of energy-momentum tensors and follows from
(14). The speed of light in the multiplier of
proportionality in (16) corresponds to the fact, that at tensors and also there is speed of
light. Thus in case of the weak field the equations (16) turn into the wave
equations for those amendments to the metrics
which distinguish the metrics of the curved space-time from the Minkowski flat space-time.
From here we can conclude, that fluctuations of the metrics as the equivalent to
fluctuations of gravitation, propagate also with the speed of light.
It is obvious, that equality of the speed of propagation of gravitation and the speed of light in GTR is not the property of gravitation itself, but the consequence of construction of the theoretical apparatus of GTR on the basis of the electromagnetic paradigm.
5. The Lorentz-invariant theory of gravitation
Unusualness of reduction of physical gravitational
force to the properties of space-time, following from GTR, impossibility to
present gravitational energy as covariant tensor, difficulty in attempts of
quantization of gravitational field within the framework of GTR caused numerous
attempts of developing theories of gravitation different from GTR. We shall
describe here one of the new approaches, the Lorentz-invariant Theory of
Gravitation (LITG) according to [2]. The essence of LITG is that the force of
gravitation is considered the real physical force. Thus the speed of
propagation of gravitational influence 
is not
necessarily equal to the speed of light c.
The equations of gravitational field in LITG are the following:
(17)
, 
,
where G – the vector of gravitational field strength or gravitational acceleration,
– the vector of
gravitational torsion field or simply torsion,
– the gravitational
constant,
– the density of
substance mass,
– the vector of density of the mass current, dependent on the
velocity of motion
of the mass unit.
Gravitational force depends on the strengths
of field and on the mass m of the particle on which the force acts: 
. Accordingly, for the density of force we have: 
.
The density of energy, the vectors of density of the energy flux and the density of the momentum of gravitational field are equal to:
, 
, 
. (18)
For a flat gravitational wave in
vacuum 
,
, 
.
The strengths of gravitational
field are expressed through scalar 
and vector D
potentials:
, 
. (19)
From (19) and (17) the wave equations for potentials of gravitational field follow:
, 
, (20)
under gauge condition 
.
The equations (20) predict freely propagating gravitational waves, which can have vector character and dipole origin. As opposed to it in GTR the gravitational field is considered tensorial, being derived in the simplest case in a quadripole way. We compare the given situation to the situation in electrodynamics. Radiation of the system of charges is usually calculated as the sum of dipole electric, dipole magnetic, quadripole electric and the subsequent multipole radiations. In a closed neutral system consisting of particles with the identical relation of the charge to the mass, dipole and magnetic radiations disappear, so that only the quadripole term and the next multipoles remain. We shall take now a closed gravitationally connected system, like two neutron stars, moving one near the other. For them the total dipole radiation also tends to zero, however quadripole radiation is not equal to zero. In the given particular case the results of LITG and GTR coincide.
The Liénard-Wiechert solution of the equations (20) for potentials of a moving point particle with mass m is the following:
, 
,
the potentials at any point 1 at
the moment of time t depend on the
distance between the particle
and point 1, and on the speed of movement of the particle.
And it is necessary to calculate and at an earlier moment
of time 
. Expressing all physical values at the early moment of time
through the values at the present time t,
similarly to (5) for uniform motion with the speed we obtain the following formula:
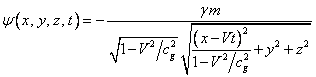, (21)
, and also: 
.
Now reference system connected with the
particle should be introduced. In the speed , and from (21) and (19) we come to the Newton law:
, 
, (22)
,
.
Outside a rotating sphere, torsion
can be expressed through the rotational momentum 
of the sphere by means
of dipolar formula:
.
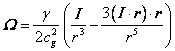Due to the the rotating sphere in
addition to Newtonian force influences bodies if they have any velocity relative
to the center of the sphere.
From (21) and (22) it is evident,
that for Lorentz-invariancy of the potential in reference systems and K it is necessary, that the coordinates
and the time should be transformed as follows:
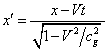, , . (23)
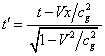. (24)
Equations (23), (24) are specific Lorentz
transformations for the case when the information about lengths and time in
different inertial systems is determined with the help of measurements of
events by the time of arrival of gravitational waves. We shall assume, that we
have learned to detect gravitational waves, to create receivers and
transmitters of gravitational signals, and also measuring devices on their
basis. Then provided that 
in inertial reference
systems, we come to the special relativity theory within the framework of LITG.
The difference of gravitational STR from electromagnetic STR then consists in
substitution of the speed of light by the speed , but the basic formulas of STR remain the same.
Logical consideration
of the gravitational STR leads to the formula for the energy of motionless bodies
as: 
. Meanwhile in usual STR the rest energy of a body is
calculated so: 
. Which formula from these two is true? Most likely, both
formulas are true, but each one is true only within the framework of
gravitational or electromagnetic representation. For the proof of validity of
the expression it is possible to
consider conditional disintegration of a gravitationally bound body of the mass
m under influence of two counter
directed gravitational-wave energy quanta. For the rest body the total energy
of quanta falling on the body is equal to 
. If the same body goes with the constant speed along the line of
distribution of quanta, the total energy of quanta from the point of view of
the reference system of the body will change due to the Doppler effect. As the
speed of quanta equals , it will be present in the formula for the shift of wave
frequency of these quanta. From here the energy of quanta will be equal to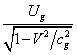
. Equating the difference of energies of quanta to the
kinetic energy of the body: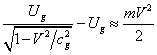 
, we will come to the formula for the energy of the
motionless body: .
During formation of a single gravitationally bound body from a set of particles, the energy generates equal by the absolute value to the binding energy of these particles. If we proceed from the virial theorem, half of the gravitational energy of the body is spent for heating the particles making up the body, and the other half of energy is carried away from the body by gravitational radiation. In its turn, the heated body radiates actively electromagnetic waves and then cools down. Thus, the energy of gravitation performing the work of aggregation of substance is partially transformed into electromagnetic form of energy.
6. LITG in the four-dimensional world of Minkowski
Lorentz-invariancy of LITG is
achieved, if all physical values are presented in the invariant form regarding
gravitational STR and in all formulas the speed of propagation of gravitation will be used. In
particular, the 4-vector of position has the form: 
. For transformation of 4-vectors and tensors from one
inertial reference system into another during the motion of reference systems
along the axis it is possible to
introduce the tensorial value 
:
,
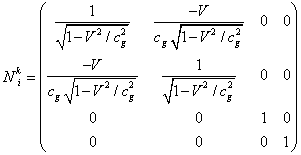so, for example, 
.
The 4-vector of the density of mass current and 4-vector of the potential are included into the equations of gravitational field:
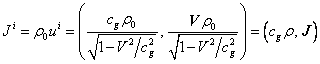, (25)
where – the density of mass
in rest reference system,
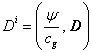. (26)
The equations of field (20) for potentials get the following form:
□2
.
The tensor of gravitational field
can be found by the formula: 
. It is expressed through the components of the vector of
gravitational acceleration G and the vector of torsion :
.
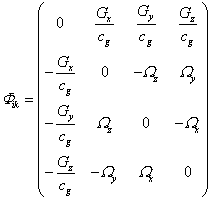With the help of the tensor 
it is possible to write
down the equations of the field (17) in another way:
, 
.
The energy-momentum tensor of the gravitational field:
, (27)
where the difference of signs
before the tensor 
and the tensor in (12) is determined
by the fact that the masses are attracted to each other, and the electric
charges of the same sign repulse from each other.
The components of the tensor include the density of
energy u and the components of the
vector of the energy flux 
:
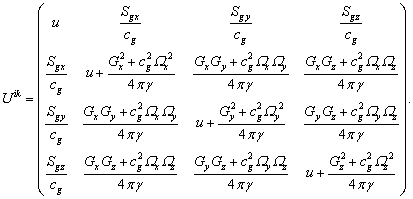
Similarly to (14) we shall write down the interrelation of energy-momentum tensors for the substance in gravitational field:
. (28)
The relation (28) expresses the
equations of motion of substance in the field. In the left part of (28) there
is the tensor for compressed liquid
or continuously distributed substance according to definitions (13). We shall
notice, that in this case 4-velocity in this tensor is expressed not through
the speed of light, but through the speed . The derivative from the tensor is the change of the
momentum of substance and extraneous forces in time unit. In the right part
(28) there is gravitational 4-force:
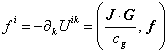, where
.
Proceeding from above-stated, LITG is completely
compatible with gravitational STR. In other words, the gravitational phenomena
will be invariant in different inertial reference systems if the gravitational
field having speed is used as the carrier
of information. Thus we come to the fact that it is possible to build a
gravitational picture of the world. The difference of gravitational and
electromagnetic pictures of the world follows from the difference of speeds of
carrying of information and c.
7. LITG and general relativity
For the beginning we will assume that there is only
the substance and the gravitational field, described by the tensors and accordingly. We want
to use again the Hilbert-Einstein equations to find
the components of the metric tensor. The common idea here as well as in GTR is that curvature of
space-time is in direct proportion to energy-momentum tensors in this
space-time.
The
equations for the metrics are similar to (16):
, (29)
the
difference is only in the use of speed and in substitution of
the tensor by the tensor .
However there is already no sense in
treating the components of the metric tensor in curved space-time as the
potentials of tensorial gravitational field. Really, LITG allows to determine
all characteristics of gravitational field in the covariant way already within
the framework of gravitational STR. As a result the metrics obtained from (29)
simply shows the degree of curvature of space-time in relation to the Minkowski
flat space-time. The metrics becomes only geometrical parameter as it should
be. The fluctuations of the metrics in (29) occur with the speed of propagation
of gravitation . The solution to the equations (29) for determining the
metrics inside and outside a motionless massive sphere was made in [2]. The
contribution to the metrics from the energy-momentum of the prper gravitational
field of the massive body makes an amendment of the second order in relation to
the form of the Schwarzschild solution in GTR. Obviously, the metric can be
changed in the absence of substance, under the influence of external
electromagnetic and gravitational waves propagating in free space. These waves
transfer energy and the momentum, that is why they influence the light
propagation if we determine the metrics and the metric field with its help.
8. Conclusion
The presence of the energy-momentum tensor in (29) leads to the
fact that any gravitational field, external or internal, stationary or free,
makes contribution to the metrics, in addition to the energy-momentum of moving
or motionless substance. And what is possible to say about the contribution of
electromagnetic field to the metrics from the point of view of LITG? The given
question demands more thorough examination. We will be limited here to that
possible case when the speeds of propagation of gravitation and electromagnetic
influences and 
are equal, reflecting
thus two sides of one phenomenon. Then the energy-momentum tensor of the
electromagnetic field simply can be added to
tensors and in the right part of
the equations for the metrics (29). The sum of the components 
, 
, and 
as of the densities of
the corresponding energies, will be equal to the sum of the rest energy of the
substance, the kinetic energy of mass-energy of differences of pressure forces,
the energy of pushing apart of charges and the currents from electric and
magnetic fields, and also the negative energy of the gravitational field. Such
order of summation of energies corresponds to the fact that the integrated
gravitational mass is made up by all kinds of energy of substance and fields
and is responsible for the curvature of space-time.
It should be noted that even Einstein pointed at essential asymmetry between the field of gravitation and other fields in GTR. As each field has energy and momentum, it has mass and consequently it contributes to gravitation. Gravitation is created by any field and in this sense it is inseparable from other fields. But the emergence of gravitation in general relativity is possible without other fields, and the gravitation is not required to produce other fields or somehow influence them.
In LITG the addition of the
energy-momentum tensor of electromagnetic field to the equations (29)
results in symmetric entering of gravitation and electromagnetism in solutions
for the metrics. Each field makes its own contribution to the metrics, the
fields are equal by the importance as the sources for determining the metrics.
If in GTR gravitation as the result of curvature of space-time is not subject to quantization, in LITG the same procedure of
quantization of gravitation is possible, as in electromagnetism.
Addition of in (29) and the use of three tensors essentially enriches and
changes the contents of LITG in comparison with GTR. The general relativity in
LITG serves as the means of description of physical phenomena in conditions
when any masses, energies and momentums of the matter influence the
distribution of electromagnetic and gravitational waves. Waves are the basic
source of information about the events and the phenomena. The account of the
metrics allows restoring the exact information about the rate of clocks, the
measured lengths and physical values in non-inertial reference systems. Thus
overcome the distortion effects introduced by the matter itself in our way of
physical observations.
In GTR there is no reason why such extreme objects as black holes should not exist. Indeed, the gravitational field in general relativity is just a consequence of the curvature of space-time, which is not imposed any restrictive conditions. However black holes as signs of singularities of space-time signify, that the field equations and the known laws of nature are not applicable to them. If GTR admits the existence of such objects and cannot describe them, it means either weakness of GTR as of a complete physical theory or inconsistency of GTR. In LITG not only the substance, but also gravitational field determines the metrics. In this case, there is a natural boundary condition. It follows from the fact that the degree of maximum aggregation of substance is determined by the interaction of gravitational and electromagnetic forces with the substance. In their turn these forces are generated by the matter on lower scale levels, from the level of elementary particles to deeper structural levels of the substance organization. In this case gravitation can not be infinitely large.
It is possible to assume that gravitation and electromagnetism are the consequence of radiations from the set of the smallest particles of matter. At the level of stars a characteristic example of similar processes is the collapse of a neutron star when spherical gravitational waves, fluxes of neutrino, electromagnetic radiation are radiated from the star, there are emissions of substance at relativistic speeds. Then we should expect that the forces of possible gravitational and electromagnetic influence on the substance are limited in their effect by the nature, at all levels of matter. Reasoning by induction, the black holes should either exist or not exist simultaneously at all scale levels. Besides the existence of black holes contradicts their capability to absorb particles and radiations. If the black holes absorb everything but release nothing from themselves, in the end they would absorb all matter on lower scale levels. But in this case the source which causes gravitation observed at our level of matter would vanish.
There is also a number of the observational data contradicting the existence of black holes. For example, the progenitor of neutron star CXO J164710.2-455216 was a very massive star with the mass of about 40 masses of the Sun [3]. Earlier it was considered that such massive stars should generate black holes at the end their evolution.
We should note that the necessity
of presence of the tensor of gravitational field in the right part of the
equations (16) can be proved even within the framework of GTR. For this purpose
it is enough to accept the following statement: As in GTR the metrics appears
to be the function of potentials of gravitational and electromagnetic fields
and additional external forces (it is well observable within the limits of the
weak field) then the addition of the tensor of the gravitational field in the Hilbert-Einstein
equations for the metrics is equivalent to self-action of the gravitational
field through the metrics. The effect of self-action in general should be
considered to be the law of the nature so it is possible to postulate the
following: if the object creates any change around itself, this change
inevitably influences object. Hence, if the matter creates in GTR a metric
field as the equivalent of gravitational field this gravitational field should
also influence somehow the matter, in its turn changing the metric field. It is
possible to say in another way – in order to achieve self-consistency of the
metric field in GTR is necessary to consider its contribution also through the
very source of the metric field in the form of the corresponding tensor.
We should repeat again that GTR is not a
theory of gravitational field but the theory of the metric field. It is known
that in the STR coordinate transformation of physical quantities such as velocity,
force, potentials, etc., and the equations of motion of bodies from one
inertial system to another are possible. In this case, the investigated bodies
are accelerated only, and inertial frames along with their observers by definition
move without acceleration, that is, at a constant velocity. The main aim of the
GTR is transformation of the coordinates and
physical quantities between any reference frames including noninertial frames
with acceleration. In this case STR is a particular case of GTR, when the acceleration of the frames being used equals
zero. For the correct examination of gravitational forces in inertial reference
frames it is necessary that gravitation should take place only between the
bodies examined and it should not accelerate the reference frames themselves.
For this purpose we should place the local reference frame in the additional
external gravitational field, opposite to the examined gravitational field.
Then the observer together with the equipment for measuring time and distance
will be located in the inertial reference frame. In such way, the potentials of
the gravitational field which is symmetrical in relation to the radius of
massive sphere, can be measured in the inertial reference frames for all points
of the sphere. Then with the help of the Lorentz- transformations for the
4-vector of the potential (26) it is easy to obtain the potentials of the field
in any other inertial reference frame. So it is possible to consider the
gravitational phenomena in the framework of the STR, with the help of the LITG
equations (17). As it was shown above, the equations of the gravitational field
we can write down in the tensor form by means of tensor . That means that gravitation can be presented without
GTR in covariant tensor form including noninertial
reference systems with any metrics. Further with the help of GTR with known initial distributions of energy-impulse of
the matter we can obtain the metrics in any reference frames and the further
motion of the matter. For each reference frame its own metrics and its own
pattern of the phenomena are obtained, that helps obtain correlation between
the same events in different reference frames.
Now we will return to the heading of the given
article. In the beginning we have shown the likelihood of existence of two
similar Lorentz-invariant theories – electromagnetisms and gravitation. For
each of these theories we can find corresponding special relativity theory
depending either on the speed of light, or on the speed of propagation of
gravitation accordingly. From the electromagnetic approach the General Theory
of Relativity (GTR) appeared while from the gravitational approach the
Lorentz-invariant Theory of Gravitation (LITG) developed, followed by the
generalization of LITG for relativity in non-inertial reference frames, similar
to GTR. The common form of equations for electromagnetism and gravitation, the
symmetry of their presence within the framework of LITG and GTR as the sources
for finding the metrics mean an opportunity to develop a more general theory of
fields. From the stated above it is evident, that under condition of 
the uniform
gravielectromagnetic field is obtained by simple summation of the appropriate
physical quantities in the equations. Thus we come to the alternativeness and
mutual complementarity of electromagnetic and gravitational pictures of the
world.
References
[1] S.G.
Fedosin, (Contemporary Issues of Physics.
In Search for the New Principles), Editorial URSS,
[2] S.G.
Fedosin, (Physics and Philosophy of
Similarity from Preons to Metagalaxies), Style-Mg,
[3] M. P. Muno at al., “A Neutron Star with a Massive Progenitor in
Westerlund 1”, arXiv:
astro-ph /0509408 v3,
Source:
http://sergf.ru/egpen.htm