In English

 

Hadronic Journal, 2012, Vol. 35, No. 4, P. 349 – 363.

 

УДК  539.1 + 53.081.6 + 539.125.4

 

Радиус протона в самосогласованной модели

 

Федосин Сергей Григорьевич

г. Пермь, Пермский край, Россия

e-mail intelli@list.ru

 

Исходя из представления о сильной гравитации, действующей на уровне элементарных частиц, и из равенства магнитного момента протона предельному магнитному моменту вращающегося неоднородно заряженного шара, находится радиус протона, согласующийся с экспериментальными данными. Одновременно выводится зависимость распределения плотности массы и заряда внутри протона. Отношение плотности в центре протона к средней плотности получается равным 1,57.   

Ключевые слова: сильная гравитация; волны де Бройля; магнитный момент; радиус протона.

PACS: 12.39.Pn, 14.20.Dh

 

1.      Введение

С момента открытия протона в 1917 году возник вопрос о том, как определить радиус этой элементарной частицы. Существует немало теоретических моделей для оценки радиуса протона. Большинство из этих моделей связано с представлением об электромагнитных форм-факторах как поправках, за счёт которых амплитуда рассеяния частиц на протоне отличается от амплитуды рассеяния на точечной частице. Расчёт форм-факторов достаточно сложный и требует учёта множества факторов, среди которых радиальное распределение плотности заряда и магнитного момента, динамика кварков, партонов и виртуальных частиц. При этом могут использоваться различные подходы – теория рассеяния, киральная теория возмущений, решёточная квантовая хромодинамика и т.д., описание которых можно найти в [1], [2]. Форм-факторы определяются из экспериментов по рассеянию, зависят от энергии взаимодействующих частиц и позволяют найти среднеквадратичные распределения заряда и магнитного момента как меры размеров частиц. Информация о радиусе протона может быть извлечена из анализа сдвига Лэмба в атоме водорода, а также в связанной системе из протона и отрицательного мюона [3].

 

2.       Другие оценки радиуса протона

Рассмотрим некоторые простые методы определения радиуса протона. Один из них основан на том, что в частицах при их возбуждении возникают стоячие электромагнитные волны. Максимальная энергия таких стоячих волн не превышает энергии покоя во избежание распада частиц. Отсюда выводится, что волны де Бройля являются электромагнитными колебаниями, обнаруживаемыми в лабораторной системе отсчёта при взаимодействии движущихся частиц. Для описания таких колебаний необходимо применить преобразования Лоренца к стоячим волнам внутри частиц и найти их вид в лабораторной системе отсчёта [4], [5].

В простейшем случае стоячие сферические волны моделируются двумя волнами, одна из которых бежит от центра к поверхности частицы, а другая в то же время движется обратно. Можно считать, что в направлении какой-либо выделенной оси, например , имеются две встречные волны следующего вида:

 

,             ,

 

,                         (1)

 

здесь ,  − начальные фазы колебаний при ,  − амплитуда периодической функции,  и  обозначают угловую частоту и волновое число, а штрихи перед переменными означают, что они рассматриваются в системе покоя частицы.

 

В качестве  может быть любая периодическая функция, удовлетворяющая волновому уравнению. Например, это может быть напряжённость или потенциал поля волны. Фазы волн в (1) должны быть сдвинуты на  для возникновения стоячей волны. Если , , то в центре частицы при  всегда будет узел как отсутствие видимых колебаний, и (1) становится таким:

 

.                                                 (2)

 

В результате колебаний (2) внутри частицы могут периодически изменяться скорости зарядов вещества частицы и потенциалы поля. Это неизбежно приводит к появлению периодических колебаний потенциалов поля и за пределами частицы, в окружающем её пространстве.

Пусть теперь частица вместе со своей стоячей волной движется вдоль оси  лабораторной системы отсчёта со скоростью . Как видоизменятся колебания поля внутри и за пределами частицы в связи с её движением? Нам необходимо выразить в (2) штрихованные координаты и время внутри движущейся частицы через координаты и время лабораторной системы отсчёта с помощью преобразований Лоренца ( обозначает скорость света):

 

,        ,       ,       ,

 

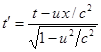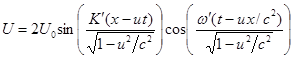.                                 (3)

 

Из (3) видно, что вследствие перемещения стоячей волны вместе с частицей, для внешнего неподвижного в лабораторной системе отсчёта наблюдателя меняются длина волны и частота. Точнее говоря, на наблюдаемой волне появляются дополнительные пучности, с длиной волны между ними, отличающимися от длины волны  в системе отсчёта частицы. Остановим на мгновение волну (3) при  и найдём длины волн как пространственное разделение между точками волны в одной и той же фазе. При  синус в (3) будет равен нулю, а при  фаза синуса изменится от  до . Отсюда имеем:

 

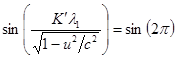,         .               (4)

 

 

Аналогично для длины волны у косинуса в (3) находим:

 

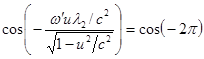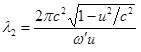,                .                     (5)

 

Оценим теперь временное разделение между точками волны в одной фазе при , считая это разделение соответствующим периодом волны:

 

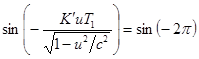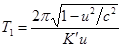,                 .                  (6)

 

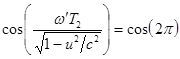,                      .                   (7)

 

Из (4) − (7) следуют следующие выражения для скоростей:

 

,                                    .                                      (8)

 

Как видно из (8), колебания волны (3), связанные с косинусом, распространяются с фазовой скоростью волны де Бройля . Кроме этого, колебания волны (3), связанные с синусом, движутся в пространстве с той же скоростью , что и сама частица. Длину волны  в (5) можно преобразовать так, чтобы привести её к стандартному виду для длины волны де Бройля. Свяжем угловую частоту колебаний внутри частицы, аналогично электромагнитной волне, с энергией колебаний: , где  – постоянная  Дирака,  – постоянная Планка. Это даёт следующее:

 

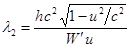.                                                      (9)

 

Аналогично из (4) имеем:

 

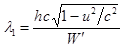.                                                     (10)

 

В предельном случае, когда энергия колебаний сравнивается с энергией покоя частицы, , из (9) следует:

 

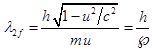,                                                  (11)

 

где – масса частицы,  – релятивистский импульс частицы.

 

Формула (11) определяет длину волны де Бройля через импульс частицы. Заметим, что и сам де Бройль написал формулу (11) при условии, что энергия частицы 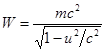 равна энергии волны, сопровождающей частицу.

 

Согласно полученному нами выражению (9), длина волны  должна присутствовать у частицы и при малой энергии возбуждения . При этом по мере уменьшения энергии возбуждения длина волны увеличивается.

Как правило, в экспериментах обнаруживается только  из (11), а не длина волны  из (9).

 

Это может происходить потому, что среди множества взаимодействующих частиц одновременно присутствуют частицы с разными энергиями возбуждения  и разными , так что волновые явления размываются. Это же касается и для волн с длиной волны  в (10). Лишь для самых энергично взаимодействующих частиц, энергии возбуждения  которых близки к энергии покоя частиц, достигается граничное значение длины волны, равное длине волны де Бройля. Тем самым эта длина волны и проявляется в эксперименте. При  можно предсказать у частиц также и волновые явления с граничной длиной волны .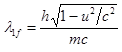

 

В частности,  есть комптоновская длина волны, обнаруживаемая в эффекте Комптона. Согласно нашей точке зрения появление волны де Бройля следует трактовать как чисто релятивистский эффект, возникающий как следствие лоренцевского преобразования стоячей волны, движущейся вместе с частицей.

В результате мы вынуждены принять, что корпускулярно-волновой дуализм реализуется в полной мере только у тех конкретных частиц, у которых энергии возбуждения достигают их энергии покоя. При этом различие частиц и квантов поля в волновом отношении стирается. При малых энергиях возбуждения частицы не могут сильно излучать свою энергию, и амплитуды колебаний потенциалов поля возле частиц будут невелики. Тогда частицы взаимодействуют между собой скорее не волновым, а обычным способом, и волновые явления становятся незаметными.

Если теперь предположить, что длина стоячей волны равна , где  – радиус протона, то из равенства энергии волны и энергии покоя протона получается:

 

,             ,              м,

 

здесь  – частота колебаний,  – масса протона.

 

 Другой способ оценки радиуса протона предполагает, что разность энергий покоя нейтрона и протона возникает вследствие электрической энергии заряда протона. В таком случае должно быть:

 

,                                                        (12)

 

где  – масса нейтрона,  – элементарный заряд,  – электрическая постоянная.

 

В (12) для случая однородного распределения заряда по объёму протона , в результате оценка радиуса протона даёт значение м.

В [6] и [7] радиус протона находился из того условия, что предельный момент импульса поля сильной гравитации внутри протона равен по величине спину протона. Это приводит к формуле:

 

м.                                                     (13)

 

В (13) используется постоянная сильной гравитации . Согласно [4] данная постоянная определяется из равенства электрической силы и силы от поля сильной гравитации, действующих в атоме водорода на электрон с массой , который находится в основном состоянии на радиусе Бора :

 

,                   м3∙кг–1∙с–2,           (14)

 

Кроме сил притяжения от гравитации и зарядов ядра и электрона, в атоме водорода на вещество электрона в виде вращающегося диска действуют и силы отталкивания в сторону от ядра. Одной из этих сил является электрическая сила расталкивания заряженного вещества электронного облака самого от себя. В той вращающейся неинерциальной системе отсчёта, в которой произвольная часть вещества электрона неподвижна, появляется также сила инерции в виде центробежной силы, зависящей от скорости вращения этого вещества вокруг ядра. В первом приближении указанные силы равны друг другу по величине, что и приводит к (14).

Напомним, что идея сильной гравитации была введена в науку в трудах Абдуса Салама и группы его сотрудников [8], [9] как альтернативное объяснение сильного взаимодействия частиц. В предположении, что адроны могут быть представлены как Керр-Ньюмановские чёрные дыры, они оценили постоянную сильной гравитации как величину порядка м3∙кг–1∙с–2.

С помощью постоянной сильной гравитации (14) можно выразить постоянную тонкой структуры:

 

.

 

Ещё одна оценка радиуса протона вытекает из равенства энергии покоя и модуля полной энергии, с учётом теоремы вириала приблизительно равной половине модуля энергии сильной гравитации, связанной с протоном [4]:

 

.                                                              (15)

 

Если взять  для случая однородного распределения массы, то из (15) следует, что м.

Все указанные выше оценки основываются на классическом подходе к протону как к материальному объекту малых размеров в виде шара радиуса . При этом предполагается, что сильная гравитация действует на уровне элементарных частиц точно так же, как обычная гравитация на уровне планет и звёзд.

В Стандартной модели элементарных частиц и в квантовой хромодинамике считается, что нуклоны и другие адроны состоят из кварков, причём у барионов три кварка, а у мезонов два кварка. Вместо сильной гравитации предполагается действие глюонных полей, удерживающих кварки в адронах. Кварки полагаются заряженными элементарными частицами, поэтому в качестве радиуса протона рассматриваются зарядовый и магнитный среднеквадратичные радиусы. Эти радиусы определяются электрическим и магнитным взаимодействием протона и могут отличаться друг от друга.

Оценка среднеквадратичного зарядового радиуса протона может быть сделана с помощью экспериментов по рассеянию заряженных частиц на протонной мишени [10]. В таких экспериментах находятся полные сечения взаимодействия частиц . Для случая рассеяния протонов на нуклонах при энергиях более 10 ГэВ можно считать, что , причём м2 . Отсюда получается, что м.

 

3.       Самосогласованная модель

Поставим своей целью найти более точное значение радиуса протона с помощью классических методов. При вычислениях мы будем использовать только табличные данные о массе, заряде и магнитном моменте протона. Протон будем рассматривать с точки зрения теории бесконечной вложенности материи [11], в которой аналогом протона на уровне звёзд является магнитар или заряженная нейтронная звезда с очень большим магнитным и гравитационным полем. Подобно магнитару, вещество протона должно быть замагниченно и скрепляться полем сильной гравитации. 

С целью учёта неоднородности плотности вещества внутри протона используем простую формулу, в которой плотность вещества изменяется линейным образом с нарастанием к центру:

 

,                                                               (16)

 

где  – центральная плотность,  – текущий радиус,  – коэффициент, подлежащий определению.

 

Формулу (16) следует рассматривать как первое приближение к реальному распределению плотности вещества внутри протона. Приблизительная линейность зависимости плотности вещества в нейтронных звёздах была показана в [12], и мы предполагаем, что это справедливо также для протона как аналога нейтронной звезды.

Для оценки величины  и радиуса  рассмотрим интеграл для массы протона в сферических координатах:

 

.                            (17)

 

Для точного расчёта состояния нейтронных звёзд, а значит и протонов как их аналогов, следует учитывать искривление пространства-времени под действием сильного гравитационного поля, а также вклад энергии гравитационного поля в общую массу-энергию. Мы будем считать, что в (16) в зависимости плотности вещества от радиуса уже учтены все релятивистские эффекты, а масса протона (17) является гравитационной массой с точки зрения удалённого наблюдателя.

В (17) содержатся три неизвестные величины, для нахождения которых требуются ещё два уравнения. Будем считать справедливой теорему вириала и приравняем энергию покоя протона к половине модуля энергии статического поля сильной гравитации:

 

,                                              (18)

 

где  − плотность энергии поля сильной гравитации согласно [4], − гравитационное ускорение.

 

В (18) интегрирование плотности энергии поля необходимо производить как внутри, так и за пределами протона. Величину  внутри протона удобно находить путём интегрирования уравнения для поля сильной гравитации , входящего в состав уравнений лоренц-инвариантной теории гравитации [13]. После интегрирования по сферическому объёму некоторого радиуса , с последующим использованием теоремы Гаусса, то есть с переходом на интегрирование по площади указанной сферы внутри протона, с учётом (17) получается:

 

,

 

.                                                      (19)

 

За пределами протона гравитационное ускорение равно:

 

.                                                                (20)

 

Подставляя (19) и (20) в (18), получаем соотношение:

 

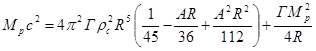.                                (21)

 

В (21) можно исключить величину  с помощью (17), что даёт зависимость  от  в виде квадратного уравнения:

 

.

 

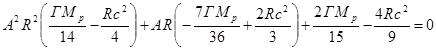Анализ данного уравнения показывает, что оно имеет следующее решение:

 

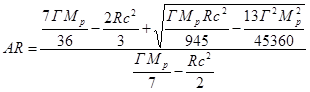,                                 (22)

 

при том условии, что когда , то соответственно .

 

Обратимся теперь к магнитному моменту протона. Как и в [4], мы предполагаем, что магнитный момент протона равен тому магнитному моменту, который формируется за счёт максимально быстрого вращения заряженного вещества протона. В сферических координатах магнитный момент можно приблизительно вычислить как сумму элементарных магнитных моментов отдельных колец с их радиусом , обладающих магнитным моментом за счёт протекания в них тока  от вращения заряда:

 

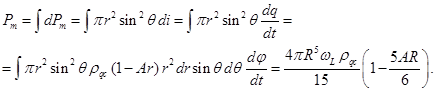                 (23)

 

Угловая скорость  максимального вращения протона может быть найдена из условия предельного вращения, при равенстве центростремительной силы и силы гравитации на экваторе: . Считаем далее, что для плотностей заряда и вещества выполняется равенство , и используем (17). Это даёт следующее:

 

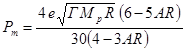.                                                  (24)

 

4.      Выводы

Соотношение (24) совместно с (22) дают возможность найти радиус протона м, а также значение . Из (17) тогда получается центральная плотность вещества кг/м3, которая превышает среднюю плотность протона в 1,57 раз. Максимальная угловая скорость вращения протона с учётом (23) будет равна рад/с. В то же время, если бы спин протона в приближении однородной плотности вещества равнялся бы стандартной величине для спина фермиона: , то такому спину соответствовала бы угловая скорость вращения рад/с.

Для сравнения с экспериментальными данными укажем на результаты расчётов электронного рассеяния из [14], где среднеквадратичный зарядовый радиус м получается при учёте только рассеяния на протонах, м с учётом данных пионного рассеяния, и м с учётом данных о рассеянии на нейтронах. В работе [3] нашли среднеквадратичный зарядовый радиус м при изучении связанной системы из протона и отрицательного мюона. Изучение сечения рассеяния поляризованных фотонов на протонах [15] даёт зарядовый радиус м и магнитный радиусм. Зарядовый радиус м и магнитный радиус м протона указаны на сайте Particle data group [16]. В базе данных CODATA [17] зарядовый радиус протона равен м.

Полученное нами в рамках самосогласованной модели значение м близко к экспериментальным значениям радиуса протона, что подтверждает возможность применения идеи сильной гравитации для описания сильного взаимодействия элементарных частиц.

 

Список использованных источников

1.        C. F. Perdrisat, V. Punjabi, and M. Vanderhaeghen. Nucleon Electromagnetic Form Factors. Prog. Part. Nucl. Phys., 2007, Vol. 59, Issue 2, P. 694–764.

2.        J. Arrington, C. D. Roberts, and J. M. Zanotti. Nucleon electromagnetic form factors. Journal of Physics G: Nuclear and Particle Physics, 2007, Vol. 34, No 7, S23.

3.        Randolf Pohl at all. The size of the proton. Nature, 2010, Vol. 466, P. 213–216.

4.        Федосин С.Г. Физика и философия подобия от преонов до метагалактик. Пермь, Стиль-МГ, 1999, 544 стр., Табл.66, Ил.93, Библ. 377 назв. ISBN 5-8131-0012-1.

5.        Федосин С.Г. Физические теории и бесконечная вложенность материи. Пермь, 2009, 842 стр., Табл. 21, Ил.41, Библ. 289 назв. ISBN 978-5-9901951-1-0.

6.        Федосин С.Г. Современные проблемы физики. М.: Эдиториал УРСС, 2002, 192 стр., Ил.26, Библ. 50 назв. ISBN 5-8360-0435-8.

7.        Федосин С.Г., Ким А.С. Момент импульса и радиус протона. Известия вузов. Физика, 2002, Т. 45, №. 5, С. 93–97.

8.        Salam A. and Sivaram C. Strong Gravity Approach to QCD and Confinement. Mod. Phys. Lett., 1993, Vol. A8(4), P. 321–326.

9.        Sivaram, C. and Sinha, K.P. Strong gravity, black holes, and hadrons. Physical Review D, 1977, Vol. 16, Issue 6, P. 1975–1978.

10.    Барашенков В.С. Сечения взаимодействия элементарных частиц. М.: Наука, 1966.

11.    Infinite Hierarchical Nesting of Matter  – en.wikiversity.org.

12.    Riccardo Belvedere, Daniela Pugliese, Jorge A. Rueda, Remo Ruffini, She-Sheng Xue. Neutron star equilibrium configurations within a fully relativistic theory with strong, weak, electromagnetic, and gravitational interactions. Nuclear Physics A, 2012, Vol. 883, P. 1–24.

13.    Fedosin S.G. Electromagnetic and Gravitational Pictures of the World. Apeiron, 2007, Vol. 14, No. 4, P. 385–413.

14.    Richard J. Hill, Gil Paz. Model independent extraction of the proton charge radius from electron scattering. Physical Review D, 2010, Vol. 82, Issue 11, 113005 (10 pages).

15.    X. Zhan, et al. High Precision Measurement of the Proton Elastic Form Factor Ratio μp GE / GM at low Q2. Phys. Lett., 2011, B705, P. 59–64.

16.    J. Beringer et al. (Particle Data Group). Review of Particle Physics. Phys. Rev. D86, 010001 (2012).

17.    P.J. Mohr, B.N. Taylor, and D.B. Newell (2011), The 2010 CODATA Recommended Values of the Fundamental Physical Constants. National Institute of Standards and Technology, Gaithersburg, MD 20899.

 

The radius of the proton in the self-consistent model

 

Based on the notion of strong gravitation, acting at the level of elementary particles, and on the equality of the magnetic moment of the proton and the limiting magnetic moment of the rotating non-uniformly charged ball, the radius of the proton is found, which conforms to the experimental data. At the same time the dependence is derived of distribution of the mass and charge density inside the proton. The ratio of the density in the center of the proton to the average density is found, which equals 1.57 .

 

Источник: http://sergf.ru/rp.htm

На научный сайт