На русском языке

Canadian Journal of Physics, Vol. 94, No. 4, P. 370-379 (2016). http://dx.doi.org/10.1139/cjp-2015-0593

 

Estimation of the physical parameters of planets and stars in the gravitational equilibrium model

Sergey G. Fedosin

Sviazeva Str. 22-79, Perm, 614088, Perm region, Russian Federation

e-mail intelli@list.ru

 

Abstract: The motion equations of matter in the gravitational field, acceleration field, pressure field and other fields are considered based on the field theory. This enables us to derive simple formulas in the framework of the gravitational equilibrium model, which allow us to estimate the physical parameters of cosmic bodies. The acceleration field coefficient  and the pressure field coefficient  are a function of the state of matter, and their sum is close in magnitude to the gravitational constant . In the presented model the dependence is found of the internal temperature and pressure on the current radius. The central temperatures and pressures are calculated for the Earth and the Sun, for a typical neutron star and a white dwarf. The heat flux and the thermal conductivity coefficient of the matter of these objects are found, and the formula for estimating the entropy is provided. All the quantities are compared with the calculation results in different models of cosmic bodies. The discovered good agreement with these data proves the effectiveness and universality of the proposed model for estimating the parameters of planets and stars and for more precise calculation of physical quantities.

Keywords: field theory; acceleration field; pressure field; gravitational field; gravitational equilibrium model.

PACS: 03.30.+p, 03.50.-s, 03.65.pm, 04.40.-b, 95.30.Sf

 

Résumé: Sur la base de la théorie des champs les équations du mouvement de la matière dans le champ gravitationnel, le champ de l'accélération, le champ de pression et dans autres champs sont considérées. Cela permet de dériver dans le domaine du modèle d'équilibre gravitationnel des formules simples qui permettent de faire des estimations des paramètres physiques des corps spatiaux. Le coefficient du champ de l'accélération  et le coefficient du champ de pression  sont une fonction de l'état de la matière, et leur somme est proche en amplitude à la constante gravitationnelle . Dans le présent modèle, les dépendances de temperature et pression intérieures du rayon actuel sont trouvées. Les températures centrales et les pressions sont calculées pour la Terre et le Soleil, pour une étoile à neutrons typique et une naine blanche. Le flux thermique et le coefficient de conductivité thermique de la matière de ces objets sont trouvés et une formule d'estimation de l'entropie est présentée. Toutes les quantités sont comparées avec les résultats des calculs en les différents modèles de corps spatiaux. Une bonne conformité trouvée avec les données confirme l'efficacité et l'universalité du modèle proposé pour estimer les paramètres des planètes et des étoiles, et pour les calculs plus précis de quantités physiques.

Les mots-clés: la théorie du champ, le champ d’accélération, le champ de pression, le champ gravitationnel, modèle d’équilibre gravitationnel.

 

1. Introduction

The most accurate models of cosmic objects include detailed numerical calculations of certain internal structures (the solid or liquid core, shell, convective zone) with the use of equations of the state of different phases of matter and acting fields. For compact objects it is necessary to take into account the quantum and relativistic effects.

However, physics has in store the models that allow us to quickly estimate the characteristic parameters of planets and stars based only on the observable data, such as radius, luminosity, spectrum, surface temperature, gravitational redshift, asteroseismology data, etc. A well-known example is a polytropic model, in which the gas pressure is related to the mass density by a polytrope at the constant thermal capacity of the matter [1-3]. With polytropic index  and  the model gives the correct order of such quantities as the central density, temperature, pressure, potential gravitational energy and a number of other quantities.

White dwarfs are objects, in which the electron gas degenerates and makes the major contribution to the pressure in the matter. For neutron stars, the same is true for the neutron gas. There is a well-known simple calculation of the state of matter in white dwarfs and neutron stars, based on the equality of the gravitational energy and quantum mechanical energy and providing the typical values of the masses and radii of these objects. A more detailed analysis leads to the Chandrasekhar limit [4-5] as the greatest mass of a white dwarf, beyond which it becomes a neutron star.

In [6] the structure of compact stars is modeled by solving the equation of hydrostatic equilibrium by parameterization of the mass density dependence on the radius. This leads to the dependence of the masses and radii of the objects on the central density and the dependence of the pressure on the radius, expressed in terms of the gamma-function and the hypergeometric function.

The natural drawbacks of the above-mentioned approaches are the limited range of application or the low accuracy of predictions of physical quantities and the internal structure of objects.

Next, we will present the model of gravitational equilibrium, which is based on the field theory. In order to illustrate the possibilities of this model, we will calculate some physical parameters of a number of objects and will compare them with the results of calculations made by other authors. The positive aspect of the proposed approach is its universality, which allows applying it to any cosmic objects. In addition, this model provides very simple formulas to estimate the parameters of planets and stars at minimum of necessary assumptions.

 

2. The model description

In the model of gravitational equilibrium it is assumed that the corresponding object (planet, star) is in a state when the processes of energy exchange between the gravitational field and other fields have finished in it. From a theoretical point of view, all the fields acting in cosmic objects can be viewed as the components of a single general field [7]. In addition to the gravitational field, which is the main component, contribution to the general field can also be made by the electromagnetic field, pressure field, acceleration field, dissipation field, strong interaction field, weak interaction field, as well as other fields in the matter of the objects under consideration. At equilibrium, all the fields are relatively independent, because the energy fluxes between the fields and the matter on the average tend to zero. The expression for the general field equations follows from the principle of least action:

 

,                        ,                                 (1)

 

where  is the general field tensor,

 is the general field coefficient,

 is the Levi-Civita symbol or completely antisymmetric unit tensor,

 is the mass four-current,

 is the mass density in the reference frame associated with the particle,

 is the four-velocity of a point particle,  is the speed of light.

 

Since the general field tensor is the sum of tensors of particular fields, then the equations of any field can be represented in the form of (1) after the respective substitution of the field tensor, the constant of this field and the four-current. A characteristic feature of (1) is the fact that the equations of the general field and of each particular field have the form of Maxwell equations for the electromagnetic field, written in a covariant form in the curved space for non-inertial reference frames.

 

3. The acceleration field and the temperature

The equations of the acceleration field according to (1) have the following form [8]:

 

,                        ,                                 (2)

 

where  is the acceleration field tensor,  is the acceleration field coefficient.

 

The tensor  includes the vector components  and , which can be found by the rule:

 

,                 ,                     (3)

 

where the indices  form a triples of non-recurring numbers of the form 1,2,3 or 3,1,2 or 2,3,1; the three-vectors  and  can be expanded into the components: ;    .

 

For simplicity, we will consider equations (2) in the flat Minkowski space, that is, within the framework of the special theory of relativity. In this case, equations (2) are written as the equations for strength  and for the solenoidal vector  of the acceleration field:

 

,      ,      ,      .         (4)

 

With the help of the vectors  and  we can form an acceleration four-vector, characteristic of the body particles moving at the velocity  and having the Lorentz factor :

 

,

.                                 (5)

 

A gravitationally bound body usually has a spherical shape, so that the four-acceleration  with a covariant index will be a certain coordinate function. The vectors  and  also allow us to calculate the stress-energy tensor of the acceleration field  and the vector , which is the vector of the energy-momentum flux density of the acceleration field.

The main reason that the acceleration field of the matter particles has its own energy density, energy flux density and field strength is the gravitation force. Under the action of this force the gradients of pressure, temperature, mass density and other quantities are formed in cosmic bodies. The closer to the center of the body we approach, the higher the temperature and, consequently, the average velocity of the particles and the value of the four-velocity become. For a single particle, the four-potential of the acceleration field is the covariant four-velocity  of this particle. However, in case of a set of closely interacting particles it is not so – in the total four-potential of the system’s acceleration field  the scalar potential  and the vector potential  of the acceleration field become independent quantities as a consequence of different rules of summation of contributions from the scalar and vector quantities of different particles.

In [9], we calculated the energy and the vector of the energy-momentum flux density  of the acceleration field for a set of similarly charged particles that form a gravitationally bound system in the form of some liquid and filling a spherical volume. The same was done for other fields, including the gravitational and electromagnetic fields, as well as the pressure field. It allowed estimating the acceleration field coefficient in a first approximation with the help of the gravitational constant , the vacuum permittivity  and the relation  for the particles in question:

.                                                      (6)

 

In article [10], the concept of acceleration field allowed us to calculate the relativistic energy of the system of particles and the gravitational mass of the system; and in [11] it allowed us to derive the relativistic Navier-Stokes equations for viscous charged matter, taking into account the pressure field and dissipation field.

Since in the definition  the acceleration tensor is expressed in terms of the four-potential of the acceleration field, in equations (2) we can pass on from the acceleration tensor to the four-potential . This leads to the wave equations for the potentials  and  of the acceleration field [12]:

 

.            (7)

 

In (7)  is the four-potential of the acceleration field, expressed with a contravariant index using the metric tensor , and  are the Christoffel symbols, which are the function of . We solved equation (7) in [9] for the case of a set of randomly moving particles without general rotation, which are connected with each other by means of gravitation and the electromagnetic field including the pressure field. In Minkowski space the scalar component (7) is reduced to the equation for the Lorentz factor, thus we obtain the following:

 

,           ,         ,                     (8)

 

where the Lorentz factor  

 

is the function of the current radius  inside the sphere and the average value for the set of particles,  is the average velocity of the particles in the reference frame , which is associated with the center of inertia of the system.

 

The solution of (8) in case of uniform density is the following expression:

 

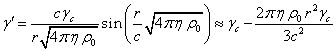,                            (9) 

 

where  is the Lorentz factor for the velocities  of the particle in the center of the sphere.

 

From (9) by raising to the square we obtain approximately the following:

 

,                                                    (10)

 

so that as the current radius  inside the sphere increases while moving from the center to the periphery of the sphere, the velocity  of the particles decreases.

 

Assuming that the velocity  is the root mean square velocity of the particles, and taking into account its relation to the kinetic temperature in the form of , where  is the Boltzmann constant, expression (10) is transformed into the temperature-radius dependence:

 

.                                    (11)

 

where  is the temperature at the center of the sphere,  is the mass of one gas particle,  is the mass within the current radius .

 

From (11) it follows that the temperature inside the cosmic bodies in the first approximation decreases parabolically, depending on the square of the radius of the observation point. Assuming in (11) that at the body radius  the body mass is equal to , and neglecting the surface temperature , we find the formula for the temperature in the center of the body:

 

.                                                           (12)

 

4. The pressure field

The four-potential of the pressure field for one particle is found by multiplying the function depending on the pressure and density by the covariant four-velocity [8-9], [12]:

 

,                                              (13)

 

where  and  denote the pressure and density in the reference frame  of the particle, the dimensionless ratio  is proportional to the pressure energy of the particle per unit mass of the particle,  and  are the scalar and vector potentials of the pressure field.

 

For a system of particles, (13) can also be considered valid, but  should be considered not as the four-velocity of an individual particle, but as the four-velocity averaged with respect to some ensemble of particles near the observation point.

The equations of the pressure field according to (1) are as follows:

 

,                      ,                            (14)

 

where  is the pressure field tensor,  is the pressure field coefficient.

 

The tensor  is the result of applying the four-curl to the four-potential :

 

,                                        (15)

 

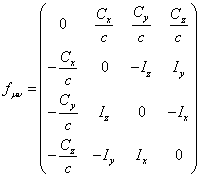.                                           (16)

 

 

 

 

here the tensor components are the components of the strength vector  and the solenoidal vector  of the pressure field.

 

In Minkowski space, equations of the pressure field (14) are considerably simplified:

 

,      ,      ,      .         (17)

 

It is sufficient to know the vectors  and  in order to determine the stress-energy tensor , the vector of the energy flux density  of the pressure field and the pressure force density in the matter.

Substituting (15) into (14) gives the wave equation for the four-potential of the pressure field:

 

.          (18)

 

In case of a self-gravitating system of particles without rotation, which occupies a spherical volume, equation (18) and its solution for the scalar potential in view of (9) is reduced to the following:

 

.                                                     (19)

 

 

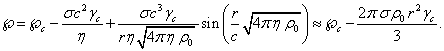
Since there is a relation , at a constant density the solution of (19) is transformed into the dependence of the pressure inside the system:

 

.                                   (20)

 

In large cosmic bodies the pressure on the surface at  is rather low and we can neglect it in (20). Then, to estimate the pressure in the center of the body we obtain a simple formula:

 

.                                                        (21)

 

5. The gravitational field and the equation of motion of matter

The equations of the gravitational field in the covariant theory of gravitation [13-16] correspond in their form to (1):

 

 ,                          ,                                   (22)

 

where  is the gravitational field tensor, which includes the components of the gravitational strength vector  and the solenoidal vector  of the torsion field:

 

.

 

 

 

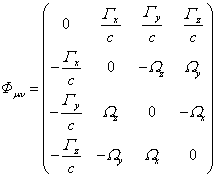The starting point of the covariant theory of gravitation is the four-potential of the gravitational field , which is described by the field’s scalar potential  and vector potential . The four-potential is part of the Lagrangian and it allows us to derive the equations of the gravitational field from the principle of least action, while the field tensor is associated with the four-potential: . This equality can be written in vector notation as follows:

 

,                    .                                           (23)

 

In Minkowski space, the mass density , the mass current density , the mass four-current , and equations (22) have the following form:

 

,      ,      ,      .

 

If in (22) we turn from the tensor  to the four-potential , we will obtain the wave equation:

 

.

 

In Minkowski space, this equation falls into two equations for the potentials of the gravitational field:

 

,                   .                    (24)

 

If the system of particles does not move in space as a whole and has no general rotation, then it has the vector potential  and the torsion field . And if the potential  does not depend on time, then the gravitational field becomes static. In this case, according to [9], the scalar potential inside the body at a constant mass density in view of (9) is defined by the formula:

 

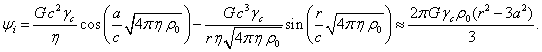   (25)

 

In the concept of the general field [7] the equation of motion of matter is as follows:

 

.

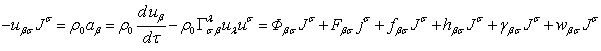(26)

 

where  is the four-acceleration in the curved space,  is the electromagnetic tensor,  is the electromagnetic four-current,  is the dissipation field tensor,  is the strong interaction field tensor ,   is the weak interaction field tensor.

 

The tensors  and  are important in the cases, when the equilibrium inside cosmic bodies is supported by the additional pressure from thermonuclear reactions or radioactive decay. The vector component (26) in view of (5) is reduced to the following:

 

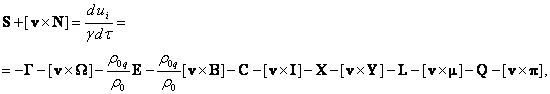    (27)

 

 

 

where the vectors ,  and  denote the strengths of the dissipation field, strong interaction field and weak interaction field, respectively, and the vectors ,  and  are the solenoidal vectors of these fields.

 

If we consider the equation of motion in Minkowski space and take into account only the gravitation, the acceleration field and the pressure field, then in the static case we can assume , , and . In view of (23) and (25) we have the following:

 

.                                   (28)

 

The pressure field strength is given by the formula: , and if the vector potential is , then using (19) we find the following:

 

.                                      (29)

 

According to (3) and the definition of the acceleration field four-potential in the form of , the acceleration field strength equals: .

For a non-rotating body both the vector potential  and the solenoidal vector  are equal to zero. In this case, using (8-9) inside the body we find the following:

 

.                               (30)

 

Substituting ,  and  in (27) in the absence of other fields, we obtain the equality for the field strengths and the relation for the field coefficients:

 

,                               .                                  (31)

 

Outside the system, near its border, we can assume that , , and there is a gravitational force acting on a certain test particle, but the pressure tends to zero due to the low mass density. Then in (31) we should assume , and the gravitational field strength  will determine the centripetal acceleration of individual particles, rotating around the system. In the non-relativistic case, this can be written as: . In view of the equality  for the kinetic temperature of the particles near the surface of the system we must obtain:

 

.                                                          (32)

 

The kinetic temperature  refers to the kinetic energy of the particles during their rotation around the system and it should exceed the average temperature  of the gas of these particles, which is the measure of the gas thermal energy near the system.

The best conditions for (32) to hold must be in gas clouds, for example, in Bok globules, small dark cosmic clouds of gas and dust. In [17] it was found that the radius of a typical globule is 0.35 parsecs, the mass is 11 Solar masses, and the recorded temperature of dust in some globules can reach 26 K.

Assuming in (32) that  is equal to an atomic mass unit, we find the temperature of particles on the surface for a typical globule:  K. If in (11) we assume , , , and taking into account equation (6) for , the temperature in the center of the globule is of the order of 22 K, which is close enough to the observations.

Using (32) for the Earth gives the kinetic temperature  of about 2500 K, and for the Sun – about 7.7 million degrees. Such temperatures are actually observed – at the Earth's ionosphere the thermal temperature  is over 2000 K, and at the Solar corona the average temperature is about 5 million degrees. Due to the action of the Sun’s gravitation the particles are orbiting around the star for a long time, almost without losing their energy. This solves the well-known coronal heating problem, according to which a fast-moving heated gas should evaporate quickly and the corona should rapidly cool down due the insufficient rate of its heating from the photosphere. It is obvious that in this analysis of the problem it is not taken into account that the particles can be fully retained by the gravitational field of the Sun and rotate around it. In addition, if the particles are always close to the Sun, they can be heated for a long time due to solar flares and similar phenomena, finally reaching the observed temperature of millions of degrees.

However, we must limit the use of formulas (31) and (32) due to their incompleteness, because along with the motion of particles in solid bodies and stellar plasma, the main contribution into the pressure is made by the interatomic forces, including the electromagnetic forces of electric charges and the strong gravitation as the component of strong interaction (in the gravitational model of strong interaction [14]). These forces can significantly change the particle acceleration in the equation of motion (27).

For an ideal solid body there is no motion of particles inside the body, , and from (31), in view of (28), and from the relation  it follows:

 

.                              (33)

 

Meanwhile, modelling of the cosmic objects is usually based on the so-called hydrostatic equilibrium equation, which has the following form without corrections of the general theory of relativity:

 

.                                                    (34)

 

We see that (34) corresponds to (33) with the difference that in (33) the mass density  is under the gradient sign together with the pressure. At constant density both expressions are equivalent, but since the density is usually a function of the radius, expressions (33) and (34) do not fully coincide. In the event of noticeable rotation of the object, in (27) we should take into account the non-zero torsion field vector  and the solenoidal vector  of the pressure field, then hydrostatic equation (34) becomes even more inaccurate.

 

6. The case of non-uniform density

In [7] and [9], we made estimates of the temperature and pressure in the center of various cosmic objects by formulas (12) and (21), and we obtained quite a good agreement with the models of stars, planets and gas clouds. In this section, we plan to increase the accuracy of our calculations.

In (11) and (20) the density was assumed to be a constant, although the temperature and pressure vary within wide ranges approximately quadratically. In general, when solving the wave equations (8) and (19) we should take into account that the density is also a certain function of the radius. We will continue to use the following approximation:

 

.                                                    (35)

 

Substituting (35) in (8), where we introduce an auxiliary function  in the form of , we express the Laplacian as the function of the current radius:

 

.                      (36)

 

It is convenient to seek the solution of this differential equation in the form of a series with constant coefficients:

 

.

 

Limiting the series by the value , after substituting  in (36) and cancelling the similar terms we can calculate the coefficients . All of these coefficients appear proportional to the coefficient , and . Specifying , taking into account the relation , we find the approximate dependence of the Lorentz factor on the current radius:

 

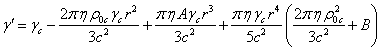.                     (37)

 

In (37) we can neglect the term  in the brackets, which is small even for neutron stars. In the first approximation, we have:

 

,           .

 

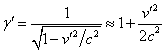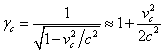Taking into account the relationship between the particle velocity  and the temperature , and passing on in (37) from the Lorentz factor to the velocities and then to the temperature, we can now specify (11) for the temperature dependence:

 

.                     (38)

 

In order to specify the pressure dependence, in (19) we will replace  and will substitute (35) and (37) into it:

 

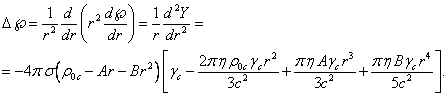             (39)

 

 

 

We will seek the solution of equation (39) in the form of a quintic polynomial with constant coefficients:

 

.

 

After substituting  in (39) and cancelling the similar terms, we see that , . Determining other coefficients, we find the function , and then the scalar potential  of the pressure field:

 

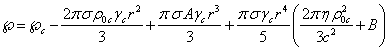.                   (40)

 

The term  in comparison with  in (40) can be neglected.

 

As we can see, the coefficients  and  in the density-radius dependence (35) make additional contribution into the dependences of the temperature (38) and the pressure field potential (40) on the current radius.

 

7. The temperature and pressure estimates

We will calculate the volume-averaged mass density by integrating (35) with respect to the radius from zero to the body’s radius :

 

(41)

 

In (38) and (40) we will assume  and substitute there , expressed from (41) in terms of the average density . We will also use the expression for the body mass . This allows us to estimate the surface temperature  and the pressure field potential at the surface :

 

.                           (42)

 

.                                  (43)

 

In (43) we can assume that the scalar potential  of the pressure field on the surface of cosmic bodies is close to zero as compared to the potential  at the center. This allows us to calculate , as well as the pressure at the center:

 

.

 

In this relation, the density at the center  can be expressed using (41) in terms of the average density and we can use the equation :

 

(44)

 

The number of terms in (44) is greater than in (21), which increases the accuracy of calculations. Let us now consider the possible values of coefficients of the pressure field and acceleration field. Based on the equation of motion, in (31) we found the equality . If we compare the pressure at the center (21) and the temperature at the center (12) at constant density , we obtain:

 

.                                                      (45)

 

On the other hand, the standard expression for the pressure in view of the radiation pressure has the following form:

 

,                                                     (46)

 

where  is the radiation density constant,

 

 is the number of nucleons per ionized gas particle, so that the gas particle can be an atom, ion, electron or a single nucleon, depending on its state.

By definition: 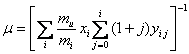, where  is the mass fraction of the element with atomic number ,  is the nuclear mass of the atom with atomic number  and atomic mass ,  is the degree of -multiple ionization of -th element, so that . In fully ionized gas, consisting of hydrogen, helium, and other elements with , the expression for  becomes as follows:, where , , .

 

If we do not take into account the radiation pressure, then comparison of (45) and (46) implies the equation: . Assuming , we find:

 

,                             .                               (47)

 

For the gas of nucleons or hydrogen atoms  and , ;  for the gas of fully ionized hydrogen  and , ;  for the gas of fully ionized helium  and , ;  for the fully ionized gas of heavier chemical elements  and , .

According to the Earth's model, the inner core temperature reaches 6000 K, and the pressure is  Pa [18]. Since the Earth is substantially inhomogeneous, we will use the data for the Earth's outer core: the radius of 3480 km, the mass  kg, the temperature on the core surface of the order of  K, and the pressure  Pa.

From the analysis of the density-radius dependence of the form of (35), for the model of Earth's core in view of (41) we can estimate the coefficients  kg/m4 and  kg/m5 with the central density  kg/m3. Based on these data, given that , , and using  as the atomic mass unit, from (42) it follows that the temperature at the center of the Earth's core is of the order of  K. It is clear that the matter at the center of the Earth is not a fully ionized gas, but rather solid crystalline matter. If we assume the temperature at the center equal to 6000 K, from (42) we can estimate the effective value of the acceleration field coefficient: .

For the pressure according to (44), provided , we obtain the value  Pa, and taking into account the additional pressure of the crust  the pressure at the center of the Earth must be  Pa. This pressure is 1.9 times less than the pressure in the standard model. We can explain this, among other things, by the fact that the equations of motion (33-34) for an ideal solid body are not completely accurate, since they do not take into account the contribution of the acceleration field explicitly. These equations imply the equality of the gravitational force and the pressure force, which leads to the equality of the acceleration inside the body to zero and to the relation . But in fact, the acceleration inside the body is different from zero and is calculated in (27) and (31) with the use of the acceleration field, as a result, according to (47) .

For the model of the Earth as a whole the coefficients in (35) are equal to  kg/m4 and  kg/m5. Substituting these coefficients in (44), we find the pressure at the center of the Earth:  Pa. This pressure is even less than the above pressure estimate made with the help of the coefficients for the core, which illustrates the effect of inhomogeneity inside the Earth.

Let us now consider a neutron star with the radius of 12 km and the mass , where  denotes the mass of the Sun. We will take as an estimate of the central stellar density the value  kg/m3, with the equation of the state of matter according to the potentials AV18 + UIX in [19]. Using the density-radius dependence from [20], we can estimate the coefficients in (35):  kg/m4,  kg/m5. Neglecting the surface temperature , with condition  in (42) we obtain the estimate of the temperature at the center of a neutron star - of the order of  K. Let us note that according to [21] up to the temperature  K stable atomic nuclei can exist in the matter of neutron stars.

For the pressure at the center of a neutron star from (44) with condition  we obtain the value  Pa. This can be compared with the pressure of the nuclear matter  Pa at the density  kg/m3 according to [22] and the pressure of the order of  Pa in [23], while in different models of neutron stars according to [20] the pressure does not exceed  Pa.

The helium white dwarf with the mass  must have the radius  m and the central density  kg/m3, according to [24]. In view of (41) from the density-radius dependence in [25] the coefficients follow in relation (35):  kg/m4,  kg/m5. With this in mind, from (42) with  we find the temperature at the center of the white dwarf:  K, and the pressure at the center, according to (44), is equal to  Pa.

In the NASA model, at the center of the Sun the supposed mass density is  kg/m3, the pressure is about  Pa and the temperature is  K [26].

Since the main sequence stars are much larger in size than white dwarfs and neutron stars, the density variation in dependence (35) moving from the core to the stellar surface is very large, and two terms are not enough for acceptable accuracy. Therefore, we will turn from the model of the Sun as a whole to the model of its core, which is much more uniform. The core radius is estimated at the value, which is five times less than the radius of the Sun, the core mass is equal to , the pressure on the core surface is not less than  Pa [27], and temperature about  K. So the coefficients for the core in (35) are as follows:  kg/m4,  kg/m5. According to [28], for the Solar core , then from (47) we obtain , .  From (42) we estimate the temperature at the center of the core:  K. From (44) for the pressure we obtain  Pa. These values are somewhat lower than in the NASA model, but it should be noted that the Sun’s crust also exerts pressure on the Solar core. If we sum up the pressures  and , the result will be much closer to .

 

8. Thermal conductivity

According to the model of stellar evolution, all of the main sequence stars over time turn into white dwarfs and neutron stars. It is assumed that in compact stars there are no observable sources of internal energy, associated with nuclear transformations. As a result, after formation white dwarfs and neutron stars have to cool down slowly over many billions of years.

The surface temperatures of some of the observed hot white dwarfs reach 150 000 K, and the surface of cooled white dwarfs has a temperature below 4000 K. The respective luminosities corresponding to these temperatures are  and  for a dwarf with the typical mass of , and cooling down up to 4000 K takes about 12 billion years [29]. To characterize the heat propagation inside a star we will consider a phenomenological differential heat-flux equation, describing the Fourier’s law of thermal conduction:

 

.                                                           (48)

 

In (48), the energy flux density vector  is proportional to the thermal conduction coefficient  and the temperature gradient.

In the considered model of gravitational equilibrium, a star or planet cannot cool down infinitely. Indeed, the temperature distribution (38) was derived by us based on the fact that the gravitational field was counteracted by the acceleration field and pressure field. The equilibrium state must be maintained at any time, as well after the star cools down. Suppose that the observed cooled white dwarfs are in such a state that the temperature distribution in them is close to the equilibrium distribution (38). Substituting the temperature-radius dependence (38) into (48) we find the vector :

 

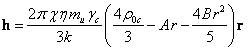.                                   (49)

 

Substituting in (49) , , ,  kg/m3 and the coefficients  and  for the white dwarf from the previous section, we obtain the absolute value of the vector of the energy flux density at the surface: . The integral of the vector  across the entire surface of the white dwarf must be equal to the stellar luminosity. Since the vector  is perpendicular to the surface of the star, then the luminosity is equal to: . On the other hand, the luminosity of a white dwarf in the steady state after long-term cooling is presumably equal to . From the equation  we find the estimate of the thermal conductivity of the stellar matter:  W/(m·K). This value mainly characterizes the thermal conductivity of the upper crust and the atmosphere of the white dwarf, while the thermal conductivity of the interior, crust and atmosphere of the star may differ many times due to the difference in temperatures and the state of matter. For comparison, the thermal conduction coefficient of a diamond with impurities at room temperature is  W/(m·K), while the purified diamond’s coefficient reaches  W/(m·K) [30], which is one of the highest experimental values for the known substances.

 The temperature of the surface of neutron stars can be  K or less, which requires about  years of cooling [31]. If we use the stellar radius of  m, then the corresponding minimal luminosity will be  with  as the Stefan–Boltzmann constant, which is close to the observed luminosities of certain stars [32].

Substituting in (49) the data for a neutron star at , , , the central density of  kg/m3 and the coefficients  and  from section 7, we obtain the absolute value of the vector of the energy flux density at the surface: . Comparison of the luminosities  and  allows us to estimate the thermal conduction coefficient of the stellar matter:  W/(m·K). This estimate is consistent with the results of calculation of the ionic thermal conductivity in the shell of a neutron star [33].

We will use (49) with  for the Earth as a whole, taking into account , the central density  kg/m3 and the corresponding coefficients  kg/m4  and  kg/m5 from section 7. The energy flux density at the surface is equal to . The measurements of the heat flux on land and in the oceans give the average value of  W/m2 [34], which leads to the thermal conduction coefficient  of   W/(m·K). According to [35], the thermal conduction coefficient in the core of the Earth must be 37 W/(m·K), corresponding to the thermal conductivity of iron, on the core-mantle boundary  is reduced to 16.4 W/(m·K) [36], and the thermal conductivity of the shell should be almost an order of magnitude less.

The value we found W/(m·K) is greater than the expected value for the shell of the Earth, which can be attributed to inaccuracy of measuring the density  using two coefficients. In addition, we did not take into account in the calculation that a significant part of the thermal energy inside the Earth was generated due to the radioactive decay of certain isotopes.

If we repeat all the calculations only for the outer core of the Earth, with its radius of 3480 km, mass of kg and the supposed total core’s heat flux of 10.6 TW, according to [36], then with the coefficients  kg/m4 and  kg/m5 we will obtain a more acceptable value for the upper core:  W/(m·K). To improve the results, the matter density should be specified in (35) with much greater accuracy and all the sources of thermal energy should be taken into account. This is even more important for modelling the main sequence stars and the Sun.

 

9. Entropy

Planets and stars consist of molecules, atoms, ions, electrons, and as for the white dwarfs and neutron stars the list of basic matter particles also includes the atomic nuclei and individual nucleons. For multicomponent systems the specific entropy per one matter nucleon is calculated by summing up for each type of particles, and taking into account the radiation entropy according to [37] it looks as follows:

 

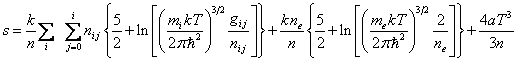,        (50)

 

where  is the concentration of nucleons,  is the atomic mass unit,  is the mass of the atomic nucleus with the charge number  and the mass number ,  is the statistical weight of the ion of -th chemical element in -th ionization state,  is the concentration of ions in the element  in -th ionization state,  is the mass fraction of the element with the charge number ,  is the degree -fold ionization of the -th element, so that ,  is Dirac constant,  is the concentration of electrons under electroneutrality conditions.

 

We will apply relation (50) to the case of a monatomic neutral gas without taking into account the contribution of the electrons:

 

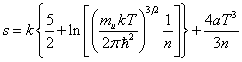.                                     (51)

 

Expression (51) can be used to estimate the specific entropy in the newly formed neutron star, consisting mostly of neutrons with admixture of protons, electrons and atomic nuclei in the shell of the star. If the star’s mass is  and its radius is  m, then  m-3. Substituting in (51) the temperature  K at the center of the neutron star, found in Section 7, we obtain the specific entropy per nucleon: . But at the initial time point the entropy is considerably higher, since at the same temperature the radius of a hot star exceeds  and the density  is less.

At this temperature, the contribution from the entropy of radiation is 31.5 times less than the contribution from the entropy of nucleons. The specific entropy value in the equilibrium state should be less than , as due to cooling the temperature in the main volume of the star would be less than the temperature at the center  K.

The estimation of the specific entropy can be done in a different way. As it was shown in [10], the energy of the acceleration field as part of the energy of random motion of particles can be expressed as follows:

 

.

 

To this energy we must add the energy of the particles due to their interaction with the four-potential of the acceleration field. For exact calculation of the kinetic energy of particles we can use the virial theorem or the kinetic energy definition as the difference between the relativistic energy of the moving particles and their rest energy. In both cases we obtain for the kinetic energy the following:

 

.

 

By definition, the increment of the specific entropy is given by the formula: , where  is the increment of the total entropy,  is the number of nucleons,  is the increment of the thermal energy at the temperature . In the neutron star formation we can assume in a first approximation that , as well . Then for the specific entropy we obtain the following relation:

 

.                                                      (52)

 

Substituting here  at  from (47) and the central temperature  K, we find , which is less than . However, this result is subject to further correction in view of the fact that the star during transition to the equilibrium radius loses its energy with the neutrinos that fly away and is getting rapidly cooled, reducing its entropy.

For comparison, there was found in [38] that a hot protoneutron star with the mass , the radius of 55.75 km and the temperature  K has the specific entropy equal to . When the star reaches its equilibrium radius of 11.15 km, its specific entropy at the effective temperature of matter of the order of  K becomes equal to  and then decreases continuously due to the subsequent cooling.

Calculating the entropy of planets and stars with the help of (50) requires knowledge of the quantitative chemical composition of matter. If we use (52) for initial estimation of the entropy, it is necessary to know the mass, radius and average temperature. For Jupiter, the specific entropy, according to (52), at  will be of the order of , if as  we use the temperature value  K expected at the center of Jupiter within the framework of the modern models of gas giants. This value of the specific entropy should be increased because as  we should use a less temperature value, averaged over the entire volume. In particular, calculations by a standard method give  for a planet like Jupiter [39].

 

10. Conclusion

In the presented model of gravitational equilibrium, an important role is played by the acceleration field and the pressure field. The equations of these fields (2) and (14) allow us to calculate the strengths and the solenoidal vectors of the fields and to determine the distribution of temperature and pressure inside the cosmic bodies, caused by gravitation, using simple formulas. Equations (22) allow us to find the gravitational field strength and the solenoidal vector of the torsion field in the covariant theory of gravitation. The knowledge of field strengths and solenoidal vectors is sufficient for the analysis of the equations of motion of matter (26) and for construction of the model basis. In particular, the equation of motion leads to correlation (31) between the coefficients of the acceleration field and the pressure field, and in (47) these coefficients are expressed in terms of the thermodynamic parameter . Using the values of these coefficients, we determine the temperature and pressure at the center of various objects – in Bok globules, inside the Earth, the Sun, in a white dwarf and a neutron star. In addition, we obtain the estimates of the heat flux and the thermal conductivity coefficient, which characterizes this or that object, and we also estimate the entropy of a neutron star and a gas planet. The analysis of the results shows that they agree well with the data provided by other authors.

Based on the significantly higher thermal conductivity of the core and crust as compared to the shell, some authors in a number of studies suggest the existence in a typical neutron star (and a white dwarf) of an almost isothermal core with a small temperature gradient. In our approach, the temperature distribution inside a star is associated with dependence (37) for the Lorentz factor, while the high value of thermal conductivity does not play an essential role and cannot lead to the isothermal core. In turn, relation (37) follows from the wave equation of the acceleration field (7) and is determined only by the matter density distribution and the matter motion.

From the physical standpoint, (37) and the similar dependence for the pressure field potential (40) are associated with the energy distribution between the gravitational field, acceleration field and pressure field. The result of this energy distribution is a certain state of equilibrium and certain distribution of physical parameters, depending on the current radius, inside of the object under consideration. If we proceed from the Le Sage's theory of gravitation, then the actual agents, performing the gravitational contraction and equilibrium heating of matter of cosmic objects, are the fluxes of gravitons. The energy density, the cross-section of interaction between the graviton field and the nucleon matter, as well as other parameters can be calculated based on the fact that the action of graviton fluxes should lead to the Newton's law of universal gravitation [40-41].

The universality of the gravitational equilibrium model is ensured by the fact that the field equations can be applied to any objects, regardless of their state of matter. A certain restriction is the need for a detailed representation of the mass density distribution in order to obtain accurate results, however the same is required in any other approaches, including the commonly used polytropic model. As a rule, to estimate the mass density distribution the measurement of the velocities of longitudinal and transverse seismic waves is used, as well as the correspondence between the radial distribution of mass density and the total body mass and its moment of inertia.

Another restriction is the use in formula (42) of the atomic mass unit as , which is permissible for the hydrogen gas and the uniform nuclear matter of nucleons. Meanwhile, in previously derived correlations (11) and (38)  has the meaning of the mass of one gas particle, which can be different from the atomic mass unit. Thus, in white dwarfs a significant contribution into the state of matter is made by electrons, the relativistic masses of which depend on the temperature. In stars and planets there are both neutral and ionized atoms with the masses of the order of , where  is the mass number of the corresponding chemical isotope. Due to the complex composition of particles in the matter, formulas (42) for the temperature and (52) for the specific entropy need to be specified for each type of cosmic objects.

 

References

1.           J.H. Lane. Am. J. Sci. 2 50, 57 (1870). doi:10.2475/ajs.s2-50.148.57.

2.           G.P. Horedt. Polytropes – applications in astrophysics and related fields. Kluwer Academic Publishers, Dordrecht. 2004.

3.           L. Herrera and W. Barreto. Phys. Rev. D. 87, 087303 (2013). doi:10.1103/PhysRevD.87.087303.

4.           S. Chandrasekhar. Astrophys. J. 74, 81 (1931). doi:10.1086/143324.

5.           Д.Г. Яковлев. УФН. 164, 653 (1994). doi:10.3367%2FUFNr.0164.199406g.0653. [In Russian.]

6.           H. Rodrigues. Eur. J. Phys. 34, 667 (2013). doi:10.1088/0143-0807/34/3/667.

7.           S.G. Fedosin. The concept of the general force vector field. 2014. viXra:1406.0173.

8.           S.G. Fedosin. About the cosmological constant, acceleration field, pressure field and energy. 2014. Accepted by Jordan Journal of Physics. viXra:1403.0023.

9.           S.G. Fedosin. Amer. J. Mod. Phys. 3, 152 (2014). doi:10.11648/j.ajmp.20140304.12.

10.       S.G. Fedosin. Jordan J. Phys. 8, 1 (2015). http://journals.yu.edu.jo/jjp/Vol8No1Contents2015.html.

11.       S.G. Fedosin. Int. J. Therm. 18, 13 (2015). doi:10.5541/ijot.5000034003.

12.       S.G. Fedosin. Advanced Studies in Theoretical Physics. 8, 771 (2014). doi:10.12988/astp.2014.47101.

13.       S.G. Fedosin. Fizika i filosofiia podobiia ot preonov do metagalaktik. Perm. 1999.

14.       S. Fedosin. The physical theories and infinite hierarchical nesting of matter, Vol. 1. LAP LAMBERT Academic Publishing, Saarbrücken. 2014.

15.       S.G. Fedosin. Hadronic J. 35, 35 (2012).

16.       S.G. Fedosin. Adv. Nat. Sci. 5, 55 (2012). doi:10.3968%2Fj.ans.1715787020120504.2023.

17.       D.P. Clemens, J.L. Yun, and M.H. Meyer. Astrophys. J. Suppl. 75, 877 (1991). doi:10.1086/191552.

18.       D. Alfè, M.J. Gillan, L. Vocadlo, J. Brodholt, and G.D. Price. Phil. Trans. Roy. Soc. 360, 1227 (2002). doi:10.1098/rsta.2002.0992.

19.       A. Akmal and V.R. Pandharipande. Phys. Rev. C. 56, 2261 (1997). doi:10.1103/PhysRevC.56.2261.

20.       J.M. Lattimer and M. Prakash. Astrophys. J. 550, 426 (2001). doi:10.1086/319702.

21.       D.Q. Lamb, J. M. Lattimer, C.J. Pethick, and D.G. Ravenhall. Phys. Rev. Lett. 41, 1623 (1978). doi:10.1103/PhysRevLett.41.1623.

22.       R. Malone, M. Johnson, and H. Bethe. Astrophys. J. 199, 741 (1975). doi:10.1086/153746.

23.       F.J. Fattoyev and J. Piekarewicz. Phys. Rev. C. 82, 025805 (2010). doi:10.1103/PhysRevC.82.025805.

24.       M. Rotondo, J.A. Rueda, R. Ruffini and S.-S. Xue. Phys. Rev. D. 84, 084007 (2011). doi:10.1103/PhysRevD.84.084007.

25.       M.I. Nouh, A.S. Saad, M.M. Elkhateeb, and B. Korany. White dwarf stars as a polytropic gas spheres. 2014. arXiv:1406.1482.

26.       D.R. Williams. Sun fact sheet. NASA, 04 January 2016. http://nssdc.gsfc.nasa.gov/planetary/factsheet/sunfact.html.

27.       J. Christensen-Dalsgaard et al. Science. 272, 1286 (1996). doi:10.1126/science.272.5266.1286.

28.       W.J. Chaplin, A.M. Serenelli, S. Basu, Y. Elsworth, R. New, and G.A. Verner. Astrophys. J. 670, 872 (2007). doi:10.1086/522578.

29.       B.M.S. Hansen and J. Liebert. Annu. Rev. Astro. Astrophys. 41, 465 (2003). doi:10.1146/annurev.astro.41.081401.155117.

30.       L. Wei, P.K. Kuo, R.L. Thomas, T.R. Anthony, and W.F. Banholzer. Phys. Rev. Lett. 70, 3764 (1993). doi:10.1103%2FPhysRevLett.70.3764.

31.       M.V. Beznogov and D.G. Yakovlev. MNRAS. 447, 1598 (2015). doi:10.1093/mnras/stu2506.

32.       V.E. Zavlin. Theory of radiative transfer in neutron star atmospheres and its applications. In Neutron stars and pulsars, ed. W. Becker, Astronomy and Space Science Library. 357, 181 (2009). doi:10.1007/978-3-540-76965-1_9.

33.       A.I. Chugunov and P. Haensel. MNRAS, 381, 1143 (2007). doi:10.1111/j.1365-2966.2007.12301.x.

34.       J.H. Davies and  D.R. Davies. Solid Earth, 1, 5 (2010). doi:10.5194/se-1-5-2010.

35.       В.Н. Жарков. Внутреннее строение Земли и планет. Наука, Москва. 1978. [In Russian.]

36.       V. Haigis, M. Salanne, and S. Jahn. Earth and Planetary Science Letters. 355-356, 102 (2012). doi:10.1016/j.epsl.2012.09.002.

37.       L.D. Landau, E.M. Lifshitz. Statistical physics, Part 1. Vol. 5 (3rd ed.). Butterworth–Heinemann, Oxford. 1980.

38.       M.G.B. de Avellar, R.A. Souza, and J.E. Horvath. RAA. 16, 21 (2016). doi:10.1088/1674–4527/16/2/021. http://www.raa-journal.org/raa/index.php/raa/article/viewFile/1837/2323 .

39.       G.-D. Marleau and A. Cumming. MNRAS. 437, 1378 (2014). doi:10.1093/mnras/stt1967.

40.       S.G. Fedosin. J. Vectorial Relativity. 4, 1 (2009).

41.       S.G. Fedosin. Phys. Scie. Int. J. 8, 1 (2015). doi:10.9734/PSIJ/2015/22197.

 

Source: http://sergf.ru/esten.htm

Scientific site