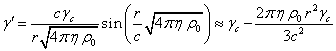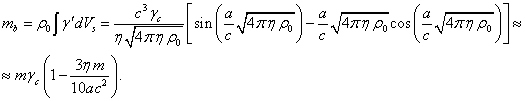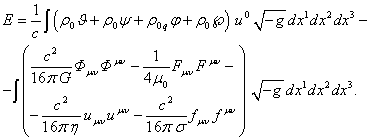In English

 

International Letters of Chemistry, Physics and Astronomy, Vol. 78, pp. 39-50 (2018). http://dx.doi.org/10.18052/www.scipress.com/ILCPA.78.39

 

Гравитационное поле в релятивистской однородной модели в рамках ковариантной теории гравитации

 

Федосин Сергей Григорьевич

ул. Свиязева 22-79, город Пермь, 614088, Пермский край, Россия

e-mail: fedosin@hotmail.com

 

Для релятивистской однородной системы с инвариантной плотностью массы определяются точные выражения для потенциалов и напряжённостей гравитационного поля, энергии частиц и поля. Показывается, что как и в классическом случае для тел с постоянной плотностью массы, в системе с нулевым векторным потенциалом гравитационного поля энергия частиц, связанная со скалярным потенциалом поля, по модулю в два раза превышает энергию, определяемую через тензорный инвариант гравитационного поля. Рассматривается вопрос о неточности использования тензоров энергии-импульса полей для вычисления массы и энергии системы. Найденные выражения для напряжённостей гравитационного поля внутри и снаружи системы позволяют объяснить возникновение крупномасштабной структуры наблюдаемой Вселенной, а также связать плотность энергии гравитонов в вакуумном поле с предельной плотностью массы внутри протона. Как Вселенная, так и протон оказываются релятивистскими однородными системами с максимально допустимыми параметрами. Описанный подход позволяет вычислить максимально возможный фактор Лоренца частиц вещества в центре нейтронной звезды и в центре протона, а также оценить радиус действия сильной и обычной гравитации в космологическом пространстве.

Ключевые слова: релятивистская однородная система; ковариантная теория гравитации; гравитационное поле; энергия.

PACS: 03.30.+p; 95.30.Sf.

 

The gravitational field in the relativistic uniform model within the framework of the covariant theory of gravitation

 

Sergey G. Fedosin

PO box 614088, Sviazeva str. 22-79, Perm, Perm Krai, Russia

E-mail fedosin@hotmail.com

 

For the relativistic uniform system with an invariant mass density the exact expressions are determined for the potentials and strengths of the gravitational field, the energy of particles and fields. It is shown that, as in the classical case for bodies with a constant mass density, in the system with a zero vector potential of the gravitational field, the energy of the particles, associated with the scalar field potential, is twice as large in the absolute value as the energy defined by the tensor invariant of the gravitational field. The problem of inaccuracy of the use of the fields’ stress-energy tensors for calculating the system’s mass and energy is considered. The found expressions for the gravitational field strengths inside and outside the system allow us to explain the occurrence of the large-scale structure of the observable Universe, and also to relate the energy density of gravitons in the vacuum field with the limiting mass density inside the proton. Both the Universe and the proton turn out to be relativistic uniform systems with the maximum possible parameters. The described approach allows us to calculate the maximum possible Lorentz factor of the matter particles at the center of the neutron star and at the center of the proton, and also to estimate the radius of action of the strong and ordinary gravitation in cosmological space.

Keywords:  Relativistic uniform system; covariant theory of gravitation; gravitational field; energy.

PACS: 03.30.+p; 95.30.Sf

 

1  Введение

Релятивистская теория более точно описывает физику явлений по сравнению с классической механикой. Это приводит к тому, что идеальная однородная модель тела с постоянной плотностью массы должна быть заменена на релятивистскую однородную модель. В релятивистской модели плотность массы может быть функцией координат, но считается постоянной инвариантной плотностью массы в системах отсчёта, сопутствующих частицам, составляющих тело. За счёт движения частиц эффективная плотность массы в системе отличаются от инвариантных значений, что вносит дополнительные поправки в значения функций поля и в энергию системы.

Различные свойства релятивистской однородной системы изучались ранее в [1, 2]. Целью настоящей работы является проверка соотношения между энергией частиц в скалярном гравитационном потенциале и собственной энергией гравитационного поля в рамках ковариантной теории гравитации и релятивистской однородной модели. Мы будем использовать ковариантную теорию гравитации, а не общепринятую общую теорию относительности. Это связано с тем, что в общей теории относительности отсутствует тензор энергии-импульса гравитационного поля, что не позволяет однозначно вычислить плотность энергии и поток энергии поля внутри тела либо за его пределами [3, 4]. С другой стороны, с помощью ковариантной теории гравитации удаётся построить модели звёзд и оценить их параметры [5], уточнить терему вириала [6]. При этом гравитационное поле в рамках ковариантной теории гравитации было включено в единое общее поле как отдельная компонента [7]. Метрика возле уединённого массивного тела была определена в [8], с помощью которой в [9] было показано, что ковариантная теория гравитации успешно объясняет аномальную прецессию перигелия Меркурия, отклонение частиц и света в гравитационном поле, гравитационное замедление времени и гравитационное красное смещение света, а также эффект Пионеров [10].

Другой особенностью ковариантной теории гравитации является наличие в ней 4-потенциала гравитационного поля, содержащего кроме скалярного потенциала поля также векторный потенциал. С помощью векторного потенциала формируются дополнительные добавки в напряжённости гравитационного поля и в поле гравитационного кручения, которые в гравитоэлектромагнетизме как частном случае общей теории относительности называются напряжённостями гравитоэлектрического поля и гравитомагнитного поля соответственно. Указанные добавки необходимы для того, чтобы учесть запаздывание распространения гравитационного взаимодействия точно также, как это происходит в электромагнетизме, при распространении электромагнитного взаимодействия. Благодаря векторному потенциалу и полю кручения возможны различные эффекты, в том числе гравитационная индукция [11, 12].

Ковариантная теория гравитации отличается также от модифицированных версий общей теории относительности, таких как , ,  модели или модель Эйнштейна с космологической постоянной  (Einstein-Λ model). Общей задачей указанных моделей является их применение в космологии, где они позволяют учесть такие эффекты, которые приписываются сейчас тёмной энергии и тёмной материи. Но в ряде работ указанные модели гравитации применяются и к ограниченной по размерам системе. Так, в  [13]  гравитация Палатини (Palatini f(R) gravity) используется для описания динамической нестабильности в коллапсирующей самогравитирующей сферической системе звёздных размеров, а в [14]  гравитация ( gravity) применяется к самогравитирующей анизотропной системе цилиндрической формы, которая может содержать внутреннюю полость как результат взрывного расширения. В [15] уравнения поля и динамические уравнения для вещества компактной звезды изучаются с помощью теории гравитации типа ,  а в [16]  гравитация (gravity) используется для моделирования уравнения состояния релятивистского вещества. Интерпретация результатов как всегда оказывается наиболее ясной в пределе слабого поля, при этом в качестве отправной точки служат обычно ньютоновский и постньютоновский пределы.

В отличие от указанных модифицированных теорий гравитации, в пределе слабого поля ковариантная теория гравитации переходит в лоренц-инвариантную теорию гравитации и не содержит элементов, связанных с тёмной энергией и тёмной материей. Однако применение ковариантной теории гравитации к релятивистской однородной системе приводит к специфическим особенностям для потенциалов и напряжённостей гравитационного поля. Как будет показано далее, эти особенности имеют наибольшее значение для объектов, в которых произведение радиуса объекта на квадратный корень от плотности массы достигает максимума. В частности, мы применим выражения для напряжённостей гравитационного поля к наблюдаемой Вселенной, к нейтронной звезде и к протону, что позволит нам объяснить некоторые свойства этих объектов.

 

2  Функции поля

В качестве релятивистской однородной системы рассматривается сферическая система, состоящая из частиц, которые могут иметь ещё электрический заряд. Стабильность системы поддерживается действием собственной гравитации, внутренним полем давления и полем ускорений частиц [17, 18]. Функции поля вычисляются в предположении, что в системе отсутствует общее вращение частиц, они движутся хаотически и потому общие векторные потенциалы полей в среднем стремятся к нулю.

Уравнение для гравитационного скалярного потенциала внутри сферы и его решение в пределе специальной теории относительности имеют следующий вид [2]:

 

,                                                          (1)

 

.

 

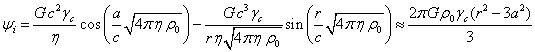В (1) фактор Лоренца частиц ,  – средняя скорость движения произвольной частицы внутри сферы,  – фактор Лоренца в центре сферы,  – скорость света,  – гравитационная постоянная,  – коэффициент поля ускорений, – плотность массы частицы в сопутствующей частице системе отсчёта,  – радиус сферы, индекс  отличает внутренний гравитационный скалярный потенциал  от внешнего потенциала , который генерирует сфера за своими пределами при . Как потенциал , так и  являются функциями текущего радиуса  внутри сферы и не зависят от угловых переменных.

 

Зависимость  от радиуса была найдена в [1]:

 

.                            (2)

 

Именно благодаря тому, что в (2) в выражении для фактора Лоренца присутствует синус, в решении (1) для  также появляются периодические функции. Приблизительные выражения в правой части (1) и (2) возникают, если взять первые члены разложения периодических функций с учётом малости их аргумента.  Как видно, выражение для  совпадает лишь в первом приближении с классическим выражением для скалярного потенциала внутри однородной сферы в правой части (1), что является следствием различия релятивистской и классической однородных систем.

Для внешнего гравитационного потенциала  неподвижной сферы, наполненной движущимися частицами, получается следующее:

 

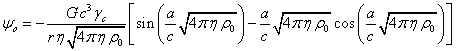.              (3)

 

По мере увеличения текущего радиуса  данный потенциал стремится к нулю. Кроме этого, на поверхности сферы при  внешний гравитационный потенциал   (3) точно совпадает с внутренним гравитационным потенциалом  в (1).

Далее будем использовать массу  как произведение плотности массы  на объём сферы . Однако фактически гравитационное поле за пределами сферы определяется массой , равной [1]:

 

(4)

 

Масса  представляет собой сумму инвариантных масс всех частиц системы, которая оказывается равной гравитационной массе системы . С учётом определения массы  из (3) следует:

 

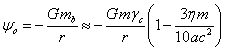.                                          (5)

 

Поскольку после усреднения по достаточному количеству частиц внутренний векторный гравитационный потенциал  и внешний векторный гравитационный потенциал  системы равны нулю из-за хаотического движения множества частиц, действующая напряжённость  гравитационного поля внутри системы и напряжённость поля  снаружи системы фактически определяются только через градиент соответствующего скалярного потенциала. С учётом (1) и (3) для напряжённостей получается следующее [1]:

 

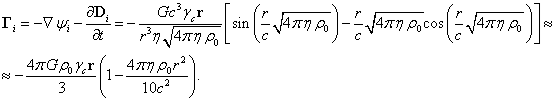
(6)

 

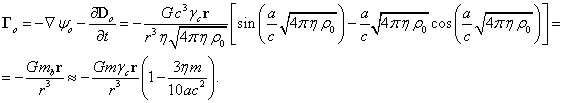
(7)

 

Поле кручения, имеющее в ковариантной теории гравитации то же значение, что и гравитомагнитное поле в гравитоэлектромагнетизме, и подобное по смыслу магнитному полю в электромагнетизме, в среднем равно нулю как внутри, так и снаружи рассматриваемой системы:

 

,                      .                               (8)

 

Напряжённость гравитационного поля  и поле кручения  в совокупности составляют тензор гравитационного поля  внутри системы, а величины  и  составляют этот же тензор за пределами системы. Поскольку все выражения в ковариантной теории гравитации выводятся из принципа наименьшего действия  аналогично тому, как это делается для электромагнитного поля в искривлённом пространстве-времени, тензор гравитационного поля по своей форме подобен тензору электромагнитного поля [19]. Соответственно, гравитационное поле рассматривается как векторное поле, а ковариантная теория гравитации представляет собой векторно-тензорную теорию с учётом метрики и космологической константы.

 

3  Энергия частиц в поле и энергия самого поля

В [18] был найден гамильтониан системы из частиц с учётом четырёх действующих в системе полей, включая поле ускорений, гравитационное поле, электромагнитное поле и поле давления, и было показано, что для стационарной системы в искривлённом пространстве-времени гамильтониан точно равен релятивистской энергии системы. Для энергии было найдено следующее:

 

                         (9)

 

 

 

где  – скалярные потенциалы поля ускорений, гравитационного поля, электрического поля и поля давления, соответственно;  – плотность заряда частицы в сопутствующей частице системе отсчёта;  – временная компонента 4-скорости произвольной частицы;  – гравитационный тензор;  – магнитная постоянная;  – электромагнитный тензор;  – тензор ускорений;  – коэффициент поля давления;  – тензор поля давления;  – движущийся инвариантный 3-объём, выражаемый через произведение  дифференциалов пространственных координат, и через квадратный корень  из детерминанта  метрического тензора, взятого с отрицательным знаком.

 

В выражении для энергии (9) первый интеграл связан с энергиями частиц в скалярных потенциалах полей, а второй интеграл содержит четыре тензорных инварианта, каждый из которых отражает энергию соответствующего поля.

Вычислим в пределе специальной теории относительности энергию частиц в гравитационном поле системы, в которой гравитационный векторный потенциал и поле гравитационного кручения в среднем равны нулю. В этом случае  и энергия частиц определяется как интеграл по объёму от произведения эффективной плотности массы внутри сферы  на внутренний скалярный потенциал . С учётом (1-2) имеем:

 

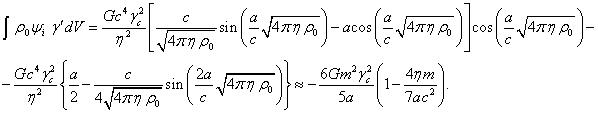
(10)

 

 

Вычислим теперь интеграл по объёму от тензорного инварианта гравитационного поля, отдельно для поля внутри и снаружи сферы. Интеграл от тензорного инварианта выражается через напряжённость гравитационного поля  и поле кручения , входящих в тензор гравитационного поля :

 

.                                (11)

 

В таком виде данный интеграл входит в энергию системы (9) и задаёт там вклад гравитационного поля. Подставляя сюда (6-8), находим:

 

 

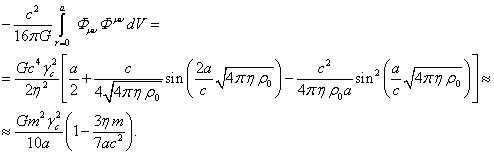
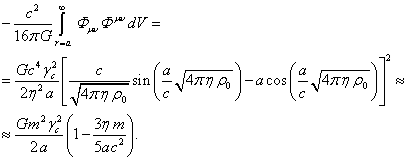
(12)

 

 

Мы можем просуммировать интегралы в (12), то есть вычислить интеграл от тензорного инварианта по всему объёму, занимаемому полем, и затем сравнить результат с (10). Получается следующее:

 

(13)

 

Согласно (13), интеграл от тензорного инварианта по модулю в два раза меньше, чем энергия частиц в гравитационном потенциале.

 

4  Тензор энергии-импульса

Если подставить (13) в энергию (9), то видно, что энергия гравитационного поля в виде тензорного инварианта вычитается из энергии частиц в гравитационном потенциале, так что полная гравитационная энергия системы становится равной половине энергии частиц в гравитационном потенциале и в таком виде делает вклад в релятивистскую энергию системы. То же самое следует и для электрического поля рассматриваемой системы, если исходить из подобия уравнений обоих полей. Действительно, электростатическая энергия также вычисляется как половина энергии частиц в электрическом потенциале.

Полную гравитационную энергию системы для рассматриваемой системы можно оценить ещё с помощью тензора энергии-импульса гравитационного поля, определяемого по формуле [9], [12], [19]:

 

,

 

где  есть метрический тензор.

 

В пределе специальной теории относительности временная компонента данного тензора равна:

 

.

 

Если учесть, что в рассматриваемой системе поле кручения  полагается равным нулю, то интеграл по объёму от  будет лишь знаком отличаться от интеграла тензорного инварианта в (11). Поэтому с учётом (13) полную гравитационную энергию системы можно выразить так:

 

.                        (14)

 

Точно также электростатическая энергия , в отсутствие магнитного поля , может быть вычислена с помощью интегрирования по объёму временной компоненты  тензора энергии-импульса электромагнитного поля:

 

.                       (15)

 

Равенства (14) и (15) нарушаются, как только в системе появляются поле кручения  и соответственно магнитное поле , например за счёт согласованного движения частиц или зарядов.

Заметим, что ни тензор энергии-импульса гравитационного поля , ни тензор энергии-импульса электромагнитного поля  не входят в выражение (9). Поэтому в общем случае использование тензоров энергии-импульса для вычисления какой-либо части энергии или всей энергии системы незаконно. Вместо этих тензоров в релятивистской энергии системы (9) присутствуют интегралы от тензорных инвариантов полей. При этом само выражение (9) выводится ковариантным способом как гамильтониан из принципа наименьшего действия, и каждое поле учитывается в лагранжиане и энергии независимо от других полей.

 

5  Гравитационное поле Вселенной

При малых размерах  и , и небольшой плотности массы , в формулах для потенциалов и напряжённостей гравитационного поля справедливы приблизительные выражения в правой части (1), (5), (6), (7). Однако если  или  достаточно велики, необходимо пользоваться точными формулами, содержащими синусы и косинусы. Возьмём для примера напряжённость гравитационного поля  за пределами тела в (7), и сделаем там обозначение: . Тогда квадратная скобка в (7) запишется как величина , так что  будет изменяться пропорционально .

Пока угол  мал, можно приблизительно ориентироваться на правую часть (7). Если же угол  увеличивать, то вначале величина  растёт, а затем начинает уменьшаться и даже меняет свой знак. Так, при  будет , при  будет , при  будет . Если решить уравнение , то можно найти угол , при котором величина  обращается в нуль. Этот угол равен приблизительно  радиан.

При  напряжённость гравитационного поля  за пределами тела в (7) меняет свой знак, так что вместо гравитационного притяжения появляется отталкивание. Мы полагаем, что условие  приводит к физически необоснованной ситуации. Таким образом, должно выполняться неравенство:

 

.                                                   (16)

 

Данное неравенство накладывает определённые ограничения на допустимые значения радиуса  физической системы и инвариантной плотности массы  в этой системе. Для примера оценим  для всей наблюдаемой Вселенной, которая на масштабе 100 Мпс и более может рассматриваться как релятивистская однородная система ввиду незначительной вариации средней плотности массы в разных точках.

Из наблюдений следует, что Вселенная очень близка к состоянию, в котором пространство-время плоское и почти Евклидово. В таком случае согласно модели Лямбда-CDM (Lambda-CDM model) суммарная плотность массы-энергии Вселенной близка к критическому значению кг/м3 [20]. Размер Вселенной можно оценить как Хаббловскую длину (Hubble length) м, где  есть параметр Хаббла. Беря  в качестве , а также  в качестве , и используя приблизительное равенство  согласно [5], находим значение   радиан.

Поскольку угол  достаточно велик, то для моделирования гравитационного поля Вселенной необходимо использовать уточнённые формулы с синусами и косинусами. Как видно из формулы для напряжённости гравитационного поля внутри системы (6), по мере увеличения текущего радиуса  до величины  и более, величины ,  и модуль напряжённости поля  вначале увеличиваются, но затем начинают уменьшаться. При граничном условии (16), то есть при  радиан, обращаются в нуль как , так и , и на границе Вселенной при некотором  гравитация стремится к нулю.

С другой стороны, наблюдательным фактом является крупномасштабная структура Вселенной, когда вещество скоплений галактик вблизи границы Вселенной формируется не в большие сферические системы, а образует сетевую структуру из скоплений галактик. Это может быть объяснено так, как будто на больших расстояниях гравитация теряет свою силу, а удалённые части Вселенной влияют слабее по сравнению с ближайшими частями, чем это требуется по закону Ньютона. Мы полагаем, что данный эффект как раз описывается формулой для напряжённости гравитационного поля внутри системы (6).

Но почему гравитация на больших расстояниях должна ослабляться? Существует модель, объединяющая в себе бесконечную вложенность материи и теорию гравитации Лесажа, и объясняющая ослабление гравитации рассеянием гравитонов на частицах космической среды [21]. В этом случае получается, что наблюдаемая Вселенная по своим масштабам достаточно близка к предельным размерам системы из звёзд и галактик, которая ещё может удерживаться от распада силой обычной гравитации.

 

6  Сильная гравитация на уровне нуклонов

Перейдём теперь от больших размеров и малой плотности массы к случаю малых размеров и большой плотности массы, и снова используем (6) для напряжённости гравитационного поля, но уже внутри протона. Протон хорошо вписывается в релятивистскую однородную модель, поскольку его средняя плотность, порядка  кг/м3 при радиусе протона м согласно [22], всего лишь в 1,5 раза меньше, чем плотность массы в центре. В качестве гравитационной постоянной на уровне атомов мы будем использовать постоянную сильной гравитации м3/(кгˑс2), полагая, что именно сильная гравитация скрепляет вещество нуклонов и других частиц [12].

Как и в (16), оценим для протона величину , используя приблизительное равенство :

 

.

 

Как видно, для протона угол  достаточно близок к предельному углу . Отсюда также следует, что необходимо использовать синусы и косинусы в (6) и (7) для описания гравитационного поля сильной гравитации внутри и снаружи протона.

Предположим теперь, что мы можем добавлять вещество внутрь объёма протона, увеличивая плотность массы протона до некоторой величины  таким образом, что угол  становится равным предельному углу . Это соответствует условию  радиан, откуда получается оценка предельной инвариантной плотности массы  кг/м3 и оценка соответствующей инвариантной плотности энергии  Дж/м3. Для того, чтобы перейти от данных инвариантных значений к наблюдаемым значениям, в первом приближении достаточно умножить инвариантные значения на фактор Лоренца  движения вещества в центре протона. Как указывается в [1], это эквивалентно тому, что вместо массы  мы используем массу , определённую в (4), и равную гравитационной массе системы .

С другой стороны, в [23, 24] в модели гравитации Лесажа была найдена плотность энергии гравитонов в вакуумном поле, равная  Дж/м3. Из равенства  получаем оценку фактора Лоренца в центре протона: . Это же следует и непосредственно из (4), где вместо  надо подставить массу протона, вместо  подставить  радиан, заменить  на радиус протона , и учесть соотношение .

Но почему же мы используем равенство ? Дело в том, что добавляя вещество внутрь протона вплоть до предельной инвариантной плотности массы  кг/м3, мы согласно (6) и (7) уменьшаем гравитационное поле на поверхности протона до нуля. Чтобы объяснить это, следует обратиться к модели гравитации Лесажа. В этой модели для возникновения силы гравитации необходим градиент потока гравитонов, падающих на пробное тело. Как правило, такой градиент возникает между двумя телами, приводя к силе гравитации, то есть к притяжению тел. Однако градиент потока гравитонов на поверхности протона исчезнет, если плотность энергии  гравитонов в вакуумном поле станет равной максимальной плотности энергии внутри протона, равной . Протон станет излучать столько же гравитонов, что и окружающий его вакуум, и станет неотличимым от вакуума по плотности энергии. В отсутствие градиента гравитонов гравитационная сила исчезает, что и отражает выражение (6) для напряжённости поля в предельном случае при .

Рассмотрим ещё одну ситуацию с участием сильной гравитации. А именно, оценим максимальный радиус  системы, удерживаемой сильной гравитацией и имеющей плотность массы, равную критической плотности кг/м3 в наблюдаемой Вселенной. Для этого аналогично (16) должно выполняться следующее условие: . Подставляя сюда приблизительное равенство , находим м. Как и в предыдущем разделе для случая Вселенной, мы можем предположить, что теперь уже сильная гравитация перестаёт работать на расстояниях более  при плотности вещества .

Разделив Хаббловскую длину м на , получим отношение . Далее мы используем коэффициент подобия  по размерам между атомным и звёздным уровнями материи, для протона и его аналога на уровне звёзд в виде нейтронной звезды. Разделив радиус типичной нейтронной звезды с массой 1,35 масс Солнца, приблизительно равный 12 км, на радиус протона, получаем . Значение  того же порядка, что и отношение . Это означает, что объект радиуса , удерживаемый в равновесии сильной гравитацией и состоящий из нуклонов или атомов водорода, подобен видимой Вселенной, удерживаемой в равновесии обычной гравитацией и состоящей из звёзд и их скоплений.

В общем случае, если в условии  увеличивать плотность массы , то соответственно уменьшается предельный размер  объекта, для которого вычисляется напряжённость гравитационного поля в (6), как для сильной, так и для обычной гравитации. При размерах, превышающих , сильная гравитация перестаёт работать в космологическом пространстве. Обычная гравитация намного слабее, чем сильная гравитация, но зато диапазон действия обычной гравитации в космологическом пространстве намного больше. Таким образом, сильная гравитация при размерах, превышающих , исчезает не до конца – вместо неё остаётся и действует обычная гравитация. Однако действие обычной гравитации также ограничено, при некотором м она начинает уменьшаться, как это показано в предыдущем разделе. Соответственно, при таких больших размерах обычная гравитация должна будет замениться на какую-то другую, более слабую гравитацию с большим радиусом действия.

 

7  Нейтронная звезда

В предыдущем разделе была получена оценка фактора Лоренца в центре протона: . Аналогично можно подсчитать фактор Лоренца для частиц в центре типичной нейтронной звезды с массой 1,35 масс Солнца, радиусом  км и средней плотностью  кг/м3. Для звезды нужно учесть соотношение  и угол  радиан. Подставляя теперь в (4) массу звезды вместо ,  вместо ,  вместо , и заменяя  на радиус звезды , находим . Это позволяет вычислить кинетическую энергию протона  как некоторой типичной частицы, движущейся в центре нейтронной звезды, и с помощью равенства  , где  – постоянная Больцмана,  – масса протона, оценить температуру в центре звезды: К. Ранее данная температура вычислялась в [5] с помощью предполагаемого из расчётов других авторов хода плотности массы внутри звезды, и там было найдено К. Указанные значения центральных температур можно считать верхним пределом, справедливым для момента образования звезды. В этот короткий промежуток времени звезда находится ещё в горячем состоянии, нуклоны в её веществе движутся хаотически и справедлив описанный выше подход. Следовательно, фактор Лоренца  для частиц в центре является предельным значением для вещества нейтронной звезды. Это же относится и к фактору Лоренца  в центре протона.

 

8  Заключение

Одним из выводов в [25] было то, что энергия покоящегося вещества однородного тела в виде сферы в собственном статическом гравитационном поле по модулю превышает в два раза энергию самого гравитационного поля. Что произойдёт, если сделать переход к релятивистской однородной системе, в которой частицы вещества не стоят на месте, а движутся с лоренц-фактором (2), зависящим от текущего радиуса? Ответ на этот вопрос следует из (13) – как в классическом, так и в релятивистском случае соотношение между энергией частиц в поле и энергией самого поля остаётся неизменным.

В разделе 4 мы показали, что в общем случае знания тензоров энергии-импульса полей недостаточно для вычисления релятивистской энергии, а значит и соответствующей инертной массы системы. Таким образом ковариантная теория гравитации существенно отличается от общей теории относительности, где допускается вычисление энергии и массы путём интегрирования по объёму суммарного тензора энергии-импульса системы [26].

Применение выражений для потенциалов и напряжённостей гравитационного поля (1), (5), (6), (7) к наблюдаемой Вселенной и к протону позволяет уточнить некоторые особенности этих объектов. Оказывается, что данные объекты находятся в состояниях, близких к предельно возможным, что требует точного учёта эффектов релятивистской однородной модели в отношении гравитационного поля. Возможны два крайних случая – максимально большие размеры объекта  и малая плотность массы  (Вселенная), и предельно большая плотность массы при небольших размерах (протон, нейтронная звезда). В (16) представлено условие  радиан, которому должны подчиняться размеры и плотность массы объекта, если данный объект удерживается в равновесии собственным гравитационным полем. Это даёт возможность оценить радиус действия сильной и обычной гравитации в космологическом пространстве. С помощью (4) удаётся также вычислить максимально возможный фактор Лоренца частиц вещества в центре нейтронной звезды и в центре протона.

Таким образом, полученные результаты в отношении зависимостей гравитационного поля внутри и снаружи тел хорошо согласуются с выводами теории гравитации Лесажа, с бесконечной вложенностью материи, с сильной гравитацией на уровне нуклонов и с представлением о динамическом силовом вакуумном поле.

На следующем этапе планируется связать выводы ковариантной теории гравитации и результаты модели Эйнштейна с космологической постоянной  (Einstein-Λ model), описанные например  в [27] и в [28], в отношении энергии частиц физической системы.

 

Ссылки

[1]         Fedosin, S.G. Relativistic Energy and Mass in the Weak Field Limit. Jordan Journal of Physics. 8 (1), 1-16 (2015).

[2]         Fedosin, S.G. The Integral Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based on the Pressure Field and Acceleration Field. American Journal of Modern Physics. 3 (4), 152-167 (2014). Doi:10.11648/j.ajmp.20140304.12.

[3]         Денисов, В. И.; ЛогуновЮ А. А. Инертная масса, определенная в общей теории относительности, не имеет физического смысла. ТМФ, 1982, том 51, номер 2, 163-170; Denisov V. I., Logunov A. A. The inertial mass defined in the general theory of relativity has no physical meaning. Theoretical and Mathematical Physics, Volume 51, Issue 2, pp. 421-426 (1982). http://dx.doi.org/10.1007/BF01036205.

[4]         Khrapko, R. I.  The Truth about the Energy-Momentum Tensor  and  Pseudotensor. ISSN 0202-2893, Gravitation and Cosmology, Vol. 20, No. 4, pp. 264-273 (2014). Pleiades Publishing, Ltd., 2014. http://dx.doi.org/10.1134/S0202289314040082;  Храпко Р.И. Правда о тензоре и псевдотензоре энергии-импульса.

[5]         Fedosin, S.G. Estimation of the physical parameters of planets and stars in the gravitational equilibrium model. Canadian Journal of Physics. 94 (4), 370-379 (2016). Doi:10.1139/cjp-2015-0593.

[6]         Fedosin, S.G. The virial theorem and the kinetic energy of particles of a macroscopic system in the general field concept. Continuum Mechanics and Thermodynamics, Vol. 29, Issue 2, pp. 361-371 (2016). https://dx.doi.org/10.1007/s00161-016-0536-8.

[7]         Fedosin, S.G. Two components of the macroscopic general field. Reports in Advances of Physical Sciences, Vol. 1, No. 2, 1750002, 9 pages (2017). http://dx.doi.org/10.1142/S2424942417500025. // Две компоненты макроскопического общего поля.

[8]         Fedosin, S.G. The Metric Outside a Fixed Charged Body in the Covariant Theory of Gravitation. International Frontier Science Letters, Vol. 1, No. 1 , pp. 41-46 (2014). http://dx.doi.org/10.18052/www.scipress.com/ifsl.1.41. // Метрика за пределами неподвижного заряженного тела в ковариантной теории гравитации.

[9]         Fedosin, S. The physical theories and infinite hierarchical nesting of matter, Volume 2, LAP LAMBERT Academic Publishing, pages: 420, ISBN-13: 978-3-659-71511-2. (2015).

[10]     Fedosin, S.G. The Pioneer Anomaly in Covariant Theory of Gravitation. Canadian Journal of Physics, Vol. 93, No. 11, pp. 1335-1342 (2015). http://dx.doi.org/10.1139/cjp-2015-0134. // Эффект "Пионера" в ковариантной теории гравитации.

[11]     Einstein, A. Gibt es eine Gravitationswirkung die der elektrodynamischen Induktionswirkung analog ist? Vierteljahrsschrift für gerichtliche Medizin und öffentliches Sanitätswesen, 44: 37-40 (1912).

[12]     Fedosin, S.G. Fizika i filosofiia podobiia: ot preonov do metagalaktik, written in Perm, (1999-06-09) 544 pages. ISBN 5-8131-0012-1.

[13]     Sharif M. and Yousaf Z. Role of adiabatic index on the evolution of spherical gravitational collapse in Palatini f(R) gravity. Astrophys. Space Sci. 355, 317-331 (2015). Doi:10.1007/s10509-014-2179-1.

[14]     Yousaf Z. and Zaeem ul Haq Bhatti M. Cavity evolution and instability constraints of relativistic interiors. Eur. Phys. J. C. 76, 267 (2016). http://dx.doi.org/10.1140/epjc/s10052-016-4109-6.

[15]     Yousaf Z., Zaeem ul Haq Bhatti M. and Farwa U. Stability of compact stars in αR2+β(RγδTγδ) gravity. Mon. Not. R. Astron. Soc. Vol. 464 (4), pp. 4509-4519 (2017). DOI: 10.1093/mnras/stw2698.

[16]     Zaeem ul Haq Bhatti M., Yousaf Z. and Hanif S. Role of f(T) gravity on the evolution of collapsing stellar model. Phys. Dark Universe. Vol. 16, pp. 34-40 (2017). DOI:10.1016/j.dark.2017.04.003.

[17]     Fedosin, S.G. The Procedure of Finding the Stress-Energy Tensor and Equations of Vector Field of Any Form. Advanced Studies in Theoretical Physics. 8 (18), 771-779 (2014). Doi:10.12988/astp.2014.47101. // Процедура для нахождения тензора энергии-импульса и уравнений векторного поля любого вида.

[18]     Fedosin, S.G. About the cosmological constant, acceleration field, pressure field and energy. Jordan Journal of Physics. 9 (1), 1-30 (2016).

[19]     Fedosin, S.G. The Principle of Least Action in Covariant Theory of Gravitation. Hadronic Journal, Vol. 35, No. 1, pp. 35-70 (2012). // Принцип наименьшего действия в ковариантной теории гравитации.

[20]     C. Patrignani et al. (Particle Data Group). The Review of Particle Physics. Chin. Phys. C, 40, 100001 (2016) and 2017 update.

[21]     Fedosin S.G. Cosmic Red Shift, Microwave Background, and New Particles. Galilean Electrodynamics, Vol. 23, Special Issues No. 1, pp. 3-13 (2012). // Красное смещение и космическое микроволновое фоновое излучение как следствие взаимодействия фотонов с новыми частицами.

[22]     Fedosin S.G. The radius of the proton in the self-consistent model. Hadronic Journal, Vol. 35, No. 4, pp. 349-363 (2012). // Радиус протона в самосогласованной модели.

[23]     Fedosin S.G. The graviton field as the source of mass and gravitational force in the modernized Le Sage’s model. Physical Science International Journal, ISSN: 2348-0130, Vol. 8, Issue 4, pp. 1-18 (2015). http://dx.doi.org/10.9734/PSIJ/2015/22197. // Поле гравитонов как источник гравитационной силы и массы в модернизированной модели Лесажа.

[24]     Fedosin S.G. The charged component of the vacuum field as the source of electric force in the modernized Le Sage’s model. Journal of Fundamental and Applied Sciences, Vol. 8, No. 3, pp. 971-1020 (2016). Doi: 10.5281/zenodo.845357. // Заряженная компонента вакуумного поля как источник электрической силы в модернизированной модели Лесажа.

[25]     Fedosin S.G. The Hamiltonian in Covariant Theory of Gravitation. Advances in Natural Science. 5 (4), 55-75 (2012). Doi:10.3968%2Fj.ans.1715787020120504.2023.

[26]     Fock V. A. (1964). "The Theory of Space, Time and Gravitation". Macmillan. Фок В.А. Теория пространства, времени и гравитации. 2-е издание. – М.: Физматгиз, 1961. –568 с.

[27]     Yousaf Z. Spherical relativistic vacuum core models in a Λ-dominated era. Eur. Phys. J. Plus. 132, 71 (2017). DOI: 10.1140/epjp/i2017-11336-9.

[28]     Yousaf Z. Stellar filaments with Minkowskian core in the Einstein-Λ gravity. Eur. Phys. J. Plus. 132, 276 (2017). DOI: 10.1140/epjp/i2017-11547-0.

 

Источник: http://sergf.ru/gpr.htm

На научный сайт