Reports
in Advances of Physical Sciences, Vol.
1, No. 2, 1750002, 9 pages (2017). http://dx.doi.org/10.1142/S2424942417500025
Две
компоненты макроскопического общего поля
Федосин
Сергей Григорьевич
г.
Пермь, Пермский край, Россия
E-mail: intelli@list.ru
Общее поле, содержащее в себе все макроскопические поля, разделяется на массовую компоненту, источником которой является массовый 4-ток, и на зарядовую компоненту, источником которой является зарядовый 4-ток. Массовая компонента включает в себя гравитационное поле, поле ускорений, поле давления, поле диссипации, поля сильного и слабого взаимодействия, другие векторные поля. Зарядовая компонента общего поля представляет собой электромагнитное поле. С помощью принципа наименьшего действия выводятся уравнения полей, уравнение движения вещества в общем поле, уравнение для метрики, энергия и импульс системы из вещества и его полей, калибруется космологическая постоянная. Компоненты общего поля связываются с соответствующими компонентами вакуумного поля таким образом, что вакуумное поле порождает общее поле на макроскопическом уровне.
Ключевые слова: общее поле; вакуумное поле; поле ускорений; поле
давления; поле диссипации.
1.
Введение
Большинство
теорий единого поля, такие как теория всего, теории Великого объединения,
петлевая квантовая гравитация, теория струн и ряд других, опираются на
квантовый подход и имеют своей целью объединить фундаментальные взаимодействия
на уровне элементарных частиц. Известны попытки объединить физические поля и на
макроскопическом уровне, для достаточно массивных тел, где гравитация
становится определяющим взаимодействием. При этом используются самые различные
подходы. Так, в теории Калуцы-Клейна [1-2] к обычному
четырёхмерному пространству-времени были добавлены до сих пор необнаруженное
пятое измерение и некоторое скалярное поле для того, чтобы вывести как
уравнения гравитационного поля, так и уравнения, эквивалентные уравнениям
Максвелла. Теории единого поля в четырёхмерном и многомерном пространствах
были рассмотрены в ряде основополагающих работ [3-6].
В [7] предполагается, что вектор напряжённости и соленоидальный вектор единого поля состоит из суммы напряжённостей и соленоидальных векторов всех известных полей с соответствующими коэффициентами. При этом единое поле подчиняется уравнениям Максвелла, в которых источником напряжённости единого поля является сумма произведений плотностей заряда полей на некоторые коэффициенты, а источником соленоидального вектора единого поля является сумма произведений токов с некоторыми коэффициентами. В результате каждый 4-ток, связанный с тем или иным полем, вносит свой вклад в векторные компоненты единого поля. Недостатком данного подхода является отсутствие ковариантности представленных уравнений единого поля.
Концепция общего силового векторного поля, в которое
были включены электромагнитное и гравитационное поле, поле ускорений, поле
давления, поле диссипации, поле сильного взаимодействия, поле слабого
взаимодействия, и другие векторные поля, была представлена в [8]. Особенностью этого подхода является то, что
4-потенциал общего поля задаётся суммой 4-потенциалов всех частных полей.
Исключением является 4-потенциал электромагнитного поля, который входит в сумму
4-потенциалов с коэффициентом, равным отношению 
плотности заряда к плотности
массы. Полученные из принципа наименьшего действия уравнения полностью
описывают общее поле и его взаимодействие с веществом.
Некоторым ограничением
данного подхода является то, что отношение плотностей в рассматриваемой
физической системе предполагается неизменным. Далее мы представляем более
полную и универсальную теорию, в которой общее поле раскладывается на две
основные компоненты. Источником первой компоненты является массовый 4-ток 
, который генерирует такие векторные поля, как гравитационное поле, поле ускорений, поле давления,
поле диссипации, макроскопические поля сильного и слабого взаимодействий.
Второй компонентой общего поля является электромагнитное поле, источником
которого является зарядовый 4-ток 
.
Особенностью макроскопических полей
является то, что их описание может не совпадать с описанием поля на
микроскопическом уровне. Так, общая теория относительности (ОТО) считается
вполне удовлетворительной теорией, хотя никак не связана с квантовой теорией
гравитации и не вытекает из неё. Из набора аксиом ОТО следует, что
гравитационное поле описывается метрическим тензором и псевдотензором энергии-импульса,
которые определяются на основе геометрии пространства-времени [9]. Данный
подход, многократно подтверждённый экспериментами, приводит к представлению о
том, что гравитационное поле является тензорным (метрическим) полем. Таким
образом гравитация в ОТО не сводится к векторному полю, а тензорный характер
поля непосредственно обуславливает отсутствие в гравитационном излучении
дипольной компоненты.
Для описания гравитации мы используем
аксиоматически построенную ковариантную теорию гравитацию (КТГ) с векторным
4-потенциалом, гравитационным тензором и тензором энергии-импульса [10]. При
этом гравитация является самостоятельным физическим полем, не требующим полного
сведения к геометрии. В КТГ для каждого отдельного тела допускается дипольное
гравитационное излучение. Поскольку для обнаружения эффектов гравитации
требуется как минимум два тела, их дипольные излучения взаимно уничтожаются, и
система тел излучает всегда квадрупольным образом либо более высокими мультиполями. Таким образом в отношении излучения тензорность поля в ОТО не противоречит векторности
поля в КТГ. Различие исходных постулатов обеих теорий не мешает описать в КТГ
все стандартные эффекты ОТО [10], представить выражение для метрического
тензора [11], объяснить эффект Пионера [12], а для макроскопических систем
рассмотреть вклад гравитационного поля в уравнении Навье-Стокса [13], в оценке параметров космических тел [14] и в
теореме вириала [15].
Хотя сильное и слабое взаимодействия на уровне
элементарных частиц описывается обычно векторными неабелевыми
полями (нелинейными полями Янга-Миллса с самодействием), на макроскопическом
уровне мы считаем возможным описывать эти взаимодействия обычными
четырёхмерными векторными полями. Действительно, квантовые эффекты на
макроуровне как правило стираются за счёт огромного количества
взаимодействующих частиц так же, как и вклады в поля от отдельных частиц,
важными становятся лишь средние значения полей. В результате для описания
макроскопических полей достаточно использовать простейшие схемы в виде
уравнений для 4-потенциалов максвелловского типа, по
крайней мере в качестве первого приближения.
2. Функция действия и
её вариация
Мы считаем, что
две компоненты общего поля и соответствующие им 4-токи являются в достаточной
степени независимыми друг от друга. Это позволяет применить принцип
суперпозиции в принципе наименьшего действия, так что каждая компонента
самостоятельно вносит свой вклад в лагранжиан. Функция действия для непрерывно
распределённого вещества, находящегося в общем поле (как в собственном, так и
во внешнем поле) в искривленном пространстве-времени
аналогично [8], [16] приобретает следующий вид:
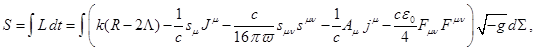(1)
где 
– лагранжиан, 
– скалярная кривизна, 
– космологическая
постоянная, 
– 4-вектор массового
тока, 
– плотность массы
точечной частицы вещества в сопутствующей частице системе отсчёта, 
– 4-скорость точечной
частицы, 
– скорость света, 
– 4-потенциал массовой компоненты общего
поля, описываемый через скалярный потенциал
и векторный потенциал 
этого поля, 
– тензор массовой
компоненты общего поля, 
– 4-потенциал электромагнитного поля,
задаваемый с помощью скалярного потенциала
и векторного потенциала 
, 
– 4-вектор зарядового
тока, 
– плотность заряда точечной частицы в сопутствующей частице
системе отсчёта, 
– электрическая
постоянная, 
– электромагнитный
тензор, 
и 
считаются постоянными
коэффициентами.
В (1) первый член под знаком интеграла пропорционален плотности
энергии, связанной с кривизной и с космологической постоянной. Второй член
задаёт плотность энергии массового 4-тока при 4-потенциале 
. Аналогично этому четвёртый член для
электромагнитного поля определяет плотность энергии зарядового 4-тока при
4-потенциале 
. Третий и пятый члены связаны соответственно с плотностью энергии массовой компоненты общего поля и с плотностью
энергии электромагнитного поля, и
не исчезают даже в пустом пространстве за пределами вещества.
4-потенциал массовой компоненты общего поля определяется как
обобщённая 4-скорость в виде суммы 4-потенциалов соответственно гравитационного поля [17], поля ускорений и поля давления [18], поля диссипации [13], полей сильного и слабого взаимодействий
[8]:
. (2)
Из (2) и компонент 4-потенциала следует, что скалярный
и векторный потенциалы массовой компоненты общего
поля являются суммами соответствующих скалярных и векторных потенциалов
рассматриваемых нами полей.
Тензор массовой компоненты общего поля 
задаётся как 4-ротор 4-потенциала . С учётом (2) тензор выражается через сумму
тензоров соответственно гравитационного поля, поля ускорений, поля
давления, поля диссипации, полей сильного и слабого взаимодействий:
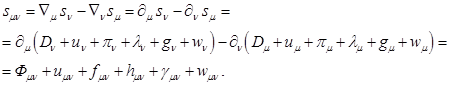(3)
Функция действия с членами,
аналогичными членам в (1), варьировалась во множестве работ, например, в [16], [19]. Для
вариации функции действия можно записать:
, (4)
,
,
,
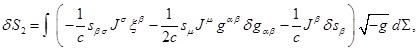
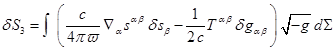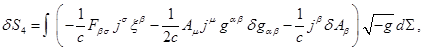
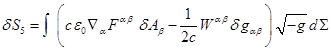где 
есть тензор Риччи, 
– вариация
метрического тензора, 
– инвариантный
4-объём, выражаемый через дифференциал временной координаты 
, через произведение 
дифференциалов
пространственных координат, и через квадратный корень 
из детерминанта 
метрического тензора,
взятого с отрицательным знаком,
представляет собой
вариацию 4-координат [19, 20], вследствие которой возникают вариации массового 4-тока 
и зарядового 4-тока 
, 
– вариация
4-потенциала массовой компоненты общего поля, 
– вариация 4-потенциала электромагнитного поля.
Тензор 
энергии-импульса массовой компоненты общего поля и тензор 
энергии-импульса электромагнитного поля определяются выражениями:
.
.
Свойства тензора энергии-импульса описаны в [8].
3. Уравнения для полей и движения вещества
Суммируя в (4) члены при одинаковых вариациях и
приравнивая эти суммы к нулю, получаем соответствующие уравнения. В частности,
находим уравнения для массовой компоненты
общего поля с источником поля в виде массового 4-тока, а также уравнения этого
поля без источников, вытекающие из антисимметрии тензора 
:
,
. (5)
Уравнения электромагнитного поля имеют стандартный вид:
,
. (6)
Применение к уравнениям поля с
источниками в (5) и (6) ковариантной производной 
даёт уравнения
непрерывности для 4-токов в искривлённом пространстве-времени:
, 
.
Условие калибровки 4-потенциалов:
, 
.
Уравнения
движения получаются из (4) путём приравнивания нулю суммы членов, содержащих вариацию
. С учётом (3) имеем:
. (7)
Тензорное произведение 
можно выразить через
4-ускорение 
с помощью оператора
производной по собственному времени [18]:
.
С учётом этого (7) превращается в четырёхмерное уравнение движения вязкого сжимаемого заряженного вещества [13], с добавкой от плотности 4-сил, возникающих от сильного и слабого взаимодействий:
.
Поскольку из
свойств тензоров для соответствующих 4-сил справедливы соотношения:
,
,
то уравнение
движения (7) можно записать через дивергенцию суммы тензоров энергии-импульса:
. (8)
4. Уравнение для
метрики и релятивистская энергия
Уравнение для метрики получается приравниванием к нулю суммы
членов, содержащих в (4) вариацию 
:
(9)
Свернём это
уравнение путём умножения на метрический тензор, учитывая, что 
, 
, 
, 
:
. (10)
Подстановка (10) в (9) упрощает уравнение для метрики:
, (11)
Решение уравнения (11) было представлено в [11] для случая гравитационного и
электромагнитного полей, при этом коэффициент 
должен определяться из
сравнения с экспериментом.
Действуя как в [18], запишем
условие калибровки космологической постоянной 
. С учётом (2) получается следующее:
. (12)
В полной физической
системе учитываются все источники поля в виде 4-токов, и все поля в такой
системе, действующие на вещество, имеют внутреннее происхождение. Согласно
(12), для каждого элемента вещества получается своё значение 
, зависящее от 4-потенциалов двух компонент общего поля, и
соответствующих им 4-токов. Мы можем предположить, что начальным состоянием
рассматриваемой системы было рассеянное в пространстве неподвижное вещество
малой плотности в виде отдельных частиц. Затем это вещество под действием гравитации разбилось на
фрагменты и было собрано в более плотную систему. В таком случае постоянная отражает суммарную
плотность энергии вещества в собственных полях в начальном состоянии.
При калибровке
(12) из (10) следует связь между скалярной кривизной и космологической
постоянной:
.
(13)
После применения
ковариантной производной 
ко всем членам в (11),
с учётом (8) и равенства 
как свойства тензора
Эйнштейна, остаётся равенство 
или эквивалентное ему
равенство 
. Из (13) следует тогда равенство 
, а если учесть (12), это приводит к равенству, которое
должно соблюдаться внутри вещества:
.
Энергию системы,
состоящей из вещества и полей, можно вычислить тем же способом, что и в [18]. С
учётом калибровки (12) для энергии получается:
.
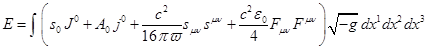Энергия зависит
только от временных компонент 4-потенциалов и 4-токов и не
зависит от их пространственных компонент. Для 4-импульса системы имеем: 
, где 
и 
обозначают импульс системы и скорость движения
центра масс системы.
5. Заключение
Все известные поля мы разделяем на две группы. В первую
группу входят гравитационное поле, поле
ускорений, поле давления, поле диссипации, поле сильного взаимодействия, поле
слабого взаимодействия, и другие векторные поля, источником которых является
массовый 4-ток 
. Данная группа полей предстаёт как массовая компонента
общего поля. Второй (зарядовой) компонентой общего поля оказывается электромагнитное
поле, источником которого является
зарядовый 4-ток 
. Все уравнения для полей, тензоры энергии-импульса,
уравнение движения вещества, уравнение для метрики и релятивистская энергия
находятся из принципа наименьшего действия в ковариантном виде. Как было
показано в [21, 22], потенциалы и напряжённости всех полей подчиняются
волновому уравнению и потому в ряде случаев имеют одинаковую зависимость от
координат и времени. При этом потенциалы полей, тензоры полей и тензоры
энергии-импульса могут быть найдены по стандартной процедуре [23].
Обе компоненты общего поля связаны друг с другом не только в уравнениях, но и в реальных процессах. Так, зарядовый 4-ток всегда сопровождается соответствующим массовым 4-током носителей заряда, каждый из которых имеет собственную массу и скорость движения. В свою очередь, гравитационное поле, поле давления и другие поля могут порождать некоторый зарядовый 4-ток. Примером является возникновение магнитных полей в космических объектах в электрокинетической модели [24], за счёт механизма разделения зарядов и их вращения вместе с веществом объектов.
Разделение общего поля на две компоненты наиболее естественно
объясняется в модернизированной модели Фатио-Лесажа [25, 26],
в которой вакуумное поле также имеет две компоненты – поле гравитонов и поле
заряженных частиц (праонов). При этом один и тот же физический механизм может
быть ответственен как за возникновение гравитационной силы [27] посредством действия поля
гравитонов, так и за возникновение электромагнитного взаимодействия [28, 29]
под действием поля заряженных частиц.
В данной модели потоки мельчайших частиц вакуумного поля пронизывают
все тела и осуществляют электромагнитное и гравитационное взаимодействие
между удалёнными друг от друга частицами вещества. Возникающие вследствие этого
различные взаимодействия между частицами вещества могут быть представлены как
действие поля давления, поля ускорений, поля диссипации и других полей,
входящих в общее поле. Так компоненты вакуумного поля приводят к компонентам
общего поля.
Единый механизм
взаимодействия вакуумного и общего полей позволяет объяснить причину того, что
все частные поля как компоненты общего поля могут быть описаны одинаковыми
уравнениями максвелловского типа. Например, путём
решения волновых уравнений для 4-потенциалов поля ускорений и поля давления
удаётся найти температуру и давление внутри звёзд и планет [14] в согласии с
расчётами, выполненными другими методами. Указанный подход для четырёх частных
полей был успешно применён для оценки тремя различными способами кинетической
энергии частиц макроскопической системы [15].
Список использованных источников
1.
Kaluza T. Zum Unitätsproblem
in der Physik. Sitzungsber. Preuss. Akad. Wiss. Berlin. (Math. Phys.) pp. 966-972 (1921).
2.
Klein
O. Quantentheorie und fünfdimensionale
Relativitätstheorie. Zeitschrift
für Physik
A, Vol. 37 (12),
pp. 895-906 (1926).
3. Hilbert D. Die Grundlangen
der physic (Erste Mitteilung),
Nachr. Koenigl. Gesellsch Wiss. Goettingen, Math-Phys. Kl., pp. 395-407 (1915).
4. Eddington A.S. A generalisaton
of Weyl’s theory of the electromagnetic and gravitational field. Proc. R. Soc.
London, A 99, pp. 104-122 (1921).
5. Weyl H. Raum,
Zeit und Matter, 4 edition, Springer, Berlin (1923).
6. Einstein A. Riemann-Geometrie mit Auufrechterhaltung
des Begriffs des Fernparallelismus.
Sitzungsber. Preuss. Akad. Wiss. Vol. 17, 217-221 (1928).
7.
Науменко Ю. В. Единая теория
векторных полей (от электродинамики Максвелла к единой теории поля). Армавир, Армавирское
полиграф-предприятие, 2006.
8.
Fedosin S.G. The concept of the general force vector field. OALib Journal,
Vol. 3, pp. 1-15 (2016). doi: 10.4236/oalib.1102459; Концепция общего силового векторного поля.
9. Fedosin S.G. The General Theory of Relativity, Metric Theory of Relativity and Covariant Theory of Gravitation. Axiomatization and Critical Analysis. International Journal of Theoretical and Applied Physics (IJTAP), Vol. 4, No. I , pp. 9-26 (2014); Общая теория относительности, метрическая теория относительности и ковариантная теория гравитации. Аксиоматизация и критический анализ.
10. Федосин С.Г. Физические теории и бесконечная вложенность материи. – Пермь, 2009-2011, 635 стр., Табл. 21, Ил.41, Библ. 293 назв. ISBN 978-5-9901951-1-0.
11.
Fedosin S.G. The Metric Outside a Fixed Charged Body in the Covariant Theory of
Gravitation. International Frontier Science Letters (IFSL), ISSN:
2349 – 4484, Vol. 1, No. 1, pp. 48- 55 (2014). doi: 10.18052/www.scipress.com/ifsl.1.41; Метрика за пределами неподвижного заряженного тела в ковариантной теории гравитации.
12.
Fedosin S.G. The Pioneer Anomaly in Covariant
Theory of Gravitation. Canadian Journal of Physics, Vol.
93, No. 11, pp. 1335-1342 (2015). doi: 10.1139/cjp-2015-0134. // Эффект "Пионера"
в ковариантной теории гравитации.
13.
Fedosin
S.G. Four-Dimensional Equation
of Motion for Viscous Compressible and Charged Fluid with Regard to the
Acceleration Field, Pressure Field and Dissipation Field. International Journal of Thermodynamics,
Vol. 18, No. 1, pp. 13-24, (2015). doi: 10.5541/ijot.5000034003; Четырёхмерное уравнение движения вязкого сжимаемого вещества с учётом поля ускорений, поля давления и поля диссипации.
14. Fedosin S.G. Estimation of the physical parameters of planets and stars in the gravitational equilibrium model. Canadian Journal of Physics, Vol. 94, No. 4, pp. 370-379 (2016). doi: 10.1139/cjp-2015-0593. // Оценка физических параметров планет и звёзд в модели гравитационного равновесия.
15. Fedosin S.G. The virial theorem and the kinetic energy of particles of a macroscopic system in the general field concept. Continuum Mechanics and Thermodynamics, Vol. 29, Issue 2, pp. 361-371 (2016). doi: 10.1007/s00161-016-0536-8.
16. Fedosin S.G. The Principle of Least Action in Covariant Theory of Gravitation. Hadronic Journal, Vol. 35, No. 1, pp. 35-70 (2012); Принцип наименьшего действия в ковариантной теории гравитации.
17. Федосин С.Г. Физика и философия подобия от преонов до метагалактик. Пермь: Стиль-МГ, 1999, 544 стр., Табл.66, Ил.93, Библ. 377 назв. ISBN 5-8131-0012-1.
18. Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy. Jordan Journal of Physics, Vol. 9, No. 1, pp. 1-30 (2016); О космологической постоянной, поле ускорения, поле давления и об энергии.
19. Fock V. A. (1964). "The Theory of Space, Time and Gravitation". Macmillan. Фок В.А. Теория пространства, времени и гравитации. 2-е издание. – М.: Физматгиз, 1961. –568 с.
20. Dirac P.A.M. General theory of relativity. Florida State University. John Wiley & Sons, Inc., New York - London • Sydney • Toronto, 1975. Дирак П. А. М. Общая теория относительности: Пер. с англ./ Под. ред. Д. И. Блохинцева. – Пер. изд.: США, 1975. – М.: Атомиздат, 1978. – 64 с.
21. Fedosin S.G. The Integral Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based on the Pressure Field and Acceleration Field. American Journal of Modern Physics, Vol. 3, No. 4, pp. 152-167 (2014). doi: 10.11648/j.ajmp.20140304.12; Интегральный 4-вектор энергии-импульса и анализ проблемы 4/3 на основе поля давления и поля ускорений.
22. Fedosin S.G. Relativistic Energy and Mass in the Weak Field Limit. Jordan Journal of Physics, Vol. 8, No. 1, pp. 1-16 (2015); Релятивистская энергия и масса в пределе слабого поля.
23.
Fedosin S.G. The procedure of finding the stress-energy tensor and vector field
equations of any form. Advanced
Studies in Theoretical Physics, Vol. 8, pp. 771-779
(2014). doi: 10.12988/astp.2014.47101; Процедура для нахождения тензора энергии-импульса и уравнений векторного поля любого вида.
24.
Fedosin S.G. Generation of magnetic fields in
cosmic objects: electrokinetic model. Advances
in Physics Theories and Applications, Vol. 44, pp. 123-138 (2015); Возникновение магнитных полей в
космических объектах: электрокинетическая модель.
25. Sergey Fedosin, The physical theories and infinite hierarchical nesting of matter, Volume 2, LAP LAMBERT Academic Publishing, pages: 420, ISBN-13: 978-3-659-71511-2. (2015).
26.
Fedosin S.G. The force vacuum field as an alternative to the
ether and quantum vacuum. WSEAS Transactions on Applied and
Theoretical Mechanics, Vol. 10, Art. #3, pp. 31-38 (2015); Силовое вакуумное поле как альтернатива эфиру и квантовому вакууму.
27.
Fedosin S.G. The graviton field as the source of mass and gravitational force in the
modernized Le Sage’s model. Physical Science International Journal,
Vol. 8, Issue 4, pp. 1-18 (2015). doi: 10.9734/PSIJ/2015/22197; Поле гравитонов как
источник гравитационной силы и массы в
модернизированной модели Лесажа.
28.
Fedosin S.G. The charged component of the vacuum field as the source of electric
force in the modernized Le Sage’s model. Journal of Fundamental
and Applied Sciences, Vol. 8, No. 3, pp. 971-1020 (2016). doi: 10.4314/jfas.v8i3.18; Заряженная компонента вакуумного поля как источник электрической силы в
модернизированной модели Лесажа.
29.
Fedosin S.G. The substantial model of the photon. Journal of Fundamental and Applied
Sciences, Vol. 9, No. 1, pp.
411-467 (2017). doi: 10.4314/jfas.v9i1.25; Субстанциональная модель фотона.
Источник: http://sergf.ru/tc.htm