International
Frontier Science Letters, ISSN: 2349 – 4484, Vol. 1, No. I (2014), pp. 41 – 46. http://dx.doi.org/10.18052/www.scipress.com/ifsl.1.41
Метрика за пределами
неподвижного заряженного тела в ковариантной теории гравитации
Федосин Сергей Григорьевич
г. Пермь, Пермский край, Россия
E-mail: intelli@list.ru
Вычислена метрика за пределами
заряженного тела. В рамках представленного подхода показывается, что
гравитационное и электромагнитное поля в равной мере участвуют в формировании
компонент метрического тензора. При этом вклад полей в метрику оказывается
пропорциональным энергии этих полей. Из уравнений для метрики следует, что
компоненты метрического тензора определяются с точностью до двух постоянных.
Ключевые слова: метрика; статическое решение; энергия поля; ковариантная теория гравитации.
The Metric Outside a
Fixed Charged Body in the Covariant Theory of Gravitation
Sergey G. Fedosin
PO box 614088, Sviazeva
str. 22-79, Perm, Russia
E-mail: intelli@list.ru
The metric outside a charged body is calculated. As
part of the given approach it is shown that the gravitational and
electromagnetic fields are equally involved in the formation of the metric
tensor components. And the contribution of fields in the metric is proportional
to the energy of these fields. From equations for the metric it follows that
the metric tensor components are determined up to two constants.
Keywords:
metric; static solution; field energy; covariant theory of gravitation.
1. Введение
В теории гравитации метрика необходима для корректного
отображения теоретических выводов и результатов экспериментов. Представление о
метрике наиболее актуально в общей теории относительности (ОТО), в которой поле
метрического тензора играет роль гравитационного поля. В результате переход ОТО
в теорию тяготения Ньютона осуществляется всегда посредством разложения
компонент метрического тензора до главных членов разложения. Например, для
потенциала гравитационного поля получается выражение: 
, где 
является временной компонентой метрического
тензора. Каким бы малым ни было поле, в ОТО вначале необходимо найти , чтобы
затем оценить потенциал 
.
В отличие от
этого, в ковариантной теории гравитации (КТГ) метрика в слабом поле
автоматически стремится к метрике плоского пространства Минковского, при этом
уравнения гравитационного поля не изменяют свой вид ввиду ковариантной записи
уравнений. В КТГ вначале определяются скалярные потенциалы и 
гравитационного и электромагнитного полей, векторные
потенциалы полей, соответствующие этим полям тензоры, и только после этого
высчитывается метрика пространства-времени за пределами тела [1].
2. Решение уравнения для метрики
Тензорное
уравнение для метрики, найденное в [2] из принципа наименьшего действия с учётом
калибровки космологической постоянной, в смешанных индексах имеет следующий
вид:
.
(1)
За пределами
тела, где плотности массы и заряда равны нулю, скалярная кривизна 
и тензоры энергии-импульса 
поля ускорений и 
поля давления также равны нулю. Это связано с
тем, что поле ускорений описывает движение частиц тела, а поле давлений
относится к давлению частиц тела друг на друга. Оба этих поля существуют лишь в
объёме рассматриваемого тела. Равенство нулю скалярной кривизны связано с условием калибровки космологической
постоянной.
В правой
части (1) остаются два тензора энергии-импульса гравитационного 
и электромагнитного 
полей:
.
(2)
. (3)
Здесь 
– гравитационная постоянная, 
– электрическая постоянная, 
и 
являются гравитационным и электромагнитным
тензором, соответственно, 
– единичный тензор или символ Кронекера. Мы считаем, что
скорость света 
одна и та же для распространения
электромагнитного и для распространения гравитационного воздействия посредством
поля. Тензор энергии-импульса гравитационного поля в виде (2) был представлен в
[1].
С учётом (2) и (3) из (1) имеем:
.
(4)
Согласно (4),
тензор Риччи 
,
связанный с кривизной пространства-времени, за пределами уединённого тела
зависит от напряжённостей гравитационного и электромагнитного полей этого тела. Далее мы
будем использовать обозначения, описанные в [3].
Пусть имеется
тело, имеющее сферическую форму и симметричное относительно центра сферы
распределение вещества. В статическом случае метрика не будет зависеть ни от
времени, ни от углов сферической системы отсчёта. Тогда метрика в произвольной
точке вокруг тела будет зависеть лишь от радиальной координаты 
,
соединяющей данную точку с центром сферы. Удобно поэтому использовать
сферические координаты 
, 
, 
, 
,
связанные с декартовыми координатами соотношениями: 
, 
, 
.
Метрический тензор будем искать в следующем виде:
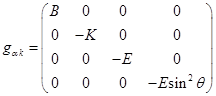, (5)
где 
являются функциями только радиальной
координаты .
Поскольку 
, то можно найти метрический тензор
с контравариантными индексами:
.
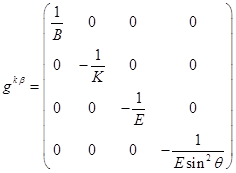(6)
Согласно (5) ненулевые компоненты 
, 
, 
, 
.
Тензор
напряжённостей гравитационного поля и аналогичный тензор электромагнитного поля
выражаются через соответствующие 4-векторы потенциала с ковариантным индексом [1]:
, 
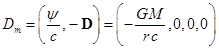, (7)
, 
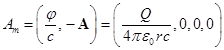, (8)
здесь – скалярный потенциал гравитационного поля
вокруг массивного тела с гравитационной массой 
, – скалярный потенциал электромагнитного поля
вокруг тела с зарядом 
,
величины 
и 
обозначают векторные потенциалы
гравитационного и электромагнитного поля.
Будем
считать, что векторный потенциал тела равен нулю, так как тело не вращается, а
его частицы хаотично движутся в разных направлениях и векторные потенциалы
частиц компенсируют друг друга. Аналогично считаем, что направленные
электрические токи внутри тела отсутствуют, магнитные моменты частиц вещества
скомпенсированы и 
.
С помощью (7)
и (2) находим ненулевые компоненты 
и :
, 
, 
,
, 
. (9)
Из (8) и (3)
вычисляем ненулевые компоненты 
и :
, 
, 
,
, 
. (10)
Тензор Риччи 
вычисляется по стандартной процедуре через
коэффициенты Кристоффеля 
, то
есть через метрический тензор и его производные:
.
(11)
.
(12)
Если
обозначить производные по 
штрихами, то ненулевые коэффициенты
Кристоффеля, выраженные через функции 
в метрическом тензоре (5) и (6), согласно (11)
равны:
, 
, 
, 
, 
,
, 
, 
. (13)
Подставляя
(13) в (12), находим ненулевые компоненты тензора Риччи, при этом оказывается,
что 
.
Выражение для тензора Риччи в смешанных индексах получается с помощью
метрического тензора: 
.
Используя найденные компоненты 
в левой части (4), а в правой части (4)
компоненты тензоров из (9) и 
из (10), приходим к трём независимым
уравнениям:
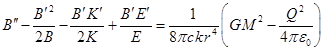. (14)
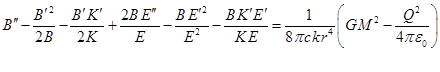. (15)
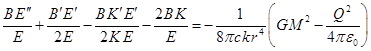. (16)
Уравнения
(14) – (16) содержат вторые производные по текущему радиусу 
,
обозначенные двумя штрихами. Если вычесть (15) из (14), а результат умножить на
, то
это даёт следующее:
, 
,
, 
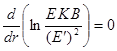, (17)
где 
– некоторая константа.
Подставим в
(16) значения 
и 
из (17):
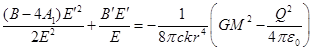. (18)
Соотношение
(18) является квадратным уравнением для 
со следующим решением:
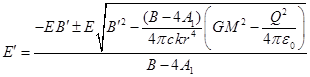. (19)
Из (19) можно
найти вторую производную от 
по , то
есть 
.
Подставляя и в (14), а также используя (17) для замены в (14) получим дифференциальное уравнение
второго порядка для 
:
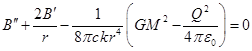. (20)
Решением
уравнения (20) является следующее выражение:
,
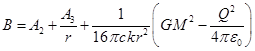(21)
где 
и 
– некоторые постоянные.
На
бесконечности, где гравитационное и электромагнитное поля близки к нулю,
метрический тензор (5) должен иметь вид тензора для пространства-времени
Минковского в сферических координатах, для которого 
, 
.
Следовательно, в (21) 
, а в
(17) и в (19) 
.
Подставляя эти коэффициенты и из (21) в (19), находим: . При
известных и из (17) видно, что 
. С
учётом этого искомые функции для метрики вокруг одиночного тела в ковариантной
теории гравитации будут равны:
, 
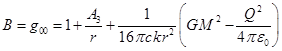, (22)
, 
.
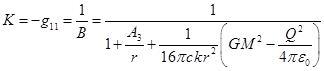3. Заключение
В (22)
константы 
и 
оказываются не определёнными из уравнений для
метрики, но значения этих констант могут быть найдены из сравнения с
экспериментом. Согласно (22), вклад заряда 
тела в метрику противоположен вкладу
гравитационной массы 
.
Для
сравнения, приведём метрику Райсснера-Нордстрёма [4-5] для заряженного тела в общей теории
относительности (ОТО):
, 
, 
, 
.
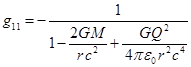(23)
Выражения
(23) в ОТО не содержат неопределённых коэффициентов, и в 
член, содержащий в знаменателе 
,
зависит только от заряда 
. Это
является следствием отсутствия в ОТО представления о гравитации как о самостоятельном
поле, так что в ОТО нет тензора энергии-импульса гравитационного поля и этот
тензор не участвует в определении метрики в уравнении (1). В результате метрика
за пределами даже незаряженного тела в ОТО каким-то таинственным способом
зависит от тела и его массы. Действительно, если не существует гравитационного
поля, а тело тем не менее изменяет метрику возле себя, то должен иметься
механизм, изменяющий метрику и переносящий влияние от тела в любую заданную
точку пространства. Указанный механизм в ОТО до сих пор не представлен.
В метрике
(22) ковариантной теории гравитации оба поля, гравитационное и
электромагнитное, представлены в равной мере в 
в члене, содержащем в знаменателе 
. Оба поля являются причиной того, что метрика вокруг тела изменяется.
Предположим теперь, что константы 
и зависят от параметров системы
следующим образом:
,
,
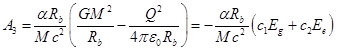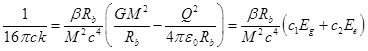где 
– радиус тела, 
и 
обозначают гравитационную и электрическую
энергии полей тела, численные коэффициенты 
и 
подлежат дальнейшему определению, коэффициенты
и 
зависят от распределения массы и заряда и в
случае однородной плотности массы и заряда тела будут одинаковы и равны
приблизительно величине 5/3.
В этом случае 
из (22) можно записать следующим
образом:
.
Данное соотношение можно трактовать так, что в
статическом случае компоненты метрики 
и 
фактически зависят от энергии
собственных полей тела.
С нашей точки зрения перспективной теорией,
позволяющей физически объяснить механизм передачи воздействия от одних масс и
зарядов к другим на расстоянии посредством поля, является теория гравитации
Фатио-Лесажа. В модели Фатио-Лесажа становится возможным понять не только взаимодействие между
массами [6], но и между электрическими зарядами [3]. Ранее мы находили метрику вида (22) в [3], теперь же мы рассмотрели
случай заряженного тела и учли вклад электрической энергии в компоненты
метрического тензора.
4. Список использованных источников
1. Федосин С.Г. Физика
и философия
подобия от преонов до метагалактик. Пермь, Стиль-МГ, 1999, 544 стр., Табл.66,
Ил.93, Библ. 377 назв. ISBN 5-8131-0012-1.
2. Fedosin S.G. About the cosmological constant, acceleration field, pressure
field and energy. vixra.org, 5 Mar 2014; О
космологической постоянной, поле ускорения, поле давления и об энергии.
3.
Федосин С.Г. Физические теории и бесконечная вложенность материи. Пермь,
2009-2012, 858 стр., Табл. 21, Ил.41, Библ. 293 назв. ISBN 978-5-9901951-1-0.
4.
Reissner,
H. (1916). Über die Eigengravitation des elektrischen Feldes nach der
Einsteinschen Theorie. Annalen der
Physik (in German) 50: 106–120. doi:10.1002/andp.19163550905.
5. Nordström, G. (1918). On the Energy of the
Gravitational Field in Einstein's Theory. Verhandl.
Koninkl. Ned. Akad. Wetenschap., Afdel. Natuurk., Amsterdam 26: 1201–1208.
6. Fedosin S.G. Model of Gravitational Interaction in the Concept of Gravitons. Journal of Vectorial Relativity, March 2009, Vol. 4, No. 1, P.1 – 24. // Модель гравитационного взаимодействия в концепции гравитонов.
Источник: http://sergf.ru/om.htm