International
Frontier Science Letters, ISSN: 2349 – 4484, Vol. 1, No. I (2014), pp. 41 – 46. http://dx.doi.org/10.18052/www.scipress.com/ifsl.1.41
The Metric
Outside a Fixed Charged Body in the Covariant Theory of Gravitation
Sergey G. Fedosin
PO box 614088, Sviazeva str. 22-79,
Perm, Russia
E-mail: intelli@list.ru
The metric outside a charged body is calculated. As part of the given
approach it is shown that the gravitational and electromagnetic fields are
equally involved in the formation of the metric tensor components. And the
contribution of fields in the metric is proportional to the energy of these
fields. From equations for the metric it follows that the metric tensor
components are determined up to two constants.
Keywords: metric; static solution; field energy; covariant
theory of gravitation.
1. Introduction
In the theory of gravitation the metric is needed for correct
representation of theoretical conclusions and experimental results. The concept
of metric is most important in the general theory of relativity (GTR), in which
the metric tensor field plays the role of the gravitational field. As a result,
transition of GTR to the Newtonian theory of gravitation is always performed by
expanding the metric tensor components to the principal expansion terms. For
example, for the gravitational field potential we obtain the following
expression: 
, where 
is the
time component of the metric tensor. No matter how small the field is, in GTR
first we must find , in order to evaluate then the potential 
.
In contrast to this, in the covariant theory of gravitation (CTG) the
metric in the weak field automatically tends to the metric of the Minkowski flat
space, while the gravitational field equations do not change their form due to
the covariant notation of equations. In CTG first we obtain the scalar
potentials and 
of the
gravitational and electromagnetic fields, the vector field potentials, the
tensors, corresponding to these fields, and only after that we calculate the
spacetime metric outside the body [1].
2. The solution of the equation for the
metric
The tensor equation for the metric, which was found in [2] from the
principle of least action, taking into account the cosmological constant gauge,
in mixed indices has the following form:
.
(1)
Outside the body, where the mass and charge densities are equal to zero,
the scalar curvature 
and the
stress-energy tensors 
of the
acceleration field and 
of the
pressure field are also equal to zero. This is due to the fact that the
acceleration field describes the motion of the body particles, and the pressure
field is associated with the pressure of the body particles on each other. Both
of these fields exist only in the volume of the body under consideration. The
equality of the scalar curvature to zero is
associated with the gauge condition of the cosmological constant.
In the right side of (1) there are two stress-energy tensors of the
gravitational 
and
electromagnetic 
fields:
.
(2)
.
(3)
Here 
is the
gravitational constant, 
is the vacuum permittivity, 
and 
are the
gravitational and electromagnetic tensors, respectively, 
is the unit tensor or the
Kronecker delta. We consider that the speed of light 
is the
same for the propagation of electromagnetic and gravitational effects through
the field. The stress-energy tensor of the gravitational field in the form of
(2) was presented in [1].
With regard to (2) and (3), from (1) we obtain:
.
(4)
According to (4), the Ricci tensor 
, associated with the spacetime curvature outside
a single body, depends on the gravitational and electromagnetic field strengths
of this body. Next, we will use the notation described in
[3].
Suppose there is a body with a spherical shape and the mater
distribution which is symmetrical relative to the center of the sphere. In the
static case, the metric depends neither on time nor on the angles of the
spherical reference frame. Then the metric at an arbitrary point around the
body will depend only on the radial coordinate 
connecting
this point with the center of the sphere. It is therefore convenient to use the
spherical coordinates 
, 
, 
, 
, associated with the Cartesian coordinates by
relations: 
, 
, 
. The metric tensor will be found in the
following form:
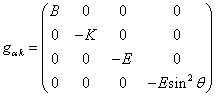, (5)
where 
are the functions
only of the radial coordinate .
Since 
, it is
possible to find the metric tensor with contravariant indices:
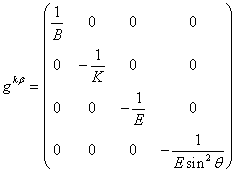. (6)
According to (5) the non-zero components are 
, 
, 
, 
.
The tensor of the gravitational field strength and the similar
electromagnetic field tensor are expressed with the help of the corresponding
4-potentials with the covariant index [1]:
,
, (7)
,
, (8)
here is the
scalar potential of the gravitational field around the massive body with the
gravitational mass 
, is the
scalar potential of the electromagnetic field around the body with the charge 
, the quantities 
and 
denote the
vector potentials of the gravitational and electromagnetic fields.
We will assume that the vector potential of the
body is equal to zero, since that the body does not rotate, its particles move
randomly in different directions and the vector potentials of particles compensate
each other. Similarly, we assume that there are no directed electrical currents
within the body, the magnetic moments of the substance particles are
compensated and 
.
Using (7) and (2), we find the non-zero components 
and :
,
,
,
, 
. (9)
From (8) and (3) we calculate the non-zero components 
and :
,
,
,
, 
.
(10)
The Ricci tensor 
is
calculated according to the standard procedure using the Christoffel
coefficients 
, i.e. the metric tensor and its derivatives:
. (11)
. (12)
If we denote the derivatives with respect to by primes,
then the non-zero Christoffel coefficients, expressed in terms of functions in the
metric tensor (5) and (6), according to (11) are equal to:
, 
, 
, 
, 
,
, 
, 
.
(13)
Substituting (13) into (12), we find non-zero components of the Ricci
tensor, and it also turns out that 
. We obtain the expression for the Ricci tensor
in mixed indices with the help of the metric tensor: 
. Using the obtained components in the
left side of (4), and the tensor components from (9)
and from (10)
in the right side (4), we find three independent equations:
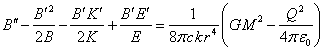. (14)
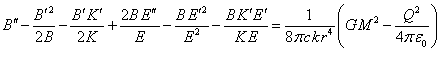. (15)
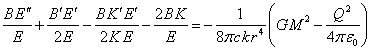. (16)
Equations (14) – (16) contain the second derivatives with respect to the
current radius , marked by two primes. If we subtract (15) from
(14) and multiply the result by 
, it gives the following:
, 
,
, 
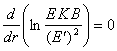, (17)
where 
is a
constant.
We will substitute in (16) the quantities 
and 
from (17):
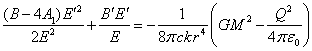. (18)
Equation (18) is a quadratic equation for 
with the
following solution:
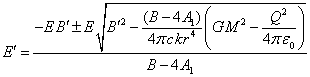. (19)
From (19) we can find the second derivative of 
with
respect to , that is 
. Substituting and in (14)
and also using (17) to substitute in (14),
we obtain a differential equation of the second order for 
:
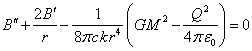. (20)
The solution of equation (20) is the following expression:
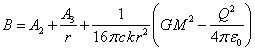, (21)
where 
and 
are some
constants.
At infinity, where the gravitational and electromagnetic fields are
close to zero, the metric tensor (5) must have the form of a tensor for
Minkowski spacetime in spherical coordinates, for which 
, 
. Therefore, in (21) 
and in
(17) and (19) 
. Substituting these coefficients and from (21)
in (19), we find: . With the known and from (17)
we see that 
. With this in mind, the required functions for
the metric around a single body in the covariant theory of gravitation will
equal:
, 
,
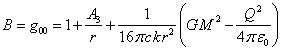(22)
, 
.
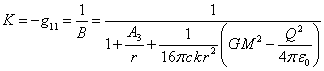3. Conclusion
In (22) the constants 
and 
are not
determined from the equations for the metric, but the values of these constants
can be found by comparison with the experimental data. According to (22), the
contribution of the body charge into the
metric is opposite to the contribution of the gravitational mass .
For comparison, we will use the Reissner-Nordström metric [4-5] for a
charged body in the general theory of relativity (GTR):
, 
, 
, .
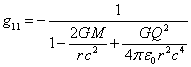(23)
Expressions (23) in GTR do not contain indefinite coefficients, and in the term,
containing 
in the
denominator, depends only on the charge . This reflects the absence of understanding of
gravitation as an independent field in
GTR, so in GTR there is no stress-energy tensor of the gravitational field and this
tensor is not used in determining the metric in equation (1). As a result, the
metric outside even uncharged body in GTR depends on the body and its mass in
some mysterious way. Indeed, if there is no gravitational field, and
nevertheless the body changes the metric near itself, there should be a
mechanism that changes the metric and transfers the body’s influence to any
given point in space. This mechanism is not yet represented in GTR.
In the metric (22) of the covariant theory of gravitation, both gravitational
and electromagnetic fields are equally represented in in the
term, containing 
in the
denominator. Both fields are the reason due to which the metric around the body
is changed.
Let us suppose now that the constants and depend on
the system’s parameters as follows:
,
,
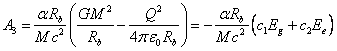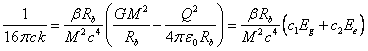where 
is the
radius of the body, 
and 
denote the gravitational and electrical
energies of the body’s fields, the numerical coefficients 
and 
should be
determined further, the coefficients 
and 
depend on
the mass and charge distribution, and in case of uniform density of the mass
and charge of the body, are the same and are approximately equal to the value
5/3.
In this case for from (22)
we can write the following:
.
This relation can be interpreted so that in the static case the metric
components and 
actually
depend on the energy of the body's proper fields.
In our opinion a perspective theory, that allows us to explain from the physical
standpoint the mechanism which transfers influence from some masses and charges
to others at a distance by means of the field, is Fatio–Le Sage’s theory of
gravitation. In Fatio–Le Sage’s model it is also possible to understand not
only the interaction between the masses [6], but also between the electric
charges [3]. Previously, we found the metric of
the form (22) in [3], but now we considered the case of a charged body and took
into account the contribution of the electric energy into the metric tensor
components.
4. References
1. Fedosin S. G. Fizika i filosofiia
podobiia ot preonov do metagalaktik. (Perm,
1999).
2. Fedosin S.G. About the cosmological constant, acceleration field,
pressure field and energy. vixra.org, 5 Mar 2014.
3.
Fedosin
S. G. Fizicheskie
teorii i beskonechnaia vlozhennost’ materii
(Perm, 2009).
4.
Reissner, H. (1916). Über die Eigengravitation des elektrischen Feldes
nach der Einsteinschen Theorie. Annalen der Physik 50: 106–120. doi:10.1002/andp.19163550905.
5. Nordström, G. (1918). On
the Energy of the Gravitational Field in Einstein's Theory. Verhandl. Koninkl. Ned. Akad. Wetenschap.,
Afdel. Natuurk., Amsterdam 26: 1201–1208.
6. Fedosin S.G. Model of Gravitational Interaction in the Concept of Gravitons. Journal of Vectorial Relativity, 2009, Vol. 4, No. 1, P.1 – 24.
Source:
http://sergf.ru/omen.htm