Journal of
Fundamental and Applied Sciences, Vol. 8, No. 3, P. 971-1020 (2016). https://dx.doi.org/10.5281/zenodo.845357
Заряженная компонента вакуумного поля как источник
электрической силы в модернизированной модели Лесажа
Федосин Сергей Григорьевич
ул. Свиязева 22-79, город Пермь, 614088, Пермский край, Россия
e-mail intelli@list.ru
Выводится формула для электрической силы внутри однородно заряженного
сферического тела, а также для силы Кулона между заряженными телами с точки
зрения модели вакуумного поля с заряженными частицами. Оцениваются параметры
потоков заряженных частиц, включая плотность энергии, поток энергии и сечение
взаимодействия с заряженным веществом. Сечение взаимодействия оказывается почти
точно равно геометрическому сечению нуклонов и становится равным сечению взаимодействия
гравитонов с веществом, если полагать, что отношение плотности энергии потоков
гравитонов к плотности энергии заряженных частиц вакуумного поля равно
отношению масс протона и электрона. При этом плотность энергии гравитонов в
модели гравитации Лесажа выражается через постоянную сильной гравитации, что
устанавливает связь между обычной гравитацией на уровне звёзд и сильной
гравитацией на атомно-нуклонном уровне материи. Выводится соотношение,
связывающее заряд тела и мощность излучения из тела тех заряженных частиц
вакуумного поля, которые взаимодействовали с веществом и передали телу свой
импульс. Определяется отношение заряда к массе для заряженных частиц,
составляющих фотоны и заряженную компоненту вакуумного поля. Указанные частицы
идентифицируются как праоны, причём праонный уровень материи является нижним
уровнем по отношению к нуклонному уровню материи. Праоны соотносятся с
нуклонами так же, как нуклоны с нейтронными звёздами. На основе теории бесконечной вложенности
материи делается заключение о том, что заряженные частицы вакуумного поля
порождаются на всех уровнях материи самыми плотными объектами типа праонов,
нуклонов и нейтронных звёзд. Анализ основных проблем модели Лесажа показывает,
что эти проблемы могут быть сняты в модернизированной модели, в которой
учитываются выводы специальной теории относительности и особенности
взаимодействия релятивистских частиц с веществом.
Ключевые
слова: вакуумное
поле; поле гравитонов;
электрическая сила; праоны; бесконечная вложенность материи.
PACS: 03.50.Kk; 04.50.+h; 14.80.-j
The
charged component of the vacuum field as the source of electric force in the
modernized Le Sage’s model
Sergey G. Fedosin
Sviazeva Str. 22-79, Perm, 614088, Perm region,
Russian Federation
e-mail intelli@list.ru
The formula is derived
for the electric force inside a uniformly charged spherical body, as well as
for the Coulomb force between the charged bodies from the standpoint of the
model of the vacuum field with charged particles. The parameters of the fluxes
of charged particles are estimated, including the energy density, energy flux
and cross-section of interaction with the charged matter. The interaction
cross-section is almost exactly equal to the geometric cross-section of
nucleons and becomes equal to the cross-section of interaction of gravitons
with the matter, if it is assumed that the ratio of the energy density of
graviton fluxes to the energy density of the charged particles in the vacuum
field is equal to the ratio of masses of the proton and the electron. In this
case, the energy density of gravitons in the Le Sage’s gravitation model is
expressed in terms of the strong gravitational constant, which establishes
connection between the ordinary gravitation at the level of stars and the
strong gravitation at the atomic-nucleon level of matter. The relation is
derived, which connects the body charge and the rate of emission from the body
of the charged particles of the vacuum field, which interacted with the matter
and transferred their momentum to the body. The charge to mass ratio is
determined for the charged particles that make up photons and the charged
component of the gravitational field. These particles are identified as praons,
while the praon level of matter is considered a lower level relative to the
nucleon level of matter. Praons are related to nucleons the same way as
nucleons are related to neutron stars. Based on the theory of infinite nesting
of matter a conclusion is made that the charged particles of the vacuum field
are generated at all levels of matter by the densest objects, such as praons, nucleons and neutron stars. The analysis of the main problems of the Le
Sage’s model shows that these problems can be eliminated in the modernized
model, which takes into account the conclusions of the special theory of
relativity and the peculiarities of interaction of the relativistic particles
with the matter.
The keywords: vacuum field; graviton field; electric force; praons; infinite nesting
of matter.
PACS: 03.50.Kk; 04.50.+h; 14.80.-j
1. Введение
Подобие уравнений Максвелла для электромагнитного поля, с одной стороны,
и уравнений Хевисайда для гравитационного поля в Лоренц-инвариантной теории
гравитации [1-2], с другой стороны, а также
подобие формул для силы Кулона и силы Ньютона допускает большую вероятность
того, что за это ответственен один и тот же физический механизм. Так, в [3]
выводится, что гравитация может быть следствием действия электромагнитных микроквантов
с длиной волны, равной планковской длине.
Ранее в [2] и [4] мы вывели формулу для ньютоновского закона всемирного тяготения и выражение гравитационной постоянной через параметры поля гравитонов, используя модернизированную теорию гравитации Лесажа. В дополнение к этому в [5] было найдено выражение для массы тела как функции от светимости гравитонов, взаимодействующих с телом, а также выражение для напряжённости гравитационного поля внутри тела.
Теперь же мы намереваемся вывести формулу для кулоновской силы, действующей между заряженными телами, и уточнить параметры вакуумного поля, состоящего из поля гравитонов и поля заряженных частиц. В модернизированной теории гравитации Лесажа всёпроникающие потоки частиц вакуумного поля состоят из нейтрино, фотонов и заряженных частиц, свойства которых подобны космическим лучам высокой энергии. Присутствие заряженных частиц в динамическом вакуумном поле позволяет описать электростатические силы и как следствие обосновать электромагнитные явления.
2. Картина взаимодействия
Чтобы понять электрическое взаимодействие тел на расстоянии друг от
друга, рассмотрим на рисунке 1 движение малых заряженных частиц вакуумного поля
вблизи двух тел, одно из которых нейтрально, а второе заряжено положительно.
Как видно, и положительные и отрицательные частицы действуют на положительно
заряженное тело симметрично, что не приводит к возникновению какой-либо
дополнительной силы по сравнению с силой гравитации. Это же касается и второго,
нейтрального тела.
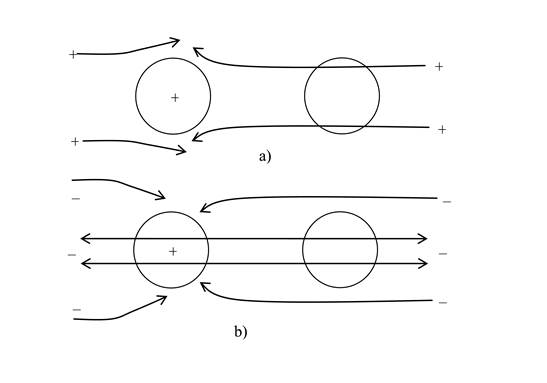
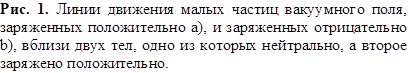
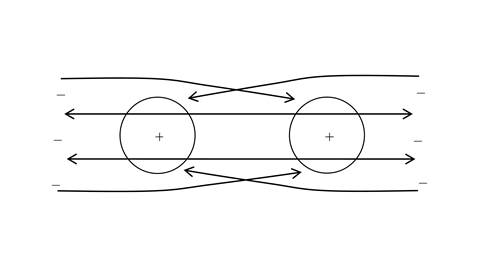
На рисунке 2 a)
видно, что положительные частицы толкают отрицательно заряженное тело влево, а
на рисунке 2 b)
отрицательные частицы толкают положительно заряженное тело вправо (когда
мельчайшие частицы проходят сквозь тела подобно гравитонам, они передают им
свой импульс). Следовательно, оба тела будут притягиваться друг к другу.
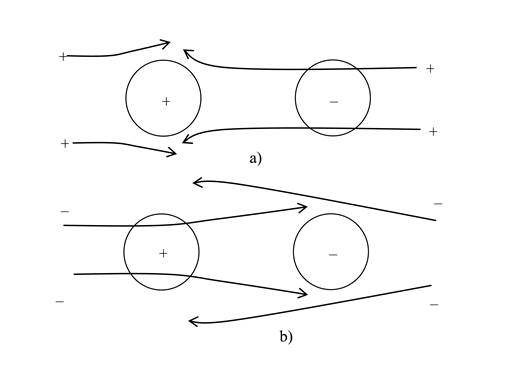
На рисунке 3 приведены линии движения отрицательных частиц вакуумного поля вблизи двух положительно заряженных тел. Оба тела притягивают отрицательные частицы и получают от них дополнительный импульс, приводящий к отталкиванию тел. Движение положительных частиц вакуумного поля на рисунке 3 не показано. Предполагается, что они отталкиваются от этих тел и потому взаимодействуют с ними в меньшей степени.
Для двух отрицательно заряженных тел взаимодействие подобно показанному
на рисунке 3, необходимо лишь заменить знаки у всех зарядов. Отсюда получается
отталкивание одноимённо заряженных тел. Описанную выше картину можно найти в
[6]. Общим для всех рисунков является то, что в зависимости от знаков зарядов
двух тел количество падающих на тела заряженных частиц меняется так, что после
подсчёта переданного импульса от этих частиц появляется электрическая сила
необходимого направления. Таким образом, взаимодействие между зарядами на
расстоянии мы сводим к взаимодействию посредством заряженных частиц вакуумного
поля.
3. Сила Кулона
Для определения выражения для электрической силы используем подход,
применённый в [4-5]. Пусть мощность
флюенса заряженных частиц вакуумного поля задаётся
идеализированным сферическим распределением следующего вида:
![]() .
(1)
.
(1)
Согласно (1) предполагается, что некоторый
детектор в единицу времени ![]() измеряет заряженные частицы вакуумного поля в
количестве
измеряет заряженные частицы вакуумного поля в
количестве ![]() ,
падающих на детектор из телесного угла
,
падающих на детектор из телесного угла ![]() на единичную площадь поверхности
на единичную площадь поверхности ![]() перпендикулярно этой поверхности.
перпендикулярно этой поверхности.
Будем считать, что в веществе каждого
заряженного тела происходит экспоненциальное изменение количества заряженных
частиц вакуумного поля по мере того, как поток этих
частиц проходит
в веществе некоторый путь ![]() :
:
![]() ,
, ![]() , (2)
, (2)
где ![]() есть сечение взаимодействия движущихся
заряженных частиц с веществом,
есть сечение взаимодействия движущихся
заряженных частиц с веществом, ![]() – концентрация зарядов, связанных с веществом.
– концентрация зарядов, связанных с веществом.
Обозначая положительный по величине
элементарный заряд через ![]() , для модулей зарядов и площади
, для модулей зарядов и площади ![]() шаровых сегментов на
рисунке 4 имеем:
шаровых сегментов на
рисунке 4 имеем:
![]() ,
, ![]() ,
, 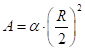 . (3)
. (3)
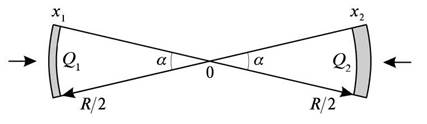
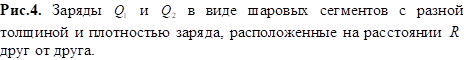
Детектор находится в точке ![]() посередине между двумя сегментами. Для него
каждый сегмент виден под одним и тем же телесным углом
посередине между двумя сегментами. Для него
каждый сегмент виден под одним и тем же телесным углом ![]() на расстоянии
на расстоянии ![]() , при
этом поперечные площади сегментов одинаковы и равны
, при
этом поперечные площади сегментов одинаковы и равны ![]() . Это
означает, что прежде чем применять дальнейшие рассуждения для двух больших тел,
эти тела следует нарезать на сегменты и затем вычислять суммарную электрическую
силу между всеми возможными парами сегментов путём векторного суммирования
отдельных сил.
. Это
означает, что прежде чем применять дальнейшие рассуждения для двух больших тел,
эти тела следует нарезать на сегменты и затем вычислять суммарную электрическую
силу между всеми возможными парами сегментов путём векторного суммирования
отдельных сил.
Рассмотрим вначале случай, когда заряд ![]() положителен, а заряд
положителен, а заряд ![]() отрицателен. Сравнение с рисунком 2 показывает,
что взаимодействие приводит к притяжению за счёт поглощения и рассеяния
заряженных частиц, падающих на заряды и проходящих через них. В первом
приближении можно считать, что основной вклад делают поток отрицательных
заряженных частиц, падающих на заряд
отрицателен. Сравнение с рисунком 2 показывает,
что взаимодействие приводит к притяжению за счёт поглощения и рассеяния
заряженных частиц, падающих на заряды и проходящих через них. В первом
приближении можно считать, что основной вклад делают поток отрицательных
заряженных частиц, падающих на заряд ![]() слева, и поток положительных заряженных
частиц, падающих на заряд
слева, и поток положительных заряженных
частиц, падающих на заряд ![]() справа.
справа.
Изменение потока заряженных частиц с левой стороны после прохождения первого сегмента на рисунке 4 согласно (2) зависит от толщины этого сегмента и концентрации заряда:
![]() .
.
После этого поток заряженных частиц проходит
через второй сегмент с дополнительным изменением потока:
![]() .
.
Обозначим через ![]() средний импульс
заряженной частицы вакуумного поля, и далее будем считать, что в случае
взаимодействия одной такой частицы с заряженным веществом изменение импульса
частицы приблизительно равно
средний импульс
заряженной частицы вакуумного поля, и далее будем считать, что в случае
взаимодействия одной такой частицы с заряженным веществом изменение импульса
частицы приблизительно равно ![]() . Это возможно,
если заряженная частица останавливается веществом либо отражается
электромагнитным полем в сторону так, что изменение вектора импульса имеет тот
же порядок величины, что и сам вектор импульса частицы.
. Это возможно,
если заряженная частица останавливается веществом либо отражается
электромагнитным полем в сторону так, что изменение вектора импульса имеет тот
же порядок величины, что и сам вектор импульса частицы.
Тогда сила, действующая на второй сегмент слева,
с учётом (1) будет равна:
![]() .
.
Изменение потока заряженных частиц, проходящего
справа через второй сегмент, и сила с этой стороны равны соответственно:
![]() ,
, ![]() .
.
Для силы электрического действия на второй сегмент находим симметричное выражение, по модулю равное силе электрического действия на первый сегмент:
![]() .
.
Раскладывая экспоненты в линейном приближении по правилу: ![]() , с учётом
(3) для силы притяжения двух противоположно заряженных сегментов получим:
, с учётом
(3) для силы притяжения двух противоположно заряженных сегментов получим:
![]() ,
, ![]() . (4)
. (4)
В (4) сила ![]() направлена противоположно вектору
направлена противоположно вектору ![]() расстояния от первого сегмента до второго, так
как заряд
расстояния от первого сегмента до второго, так
как заряд ![]() отрицателен.
отрицателен.
Согласно закону Кулона, формула для электрической силы между двумя заряженными телами имеет следующий вид:
![]() .
(5)
.
(5)
Сравнивая значения для сил в (4) и (5), приходим к выражению для электрической постоянной через параметры вакуумного поля при идеализированном сферическом распределении потоков заряженных частиц вакуумного поля:
![]() .
(6)
.
(6)
Электрическая постоянная в (6) зависит от
сечения ![]() взаимодействия заряженных частиц вакуумного поля с веществом, от среднего импульса одной частицы
взаимодействия заряженных частиц вакуумного поля с веществом, от среднего импульса одной частицы ![]() , от
мощности флюенса заряженных частиц
, от
мощности флюенса заряженных частиц ![]() и от элементарного заряда
и от элементарного заряда ![]() .
.
Из выражения для силы определяется напряжённость электрического поля одного заряда в месте расположения второго заряда:
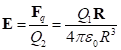 .
(7)
.
(7)
Будем считать теперь, что заряд ![]() на рисунке 4 положителен, как и заряд
на рисунке 4 положителен, как и заряд ![]() . Эта
ситуация соответствует рисунку 3, из которого следует, что после прохождения
заряда
. Эта
ситуация соответствует рисунку 3, из которого следует, что после прохождения
заряда ![]() поток заряженных частиц эффективно
увеличивается перед падением на заряд
поток заряженных частиц эффективно
увеличивается перед падением на заряд ![]() . Для
потока частиц, движущихся со стороны заряда
. Для
потока частиц, движущихся со стороны заряда ![]() и падающих на заряд
и падающих на заряд ![]() ,
ситуация симметрична. Чтобы учесть эффект увеличения потока заряженных частиц,
введём дополнительный коэффициент
,
ситуация симметрична. Чтобы учесть эффект увеличения потока заряженных частиц,
введём дополнительный коэффициент ![]() .
Тогда поток заряженных частиц с левой стороны
после прохождения первого сегмента на рисунке 4 с учётом (2) изменится до
величины:
.
Тогда поток заряженных частиц с левой стороны
после прохождения первого сегмента на рисунке 4 с учётом (2) изменится до
величины:
![]() .
.
При прохождении через второй сегмент поток уменьшается:
![]() .
.
Сила, действующая на второй сегмент слева, с
учётом (1) будет равна:
![]() .
.
Для потока заряженных частиц, проходящего
справа через второй сегмент, и сила с этой стороны равны соответственно:
![]() ,
, ![]() .
.
Для силы электрического действия на второй сегмент получим:
![]() .
.
В данном выражении разложим экспоненты и используем (3):
![]() . (8)
. (8)
Сила отталкивания (8) при смене знака у заряда ![]() должна равняться по модулю силе притяжения в
(4). Для этого должно выполняться следующее условие:
должна равняться по модулю силе притяжения в
(4). Для этого должно выполняться следующее условие: ![]() .
Существует способ проверить это соотношение. Для этого нужно рассмотреть
ситуацию на рисунке 3, оценить потоки заряженных частиц со всех сторон и их взаимодействие
с заряженными телами, чтобы в итоге определить, насколько увеличиваются эти
потоки при падении на тела по сравнению с ситуацией на рисунке 1. Мы вернёмся
ещё к этому вопросу в разделе 6.
.
Существует способ проверить это соотношение. Для этого нужно рассмотреть
ситуацию на рисунке 3, оценить потоки заряженных частиц со всех сторон и их взаимодействие
с заряженными телами, чтобы в итоге определить, насколько увеличиваются эти
потоки при падении на тела по сравнению с ситуацией на рисунке 1. Мы вернёмся
ещё к этому вопросу в разделе 6.
Из рисунка (1) видно, что если у одного из тел нет никакого заряда, то заряженные частицы вакуумного поля не взаимодействуют с этим телом электрическим образом. Они проходят через него почти свободно, если не считать гравитационного действия. В результате между заряженным и незаряженным телами будет лишь сила гравитационного притяжения.
4. Напряжённость электрического поля внутри шара
Для оценки поля внутри однородного шара удобно от сферического распределения (1) перейти к кубическому распределению в виде смешанной производной для направленного в одну сторону потока заряженных частиц вакуумного поля:
![]() ,
(9)
,
(9)
где мощность флюенса ![]() обозначает количество заряженных частиц
обозначает количество заряженных частиц ![]() ,
попавших за время
,
попавших за время ![]() на перпендикулярную потоку площадь
на перпендикулярную потоку площадь ![]() одной из граней некоторого куба,
ограничивающего рассматриваемый объём.
одной из граней некоторого куба,
ограничивающего рассматриваемый объём.
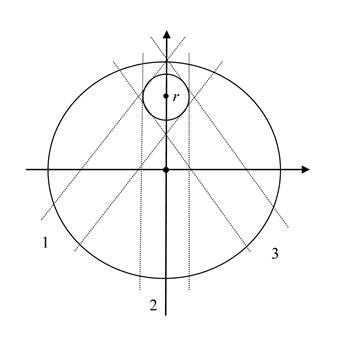
На рисунке 5 показано сечение однородно заряженного шара радиуса ![]() ,
внутри которого находится небольшое пробное тело, также в форме шара, с
радиусом
,
внутри которого находится небольшое пробное тело, также в форме шара, с
радиусом ![]() .
.
![]()
Потоки заряженных частиц вакуумного поля идут по путям 1, 2 , 3 , а также по другим путям, пересекая
сечение малого шара, находящегося на расстоянии ![]() от центра большого шара. Если заменить малый
шар кубом таких же размеров, то при идеализированном кубическом распределении
достаточно рассмотреть вертикальные потоки вдоль пути 2. Потоки заряженных частиц через другие грани малого куба будут
симметричны и не влияют на электрическую силу. Это значит, что при таком
подходе мы будем не прямо, а косвенно учитывать потоки по наклонным путям 1 и
3. Все эти потоки при векторном сложении дают силу, действующую на малый шар и
добавляются к силе, вычисляемой на пути 2.
от центра большого шара. Если заменить малый
шар кубом таких же размеров, то при идеализированном кубическом распределении
достаточно рассмотреть вертикальные потоки вдоль пути 2. Потоки заряженных частиц через другие грани малого куба будут
симметричны и не влияют на электрическую силу. Это значит, что при таком
подходе мы будем не прямо, а косвенно учитывать потоки по наклонным путям 1 и
3. Все эти потоки при векторном сложении дают силу, действующую на малый шар и
добавляются к силе, вычисляемой на пути 2.
Пусть объём малого шара равен объёму некоторого куба. Тогда для объёма
куба с ребром ![]() , и
для модуля заряда
, и
для модуля заряда ![]() этого куба получаются соотношения:
этого куба получаются соотношения:
![]() ,
, ![]() , (10)
, (10)
где ![]() – концентрация заряда в маленьком шаре.
– концентрация заряда в маленьком шаре.
Распределение (9) заменяет фактическое распределение потоков заряженных частиц вакуумного поля в пространстве на идеализированное кубическое распределение, когда на данный кубический объём падает всего шесть потоков заряженных частиц, перпендикулярно граням куба.
По аналогии с (2) можно записать зависимость мощности флюенса заряженных частиц вакуумного поля от пройденного в веществе расстояния:
![]() ,
, ![]() . (11)
. (11)
Пусть для начала заряд ![]() малого шара на рисунке 5 отрицателен, а заряд
большого шара положителен.
малого шара на рисунке 5 отрицателен, а заряд
большого шара положителен.
Падающий сверху поток заряженных частиц проходит путь ![]() в большом шаре с концентрацией заряда
в большом шаре с концентрацией заряда ![]() , и
достигает малого куба, которым мы заменили малый шар. Согласно (11) к этому
моменту мощность флюенса уменьшится до величины:
, и
достигает малого куба, которым мы заменили малый шар. Согласно (11) к этому
моменту мощность флюенса уменьшится до величины:
![]() .
.
Далее поток проходит через малый куб с концентрацией нуклонов
![]() и снова уменьшается:
и снова уменьшается:
![]() .
.
Сила от этого потока заряженных частиц пропорциональна площади
грани малого куба и количеству заряженных частиц, передавших свой импульс в
единицу времени веществу куба:
![]() . (12)
. (12)
С нижней стороны большого шара поток заряженных частиц проходит
вначале путь ![]() до малого куба, а затем проходит через этот
куб:
до малого куба, а затем проходит через этот
куб:
![]() ,
, ![]() .
.
Сила, действующая на малый куб с этой стороны, равна:
![]() . (13)
. (13)
Суммарная сила есть разница сил (12) и (13):
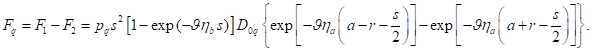
Так как в данном выражении показатели экспонент достаточно малы,
их можно разложить по малому параметру по правилу: ![]() . С
учётом этого имеем:
. С
учётом этого имеем:
![]() .
.
В данном выражении учтём, что плотность заряда большого шара
выражается формулой: ![]() , и используем (10):
, и используем (10):
![]() ,
, ![]() .
.
Сила ![]() действует на маленький шар с отрицательным
зарядом
действует на маленький шар с отрицательным
зарядом ![]() на рисунке 5 так, что сила направлена к центру
большого шара и противоположно радиус-вектору
на рисунке 5 так, что сила направлена к центру
большого шара и противоположно радиус-вектору ![]() от центра большого шара до малого шара. По
определению, напряжённость электрического поля есть отношение силы, действующей
на пробное тело, к заряду пробного тела. Тогда вектор напряжённости
электрического поля внутри большого шара будет такой:
от центра большого шара до малого шара. По
определению, напряжённость электрического поля есть отношение силы, действующей
на пробное тело, к заряду пробного тела. Тогда вектор напряжённости
электрического поля внутри большого шара будет такой:
![]() .
(14)
.
(14)
В электростатике вектор напряжённости электрического поля внутри однородно заряженного шара определяется формулой:
![]() .
(15)
.
(15)
Из сравнения (14) и (15) находим выражение электрической постоянной через параметры вакуумного поля в приближении кубического распределения потоков заряженных частиц
вакуумного поля:
![]() .
(16)
.
(16)
Различие используемых нами кубического (9) и сферического (1)
распределений приводит к тому, что формулы для электрической постоянной (16) и
(6) отличаются численным множителем.
Если малый шар на рисунке 5 имеет не отрицательный, а
положительный заряд ![]() , то
его взаимодействие с зарядом большого шара следует рассматривать с учётом
рисунка 3 для взаимодействия двух положительных зарядов. Это значит, что следует ввести дополнительный
коэффициент
, то
его взаимодействие с зарядом большого шара следует рассматривать с учётом
рисунка 3 для взаимодействия двух положительных зарядов. Это значит, что следует ввести дополнительный
коэффициент ![]() ,
чтобы учесть эффект увеличения потока заряженных частиц.
,
чтобы учесть эффект увеличения потока заряженных частиц.
В результате мощности флюенса ![]() и
и ![]() , и
сила (12) от падающего сверху потока заряженных частиц на малый куб,
которым мы заменили малый шар, изменяются и будут равны:
, и
сила (12) от падающего сверху потока заряженных частиц на малый куб,
которым мы заменили малый шар, изменяются и будут равны:
![]() ,
, ![]() ,
,
![]() . (17)
. (17)
Аналогично с нижней стороны большого шара для мощности флюенса и силы имеем вместо (13):
![]() ,
, ![]() ,
,
![]() . (18)
. (18)
Суммарная сила есть разница сил (18) и (17):
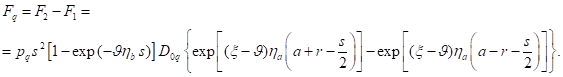
Раскладывая экспоненты по правилу: ![]() , находим:
, находим:
![]() .
.
Положим, что плотность заряда большого шара выражается формулой: ![]() , а
для коэффициента
, а
для коэффициента ![]() справедливо соотношение
справедливо соотношение ![]() ,
найденное в предыдущем разделе. Тогда с учётом (10) имеем:
,
найденное в предыдущем разделе. Тогда с учётом (10) имеем:
![]() .
.
Сила ![]() направлена радиально от центра большого шара,
а выражение для этой силы после деления на заряд
направлена радиально от центра большого шара,
а выражение для этой силы после деления на заряд ![]() приводит к напряжённости электрического поля
(14).
приводит к напряжённости электрического поля
(14).
5. Параметры
потоков заряженных частиц вакуумного
поля
Оценим плотность энергии для кубического распределения потоков заряженных частиц вакуумного
поля в пространстве. Пусть есть куб с ребром ![]() , в
который влетают частицы с шести сторон перпендикулярно граням куба. Скорость заряженных частиц
предполагается равной скорости света
, в
который влетают частицы с шести сторон перпендикулярно граням куба. Скорость заряженных частиц
предполагается равной скорости света ![]() , так
что за время
, так
что за время ![]() куб будет полностью заполнен. С учётом
распределения (9) количество частиц в кубе будет равно:
куб будет полностью заполнен. С учётом
распределения (9) количество частиц в кубе будет равно: ![]() .
Если энергия одной частицы равна
.
Если энергия одной частицы равна ![]() , то
для плотности энергии заряженных
частиц вакуумного поля с помощью (16) находим:
, то
для плотности энергии заряженных
частиц вакуумного поля с помощью (16) находим:
![]() . (19)
. (19)
Используем теперь сферическое распределение (1) для оценки плотности
энергии заряженных частиц
вакуумного поля. Пустая сфера радиуса ![]() может быть заполнена частицами за время
может быть заполнена частицами за время ![]() ,
если потоки частиц
направлены радиально и укладываются в полный телесный угол
,
если потоки частиц
направлены радиально и укладываются в полный телесный угол ![]() .
Число частиц внутри
сферы будет равно
.
Число частиц внутри
сферы будет равно ![]() .
Умножая это число на энергию одного частицы и разделив на объём сферы, можно найти плотность энергии.
С учётом (6) и условия
.
Умножая это число на энергию одного частицы и разделив на объём сферы, можно найти плотность энергии.
С учётом (6) и условия ![]() ,
имеем:
,
имеем:
![]() . (20)
. (20)
Плотность энергии (20) при сферическом распределении в 3/2 раза больше, чем при кубическом распределении (19), что подчёркивает приблизительность наших оценок из-за использования двух идеализированных распределений.
Ранее в [5] мы применили концепцию поля
гравитонов для вычисления гравитационной силы Ньютона между двумя телами и
гравитационной постоянной. Это дало возможность оценить плотность энергии поля
гравитонов для кубического распределения и мощность потока энергии поля
гравитонов в одном направлении:
![]() Дж/м3 , (21)
Дж/м3 , (21)
![]() Вт/м2 ,
Вт/м2 ,
здесь ![]() есть средняя энергия одного гравитона,
есть средняя энергия одного гравитона, ![]() – средний импульс гравитона,
– средний импульс гравитона, ![]() – количество гравитонов, падающих в единицу
времени на единичную площадку с одного из
6 пространственных направлений при кубическом распределении,
– количество гравитонов, падающих в единицу
времени на единичную площадку с одного из
6 пространственных направлений при кубическом распределении, ![]() ,
, ![]() – гравитационная постоянная,
– гравитационная постоянная, ![]() – масса одного нуклона вещества,
– масса одного нуклона вещества, ![]() м2 – сечение взаимодействия
гравитонов с веществом.
м2 – сечение взаимодействия
гравитонов с веществом.
Плотность энергии ![]() в (21) связана с гравитационной постоянной
в (21) связана с гравитационной постоянной ![]() и с действием гравитации на нуклоны вещества.
Аналогично, плотность энергии заряженных частиц вакуумного поля
и с действием гравитации на нуклоны вещества.
Аналогично, плотность энергии заряженных частиц вакуумного поля ![]() в (19) связана с электромагнитным действием
поля на каждый из элементарных зарядов
в (19) связана с электромагнитным действием
поля на каждый из элементарных зарядов ![]() вещества.
вещества.
Для дальнейшего нам понадобятся коэффициенты подобия, с помощью которых в
теории бесконечной вложенности материи [2], [6]
вычисляются физические величины, присущие тому или иному уровню материи. В
качестве типичных параметров нейтронной звезды возьмём массу 1,35 массы Солнца
или ![]() кг,
а также радиус звезды
кг,
а также радиус звезды ![]() км.
км.
Разделив массу нейтронной звезды на массу протона ![]() ,
находим коэффициент подобия по массе:
,
находим коэффициент подобия по массе: ![]() .
Аналогично вычислим коэффициент подобия по размерам как отношение радиуса
звезды к радиусу протона:
.
Аналогично вычислим коэффициент подобия по размерам как отношение радиуса
звезды к радиусу протона: ![]() ,
здесь было использовано значение
,
здесь было использовано значение ![]() м в самосогласованной модели протона [7]. Мы можем оценить минимально допустимый радиус
нейтронной звезды, исходя из соотношения между объёмом звезды и суммарным
объёмом всех нуклонов в звезде:
м в самосогласованной модели протона [7]. Мы можем оценить минимально допустимый радиус
нейтронной звезды, исходя из соотношения между объёмом звезды и суммарным
объёмом всех нуклонов в звезде: ![]() ,
, ![]() км.
Звезда с радиусом 12 км превышает этот предел, между нуклонами ещё имеются
некоторые промежутки и нуклоны остаются самостоятельными частицами.
км.
Звезда с радиусом 12 км превышает этот предел, между нуклонами ещё имеются
некоторые промежутки и нуклоны остаются самостоятельными частицами.
Коэффициент подобия по скоростям равняется отношению характерных
скоростей вещества внутри звезды и протона соответственно. Для звезды
характерная скорость ![]() вычисляется из равенства энергий с точки
зрения общего принципа эквивалентности массы и энергии, обобщённого в отношении
модуля полной энергии на любые космические объекты:
вычисляется из равенства энергий с точки
зрения общего принципа эквивалентности массы и энергии, обобщённого в отношении
модуля полной энергии на любые космические объекты:
![]() ,
, 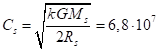 м/с.
м/с.
Аналогично этому для протона находим равенство характерной скорости его вещества и скорости света:
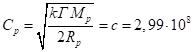 м/с,
м/с,
при этом ![]() м3·кг-1·с-2
есть постоянная сильной гравитации, вычисляемая из равенства электрической и
гравитационной сил в атоме водорода,
м3·кг-1·с-2
есть постоянная сильной гравитации, вычисляемая из равенства электрической и
гравитационной сил в атоме водорода, ![]() есть электрическая постоянная,
есть электрическая постоянная, ![]() есть масса электрона, и согласно [7] для протона
есть масса электрона, и согласно [7] для протона ![]() .
Отсюда коэффициент подобия по скоростям будет равен:
.
Отсюда коэффициент подобия по скоростям будет равен: ![]() .
.
Как было показано в [2], отношение модуля
плотности энергии сильной гравитации к плотности электромагнитной энергии для
протона равно отношению массы протона к массе электрона ![]() .
Действительно, для энергии полей и их отношения с учётом определения постоянной
сильной гравитации
.
Действительно, для энергии полей и их отношения с учётом определения постоянной
сильной гравитации ![]() имеем:
имеем: ![]() ,
, ![]() ,
, 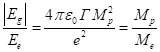 .
.
Мы считаем, что такое же соотношение имеется и для плотностей энергии поля гравитонов и заряженных частиц в вакуумном поле, что позволяет оценить плотность энергии заряженных частиц вакуумного поля:
![]() Дж/м3.
(22)
Дж/м3.
(22)
Подставим (22) в (19), используя значение ![]() из (21), учтём близость массы протона и
средней массы нуклона
из (21), учтём близость массы протона и
средней массы нуклона ![]() , а
также определение постоянной сильной гравитации в виде
, а
также определение постоянной сильной гравитации в виде ![]() .
Это даёт оценку сечения взаимодействия заряженных частиц вакуумного поля с
заряженным веществом:
.
Это даёт оценку сечения взаимодействия заряженных частиц вакуумного поля с
заряженным веществом:
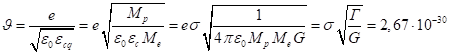 м2 . (23)
м2 . (23)
Данное сечение имеет величину, почти точно совпадающую с геометрическим
сечением нуклона, и существенно превышает сечение ![]() м2 взаимодействия гравитонов с
веществом. Чтобы выяснить большое различие между
м2 взаимодействия гравитонов с
веществом. Чтобы выяснить большое различие между ![]() и
и ![]() ,
выразим
,
выразим ![]() из (22), используем
из (22), используем ![]() из (19) и учтём определение
из (19) и учтём определение ![]() :
:
![]() . (24)
. (24)
Из сравнения (24) и (21) при условии ![]() следует, что если в (21) перейти от сечения
следует, что если в (21) перейти от сечения ![]() к сечению
к сечению ![]() , то
одновременно с этим необходимо гравитационную постоянную
, то
одновременно с этим необходимо гравитационную постоянную ![]() заменить на постоянную сильной гравитации
заменить на постоянную сильной гравитации ![]() . В
(24) плотность энергии
. В
(24) плотность энергии ![]() поля гравитонов на уровне нуклонов полностью
выражена через параметры нуклонного уровня материи. Точно так же, в (19)
плотность энергии
поля гравитонов на уровне нуклонов полностью
выражена через параметры нуклонного уровня материи. Точно так же, в (19)
плотность энергии ![]() заряженных частиц вакуумного поля выражена
через параметры нуклонного уровня материи. При этом и в (19) и в (24)
используется одно и то же сечение
заряженных частиц вакуумного поля выражена
через параметры нуклонного уровня материи. При этом и в (19) и в (24)
используется одно и то же сечение ![]() взаимодействия частиц вакуумного поля с
веществом, состоящим из нуклонов. Заметим, что в [4]
было найдено, что сечение
взаимодействия частиц вакуумного поля с
веществом, состоящим из нуклонов. Заметим, что в [4]
было найдено, что сечение ![]() взаимодействия гравитонов с веществом из
нуклонов по порядку величины должно равняться сечению протона.
взаимодействия гравитонов с веществом из
нуклонов по порядку величины должно равняться сечению протона.
По аналогии с (24) для поля гравитации на уровне звёзд можно записать:
![]() .
.
Если в этом выражении учесть следующие соотношения с использованием теории размерностей, коэффициентов подобия и (24):
![]() ,
, ![]() ,
, ![]() ,
,
то получится соотношение ![]() Дж/м3, в котором плотность энергии
поля гравитонов на уровне звёзд
Дж/м3, в котором плотность энергии
поля гравитонов на уровне звёзд ![]() ,
необходимая для удержания вещества нейтронных звёзд, связана с плотностью
энергии
,
необходимая для удержания вещества нейтронных звёзд, связана с плотностью
энергии ![]() .
Поскольку плотность энергии
.
Поскольку плотность энергии ![]() необходима для целостности нуклонов в поле
сильной гравитации, то
необходима для целостности нуклонов в поле
сильной гравитации, то ![]() .
.
С учётом (16), (19), (22) и соотношения ![]() ,
для мощности потока энергии поля заряженных частиц в одном направлении находим:
,
для мощности потока энергии поля заряженных частиц в одном направлении находим:
![]() Вт/м2 . (25)
Вт/м2 . (25)
Ввиду того, что выше плотность энергии ![]() поля заряженных частиц меньше плотности
энергии
поля заряженных частиц меньше плотности
энергии ![]() поля гравитонов в (21), мощность потока
энергии поля заряженных частиц
поля гравитонов в (21), мощность потока
энергии поля заряженных частиц ![]() оказывается меньше мощности потока энергии
поля гравитонов
оказывается меньше мощности потока энергии
поля гравитонов ![]() .
.
6. Оценки сил и
энергий
В [2] и [6] делается предположение о том, что
нейтронные звёзды – магнитары могут обладать положительным электрическим
зарядом величиной до ![]() Кл, где
Кл, где ![]() – элементарный электрический заряд. В данном
соотношении для зарядов используются коэффициенты подобия в соответствии с
теорией размерностей.
– элементарный электрический заряд. В данном
соотношении для зарядов используются коэффициенты подобия в соответствии с
теорией размерностей.
Электрическая энергия протона на
поверхности заряженного магнитара будет достигать ![]() Дж или
Дж или ![]() эВ.
Соответствующая электрическая сила будет равна
эВ.
Соответствующая электрическая сила будет равна ![]() Н.
Н.
Предполагается, что именно электрическая энергия в поле магнитара является источником энергии космических лучей высокой энергии.
Для модуля гравитационной энергии протона на поверхности магнитара
аналогично имеем: ![]() Дж.
Дж.
Эта энергия и связанная с ней сила гравитации явно
недостаточны, чтобы удержать протон, на который действует сила отталкивания со
стороны всего заряда магнитара. Однако магнитар выглядит как огромное атомное
ядро, состоящее из множества близко расположенных друг к другу нуклонов. Между
нуклонами действует сильное взаимодействие, удерживающее их вместе. В
гравитационной модели сильного взаимодействия [6]
для описания сильного взаимодействия используется идея сильной гравитации.
Нуклоны в ядрах атомов притягиваются друг к другу посредством сильной
гравитации и отталкиваются друг от друга посредством поля кручения,
возникающего от быстрого вращения нуклонов. Согласно лоренц-инвариантной теории
гравитации [1-2], поле кручения возникает аналогично магнитному полю в
электромагнетизме, а в общей теории относительности соответствует
гравитомагнитному полю. Баланс сил притяжения и отталкивания, возникающих от
сильной гравитации, может быть ответственен за целостность атомных ядер, а
также и за целостность заряженной нейтронной звезды.
Оценки сил и энергий в атомных ядрах мы делали в [6].
Например, ядро никеля ![]() состоит из
состоит из ![]() нуклонов, среди которых 28
протонов и 34 нейтрона. Масса этого ядра
нуклонов, среди которых 28
протонов и 34 нейтрона. Масса этого ядра ![]() кг,
а радиус получается из экспериментов по рассеянию электронов по формуле:
кг,
а радиус получается из экспериментов по рассеянию электронов по формуле: ![]() м,
где
м,
где ![]() м. С
этими данными оценим силу, действующую со стороны ядра на протон, находящийся
на поверхности ядра, с помощью сильной гравитации:
м. С
этими данными оценим силу, действующую со стороны ядра на протон, находящийся
на поверхности ядра, с помощью сильной гравитации: ![]() Н.
Н.
Поверхность магнитара как нейтронной звезды состоит по
всей видимости из ядер элементов типа железа, никеля и более тяжёлых ядер, так
как у них энергия связи на один нуклон максимальна. Если бы протон был вблизи
одного из таких ядер на поверхности магнитара, сила ![]() удержала бы протон, действуя против силы
электрического отталкивания
удержала бы протон, действуя против силы
электрического отталкивания ![]() Н от
заряда магнитара. Но концентрация ядер на поверхности звезды такова, что протон
в среднем будет находится где-то между ядрами на некотором расстоянии
Н от
заряда магнитара. Но концентрация ядер на поверхности звезды такова, что протон
в среднем будет находится где-то между ядрами на некотором расстоянии ![]() от них.
от них.
Для удержания протона необходимо условие ![]() ,
откуда вытекает, что должно быть
,
откуда вытекает, что должно быть ![]() м.
Для куба с ребром, равным
м.
Для куба с ребром, равным ![]() , в
вершинах которого расположены 8 ядер
, в
вершинах которого расположены 8 ядер ![]() , а протон находится в центре куба, плотность вещества получается
равной
, а протон находится в центре куба, плотность вещества получается
равной ![]() кг/м3. Плотность вещества на
поверхности магнитара должна превышать это значение, чтобы могло выполняться
условие устойчивости в отношении электрических сил. С другой стороны, оценки в [8] плотности вещества в коре нейтронной звезды дают, что при плотности, равной
кг/м3. Плотность вещества на
поверхности магнитара должна превышать это значение, чтобы могло выполняться
условие устойчивости в отношении электрических сил. С другой стороны, оценки в [8] плотности вещества в коре нейтронной звезды дают, что при плотности, равной ![]() кг/м3 и более, ядра
кг/м3 и более, ядра ![]() начинают распадаться.
Следовательно, в коре магнитара должны преобладать более тяжёлые
ядра, и в частности, типичным ядром согласно [8]
оказывается
начинают распадаться.
Следовательно, в коре магнитара должны преобладать более тяжёлые
ядра, и в частности, типичным ядром согласно [8]
оказывается ![]() .
Из приведённых расчётов следует, что заряд магнитара является практически
максимальным зарядом, который может нести звезда без ущерба для своей
целостности. При этом основной вклад в устойчивость звезды вносит не обычная, а
сильная гравитация, действующая на уровне атомных ядер.
.
Из приведённых расчётов следует, что заряд магнитара является практически
максимальным зарядом, который может нести звезда без ущерба для своей
целостности. При этом основной вклад в устойчивость звезды вносит не обычная, а
сильная гравитация, действующая на уровне атомных ядер.
С помощью коэффициентов подобия можно вычислить массу, радиус и заряд
праона – частицы, которая относится к протону так же, как протон относится к
магнитару: ![]() кг,
кг, ![]() м,
м, ![]() Кл. Если праон расположен на поверхности протона, его
электрическая энергия и гравитационная энергия в поле сильной гравитации будут
равны:
Кл. Если праон расположен на поверхности протона, его
электрическая энергия и гравитационная энергия в поле сильной гравитации будут
равны: ![]() Дж,
Дж, ![]() Дж.
Дж.
Отношение этих энергий даёт то же самое, что и
отношение электрической энергии протона на поверхности магнитара к
гравитационной энергии этого протона в поле тяжести магнитара. В
субстанциональной модели протона и нейтрона, представленной в [6], предполагается, что нуклоны состоят
из нейтральных и заряженных праонов аналогично тому, как нейтронные звёзды
состоят из нуклонов. Кроме этого, по аналогии с составом космических лучей, состоящих
в основном из релятивистских протонов, мы можем предположить, что заряженная
компонента вакуумного поля может состоять из праонов,
ускоренных положительно заряженными атомными ядрами до высоких энергий.
В настоящее время регистрируются космические лучи с
энергией до ![]() эВ
или 9,6 Дж в расчёте на 1 нуклон [9]. Полагая, что это есть энергия ускоренного
протона, разделим её на коэффициент подобия по энергии и найдём соответствующую
энергию праона:
эВ
или 9,6 Дж в расчёте на 1 нуклон [9]. Полагая, что это есть энергия ускоренного
протона, разделим её на коэффициент подобия по энергии и найдём соответствующую
энергию праона: ![]() Дж.
Приравнивая эту энергию к энергии
Дж.
Приравнивая эту энергию к энергии ![]() одной заряженной частицы вакуумного поля,
можно оценить концентрацию этих заряженных частиц как концентрацию
релятивистски движущихся праонов. С учётом (19) и (22) имеем:
одной заряженной частицы вакуумного поля,
можно оценить концентрацию этих заряженных частиц как концентрацию
релятивистски движущихся праонов. С учётом (19) и (22) имеем:
![]() м-3
.
м-3
.
Умножая данную концентрацию заряженных частиц на заряд одного праона ![]() и на скорость света, можно оценить плотность
тока в вакууме в одном направлении, возникающую от потока положительно
заряженных праонов в одном направлении при кубическом распределении:
и на скорость света, можно оценить плотность
тока в вакууме в одном направлении, возникающую от потока положительно
заряженных праонов в одном направлении при кубическом распределении:
![]() А/м2
.
А/м2
.
Кроме плотности тока ![]() , мы
должны ожидать ещё аналогичную плотность тока
, мы
должны ожидать ещё аналогичную плотность тока ![]() в том же направлении, возникающую от потока
отрицательно заряженных праонов. Это должно обеспечивать определённую степень
электронейтральности вакуума и существование электрических сил отталкивания и
притяжения.
в том же направлении, возникающую от потока
отрицательно заряженных праонов. Это должно обеспечивать определённую степень
электронейтральности вакуума и существование электрических сил отталкивания и
притяжения.
Рассмотрим теперь вопрос о проницаемости вещества нейтронной звезды для гравитонов и заряженных частиц вакуумного поля, соответственно. Мощности флюенса из единичного телесного угла аналогично (2) имеют вид:
![]() ,
, ![]() .
.
Если нейтронная звезда имеет радиус 12 км и массу 1,35 массы Солнца, то
средняя концентрация нуклонов составит ![]() м-3
. Средняя концентрация положительного заряда в магнитаре равна
м-3
. Средняя концентрация положительного заряда в магнитаре равна ![]() м-3
. Полагая, что
м-3
. Полагая, что ![]() км,
для показателей экспонент с учётом (21) и (23) находим:
км,
для показателей экспонент с учётом (21) и (23) находим: ![]() ,
, ![]() .
Отсюда следует, что если на пути потока гравитонов поставить три нейтронных
звезды, то поток уменьшится приблизительно в
.
Отсюда следует, что если на пути потока гравитонов поставить три нейтронных
звезды, то поток уменьшится приблизительно в ![]() раз, где
раз, где ![]() – основание натурального логарифма. Но для
потока заряженных частиц вакуумного поля для заметного уменьшения этого потока
нужно поставить в ряд уже порядка 140 магнитаров.
– основание натурального логарифма. Но для
потока заряженных частиц вакуумного поля для заметного уменьшения этого потока
нужно поставить в ряд уже порядка 140 магнитаров.
Это различие потоков позволяет объяснить эффект насыщения удельной
энергии связи, когда энергия связи ядра в расчёте на один нуклон в зависимости
от количества нуклонов в ядрах вначале растёт, достигает максимума 8,79 МэВ на
один нуклон для ядра ![]() , и затем начинает уменьшаться. Для лёгких ядер рост удельной
энергии хорошо соответствует росту удельной гравитационной энергии ядра в поле
сильной гравитации, когда энергия растёт пропорционально квадрату массы и
обратно пропорционально радиусу ядра. Эффект насыщения начинает сказываться в
диапазоне от 17 до 23 нуклонов, составляющих ядро. При этом добавление нового
нуклона к ядру увеличивает энергию не пропорционально квадрату массы, а в
меньшей степени. Это связано с тем, что гравитоны сильной гравитации не могут
пройти сквозь ядро с множеством нуклонов, как это видно из показателя
экспоненты. Каждый новый нуклон просто прижимается к ядру извне сильной
гравитацией, пока для больших ядер эта сила не достигнет максимума,
обусловленного давлением потока гравитонов. Однако заряженные частицы
вакуумного поля в этих условиях имеют почти в 50 раз большую длину пробега и
потому положительная электрическая энергия протонов ядра дополнительно
уменьшает отрицательную гравитационную энергию ядра, давая основной вклад в
наблюдаемое уменьшение удельной энергии связи массивных ядер.
, и затем начинает уменьшаться. Для лёгких ядер рост удельной
энергии хорошо соответствует росту удельной гравитационной энергии ядра в поле
сильной гравитации, когда энергия растёт пропорционально квадрату массы и
обратно пропорционально радиусу ядра. Эффект насыщения начинает сказываться в
диапазоне от 17 до 23 нуклонов, составляющих ядро. При этом добавление нового
нуклона к ядру увеличивает энергию не пропорционально квадрату массы, а в
меньшей степени. Это связано с тем, что гравитоны сильной гравитации не могут
пройти сквозь ядро с множеством нуклонов, как это видно из показателя
экспоненты. Каждый новый нуклон просто прижимается к ядру извне сильной
гравитацией, пока для больших ядер эта сила не достигнет максимума,
обусловленного давлением потока гравитонов. Однако заряженные частицы
вакуумного поля в этих условиях имеют почти в 50 раз большую длину пробега и
потому положительная электрическая энергия протонов ядра дополнительно
уменьшает отрицательную гравитационную энергию ядра, давая основной вклад в
наблюдаемое уменьшение удельной энергии связи массивных ядер.
Ранее в [4] мы оценили максимальную силу между двумя звёздными объектами:
![]() Н,
Н,
где ![]() для случая однородной плотности каждого
объекта, и предполагается, что потоки гравитонов полностью задерживаются этими
объектами, расположенными вблизи друг друга.
для случая однородной плотности каждого
объекта, и предполагается, что потоки гравитонов полностью задерживаются этими
объектами, расположенными вблизи друг друга.
Аналогичное выражение для максимальной силы на нуклонном уровне материи
после замены гравитационной постоянной на постоянную сильной гравитации с
учётом коэффициента подобия по скоростям ![]() имеет вид:
имеет вид:
![]() Н.
Н.
Отметим, что соответствующее отношение гравитационной энергии и силы
между двумя протонами к их электростатической энергии и силе равно отношению массы
протона к массе электрона. Действительно, для сил и их отношения с учётом
определения постоянной сильной гравитации ![]() имеем:
имеем:
![]() ,
, ![]() ,
, ![]() .
.
Мы можем объяснить это тем, что в выражении для ![]() показатель экспоненты для потока заряженных
частиц вакуумного поля в магнитаре, а значит, и в протоне, меньше, чем
соответствующий показатель экспоненты для потока гравитонов в выражении для
показатель экспоненты для потока заряженных
частиц вакуумного поля в магнитаре, а значит, и в протоне, меньше, чем
соответствующий показатель экспоненты для потока гравитонов в выражении для ![]() .
Гравитоны сильнее задерживаются в веществе протона, чем заряженные частицы
вакуумного поля, и потому гравитационная сила больше, чем электрическая сила.
.
Гравитоны сильнее задерживаются в веществе протона, чем заряженные частицы
вакуумного поля, и потому гравитационная сила больше, чем электрическая сила.
При переходе от плотных и
заряженных объектов типа магнитаров и протонов к окружающим нас телам ситуация
с отношением сил меняется. Гравитационная сила быстро убывает по мере
уменьшения массы тел и мы мало можем влиять на это. Однако путём изменения зарядов
тел мы можем менять их электрическое взаимодействие, так что электрическая сила
может оказаться во много раз больше гравитационной силы между этими телами. Это
видно из отношения электрической и гравитационной сил для двух одинаковых тел с
массами ![]() и зарядами
и зарядами ![]() ,
которое пропорционально квадрату заряда:
,
которое пропорционально квадрату заряда: ![]() .
.
Возьмём к примеру два железных шара радиуса ![]() см
каждый. При плотности железа 7874 кг/м3 это даёт массу каждого шара,
равную приблизительно 4,1 кг. Для равенства величин гравитационной и
электрической сил достаточно зарядить шары до заряда
см
каждый. При плотности железа 7874 кг/м3 это даёт массу каждого шара,
равную приблизительно 4,1 кг. Для равенства величин гравитационной и
электрической сил достаточно зарядить шары до заряда ![]() Кл,
так что потенциал каждого шара достигнет величины
Кл,
так что потенциал каждого шара достигнет величины ![]() В.
Оценим электрическую энергию праона, пролетающего рядом с шаром, учитывая, что
выше мы оценили заряд праона величиной
В.
Оценим электрическую энергию праона, пролетающего рядом с шаром, учитывая, что
выше мы оценили заряд праона величиной ![]() Кл :
Кл : ![]() Дж.
Дж.
С другой стороны, энергия праона, рассматриваемого как релятивистская
частица и подобная по свойствам космическим лучам, была найдена выше в виде: ![]() Дж.
Дж.
Сравнение этих двух энергий позволяет сделать следующие выводы. Во-первых, даже слабо заряженные тела, взаимодействующие на уровне малой по величине гравитационной силы, могут влиять на движение праонов рядом с ними и отклонять их в сторону. Это обосновывает картину движения заряженных частиц вакуумного поля вблизи заряженных тел на рисунках 1-3 и наши расчёты электрической силы. Во-вторых, если уменьшать заряды и увеличивать размеры тел, то могут проявиться отклонения от закона Кулона. Однако эти отклонения нужно будет отличить от гравитационной силы, которая при этом становится больше электрической силы.
Последний вывод можно уточнить следующим образом. Для того чтобы искать
отклонения от закона Кулона, желательно выполнение условия небольших
потенциалов ![]() В. Чтобы уменьшить зависимость от
гравитационной силы, следует условие
В. Чтобы уменьшить зависимость от
гравитационной силы, следует условие ![]() или
или ![]() . Из
этого для подходящего электрического потенциала одного шара имеем:
. Из
этого для подходящего электрического потенциала одного шара имеем: 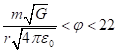 В,
или
В,
или ![]() кг/м.
кг/м.
Для шаров из железа это даёт ![]() см,
см, ![]() кг.
Ещё одно осложнение в экспериментах по поиску отклонения от закона Кулона
связано с тем, что в проводящих телах некомпенсированные заряды расположены в
тонком слое на поверхности тел, с толщиной порядка 1 или 2 атомных слоёв.
Свободные электроны легко смещаются от равновесного положения во внешнем
электрическом поле, либо отталкиваясь, либо притягиваясь к источнику внешнего
поля, изменяя тем самым свою концентрацию на теле. За счёт этого у двух
взаимодействующих металлических заряженных шаров появляются дополнительные
электрические силы, которые обычно вычисляются методом изображений.
кг.
Ещё одно осложнение в экспериментах по поиску отклонения от закона Кулона
связано с тем, что в проводящих телах некомпенсированные заряды расположены в
тонком слое на поверхности тел, с толщиной порядка 1 или 2 атомных слоёв.
Свободные электроны легко смещаются от равновесного положения во внешнем
электрическом поле, либо отталкиваясь, либо притягиваясь к источнику внешнего
поля, изменяя тем самым свою концентрацию на теле. За счёт этого у двух
взаимодействующих металлических заряженных шаров появляются дополнительные
электрические силы, которые обычно вычисляются методом изображений.
7. Взаимодействие заряда тела с вакуумным полем
Закон Кулона благодаря наличию заряженных частиц в вакуумном поле может быть объяснён с помощью модели Лесажа. Однако не только потоки заряженных частиц оказывают влияние на взаимодействие заряженных тел, но и сами заряды тел влияют на потоки заряженных частиц вокруг тел. Одно из таких воздействий заключается в отклонении заряженных частиц от их траекторий, как описано в предыдущем разделе. Кроме этого, у каждого заряженного тела возникает определённый баланс энергии и импульса при взаимодействии с вакуумным полем.
Рассмотрим плотность энергии поля заряженных частиц внутри заряженного
тела и рядом с ним. Пусть имеется тело в виде куба с ребром ![]() .
Количество заряженных частиц
.
Количество заряженных частиц ![]() в единицу времени через единичную площадку при
движении в веществе уменьшается по формуле (11). За время
в единицу времени через единичную площадку при
движении в веществе уменьшается по формуле (11). За время ![]() шесть потоков заряженных частиц с каждой из
сторон пройдут куб насквозь через грани с площадью
шесть потоков заряженных частиц с каждой из
сторон пройдут куб насквозь через грани с площадью ![]() и изменятся до величины:
и изменятся до величины:
![]() ,
, ![]() ,
,
где ![]() есть число прошедших через куб заряженных
частиц.
есть число прошедших через куб заряженных
частиц.
Если бы заряженные частицы пролетали через такой же пустой объём, их
количество на выходе было бы ![]() .
Следовательно, количество заряженных частиц, которые взаимодействовали с
веществом заряженного тела в течение времени
.
Следовательно, количество заряженных частиц, которые взаимодействовали с
веществом заряженного тела в течение времени ![]() ,
составит:
,
составит:
![]() .
.
Как было показано в [5], практически вся энергия поля гравитонов, которые взаимодействуют с веществом, переизлучается обратно в поле гравитонов, не нагревая существенно вещество тел. Это относится и к потокам заряженных частиц вакуумного поля, которые передают веществу импульс силы с возвратом энергии в вакуумное поле.
Оценим с учётом (19) плотность энергии тех заряженных частиц, которые взаимодействуют с веществом тел:
![]() .
(26)
.
(26)
Вычислим из (26) мощность излучения энергии от заряженных частиц из тела
в виде куба, умножая ![]() на объём
на объём ![]() и деля на время
и деля на время ![]() .
Выражая концентрацию заряда через заряд тела, с учётом (19) имеем:
.
Выражая концентрацию заряда через заряд тела, с учётом (19) имеем:
![]() ,
, ![]() . (27)
. (27)
Из (27) следует, что мощность излучения ![]() ,
понимаемая как мощность излучения тех потоков заряженных частиц вакуумного
поля, которые взаимодействовали с заряженным веществом тела и передали ему свой
импульс, пропорциональна заряду тела
,
понимаемая как мощность излучения тех потоков заряженных частиц вакуумного
поля, которые взаимодействовали с заряженным веществом тела и передали ему свой
импульс, пропорциональна заряду тела ![]() .
Это означает, что заряд, имеющийся у тела, может быть выражен через параметры
потоков заряженных частиц вакуумного поля, взаимодействующих с телом.
.
Это означает, что заряд, имеющийся у тела, может быть выражен через параметры
потоков заряженных частиц вакуумного поля, взаимодействующих с телом.
В (27) присутствует произведение ![]() ,
равное количеству некомпенсированных элементарных зарядов в рассматриваемом
теле. Тогда мощность излучения в расчёте на один элементарный заряд с учётом
(19), (22-23) будет равна:
,
равное количеству некомпенсированных элементарных зарядов в рассматриваемом
теле. Тогда мощность излучения в расчёте на один элементарный заряд с учётом
(19), (22-23) будет равна:
![]() Вт. (28)
Вт. (28)
Отношение мощности излучения ![]() к средней энергии заряженной частицы
к средней энергии заряженной частицы ![]() даёт количество заряженных частиц, которые в
единицу времени взаимодействуют с одним некомпенсированным элементарным зарядом
вещества и передают ему свой импульс. Согласно (28), это количество заряженных
частиц равно произведению
даёт количество заряженных частиц, которые в
единицу времени взаимодействуют с одним некомпенсированным элементарным зарядом
вещества и передают ему свой импульс. Согласно (28), это количество заряженных
частиц равно произведению ![]() ,
причём сечение
,
причём сечение ![]() характеризует эффективную площадь
взаимодействия элементарного заряда с заряженными частицами, а коэффициент 6
связан с шестью сторонами кубического распределения потоков частиц
характеризует эффективную площадь
взаимодействия элементарного заряда с заряженными частицами, а коэффициент 6
связан с шестью сторонами кубического распределения потоков частиц ![]() в (11).
в (11).
Выражению (27) можно придать другой смысл, если положить, что площадь
грани куба связана с сечением ![]() следующим соотношением:
следующим соотношением: ![]() ,
где
,
где ![]() некоторый численный коэффициент,
некоторый численный коэффициент, ![]() – количество некомпенсированных элементарных
зарядов в кубе. Тогда при условии
– количество некомпенсированных элементарных
зарядов в кубе. Тогда при условии ![]() (27) переписывается так:
(27) переписывается так:
![]() .
.
Из этого соотношения видно, что мощность излучения пропорциональна, с
точностью до коэффициента ![]() , электрической энергии заряженного тела,
извлекаемой из тела за время
, электрической энергии заряженного тела,
извлекаемой из тела за время ![]() прохождения заряженными частицами характерного
размера тела.
прохождения заряженными частицами характерного
размера тела.
Отметим ещё один аспект, касающийся взаимодействия между электромагнитным и гравитационным полями. В концепции общего поля [10] показывается, что векторные поля, включая электромагнитное и гравитационное поля, являются компонентами одного общего поля. При этом в случае выполнения теоремы о равнораспределении энергии уравнения частных полей перестают зависеть друг от друга и по форме аналогичны уравнениям Максвелла. Если же поля взаимодействуют друг с другом, то в гамильтониане это проявляется в членах с энергией поля, где появляются перекрёстные члены с произведениями напряжённостей разных полей. Такое возможно, например, в неустановившихся процессах в системах, не достигших равновесия. С точки зрения вакуумного поля это означает, что в стационарных условиях гравитоны и заряженные частицы вакуумного поля относительно независимо взаимодействуют с веществом, создавая гравитационные и электромагнитные силы. Если же равновесие в системе отсутствует, то кинетическая энергия вещества и энергии одних полей переходят в энергию других полей, в том числе возможен обмен энергиями между гравитонами и заряженными частицами вакуумного поля. Это и приводит к перекрёстным членам в энергии системы.
8. Фотоны и праоны
В этом разделе мы попытаемся уточнить, какие именно частицы могут быть
ответственны за электромагнитные явления. Заряженные частицы вакуумного поля не
только приводят к электрическим силам в законе Кулона, но и должны входить в
состав фотонов, то есть электромагнитных квантов, излучаемых атомами.
Рассмотрим для примера фотон с длиной волны ![]() м и угловой частотой
м и угловой частотой ![]() с-1,
возникающий в атоме водорода при переходе электрона со второго на первый
уровень в серии Лаймана. Вероятность этого перехода равна
с-1,
возникающий в атоме водорода при переходе электрона со второго на первый
уровень в серии Лаймана. Вероятность этого перехода равна ![]() с-1 [11], что даёт среднее время жизни
электрона на втором уровне
с-1 [11], что даёт среднее время жизни
электрона на втором уровне ![]() с,
с,
как некоторую меру длительности излучения фотона во
время перехода. В квантовой механике [12] известна формула для
времени затухания колебаний осциллятора в ![]() раз, где
раз, где ![]() – основание натурального логарифма, с помощью которой получаем следующую оценку:
– основание натурального логарифма, с помощью которой получаем следующую оценку:
![]() с.
с.
где ![]() есть магнитная постоянная.
есть магнитная постоянная.
Длительность излучения фотона можно вычислить
непосредственно в рамках боровской модели атома водорода. В этой модели
электрическая сила между протоном и электроном выступает в роли
центростремительной силы при вращения электрона вокруг ядра в виде протона. При
таком вращении электрон должен излучать электромагнитную волну, так как он всё
время ускоряется в направлении ядра. Формула для мощности излучения заряда при
его вращении хорошо известна, что позволяет связать скорость электрона и
эффективную силу, действующую на электрон от излучения. Момент данной силы
уменьшает момент импульса электрона, приводя к уменьшению радиуса вращения.
Отсюда выводится зависимость радиуса от времени [6]. Из этой зависимости находим длительность излучения фотона как
время перехода электрона со второго на первый уровень энергии. Учитывая, что
средний радиус вращения электрона на втором уровне равен ![]() , а средний радиус вращения
электрона на первом уровне есть радиус Бора
, а средний радиус вращения
электрона на первом уровне есть радиус Бора ![]() ,
имеем:
,
имеем:
![]() с. (29)
с. (29)
Для мгновенной мощности электромагнитного излучения получается формула:
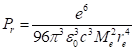 .
.
Отсюда следует сильная зависимость мощности излучения от текущего радиуса
![]() вращения электрона, обратно пропорциональная
четвёртой степени этого радиуса. Получается, что основная энергия фотона
излучается тогда, когда электрон приближается к нижнему уровню энергии.
вращения электрона, обратно пропорциональная
четвёртой степени этого радиуса. Получается, что основная энергия фотона
излучается тогда, когда электрон приближается к нижнему уровню энергии.
Зная длительность излучения, мы можем найти длину фотона: ![]() .
Для вычисления объёма фотона нам понадобится ещё его среднее сечение. В первом
приближении положим, что средний радиус фотона равен
.
Для вычисления объёма фотона нам понадобится ещё его среднее сечение. В первом
приближении положим, что средний радиус фотона равен ![]() ,
что равно
,
что равно ![]() .
Заметим, что в субстанциональной модели электрона [6]
последний рассматривается как тонкий диск, имеющий на основном уровне энергии
внутренний радиус
.
Заметим, что в субстанциональной модели электрона [6]
последний рассматривается как тонкий диск, имеющий на основном уровне энергии
внутренний радиус ![]() и внешний край
и внешний край ![]() , а
радиус Бора
, а
радиус Бора ![]() получается как некоторый характерный радиус
диска и как средний радиус вращения электрона. На втором уровне внешний край
электронного диска также больше, чем средний радиус вращения электрона
получается как некоторый характерный радиус
диска и как средний радиус вращения электрона. На втором уровне внешний край
электронного диска также больше, чем средний радиус вращения электрона ![]() на этом уровне. С учётом этого объём фотона
будет равен:
на этом уровне. С учётом этого объём фотона
будет равен: ![]() .
.
Далее мы будем использовать упрощённую модель фотона из [2], [13], согласно которой фотон состоит из заряженных
частиц, вращение которых вокруг оси фотона создаёт момент импульса фотона.
Кроме этого, внутри фотона как и в электромагнитной волне должны быть взаимно
перпендикулярные периодически изменяющиеся электрические и магнитные поля.
Электромагнитная энергия фотона состоит поровну из электрической и магнитной
компонент, и для суммарной плотности энергии можно записать: ![]() ,
так как в волне
,
так как в волне ![]() .
Напряжённость
.
Напряжённость ![]() электрического поля внутри фотона мы будем
характеризовать амплитудой
электрического поля внутри фотона мы будем
характеризовать амплитудой ![]() .
Поле внутри фотона осциллирует, меняясь от нуля до амплитудного значения,
поэтому для средней плотности электромагнитной энергии фотона мы положим, что
.
Поле внутри фотона осциллирует, меняясь от нуля до амплитудного значения,
поэтому для средней плотности электромагнитной энергии фотона мы положим, что ![]() .
Предположим также, что энергия фотона поровну делится между механической
энергией заряженных частиц и электромагнитной энергией. Энергия фотона
.
Предположим также, что энергия фотона поровну делится между механической
энергией заряженных частиц и электромагнитной энергией. Энергия фотона ![]() пропорциональна постоянной Дирака
пропорциональна постоянной Дирака ![]() и угловой частоте
и угловой частоте ![]() .
Разделив энергию фотона на объём фотона, получим плотность энергии, которую
можно приравнять к удвоенной плотности электромагнитной энергии внутри фотона:
.
Разделив энергию фотона на объём фотона, получим плотность энергии, которую
можно приравнять к удвоенной плотности электромагнитной энергии внутри фотона:
![]() ,
, ![]() . (30)
. (30)
Подставляя в (30)
угловую частоту фотона ![]() с-1, длительность излучения фотона
с-1, длительность излучения фотона ![]() из (29) и радиус фотона
из (29) и радиус фотона ![]() ,
оценим амплитуду напряжённости электрического поля внутри фотона:
,
оценим амплитуду напряжённости электрического поля внутри фотона: ![]() В/м.
Для сравнения, протон создаёт на радиусе Бора напряжённость электрического поля
В/м.
Для сравнения, протон создаёт на радиусе Бора напряжённость электрического поля
![]() В/м.
В/м.
Упрощённо с механической точки зрения фотон можно рассматривать как
длинный тонкий цилиндр, вращающийся с угловой частотой ![]() .
Если в цилиндре находится
.
Если в цилиндре находится ![]() частиц, каждая из которых имеет релятивистскую
массу
частиц, каждая из которых имеет релятивистскую
массу ![]() , то
при однородном распределении частиц момент импульса цилиндра должен равняться
постоянной Дирака, как это подразумевается для всех фотонов:
, то
при однородном распределении частиц момент импульса цилиндра должен равняться
постоянной Дирака, как это подразумевается для всех фотонов:
![]() .
(31)
.
(31)
Из (31) следует, что
механическая энергия вращения частиц, вычисляемая как половина произведения
момента импульса ![]() на угловую скорость вращения, равна половине энергии фотона:
на угловую скорость вращения, равна половине энергии фотона: ![]() .
Другая половина энергии фотона должна быть электромагнитной энергией, что мы
учли в (30). Поскольку момент импульса электрона в атоме квантуется и
пропорционален
.
Другая половина энергии фотона должна быть электромагнитной энергией, что мы
учли в (30). Поскольку момент импульса электрона в атоме квантуется и
пропорционален ![]() , из
(31) следует, что суммарная релятивистская масса
, из
(31) следует, что суммарная релятивистская масса ![]() заряженных частиц, вращающихся внутри фотона,
должна быть порядка массы электрона, чтобы обеспечивать момент импульса
заряженных частиц, вращающихся внутри фотона,
должна быть порядка массы электрона, чтобы обеспечивать момент импульса ![]() фотона. Однако масса
фотона. Однако масса ![]() является лишь малой частью массы всего потока
заряженных частиц вакуумного поля, прошедших через электронный диск за
время излучения фотона
является лишь малой частью массы всего потока
заряженных частиц вакуумного поля, прошедших через электронный диск за
время излучения фотона ![]() из (29). Общая релятивистская масса частиц
всего потока за время
из (29). Общая релятивистская масса частиц
всего потока за время ![]() выражается произведением мощности потока
энергии (25) на время
выражается произведением мощности потока
энергии (25) на время ![]() и на площадь электронного диска
и на площадь электронного диска ![]() , с
последующим делением на квадрат скорости света для перехода от энергии к массе:
, с
последующим делением на квадрат скорости света для перехода от энергии к массе:
![]() кг,
что много больше массы электрона.
кг,
что много больше массы электрона.
Рассмотрим движение некоторой заряженной частицы внутри фотона,
находящейся на радиусе ![]() .
Эта частица вращается с некоторой скоростью
.
Эта частица вращается с некоторой скоростью ![]() вокруг оси фотона, и кроме того, движется со
скоростью света, как и сам фотон, в направлении его распространения. Для периода
вращения частицы можно записать:
вокруг оси фотона, и кроме того, движется со
скоростью света, как и сам фотон, в направлении его распространения. Для периода
вращения частицы можно записать:
![]() ,
, ![]() . (32)
. (32)
В данной модели
фотона существует связь между центростремительной силой, требуемой для вращения
частицы, и электрической силой, действующей на частицу с зарядом ![]() и массой
и массой ![]() . С
учётом (32) имеем:
. С
учётом (32) имеем:
![]() .
(33)
.
(33)
Выразим из (30)
![]() и подставим в (33) для того, чтобы определить
отношение
и подставим в (33) для того, чтобы определить
отношение ![]() для заряженных частиц внутри фотона. С учётом
(29) для
для заряженных частиц внутри фотона. С учётом
(29) для ![]() , а
также принятого нами соотношения
, а
также принятого нами соотношения ![]() и значения угловой частоты фотона
и значения угловой частоты фотона ![]() с-1, находим:
с-1, находим:
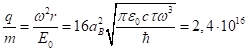 Кл/кг. (34)
Кл/кг. (34)
Для уровня звёзд
отношение заряда к массе должно быть наибольшим у заряженного магнетара, как
нейтронной звезды массы ![]() кг,
несущей согласно нашему предположению электрический заряд
кг,
несущей согласно нашему предположению электрический заряд ![]() Кл. Это даёт:
Кл. Это даёт: ![]() Кл/кг. На уровне атомов то же самое
справедливо для протона, у которого
Кл/кг. На уровне атомов то же самое
справедливо для протона, у которого ![]() Кл/кг. Что же даёт нам соотношение (34)? Из
него следует, что мы должны обратиться к ещё более низкому уровню материи, то
есть к праонному уровню материи. Для покоящегося заряженного праона отношение заряда к массе с учётом
результатов раздела 6 равно:
Кл/кг. Что же даёт нам соотношение (34)? Из
него следует, что мы должны обратиться к ещё более низкому уровню материи, то
есть к праонному уровню материи. Для покоящегося заряженного праона отношение заряда к массе с учётом
результатов раздела 6 равно: ![]() Кл/кг. Учтём теперь, что в (34) масса
заряженной частицы есть релятивистская масса, то есть отношение энергии частицы
к квадрату скорости света. Эту массу можно записать так:
Кл/кг. Учтём теперь, что в (34) масса
заряженной частицы есть релятивистская масса, то есть отношение энергии частицы
к квадрату скорости света. Эту массу можно записать так: ![]() ,
где
,
где ![]() есть фактор Лоренца для частицы, движущейся
практически со скоростью света. Подставляя массу
есть фактор Лоренца для частицы, движущейся
практически со скоростью света. Подставляя массу ![]() в (34) и используя значение
в (34) и используя значение ![]() для праона, определяем фактор Лоренца:
для праона, определяем фактор Лоренца: ![]() .
.
Ранее в разделе 6 мы ссылались на то, что протоны в космических лучах достигают
энергии ![]() эВ,
при энергии покоя протона, равной
эВ,
при энергии покоя протона, равной ![]() эВ.
Следовательно, у самых энергичных протонов космических лучей фактор Лоренца
будет следующий:
эВ.
Следовательно, у самых энергичных протонов космических лучей фактор Лоренца
будет следующий: ![]() .
.
Мы видим, что факторы Лоренца для праонов и для протонов достаточно близки друг к другу. Всё это означает, что фотон представляет собой тесно связанный поток праонов, энергия которых максимальна и соответствует энергии космических лучей на нуклонном уровне материи. При этом праоны соотносятся с протоном так же, как протоны соотносятся с заряженной нейтронной звездой – магнетаром. Из нейтральности фотона так же вытекает, что в его составе должны быть положительно и отрицательно заряженные праоны.
9. Анализ критики теории Лесажа
Если считать, что заряженными частицами вакуумного поля являются
релятивистские праоны, то согласно (28) мощность энергии потоков праонов,
взаимодействующих с каждым некомпенсированным элементарным зарядом некоторого
заряженного тела, равна ![]() Вт.
В [5] мы нашли, что мощность энергии потоков
гравитонов, создающих обычную гравитацию, в расчёте на один нуклон тела равна:
Вт.
В [5] мы нашли, что мощность энергии потоков
гравитонов, создающих обычную гравитацию, в расчёте на один нуклон тела равна:
![]() Вт.
(35)
Вт.
(35)
На нуклонном масштабном уровне материи мы должны перейти от обычной
гравитации к сильной гравитации, которая скрепляет вещество нуклонов. Как
следует из (21-24), для этого сечение взаимодействия гравитонов ![]() в (35) следует заменить на сечение
взаимодействия
в (35) следует заменить на сечение
взаимодействия ![]() :
:
![]() Вт. (36)
Вт. (36)
Из (22) тогда следует, что ![]() ,
,
то есть отношение мощности излучения потоков гравитонов сильной гравитации в расчёте на каждый нуклон тела к мощности излучения потоков заряженных праонов в расчёте на каждый некомпенсированный элементарный заряд тела равно отношению массы протона к массе электрона.
Согласно (35), каждую секунду один нуклон гравитационно-связанного тела
должен переизлучать энергию ![]() Дж
падающих на этот нуклон потоков гравитонов для того, чтобы при этом была
возможна обычная гравитация. Если бы такого переизлучения не было, то из
равенства
Дж
падающих на этот нуклон потоков гравитонов для того, чтобы при этом была
возможна обычная гравитация. Если бы такого переизлучения не было, то из
равенства ![]() можно оценить температуру, на которую должен
был бы нагреться каждый нуклон и любое тело из нуклонов от потоков гравитонов
за одну секунду:
можно оценить температуру, на которую должен
был бы нагреться каждый нуклон и любое тело из нуклонов от потоков гравитонов
за одну секунду: ![]() К. Если же в качестве
К. Если же в качестве ![]() подставить энергии, вытекающие из (28) и (36),
то соответствующие температуры были бы ещё выше.
подставить энергии, вытекающие из (28) и (36),
то соответствующие температуры были бы ещё выше.
Именно проблема нагрева тел является основной проблемой теории Лесажа, как для потоков гравитонов, приводящих к гравитации, так и для потоков заряженных праонов, создающих электромагнитное взаимодействие на нуклонном уровне материи. Действительно, поскольку потоки гравитонов и заряженных частиц должны передать часть своего импульса веществу для возникновения гравитационных и электромагнитных сил, то кажется, что и часть энергии этих потоков должна перейти в кинетическую энергию движения вещества и тем самым нагреть его до высоких температур, что не наблюдается. Многие исследователи теории Лесажа, в том числе Томсон [14] и Пуанкаре [15], основываясь на доводах классической механики и связи между энергией и импульсом, указывали на это и другие обстоятельства, считая их препятствием к признанию теории.
Мы ставим теперь следующий вопрос: возможен ли такой механизм, когда потоки мельчайших релятивистских частиц передают веществу тела некоторый импульс, но при этом почти полностью сохраняют свою энергию и излучаются обратно в окружающее пространство, не нагревая существенно тело? Для ответа на этот вопрос вспомним, что в физике известны поля, не совершающие работы над частицами и не изменяющие их энергии. Это магнитное поле, а также поле кручения в ковариантной теории гравитации [6], известное как гравитомагнитное поле в общей теории относительности. Быстрая заряженная частица, проходящая через область пространства с магнитным полем, отклоняется от первоначального направления движения силой Лоренца, при этом амплитуда импульса частицы и её энергия не меняются. Несмотря на это, возникает сила давления со стороны частицы на источник магнитного поля. Так происходит потому, что импульс как любой вектор может меняться как по величине, так и по направлению, а любое изменение импульса связано с соответствующей силой.
Аналогом нуклонов на уровне звёзд является нейтронная звезда, а потоки праонов соответствуют космическим лучам. Проходящие рядом с нейтронной звездой космические лучи будут взаимодействовать с сильным магнитным полем звезды и отклоняться им. Очевидно, что если с одной из сторон звезды поток космических лучей сильнее, чем с других сторон, то более сильный поток начнёт сдвигать звезду за счёт магнитного давления. Такой же эффект получается и за счёт поля кручения, которое особенно сильное у быстро вращающихся нейтронных звёзд и взаимодействует даже с нейтральными быстро движущимися частицами, так как действует не на движущийся заряд, а на импульс частиц.
На движущиеся в веществе потоки праонов действуют не только магнитные поля нуклонов, но и электрические поля от нескомпенсированных зарядов отдельных протонов и электронов. Эти поля также отклоняют потоки праонов без существенного изменения энергии праонов, что является следствием потенциальности электрического поля. Действительно, если потоки положительно заряженных праонов летят в сторону протона, они вначале тормозятся электрическим полем протона и уменьшают свою энергию, а затем, когда пролетят мимо протона, начинают ускоряться от протона под действием этого же поля и увеличивают свою энергию до прежнего уровня. Аналогично действует на гравитоны и гравитационная сила.
С помощью описанного механизма потоки гравитонов и праонов способны
создавать гравитационное и электромагнитное взаимодействия в веществе тел без
существенного нагрева этих тел. Проходя через вещество, потоки гравитонов и
праонов, состоящие из огромного количества мельчайших частиц, синхронно
действуют на нуклоны, электроны и атомные ядра, сжимая их в направлении
градиента соответствующего потока и создавая гравитационное и электромагнитное
ускорения. То, что сечение взаимодействия ![]() характеризует одновременно электромагнитное
взаимодействие потоков праонов с нуклонами и сильную гравитацию от потоков
гравитонов на уровне нуклонов, и по порядку величины равно сечению нуклона,
говорит о том, что силы взаимодействия действительно могут возникать рядом с
поверхностью нуклонов. Здесь электрическое и гравитационное поля, магнитное
поле и поле кручения нуклонов достигают максимума и способны эффективно
взаимодействовать с потоками праонов и гравитонов. В
качестве гравитонов, приводящих к сильной гравитации, в [5] были предложены
граоны как частицы, которые составляют праон так же, как праоны составляют
нуклон или нуклоны составляют нейтронную звезду. Для того, чтобы граоны могли
стать гравитонами, они должны быть ускорены до релятивистских энергий в
процессах вблизи поверхности праонов.
характеризует одновременно электромагнитное
взаимодействие потоков праонов с нуклонами и сильную гравитацию от потоков
гравитонов на уровне нуклонов, и по порядку величины равно сечению нуклона,
говорит о том, что силы взаимодействия действительно могут возникать рядом с
поверхностью нуклонов. Здесь электрическое и гравитационное поля, магнитное
поле и поле кручения нуклонов достигают максимума и способны эффективно
взаимодействовать с потоками праонов и гравитонов. В
качестве гравитонов, приводящих к сильной гравитации, в [5] были предложены
граоны как частицы, которые составляют праон так же, как праоны составляют
нуклон или нуклоны составляют нейтронную звезду. Для того, чтобы граоны могли
стать гравитонами, они должны быть ускорены до релятивистских энергий в
процессах вблизи поверхности праонов.
Рассмотрим теперь вторую проблему теории
Лесажа, согласно которой при движении должно возникать избыточное давление
гравитонов и заряженных частиц спереди (drag effect), пропорциональное скорости движения тел. В
результате сопротивления движению тел от потоков гравитонов невозможно было бы
долговременное вращение планет вокруг Солнца и не выполнялся бы принцип
свободного движения по инерции в отсутствие сил. Используя кубическое
распределение заряженных частиц вакуумного
поля (9) и мощность флюенса (11) этих частиц, находим для изменения флюенса и
для силы, действующей с одной стороны на неподвижный заряженный куб с ребром ![]() :
:
![]() ,
,
![]() . (37)
. (37)
Величина ![]() в (37) по порядку величины равна
релятивистскому импульсу одного заряженного праона. Пока куб неподвижен в
изотропной системе отсчёта, потоки праонов симметрично проходят через куб со
всех сторон и он неподвижен. Пусть
теперь куб движется вдоль
оси
в (37) по порядку величины равна
релятивистскому импульсу одного заряженного праона. Пока куб неподвижен в
изотропной системе отсчёта, потоки праонов симметрично проходят через куб со
всех сторон и он неподвижен. Пусть
теперь куб движется вдоль
оси ![]() слева направо так, что одна грань куба
перпендикулярна оси
слева направо так, что одна грань куба
перпендикулярна оси ![]() .
При движении куба приходящие с его правой стороны праоны будут иметь
увеличенную энергию
.
При движении куба приходящие с его правой стороны праоны будут иметь
увеличенную энергию ![]() ,
кроме этого увеличивается амплитуда флюенса
,
кроме этого увеличивается амплитуда флюенса ![]() вследствие увеличения частоты появления
праонов, падающих на куб. Так как праоны являются ультрарелятивистскими
частицами, их импульс пропорционален энергии:
вследствие увеличения частоты появления
праонов, падающих на куб. Так как праоны являются ультрарелятивистскими
частицами, их импульс пропорционален энергии: ![]() ,
кроме этого
,
кроме этого ![]() .
Данные соотношения вытекают из преобразований Лоренца, применённых к импульсу и
частоте появления частиц.
.
Данные соотношения вытекают из преобразований Лоренца, применённых к импульсу и
частоте появления частиц.
С другой стороны, мы можем ожидать, что сечение взаимодействия праонов с
веществом должно быть прямо пропорционально квадрату длины де Бройля и обратно
пропорционально квадрату энергии праонов: ![]() .
.
Подобная зависимость сечения является типичной в квантовой теории рассеяния ультрарелятивистских фотонов – чем больше их энергия, тем слабее они взаимодействуют друг с другом [16-17]. При этом мы предполагаем, что фотоны состоят из праонов, а взаимодействие праонов с электромагнитным полем нуклонов является частным случаем взаимодействия фотона на виртуальных фотонах.
Если ![]() ,
, ![]() и
и ![]() зависят от энергии праонов, как указано выше,
то сила в (37) остаётся неизменной как для покоящегося, так и для движущегося
куба. В (37) есть ещё произведение
зависят от энергии праонов, как указано выше,
то сила в (37) остаётся неизменной как для покоящегося, так и для движущегося
куба. В (37) есть ещё произведение ![]() ,
равное количеству некомпенсированных зарядов внутри куба и не зависящее от
движения куба. Сила
,
равное количеству некомпенсированных зарядов внутри куба и не зависящее от
движения куба. Сила ![]() в (37) есть сила с одной стороны, действующая
на куб, ей противостоит аналогичная сила с противоположной стороны куба. Таким
образом, куб может двигаться по инерции, и тормозящая сила от потоков
заряженных частиц вакуумного поля, которая была бы пропорциональна скорости
движения, не возникает. Данный подход к проблеме давления на движущиеся тела от
потоков гравитонов ранее был использован в [2].
в (37) есть сила с одной стороны, действующая
на куб, ей противостоит аналогичная сила с противоположной стороны куба. Таким
образом, куб может двигаться по инерции, и тормозящая сила от потоков
заряженных частиц вакуумного поля, которая была бы пропорциональна скорости
движения, не возникает. Данный подход к проблеме давления на движущиеся тела от
потоков гравитонов ранее был использован в [2].
Проблема аберрации в теории Лесажа иллюстрируется примером, в котором при движении двух гравитационно связанных тел друг возле друга кажется, что с учётом ограниченной скорости движения гравитонов появляется некоторая дополнительная сила. Действительно, пока гравитоны от одного тела дойдут до второго тела, оно сдвинется по орбите от того положения, которое предписывает теория тяготения Ньютона для мгновенно действующей гравитации. В результате гравитоны достигнут второе тело под каким-то другим углом к орбите, что даёт добавочную компоненту силы. Данная проблема была рассмотрена в [4] для случая, когда два тела движутся синхронно в направлении, перпендикулярном линии, соединяющей тела. При этом было показано, что проблема аберрации гравитационной силы исчезает, если к гравитонам применить соотношения специальной теории относительности, учитывающие, что скорость ультрарелятивистских частиц не бесконечна и практически равна скорости света. В обоих случаях, как для покоящихся, так и для движущихся тел, гравитоны приходят к этим телам под одним и тем же углом по отношению к осям собственной системы координат.
Гипотетическая проблема гравитационного экранирования в теории Лесажа
предполагает, что если между двумя телами поместить третье тело, то это
приведёт к более заметному изменению сил между телами, чем это следует из
закона тяготения Ньютона для трёх тел. Измерения возможного экранирования Луной
гравитационного влияния Солнца на Земле в моменты солнечных затмений в пределах
ошибок измерений не находят каких-либо отклонений от теории [18]. Согласно [4],
такое положение дел связано с малостью сечения ![]() взаимодействия гравитонов с веществом. Это
позволяет с достаточно большой точностью раскладывать экспоненты в выражениях
для сил на двучлены и обеспечивает принцип суперпозиции гравитационных сил для
нескольких тел. Заметное отклонение появляется лишь для таких плотных объектов,
как белые карлики и особенно нейтронные звёзды. Согласно (23), сечение
взаимодействия гравитонов с веществом. Это
позволяет с достаточно большой точностью раскладывать экспоненты в выражениях
для сил на двучлены и обеспечивает принцип суперпозиции гравитационных сил для
нескольких тел. Заметное отклонение появляется лишь для таких плотных объектов,
как белые карлики и особенно нейтронные звёзды. Согласно (23), сечение ![]() взаимодействия праонов с заряженным веществом
на 20 порядков больше, чем сечение
взаимодействия праонов с заряженным веществом
на 20 порядков больше, чем сечение ![]() взаимодействия гравитонов с веществом. Однако
концентрации
взаимодействия гравитонов с веществом. Однако
концентрации ![]() некомпенсированных зарядов в веществе как
правило на много порядков меньше, чем концентрации
некомпенсированных зарядов в веществе как
правило на много порядков меньше, чем концентрации ![]() нуклонов. Это позволяет раскладывать
экспоненты в выражениях для сил также и в случае электромагнитного
взаимодействия тел посредством заряженных частиц вакуумного поля, обосновывая
принцип суперпозиции сил.
нуклонов. Это позволяет раскладывать
экспоненты в выражениях для сил также и в случае электромагнитного
взаимодействия тел посредством заряженных частиц вакуумного поля, обосновывая
принцип суперпозиции сил.
10. Заключение
Исходя из предположения, что электрическая сила возникает под действием потоков заряженных частиц, существующих в вакуумном поле, мы вывели выражения для напряжённостей электрического поля внутри шара (14) и за его пределами (7). Эти выражения согласуются с формулами для напряжённостей поля в электростатике. От напряжённостей поля нетрудно перейти к скалярным потенциалам электрического поля, поскольку напряжённость с точностью до знака определяется как градиент потенциала.
Как только электрический скалярный потенциал становится известным, с
помощью специальной процедуры [19] можно найти
4-потенциал, тензор энергии-импульса электромагнитного поля, уравнения
электромагнитного поля, электромагнитную силу, а также вклад электромагнитного
поля в уравнение для определения метрики. Это означает, что теория электромагнитного
поля как в плоском пространстве Минковского, так и в искривлённом
пространстве-времени, полностью обосновывается на субстанциональном уровне,
через потоки заряженных частиц вакуумного поля. При этом зависимость метрики от
потенциала электромагнитного поля позволяет учесть влияние неоднородного
вакуумного поля на результаты пространственно-временных экспериментов,
проводимых как правило на основе использования электромагнитных волн и
приборов.
В (19) и (22) мы сделали оценку плотности энергии поля заряженных частиц, в (23) представили сечение взаимодействия заряженных частиц с веществом, в (25) оценили мощность потока энергии поля заряженных частиц в одном направлении. На основе принципов теории бесконечной вложенности материи в качестве источников поля заряженных частиц предлагаются самые плотные объекты на каждом уровне материи – нейтронные звёзды и магнитары, нуклоны и атомы, праоны как компоненты, составляющие нуклоны, и т.д. Указанные объекты излучают нейтрино, фотоны, высокоэнергичные космические лучи, которые могут давать свой вклад в вакуумное поле, причём на всех уровнях материи.
В формуле (27) мы выразили заряд тела через мощность излучения тех
потоков заряженных частиц вакуумного поля, которые взаимодействовали с веществом
тела и передали ему свой импульс. Благодаря такому взаимодействию,
осуществляется вклад заряженной компоненты вакуумного поля в массу как в меру
инерции тела. Инерция тела проявляется при его ускорении, когда меняется баланс
между падающими на тело и исходящими от него потоками энергии вакуумного поля.
Мы можем выделить в вакуумном поле три компоненты, одна из которых с плотностью
энергии ![]() связана с сильной гравитацией и энергией покоя
частиц, обуславливает целостность нуклонов и атомных ядер и в основном
ответственна за инерцию тел. Другая компонента с плотностью энергии
связана с сильной гравитацией и энергией покоя
частиц, обуславливает целостность нуклонов и атомных ядер и в основном
ответственна за инерцию тел. Другая компонента с плотностью энергии ![]() отвечает за обычную гравитацию, третья
компонента в виде заряженных частиц с плотностью энергии
отвечает за обычную гравитацию, третья
компонента в виде заряженных частиц с плотностью энергии ![]() приводит к электромагнетизму. Две последние
компоненты делают свой собственный вклад в массу тел.
приводит к электромагнетизму. Две последние
компоненты делают свой собственный вклад в массу тел.
Отметим ещё различие в том, как понимается происхождение электрической силы. В нашем подходе потоки заряженных частиц вакуумного поля являются источником электрической силы, существуют как необходимое дополнение к материи в виде элементарных частиц и сложенных из них тел, участвуют в процессах гравитационного скучивания рассеянного вещества, и порождаются сами через излучение от самых плотных объектов типа праонов, нуклонов и нейтронных звёзд. Именно потоки заряженных частиц вакуумного поля являются причиной так называемых токов смещения в вакууме, пропорциональных скорости изменения электрического поля со временем. Примером здесь является заряжаемый конденсатор, между обкладками которого появляется магнитное поле, несмотря на отсутствие тока электронов внутри конденсатора.
В электростатике электрическая сила никак не объясняется, а в квантовой электродинамике путём подбора лагранжиана взаимодействия поля с веществом выводится формула, напоминающая формулу для электрической энергии взаимодействия двух зарядов в электростатике [20]. В качестве интерпретации предлагается картина, в которой заряженные тела обмениваются друг с другом виртуальными фотонами, что приводит к электрическому взаимодействию. При этом используется принцип неопределённости, ограничивающий время жизни виртуальных фотонов. Благодаря виртуальности, фотонам приписываются крайне экзотические свойства, включая возможность отрицательности энергии или наличие импульса без энергии. Энергия фотонов считается пропорциональной постоянной Планка и следовательно, возможность существования фотонов и частиц, принадлежащих низшим уровням материи и с другой постоянной Планка, не рассматривается. Очевидным недостатком такого подхода является трудность с объяснением происхождения виртуальных частиц как таковых и их уникальных свойств.
Если же считать источником электрических сил потоки заряженных частиц в
вакуумном поле, то появляется возможность рассмотреть их рассеяние в процессе
квантовых переходов в атомах. В [6] рассматривается
субстанциональная модель электрона в виде диска, заряженное вещество в котором
вращается дифференциально и обеспечивает магнитный момент электрона. Кроме
этого, спин электрона объясняется как результат сдвига центра диска
относительно ядра и вращения этого центра в дополнение к вращению вещества в
электронном облаке. Если электрон переходит в квантовое состояние с меньшей
энергией, он излучает фотон, уносящий с собой момент импульса, пропорциональный
постоянной Дирака. В таком процессе рассеяние заряженных частиц вакуумного
поля на электронном диске, с учётом действия
магнитного и электрического полей в волновой зоне, приводит к формированию
фотона как некоторого долговременно сохраняющего свою структуру объекта.
В разделе 8 мы рассмотрели модель фотона,
излучаемого в атомном переходе в атоме водорода. Связывая параметры фотона и
его структуру с параметрами излучателя – заряженного электронного диска, нам
удалось определить отношение заряда к массе для частиц, составляющих фотон. В
итоге получилось, что фотоны состоят из праонов очень высоких энергий,
сопоставимых с энергиями, которые имеют космические лучи, если бы эти лучи
создавались на нуклонном уровне материи вблизи протонов. Данные релятивистские
праоны должны составлять основу заряженных частиц вакуумного поля. Действительно, при взаимодействии праонов вакуумного
поля с электроном при атомном переходе происходит
закручивание праонов под действием полей вдоль оси электронного диска, и
возникающий фотон уносит избыточный момент импульса электрона из атома. При
этом часть праонов вакуумного поля входит в
состав фотона, так что скорость фотона практически есть скорость движения
праонов в потоках частиц вакуумного поля.
В отличие от хаотического движения праонов в вакуумном
поле, праоны в фотоне жёстко связаны друг с другом как
электромагнитными, так и гравитационными силами. Ситуация здесь аналогична
положению дел с нуклонами, которые только при особых обстоятельствах могут
образовывать чрезвычайно устойчивые образования – атомные ядра. Согласно
гравитационной модели сильного взаимодействия [6], нуклоны в ядрах атомов
притягиваются друг к другу посредством сильной гравитации и отталкиваются друг
от друга посредством поля кручения, возникающего от быстрого вращения нуклонов.
Для образования ядра нуклоны должны взаимодействовать друг с другом только при
строго определённой ориентации спинов и магнитных моментов и иметь достаточную
начальную энергию, которая позволяет раскрутить нуклоны до нужной скорости
вращения посредством гравитационной индукции. Праоны в фотоне могут взаимодействовать
друг с другом аналогично. Мы можем даже рассчитать постоянную гравитации для
праонного уровня материи с помощью коэффициентов подобия из раздела 5 и
постоянной сильной гравитации ![]() м3·кг-1·с-2
следующим образом, используя теорию размерностей и SPФ симметрию согласно [2]:
м3·кг-1·с-2
следующим образом, используя теорию размерностей и SPФ симметрию согласно [2]: ![]() м3·кг-1·с-2 .
м3·кг-1·с-2 .
В гравитационном поле со столь большой постоянной гравитации праоны фотона могут составлять достаточно жёсткую структуру для того, чтобы фотон мог, не распадаясь, пролетать большие космические расстояния.
В разделе 5 для отношения модуля энергии поля сильной гравитации к
энергии электрического поля протона мы нашли: 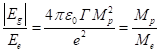 .
Аналогичное равенство следует и для праона, для чего необходимо постоянную
сильной гравитации
.
Аналогичное равенство следует и для праона, для чего необходимо постоянную
сильной гравитации ![]() заменить на постоянную
гравитации для праонного уровня материи
заменить на постоянную
гравитации для праонного уровня материи ![]() и подставить массу и заряд праона из раздела
6:
и подставить массу и заряд праона из раздела
6: 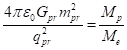 .
.
Совместное рассмотрение эволюции объектов на разных уровнях материи,
например праонов, нуклонов и нейтронных звёзд, позволяет сделать выводы не
только в отношении происхождения гравитационных и электромагнитных сил.
Например, если для нейтронной звезды с массой ![]() массы Солнца и радиусом звезды
массы Солнца и радиусом звезды ![]() км вычислить среднюю
энергию связи в расчёте на один нуклон, то получится
км вычислить среднюю
энергию связи в расчёте на один нуклон, то получится ![]() Дж или 47 МэВ на один нуклон, что
больше, чем энергия связи в атомных ядрах.
Дж или 47 МэВ на один нуклон, что
больше, чем энергия связи в атомных ядрах.
Учитывая, что нейтронные звёзды рождаются во
взрывах сверхновых, когда энергия взрыва уносится нейтрино, излучением и
переходит в кинетическую энергию сбрасываемой оболочки, заметная доля энергии
связи излучается из звезды и переходит в окружающую среду. В [13] мы оценили,
что 61 % всех праонов входят в состав нуклонов, а остальные 39 % формируют
новые частицы – нюоны (являющиеся по своей структуре аналогами белых карликов
на уровне элементарных частиц) или существуют отдельно. Эта же пропорция
остаётся и на уровне звёзд: 61 % всех нуклонов с течением времени войдёт в
состав нейтронных звёзд, а остальные нуклоны останутся либо в виде газа, либо в
виде вещества белых карликов. Нюоны как аналоги белых карликов ввиду своего
значительного присутствия в космическом пространстве могут обеспечить эффект
красного смещения в спектрах далёких галактик, объяснить фоновое излучение и
тёмную материю, и т.д.
Следовательно, концентрация свободных протонов
в видимой Вселенной должна быть того же порядка, что и усреднённая по всему
пространству концентрация нуклонов в звёздах, то есть порядка концентрации
барионов ![]() м-3 , согласно выводам Lambda-Cold Dark Model [21]. С учётом этого, произведение концентрации барионов и энергии связи нейтронной звезды в
расчёте на один нуклон даст нам оценку максимальной плотности энергии излучения
в космическом пространстве:
м-3 , согласно выводам Lambda-Cold Dark Model [21]. С учётом этого, произведение концентрации барионов и энергии связи нейтронной звезды в
расчёте на один нуклон даст нам оценку максимальной плотности энергии излучения
в космическом пространстве: ![]() Дж/м3
. И действительно, плотность энергии в реликтовом излучении равна
Дж/м3
. И действительно, плотность энергии в реликтовом излучении равна ![]() Дж/м3,
и такого же порядка плотности энергии в излучении звёзд, магнитных полях, в
космических лучах и в кинетической энергии движения частиц газа. Сумма этих
плотностей энергии не превышает максимальной
плотности энергии
Дж/м3,
и такого же порядка плотности энергии в излучении звёзд, магнитных полях, в
космических лучах и в кинетической энергии движения частиц газа. Сумма этих
плотностей энергии не превышает максимальной
плотности энергии ![]() .
.
В заключение оценим длину свободного пробега заряженных
частиц вакуумного поля в космическом
пространстве, беря в первом приближении в качестве концентрации зарядов
величину ![]() элементарного заряда на кубический метр, что
равно средней концентрации барионов во Вселенной. Данное приближение даёт лишь
минимальное значение длины свободного пробега, так как в среднем вещество во
Вселенной нейтрально, а
элементарного заряда на кубический метр, что
равно средней концентрации барионов во Вселенной. Данное приближение даёт лишь
минимальное значение длины свободного пробега, так как в среднем вещество во
Вселенной нейтрально, а ![]() должно отражать среднюю концентрацию общего
заряда Вселенной. Из соотношения
должно отражать среднюю концентрацию общего
заряда Вселенной. Из соотношения ![]() при данной концентрации зарядов и значении
при данной концентрации зарядов и значении ![]() согласно (23) находим длину свободного пробега
заряженных частиц:
согласно (23) находим длину свободного пробега
заряженных частиц: ![]() м.
Эта величина почти на 3 порядков больше видимого размера Вселенной,
оцениваемого величиной 14 миллиардов парсек или
м.
Эта величина почти на 3 порядков больше видимого размера Вселенной,
оцениваемого величиной 14 миллиардов парсек или ![]() м.
Следовательно, заряженные частицы вполне могут
достичь нашей Вселенной издалека, где они могут быть рождены в достаточной
концентрации, чтобы соответствовать требуемой плотности энергии. Мы не
поддерживаем модель Большого взрыва, ограничивающее время жизни Вселенной
величиной 13,8 млрд. лет, объясняя другим путём
явления, связанные с этой моделью [13]. Тогда у заряженных частиц вакуумного
поля может быть достаточно времени для того, чтобы
попасть в нашу Вселенную извне и достичь здесь равновесной концентрации
м.
Следовательно, заряженные частицы вполне могут
достичь нашей Вселенной издалека, где они могут быть рождены в достаточной
концентрации, чтобы соответствовать требуемой плотности энергии. Мы не
поддерживаем модель Большого взрыва, ограничивающее время жизни Вселенной
величиной 13,8 млрд. лет, объясняя другим путём
явления, связанные с этой моделью [13]. Тогда у заряженных частиц вакуумного
поля может быть достаточно времени для того, чтобы
попасть в нашу Вселенную извне и достичь здесь равновесной концентрации ![]() м-3
.
м-3
.
В последнем разделе мы рассмотрели основные возражения против теории Лесажа и представили свои аргументы, поддерживающие эту теорию. Это стало возможным благодаря учёту специальной теории относительности и особенностей взаимодействия гравитонов и заряженных частиц вакуумного поля с веществом. По нашему мнению, модернизированная модель Лесажа наиболее естественным образом объясняет происхождение гравитационных и электромагнитных сил, а теория бесконечной вложенности материи – эволюционное происхождение гравитонов и заряженных частиц вакуумного поля. Кроме этого мы можем предположить, что роль гравитонов обычной гравитации играют заряженные праоны, а роль гравитонов сильной гравитации играют заряженные граоны. Для нейтральных тел действие потоков этих частиц приводит к гравитационным силам, а у заряженных тел возникают ещё электромагнитные силы.
Список использованных источников
1. Oliver
Heaviside. A
Gravitational and Electromagnetic Analogy, Part I, The Electrician, Vol.
31, 281-282 (1893).
2. Федосин С.Г. Физика и философия подобия от преонов до метагалактик. Пермь, Стиль-МГ, 1999, 544 стр., Табл.66, Ил.93, Библ. 377 назв. ISBN 5-8131-0012-1.
3.
Maurizio
Michelini. A Flux of Micro Quanta Explains Relativistic Mechanics
and the Gravitational Interaction. Apeiron.
2007, Vol. 14, No 2, P. 65-94.
4. Fedosin S.G. Model of Gravitational Interaction
in the Concept of Gravitons. Journal of Vectorial Relativity, 2009, Vol. 4, No.
1, P. 1 – 24; Модель гравитационного взаимодействия в концепции гравитонов.
5. Fedosin S.G. The graviton field as
the source of mass and gravitational force in the modernized Le Sage’s model. Physical Science International Journal, ISSN:
2348-0130, Vol. 8, Issue 4, P. 1-18 (2015). http://dx.doi.org/10.9734/PSIJ/2015/22197.
6. Федосин С.Г. Физические теории и бесконечная вложенность материи. Пермь, 2009, 842 стр., Табл. 21, Ил.41, Библ. 289 назв. ISBN 978-5-9901951-1-0.
7. Fedosin S.G. The radius of the proton in the self-consistent model. Hadronic Journal, 2012, Vol. 35, No. 4, P. 349 – 363; Радиус протона в самосогласованной модели.
8. Riccardo Belvedere, Daniela
Pugliese, Jorge A. Rueda, Remo Ruffini, She-Sheng Xue. Neutron star equilibrium configurations within a fully relativistic
theory with strong, weak, electromagnetic, and gravitational interactions. Nuclear Physics A, 2012, Vol. 883,
1 , P. 1–24. http://dx.doi.org/10.1016/j.nuclphysa.2012.02.018 .
9. T. K. Gaisser. Spectrum of
cosmic-ray nucleons, kaon production, and the atmospheric muon charge ratio.
Astropart. Phys. 2012, Vol. 35, P. 801-806. http://dx.doi.org/10.1016/j.astropartphys.2012.02.010.
10. Fedosin S. G. The concept of the general force vector field. OALib Journal, Vol. 3, P. 1-15 (2016). http://dx.doi.org/10.4236/oalib.1102459; Концепция общего силового векторного поля.
11.
WolframAlpha, computational knowledge engine.
12.
Яворский Б.М., Детлаф А.А., Лебедев А.К.
Справочник по физике. 8 изд-е, М: Оникс, 2006.
13. Fedosin S.G. Cosmic Red Shift, Microwave Background, and New Particles. Galilean Electrodynamics, 2012, Vol. 23, Special Issues No. 1, P. 3 – 13; Красное смещение и космическое микроволновое фоновое излучение как следствие взаимодействия фотонов с новыми частицами.
14.
Thomson W. (Lord Kelvin) (1873).
On the
ultramundane corpuscles of Le Sage. Phil.
Mag. Vol. 45, P.
321–332.
15.
Poincaré H. (1913). The New Mechanics. The foundations of science
(Science and Method). New York: Science Press, pp. 517–522 (The Theory of
Lesage).
16.
Karplus
R. and Neuman M. The Scattering of Light by Light. Phys. Rev. Vol. 83, P.776
(1951). http://dx.doi.org/10.1103/PhysRev.83.776.
17.
Berestetskii
V.B., Lifshitz E.M. and Pitaevskii L.P. Relativistic Quantum Theory. Pergamon
Press, 1974.
18.
Unnikrishnan
C. S., Mohapatra A. K. and Gillies G. T. Anomalous gravity data during the 1997
total solar eclipse do not support the hypothesis of gravitational shielding.
Physical Review D, Vol 63, 062002 (2001).
http://dx.doi.org/10.1103/PhysRevD.63.062002.
19.
Fedosin S.G. The Procedure of
Finding the Stress-Energy Tensor and Equations of Vector Field of Any Form. Advanced
Studies in Theoretical Physics, Vol. 8, 2014, no. 18, 771 – 779. http://dx.doi.org/10.12988/astp.2014.47101; Процедура для нахождения тензора энергии-импульса и уравнений векторного поля любого вида.
20. Peierls R. E. The laws of nature. (New York: Charles Scribner's Sons, 1956), 284 pages. ISBN 9780191010255.
21.
Hinshaw, G.F., et.al. Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP)
Observations: Cosmological Parameter Results. ApJS., 2013, Vol.
208, 19H.
Источник: http://sergf.ru/zk.htm