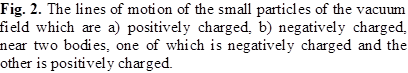Journal of Fundamental and Applied Sciences, Vol. 8, No. 3, pp. 971-1020
(2016). https://dx.doi.org/10.5281/zenodo.845357
S. G. Fedosin
Sviazeva Str. 22-79, Perm,
614088, Perm region, Russian Federation
e-mail:
intelli@list.ru
ABSTRACT
The formula is derived for the electric force inside a
uniformly charged spherical body, as well as for the Coulomb force between the
charged bodies from the standpoint of the model of the vacuum field with
charged particles. The parameters of the fluxes of charged particles are
estimated, including the energy density, energy flux and cross section of
interaction with the charged matter. The energy density of gravitons in the Le
Sage’s gravitation model is expressed in terms of the strong gravitational
constant. The charge to mass ratio is determined for the charged particles that
make up photons and the charged component of the gravitational field. These
particles are identified as praons, while the praon level of matter is
considered a lower level relative to the nucleon level of matter. The analysis
of the main problems of the Le Sage’s model shows that these problems can be
eliminated in the modernized model.
Keywords: vacuum field; graviton field; electric
force; praons; infinite nesting of matter.
1. INTRODUCTION
The similarity of Maxwell equations for the
electromagnetic field, on the one hand, and the Heaviside equations for the
gravitational field in the Lorentz-invariant theory of gravitation [1,2], on
the other hand, as well as the similarity of formulas for the Coulomb force and
the Newton force implies a large probability that the same physical mechanism
is responsible for that. For example, as it was shown in [3], gravity may be
due to the action of electromagnetic micro quanta with a wavelength equal to
the Planck length.
Earlier in [2] and [4],
we derived the formula for the Newton's law of universal gravitation and the
expression of the gravitational constant in terms of the graviton field
parameters, using the modernized Le Sage's theory of gravitation. In addition,
in [5] we found the expression for the body mass as the
function of luminosity of the gravitons interacting with the body, as well as
the expression for the strength of the gravitational field inside the body.
Now we intend to derive the formula for the Coulomb
force between the charged bodies and to specify the parameters of the vacuum
field, consisting of the graviton field and the field of charged particles. In
the modernized Le Sage's theory of gravitation the all-permeating fluxes of the
vacuum field particles consist of neutrinos, photons and charged particles, the
properties of which are similar to high-energy cosmic rays. The presence of
charged particles in the dynamic vacuum field allows us to describe the
electrostatic forces and as a result to justify the electromagnetic phenomena.
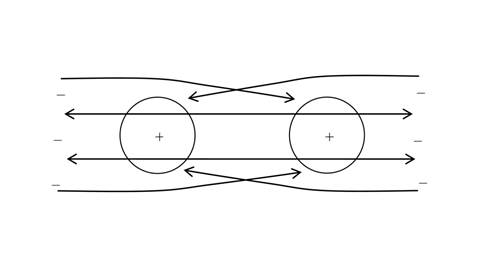
2. THE INTERACTION PICTURE
To understand the electric interaction of the bodies
at a distance from each other, consider Figure 1 which shows the motion of
small charged particles of the vacuum field near the two bodies, one of which is neutral
and the other is positively charged. As can be seen, both positive and negative
particles act symmetrically on the positively charged body, which does not
result in emerging of any additional force in comparison with the force of
gravitation. The same applies to the second neutral body.
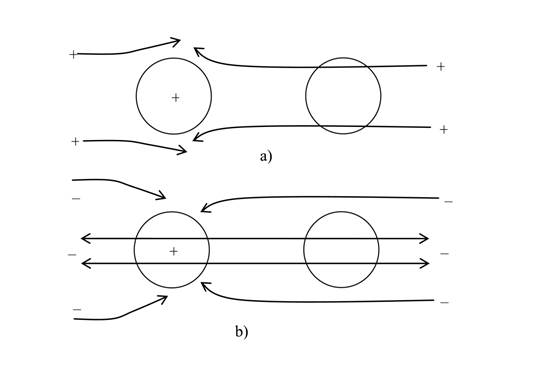
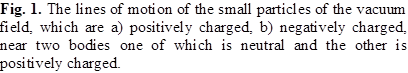
Figure 2 a) shows that the positive particles push the
negatively charged body to the left, and Figure 2 b) shows that the negative
particles push the positively charged body to the right (when the smallest
particles pass through the body similarly to gravitons, they transfer their
momentum to them). Consequently, both bodies will be attracted to each other.
Figure 3 shows the lines of motion of the negative
particles of the vacuum field near two positively charged bodies. Both bodies
attract the negative particles and obtain an additional momentum from them,
which leads to repulsion of bodies. The motion of the positive particles of the
vacuum field in Figure 3 is not shown. It is assumed that
they are repelled from the bodies and therefore their interaction with them is
weak.
For two negatively charged bodies the interaction is
similar to the one shown in Figure 3, only it is necessary to replace the signs
of all charges. This results in the repulsion of similarly charged bodies. The
described above picture can be found in [6].
The common in all the Figures is the fact that depending on the sign of the
charge of two bodies the number of charged particles falling on the body
changes so that after calculating the momentum transferred from these particles
the electric force with required direction emerges. Thus, we reduce the
interaction between the charges at a distance to the interaction by means of
the charged particles of the vacuum field.
3. THE COULOMB FORCE
To determine the expression for the electric force we
use the approach applied in [4-5]. Let’s assume that the fluence rate of the charged
particles of the vacuum field is defined by idealized spherical distribution of
the following form:
.
(1)
According to (1) we suggest that some detector per
unit time 
measures the charged
particles of the vacuum field in the amount 
that fall on the
detector from the solid angle 
per unit surface area 
perpendicularly to
this surface.
We will assume that inside the matter of each charged
body an exponential change in the number of charged particles of the vacuum
field takes place, as the flux of these particles travels some path 
in this matter:
,
,
(2)
where 
is the cross section
of interaction of the moving charged particles with the matter, 
is the concentration
of charges associated with the matter.
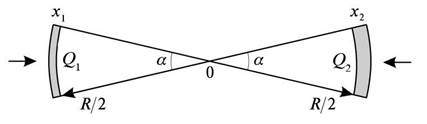
Denoting the positive elementary charge by 
, for the absolute values of charges and the area 
of ball segments in
Figure 4 we obtain the following:
, 
, 
. (3)
The detector is located at point 0 in the middle between
the two segments. For it, each segment is seen at the same solid angle 
at the distance 
, while the transverse areas of the segments are the same and
equal 
. It means that before we apply further arguments for the two
large bodies, we should cut these bodies into segments and then calculate the
total electric force between all the possible pairs of segments by means of
vector summation of particular forces.
Let us first consider the case when the charge 
is positive and the
charge 
is negative.
Comparison with Figure 2 shows that interaction leads to attraction due to
absorbing and scattering of charged particles falling on the charges and
passing through them. As a first approximation we can assume that the main
contribution is made by the flux of negatively charged particles falling on the
charge from the left and the
flux of positively charged particles falling on the charge 
from the right.
Decrease of the flux of charged particles on the left
side after passing the first segment in Figure 4 according to (2) depends on
the thickness of this segment and on the concentration of charge:
.
After that the flux of charged particles passes through
the second segment with further decrease of the flux:
.
We will denote the average momentum of a charged
particle of the vacuum field with 
, and further we will assume that in case of interaction of
such a particle with the charged matter the change in the momentum of the
particle is approximately equal to 
. This is possible if the charged particle is stopped by the
matter or is reflected by the electromagnetic field sideways so that the change
in the momentum vector has the same order of magnitude as the particle momentum
vector itself.
Then the force acting on the second segment from the
left, taking into account (1) is equal to:
.
Decrease of the flux of charged particles, passing through the second segment from the right side, and the force from this side are, respectively:
, 
.
For the force of electrical action on the second
segment we find a symmetrical expression, which is equal by its absolute value
to the force of electrical action on the first segment:
.
Expanding the exponents in the linear approximation by
the rule 
, taking into account (3), we obtain for the force of
attraction between two oppositely charged segments the following:
, 
. (4)
In (4) the force 
is directed oppositely
to the vector 
of the distance from
the first segment to the second segment, since the charge 
is negative.
According to the Coulomb's law, the formula for the electric force between two charged bodies is as follows:
. (5)
Comparing the values of the forces in (4) and (5), we
arrive at the expression for the vacuum permittivity in terms of the parameters
of charged particles fluxes in case of idealized
spherical distribution:
.
(6)
The vacuum permittivity in (6) depends on the cross
section 
of
interaction of charged particles fluxes with the matter, on the
average momentum of one charged particle 
, on the fluence rate 
and on the elementary
charge 
.
From the expression for the force we determine the
electric field strength of one charge at the place of the second charge:
.
(7)
We will assume now that the charge in Figure 4 is
positive like the charge 
. This situation corresponds to Figure 3, from which it follows
that after the passing the charge 
the flux of charged
particles effectively increases before falling on the charge . For the flux of particles moving from the charge 
and falling on the
charge 
the situation is
symmetric. In order to take into account the effect of increasing of the flux
of charged particles, we will introduce an additional coefficient 
. Then the flux of charged particles from the left side after
passing the first segment in Figure 4, taking into account (2), changes to the
value:
.
When passing through the second segment the flux
decreases:
.
The force acting on the second segment from the left,
taking into account (1), is equal to:
.
For the flux of charged particles passing through the
second segment from the right and the force from this side we obtain,
respectively:
, .
For the force of electrical action on the second segment
we obtain:
.
In this expression, we will expand the exponent and
use (3):
. (8)
The repulsion force (8) after changing of the sign of
the charge must be equal by its
magnitude to the attraction force in (4). For this the following condition must
hold: 
. There is a way to prove this relation. To do this, we
should consider the situation in Figure 3, estimate the fluxes of charged
particles from all sides and their interaction with the charged bodies, so that
we could determine how much these fluxes increase when falling on the bodies as
compared to the situation in Figure 1. We will return to this issue again in Section 6.
In Figure (1) we see that if one of the bodies has no
charge, then the charged particles of the vacuum field do not interact with
this body electrically. They pass through it almost freely, except for the
gravitational action. As a result, between the charged and uncharged bodies
there will be only the force of gravitational attraction.
4. THE ELECTRIC FIELD
STRENGTH INSIDE THE BALL
In order to estimate the field inside a uniform ball
it is more convenient to proceed from spherical distribution (1) to cubic
distribution in the form of a mixed derivative for the flux of charged
particles of the vacuum field directed in one way:
,
(9)
where the fluence rate 
indicates the number of charged
particles 
, that during time 
fell on the area 
of one of the cube faces, limiting the volume under consideration, which is perpendicular to the flux.
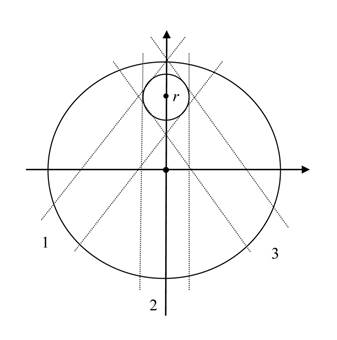
Figure 5 shows the section of a uniform charged ball
with a radius 
, inside which there is a small test body in form of a ball
with a radius 
.
The fluxes of charged particles of the vacuum field
move along the paths 1, 2, 3, as well as other paths, passing the section of
the small ball, which is at a distance 
from the center of the
large ball. If we replace the small ball with the cube of the same size, then
in case of idealized cubic distribution it is enough to consider the vertical
fluxes along the path 2. The fluxes of charged particles passing through the
other faces of the small cube will be symmetrical and will not influence the
electric force. This means that with this approach we will take into account
the fluxes along inclined paths 1 and 3 not directly, but indirectly. All these
fluxes in case of vector summation will give the force, acting on the small
ball and should be added to the force, calculated for path 2.
Let the volume of the small ball be equal to the
volume of some cube. Then for the volume of a cube with an edge 
and
for the absolute value of charge 
of this cube we obtain
the relations:
, 
,
(10)
where 
is the concentration
of charge in the small ball.
Distribution (9) replaces the actual distribution of
the charged particles of the vacuum field in space with the idealized cubic
distribution, when only six fluxes of charged particles fall on the given cubic
volume perpendicularly to the faces of the cube.
By analogy with (2) we can write the dependence of the
fluence rate of the charged particles of the vacuum field on the distance
traveled in the matter:
, 
.
(11)
Let us first assume the charge 
of the small ball in
Figure 5 as negative and the charge of the large ball as positive.
The flux of charged particles falling from above
travels the path 
in the large ball with
the concentration of charge 
in its matter, and
reaches the small cube, with which we replaced the small ball. According to
(11) at this point the fluence rate decreases to the value:
.
Then the flux passes through the small cube with
concentration of charge and decreases again:
.
The force from this flux of charged particles is
proportional to the square of the face of the small cube and to the number of
charged particles, which transferred their momentum per time unit to the cube
matter:
.
(12)
On the lower side of the large ball the flux of charged
particles first passes the path 
to a small cube and
then passes through the cube:
,
.
The force acting on the small cube from this side
equals:
.
(13)
The total force is the difference between the forces
(12) and (13):
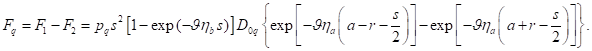
Since exponents in this expression are small
enough, the exponents can be expanded in the small parameter
by the rule: 
. With this in mind, we obtain:
.
In this expression, we will take into account that the
charge density of the large ball is given by the formula: 
, and will use (10):
,
.
The force 
acts on the small ball
with the negative charge in Figure 5 so that
the force is directed toward the center of the large ball and oppositely to the
radius vector 
from the center of the
large ball to the small ball. By definition, the electric field strength is the
ratio of the force, acting on the test body, to the charge of the test body. Then
the vector of the electric field strength inside the large ball will be:
.
(14)
In electrostatics, the vector of the electric field
strength inside a uniform charged ball is determined by the formula:
.
(15)
From comparison of (14) and (15) we find the expression of the vacuum permittivity in
terms of the parameters of charged particles fluxes in the cubic distribution
approximation:
.
(16)
The difference between the used cubic (9) and
spherical (1) distributions leads to the fact that the formulas for vacuum
permittivity (16) and (6) differ by a numerical factor.
If the small ball in Figure 5 has not a negative
charge but a positive charge 
, then its interaction with the charge of the large ball
should be considered in view of Figure 3 for the interaction of two positive
charges. It means that it is necessary to introduce an additional coefficient 
in order to take into
account the effect of increasing of the flux of charged particles.
As a result, the fluence rates 
and 
and the force (12) from
the flux of charged particles falling from above on the small cube, by which we
replaced the small ball, will change and be equal to:
, 
,
. (17)
Similarly, at the lower side of the large ball for the
fluence rate and the force, instead of (13), we have:
,
,
. (18)
The total force equals the difference between the
forces (18) and (17):
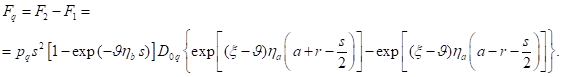
Expanding the exponents by the rule: 
, we find:
.
Let us assume that the charge density of the large
ball is given by the formula: 
, and for the coefficient the relation holds: 
, which was found in the previous section. Then, with regard to
(10), we obtain:
.
The force 
is directed radially
from the center of the large ball, and the expression for this force after
dividing by the charge leads to the electric
field strength (14).
5. THE PARAMETERS OF THE
FLUXES OF CHARGED PARTICLES OF THE VACUUM FIELD
We will estimate the energy density for cubic
distribution of charged particles fluxes of vacuum field in space. Suppose
there is a cube with an edge 
, into which charged particles fly from six sides
perpendicularly to the faces of the cube. The speed of charged particles is
assumed to be equal to the speed of light, so that in the time 
the cube will be
completely filled. In view of distribution (9) the number of charged particles
in the cube will be: 
. If the energy of one charged particle is 
, then with the help
of (16) for the energy density of charged particles of vacuum field we find:
. (19)
Now we will use the spherical distribution (1) to
estimate the energy density of charged particles of vacuum field. An empty
sphere with radius 
can be filled with
charged particles in the time 
, if the graviton fluxes are directed radially and correspond
to the full solid angle 
. The number of charged particles inside the sphere will
equal 
. Multiplying this number by the energy of one charged
particle and dividing by the sphere’s volume we can find the energy density. In view of
(6) and the condition 
, we obtain:
. (20)
The energy density (20) with spherical distribution is
3/2 times greater than with cubic distribution (19), which emphasizes that our
estimates are approximate due to the use of two idealized distributions.
Earlier in [5] we have applied the concept of the graviton field to
calculate the Newton’s gravitational force between two bodies and the
gravitational constant. This allowed us to estimate the energy density of the
graviton field for cubic distribution and the rate of the energy flux of the
graviton field in one direction:
J/m3
, (21)
W/m2 ,
here 
is the average energy
of one graviton, 
is the average momentum of one graviton, 
is the number of
gravitons falling per unit time on unit area from one of the six spatial
directions in cubic distribution, 
, 
is the gravitational
constant, 
is the mass of one
nucleon of the matter, 
m2 is the cross section of interaction of
gravitons and the matter.
The energy density 
in (21) is associated
with the gravitational constant and with gravitation
at the level of nucleons. Similarly, the energy density of the charged
particles of the vacuum field 
in (19) is associated
with the electromagnetic action of the field on each elementary charge 
of the matter.
Further we will need the similarity coefficients, with
the help of which in the theory of infinite nesting of matter [2],
[6] we will calculate the physical quantities inherent
in each particular level of matter. As the typical parameters of a neutron star
we will take the mass equal to 1.35 Solar mass or 
kg and the stellar radius equal to 
km.
Dividing the mass of the neutron star by the proton
mass 
, we find the coefficient of similarity in mass: 
. Similarly, we calculate the coefficient of similarity in
size as the ratio of the stellar radius to the proton radius: 
,
here the quantity 
m in the self-consistent model of the proton [7]
was used. We can estimate the minimum possible radius of the neutron star based
on the ratio of the star volume to the total volume of all the nucleons in the
stars: 
, 
km. A star with the
radius of 12 km exceeds this limit, there are some gaps between the nucleons
and the nucleons remain to be independent particles.
The coefficient of similarity in speed equals the
ratio of the characteristic speeds of the matter inside the star and the
proton, respectively. For the star the characteristic speed 
is calculated from the
energy equality from the standpoint of the general principle of equivalence of
mass and energy, generalized with respect to the absolute value of the total
energy to any space objects:
, 
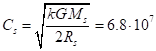m/s.
Similarly, we find for the proton the equality of the
characteristic speed of its matter and the speed of light:
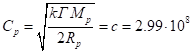m/s,
while 
m3·kg-1·s-2 is the strong
gravitational constant, calculated from the equality of electric and
gravitational forces in the hydrogen atom, 
is the vacuum
permittivity, 
is the electron
mass and according to [7]
for the proton 
. Hence, the coefficient of similarity in speed is equal to: 
.
As it was shown in [2],
the ratio of the absolute value of strong gravitation energy density to the
electromagnetic energy density of the proton is equal to the ratio of the
proton mass to the electron mass 
. Indeed, for the energy of the fields and their ratios, in view
of the definition of the strong gravitational constant 
, we have: 
, 
, 
.
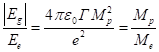We believe that the same ratio exists for the energy
densities of graviton field and charged particles of the vacuum field, which
allows us to estimate the energy density of charged particles of the vacuum
field:
J/m3.
(22)
Let us substitute (22) into (19), using the value of 
from (21), and take
into account the proximity of the proton mass and the average mass of a nucleon
, as well as the definition of the strong gravitational
constant in the form 
. This gives an estimate of the cross section of interaction
of the charged particles of the vacuum field with the charged matter:
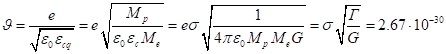m2 .
(23)
This cross section has a value that almost exactly
coincides with the geometrical cross section of a nucleon and significantly
exceeds the cross section 
m2 of interaction of gravitons with the matter. In
order to find the significant difference between 
and 
, we will express from (22), use 
from (19) and take
into account the definition of 
:
. (24)
From comparison of (24) and (21), provided that 
, it follows that if in (21) we pass from the cross section to the cross section , then at the same time it is necessary to substitute the
gravitational constant 
with the strong
gravitational constant 
. In (24) the energy density of the graviton field at
the level of nucleons is fully expressed in terms of the parameters of the
nucleon level of matter. Similarly, in (19) the energy density 
of the charged particles
of the vacuum field is expressed in terms of the parameters of the nucleon
level of matter. In this case, both in (19) and (24) the same cross section 
of interaction of the
vacuum field particles with the matter consisting of nucleons is used. Note
that in [4] it was found that the cross-section of the interaction
between the gravitons and the matter of nucleons must be equal by the order of
magnitude to the cross-section of the proton.
By analogy with (24) for the graviton field at
the stellar level we can write:
.
If in this expression we shall consider the following
relations in accordance with the dimensional analysis,
coefficients of similarity and (24):
, 
, 
,
then we obtain the relation 
J/m3,
in which the energy density of graviton field at the stellar level
, needed to keep the matter in neutron stars, linked
to the energy density 
. Since the energy density is required for
the integrity of the nucleons in the field of strong gravitation, then 
.
In view of (16), (19), (22) and the relation 
, for the rate of the energy flux of charged particles of the
vacuum field in one direction we find:
W/m2
. (25)
Due to the fact that the above-mentioned energy
density of charged particles
of the vacuum field is less than the energy density of graviton field in
(21), the rate of the energy flux of charged particles of the vacuum field 
is less than the rate
the energy flux of the graviton field 
.
6. THE ESTIMATES OF FORCES
AND ENERGIES
In [2] and [6] the assumption is made that some neutron stars – magnetars can have a positive electric charge of up to
C, where 
is the elementary
electric charge and the similarity coefficients are used in accordance with the
dimensional analysis.
The
proton electric energy on the surface of the charged magnetar will reach 
J or 
eV. The corresponding electric force will be equal to 
N. It is
assumed that it is precisely the electrical energy in the magnetar field that
is the energy source of high energy cosmic rays.
For the absolute value of the gravitational energy of
the proton on the surface of the magnetar similarly we have: 
J.
This energy and the gravitational force, associated
with it, are clearly not enough to keep the proton, on which the repulsive
force is acting from the entire charge of the magnetar. However the magnetar
looks like a huge atomic nucleus consisting of a number of closely-spaced
nucleons. Between nucleons there is strong interaction, which holds them
together. In the gravitational model of strong interaction [6]
the idea of strong gravitation is used to describe the strong interaction. The nucleons in the atomic nuclei are attracted to
each other by strong gravitation and repel from each other by means of the
torsion field, which arises from the rapid rotation of the nucleons. According
to the Lorentz-invariant theory of gravitation [1-2],
the torsion field arises similarly to the magnetic field in electromagnetism,
and in the general theory of relativity it corresponds to the gravitomagnetic
field. The balance of attractive and repulsive forces, arising from strong
gravitation, can be responsible for the integrity of the atomic nuclei, as well
as for the integrity of the charged neutron star.
We did the estimates of forces and energies in the
atomic nuclei in [6]. For example, the nickel nucleus 
consists of 
nucleons, among which
there are 28 protons and 34 neutrons. The mass of this nucleus is 
kg, and the radius is obtained from experiments on the
scattering of electrons by the formula: 
m, where 
m. Based on these data we will estimate the force, acting
from the nucleus on the proton located on the nucleus surface, with the help of
strong gravitation: 
N.
The surface of the magnetar as a neutron star
apparently consists of the nuclei of such elements as iron, nickel and heavier
nuclei, since their binding energy per nucleon is maximum. If the proton was
near one of these nuclei on the magnetar surface, the force 
would keep the proton,
acting against the force of electrical repulsion 
N from the magnetar charge. But the concentration of nuclei
on the stellar surface is such that the proton on the average will be located
somewhere between the nuclei at a distance 
from them.
To keep the proton the condition 
must hold, which
implies that 
m. For a cube with the edge 
, at the corners of which there are 8 nuclei 
, and the proton is in the center of the cube, the
matter density is equal to 
kg/m3. The matter density on the magnetar surface
must exceed this value, so that the condition of stability with respect to
electric forces is satisfied. On the other hand, the estimates in [8]
of the matter density in the crust of the neutron star imply that at a density
of 
kg/m3 and
more the nuclei 
begin to decay.
Consequently, heavier nuclei must prevail in the magnetar crust, in particular,
a typical nucleus according to [8] is 
. From these calculations it follows that the magnetar
charge is almost the maximum charge that the star can have without loss of its
integrity. And the main contribution into the stability of a star is made by
not ordinary but strong gravitation, acting at the level of atomic nuclei.
With the help of the similarity coefficients we can
calculate the mass, radius and charge of the praon – the particle, which relates
to the proton, as the proton relates to the magnetar: 
kg, 
m, 
C. If the praon is located at the surface of the proton,
its electrical energy and gravitational energy in the strong gravitational
field will be equal: 
J, 
J.
The ratio of these energies is the same as the ratio
of the electric energy of the proton at the surface of the magnetar to the gravitational
energy of this proton in the gravitational field of the magnetar. In the
substantial model of the proton and neutron, presented in [6],
it is assumed that the nucleons consist of neutral and charged praons, just as
neutron stars consist of nucleons. In addition, by analogy with the composition
of cosmic rays, consisting mainly of relativistic protons, we can assume that
the charged component of the vacuum field can consist of praons accelerated by
positively charged atomic nuclei up to high energies.
At the present time cosmic rays are registered with
energies up to 
eV or 9.6 J per nucleon [9].
Assuming that this is the energy of the accelerated proton, we will divide it
by the coefficient of similarity in energy and will find the corresponding
energy of the praon: 
J. Equating this energy to the energy 
of a charged particle
of the vacuum field, we can estimate the concentration of these charged
particles as the concentration of relativistically moving praons. In view of
(19) and (22) we obtain:
m-3 .
Multiplying this concentration of charged particles by
the charge of one praon 
and the speed of
light, we can estimate the density of the current in the vacuum in one
direction, which arises from the flux of positively charged praons in one
direction at cubic distribution:
A/m2 .
Beside the current density 
, we should expect another similar current density 
in the same direction,
which arises from the flux of negatively charged praons. This should ensure a
certain degree of vacuum electroneutrality and existence of electrical forces
of repulsion and attraction.
Now we will consider the question of neutron star’s
matter permeability for gravitons and charged particles of the vacuum field,
respectively. The fluence rates from a unit solid angle similarly to (2) have
the form:
,
.
If the neutron star has a radius of 12 km and a mass
of 1.35 solar masses, then the average concentration of nucleons will equal 
m-3. The average concentration of the positive
charge in the magnetar is 
m-3. Assuming that 
km, for the exponents in view of (21) and (23) we find: 
, 
. It follows that if we put three neutron stars in the way of
the flux of gravitons, the flux will reduce approximately by a factor of 
, where 
is the base of the natural logarithm. But for the flux of
charged particles of the vacuum field in order to reduce it noticeably we need
to put in a line about 140 magnetars.
This difference in fluxes allows us to explain the
saturation effect of the specific binding energy, when the nuclear binding
energy per nucleon, depending on the number of nucleons in nuclei, first
increases, reaching a maximum of 8.79 MeV per nucleon for the nucleus , and then begins to decrease. For light nuclei the
increase in the specific energy agrees well with the increase of the specific gravitational
energy of the nucleus in the strong gravitational field, when the energy
increases in direct proportion to the square of mass and in inverse proportion
to the radius of the nucleus. The saturation effect comes into play in the
range of 17 to 23 nucleons, forming the nucleus. Besides, adding a new nucleon
to the nucleus increases the energy not proportionally to the square of mass,
but to a lesser extent. This is due to the fact that gravitons of strong
gravitation cannot permeate the nucleus with a lot of nucleons, as is evident
from the exponent. Each new nucleon is simply pressed to the nucleus from the
outside by the strong gravitation, until for the large nuclei this force
reaches the maximum, conditioned by the pressure of the graviton flux. However,
the charged particles of the vacuum field in these conditions have almost 50
times larger path length, and therefore the positive electrical energy of the
nucleus’ protons further decreases the negative gravitational energy of the
nucleus, making the main contribution into the observed decrease in the
specific binding energy of massive nuclei.
Earlier in [4] we estimated the maximum force between
two stellar objects:
N,
where 
for the case of
uniform density of each object, and it is assumed that the graviton fluxes are
fully retained by these objects, which are located close to each other.
A similar expression for the maximum force at the
nucleon level of matter, after replacing the gravitational constant by the
strong gravitational constant, in view of the coefficient of similarity in
speed 
has the form:
N.
We should note that the corresponding ratio of the
gravitational energy and the force between two protons to their electrostatic
energy and force is equal to the ratio of the proton mass to the electron mass.
Indeed, for the forces and their ratios in view of the definition of the strong
gravitational constant 
, we have: 
, 
, 
.
We can explain this by the fact that in the expression
for 
the exponent for the
flux of charged particles of the vacuum field in the magnetar and hence in the
proton is less than the corresponding exponent for the flux of gravitons in the
expression for 
. The gravitons are retained in the proton matter more than
the charged particles of the vacuum field, and therefore the gravitational
force is greater than the electric force.
After passing from dense and charged objects such as
magnetars and protons to the bodies surrounding us the situation with the ratio
of forces is changing. The gravitational force decreases rapidly with
decreasing of the mass of bodies, and we can hardly influence it. However, by
changing the charges of bodies we can change their electrical interaction, so
that the electric force can be many times greater than the gravitational force
between these bodies. This can be seen from the ratio of the electric and
gravitational forces for two identical bodies with the mass 
and charge 
, which is proportional to the squared charge: 
.
Let us take for example two iron balls with the radius
cm each. With the density of iron 7874 kg/m3 it
gives the mass of each ball of approximately 4.1 kg. For the equality of the
gravitational and electrical forces it is enough to charge the balls up to 
C, so that the potential of each ball reaches the value 
V. Let us estimate the electrical energy of the praon, flying
near the ball, taking into account that above we estimated the charge of the
praon with the value 
C: 
J. On the other hand, the energy of a praon, regarded as a
relativistic particle similar by its properties to cosmic rays, has been found
above in the form: 
J. Comparison of these two energies allows us to make the
following conclusions. Firstly, even weakly charged bodies, which interact at
the level of low gravitational force, can influence the motion of praons near
them and deflect them aside. This substantiates the pattern of motion of the
charged particles of the vacuum field near the charged bodies in Figures 1-3
and our calculations of the electric force. Secondly, if we decrease the
charges and increase the sizes of bodies, there can be deviations from the
Coulomb law. However, these deviations should be distinguished from the
gravitational force, which in this case becomes greater than the electric
force.
The last conclusion can be specified as follows. In
order to find the deviations from the Coulomb law, it is desirable that the
condition of small potentials is satisfied 
V. To reduce the dependence on the gravitational force, there
are the following conditions 
or 
. Hence for the corresponding electrical potential of one
ball, we have: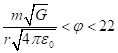 
V or 
kg/m.
For the iron balls it gives 
cm, 
kg. Another
complication in the experiments for finding deviations from the Coulomb law
occurs due to the fact that in conductive bodies the uncompensated charges are
located in the thin layer on the bodies’ surface, with a thickness of the order
of 1 or 2 atomic layers. Free electrons easily go out of the equilibrium
position in the external electric field, either repelling or being attracted to
the source of the external field, thereby changing their concentration on the
body. Due to this, in two interacting charged metal balls additional electrical
forces appear, which are usually calculated by the method of images.
7. INTERACTION OF THE
BODY’S CHARGE WITH THE VACUUM FIELD
The Coulomb law, due to the presence of charged
particles in the vacuum field, can be explained with the help of Le Sage’s
model. However, not only the fluxes of charged particles influence the
interaction of charged bodies, but the charges of bodies themselves influence
the fluxes of charged particles around the bodies. One example of this
influence is deflection of the charged particles from their trajectories, as it
was described in the previous section. In addition, each charged body achieves
a certain balance of energy and momentum during interaction with the vacuum
field.
Let us consider the energy density of the charged
particles of the vacuum field inside the charged body
and near it. Suppose there is a body in the form of a cube with an edge 
. The number of charged particles 
per unit time through
a unit area during particles’ motion in the matter decreases according to
formula (11). During time 
six fluxes of charged
particles from each side will pass inside the cube through the faces with the
area 
and will change up to
the value:
,
,
where 
is the number of
charged particles that passed through the cube.
If charged particles flew through the same empty
volume, the number of charged particles coming out would be 
. Consequently, the number of charged particles, which
interacted with the matter of charged body during time , equals:
.
As it was shown in [5], almost all the energy of the
graviton field, which interacts with the matter, is re-emitted back to the
graviton field, without heating the bodies significantly. This also applies to
the fluxes of charged particles the vacuum field, that transfer their momentum
to the matter with return of the energy back to the vacuum field.
Let us estimate in view of (19) the energy density of
those charged particles that interact with the bodies’ matter:
.
(26)
From (26) we will calculate the luminosity of charged
particles of a body in the form of a cube, multiplying 
by the volume 
and dividing by the
time . Expressing the charge concentration in terms of the charge,
in view of (19) we have:
,
.
(27)
From (27) it follows that the luminosity 
of
the charged particles, understood as the luminosity of those charged particles
fluxes that interacted with the charged matter of body and gave their momentum
to it, is proportional to body charge 
. This means that the body charge can be expressed in terms
of the parameters of the charged particles fluxes interacting with the body.
In (27) there is a product 
equal to the number of
uncompensated elementary charges in the body under consideration. Then the charged
particles luminosity per one elementary charge, in view of
(19), (22-23) will equal:
W. (28)
The ratio of the luminosity 
to the average energy
of a charged particle 
gives the number of
charged particles that interact with one uncompensated elementary charge of
matter per unit time and gave their momentum to it. According to (28), this
number of charged particles is equal to the product 
, while the cross section 
characterizes the
effective area of elementary charge’s interaction with charged particles, and
the coefficient 6 is associated with the six sides of cubic distribution of
charged particles fluxes 
in (11).
Expression (27) can be given a different meaning, if
we assume that the area of the cube face is connected with the cross section by the following
relation: 
, where 
is some numerical
coefficient, 
is the number of
uncompensated elementary charges in the cube. Then under the condition 
(27) can be rewritten as follows:
.
This relation shows that the emission rate is
proportional with accuracy to a coefficient 
to the electric energy
of the charged body, derived from the body in the time of passing the body
characteristic size by the charged particles.
We note one more aspect concerning the interaction
between the electromagnetic and gravitational fields. The concept of the
general field [10] shows that the vector fields, including the electromagnetic
and gravitational fields, are the components of one general field. And in case
if the theorem of equipartition of the energy is satisfied, the equations of
particular fields no longer depend on each other and are similar in form to the
Maxwell equations. If the fields interact with each other, then in the
Hamiltonian it is manifested in the terms with the field energy, where the
cross-terms with the products of different field strengths appear. This is
possible, for example, in non-stationary processes in the systems that have not
reached equilibrium. From the viewpoint of the vacuum field, it means that in
stationary conditions the gravitons and charged particles of the vacuum field
interact with the matter relatively independently, creating gravitational and
electromagnetic forces. If there is no equilibrium in the system, then the
kinetic energy of matter and the energies of some fields are transformed into
the energy of other fields, and the exchange of energies between gravitons and
charged particles in the vacuum field is possible as well. This leads to the
cross-terms in the system’s energy.
8. PHOTONS AND PRAONS
In this section we will try to specify which particles
can be responsible for electromagnetic phenomena. The charged particles of the
vacuum field not only lead to the electric forces in the Coulomb law, but
should be part of the photons, i.e. the electromagnetic quanta emitted by
atoms. Let us consider, for example, a photon with the wavelength 
m and the angular frequency 
s-1, arising in the hydrogen atom in the
transition of an electron from the second to the first level in the Lyman
series. The probability of this transition equals 
s-1
[11], which gives the average lifetime of an electron at the second level 
s, as a measure of duration of photon emission during
the transition. In quantum mechanics [12] there is a formula for the oscillator’s
oscillations decay time in times, where 
is the base of the
natural logarithm, with the help of which we obtain the following estimate:
s.
where 
is the vacuum
permeability.
The duration of photon emission can be calculated
directly within the Bohr model of a hydrogen atom. In this model, the electric
force between a proton and an electron acts as a centripetal force in the
electron’s rotation around the nucleus in the form of a proton. In this
rotation, the electron must emit an electromagnetic wave, since it is
constantly accelerated towards the nucleus. The formula for the charge emission
rate during its rotation is well known, which allows us to relate the electron
velocity and the effective force acting on the electron from emission. Moment
of this force decreases the angular momentum of the electron, leading to a
decrease in the radius of rotation. Hence we can derive the dependence of the
radius on the time [6]. From this dependence we find the duration of photon
emission as the time of transition of an electron from the second to the first
level of energy. Given that the average radius of the electron rotation on the
second level equals 
, and the average radius of the electron rotation on the
first level is the Bohr radius 
, we have the following:
s. (29)
For the instantaneous power of electromagnetic
emission we obtain the formula:
.
This implies a strong dependence of the emission rate
on the current radius 
of the electron
rotation, which is inversely proportional to the fourth power of this radius. It
turns out that the main photon energy is emitted when the electron approaches
the lower energy level.
Knowing the emission duration we can find the length
of the photon 
. To calculate the volume of the photon we also need its
midsection. In the first approximation, we assume that the mean radius of the
photon equals 
, which is equal to 
. We note that in the substantial model of electron [6], it is
considered as a thin disk that has on the main energy level the inner radius 
and the outer edge 
, and the Bohr radius 
is obtained as a
certain characteristic radius of the disk and the average radius of the
electron rotation. On the second level, the outer edge of the electron disk is
greater than the average radius of the electron rotation on this level. With
this in mind, the volume of the photon will equal: 
.
Further on we will use a simplified model of photon
from [2], [13], according to which the photon consists of charged particles, the
rotation of which around the photon’s axis creates the angular momentum of the
photon. In addition, inside the photon as well as in the electromagnetic wave
there must be mutually-perpendicular periodically varying electric and magnetic
fields. Electromagnetic energy of the photon consists of the equal electric and
magnetic components, and for the total energy density we can write: 
, since in the wave 
. The electric field strength 
inside the photon will
be characterized by the amplitude 
. The field inside the photon oscillates, varying from zero
to the peak value, so for the average density of the electromagnetic energy of
the photon, we assume that 
. We also assume that the photon energy is equally divided
between the mechanical energy of the charged particles and the electromagnetic
energy. The photon energy 
is proportional to the
Dirac constant 
and the angular
frequency 
. Dividing the photon energy by the photon volume, we obtain
the energy density, which can be equated to the doubled density of
electromagnetic energy inside the photon:
, 
.
(30)
Substituting in (30) the photon angular frequency 
s-1, the duration of the photon emission 
from (29) and the
photon radius , we estimate the amplitude of the electric field strength
inside the photon: 
V/m. For comparison, the proton creates at the Bohr radius
the electric field strength 
V/m.
From the mechanical point of view we can consider in a
simplified way the photon as a long thin cylinder, rotating with the angular
frequency . If inside the cylinder there are particles, each of
which has a relativistic mass 
, then in case of uniform distribution of particles the
angular momentum of the cylinder must be equal to the Dirac constant, as it is
supposed for all photons:
.
(31)
From (31) it follows that the mechanical energy of the
particles’ rotation, calculated as half the product of the angular momentum 
and the angular
velocity of rotation, is equal to the half of the photon energy: 
. The other half of the photon energy must be the
electromagnetic energy, which was taken into account in (30). Since the angular
momentum of the electron in the atom is quantized and proportional to 
, from (31) it follows that the total relativistic mass 
of the charged
particles rotating inside the photon must be of the order of the electron mass,
in order to ensure the angular momentum of the photon.
However, the mass 
is only a small part
of the mass of the entire flux of charged particles of the vacuum field, that
pass through the electron disk per time of the photon emission 
from (29). The total
relativistic mass of particles of the entire flux per time 
is expressed by the
product of the energy flux rate (25), the time and the area of the
electron disk 
, and then dividing by the square of the speed of light in
order to pass from the energy to the mass: 
kg, which is much
greater than the electron mass.
Let us consider the motion of some charged particle
inside the photon, located on the radius 
. This particle rotates at a certain velocity 
around the axis of the
photon, and besides it moves at the speed of light, as well as the photon, in
the direction of its propagation. For the particle’s period of rotation we can
write:
, 
.
(32)
In this model of a photon, there is a relationship
between the centripetal force, required for the particle’s rotation, and the
electric force, exerted on the particle with the charge 
and the mass . In view of (32) we have:
. (33)
Let us express from (30) and substitute it in
(33) in order to determine the ratio 
for the charged
particles inside the photon. In view of (29) for , as well as the assumed relation 
and
the value of the photon angular frequency 
s-1, we find:
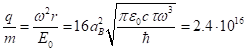C/kg. (34)
For the level of stars, the charge to mass ratio
should be the highest for the charged magnetar, as a neutron star with the mass
kg that, according to our assumption, bears the electric
charge 
C. This gives: 
C/kg. At the level of atoms, the same is true for the proton,
for which 
C/kg. What does the relation (34) give to us? From this
relation it follows that we must refer to a lower level of matter, that is, the
praon level of matter. For the charged praon at rest, the charge to mass ratio,
in view of the results of Section 6, is: 
C/kg.
Now we will take into account that in (34) the mass of
the charged particle is the relativistic mass, i.e. the ratio of the particle’s
energy to the square of the speed of light. This mass can be written as: 
, where 
is the Lorentz factor
for the particle, moving almost at the speed of light. Substituting the mass 
in (34) and using the
value 
for the praon, we can
determine the Lorentz factor: 
.
Earlier in Section 6, we referred to the fact that the
protons in cosmic rays reach the energy 
eV, while the rest energy of the proton is 
eV. Consequently, for the most energetic cosmic-ray protons
the Lorentz factor is as follows: 
.
We see that the Lorentz factors for praons and protons
are close enough to each other. All this means that the photon is a tightly
bound flux of praons, the energy of which is maximum and corresponds to the
energy of cosmic rays at the nucleon level of matter. Besides, praons are
related to protons, just as protons are related to a charged neutron star – a
magnetar. From photon’s neutrality it follows that it must consist both of
positively and negatively charged praons.
9. THE ANALYSIS OF
CRITICISM OF THE LE SAGE’S THEORY
If we assume that the charged particles of the vacuum
field are relativistic praons, then according to (28) the power of energy of
the fluxes of praons interacting with each uncompensated elementary charge of some
charged body is equal to 
W. In [5] we found
that the power of energy of the fluxes of gravitons, creating the ordinary
gravitation, calculated per body’s nucleon is equal to:
W.
(35)
At the nucleon scale level of matter we must move from
ordinary gravitation to strong gravitation, which holds the matter of nucleons.
As it follows from (21-24), for this the cross-section of the interaction of
gravitons 
in (35) should be
replaced by the interaction cross-section 
:
W. (36)
Then it follows from (22) that 
,
that is the ratio of the emission power of the fluxes
of gravitons of strong gravitation calculated per body’s nucleon to the
emission power of the fluxes of charged praons calculated per each body’s
uncompensated elementary charge is equal to the ratio of the proton mass to the
electron mass.
According to (35), every second one nucleon of a
gravitationally bound body should re-emit the energy 
J of the graviton
fluxes incident on this nucleon so that ordinary gravitation would be possible.
If there were no such re-emission, then we could estimate from the equation 
the temperature, to
which each nucleon and any body of nucleons could be heated from the fluxes of
gravitons per second: 
K. If we substitute as
the energies,
resulting from (28) and (36), then the corresponding temperatures would be even
higher.
It is the problem of heating of bodies, which is the
main problem of Le Sage’s theory, both for the fluxes of gravitons leading to
gravitation and for the fluxes of charged praons creating electromagnetic
interaction at the nucleon level of matter. Actually, since the fluxes of
gravitons and charged particles must transfer some part of their momentum to
the matter to give rise to gravitational and electromagnetic forces, it also
seems that some part of the energy of these fluxes should turn into the kinetic
energy of motion of the matter and thus heat it to high temperatures, which is
not observed. Many researchers of Le Sage’s theory, including Thomson [14] and
Poincaré [15], based on the arguments of classical mechanics and the
relationship between energy and momentum, pointed to this and other
circumstances, considering them an obstacle to the theory’s acceptance.
Now we raise the following question: is such a
mechanism possible, when the fluxes of smallest relativistic particles transfer
some momentum to the body’s matter, but at the same time they almost completely
conserve their energy and are re-emitted into the surrounding space without
heating the body significantly? To answer this question, let us remember that
there are fields known in physics that do not perform work on the particles and
do not change their energy. This is the magnetic field, as well as the torsion
field in the covariant theory of gravitation [6], known as the
gravitomagnetic field in the general theory of relativity. A fast charged
particle, passing through the region of space with the magnetic field, is
deflected from the original direction of motion by the Lorentz force, in which
case the amplitude of the particle’s momentum and its energy do not change.
Despite this, the pressure force from the particle is exerted on the source of
the magnetic field. This happens because the momentum like any vector can
change both in magnitude and in direction, and any change in the momentum is
associated with the corresponding force.
The analogue of nucleons at the level of stars is a
neutron star, and the fluxes of praons correspond to cosmic rays. The cosmic
rays, passing close to a neutron star, will interact with the strong magnetic
field of the star and be deflected by it. Obviously, if the flux of cosmic rays
on one side of the star is stronger than on the others, then the stronger flux
will start to shift the star due to the magnetic pressure. The same effect
takes place also due to the torsion field, which is especially strong in
rapidly rotating neutron stars and it interacts even with neutral fast-moving
particles, since it does not act on the moving charge but on the momentum of
particles.
The fluxes of praons moving in the matter are
influenced not only by the magnetic fields of nucleons, but also by the
electric fields of uncompensated charges of individual protons and electrons.
These fields also deflect the fluxes of praons without significant changes in
the energy of praons, which is a consequence of potentiality of the electric
field. Actually, if the fluxes of positively charged praons fly towards the
proton, they are first decelerated by the electric field of the proton and
decrease their energy, and then when they fly past the proton, they start
accelerating from the proton under the influence of the same field and increase
their energy up to the previous level. The gravitational force acts on the
gravitons in a similar way.
With the help of the described mechanism the fluxes of
gravitons and praons can create the gravitational and electromagnetic
interactions in the matter of bodies without heating these bodies
significantly. Passing through the matter the fluxes of gravitons and praons,
consisting of a large number of tiny particles, act simultaneously on the
nucleons, electrons and atomic nuclei, compressing them in the direction of the
gradient of the corresponding flux and creating the gravitational and
electromagnetic acceleration. The fact that the interaction cross-section characterizes both the
electromagnetic interaction of the fluxes of praons with nucleons and the
strong gravitation from the fluxes of gravitons at the level of nucleons, and
is equal by the order of magnitude to the cross-section of the nucleon,
suggests that the interaction forces can actually emerge near the surface of
nucleons. Here, the electric and gravitational fields, the magnetic field and
the torsion field of nucleons reach the maximum and can effectively interact
with the fluxes of praons and gravitons. As gravitons, leading to strong
gravitation, in [5] we suggested graons as the particles that make up praons
just as praons make up nucleons or as nucleons make up a neutron star. For
graons in order to become gravitons they must be accelerated up to relativistic
energies in the processes near the surface of praons.
Let us now consider the second problem of the Le
Sage’s theory, according to which during motion excess pressure of gravitons
and charged particles in front should emerge (drag effect), proportional to the
velocity of the bodies’ motion. As a result of resistance to the bodies’ motion
from the fluxes of gravitons, long-term rotation of planets around the Sun
would not be possible and the principle of free inertial motion in the absence
of forces would not hold true. Using cubical distribution of the charged
particles of the vacuum field (9) and the fluence rate (11) of these particles,
for the change of fluence and for the force, acting on a fixed charged cube
with an edge 
from one side, we find
the following:
,
.
(37)
The quantity 
in (37) is equal by
the order of magnitude to the relativistic momentum of one charged praon. While
the cube is fixed in an isotropic reference frame, the fluxes of praons pass
symmetrically through the cube from all sides and it remains motionless. Now
suppose the cube is moving along the axis 
from left to right so
that one cube’s face is perpendicular to the axis . In case of the cube’s motion, the praons coming from its
right side would have increased energy 
, besides the fluence amplitude 
would increase due to
the increased rate of occurrence of the praons incident on the cube. Since
praons are ultrarelativistic particles, their momentum is proportional to the
energy: 
, besides 
. These relations follow from the Lorentz transformations
applied to the momentum and the rate of occurrence of particles.
On the other hand, we can expect that the
cross-section of the praons’ interaction with the matter should be directly
proportional to the square of the de Broglie wavelength, and inversely
proportional to the square of the energy of praons: 
.
This dependence of cross-section in the quantum theory
of elastic scattering is typical of ultrarelativistic photons – the greater
their energy is, the weaker they interact with each other [16-17]. At the same
time, we assume that photons are composed of praons, and the interaction of
praons with the electromagnetic field of nucleons is a special case of photon’s
interaction on virtual photons.
If , and 
depend on the energy
of praons, as described above, then the force in (37) remains unchanged both
for a fixed and a moving cube. In (37) there is also a product 
, which is equal to the number of uncompensated charges
inside the cube and is independent of the cube’s motion. The force 
in (37) is the force,
acting on the cube from one side, it is opposed by a similar force from the
opposite side of the cube. Thus, the cube can move by inertia and the
decelerating force from the fluxes of charged particles of the vacuum field,
proportional to the velocity of motion, does not arise. This approach to the
problem of pressure on the moving bodies from the fluxes of gravitons has been
previously used in [2].
The problem of aberration in the Le Sage’s theory is illustrated
by an example, in which in the motion of two gravitationally bound bodies near
each other it seems that in view of the limited velocity of the gravitons’
motion, a certain additional force takes place. Indeed, while the gravitons
moving from one body reach the second body, it will move in its orbit from the
position that is dictated by the Newton’s theory of gravitation for
instantaneous gravitation. As a result,
the gravitons will reach the second body at some other angle to the orbit,
which gives an additional force component. This problem has been considered in
[4] for the case, when two bodies are moving synchronously in the direction
perpendicular to the line connecting the bodies. In this case it was shown that
the problem of aberration of the gravitational force disappears, if we apply
the relations of special theory of relativity to gravitons, which take into
account that the velocity of ultrarelativistic particles is not infinite and is
almost equal to the speed of light. In both cases, for fixed and moving bodies,
gravitons reach these bodies at the same angle with respect to the axes of the
proper coordinate system.
The hypothetical problem of gravitational shielding in
Le Sage’s theory suggests that if we place between two bodies the third body,
it will lead to a more noticeable change in the forces between the bodies, than
in case of the Newton's law of gravitation for three bodies. The measurements
of the possible Moon’s shielding of the Sun’s gravitational influence on the
Earth during Solar eclipses do not find any deviation from the theory within
the limits of measurement error [18]. According to [4], this situation is due to the
smallness of the cross-section 
of gravitons’
interaction with the matter. This allows us to expand the exponents in the
expressions for the forces into binomials with sufficiently high accuracy and
ensures the principle of superposition of gravitational forces for several
bodies. A noticeable deviation occurs only for such dense objects as white
dwarfs and especially for neutron stars. According to (23), the cross-section of praons’ interaction
with the charged matter is 20 orders of magnitude greater than the
cross-section of gravitons’
interaction with the matter. However, the concentration of uncompensated
charges in the matter is usually many orders of magnitude less than the
concentration 
of nucleons. This
allows us to expand the exponents in the expressions for the forces just as in
the case of electromagnetic interaction of bodies by means of charged particles
of the vacuum field, and thus to substantiate the principle of superposition of
forces.
10. CONCLUSION
Based on the assumption that the electric force
appears due to the action of the fluxes of charged particles that exist in the
vacuum field, we derived an expression for the electric field strengths inside
the ball (14) and outside it (7). These expressions are in good agreement with
the formulas for the field strengths in electrostatics. From the field
strengths we can easily proceed to the scalar potentials of the electric field,
since the strength is up to a sign determined as the potential gradient.
Once we find the electric scalar potential, then with
the help of a special procedure [19] we can find the 4-potential, the
stress-energy tensor of the electromagnetic field, the electromagnetic field
equations, the electromagnetic force, as well as the contribution of the
electromagnetic field into the equation for the metric. This means that the
electromagnetic field theory both in the flat Minkowski space and in the curved
spacetime is fully proved at the substantial level through the charged
particles fluxes of vacuum field. And the dependence of metric on the
electromagnetic field potential allows us to take into account the influence of
the inhomogeneous charged particles fluxes on the results of space-time
experiments, based as a rule on the use of electromagnetic waves and devices.
In (19) and (22) we made an estimate of the energy
density of the charged component of the vacuum
field, in (23) we presented the cross section of charged particles’
interaction with the matter, in (25) we estimated the rate of the energy flux
of the charged particles in one direction. Based on the principles of the
theory of infinite nesting of matter, the densest objects at each level of
matter are assumed as the sources of the charged particles of vacuum field –
neutron stars and magnetars, nucleons and atoms, praons as the components that
make up nucleons, etc. These objects emit neutrinos, photons and high-energy
cosmic rays that can make contribution to the vacuum field at all levels of
matter.
In the formula (27) we expressed the body charge in
terms of the emission rate of those fluxes of charged particles of the vacuum
field, which interacted with the body’s matter and transferred their momentum
to it. Due to this interaction, the contribution was made by the charged
component of the vacuum field into the mass as the measure of body’s inertia.
The inertia of the body is manifested in its acceleration, when the balance
changes between the falling on the body and outgoing energy fluxes of the
vacuum field. We can distinguish in the vacuum field three components, one of
which with the energy density 
is
associated with the strong gravitation and the rest energy of particles, determines
the integrity of nucleons and atomic nuclei, and is mainly responsible for the
inertia of bodies. Another component with the energy density 
is
responsible for the ordinary gravitation, and the third component in the form
of charged particles with the energy density 
leads
to electromagnetism. The last two components make their own contribution to the
mass of bodies.
We will also note the difference in how the origin of
the electrical force is understood. In our approach, the fluxes of charged
particles of the vacuum field are the source of electrical force, they exist as
a necessary complement to the matter in the form of elementary particles and
the bodies composed of them, are involved in the processes of gravitational
clustering of the scattered matter, and are generated by the emission from the
densest objects, such as praons, nucleons and neutron stars. It
is precisely the fluxes of charged particles of the vacuum field that are the
cause of the so-called displacement currents in the vacuum, which are
proportional to the rate of change of the electric field with the time. Here,
an example is the chargeable capacitor, between the plates of which there is a
magnetic field, despite the absence of the electron current in the capacitor.
In electrostatics, the electric force is not
explained. In quantum electrodynamics by means of selecting the Lagrangian of
the field’s interaction with the matter the formula is derived that resembles
the formula for the electric energy of the interaction between two charges in
electrostatics [20]. As interpretation the pattern is suggested, in which the
charged bodies exchange virtual photons with each other, which leads to the
electrical interaction. Besides, here the uncertainty principle is used,
limiting the lifetime of virtual photons. Due to virtuality, the photons are attributed
very exotic properties, including the possibility of energy negativity or the
presence of the momentum without energy. The photons’ energy is considered to
be proportional to the Planck constant, and therefore the possibility of
existence of photons and particles, belonging to the lower levels of matter and
with another Planck constant, is not considered. The obvious disadvantage of
this approach is the difficulty to explain the origin of virtual particles as
such and their unique properties.
If we consider the fluxes of charged particles in the
vacuum field as the source of the electric forces, it becomes possible to
consider their scattering in the process of quantum transitions in atoms. In
[6] the substantial model of electron in the form of a disk is considered, in
which the charged matter rotates differentially, and ensures the magnetic
moment of the electron. In addition, the electron spin is explained as the
result of the shift of the disk’s center relative to the nucleus and rotation
of this center in addition to the matter rotation in the electron cloud. If the
electron transits into the quantum state with lower energy, it emits a photon,
which carries with it the angular momentum that is proportional to the Dirac
constant. In this process, the scattering of charged particles of the vacuum
field on the electron disk, taking into account the action of the magnetic and
electric fields in the wave zone, leads to the formation of a photon as an
object preserving its structure for a long time.
In Section 8, we studied the model of the photon,
emitted in atomic transition in the hydrogen atom. Associating the photon
parameters and its structure with the parameters of the emitter – the charged
electron disk, we managed to determine the charge to mass ratio for the
particles that make up the photon. As a result, it turned out that photons
consist of praons of very high energies, comparable to the energies that cosmic
rays would have if these rays emerged at the nucleon level of matter near the
protons. These relativistic praons must form the basis of the charged particles
of the vacuum field. Indeed, in the interaction of praons of the vacuum field
with the electron in atomic transition, the twisting of praons takes place
under action of the fields along the axis of the electron disk, and the
appearing photon carries away the excess angular momentum of the electron from
the atom. Meanwhile, part of praons of the vacuum field is part of the photon,
so that the speed of the photon actually is the speed of praons in the fluxes
of particles of the vacuum field.
In contrast to the chaotic motion of the praons in the
vacuum field, the praons in the photon are rigidly bound to each other by both
electromagnetic and gravitational forces. The situation here is similar to the
situation with the nucleons, which only in special circumstances can form
extremely stable formations – the atomic nuclei. According to the gravitational
model of strong interaction [6], the nucleons in atomic nuclei are attracted to
each other by strong gravitation and repel each other by means of the torsion
field, arising from the rapid rotation of the nucleons. In order to form the
nucleus, the nucleons must interact with each other only in a strictly defined
orientation of the spins and magnetic moments and must have sufficient initial
energy that allows rotating the nucleons up to the desired rotation speed by
means of gravitational induction. The praons in the photon can interact with
each other in a similar way. We can even calculate the gravitational constant
for the praon level of matter with the help of the coefficients of similarity
from Section 5 and the strong gravitational constant 
m3·kg-1·s-2 in the following
way, using the theory of dimensions and SPФ
symmetry, according to [2]: 
m3·kg-1·s-2 .
In the gravitational field with this large
gravitational constant, the praons of the photon can form sufficiently rigid
structure, so that the photon could fly large cosmic distances without
decaying.
In Section 5, for the ratio of the absolute value of
energy in the field of strong gravitation to the energy of electric field of
the proton we found: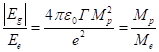 
. Аналогичное
равенство следует и для праона, для чего необходимо постоянную сильной
гравитации 
заменить на постоянную
гравитации для праонного уровня материи 
и подставить массу и заряд праона из раздела
6: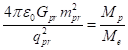 
.
Concurrent consideration of the evolution of objects
at different levels of matter, such as the level of praons, nucleons and
neutron stars, allows us to draw conclusions not only as to the origin of
gravitational and electromagnetic forces. For example, if for a neutron star
with the mass 
Solar
mass and the stellar radius 
km we calculate the average binding energy per nucleon, we
will obtain 
J or 47 MeV per nucleon,
which is greater than the binding energy of atomic
nuclei. Taking into account that neutron stars are born in supernova
explosions, when the explosion energy is carried away by neutrinos and emission,
and is converted into the kinetic energy of the discharged shell, a significant
part of the binding energy is emitted from the star and transferred into the
environment. In [13], we estimated that 61% of all praons are part of nucleons,
and the rest 39% form new particles – nuons (which are structurally the analogues of white dwarfs
at the level of elementary particles) or exist separately. The same proportion
remains at the level of stars: 61% of all nucleons over time will be part of
neutron stars, and the rest of nucleons remain either as a gas or as the matter
of white dwarfs. Nuons as the analogues of white dwarfs, due to their
significant presence in cosmic space, can ensure the red shift effect in the
spectra of distant galaxies, explain the background radiation and the dark
matter, etc.
Consequently, the concentration of free protons in the
visible Universe must be of the same order as the averaged over the entire
space concentration of nucleons in stars, that is of the order of concentration
of baryons 
m-3, according to the findings of the
Lambda-Cold Dark Model [21]. With this in mind, the product of the concentration
of baryons and the binding energy of a neutron star in the calculation per
nucleon will give us the estimate of the maximum energy density of emission in
cosmic space: 
J/m3. Indeed, the energy density in the relic
radiation equals 
J/m3, and the energy density in the stellar
radiation, magnetic fields and cosmic rays is of the same order of magnitude,
as well as the kinetic energy of the motion of gas particles. The sum of these
energy densities does not exceed the maximum energy density 
.
In conclusion, we will estimate the length of free
path of the charged particles of the vacuum field in the cosmic space, taking
as the charge concentration in a first approximation the value 
of the elementary
charge per cubic meter, which is equal to the average concentration of baryons
in the Universe. This approach gives only the minimum value of the free path
length, since on the average the matter in the Universe is neutral, and 
must reflects the
average concentration of the total charge of the Universe. From the ratio 
at a given
concentration of charges and the value 
according to (23), we
find the free path length of charged particles: 
m. This value is 3 orders of magnitude greater than the
visible size of the Universe, which is estimated by the value of 14 billion
parsecs or 
m. Consequently, the charged particles can easily reach our
Universe from a distance, where they can be produced in a concentration
sufficient to meet the required energy density. We do not support the model of
the Big Bang, which limits the lifetime of the Universe to the value of 13.8
billion years, explaining in a different way the phenomena associated with this
model [13]. Then the charged particles of the vacuum field can have enough time
to get into our Universe from the outside and reach here the equilibrium
concentration with the value 
m-3.
In the last section, we considered the main objections
to the Le Sage’s theory and presented our arguments supporting this theory.
This was possible due to taking into account the special theory of relativity
and the peculiarities of interaction of gravitons and charged particles of the
vacuum field with the matter. In our opinion, the modernized Le Sage’s model
most naturally explains the origin of gravitational and electromagnetic forces,
and the theory of infinite nesting of matter explains the evolutionary origin
of gravitons and charged particles of the vacuum field. In addition, we can
assume that the role of gravitons of ordinary gravitation is played by charged
praons, and the role of gravitons of strong gravitation is played by charged
graons. For neutral bodies the action of fluxes of these particles leads to
gravitational forces, while in charged bodies there are also electromagnetic
forces.
REFERENCES
[1] Heaviside O. A Gravitational and Electromagnetic Analogy. Part I. The Electrician, 1893, 31,
281-282
[2] Fedosin S. G. Fizika
i filosofiia podobiia ot preonov do metagalaktik. Perm: Style-MG, 1999, pp. 402-425
[3] Michelini M. A Flux of Micro Quanta Explains Relativistic Mechanics
and the Gravitational Interaction. Apeiron, 2007,
14(2), 65-94
[4] Fedosin S. G. Model of Gravitational Interaction in the Concept of
Gravitons. Journal of Vectorial Relativity, 2009,
4(1), 1- 24
[5] Fedosin S. G. Physical Science International
Journal, 2015, 8(4), 1-18. doi: 10.9734/PSIJ/2015/22197
[6] Fedosin S. G. Fizicheskie teorii i
beskonechnaia vlozhennost’ materii. Perm, 2009
[7] Fedosin S. G. The
radius of the proton in the self-consistent model. Hadronic Journal, 2012, 35(4), 349- 363
[8] Belvedere
R., Pugliese D., Rueda J. A., Ruffini R., Xue She-Sheng. Nuclear Physics A,
2012, 883(1), 1-24. doi: 10.1016/j.nuclphysa.2012.02.018
[9] Gaisser
T. K. Astropart. Phys. 2012, 35, 801-806. doi:
10.1016/j.astropartphys.2012.02.010
[10]
Fedosin S. G. OALib Journal, 2016, 3, 1-15. doi:
10.4236/oalib.1102459
[11]
WolframAlpha, computational
knowledge engine http://www.wolframalpha.com/input/?i=Lyman+series
[12]
Яворский
Б. М., Детлаф А. А., Лебедев А. К. Справочник по физике. 8 изд-е, М: Оникс,
2006
[13]
Fedosin S. G. Cosmic Red Shift,
Microwave Background, and New Particles. Galilean
Electrodynamics, 2012, 23(1), 3-13
[14]
Thomson W. (Lord Kelvin).
On the ultramundane corpuscles of Le Sage. Phil. Mag. 1873, 45, 321-332
[15]
Poincaré H. The New Mechanics. The foundations
of science (Science and Method). New York: Science Press, 1913, pp. 517-522
[16]
Karplus R. and Neuman M. Phys. Rev. 1951, 83, 776.
doi: 10.1103/PhysRev.83.776
[17]
Berestetskii V. B., Lifshitz E. M. and Pitaevskii L.
P. Relativistic Quantum Theory. Pergamon Press, 1974
[18]
Unnikrishnan C. S., Mohapatra A. K. and Gillies G. T.
Physical Review D, 2001, 63, 062002. doi: 10.1103/PhysRevD.63.062002
[19]
Fedosin S. G. Advanced
Studies in Theoretical Physics, 2014, 8(18), 771-779. doi: 10.12988/astp.2014.47101
[20]
Peierls R. E. The laws of nature.
New York: Charles Scribner's Sons, 1956
[21]
Hinshaw G. F., et.al. ApJS,
2013, 208, 19H.
doi: 10.1088/0067-0049/208/2/19
Source: http://sergf.ru/zken.htm