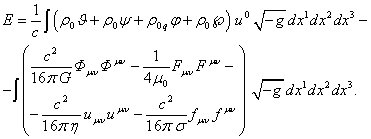International Letters of Chemistry, Physics and Astronomy, Vol. 78, pp.
39-50 (2018). http://dx.doi.org/10.18052/www.scipress.com/ILCPA.78.39
The
gravitational field in the relativistic uniform model within the framework of
the covariant theory of gravitation
Sergey G. Fedosin
PO box
614088, Sviazeva
str. 22-79, Perm, Perm Krai, Russia
E-mail fedosin@hotmail.com
For the relativistic uniform
system with an invariant mass density the exact expressions are determined for
the potentials and strengths of the gravitational field, the energy of particles
and fields. It is shown that, as in the classical case for bodies with a
constant mass density, in the system with a zero vector potential of the
gravitational field, the energy of the particles, associated with the scalar
field potential, is twice as large in the absolute value as the energy defined
by the tensor invariant of the gravitational field. The problem of inaccuracy of the use
of the field’s stress-energy tensors for calculating the system’s mass and
energy is considered. The found expressions for the gravitational field
strengths inside and outside the system allow us to explain the occurrence of
the large-scale structure of the observable Universe, and also to relate the
energy density of gravitons in the vacuum field with the limiting mass density
inside the proton. Both the Universe and the proton
turn out to be relativistic uniform systems with the maximum possible
parameters. The described approach allows us to calculate the maximum possible
Lorentz factor of the matter particles at the center of the neutron star and at
the center of the proton, and also to estimate the radius of action of the
strong and ordinary gravitation in cosmological space.
Keywords: Relativistic uniform system; covariant theory of gravitation; gravitational field; energy.
PACS:
03.30.+p; 95.30.Sf
1. Introduction
The relativistic theory
describes the physics of phenomena more precisely than classical mechanics.
This leads to the fact that an ideal uniform model of a body with a constant
mass density must be replaced by the relativistic uniform model. In the relativistic model the mass density can
be the coordinate function, but it is considered a constant invariant mass
density in the reference frames, associated with the particles that make up the
body. Due to the motion of the particles the effective mass density in the
system differs from the invariant values, which introduces additional
corrections into the values of the field functions and into the system’s
energy.
Various properties of the
relativistic uniform system were discussed earlier in [1-2]. The purpose of
this paper is to verify the relation between the energy of the particles in the
scalar gravitational potential and the proper energy of the gravitational
field, in the framework of the covariant theory of gravitation and relativistic
uniform model. We will use the
covariant theory of gravitation instead of the generally accepted general
theory of relativity. This is due to the
fact that in the general theory of relativity there is no stress-energy tensor
of the gravitational field, which does not allow to uniquely calculate the
energy density and the energy flux of the field inside or outside the body [3,
4]. On the other hand, with the help of the covariant theory of gravitation it
is possible to construct the models of stars and to estimate their parameters
[5], and to refine the virial theorem [6]. Besides in the framework of the
covariant theory of gravitation the gravitational field was included into the
general field as a separate component [7]. The metric near the solitary massive body was
determined in [8], with the help of which it was shown in [9] that the
covariant theory of gravitation successfully explains the anomalous precession
of Mercury's perihelion, the deviation of particles and light in the
gravitational field, the gravitational time delay and the gravitational
redshift of light, as well as the Pioneer anomaly [10].
Another characteristic feature
of the covariant theory of gravitation is the presence of the four-potential of
the gravitational field, which contains the vector potential in addition to the
scalar potential of the field. With the help of
the vector potential, the supplementary additives to the gravitational field
strengths and to the gravitational torsion field are formed, which in
gravitoelectromagnetism, as a special case of the general theory of relativity,
are called the gravitoelectric field strengths and gravitomagnetic field
strengths, respectively. These additives are required to take into account the
delay in the propagation of the gravitational interaction, just as it occurs in
electromagnetism with the propagation of the electromagnetic interaction. Due
to the vector potential and the torsion field various effects are possible,
including gravitational induction [11, 12].
The covariant theory of
gravitation also differs from modified versions of the general theory of
relativity, such as 
, 
, 
models or the Einstein’s model with the cosmological
constant 
(Einstein-Λ model). The common purpose of these models is
their application in cosmology, where they allow taking into account the
effects, which are now attributed to the dark energy and dark matter. But in a
number of works, these gravitation models are also applied to a system of
limited size. For example, in [13] the Palatini gravity is used to describe dynamical instability in a collapsing
self-gravitating spherical system of stellar sizes, and in [14] gravity is applied to a self-gravitating anisotropic cylindrical system,
which can contain an internal cavity as a result of explosive expansion. In
[15], the field equations and dynamic equations for the matter of a compact
star are studied using 
gravity, and in [16] 
gravity is used to simulate the equation of the state of the
relativistic matter. Interpretation of the results, as always, is most clear in
the weak field approximation, while Newtonian and post-Newtonian approximations
usually serve as the starting point.
In contrast to these modified
theories of gravitation, in the weak field limit the covariant theory of
gravitation turns into the Lorentz-invariant theory of gravitation and does not
contain any elements associated with the dark energy and dark matter. However,
the application of the covariant theory of gravitation to the relativistic
uniform system leads to specific features for the potentials and the
gravitational field strengths. As will be shown later, these features are of
greatest importance for the objects, in which the product of the object’s
radius by the square root of the mass density reaches its maximum. In
particular, we will apply the expressions for the gravitational field strengths
to the observable Universe, to the neutron star and to the proton, which will
allow us to explain some properties of these objects.
2. The field functions
As a uniform relativistic
system the spherical system is considered, which consists of the particles that
can also have the electrical charge. The stability of the system is maintained
by the action of its proper gravitation, the internal pressure field and the
acceleration field of the particles [17, 18]. The field functions are calculated on the assumption that there is no
general rotation of the particles in the system, they move randomly and
therefore the total vector field potentials on the average tend to zero.
The equation for the
gravitational scalar potential inside the sphere and its solution in the special relativity limit have the following form [2]:
,
(1)
.
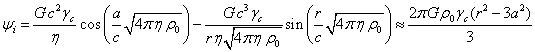In (1) the Lorentz factor of
the particles is 
, 
is the average velocity of an arbitrary particle
inside the sphere, 
is the Lorentz factor of the particles at
the center of the sphere, 
is the speed of light, 
is the acceleration field coefficient, 
is the gravitational constant, 
is the mass density of the particle in the reference
frame associated with the particle, 
is the radius of the sphere, the index 
differentiates the internal
gravitational scalar potential 
from external potential 
, which is generated by the sphere
outside its limits with 
. Both
potential and 
are the functions of the current radius 
inside the sphere and do not depend
on the angular variables.
The dependence of on the radius was found in [1]:
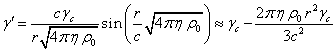. (2)
It is precisely because of the
presence of a sine in the expression for the Lorentz factor in (2), that the
periodic functions also appear in the solution of (1) for 
. The
approximate expressions on the right-hand side of (1) and (2) appear if we take
the first expansion terms of the periodic functions with regard to the
smallness of their argument. As we can see, the expression for only in the first approximation coincides with
the classical expression for the scalar potential inside the uniform sphere in
the right-hand side of (1), which is a consequence of the difference between
the relativistic and classical uniform systems.
For the external gravitational
potential 
of the fixed sphere, filled with moving particles, we obtain the
following:
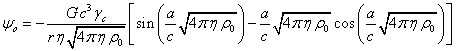. (3)
As the current radius 
increases, this potential tends to zero. In
addition, on the surface of the sphere at 
the external gravitational
potential in (3) coincides exactly with the internal
gravitational potential 
in (1).
The mass 
is defined as the product of the mass density by the sphere’s volume 
. However,
the actual gravitational field outside the sphere is defined by the mass 
,
which according to [1] is equal to:
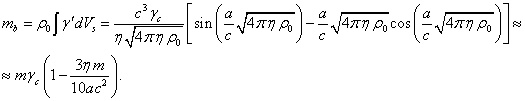
(4)
The mass 
represents the sum of the invariant masses of all the
particles in the system, which is equal to the gravitational mass of the system
. In view of the definition of the mass 
, from (3) it follows:
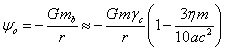. (5)
Since after averaging over a
sufficient number of particles, the internal vector gravitational potential 
and the external vector gravitational potential 
of the system are equal to zero because of the
chaotic motion of the set of particles, the acting gravitational field strength
inside the system and strength 
outside the system are actually defined only
by the gradient of the corresponding scalar potential. In view of (1) and (3),
for the strengths we obtain the following [1]:
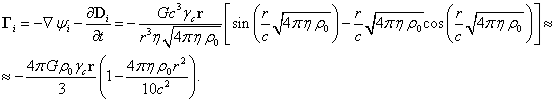
(6)
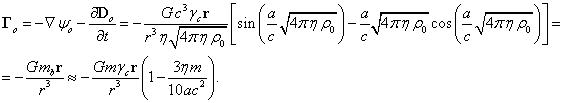
(7)
The torsion field, which has the same meaning in the covariant theory of gravitation as the gravitomagnetic field in gravitoelectromagnetism, and similar in meaning to the
magnetic field in electromagnetism, on the average is equal to zero, both inside and outside of the system under consideration:
, 
. (8)
The gravitational field
strength 
and the torsion field 
together constitute the gravitational field
tensor 
inside the system, and the quantities and 
constitute the same tensor outside the system.
Since all the expressions in the covariant theory of gravitation are derived
from the principle of least action in the same way as it is done for the
electromagnetic field in the curved spacetime, the gravitational field tensor
is similar in its form to the electromagnetic field tensor [19]. Accordingly,
the gravitational field is considered as a vector field, and the covariant
theory of gravitation represents a vector-tensor theory with regard to the
metric and the cosmological constant.
3. The energy of the particles
in the field and the energy of the field itself
In [18] the Hamiltonian of the
system of particles was found taking into account the four fields acting in the
system, including the acceleration field, the gravitational field, the
electromagnetic field and the pressure field, and it was shown that for a
stationary system in the curved spacetime the Hamiltonian is exactly equal to
the relativistic energy of the system. For energy the following was found:
(9)
where
are the scalar potentials of the acceleration
field, gravitational field, electric field and pressure field, respectively; 
is the charge density of a particle in the
reference frame associated with the particle; 
is the time component of the four-velocity of
an arbitrary particle; 
is the gravitational tensor; 
is the magnetic constant; 
is the electromagnetic tensor; 
is the acceleration tensor; 
is the coefficient of the pressure field; 
is the pressure field tensor; 
is the moving invariant three-volume expressed
in terms of the product 
of the differentials of the space
coordinates, and in terms of the square root 
of the determinant 
of the metric tensor taken with a negative
sign.
In the expression for the
energy (9) the first integral is related to the particles’ energies in the
fields’ scalar potentials, and the second integral contains four tensor
invariants, each of which reflects the energy of the respective field.
We will calculate in the limit
of the special theory of relativity the energy of the particles in the
gravitational field of the system, in which the gravitational vector potential
and the gravitational torsion field on the average are equal to zero. In this
case 
and the energy of the particles is defined as
the volume integral taken of the product of the effective mass density inside
the sphere 
by the internal scalar potential 
. In view of (1-2) we obtain the following:
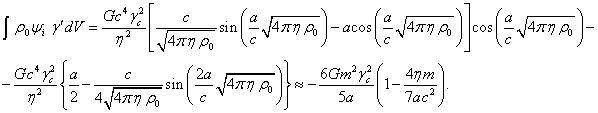
(10)
We will now calculate the
volume integral taken of the tensor invariant of the gravitational field,
separately for the field inside and outside the sphere. The integral of the
tensor invariant is expressed in terms of the gravitational field strength 
and the torsion field 
entering into the gravitational tensor 
:
. (11)
This integral part is included
in this form in the energy of the system (9) and defines there the contribution
of the gravitational field. Substituting here (6-8), we find:
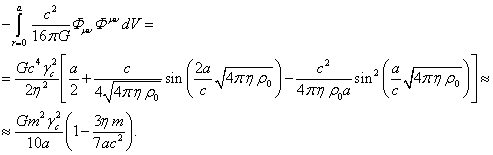
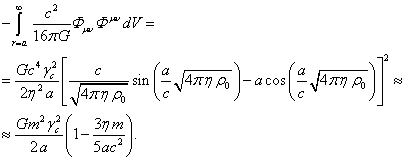
(12)
We can sum up the integrals in
(12), that is, calculate the integral of the tensor invariant over the entire
volume, occupied by the field, and then compare the result with (10). We obtain
the following:
(13)
If we substitute (13) into the energy
(9), we will see that the gravitational field energy in the form of the tensor
invariant is subtracted from the energy of particles in the gravitational
potential, so that the total gravitational energy of the system becomes equal
to half of the energy of particles in the gravitational potential, and in this
form it makes contribution into the relativistic energy of the system. The same
is true for the electric field of the system under consideration, if we proceed
from the similarity of the equations of both fields. Indeed, the electrostatic
energy is also calculated as half of the energy of particles in the electric
potential.
The total system’s gravitational
energy for the system under consideration can also be estimated with the help
of the stress-energy tensor of the gravitational field, determined by the
formula [9], [12], [19]:
,
where 
is the metric tensor.
In the limit of the
special theory of relativity, the time component of the given tensor is equal
to:
.
If we take into account that in the
system under consideration the torsion field 
is assumed to be equal to zero,
then the volume integral of 
will differ only by the sign from
the integral of the tensor invariant in (11). Therefore, in view of (13) the
total gravitational energy of the system can be expressed as follows:
. (14)
Similarly, the electrostatic energy 
in the absence of the magnetic
field 
can be calculated by volume
integration of the time component 
of the stress-energy tensor of
the electromagnetic field:
. (15)
Equations
(14) and (15) get violated as soon as the torsion field and, consequently, the magnetic field 
appear in the system, for example, due to the
coordinated motion of particles or charges.
We
note that neither the stress-energy tensor of the gravitational field 
nor the stress-energy tensor of the
electromagnetic field 
are part of expression (9). Therefore, in the
general case, the use of the stress-energy tensors to calculate any part of the
energy or the total system’s energy is inappropriate. Instead of these tensors,
the relativistic energy of the system (9) includes the integrals of the fields’
tensor invariants. In this case, expression (9) is derived in a covariant way
as the Hamiltonian from the principle of least action, and each field is taken
into account in the Lagrangian and the energy independently of the other
fields.
5. Gravitational field of the
Universe
In case of small sizes of 
and 
and the low mass density 
in the expressions for the
potentials and the gravitational field strengths, the approximate expressions
on the right-hand side of (1), (5), (6), (7) are valid. However, if or are large enough, it is necessary
to use the exact formulas containing sines and cosines. Let us take, for
example, the gravitational field strength outside the body in (7), and let
us denote: 
. Then the square brackets in (7) will be written as the quantity 
, so that 
will vary proportionally to 
.
As long as the angle 
is small, we can approximately
rely on the right-hand side of (7). If the angle is increased, then the quantity would first increase, and then
would begin to decrease and even change its sign. So, at 
we will have 
, at 
we will have 
, and at 
we will have 
. If we solve the equation 
, we can find the angle , at which the quantity vanishes. This angle is
approximately equal to 
radians.
At 
the gravitational field strength outside the body in (7) changes
its sign, so that instead of the gravitational attraction the repulsion
appears. We assume that the condition leads to a physically unjustified
situation. Thus, the following inequality must hold:
.
(16)
This inequality imposes certain
restrictions on the acceptable values of the radius of the physical system and the
invariant mass density in this system. For an example,
we will estimate 
for the entire observable
Universe, which at a scale of 100 Mpc or more can be considered as a
relativistic uniform system due to slight variation in the average mass density
at different points.
From observations it follows that the
Universe is very close to a state, in which spacetime is flat and almost
Euclidean. In this case, according to the Lambda-CDM model the total
mass-energy density of the Universe is close to the critical value 
kg/m3 [20]. The size
of the Universe can be estimated as the Hubble length 
m, where 
is the Hubble parameter. Taking 
in place of , and also 
in place of and using the approximate
equality 
according to [5], we find the
value 
radians.
Since the angle 
is sufficiently large, for
modeling the gravitational field of the Universe it is necessary to use the
refined formulas with sines and cosines. As can be seen from the formula for
the gravitational field strength inside the system (6), as the current radius 
increases to the value or more, the values 
, 
and the magnitude of the field
strength first increase, but then begin to
decrease. Under the boundary condition (16), that is at radians, both 
, and , vanish, and at the boundary of the Universe, at 
, gravitation tends to zero .
On the other hand, the large-scale
structure of the Universe is an observational fact, when the matter of clusters
of galaxies near the boundary of the Universe does not form large spherical
systems, but forms a network structure of clusters of galaxies. This can be
explained as follows: at large distances gravitation seems to lose its
strength, and the distant parts of the Universe have weaker influence, as
compared to the closer parts, than they should by the Newton’s law. We suppose
that this effect is exactly described by the formula for the gravitational
field strength inside the system (6).
But why should gravitation weaken at
large distances? There is a model that combines the infinite nesting of matter
and the Le Sage’s theory of gravitation, and explains the weakening of
gravitation by scattering of gravitons on the particles of space environment
[21]. In this case, it turns out that the observable Universe in its scale is
close enough to the limiting sizes of a system of stars and galaxies that can be
kept from disruption by the ordinary gravitation force.
6. Strong gravitation at the level of nucleons
Let us now pass on from large sizes
and low mass density to the case of small sizes and high mass density, and
again we will use (6) for the gravitational field strength, but already inside
the proton. The proton fits well into the relativistic uniform model, since its
average density of the order of 
kg/m3 at the proton
radius 
m, according to [22], is only 1.5
times less than the mass density in the center. As the gravitational constant
at the atomic level we will use the strong gravitational constant 
m3/(kg×s2), assuming that it is
the strong gravitation that holds together the matter of nucleons and other
particles [12].
Just as in (16), we will estimate the
value for the proton using the
approximate equality 
:
.
As we can see, for the proton the
angle 
is close enough to the limiting
angle 
. Hence it also follows that it is necessary to use sines and cosines in
(6) and (7) in order to describe the gravitational field of strong gravitation
inside and outside the proton.
Suppose now that we can add matter
inside the proton volume, increasing the proton’s mass density to a certain
value 
in such a way that the angle becomes equal to the limiting
angle . This corresponds to the condition 
radians, from which we obtain the
estimate of the limiting invariant mass density 
kg/m3 and the estimate
of the corresponding invariant energy density 
J/m3. In order to turn
from these invariant values to the observed values, in the first approximation
it suffices to multiply the invariant values by the Lorentz factor 
of the motion of matter in the
center of the proton. As is indicated in [1], this is equivalent to the fact
that instead of mass 
we use the mass 
, determined in (4), which is equal to
the gravitational mass 
of the system.
On the other hand, in [23, 24] in the
Le Sage’s model of gravitation, the energy density of gravitons in the vacuum
field was found, which was equal to 
J/m3. From the
equality 
we obtain the estimate of the
Lorentz factor in the center of the proton: 
. This also follows directly from (4), where we replace with the proton mass, replace 
with 
radians, replace with the proton radius 
, and take into account the ratio .
But why do we use equality ? The point is that by adding matter inside the proton up to the
limiting invariant mass density kg/m3, according to
(6) and (7) we decrease the gravitational field on the proton’s surface to
zero. In order to explain this, we need to refer to the Le Sage’s model of
gravitation. In this model, for the emergence of the gravitation force the
gradient of the gravitons’ flux is required that falls on the test body. As a
rule, such a gradient arises between two bodies, leading to the gravitation
force, that is, to the attraction of bodies. However, the gradient of the
gravitons’ flux on the proton’s surface will disappear if the energy density 
of the gravitons in the vacuum field
becomes equal to the maximum energy density inside the proton, equal to 
. The proton will emit as many gravitons as the surrounding vacuum, and
will become indistinguishable from the vacuum with respect to the energy
density. In the absence of the gravitons’ gradient the gravitational force
disappears, which is reflected in expression (6) for the field strength in the
limiting case at 
.
Let us consider another situation
involving strong gravitation. In particular, we will estimate the maximum
radius 
of the system, which is held by
strong gravitation and has the mass density equal to the critical density kg/m3 in the observable
Universe. For this, similarly to (16), the following condition must be
fulfilled: 
. Substituting here the approximate equality , we find 
m. As in the previous section for
the case of the Universe, we can now assume that the strong gravitation stops
acting at distances more than at the matter density .
Dividing the Hubble length m by , we will obtain the relation 
. Next, we will use the coefficient 
of similarity in sizes between the
atomic and stellar matter levels, for the proton and its analogue at the
stellar level in the form of a neutron star. Dividing the radius of a typical
neutron star with the mass of 1.35 Solar masses, which is approximately equal
to 12 km, by the radius of the proton, we will obtain 
. The value is of the same order as the ratio
. This means that the object with the radius , held in equilibrium by the strong gravitation and consisting of
nucleons or hydrogen atoms, is similar to the observable Universe, held in
equilibrium by the ordinary gravitation and consisting of stars and their
clusters.
In the general case, if in the condition
the mass density is increased, then consequently
the limiting size of the object decreases, for
which the gravitational field strength is calculated in (6), for both the
strong and ordinary gravitation. At sizes exceeding , the strong gravitation ceases to act in the cosmological space. The
ordinary gravitation is much weaker than the strong gravitation, but the range
of action of the ordinary gravitation in cosmological space is much greater.
Thus, the strong gravitation at the sizes exceeding does not fully disappear – the
ordinary gravitation remains and acts instead of it. However, the action of the
ordinary gravitation is also limited, at approximately 
m it starts to decrease, as was
shown in the previous section. Accordingly, at such large sizes the ordinary
gravitation should be replaced by some other weaker gravitation with a larger
radius of action.
7. The neutron star
In the previous section the estimate
of the Lorentz factor at the center of the proton was obtained: . Similarly, it is possible to calculate the Lorentz factor for the
particles at the center of a typical neutron star with the mass of 1.35 Solar
masses, the radius of 
km, and the average density of 
kg/m3. For the star we
need to take into account the ratio and the angle of 
radians. Substituting now in (4)
the star mass instead of , 
instead of , 
instead of 
, and replacing by the star radius 
, we find 
. This allows us to calculate the kinetic energy 
of the proton as a certain
typical particle, moving at the center of the neutron star, and to estimate the
temperature at the center of the star: 
K using the equation 
, where 
is the Boltzmann constant and 
is the proton mass. Previously,
this temperature was calculated in [5] using the assumed, based on the
calculations of other authors, changing of the mass density inside the star,
where the following was obtained: 
K. These values of the central
temperatures can be considered the upper limit, which is valid for the moment
of the star formation. In this short period of time the star is still in a hot
state, the nucleons are moving randomly in its matter, and the approach
described above is valid. Consequently, the Lorentz factor for the particles at the center
is the limiting value for the neutron star’s matter. The same applies to the
Lorentz factor at the center of the proton.
8. Conclusions
One of the conclusions in [25]
was that the energy of the motionless matter of the uniform body in the form of
a sphere in its proper static gravitational field is twice as large in its
absolute value as the energy of the gravitational field itself. What will
happen, if we turn into the relativistic uniform system, in which the matter
particles are not motionless, but are moving with the Lorentz factor (2),
depending on the current radius? The answer to this question follows from (13) –
both in the classical and in the relativistic case, the relation between the energy of the
particles in the field and the energy of the field itself remains unchanged.
In Section 4 we showed that,
in the general case, the knowledge of the stress-energy tensors of fields is
not enough to calculate the relativistic energy, and hence the corresponding
inertial mass of the system. Thus, the covariant theory of gravitation differs
significantly from the general theory of relativity, where it is possible to
calculate the energy and mass by volume integration of the total stress-energy
tensor of the system [26].
Applying the expressions for
the potentials and the gravitational field strengths (1), (5), (6), (7) to the
observable Universe and to the proton allows us to specify certain
characteristic features of these objects. It turns out that these objects are
in states close to the maximum possible, which requires an accurate account of
the effects of the relativistic uniform model with respect to the gravitational
field. Two extreme cases are possible – the largest possible sizes of the
object 
and the low mass density (the Universe), and the extremely large mass
density with small sizes (the proton, the neutron star). In (16) the condition 
radians is provided, to which the object’s
sizes and mass density must correspond, if this object is held in equilibrium
by its proper gravitational field. This allows us to estimate the radius of
action of the strong and ordinary gravitation in the cosmological space. With
the help of (4) it is also possible to calculate the maximum possible Lorentz factor
of the matter particles at the center of the neutron star and at the center of
the proton.
Thus, the results obtained
with respect to the dependencies of the gravitational field inside and outside
the bodies are in good agreement with the conclusions of the Le Sage’s theory
of gravitation, with the infinite nesting of matter, with the strong
gravitation at the level of nucleons and with the concept of the dynamic force
vacuum field.
At the next stage, it is
planned to relate the conclusions of the covariant theory of gravitation and
the results of the Einstein-Λ model, described, for example, in [27] and [28], with respect to the
energy of particles of the physical system.
References
[1]
Fedosin S.G. Relativistic Energy and Mass
in the Weak Field Limit. Jordan
Journal of Physics. 8
(1), 1-16 (2015).
[2]
Fedosin S.G. The Integral Energy-Momentum
4-Vector and Analysis of 4/3 Problem Based on the Pressure Field and
Acceleration Field. American Journal of Modern Physics. 3 (4), 152-167 (2014). Doi:10.11648/j.ajmp.20140304.12.
[3]
Denisov V.I. and Logunov A.A. The inertial mass defined in the general theory of relativity has no physical meaning. Theoretical
and Mathematical Physics. 51(2), 421-426
(1982). Doi:10.1007/BF01036205.
[4]
Khrapko R.I. The Truth about the Energy-Momentum Tensor and
Pseudotensor. Gravitation
and Cosmology. 20 (4), 264-273 (2014). Doi:10.1134/S0202289314040082.
[5]
Fedosin S.G. Estimation of the physical
parameters of planets and stars in the gravitational equilibrium model.
Canadian Journal of Physics. 94 (4), 370-379 (2016). Doi:10.1139/cjp-2015-0593.
[6]
Fedosin S.G. The virial
theorem and the kinetic energy of particles of a macroscopic system in the
general field concept. Continuum Mechanics and Thermodynamics. 29 (2), 361-371 (2016). Doi:10.1007/s00161-016-0536-8.
[7]
Fedosin S.G. Two
components of the macroscopic general field. Reports in Advances of Physical
Sciences. 1 (2), 1750002, 9 pages
(2017). Doi:10.1142/S2424942417500025.
[8]
Fedosin S.G. The Metric Outside a Fixed Charged Body in the Covariant Theory of
Gravitation. International Frontier Science Letters, 1 (1), 41-46 (2014). Doi:10.18052/www.scipress.com/ifsl.1.41.
[9]
Fedosin, S. The
physical theories and infinite hierarchical nesting of matter, Volume 2, LAP LAMBERT Academic
Publishing, pages: 420, ISBN-13: 978-3-659-71511-2. (2015).
[10] Fedosin
S.G. The Pioneer
Anomaly in Covariant Theory of Gravitation. Canadian Journal of Physics. 93
(11), 1335-1342 (2015). Doi:10.1139/cjp-2015-0134.
[11] Einstein A. Gibt es eine
Gravitationswirkung die der elektrodynamischen Induktionswirkung analog ist?
Vierteljahrsschrift für gerichtliche Medizin und öffentliches Sanitätswesen. 44, 37-40 (1912).
[12] Fedosin S.G. Fizika i filosofiia podobiia: ot preonov do metagalaktik, written in Perm, 544 pages. ISBN 5-8131-0012-1. (1999).
[13] Sharif
M. and Yousaf Z. Role of adiabatic index on the evolution of spherical
gravitational collapse in Palatini f(R) gravity. Astrophys. Space Sci. 355, 317-331 (2015). Doi:10.1007/s10509-014-2179-1.
[14] Yousaf
Z. and Zaeem ul Haq Bhatti M. Cavity evolution and instability constraints of
relativistic interiors. Eur. Phys. J. C. 76, 267 (2016).
Doi:10.1140/epjc/s10052-016-4109-6.
[15] Yousaf
Z., Zaeem ul Haq Bhatti M. and Farwa U. Stability of compact stars in αR2+β(RγδTγδ)
gravity. Mon. Not. R. Astron. Soc. 464 (4),
4509-4519 (2017). DOI:10.1093/mnras/stw2698.
[16] Zaeem
ul Haq Bhatti M., Yousaf Z. and Hanif S. Role of f(T) gravity on the evolution
of collapsing stellar model. Phys. Dark Universe. 16,
34-40 (2017). DOI: 10.1016/j.dark.2017.04.003.
[17] Fedosin
S.G. The
Procedure of Finding the Stress-Energy Tensor and Equations of Vector Field of
Any Form. Advanced Studies in
Theoretical Physics. 8 (18),
771-779 (2014). Doi:10.12988/astp.2014.47101.
[18] Fedosin
S.G. About
the cosmological constant, acceleration field, pressure field and energy. Jordan
Journal of Physics. 9
(1), 1-30 (2016).
[19] Fedosin
S.G. The
Principle of Least Action in Covariant Theory of Gravitation. Hadronic Journal. 35 (1), 35-70 (2012).
[20] Patrignani C. et al.
(Particle Data Group). The Review of Particle Physics. Chin. Phys. C, 40, 100001 (2016) and 2017 update.
[21] Fedosin
S.G. Cosmic Red Shift, Microwave Background, and New
Particles. Galilean Electrodynamics. 23 (1),
3-13 (2012).
[22] Fedosin
S.G. The radius of the proton in the self-consistent
model. Hadronic Journal. 35 (4), 349-363 (2012).
[23] Fedosin
S.G. The
graviton field as the source of mass and gravitational force in the modernized
Le Sage’s model. Physical Science
International Journal. 8 (4), 1-18
(2015). Doi:10.9734/PSIJ/2015/22197.
[24] Fedosin
S.G. The charged
component of the vacuum field as the source of electric force in the modernized
Le Sage’s model. Journal of Fundamental and Applied Sciences. 8 (3), 971-1020 (2016). Doi: 10.5281/zenodo.845357.
[25] Fedosin S.G. The Hamiltonian in
Covariant Theory of Gravitation.
Advances in Natural Science. 5
(4), 55-75 (2012). Doi:10.3968%2Fj.ans.1715787020120504.2023.
[26] Fock V. A. The Theory of Space, Time
and Gravitation. Macmillan. (1964).
[27] Yousaf
Z. Spherical relativistic vacuum core models in a Λ-dominated
era. Eur. Phys. J. Plus. 132, 71 (2017).
DOI: 10.1140/epjp/i2017-11336-9.
[28] Yousaf
Z. Stellar filaments with Minkowskian core in the Einstein-Λ
gravity. Eur. Phys. J. Plus. 132, 276
(2017). DOI: 10.1140/epjp/i2017-11547-0.
Source: http://sergf.ru/gpren.htm