Гравитационная постоянная

Гравитационная постоянная G лежит в основе закона всемирного тяготения.

Содержание

1 Введение
2 История измерения
3 Теоретическое определение
4 Ссылки
5 См. также
6 Внешние ссылки
7 Литература

Введение

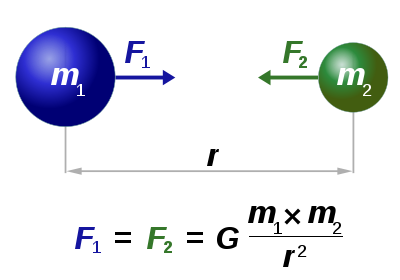
Согласно Ньютоновскому закону всемирного тяготения, сила гравитационного притяжения между двумя материальными точками с гравитационными массами m₁ и m₂, находящимися на расстоянии R , равна:

$F=G{\frac {m_{1}m_{2}}{R^{2}}}.$

Коэффициент пропорциональности G в этом уравнении называется гравитационной постоянной. Численно она равна модулю силы тяготения, действующей на точечное тело единичной массы со стороны другого такого же тела, находящегося от него на единичном расстоянии.

В единицах СИ рекомендованное на 2014 год значение: ^[1] $G=(6{,}67408(31)\cdot 10^{{-11}}$ м³•с^-²•кг⁻¹, или Н•м²•кг^-².

Гравитационная постоянная присутствует в большинстве формул, связанных с гравитационным взаимодействием. В частности, она входит в уравнения общей теории относительности и ковариантной теории гравитации, а также используется в формулах при определении поля гравитационного кручения. Значение гравитационной постоянной и её константа взаимодействия таковы, что гравитационное взаимодействие между элементарными частицами на много порядков меньше, чем слабое, электромагнитное или сильное взаимодействия.

В теории бесконечной вложенности материи на основании SPФ-симметрии предполагается существование сильной гравитации, действующей на уровне элементарных частиц. Постоянная сильной гравитации получается из обычной гравитационной постоянной путём умножения на коэффициенты подобия, находимые с помощью подобия уровней материи.

История измерения

Гравитационная постоянная фигурирует в современном законе всемирного тяготения, однако отсутствовала у Ньютона и в работах других ученых вплоть до начала XIX века. Гравитационная постоянная впервые была введена в закон всемирного тяготения, по-видимому, только после перехода к единой метрической системе мер. Возможно впервые это было сделано французским физиком Пуассоном в «Трактате по механике» (1809), по крайней мере никаких более ранних работ, в которых фигурировала бы гравитационная постоянная, историками не выявлено. В 1798 году Генри Кавендиш подготовил и провёл эксперимент Кавендиша с целью определения средней плотности Земли с помощью крутильных весов, изобретённых Джоном Мичеллом (Philosophical Transactions 1798). Кавендиш сравнивал маятниковые колебания пробного тела под действием тяготения шаров известной массы и под действием тяготения Земли. Численное значение гравитационной постоянной было вычислено позже на основе значения средней плотности Земли и привело к значению $G=6{,}754\cdot 10^{{-11}}$ м³•с^-²•кг⁻¹. ^[2] Точность измеренного значения G со времён Кавендиша увеличилась незначительно.

Теоретическое определение

Maurizio Michelini для вычисления гравитационной постоянной использовал идею микро-квантов, заполняющих всё пространство, взаимодействующих с частицами тел и в результате подталкивающих тела друг к другу. ^[³^] Для вещества, состоящего в основном из нуклонов, получается следующее:

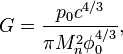
$~G={\frac {p_{0}c^{{4/3}}}{\pi M_{n}^{2}\phi _{0}^{{4/3}}}},$

где $~\ p_{0}=4,33\cdot 10^{{61}}$ Дж/м³ – плотность энергии потоков микро-квантов; $~M_{n}$ – масса нуклона; – скорость света; $~\phi _{0}=1,35\cdot 10^{{102}}$ м^-2•с^-1 – мощность флюенса потоков микро-квантов в одном направлении.

Сергей Федосин выразил гравитационную постоянную в рамках теории гравитации Лесажа через параметры, описывающие вакуумное поле гравитонов. ^[^4] ^[^5] ^[^6] В модели кубического распределения потоков гравитонов:

$~G={\frac {3p_{g}D_{0}\sigma ^{2}}{2\pi M_{n}^{2}}}={\frac {\varepsilon _{c}\sigma ^{2}}{4\pi M_{n}^{2}}}.$

Здесь $~p_{g}$ есть импульс гравитонов, взаимодействующих с нуклонным веществом; мощность флюенса $~D_{0}$ обозначает количество гравитонов dN, попавших за время dt на перпендикулярную потоку площадь dA одного из граней некоторого куба, ограничивающего рассматриваемый объём; $~\sigma =5,6\cdot 10^{{-50}}$ м² представляет собой сечение взаимодействия гравитонов с нуклонами; $~M_{n}$ – масса нуклона; $~\varepsilon _{c}=7,4\cdot 10^{{35}}$ Дж/м³ – плотность энергии потоков гравитонов для кубического распределения.

В модели сферического распределения потоков гравитонов:

$~G={\frac {4p_{g}B_{0}\sigma ^{2}}{M_{n}^{2}}}={\frac {\varepsilon _{s}\sigma ^{2}}{6\pi M_{n}^{2}}},$

где мощность флюенса $~B_{0}$ обозначает количество гравитонов dN, попавших за время dt из единичного телесного угла $d{\alpha }$ внутрь сферической поверхности dA; $~\varepsilon _{s}=1,1\cdot 10^{{36}}$ Дж/м³ – плотность энергии потоков гравитонов для сферического распределения.

Поскольку гравитационная постоянная выражается через другие переменные, она становится динамической переменной, являясь постоянной лишь в среднем.

Сечение взаимодействия $~\sigma$ может быть выражено через сечение взаимодействия $~\vartheta =2,67\cdot 10^{{-30}}$ м² заряженных частиц вакуумного поля (праонов) с нуклонами: ^[6]

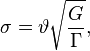
$~\sigma =\vartheta {\sqrt {{\frac {G}{\Gamma }}}},$

где $\Gamma$ – постоянная сильной гравитации. Сечение взаимодействия $~\vartheta$ очень близко по величине к геометрическому сечению нуклона и используется для вычисления электрической постоянной. Если подставить выражение $~\sigma$ через $~\vartheta$ в формулу для гравитационной постоянной в модели кубического распределения, получится связь между постоянной сильной гравитации, параметрами нуклона и плотностью энергии потоков гравитонов на нуклонном уровне материи:

$~\Gamma ={\frac {\varepsilon _{c}\vartheta ^{2}}{4\pi M_{n}^{2}}}.$

Точно также для гравитационной постоянной звёздного уровня материи возникает связь между соответствующей плотностью энергии потоков гравитонов и параметрами нейтронной звезды, являющейся аналогом нуклона:

$~G={\frac {\varepsilon _{{cs}}\vartheta _{s}^{2}}{4\pi M_{s}^{2}}},$

где $\varepsilon _{{cs}}=\varepsilon _{c}{\frac {\Phi 'S'^{2}}{P'^{3}}}=2,3\cdot 10^{{34}}$ Дж/м³ – плотность энергии потоков гравитонов на уровне звёзд для кубического распределения; $~\vartheta _{s}=\vartheta P'^{2}=5,2\cdot 10^{{8}}$ м² – сечение взаимодействия гравитонов с нейтронной звездой; $~M_{s}=M_{n}\Phi '=2,7\cdot 10^{{30}}$ кг – масса нейтронной звезды. В расчёте использованы коэффициенты подобия согласно подобию уровней материи: $~\Phi '=1,62\cdot 10^{{57}}$ по массе, $~P'=1,4\cdot 10^{{19}}$ по размерам, по скоростям протекания однотипных процессов.

Таким образом, на каждом уровне материи предполагается своя собственная постоянная гравитации, причём плотность энергии соответствующих потоков гравитонов увеличивается по мере перехода к низшим уровням материи.

Величину $\varepsilon _{{cs}}$ можно сравнить с плотностью энергии гравитационной волны в событии GW150914. Предполагается, что это событие было вызвано слиянием двух чёрных дыр массой 30 и 35 солнечных масс, вращающихся друг возле друга под действием гравитации, при уменьшении расстояния между ними до 350 км, при этом максимальная мощность гравитационного излучения достигла $3,6\cdot 10^{{49}}$ Вт. ^[7] Если разделить эту мощность на поверхность сферы радиусом 175 км, получается оценка плотности потока энергии через поверхность сферы. Эту величину можно затем разделить на скорость света и оценить плотность энергии в волне: $\approx 10^{{30}}$ Дж/м³. Плотность энергии волны получается существенно ниже, чем плотность энергии вакуумного поля гравитонов. Тем самым гравитационная волна от большинства мощных источников излучения лишь незначительно модулирует потоки гравитонов в космическом пространстве.

Ссылки

1. Newtonian constant of gravitation G. CODATA, NIST.

2. Brush, Stephen G.; Holton, Gerald James (2001), Physics, the human adventure: from Copernicus to Einstein and beyond, New Brunswick, N.J: Rutgers University Press, p. 137, ISBN 0-8135-2908-5.

3. Maurizio Michelini. Discussion on Fundamental Problems of Physics Hidden in Cosmology. Applied Physics Research. Vol. 8, No. 5. pp.19-43 (2016). http://dx.doi.org/10.5539/apr.v8n5p19.

4. Fedosin S.G. The graviton field as the source of mass and gravitational force in the modernized Le Sage’s model. Physical Science International Journal, ISSN: 2348-0130, Vol. 8, Issue 4, pp. 1-18 (2015). http://dx.doi.org/10.9734/PSIJ/2015/22197; статья на русском языке: Поле гравитонов как источник гравитационной силы и массы в модернизированной модели Лесажа.

5. Fedosin S.G. The Force Vacuum Field as an Alternative to the Ether and Quantum Vacuum. WSEAS Transactions on Applied and Theoretical Mechanics, ISSN / E-ISSN: 1991-8747 / 2224-3429, Volume 10, Art. #3, pp. 31-38 (2015); статья на русском языке: Силовое вакуумное поле как альтернатива эфиру и квантовому вакууму.

6. ^6,0 ^6,1 Fedosin S.G. The charged component of the vacuum field as the source of electric force in the modernized Le Sage’s model. Journal of Fundamental and Applied Sciences, Vol. 8, No. 3, pp. 971-1020 (2016). http://dx.doi.org/10.4314/jfas.v8i3.18, https://dx.doi.org/10.5281/zenodo.845357; статья на русском языке: Заряженная компонента вакуумного поля как источник электрической силы в модернизированной модели Лесажа.

7. Abbott, B. P.; et al. (LIGO Scientific Collaboration, Virgo Collaboration), Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 116, 061102 (2016). https://dx.doi.org/10.1103/PhysRevLett.116.061102.

См. также

Внешние ссылки

Иванов И. «Гравитационная постоянная измерена новыми методами» // Элементы.ру. — 22.01.2007.
Gravitational constant
При написании этой статьи использовались материалы страницы «Гравитационная постоянная» Русской Википедии.

Литература

Милюков В. К. Гравитационная постоянная // Физическая энциклопедия. — М.: Советская энциклопедия, 1988. — Т. 1. — С. 523.
Speake C., Quinn T. «The search for Newton’s constant» // Physics Today. — 2014. — № 7.

Источник: http://sergf.ru/gpo.htm

На список страниц