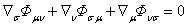International
Journal of Modern Physics A, Vol. 40, No. 02, 2450163 (2025). https://doi.org/10.1142/S0217751X2450163X
Лагранжев формализм в
теории релятивистских векторных полей
Федосин Сергей Григорьевич
ул. Свиязева 22-79,
город Пермь, 614088, Пермский край, Россия
e-mail: fedosin@hotmail.com
Лагранжев
формализм используется для вывода ковариантно определённых формул и уравнений,
пригодных для использования в непрерывно распределённом веществе в искривлённом
пространстве-времени. Особое внимание уделяется теоретическому представлению, в
котором непосредственно участвует лагранжиан и его производные. Полученные
результаты, включая уравнение для метрики, уравнение движения, уравнения для
полей, применяются к чисто векторным полям. Как следствие, определяются формулы
для вычисления основных величин, необходимые для описания физических систем.
При этом учитываются не только поле давления и поле ускорений, но и электромагнитное
и гравитационные поля за пределами вещества, делающие свой вклад в 4-импульс и
в четырёхмерный псевдотензор момента импульса каждой системы. Каждое из
представленных полей, включая гравитационное поле, имеет свой собственный
4-потенциал и свой собственный тензор, что позволяет производить все расчёты
ковариантным образом. В частности, при применении принципа наименьшего
действия оптимальным является подход, в котором 4-токи, 4-потенциалы полей и
метрический тензор зависят от точки наблюдения и варьируются независимо друг от
друга. В дополнение к уравнению Эйлера-Лагранжа выводится другое
уравнение движения, содержащее плотность обобщённой 4-силы и временную
производную объёмной плотности обобщённого 4-импульса. С целью уникальной калибровки
энергии, являющейся скалярной величиной, используется космологическая
постоянная, входящая в лагранжиан. Это приводит к тому, в выражении для
4-импульса системы исчезает как скалярная кривизна, так и космологическая
постоянная. Кроме этого, упрощается уравнение для метрики. Особенностью
уравнения для метрики оказывается то, что суммарный тензор энергии-импульса физической
системы, представленный в правой части уравнения для метрики, связан только с
тензорами полей и не зависит от 4-скоростей частиц. При этом след тензора
энергии-импульса равен нулю. Для вычисления тензора энергии-импульса
используется функциональная производная от лагранжиана по метрическому тензору.
Ковариантная производная от тензора энергии-импульса приводит к уравнению
движения частиц под действием полей, и к обобщённой теореме Пойнтинга. Свёртки
тензоров полей с тензором Риччи получаются равными нулю, так что каждое поле
делает свой собственный вклад в искривление пространства-времени в системе. Инертная масса системы
определяется как величина, связывающая 4-импульс и 4-скорость центра импульсов
системы, и может быть вычислена через квадрат 4-импульса. Показывается, что каноническим представлением
псевдотензора момента импульса является его представление с ковариантными
индексами. В ковариантном виде определяется радиус-вектор центра импульсов физической
системы.
Ключевые слова: Лагранжев формализм; интеграл движения; векторное поле; ковариантная
теория гравитации; псевдотензор момента импульса.
MSC: 70H03, 70H40, 70S05
PACS: 04.20.Fy, 11.10.Ef,
45.20.Jj
Lagrangian
formalism in the theory of relativistic vector fields
Sergey G. Fedosin
22 Sviazeva str., apt. 79,
Perm, Perm Krai, 614088, Russia
E-mail: fedosin@hotmail.com
The
Lagrangian formalism is used to derive covariant equations that are suitable
for use in continuously distributed matter in curved spacetime. Special
attention is given to theoretical representation, in which the Lagrangian and
its derivatives are directly involved. The obtained results, including equation
for metric, equation of motion, equations for fields, are applied to purely
vector fields. As a
consequence, formulas are determined for calculating the basic quantities
necessary to describe physical systems. In this case, not only the pressure
field and acceleration field are taken into account, but also the
electromagnetic and gravitational fields outside the matter, which contribute
to the four-momentum and to the four-dimensional angular momentum pseudotensor
of each system. Each of the presented fields, including gravitational field,
has its own four-potential and its own tensor,
which allows all calculations to be performed in covariant way. In particular,
when applying the principle of least action, the optimal approach is one in
which the four-currents, field four-potentials and metric tensor depend on the
observation point and vary independently from each other. In addition to the
Euler-Lagrange equation, another equation of motion is derived containing the
density of generalized four-force and the time derivative of volume density of
generalized four-momentum. In order to uniquely calibrate the energy, which is
a scalar quantity, the cosmological constant included in the Lagrangian is
used. This leads to the fact that both the scalar curvature and the
cosmological constant disappear in expression for the four-momentum of the
system. In addition, the equation for the metric is simplified. The peculiarity
of equation for the metric is that the total stress-energy tensor of the
physical system, presented in the right part of equation for the metric, is associated
only with field tensors and does not depend on particle four-velocities. Moreover,
the trace of stress-energy tensor is zero. To calculate the stress-energy
tensor, the functional derivative of Lagrangian density with respect to the
metric tensor is used. The covariant derivative of stress-energy tensor leads
to equation of particle motion under action of fields, and to generalized
Poynting theorem. The contractions of the field tensors with the Ricci tensor
are equal to zero, so that each field makes its own contribution to the
curvature of spacetime in the system. The inertial mass of a system is defined
as the value connecting the four-momentum and four-velocity of the center of momentum
of the system, and can be calculated using the square of the four-momentum. It
is shown that the canonical representation of the angular momentum pseudotensor
is its representation with covariant indices. The radius-vector of the center of momentum of a
physical system is determined in covariant form.
Keywords: Lagrangian formalism;
integral of motion; vector field; covariant theory of gravitation; angular
momentum pseudotensor.
1. Введение
В теории поля
принцип наименьшего действия является основным принципом, позволяющим находить
уравнения поля и уравнения движения частиц в заданных полях. Если действие
обозначить через 
, а лагранжиан (Lagrangian density) как объёмную плотность функции
Лагранжа обозначить через 
,
то для действия справедливо соотношение 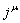[1]:
.
(1)
Обычно лагранжиан 
содержит энергии
частиц в полях, находимые через произведение 4-потенциала соответствующего поля
на массовый 4-ток 
, причём в случае электромагнитного поля используется
зарядовый 4-ток 
. Кроме этого, в лагранжиане присутствуют члены, задающие плотность
энергии самих полей и выражаемые с помощью тензорных инвариантов этих полей. Скалярная
кривизна является инвариантом тензора кривизны и задаёт в лагранжиане член,
пропорциональный плотности энергии системы и возникающий за счёт учёта метрики
системы. Наконец, космологическая постоянная в лагранжиане представляет собой
тот единственный член, с помощью которого можно уникальным способом осуществить
калибровку энергии системы. Действительно, энергия как скалярная физическая
величина определяется с точностью до константы, так что однозначность в
определении состояния системы возможна лишь с учётом калибровки энергии.
Варьирование в (1) производится для
каждого члена, входящего в лагранжиан, отдельно для каждой варьируемой
переменной 
, в качестве которой выступает, например, 4-потенциал поля,
4-ток или метрический тензор. Затем суммируют все члены, содержащие вариацию
какой-либо варьируемой переменной, и приравнивают сумму к нулю. В результате
вариация действия по 4-токам приводит к уравнению движения, вариации действия
по 4-потенциалам полей дают уравнения для полей, а вариация по метрическому
тензору даёт уравнение для определения метрики. Таков практический подход в
лагранжевом формализме.
С другой стороны,
существует теоретический подход, в котором процедура определения экстремума
действия в (1) даёт уравнения Эйлера-Лагранжа, также приводящие к уравнениям
движения частиц и полей. Если лагранжиан зависит от некоторой варьируемой
переменной 
и от её четырёхмерной
производной 
по координатам и
времени, так что 
, то соответствующее классическое уравнение Эйлера-Лагранжа может быть записано так 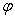[2]:
.
(2)
Нашей целью в
данной статье является конкретизация соотношений (1) и (2) таким образом, чтобы
они были пригодны в искривлённом пространстве-времени в произвольной системе
отсчёта, для непрерывно распределённого вещества. Далее мы представим уравнения
Эйлера-Лагранжа в ковариантной форме и сравним полученные уравнения с уравнениями,
которые получаются путём обычного варьирования функции действия. Кроме этого,
будут представлены ковариантные формулы для энергии, импульса, 4-импульса,
момента импульса и четырёхмерного псевдотензора момента импульса.
Необходимость
данной статьи вызвана тем, что основной поток литературы по лагранжеву
формализму и связанному с ним гамильтонову формализму посвящён отдельным
частицам и телам [3-5], между тем как зачастую
требуется проводить расчёты для непрерывной среды. В этом случае лагранжев
формализм должен применяться к интегралам по объёму вещества, что заметно
усложняет ситуацию в случае искривлённого пространства-времени. Вероятно, этим
и объясняется явный недостаток работ в указанной области, а также неполнота охвата
рассматриваемых проблем. Это же указывается и в [6], где с целью построения ковариантного
представления общей теории относительности на основе Гамильтониана в DeDonder-Weyl формализме в учёт берутся
четыре дополнительные аксиомы.
В связи с этим мы
попытаемся систематизировать различные подходы и составить из них единую
картину, представив также и собственное видение проблемы. В наших расчётах мы
будем везде использовать сигнатуру метрики вида (+,–,–,–). Все полученные результаты будут
иллюстрироваться на примере чисто векторных полей, включая гравитационное поле
в рамках ковариантной
теории гравитации (КТГ). В КТГ лагранжиан гравитационного поля подобен по форме лагранжиану электромагнитного поля.
В связи с этим сошлёмся на [7], где указывается, что только теории
максвелловского типа (Maxwell type) могут быть
самосогласованы и в них не будут появляться нефизические состояния с точки
зрения квантовой теории поля.
2. Методы
В искривлённом пространстве-времени
элемент четырёхмерного объёма следует записать в ковариантном виде. В
результате вместо (1) получается следующее стандартное выражение:
где 
есть элемент
ковариантного 4-объёма, 
есть произведение
дифференциалов пространственных координат, 
, 
есть скорость света, величина
представляет собой
детерминант метрического тензора 
.
В соответствии с
принципом наименьшего действия, для нахождения уравнений движения частиц и
полей следует приравнять к нулю вариацию действия в (3):
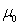. (4)
Определим теперь,
от каких переменных может зависеть лагранжиан. В общем случае в качестве таких
переменных могут выступать скалярные функции, 4-векторы и 4-тензоры, а также различные
четырёхмерные производные от этих величин. Для того, чтобы говорить более
определённо, будем использовать далее в качестве примера лагранжиан для четырёх векторных полей согласно [8-9]:
где 
– 4-потенциал
электромагнитного поля, задаваемый с помощью скалярного потенциала
и векторного
потенциала 
этого поля,
–
зарядовый 4-ток,
– инвариантная плотность
заряда, определяемая в системе отсчёта,
сопутствующей частице или элементу вещества,
– 4-скорость точечной
частицы или элемента вещества,
– 4-потенциал
гравитационного поля, описываемый через скалярный потенциал
и векторный потенциал 
этого поля в рамках
ковариантной теории гравитации,
– массовый 4-ток,
– инвариантная плотность
массы, определяемая в системе отсчёта, сопутствующей частице или элементу
вещества,
– 4-потенциал поля
ускорений, где 
и 
обозначают скалярный и
векторный потенциалы, соответственно,
– 4-потенциал поля
давления, состоящий из скалярного потенциала 
и векторного
потенциала 
,
– магнитная
постоянная,
– электромагнитный
тензор,
– гравитационная
постоянная,
– гравитационный
тензор,
– коэффициент поля
ускорений,
– тензор ускорений,
вычисляемый как 4-ротор от 4-потенциала поля ускорений,
– коэффициент поля
давления,
– тензор поля
давления,
, где 
– коэффициент порядка
единицы, подлежащий определению,
– скалярная кривизна,
– космологическая
постоянная.
Инвариантная плотность заряда , входящая в выражение зарядового тока , и инвариантная плотность массы , входящая в выражение массового тока , определяются таким же образом, как и в [10].
Описание гравитации с помощью 4-потенциала гравитационного
поля 
существенно отличает ковариантную
теорию гравитации (КТГ) от общей теории относительности (ОТО), где все
гравитационные эффекты учитываются только через метрический тензор, а отсутствует. Благодаря
гравитация может проявляться
в КТГ как самостоятельная физическая сила, ведя себя подобно электромагнитной
силе. В простейшем случае учёт метрики в КТГ приводит лишь к тому изменению
результатов пространственно-временных измерений, которое возникает под действием
полей рассматриваемой системы.
В соответствии с (5), лагранжиан зависит от следующих величин:
.
(6)
Мы можем считать,
что все величины в (6) так или иначе зависят от 4-положения 
,
задающего произвольную точку в пространстве-времени системы. Кроме этого, часть
этих величин зависит от 4-скорости 
материальной частицы
или рассматриваемого точечного элемента вещества, например, массовый 4-ток 
и зарядовый 4-ток 
. В (6) мы включили 4-потенциалы и тензоры всех полей, а
также метрический тензор 
, от которого прямо зависят некоторые члены в (4) и в (5). В
случае, если лагранжиан зависит от других переменных, они также могут быть
добавлены в (6).
Отметим различие
вида производных в (6). Так, 4-скорость определяется как производная 4-положения
по интервалу движущейся частицы: 
,
где 
обозначает интервал. В
то же время тензор векторного поля находится обычно как 4-ротор от
4-потенциала, то есть с помощью антисимметричной комбинации двух ковариантных
производных. Для тензоров полей в (5) и
(6) можно записать:
, 
, (7)
Предположим
теперь, что все величины в (5), кроме метрического тензора, полностью выражены
через и , так что вместо (6) будет 
. В этом случае метрический тензор удобно рассматривать как
самостоятельную переменную, и тогда варьирование действия по метрическому
тензору даёт уравнение для определения метрического тензора через и .
Для того, чтобы вывести уравнение движения системы в
случае заданных величин 4-токов, 4-потенциалов и 4-тензоров и полей как функций
и , выразим вариацию действия (4) следующим
образом:
.
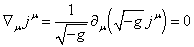(8)
Определитель метрического тензора зависит
непосредственно от компонент метрического тензора 
, так что следуя, например, [10],
можно записать:
.
(9)
Для вариации
действия в (8) с учётом (9) получается следующее:
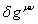. (10)
В (10) следует
учесть ещё вариацию лагранжиана , выраженную через вариации переменных
величин:
. (11)
В общем случае
производные по 4-векторам и по 4-тензорам при вариации лагранжиана должны
рассматриваться как функциональные производные.
3. Результаты
3.1. Уравнение движения и обобщённая 4-сила
В данном разделе
рассмотрим, что даёт вариация 
в (11). Данная
вариация связана с вариацией 
, причём обе вариации присутствуют только в первом интеграле
в (10). Следовательно, можно записать:
.
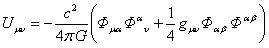(12)
Согласно [11], равенство нулю вариации 
в (12) приводит к
следующему уравнению:
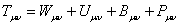. (13)
Выражение (13) отличается
от уравнения Эйлера-Лагранжа (2) тем, что в левой части производная берётся по
отношению ко времени, а не по отношению к 
. Определим объёмную плотность обобщённого 4-импульса
и выразим через
неё (13):
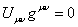. (15)
Уравнение (15)
представляет собой уравнение движения вещества, выраженное через производную от
плотности обобщённого 4-импульса по времени. При
этом мы ввели величину 
как объёмную плотность
обобщённой 4-силы. Фактически (15) есть обобщение второго закона Ньютона, с
заменой трёхмерных величин на четырёхмерные величины.
Уравнения движения
(13) и (15) впервые были выведены в [11], и там же была определена объёмная плотность обобщённого 4-импульса 
(14). При этом использовалось
условие постоянства компоненты 
каждой частицы
на каждом временном интервале 
в процессе
варьирования, что обосновывалось применением концепции типичных частиц. По
определению, типичные частицы задают основные свойства вещества физической
системы и потому их удобно использовать для описания непрерывно распределённого
вещества. После замены реальных частиц на типичные частицы физические величины
и уравнения должны быть связаны именно с типичными частицами.
Свойства типичных частиц выявляются после усреднения свойств
реальных частиц по времени и по малому объёму, окружающему избранную точку
наблюдения. В результате компонента
типичной
частицы в точке наблюдения действительно оказывается постоянной величиной, по
крайней мере для физической системы, находящейся в равновесии или в состоянии
непрерывного стационарного движения. С другой стороны, можно считать, что если время варьирования мало и сравнимо с , компонента каждой частицы
не успевает существенно измениться. В таком случае в (14) будет мгновенной плотностью обобщённого
4-импульса.
Чтобы понять
смысл (13), подставим в него лагранжиан из (5), который мы
разделим на две такие части, что 
. Так как 4-токи определяются выражениями , 
, то 4-скорость становится в 
общим множителем:
. (16)
.
(17)
Рассмотрим простейший случай, когда 4-потенциалы полей не
зависят от 4-скорости элементов вещества.
Так как тензоры полей получаются из 4-потенциалов с помощью 4-ротора, то в этом
случае тензоры полей и 
в целом не будут
зависеть от . Подставим в (14-15):
. (18)
Как видно в (18), в выражении объёмной
плотности обобщённого 4-импульса участвуют все поля,
присутствующие в системе. При этом будет зависеть только
от 4-потенциалов полей.
Предположим теперь, что правые части (15) и (19) в любой
части рассматриваемой системы равны нулю. Это возможно, например, если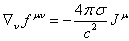 
, и все переменные величины в системе не зависят ни от
времени, ни от координат по крайнем мере в среднем. В этом случае в системе
сохраняется как плотность обобщённого 4-импульса , так и интеграл от по объёму системы,
дающий суммарный обобщённый 4-импульс.
Как правило, такая ситуация характерна для закрытых
систем, движущихся по инерции. Сохранение плотности обобщённого 4-импульса возможно
также в однородных внешних полях с особой конфигурацией. Так, в скрещённых
перпендикулярных друг другу электрическом и магнитном полях заряженная частица
может двигаться с некоторой постоянной скоростью, зависящей от величины и
направления полей, вдоль оси, перпендикулярной обоим полям.
Если определить, что 
, 
, где 
есть плотность трёхмерного
обобщённого импульса, 
есть плотность трёхмерной
обобщённой силы, то пространственная компонента четырёхмерного уравнения (15)
запишется так:
где с учётом (18) выражается через
векторные потенциалы полей:
Если величина 
явно не зависит от
координат, плотность обобщённой силы обнуляется и плотность
обобщённого импульса в (20) и (21) сохраняется.
Выразим теперь временную компоненту четырёхмерного
уравнения (15):
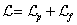, (22)
где с учётом (18) 
выражается через
скалярные потенциалы полей:
. (23)
Согласно (22), если частная производная величины 
по времени равна нулю, то обнуляется и
временная компонента плотности обобщённой 4-силы, а временная компонента (23) плотности
обобщённого 4-импульса сохраняется со временем.
Заметим теперь, что величина в (23) есть плотность энергии
частиц системы в скалярных потенциалах векторных полей, делённая на скорость
света. Для векторных полей известно, что если добавить
к энергии частиц системы в скалярных потенциалах полей энергию
самих полей, получается релятивистская энергия всей системы [8]. При этом
если выполняется соотношение:
, (24)
то релятивистская энергия системы сохраняется, как
следствие симметрии, связанной с однородностью времени. Для этого в (24)
необходимо, чтобы одновременно выполнялись условия 
и 
, то есть ни лагранжиан, ни метрика не должны зависеть от координатного
времени. В равновесной замкнутой системе следует ожидать, что величина 
не зависит прямо от
времени и в (22) сохраняется . Более того, мы можем ожидать, что сохраняется и энергия
самих полей, как часть релятивистской энергии системы.
В рамках специальной теории относительности справедливо
соотношение . Тогда, если сохраняется какая-то одна энергия – либо вся релятивистская
энергия, либо энергия частиц в скалярных потенциалах полей, либо энергия от
тензорных инвариантов полей в лагранжиане (17), – то
одновременно сохраняются и другие две энергии.
Заметим, что в механике используется соотношение
, где 
и 
обозначают плотность обычного
трёхмерного импульса и плотность обычной трёхмерной силы. Найдём связь между плотностью силы и плотностью обобщённой
силы для случая
прямолинейного движения точечной частицы, рассматриваемой как твёрдое тело. Из
(20-21) следует:
. (25)
В случае свободной твёрдой точечной частицы 4-потенциал
поля ускорений совпадает с 4-скоростью частицы, 
. В рамках специальной теории относительности 
, где 
– фактор Лоренца
частицы, 
– скорость частицы.
Следовательно, 
, и (25) можно преобразовать, перенося часть членов в правую
часть:
. (26)
Различие между плотностью силы и плотностью обобщённой
силы видно из правой части
(26). Полная производная по времени должна рассматриваться как производная
Лагранжа, 
, и следовательно, различие сил и связано с частными производными
по времени и с градиентами от векторных потенциалов как электромагнитного и
гравитационного полей, так и поля давления в веществе частицы.
3.2. Уравнение для метрики
Разделим используемый нами лагранжиан (5) и (16-17) на
две части таким образом, чтобы в первой части 
были только члены с
4-токами, а в членах второй части 
явно появился
метрический тензор:
.
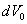(27)
Используя в (10) вместо 
последний член 
в (11), запишем
вариацию действия по метрическому тензору:
.
(28)
В (28) , а также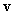 
.
Возможны два разных подхода при анализе функциональной
производной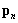 
.
В первом подходе предполагается, что независимыми
переменными в лагранжиане являются 4-потенциалы полей, 4-токи и метрический
тензор. Тогда при вариации по метрическому тензору 4-потенциалы и 4-токи не
варьируются и ведут себя как константы подобно тому, как при взятии частной
производной по одной переменной другие переменные считаются постоянными. Это
означает, что 
, и тогда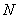 
.
Применение принципа наименьшего действия позволяет
вывести уравнения для определения 4-потенциалов и метрического тензора
(уравнения поля и уравнения для метрики) в рассматриваемой физической системе
как функций от 4-положения . Что касается 4-токов, то они также находятся из уравнений движения
как некоторые функции от . Таким образом, 4-потенциалы полей, 4-токи и метрический
тензор оказываются в одном положении по отношению к зависимости от . Указанный подход был использован в [8-10].
Другой подход
основан на том, что независимыми переменными в лагранжиане являются
4-потенциалы, 4-положение и метрический тензор.
В этом случае получается, что
,
(29)
поскольку как 4-потенциалы
согласно [10] , так и произведения 
и 
предполагаются не
зависящими прямо от метрического тензора 
. В этом случае 
в (28) будет зависеть
только от и в уравнении для
метрики члены, содержащие произведения 4-потенциалов на 4-токи,
исчезают. В качестве обоснования такой ситуации в [12]
указывают на то, что уравнения неразрывности для 4-токов в виде
, 
, (30)
определяют полностью 4-токи and в каждой точке линий тока через
начальные значения этих 4-токов. Как предполагается, это должно приводить к тому, что произведения
и не меняются при
вариации метрики и тогда их частные производные по метрическому тензору
обнуляются.
В связи с этим следует возразить, что вышеприведённые
уравнения неразрывности (30) показывают лишь то, что произведения и не зависят от
координат. Что касается зависимости этих произведений от метрики, то здесь
ситуация остаётся неопределённой.
Далее мы будем
придерживаться первого подхода при вариации действия по метрическому
тензору с целью вывода уравнения для метрики. Следовательно, согласно (28) уравнение
для метрики будет иметь следующий вид:
. (31)
В (27) метрический тензор присутствует в четырёх членах
с тензорами полей, а также в члене с тензором Риччи
, свёртка которого с метрическим тензором даёт скалярную
кривизну: 
. Учтём, что в членах с тензорами полей метрический тензор
появляется дважды. Поэтому вариация по метрическому тензору, например для члена
с электромагнитным полем, будет такова:
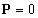
(32)
Множитель перед 
в правой части (32)
будет равен функциональной производной 
в отношении электромагнитного поля. Аналогичные вариации
будут в членах с тензорами и других полей. С учётом этого в (31) имеем:
.
(33)
При выводе (33) мы использовали тот факт, что
функциональная производная по метрическому тензору от скалярной кривизны 
даёт просто 
[13]. Это связано со
свойствами самого тензора Риччи .
Подставим теперь 
(33) в (31) и учтём
ещё лагранжиан 
в виде (5):
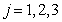
(34)
Вид уравнения (34) можно упростить, если использовать
определения тензоров энергии-импульса полей. Стандартное выражение симметричного
по своим индексам тензора энергии-импульса электромагнитного поля таково:
. (35)
В таком же виде выражаются тензоры энергии-импульса
других векторных полей. В частности, для гравитационного поля в рамках
ковариантной теории гравитации [8], для поля ускорений и для поля давления
можно записать:
, 
,
. (36)
С учётом (35-36) в (34) получается следующее:
, (37)
где 
есть суммарный тензор
энергии-импульса системы.
Умножим обе части уравнения (37) на 
и учтём, что 
, 
, а также 
, поскольку справедливы соотношения 
, 
, 
, 
:
.
(38)
Согласно [8], с целью калибровки релятивистской энергии
системы космологическая постоянная задаётся так:
. (39)
Подстановка (39) в (38) и в (37) при 
, где 
– константа порядка единицы, даёт следующее:
.
. (40)
Уравнение (40) представляет собой уравнение для метрики
и имеет тот же вид, что и в [8]. Это уравнение позволяет находить компоненты
метрического тензора при заданном тензоре энергии-импульса 
.
Следует заметить, что тензор 
энергии-импульса поля
ускорений в (36) отвечает за плотности потоков энергии, связанные с
присутствием покоящихся и движущихся частиц вещества физической системы. По
своему смыслу тензор играет ту же роль, что
и тензор энергии-импульса частиц вещества 
, используемый в общей теории относительности. Представление
тензора в (40) в составе 
происходит подобно
тому, как представляется тензор 
в соответствующем
уравнении для метрики в общей теории относительности. Однако векторное поле
ускорений учитывает движение частиц через 4-потенциал и тензор поля и потому
более точно описывает физическую систему, чем скалярное поле ускорений в общей
теории относительности. Действительно, тензор содержит лишь
4-скорости 
частиц, но не включает
в себя члены, связанные с 4-ускорением частиц. Очевидно, что энергия и импульс
ускоряемых частиц отличается от энергии и импульса тех частиц, у которых нет
ускорения.
Тензор состоит из суммы тензоров
энергии-импульса всех векторных полей, которые присутствуют в системе и учтены
нами в лагранжиане. Выделим в лагранжиане (5) ту его часть, которая содержит
тензорные инварианты полей:
. (41)
Можно заметить, что тензор выражается через 
(41) по формуле:
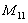. (42)
Правая часть (42) учитывает соотношение 
.
В общей теории относительности используется аналогичная
формула для определения тензора энергии-импульса Гильберта, как суммарного
тензора энергии-импульса материи и негравитационных полей (Hilbert
stress–energy tensor). При этом вместо лагранжиана в (42) подставляется
та часть лагранжиана, которая в общей теории относительности не содержит
скалярную кривизну и космологическую постоянную, и ответственна за материю и негравитационные
поля [14-15].
3.3. Уравнения поля
Запишем для лагранжиана (5) зависимость от переменных
величин в следующем виде:
. (43)
Мы можем считать, что 4-токи, 4-потенциалы, тензоры
полей и метрический тензор в (43) существуют самостоятельно и потому должны
варьироваться независимо друг от друга. Вариация лагранжиана (43) выглядит
следующим образом:
(44)
Используем (44) для вывода уравнений электромагнитного
поля. В (44) только два члена связаны с 4-потенциалом 
, а именно это 
и 
.
Вариация действия, связанная с вариацией 4-потенциала , должна обращаться в нуль. Подставим вышеуказанные два члена
в первый интеграл в (10):
.
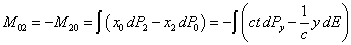(45)
Как показано в Приложении A,
результат вариации в (45) приводит к стандартным уравнениям электромагнитного
поля в ковариантном виде:
, 
. (46)
Повторяя аналогичные шаги в отношении других полей,
находим уравнения соответственно для гравитационного поля, поля ускорений и
поля давления, рассматриваемых как векторные поля:
, 
,
, 
,
, 
.
(47)
Вторые уравнения в (46) и (47) для каждого поля выполняются
тождественно и являются следствием того, что тензоры полей определены через
4-роторы от 4-потенциалов полей [8], [10].
3.4. Уравнение движения с тензорами полей
В (19) мы нашли уравнение движения физической системы,
выраженное через производную по времени от 4-потенциалов полей. Но кроме
4-потенциалов, лагранжиан содержит ещё тензоры полей, и зачастую оказывается,
что уравнение движения удобнее выражать именно через тензоры полей. Это
означает, что вместо потенциалов полей можно воспользоваться напряжённостями
полей.
Возьмём в вариации лагранжиана (44) ту его часть,
которая связана с вариациями 4-токов, и подставим эту часть в первый интеграл в
(10):
.
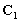(48)
Поскольку 
, 
, то
вариации 4-токов связаны с вариациями инвариантной плотности заряда 
, инвариантной плотности массы 
и 4-скорости 
:
, 
. (49)
Как правило, на 4-токи накладываются условия калибровки
следующего вида: 
, 
, так что ковариантные дивергенции 4-токов равны нулю. Условия
калибровки представляют собой так называемые уравнения непрерывности,
связывающие между собой плотность заряда (массы) и
4-скорость движущегося элемента вещества. Благодаря такой связи вариации 
и 
, 
и
становятся в (49) зависимыми
друг от друга.
С другой стороны, мы можем считать, что все вариации , и вызываются одной и той
же вариацией 
, поскольку плотность заряда (массы) и
4-скорость могут быть функциями от 4-положения 
, то есть функциями от координат и времени. Следовательно, в
(49) вариации 4-токов могут быть выражены через . При движении элемента вещества могут меняться скорость его
движения и плотность заряда (массы), но заряд и масса этого вещества как
правило являются инвариантами движения и сохраняются. Это условие было
использовано в [10], [13] для того, чтобы определить вариации 4-токов через
вариации :
,
. (50)
Используя выражение для лагранжиана 
с учётом (27), находим
функциональные производные по 4-токам:
, 
. (51)
Подставим производные (51) и вариации 4-токов (50) в (48):
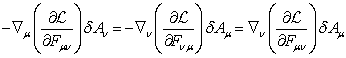. (52)
Преобразуем по частям первый член в (52), связанный с
зарядовым 4-током 
:
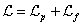(53)
Первый интеграл в правой части (53) равен нулю
аналогично (A4) в Приложении A , так как
является интегралом от дивергенции некоторого 4-вектора. Подынтегральное
выражение в последнем члене в правой части (53) можно преобразовать путём
перемены индексов:
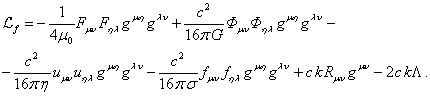
(54)
Повторяя то же самое, как в (53-54), для гравитационного
поля, поля ускорений и поля давления в отношении массового 4-тока 
, для (52) находим:
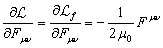. (55)
Из (55) следует, аналогично [8-9], [16-17], уравнение
движения заряженного вещества в четырёх векторных
полях:
. (56)
Отметим, что уравнение движения (56) выводится и без
варьирования по переменной . Если подставить (39) в (37), то уравнение для метрики будет
выглядеть так:
. (57)
В (57) слева находится тензор Эйнштейна 
, умноженный на 
. Поскольку дивергенция этого тензора равна нулю: 
, то будет равна нулю и дивергенция правой части:
.
(58)
Космологическая постоянная 
является постоянной в
том смысле, что для неё 
. Следовательно, в (58) должно выполняться соотношение
. (59)
Подставляя в (59) тензоры энергии-импульса полей (35) и
(36), и учитывая соотношения из [8-9]:
, 
,
, 
, (60)
приходим к уравнению движения (56).
При выводе уравнения (56) использовались вариации (50),
справедливые при условии, что выполняются уравнения непрерывности: , .
Аналогично [8], возьмём дивергенции уравнений поля (46)
и (47), и учтём уравнения непрерывности. Это приведёт к соотношениям:
, 
, 
.
(61)
Согласно (61) в искривлённом пространстве-времени
возникает дополнительная связь между тензором Риччи 
и тензорами полей, так
что свёртка с тензорами полей
должна равняться нулю.
Если учесть уравнение движения (59) и формулу (42), то
для уравнения движения получается следующая формула:
, (62)
где представляет ту часть
лагранжиана, которая содержит тензорные инварианты полей и для векторных полей
имеет вид (41). При этом временная компонента уравнения (62) описывает
обобщённую теорему Пойнтинга для энергии и потоков энергии полей [18].
3.5. Релятивистская энергия
В соответствии с
[19] и с формулой (B10)
в Приложении B, релятивистская энергия системы определяется
выражением:
, (63)
где 
есть скорость движения
элемента вещества.
Действуя далее как в [20], в (63) можно перейти от
суммирования по частицам к интегралу по объёму системы, а от производной 
перейти к
соответствующей производной от 
внутри интеграла по
объёму. Это даёт следующее:
. (64)
В (64) даётся выражение для релятивистской энергии
системы, содержащей непрерывно распределённое вещество. Так как 
, то с учётом (16-17) для и 
энергию (64) можно
представить так:
(65)
В (65) учтено условие калибровки энергии в виде 
, вытекающее из первого соотношения в (40).
Существуют случаи, когда производными по скоростям в (65)
можно пренебречь. Пусть физическая система в целом неподвижна и не вращается, и
состоит из множества хаотически движущихся с небольшой скоростью элементов
вещества в виде типичных частиц. Напряжённости и соленоидальные векторы полей в
каждой точке пространства находятся путём векторной суперпозиции полей,
порождаемых всеми типичными частицами. Образующиеся таким способом поля могут
многократно превышать собственные поля, генерируемые отдельной типичной
частицей. Если это выполняется, то в первом приближении можно считать, что
потенциалы полей и 
не зависят от
скоростей отдельных частиц внутри системы. Тогда 
и последний член в (65)
будет мал по сравнению с другими членами. Исчезают и производные по скоростям
от потенциалов полей. Это было использовано для оценки энергии релятивистской
однородной системы в [8] и в [20].
Ситуация меняется, когда частиц в системе мало и они
двигаются с релятивистскими скоростями, или когда система целиком движется со
скоростью, близкой к скорости света. В этом случае последний член в (64-65)
может уже давать достаточно существенный вклад в энергию системы. Существенными
становятся и производные по скоростям от потенциалов полей.
3.6. Преобразование Лежандра и гамильтониан
Математическая процедура, позволяющая переходить от
функции Лагранжа (Lagrangian) 
к функции Гамильтона (Hamiltonian)
, называется преобразованием Лежандра. Важность функции
Гамильтона заключается в том, что она связывается с релятивистской энергией
физической системы. Это видно из определения , которое мы запишем с учётом (63-64):
(66)
Если функция Лагранжа явно зависит от времени и 
, то как функция Лагранжа, так и функция Гамильтона
изменяются со временем.
С целью упрощения рассмотрим простейший случай, когда плотность
массы и плотность заряда 
, а также потенциалы полей явно не зависят от скоростей
частиц. В этом случае тензорные инварианты и также не зависят от
скоростей частиц, так что 
. Далее нам понадобится соотношение из [2]:
, (67)
где 
есть элемент объёма в
системе отсчёта, связанной с движущимся элементом вещества, 
есть элемент
ковариантного 4-объёма данного вещества с точки зрения внешнего координатного
наблюдателя.
В (16) можно выразить через
скорость 
типичных частиц
системы:
. (68)
С учётом (67-68) имеем:
,
(69)
Напомним, что 
согласно (21) было
следствием (14), где вычислялась производная лагранжиана 
по 4-скорости , тогда как в (69) находится через
производную по трёхмерной скорости 
в виде 
.
В рассматриваемом случае величина 
в (69) представляет
собой трёхмерный обобщённый импульс одного элемента вещества, имеющего
инвариантный объём 
и скорость
движения 
.
Подстановка (69) в (66) даёт преобразование Лежандра для
непрерывно распределённого вещества, позволяющее перейти от функции Лагранжа к функции
Гамильтона:
. (70)
Сумма в (70) означает, что вся система может быть
разбита на 
элементов объёма, каждому
из которых можно приписать свой собственный обобщённый импульс и свою скорость
движения . Указанная сумма в правой части (70) заменена на интеграл по
всему объёму, занимаемому частицами системы.
В классическом подходе функция Гамильтона должна зависеть не от
скорости , а от обобщённого импульса частиц и полей каждого элемента
объёма, 
. Если в (70) взять дифференциалы от 
и от , то окажется, что выполняются соотношения:
, 
. 
, 
. (71)
Если подставить в уравнение Эйлера-Лагранжа (B3)
в Приложении B соотношения и из (71), получается
следующее:
. (72)
Соотношения (71-72) представляют собой стандартные
уравнения Гамильтона. При этом трёхмерное уравнение (72) повторяет более общее
четырёхмерное уравнение (15) и может быть получено из пространственной
компоненты (20) этого уравнения. Чтобы прийти к (72), достаточно
проинтегрировать (20) по инвариантному объёму одного элемента вещества с учётом
определения 
в (69), соотношения в (71) и выражения
функции Лагранжа 
.
3.7. Релятивистский импульс системы
В разделе 3.5 было показано, что если в рассматриваемой
физической системе функция Лагранжа не зависит явно от времени и 
, то сохраняется энергия 
системы, как некоторая
аддитивная функция. Импульс системы также является аддитивной функцией. Для
определения импульса и закона его сохранения используется свойство однородности
пространства, когда при одновременном переносе всех частиц замкнутой системы на
некоторый постоянный малый вектор 
состояние системы не
изменяется. Согласно [19], импульс физической системы определяется по формуле:
. (73)
В (73)
представляет собой
трёхмерный импульс одного элемента объёма, функция Лагранжа есть 
. Для непрерывного распределения
вещества в (73) от суммы следует перейти к интегралу и тогда импульс
системы оказывается равным
где
интегрирование должно осуществляться уже по всему объёму системы, и в сумме дают
лагранжиан системы.
Если в (74)
использовать выражения для (68) и (17), то видно, что основной вклад в импульс системы делает величина 
, содержащая векторные потенциалы полей внутри вещества и которую необходимо проинтегрировать по объёму:
(75)
Производные 
в (75) учитывают
возможную зависимость потенциалов полей от скорости движения элементов
вещества. Кроме этого, в импульсе следует учесть сумму 
в случае, когда часть
лагранжиана 
, содержащая тензорные инварианты, зависит от скоростей движения частиц. Это
означает, что вклад в импульс системы делает и та часть поля, которая выходит
за пределы вещества и движется вместе с веществом. Импульс 
в виде (75) был также
найден в [20].
3.8. 4-импульс
системы
Согласно
стандартному определению, 4-импульс определяется как 4-вектор, в компоненты
которого входят энергия и импульс. Заметим, что в (75) импульс в основном
образуется с помощью векторных потенциалов полей внутри вещества, а векторные
потенциалы являются компонентами 4-потенциалов полей, являющихся ковариантными
4-векторами. В связи с этим аналогично [20] 4-импульс
можно определить как ковариантный 4-вектор следующего вида:
.
(76)
Как
правило, движение физической системы относительно некоторой системы отсчёта 
учитывается через
движение центра импульсов физической системы. По определению, в системе отсчёта
центра импульсов всегда 
, а энергия становится минимальной и равной инвариантной
энергии покоя 
. В такой системе отсчёта 
, связанной с центром импульсов, должно быть
.
(77)
Предположим,
что четырёхмерные координаты 
системы отсчёта связаны с координатами
системы отсчёта функциональными
соотношениями
, 
.
, 
.
(78)
Тогда
4-импульс 
(77) можно
преобразовать в 4-импульс 
, наблюдаемый в системе отсчёта , по формуле:
.
(79)
В
(79) компоненты якобиана 
вычисляются с помощью
функций (78).
Из
(76-79) для временной и пространственных компонент следуют выражения:
.
.
(80)
В
(80) индекс 
, при этом компоненты 
, 
, 
равны нулю согласно (77).
Из (77) и (80) для энергии и компонент импульса в системе отсчёта получается следующее
, 
. (81)
Определим
инертную массу 
физической системы как
скалярный множитель, на который надо умножить 4-скорость центра импульсов,
чтобы получить 4-импульс в системах отсчёта и :
, 
. (82)
Поскольку
квадрат 4-скорости равен квадрату скорости света, 
, то инертная масса может быть найдена в
любой системе отсчёта через квадрат 4-импульса по формуле 
.
Из
(76-77) и (81-82) следует:
, 
.
, 
.
(83)
Согласно
(83), энергия покоя в системе отсчёта центра импульсов
зависит от временной компоненты 4-скорости 
центра импульсов. Для
вычисления энергии 
и импульса в произвольной системе
отсчёта необходимо знать ещё
временные компоненты якобиана 
(79).
В
специальной теории относительности соотношения (83)
упрощаются. Пусть система отсчёта движется вдоль оси 
системы отсчёта
с постоянной скоростью
. В начальный момент времени центр импульсов физической
системы, связанный с началом системы координат , находится в начале системы координат . В этом случае будет 
, а якобиан 
соответствует
преобразованиям Лоренца и имеет следующий вид:
.
(84)
С
учётом (84) из (83) следуют стандартные
выражения для энергии и импульса в специальной теории относительности:
, 
.
,
. (85)
В
(14) была определена объёмная плотность обобщённого 4-импульса 
. Мы можем проинтегрировать эту плотность по собственным
объёмам всех частиц и найти обобщённый 4-импульс системы:
. (86)
В
силу своего построения обобщённый 4-импульс 
(86) является 4-вектором,
при этом энергия 
связана с энергией
частиц, выражаемой через скалярные потенциалы полей.
Подставим
лагранжиан (5) в выражение и снова предположим,
что 4-потенциалы и тензоры полей прямо не зависят от 4-скорости того или иного
элемента вещества. Тогда для 
будет справедливо
соотношение (19) и из (86) следуют величины и 
, входящие в обобщённый 4-импульс:
.
.
(87)
Как
видно в (87), энергия и импульс частиц системы являются частью энергии системы (65) и
импульса системы 
(75), соответственно.
При этом в случае, когда 4-потенциалы и тензорные инварианты полей прямо не
зависят от скоростей частиц, импульсы и совпадают друг с
другом.
3.9. Момент импульса
Для определения момента импульса и закона его сохранения
используется свойство изотропии пространства, когда при одновременном повороте относительно
некоторой оси всех частиц замкнутой системы на постоянный малый угловой вектор 
состояние системы не
изменяется.
Согласно [19], в замкнутой системе частиц сохраняется
вектор момента импульса, с учётом (73) равный:
Величина представляет собой трёхмерный
импульс одного элемента объёма системы, связанный с частицей с номером 
.
Подставим в (88) функцию Лагранжа, состоящую из двух
частей . При этом для 
от суммирования в (88)
можно перейти к интегрированию по объёму:
. (89)
Мы можем ещё подставить в (89) из (68):
(90)
В (90) видно, что основную часть момента импульса
системы с непрерывным распределением вещества создают векторные потенциалы всех
полей в веществе. Свой вклад делают также производные от потенциалов полей. В
(90) присутствует ещё добавка, зависящая от производных части лагранжиана по скоростям частиц
системы в случае, когда тензорные инварианты полей зависят от этих скоростей.
Следует заметить, что момент импульса 
является
псевдовектором. Это видно из того, что если заменить
правостороннюю систему пространственных координат на левостороннюю систему
координат, поменяет свой знак.
3.10. Псевдотензор момента импульса системы частиц
В (76) мы определили 4-импульс , с помощью которого зададим теперь четырёхмерный
псевдотензор момента импульса. Для системы из 
частиц данный
псевдотензор с ковариантными индексами вычислим по формуле:
. (91)
В (91) все величины в скобке относятся к одной частице с
текущим номером 
, а псевдотензор для всей системы находится путём
суммирования по всем частицам. В скобке находится векторное произведение двух величин
– 4-положения и 4-импульса, взятых с ковариантными индексами. Поскольку 4-положение
не является
4-вектором, то это оправдывает название псевдотензор для 
.
Найдём отдельные компоненты псевдотензора (91) в рамках
специальной теории относительности, для чего используем выражения 4-положения и
4-импульса (76) для каждой частицы в декартовой системе координат:
, 
.
,
,
,
,
,
.
(92)
Так как псевдотензор антисимметричен, то его компоненты 
, 
, 
и 
равны нулю. Из (92)
видно, что компонентами псевдотензора являются компоненты двух трёхмерных
векторов. Один из этих векторов состоит из компонент 
, 
, 
и записывается так:
. (93)
Другой вектор состоит из компонент 
, 
, 
и представляет собой
момент импульса системы в форме (88):
.
(94)
С учётом (93-94) псевдотензор момента импульса системы
частиц приобретает следующий вид:
. (95)
3.11. Псевдотензор момента импульса в случае
непрерывного распределения вещества
Для перехода к приближению сплошной среды в (91) вместо следует подставить
как эквивалент
4-импульса для одного элемента объёма, а сумму по частицам заменить на интеграл
по объёму:
. (96)
Если в [2] псевдотензор момента импульса определяется в
виде 
, то есть с контравариантными компонентами, то в (96)
первичным выражением является с ковариантными
индексами. Это связано с тем, что определением 4-импульса является его
выражение с ковариантным
индексом.
Компоненты псевдотензора в (96) в декартовых
координатах будут следующие:
,
,
,
,
. (97)
В (97) компоненты псевдотензора , , образуют трёхмерный
вектор:
. (98)
В то же время, компоненты , , псевдотензора образуют
другой трёхмерный вектор, являющийся моментом импульса системы в интегральной
форме:
.
(99)
Компоненты векторов 
(98) и (99) образуют
компоненты псевдотензора момента импульса для
непрерывной среды в том же виде, что и в (95) для случая системы частиц.
3.12. Псевдотензор момента импульса тела с учётом
его полей
В общем случае компоненты псевдотензора момента импульса
должны находиться суммированием компонент в непрерывно распределённом веществе
тела, с соответствующими компонентами, связанными с полями за пределами тела.
Для объёма, занимаемого веществом, следует использовать формулы (98-99), а для
объёма за пределами вещества, где имеется только поле, необходимо использовать формулы
(93-94).
Будем исходить из выражения импульса системы (74) с
учётом функции Лагранжа , в которой лагранжиан 
состоит из двух
частей, Для объёма, занимаемого веществом, дифференциал импульса равен:
.
(100)
Поля также делают свой вклад в импульс одного элемента
объёма посредством , с учётом определения 
:
. (101)
Подставляя 
(100) в (99), а 
(101) в (94), и
суммируя результаты, приходим к моменту импульса системы в виде (89):
. (102)
В (102) одна часть момента импульса выражена через
интеграл, а другая часть выражена через сумму по всем частицам системы.
Дифференциал интегральной части энергии системы и
энергия одного элемента объёма, зависящая от производной 
, согласно (64) равны:
. (103)
.
(104)
Подставляя (100) и 
(103) в (98). найдём
вектор 
, относящийся к объёму, занимаемому веществом тела:
(105)
Подставим теперь (101) и 
(104) в (93), и найдём
вектор 
, связанный с полями:
. (106)
Суммируя (105) и (106), находим так
называемый время-зависимый динамический массовый момент (time-varying dynamic mass moment):
(107)
В (107) удобно использовать компоненту лагранжиана в виде (68), , где дана в (27). При этом
следует учесть условие калибровки энергии в виде 
, вытекающее из первого соотношения в (40).
В массовом моменте (107) выберем члены,
содержащие радиус-векторы 
и 
, и с их помощью определим радиус-вектор центра импульсов
рассматриваемой системы:
(108)
В рамках специальной теории относительности можно
считать, что центр импульсов замкнутой системы движется с некоторой постоянной
скоростью 
. При этом для импульса выполняется
соотношение 
, где энергия системы пропорциональна
фактору Лоренца 
,
инерциальной
массе системы и квадрату скорости света. С учётом этого, а также выражения в (74) и 
в (108), для массового
момента (107) имеем:
. (109)
В замкнутой системе псевдотензор сохраняется и его
компоненты являются постоянными величинами. Это означает сохранение момента
импульса, 
, а также сохранение массового момента в виде 
и энергии системы 
. В данном случае можно ввести постоянный радиус-вектор
, выражающий положение центра импульсов системы при 
. Тогда из (109) следует уравнение движения по прямой линии центра
импульсов замкнутой системы: 
.
Основной целью использования лагранжева формализма является
вывод из принципа наименьшего действия уравнений поля, уравнения для метрики и
уравнения движения для каждого конкретного лагранжиана. Более углублённый
подход даёт в общем виде формулы, связывающие лагранжиан с необходимым
уравнением или интегралом движения. Примером здесь является общее уравнение Эйлера-Лагранжа (2).
Аналогично этому, для
векторных полей мы представляем уравнение движения (13), выраженное через
лагранжиан, уравнение для метрики (31), формулу для тензора
энергии-импульса (42), уравнение
Эйлера-Лагранжа для векторных полей на примере электромагнитного поля (A7) в Приложении A, уравнения Гамильтона (71-72).
Лагранжиан также
присутствует в формулах для энергии (63-64), в гамильтониане (66), в импульсе (73-74),
в обобщённом 4-импульсе (86), в моменте импульса (88-89), в четырёхмерном
псевдотензоре момента импульса (95), в массовом моменте (107), в радиус-векторе центра
импульсов (108).
При вычислении энергии системы с помощью Лагранжева
формализма возникает проблема калибровки энергии. В искривлённом
пространстве-времени появляются дополнительные трудности, связанные с
присутствием в выражении для энергии (64) скалярной кривизны 
и космологической
постоянной 
. При этом не определена
однозначно, а величина может быть найдена
только после решения уравнения для метрики и потому содержит неопределённые
коэффициенты. С целью получения уникального выражения для энергии, в котором
отсутствуют и и , используется условие калибровки энергии в виде , вытекающее из первого соотношения в (40). В результате
получается однозначное выражение для энергии (65), которое содержит только наблюдаемые
физические величины.
При представлении
результатов особое внимание мы уделили выводу ковариантно записанных формул,
пригодных для использования в непрерывно распределённом веществе в искривлённом
пространстве-времени. В этом случае тензор Риччи не равен нулю, а его свёртка с
тензорами полей в (61) обращается в нуль. Это подчёркивает равноправие всех
полей, делающих одинаковый вклад в метрику пространства-времени. С другой
стороны, это даёт ограничение на возможную степень искривления
пространства-времени при заданных полях. Все поля, действующие в физической
системе, делают соответствующий вклад в
4-импульс и в момент импульса системы. В результате инертная масса системы
выражается через квадрат 4-импульса в виде , как и в специальной теории относительности.
В (15) мы вывели уравнение движения физической системы,
выраженное через производные от потенциалов полей. Это привело нас к понятиям плотности
обобщённого 4-импульса (14) и к плотности обобщённой 4-силы (15). Далее мы представили
уравнение для метрики, уравнения для полей и уравнение движения, записанное с
помощью тензоров полей. В следующих разделах показывается, как с помощью
лагранжева формализма определяются энергия, гамильтониан, импульс, 4-импульс, момент
импульса и псевдотензор момента импульса.
Для псевдотензора
момента импульса показывается, что его каноническим представлением является
представление с ковариантными индексами. Отдельно рассматриваются случаи, когда
физическая система состоит из малых частиц, представляет собой непрерывную
среду либо является большим телом. Для каждого их этих случаев определяются
соответствующие формулы для компонент псевдотензора момента импульса с учётом
полей системы.
Таким образом, для векторных полей оказывается возможным
вывести ковариантным способом все основные физические величины. Эти величины
необходимы для описания уравнений движения и эволюции физических систем,
содержащих непрерывно распределённое вещество и основные действующие поля,
такие как гравитационное и электромагнитное поля, поле ускорений и поле
давления.
Полученные результаты явились следствием того, что все
векторные поля, действующие в системе, имеют соответствующие 4-потенциалы и
тензоры поля. В результате уравнения для каждого поля имеют один и тот же вид [8],
что позволяет считать все поля системы компонентами единого общего поля [16].
Список использованных источников
1.
Hand L.N., Finch J.D. Analytical Mechanics,
Cambridge University Press, (2008), ISBN 978-0-521-57572-0.
2.
Landau L.D.,
Lifshitz E.M. The Classical Theory of Fields,
(1951).
Pergamon Press. ISBN 7-5062-4256-7.
3.
Vittorio De Falco, Emmanuele Battista, Maurizio
Falanga. Lagrangian formulation of the general relativistic Poynting-Robertson
effect. Phys. Rev. D. Vol. 97, Iss. 8, 084048 (2018). https://doi.org/10.1103/PhysRevD.97.084048.
4.
Richard H. Price, and Kip S. Thorne. Lagrangian
vs Hamiltonian: The best approach to relativistic orbits. American Journal of
Physics, Vol. 86, No 9, pp. 678-682
(2018). https://doi.org/10.1119/1.5047439.
5.
Schäfer G., Jaranowski
P. Hamiltonian formulation of general relativity and post-Newtonian dynamics of
compact binaries. Living Reviews in Relativity, Vol. 21, Article number: 7 (2018). https://doi.org/10.1007/s41114-018-0016-5.
6. Claudio Cremaschini
& Massimo Tessarotto. Manifest Covariant
Hamiltonian Theory of General Relativity. Applied Physics Research, Vol. 8, No.
2, pp. 66-81 (2016). http://dx.doi.org/10.5539/apr.v8n2p60 .
7. Jose Beltrán Jiménez and Antonio L.
Maroto. Viability of vector-tensor theories of gravity. Journal of Cosmology
and Astroparticle Physics, Volume 2009, 025 (2009). http://dx.doi.org/10.1088/1475-7516/2009/02/025.
8. Fedosin S.G. About the cosmological
constant, acceleration field, pressure field and energy. Jordan Journal of Physics, Vol. 9, No. 1, pp. 1-30 (2016). http://dx.doi.org/10.5281/zenodo.889304. // О космологической постоянной, поле ускорения, поле давления и об энергии.
9.
Fedosin S.G. Four-Dimensional
Equation of Motion for Viscous Compressible and Charged Fluid with Regard to
the Acceleration Field, Pressure Field and Dissipation Field.
International Journal of Thermodynamics, Vol. 18, No. 1, pp. 13-24 (2015). http://dx.doi.org/10.5541/ijot.5000034003. // Четырёхмерное уравнение движения вязкого сжимаемого вещества с учётом поля ускорений, поля давления и поля диссипации.
10. Фок В.А. Теория пространства,
времени и гравитации. 2-е
издание. М.: Физматгиз,
1961. 568 с. Fock V. A. The Theory of Space, Time and Gravitation
(Pergamon Press, London, 1959).
11. Fedosin S.G. Generalized
Four-momentum for Continuously Distributed Materials. Gazi University Journal
of Science, Vol. 37, Issue 3,
pp. 1509-1538 (2024). https://doi.org/10.35378/gujs.1231793. // Обобщённый 4-импульс для непрерывно распределённого вещества.
12. S.W. Hawking and G. F. R. Ellis, The Large Scale Structure of Space‐Time, Cambridge Monographs on
Mathematical Physics (Cambridge University Press, New York, 1999).
13. Дирак
П.А.М. Общая теория относительности: Пер. с англ./ Под. ред. Д. И. Блохинцева. – Пер. изд.: США, 1975. – М.:
Атомиздат, 1978. – 64 с. Dirac P.A.M. General Theory of
Relativity (1975), John Wiley & Sons Inc, quick presentation of the
bare essentials of GTR. ISBN
978-0471215752.
14. Leclerc
M. Canonical and Gravitational Stress-Energy Tensors. International Journal of
Modern Physics D, Vol. 15, No. 07, pp. 959-989 (2006). https://doi.org/10.1142/S0218271806008693.
15. Blau M. Lecture Notes on General
Relativity. § 7.6. Bern, University of Bern,
(2022). http://www.blau.itp.unibe.ch/GRLecturenotes.html.
16. Fedosin
S.G. Two components of the macroscopic general field. Reports in Advances of
Physical Sciences, Vol. 1, No. 2, 1750002, 9 pages (2017). http://dx.doi.org/10.1142/S2424942417500025;
Две компоненты макроскопического общего поля.
17. Fedosin S.G. Equations of Motion in
the Theory of Relativistic Vector Fields. International Letters of Chemistry,
Physics and Astronomy, Vol. 83, pp. 12-30 (2019). https://doi.org/10.18052/www.scipress.com/ILCPA.83.12. // Уравнения
движения в теории релятивистских векторных полей.
18. Fedosin
S.G. The generalized Poynting theorem for the general field and solution of the
4/3 problem. International Frontier Science Letters, Vol. 14, pp. 19-40 (2019).
https://doi.org/10.18052/www.scipress.com/IFSL.14. // Обобщённая
теорема Пойнтинга для
общего поля и
решение проблемы 4/3.
19. Ландау, Л.Д.,
Лифшиц, Е.М. Механика. Издание 4-е, исправленное. М.: Наука, 1988. 215 с. («Теоретическая физика», том I). ISBN 5-02-013850-9. Landau L.D., Lifshitz E.M. (1976). Mechanics. Vol. 1 (3rd ed.). Elsevier Butterworth-Heinemann.
ISBN 978-0-7506-2896-9.
20. Fedosin
S.G. What should we understand by the four-momentum of physical system? Physica Scripta, Vol. 99, No. 5, 055034 (2024). https://doi.org/10.1088/1402-4896/ad3b45. // Что мы должны
понимать под 4-импульсом физической системы?
Приложение A
Рассмотрим вариацию той части функции действия, которая
связана с электромагнитным полем:
.
(A1)
Тензор электромагнитного поля выражается формулой 
, и значит, 
. Используем это для преобразования в (A1):
(A2)
Интеграл по 4-объёму от разности второго и третьего
членов в правой части (A2) будет равен нулю.
Действительно, этот член равен антисимметричной разности двух дивергенций,
которые превращаются в разность двух частных
производных следующего вида:
(A3)
Применим теорему о дивергенции для первого члена в
правой части (A3):
(A4)
Трёхмерный единичный вектор 
, где
индекс 
,
представляет собой направленный наружу нормальный вектор к двумерной
поверхности 
, окружающей нашу движущуюся физическую систему. Равенство
нулю в (A4) следует из того, что вариация 
4-потенциала
электромагнитного поля в моменты времени 
и 
равна нулю по условию варьирования
функции действия. Кроме этого, при интегрировании по поверхности вариация 
на этой поверхности также считается равной
нулю.
Для второго члена в правой части (A3)
получается аналогично, в связи с чем достаточно подставить в (A1) лишь первый, четвёртый и пятый члены в правой части
(A2):
.
(A5)
Преобразуем в (A5) второй
член, поменяв вначале индексы 
и 
местами, а затем используя антисимметричность тензора
электромагнитного поля в виде 
:
.
.
(A6)
Из (A6) следует уравнение Эйлера-Лагранжа для электромагнитного поля:
.
(A7)
В качестве лагранжиана 
в (A7)
используем лагранжиан для векторных полей, равный сумме двух компонент 
, где
.
(A8)
В (A8) тензор 
содержится в 
только в одном члене. Вариация этого члена по
тензору будет равна:
(A9)
С учётом (A8) и (A9), функциональная производная лагранжиана по тензору будет такой:
. С помощью компоненты 
(A8) находим производную по электромагнитному
4-потенциалу: 
.
Подставляя всё это в (A7),
приходим к уравнению электромагнитного поля, к которому можно ещё добавить
вытекающее из антисимметрии тензора 
второе уравнение без
источника поля:
, . (A10)
Приложение B
Стандартное определение формулы для релятивистской
энергии системы осуществляется в два этапа [19]. Вначале выводится уравнение
Эйлера-Лагранжа в предположении, что функция Лагранжа зависит только от
текущего времени 
, от трёхмерного радиус-вектора 
, задающего местоположение элемента вещества системы с
текущим номером в момент времени , и от скорости движения этого
элемента вещества. Таким образом, для функции Лагранжа предполагается
зависимость 
. Далее осуществляется варьирование действия 
и вариация 
приравнивается к нулю.
При этом действие по времени не варьируется:
, 
. (B1)
Так как 
, то в (B1) будет
,
. (B2)
При этом для второго члена в (B2)
выполняется равенство
,
так как вариации 
равны нулю в моменты
времени и . Тогда из условия 
в (B2)
следует уравнение Эйлера-Лагранжа для каждого элемента вещества:
.
(B3)
На втором этапе ищется производная по времени от функции
Лагранжа, выраженной через координаты и скорость каждого из 
элементов вещества:
. (B4)
Используя в (B4) 
из (B3), находим:
.
. (B5)
Из (B5) видно, что если в
рассматриваемой физической системе функция Лагранжа не зависит явно от времени
и , то сохраняется энергия системы, определяемая
выражением:
.
(B6)
Источник: http://sergf.ru/la.htm