International Frontier Science Letters, Vol. 14, pp. 19-40 (2019). https://doi.org/10.18052/www.scipress.com/IFSL.14.19
.
Обобщённая теорема
Пойнтинга для общего поля и решение проблемы 4/3
Федосин Сергей Григорьевич
ул.
Свиязева 22-79, город Пермь, 614088, Пермский край, Россия
e-mail: fedosin@hotmail.com
Обобщённая теорема Пойнтинга применяется к равновесной
системе частиц, как внутри, так и снаружи системы. Частицы связаны друг с
другом посредством электромагнитного и гравитационного полей, поля ускорений и
поля давления. В результате обнаруживается связь между коэффициентом поля
ускорений, коэффициентом поля давления, гравитационной постоянной и
электрической постоянной. Эта связь зависит ещё от отношения плотности заряда к
плотности массы частиц внутри сферы. Благодаря
наличию связей между указанными коэффициентами полей решается проблема 4/3 и уточняется
выражение для релятивистской энергии системы.
Ключевые слова:
теорема Пойнтинга; поле ускорений; поле давления; проблема 4/3; энергия системы.
The generalized Poynting theorem
for the general field and solution of the 4/3 problem
Sergey G. Fedosin
PO
box 614088, Sviazeva str. 22-79, Perm,
Perm Krai, Russia
E-mail: fedosin@hotmail.com
The generalized Poynting
theorem is applied to the equilibrium system of particles, both inside and
outside the system. The particles are bound to each other by means of the
electromagnetic and gravitational fields, acceleration field and pressure
field. As a result, the correlation is found between the acceleration field
coefficient ![]() , the pressure field
coefficient
, the pressure field
coefficient ![]() , the gravitational constant
, the gravitational constant ![]() and the vacuum permittivity
and the vacuum permittivity ![]() . This correlation also
depends on the ratio of the charge density
. This correlation also
depends on the ratio of the charge density ![]() to the mass density
to the mass density ![]() of the particles inside the sphere. Due to the
correlation between the given field coefficients the 4/3 problem is solved and
the expression for the relativistic energy of the system is refined.
of the particles inside the sphere. Due to the
correlation between the given field coefficients the 4/3 problem is solved and
the expression for the relativistic energy of the system is refined.
Keywords: Poynting theorem;
acceleration field; pressure field; 4/3 problem; system’s energy.
PACS: 03.50.De; 03.50.Kk; 04.50.+h; 14.80.-j.
1.
Введение
Теорема
Пойнтинга наиболее широко используется в электродинамике, где описывает связь
скорости изменения плотности энергии электромагнитного поля внутри некоторого
объёма с потоком электромагнитной энергии через поверхность
данного объёма, а также с мощностью работы поля по перемещению зарядов в расчёте
на единицу объёма [1]. В полной физической системе учитываются все действующие
в ней поля, а также в рассмотрение вводится тензор энергии-импульса вещества. В
результате становится справедливой обобщённая теорема Пойнтинга (или теорема
Умова-Пойнтинга). В частности, работа полей по перемещению масс и зарядов в
единице объёма приравнивается к изменению плотности энергии и потока энергии в тензоре
энергии-импульса вещества. Это приводит к тому, что теорема Пойнтинга для
полной физической системы в произвольном объёме может быть выражена только
через скорость изменения плотности энергии всех полей и энергии вещества в этом
объёме, и через потоки энергии полей и энергии вещества через поверхность,
окружающую этот объём [2]. Таким образом, обобщённая теорема Пойнтинга
превращается в уравнение энергетического баланса для полей и вещества.
В концепции
общего поля [3] все макроскопические частные поля могут быть включены в одну из
двух компонент, в зависимости от того, какой 4-ток является их источником [4]. Массовый 4-ток ![]() генерирует такие векторные поля, как гравитационное поле, поле
ускорений, поле давления, поле диссипации, макроскопические поля сильного и
слабого взаимодействий. Все эти поля входят в массовую компоненту общего поля.
Зарядовая компонента общего поля представлена электромагнитным полем и имеет
своим источником зарядовый 4-ток
генерирует такие векторные поля, как гравитационное поле, поле
ускорений, поле давления, поле диссипации, макроскопические поля сильного и
слабого взаимодействий. Все эти поля входят в массовую компоненту общего поля.
Зарядовая компонента общего поля представлена электромагнитным полем и имеет
своим источником зарядовый 4-ток ![]() .
.
В отличие от стандартного подхода, в концепции общего поля тензор
энергии-импульса вещества не используется совсем. Вместо него применяется
тензор энергии-импульса поля ускорений [5, 6]. Это означает, что описание
кинетической энергии вещества и потока этой энергии перестаёт быть
феноменологическим, требующим подгонки под результаты экспериментов, а
осуществляется ковариантным образом, в терминах поля скоростей и соответствующего
поля ускорений.
Концепция поля
ускорений предназначена для более точного описания ускоренного движения частиц
физической системы. В первом приближении можно считать, что типичные частицы
системы при взаимодействии ведут себя как не вращающиеся твёрдые тела. Это
соответствует тому, что используется только скалярный потенциал поля ускорений,
а собственный векторный потенциал каждой частицы не учитывается. Однако даже
при параллельном переносе твёрдой частицы вдоль искривлённой линии видно, что там,
где мгновенный
радиус вращения больше, вещество движется с увеличенной скоростью по отношению
к скорости центра инерции частицы. В случае вращения частицы её энергия будет отличаться
от энергии покоя неподвижной и не вращающейся частицы. Анализ таких случаев
существенно упрощается при учёте векторного потенциала поля ускорений как новой
степени свободы в описании движения. Поскольку скалярный и векторный потенциалы
образуют 4-потенциал, поле ускорений становится векторным полем. 4-потенциал
поля ускорений движущейся прямолинейно твёрдой частицы совпадает с её
4-скоростью. Однако в общем случае 4-потениал находится путём решения волнового
уравнения поля ускорений аналогично тому, как это делается для других векторных
полей.
Такая же
ситуация складывается и в отношении поля давления. Как правило, поле давления
рассматривается либо как чисто скалярное поле, либо как некоторое эффективное
векторное поле, в котором собственный векторный потенциал поля давления типичной
частицы всегда равен нулю. В последнем случае роль 4-потенициала поля давления
в лагранжиане системы играет произведение давления на 4-скорость частицы,
делённое на квадрат скорости света. Вместо этого мы рассматриваем полноценное
векторное поле давления, когда его 4-потениал определяется из соответствующего четырёхмерного
волнового уравнения. Это означает, что для непрерывно распределённого вещества
и большого количества взаимодействующих частиц глобальные 4-потенциалы поля
ускорений и поля давления определяются одновременно всеми частицами системы и
перестают зависеть от 4-скорости рассматриваемой частицы.
Далее мы будем анализировать обобщённую теорему Пойнтинга для
обеих компонент общего поля. Это приведёт нас к соотношениям, связывающим между
собой коэффициенты общего поля, поля ускорений и поля давления. Кроме
этого, мы дадим решение проблемы 4/3 и уточним выражение для релятивистской
энергии системы. Заметим, что гравитационное поле мы рассматриваем как
векторное поле в рамках ковариантной теории гравитации, аналогично подходу,
развитому в [7].
Чтобы без потери общности получить
точные результаты, при
анализе обобщённой теоремы
Пойнтинга мы будем опираться на релятивистскую однородную модель [5]. В этой модели описывается устойчивая физическая система, частицы которой находятся в равновесном
движении под действием глобальных полей системы. В такой системе возможно
достаточно просто вычислить потенциалы и напряжённости полей, найти тензоры
полей и соответствующие тензоры энергии-импульса, необходимые для проверки обобщённой
теоремы Пойнтинга и решения проблемы 4/3.
2. Ковариантная форма
обобщённой теоремы Пойнтинга
Уравнение
движения вещества в двухкомпонентном общем поле записывается следующим образом [4]:
![]() , (1)
, (1)
где ![]() – электромагнитный
тензор,
– электромагнитный
тензор, ![]() – тензор массовой компоненты общего поля,
– тензор массовой компоненты общего поля, ![]() – тензор энергии-импульса электромагнитного
поля,
– тензор энергии-импульса электромагнитного
поля, ![]() – тензор
энергии-импульса массовой компоненты общего поля,
– тензор
энергии-импульса массовой компоненты общего поля, ![]() – суммарный
тензор энергии-импульса физической системы из вещества и всех действующих в
системе полей.
– суммарный
тензор энергии-импульса физической системы из вещества и всех действующих в
системе полей.
Обобщённая теорема
Пойнтинга следует из (1) при условии, что в уравнении движения выбрано значение
индекса ![]() :
:
![]() . (2)
. (2)
Тензорно-дифференциальное
уравнение (2) описывает скорость изменения суммарной энергии полей в
произвольном объёме в зависимости от потоков этих полей внутрь данного объёма.
Если же в (1) выбрать индекс ![]() , то это приводит к уравнению движения вещества в общем поле в
искривлённом пространстве-времени. Как показывается в [4], в левой части
уравнения движения будет стоять произведение плотности массы на 4-ускорение, а
в правой части будет сумма плотностей 4-сил от действующих на вещество полей.
, то это приводит к уравнению движения вещества в общем поле в
искривлённом пространстве-времени. Как показывается в [4], в левой части
уравнения движения будет стоять произведение плотности массы на 4-ускорение, а
в правой части будет сумма плотностей 4-сил от действующих на вещество полей.
В стандартном
подходе для обобщённой теоремы Пойнтинга используют выражение ![]() , причём в тензор
, причём в тензор ![]() включается и тензор
энергии-импульса вещества. В общей теории относительности тензор
включается и тензор
энергии-импульса вещества. В общей теории относительности тензор ![]() приобретает
дополнительное значение, поскольку в этой теории не только уравнение
приобретает
дополнительное значение, поскольку в этой теории не только уравнение ![]() рассматривается как
уравнение движения, но ещё уравнение для метрики, содержащее тензор
рассматривается как
уравнение движения, но ещё уравнение для метрики, содержащее тензор ![]() , определяет метрику, эквивалентную гравитационному полю в
тензорной форме [8].
, определяет метрику, эквивалентную гравитационному полю в
тензорной форме [8].
Проблемой такого подхода является то, что форма тензора
энергии-импульса вещества не является общепринятой и однозначно определённой, и
зависит от того, включается ли в него вклад давления, внутренней энергии
вещества и других чётко не определённых факторов. Форма этого тензора также
существенно зависит от того, в каком виде (скалярном, векторном, тензорном) учитываются
в лагранжиане данные факторы.
В нашем подходе
мы избегаем подобной неопределённости, поскольку вместо тензора энергии-импульса
вещества используется однозначно определённый тензор энергии-импульса поля
ускорений, а вклад давления учитывается отдельным, ковариантно определённым тензором
энергии-импульса поля давления. Аналогично могут быть учтены вклады от поля
диссипации [9] и других полей. Именно
благодаря полю ускорений и векторному полю давления в [9] впервые удалось
ковариантным образом точно воспроизвести в искривлённом пространстве-времени феноменологическое
уравнение Навье-Стокса.
Тензор ![]() массовой компоненты общего поля выражается через тензоры
частных полей. Для краткости мы ограничимся далее кроме электромагнитного поля ещё
тремя основными полями, такими как гравитационное поле, поле ускорений и поле
давления. Соответствующая сумма тензоров этих трёх полей даёт тензор
массовой компоненты общего поля выражается через тензоры
частных полей. Для краткости мы ограничимся далее кроме электромагнитного поля ещё
тремя основными полями, такими как гравитационное поле, поле ускорений и поле
давления. Соответствующая сумма тензоров этих трёх полей даёт тензор ![]() :
:
![]() . (3)
. (3)
Подстановка (3)
в (1) приводит к следующему:
![]() , (4)
, (4)
причём тензор
![]() энергии-импульса массовой компоненты общего
поля зависит от тензора
энергии-импульса массовой компоненты общего
поля зависит от тензора ![]() и коэффициента общего
поля
и коэффициента общего
поля ![]() :
:
![]()
(5)
В свою очередь,
тензор массовой компоненты общего поля ![]() находится из уравнений
поля:
находится из уравнений
поля:
![]() ,
,
![]() .
(6)
.
(6)
Тензор ![]() энергии-импульса и уравнения электромагнитного
поля имеют стандартный вид:
энергии-импульса и уравнения электромагнитного
поля имеют стандартный вид:
![]()
(7)
![]() ,
,
![]() . (8)
. (8)
В данных выражениях ![]() – электрическая
постоянная,
– электрическая
постоянная, ![]() – скорость света,
– скорость света, ![]() – метрический тензор,
– метрический тензор, ![]() – символ Кронекера,
– символ Кронекера, ![]() – символ Леви-Чивиты.
– символ Леви-Чивиты.
Уравнение (4) можно анализировать двумя способами. В первом
из них решаются уравнения (6) и (8), находятся тензоры ![]() и
и ![]() , а затем тензоры
, а затем тензоры ![]() и
и ![]() в (5) и (7), которые
подставляются в (4) для вычисления дивергенции суммы этих тензоров. Второй
способ не требует нахождения тензоров
в (5) и (7), которые
подставляются в (4) для вычисления дивергенции суммы этих тензоров. Второй
способ не требует нахождения тензоров ![]() и
и ![]() , при этом используется левая часть (4).
, при этом используется левая часть (4).
Тензор энергии-импульса гравитационного поля согласно [10], и тензоры энергии-импульса поля ускорений и поля давления согласно [5] имеют следующий вид:
![]()
(9)
![]()
(10)
![]()
(11)
Если считать, что все эти поля существуют
независимо друг от друга и их вклад в лагранжиан осуществляется самостоятельно,
для тензоров этих полей справедливы волновые уравнения:
![]() ,
,
![]() .
(12)
.
(12)
![]() ,
,
![]() .
(13)
.
(13)
![]() ,
,
![]() . (14)
. (14)
В (9-14) ![]() есть гравитационная
постоянная,
есть гравитационная
постоянная, ![]() – коэффициент поля
ускорений,
– коэффициент поля
ускорений, ![]() – коэффициент поля
давления.
– коэффициент поля
давления.
Складывая друг с
другом первые уравнения в (12-14), содержащие дивергенции тензоров полей,
учитывая (3) и сравнивая результат с дивергенцией массовой компоненты общего
поля ![]() в (6), приходим к
следующему:
в (6), приходим к
следующему:
![]() ,
,
![]() . (15)
. (15)
Преобразуем
теперь произведение тензоров ![]() с помощью (3):
с помощью (3):
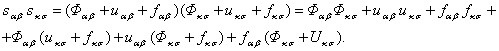
Это равенство
можно подставить в (5) и затем учесть выражения для тензоров (9-11):
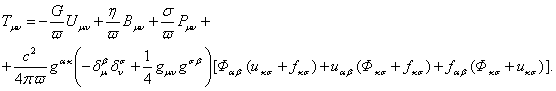
(16)
Уравнения поля
(12-14) решались в [11, 12] для сферического массивного заряженного тела, при
этом было найдено, что тензоры полей имеют подобные друг другу компоненты. В
частности, можно записать, что:
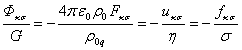 . (17)
. (17)
Подставляя (17)
в (16), с учётом (15) находим:
![]() . (18)
. (18)
Таким образом,
если считать все поля независимыми друг от друга, то внутри тела тензор
энергии-импульса массовой компоненты общего поля равен сумме тензоров
энергии-импульса всех полей, кроме электромагнитного поля, а коэффициент общего
поля
![]() выражается через
коэффициенты других полей согласно (15).
выражается через
коэффициенты других полей согласно (15).
3. Обобщённая
теорема Пойнтинга в пределе слабого поля
3.1 Анализ уравнений внутри тела
Подставим (18) в
правую часть (4) при индексе ![]() :
:
![]() . (19)
. (19)
Рассмотрим уравнение (19) в пределе слабого поля, когда
ковариантная производная превращается в 4-градиент, а искривлением
пространства-времени можно пренебречь. Этот случай соответствует пространству
Минковского специальной теории относительности. Из (19) следует:
![]() .
(20)
.
(20)
В (20) вектор Пойнтинга электромагнитного поля, вектор
Хевисайда гравитационного поля, векторы плотности потока энергии поля ускорений
и поля давления соответственно определяются формулами:
![]() ,
, ![]() ,
, ![]() ,
, ![]() . (21)
. (21)
Плотности энергии полей имеют вид:
![]() ,
, ![]() ,
,
![]() ,
, ![]() . (22)
. (22)
В (21-22) векторы плотности потока энергии и плотности
энергии выражаются через соответствующие напряжённости поля и соленоидальные
векторы поля.
Пусть имеется тело сферической формы, находящееся в
равновесии под действием собственного гравитационного и электромагнитного
полей, поля ускорений и поля давления. Данное тело в целом не вращается и неподвижно
относительно системы отсчёта ![]() , причём центр системы координат находится в центре сферы. Рассматриваемое
тело состоит из множества хаотически движущихся малых частиц, имеющих плотность
массы
, причём центр системы координат находится в центре сферы. Рассматриваемое
тело состоит из множества хаотически движущихся малых частиц, имеющих плотность
массы ![]() и плотность заряда
и плотность заряда ![]() в сопутствующих
частицам системах отсчёта. Если промежутки между частицами малы, как в жидкости,
можно считать, что вещество внутри тела распределено непрерывно. Мы изучали
такую физическую систему в [12, 13]. Ввиду хаотичности движения частиц, в
в сопутствующих
частицам системах отсчёта. Если промежутки между частицами малы, как в жидкости,
можно считать, что вещество внутри тела распределено непрерывно. Мы изучали
такую физическую систему в [12, 13]. Ввиду хаотичности движения частиц, в ![]() равны нулю векторные
потенциалы полей и соответственно, также равны нулю соленоидальные векторы:
равны нулю векторные
потенциалы полей и соответственно, также равны нулю соленоидальные векторы: ![]() (магнитная индукция),
(магнитная индукция),![]() (поле кручения),
(поле кручения),![]() и
и ![]() .
.
Кроме этого, мы нашли выражения для напряжённости
электрического поля ![]() , напряжённости гравитационного поля
, напряжённости гравитационного поля ![]() и напряжённостей поля
ускорений
и напряжённостей поля
ускорений ![]() и поля давления
и поля давления ![]() внутри тела, как
функцию текущего радиуса. После этого в [12] было сделано лоренцевское
преобразование координат из системы отсчёта
внутри тела, как
функцию текущего радиуса. После этого в [12] было сделано лоренцевское
преобразование координат из системы отсчёта ![]() в лабораторную систему
отсчёта
в лабораторную систему
отсчёта ![]() , относительно которой тело движется со скоростью
, относительно которой тело движется со скоростью ![]() вдоль оси
вдоль оси ![]() .
.
Векторы ![]() и
и ![]() входят в компоненты электромагнитного тензора
входят в компоненты электромагнитного тензора
![]() , поэтому они при преобразованиях Лоренца преобразуются
особым образом, как компоненты тензора. Знания векторов
, поэтому они при преобразованиях Лоренца преобразуются
особым образом, как компоненты тензора. Знания векторов ![]() и
и ![]() в
в ![]() достаточно, чтобы
получить их вид в лабораторной системе отсчёта
достаточно, чтобы
получить их вид в лабораторной системе отсчёта ![]() .
.
Другой способ получения векторов ![]() и
и ![]() в
в ![]() заключается в том,
чтобы вначале преобразовать 4-потенциал электромагнитного поля
заключается в том,
чтобы вначале преобразовать 4-потенциал электромагнитного поля ![]() из
из ![]() в
в ![]() с помощью
преобразований Лоренца, а затем вычислить компоненты электромагнитного тензора в
с помощью
преобразований Лоренца, а затем вычислить компоненты электромагнитного тензора в
![]() по формуле:
по формуле: ![]() . В обоих случаях для электромагнитного поля внутри движущейся
сферы после упрощения выражения для скалярного потенциала поля получается
следующее:
. В обоих случаях для электромагнитного поля внутри движущейся
сферы после упрощения выражения для скалярного потенциала поля получается
следующее:
![]() ,
, 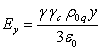 ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() . (23)
. (23)
В (23) фактор
Лоренца ![]() появляется из-за
движения сферы с постоянной скоростью
появляется из-за
движения сферы с постоянной скоростью ![]() в системе отсчёта
в системе отсчёта ![]() , а
, а ![]() есть фактор Лоренца
для скоростей
есть фактор Лоренца
для скоростей ![]() частиц в центре сферы
в системе отсчёта
частиц в центре сферы
в системе отсчёта ![]() . В момент
времени
. В момент
времени ![]() центр сферы находится
в начале системы отсчёта
центр сферы находится
в начале системы отсчёта ![]() .
.
Напряжённость гравитационного поля ![]() и поле кручения
и поле кручения ![]() внутри движущейся сферы
при тех же условиях будут таковы:
внутри движущейся сферы
при тех же условиях будут таковы:
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() . (24)
. (24)
Подобные выражения имеют и компоненты поля ускорений и поля
давления:
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() . (25)
. (25)
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() . (26)
. (26)
Как видно, в рассматриваемой физической системе напряжённости
полей и их соленоидальные векторы в (24-26), входящие в компоненты тензоров ![]() ,
, ![]() и
и ![]() , удовлетворяют соотношению (17).
, удовлетворяют соотношению (17).
С помощью (23-26) можно вычислить компоненты векторов потоков
энергии полей (21) и их дивергенции. Для электромагнитного поля:
![]() ,
, ![]() ,
,
![]() ,
, ![]() . (27)
. (27)
Для гравитационного поля:
![]() ,
, ![]() ,
,
![]() ,
, ![]() . (28)
. (28)
Для поля ускорений:
![]() ,
, ![]() ,
,
![]() ,
, ![]() . (29)
. (29)
Для поля давления:
![]() ,
, ![]()
![]() ,
, ![]() . (30)
. (30)
Выражение (28) для компонент вектора потока энергии
гравитационного поля внутри сферы получается то же самое, что и в [14],
где вычислялся импульс гравитационного поля.
С помощью (23-26) находим плотности энергии полей (22) внутри
движущейся сферы:
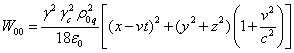 . (31)
. (31)
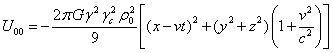 .
.
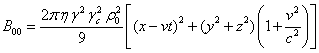 .
.
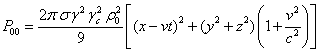 .
.
Подставим (27-31) в выражение (20) для теоремы Пойнтинга с
учётом всех четырёх действующих полей. Это даёт следующее:
![]() .
(32)
.
(32)
В (32) обнаруживается связь между коэффициентом поля
ускорений ![]() , коэффициентом поля давления
, коэффициентом поля давления ![]() , гравитационной постоянной
, гравитационной постоянной ![]() и электрической
постоянной
и электрической
постоянной ![]() . Эта связь зависит ещё от отношения плотности заряда
. Эта связь зависит ещё от отношения плотности заряда ![]() к плотности массы
к плотности массы ![]() частиц внутри сферы,
измеряемых в системах отсчёта, сопутствующих этим частицам. Предполагается, что
отношение
частиц внутри сферы,
измеряемых в системах отсчёта, сопутствующих этим частицам. Предполагается, что
отношение ![]() является постоянной
величиной. Возможен идеализированный случай, когда частицы внутри сферы не
заряжены, а весь имеющийся электрический заряд расположен в оболочке сферы.
Тогда для частиц внутри сферы
является постоянной
величиной. Возможен идеализированный случай, когда частицы внутри сферы не
заряжены, а весь имеющийся электрический заряд расположен в оболочке сферы.
Тогда для частиц внутри сферы ![]() , и вклад от электромагнитного поля в (32) пропадает. Если
подставить (32) в (15), то коэффициент общего поля внутри сферы оказывается
зависящим только от электромагнитной компоненты:
, и вклад от электромагнитного поля в (32) пропадает. Если
подставить (32) в (15), то коэффициент общего поля внутри сферы оказывается
зависящим только от электромагнитной компоненты:
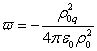 .
(33)
.
(33)
В случае, когда вещество внутри сферы нейтрально и ![]() , коэффициент
, коэффициент ![]() стремится к нулю.
стремится к нулю.
Соотношение (32) является проявлением того, что в каждой
точке рассматриваемой физической системы обнуляется сумма плотностей энергии
всех полей внутри тела, входящих во временные компоненты тензоров в (20).
Обнуляется также сумма векторов потоков энергии всех полей внутри тела.
3.2 Анализ
уравнений снаружи тела
Перейдём теперь к полям за пределами тела, где вещество
отсутствует и остаётся только электромагнитное и гравитационное поле. В системе
отсчёта ![]() напряжённости обоих
полей выглядят так, как если бы весь заряд и масса были сосредоточены в центре неподвижной
сферы. Это связано с тем, что напряжённости поля обратно пропорциональны
квадрату расстояния от центра сферы до точки, где определяются напряжённости.
Напряжённость электромагнитного поля получается прямо пропорциональной полному заряду
напряжённости обоих
полей выглядят так, как если бы весь заряд и масса были сосредоточены в центре неподвижной
сферы. Это связано с тем, что напряжённости поля обратно пропорциональны
квадрату расстояния от центра сферы до точки, где определяются напряжённости.
Напряжённость электромагнитного поля получается прямо пропорциональной полному заряду
![]() сферы, заполненной
частицами, а напряжённость гравитационного поля пропорциональна массе
сферы, заполненной
частицами, а напряжённость гравитационного поля пропорциональна массе ![]() сферы. С помощью
преобразований Лоренца из системы отсчёта
сферы. С помощью
преобразований Лоренца из системы отсчёта ![]() можно перейти в
лабораторную систему отсчёта
можно перейти в
лабораторную систему отсчёта ![]() , в которой сфера с частицами движется со скоростью
, в которой сфера с частицами движется со скоростью ![]() вдоль оси
вдоль оси ![]() . Пересчёт компонент электромагнитного и гравитационного
полей в систему отсчёта
. Пересчёт компонент электромагнитного и гравитационного
полей в систему отсчёта ![]() был осуществлён в [12]. За
пределами движущейся сферы эти компоненты равны:
был осуществлён в [12]. За
пределами движущейся сферы эти компоненты равны:
 ,
, 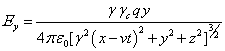 ,
,
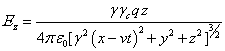 ,
, ![]() , (34)
, (34)
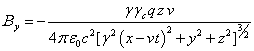 ,
, 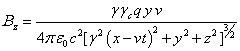 .
.
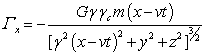 ,
, 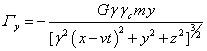 ,
,
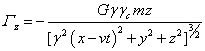 ,
, ![]() , (35)
, (35)
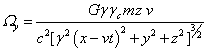 ,
, 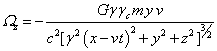 .
.
Используя (34-35), вычисляем компоненты векторов потоков
энергии полей (21) и их дивергенции. Для электромагнитного поля:
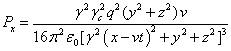 ,
, 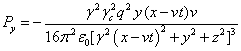 ,
,
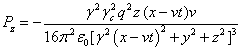 ,
,
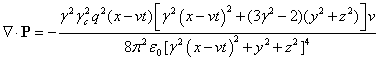 . (36)
. (36)
Для гравитационного поля:
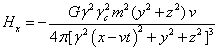 ,
, 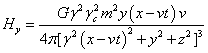 ,
,
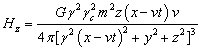 ,
,
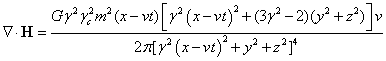 . (37)
. (37)
Плотности энергии полей (22) за пределами сферы и их частные
производные по времени для компонент полей (34-35) будут равны:
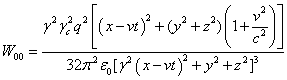 .
.
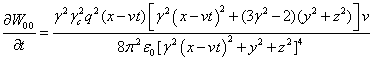 .
(38)
.
(38)
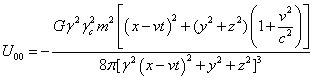 .
.
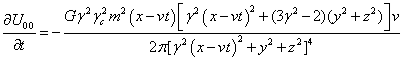 . (39)
. (39)
Обобщённая теорема Пойнтинга (20) за пределами тела запишется
так:
![]() . (40)
. (40)
После подстановки (36-39) в (40) видно, что теорема Пойнтинга
за пределами тела выполняется для каждого поля отдельно, при этом электромагнитное
и гравитационное поля не зависят друг от друга. В каждом пространственном
объёме изменение во времени плотности энергии того или иного поля точно
компенсируется дивергенцией потока энергии того же самого поля.
4.
Уравнение движения вещества
Рассмотрим левую часть уравнения движения (4) в случае
четырёх полей:
![]() .
.
В рамках
специальной теории относительности это уравнение для пространственных тензорных
компонент при значении индекса ![]() представляет собой
уравнение движения частиц вещества и может быть выражено через напряжённости и
соленоидальные векторы полей:
представляет собой
уравнение движения частиц вещества и может быть выражено через напряжённости и
соленоидальные векторы полей:
![]() . (41)
. (41)
При выводе (41) были использованы
выражения для массового 4-тока ![]() и для зарядового
4-тока
и для зарядового
4-тока ![]() , а также то обстоятельство, что тензоры полей состоят из компонент
напряжённостей и соленоидальных векторов полей. Подставим в (41) компоненты
полей из (23-26) внутри движущейся сферы, учитывая, что вектор скорости сферы
направлен вдоль оси
, а также то обстоятельство, что тензоры полей состоят из компонент
напряжённостей и соленоидальных векторов полей. Подставим в (41) компоненты
полей из (23-26) внутри движущейся сферы, учитывая, что вектор скорости сферы
направлен вдоль оси ![]() , имея компоненты вида
, имея компоненты вида ![]() . После сокращения не равных нулю множителей это даёт:
. После сокращения не равных нулю множителей это даёт:
![]() .
.
Полученное соотношение совпадает с (32), которое было выведено для временных компонент тензорного уравнения (4) внутри движущегося тела. Это подтверждает самосогласованность найденных компонент полей с уравнениями движения.
5. Решение проблемы
4/3
Вычислим суммарную массу-энергию всех четырёх полей внутри движущегося
с постоянной скоростью сферического тела, для чего возьмём интеграл от суммы
плотностей энергии полей по объёму движущегося тела и разделим его на квадрат
скорости света и на фактор Лоренца. Используем для этого выражения (31):
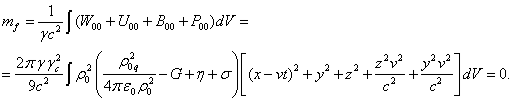 (42)
(42)
Равенство ![]() в (42) следует из
выражения (32), полученного из обобщённой теоремы Пойнтинга для полей внутри
тела, и входящего как множитель внутри интеграла в (42).
в (42) следует из
выражения (32), полученного из обобщённой теоремы Пойнтинга для полей внутри
тела, и входящего как множитель внутри интеграла в (42).
Вычислим теперь суммарную массу-энергию ![]() всех четырёх полей
внутри движущегося с постоянной скоростью тела, связанную с суммарным импульсом
этих полей. Для этого необходимо взять интеграл по объёму движущегося тела от
суммы плотностей импульсов полей, причём плотность импульса каждого поля равна
плотности потока энергии этого поля, делённой на квадрат скорости света.
Полученный путём интегрирования суммарный импульс полей внутри тела должен
равняться произведению массы-энергии
всех четырёх полей
внутри движущегося с постоянной скоростью тела, связанную с суммарным импульсом
этих полей. Для этого необходимо взять интеграл по объёму движущегося тела от
суммы плотностей импульсов полей, причём плотность импульса каждого поля равна
плотности потока энергии этого поля, делённой на квадрат скорости света.
Полученный путём интегрирования суммарный импульс полей внутри тела должен
равняться произведению массы-энергии ![]() на фактор Лоренца
на фактор Лоренца ![]() и на скорость движения
тела
и на скорость движения
тела ![]() в системе отсчёта
в системе отсчёта ![]() . Для случая,
когда скорость тела направлена точно вдоль оси
. Для случая,
когда скорость тела направлена точно вдоль оси ![]() системы отсчёта
системы отсчёта ![]() , можно использовать
выражения для компонент плотностей потоков энергии полей в (27-30):
, можно использовать
выражения для компонент плотностей потоков энергии полей в (27-30):
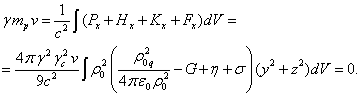 (43)
(43)
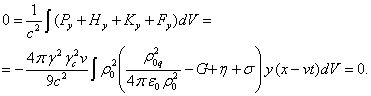 (44)
(44)
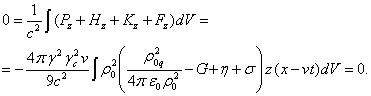
В (43) масса ![]() равна нулю в силу
соотношения (32), находящегося в (43) как отдельный множитель внутри интеграла.
Нуль в левой части (44) следует из того, что суммарный импульс полей не может
быть направлен вдоль осей
равна нулю в силу
соотношения (32), находящегося в (43) как отдельный множитель внутри интеграла.
Нуль в левой части (44) следует из того, что суммарный импульс полей не может
быть направлен вдоль осей ![]() и
и ![]() системы отсчёта
системы отсчёта ![]() . Нуль в правой части (44) связан как с соотношением (32),
так и с симметрией сферы относительно пределов интегрирования, а также с формой
подынтегрального выражения. Из (42-44) следует, что
. Нуль в правой части (44) связан как с соотношением (32),
так и с симметрией сферы относительно пределов интегрирования, а также с формой
подынтегрального выражения. Из (42-44) следует, что ![]() . Это означает, что суммарные массы-энергии полей, найденные
из плотностей энергии и из плотностей потоков энергии внутри тела, равны друг
другу, поскольку они равны нулю.
. Это означает, что суммарные массы-энергии полей, найденные
из плотностей энергии и из плотностей потоков энергии внутри тела, равны друг
другу, поскольку они равны нулю.
Рассмотрим теперь ситуацию за пределами движущегося тела, где
имеются только электромагнитное и гравитационное поля. Используя (38-39),
аналогично (42) находим суммарную массу-энергию внешних полей через интеграл от
плотностей энергии:
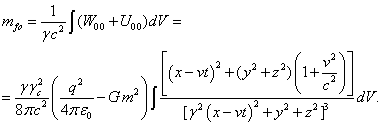 (45)
(45)
Вследствие движения тела возникает масса-энергия внешних полей,
связанная с движением этих полей вместе с телом, то есть с импульсом полей.
Аналогично (43-44) с учётом (36-37) для движения тела вдоль оси ![]() имеем:
имеем:
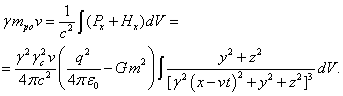 (46)
(46)
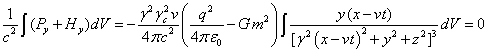 . (47)
. (47)
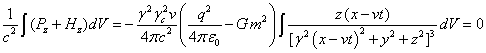 .
.
Интегралы вида (45-47) неоднократно вычислялись в работах,
посвящённых проблеме 4/3, например в [15, 16]. Первоначально
суть этой проблемы заключалась в том, что масса-энергия, связанная с плотностью
импульса электромагнитного поля движущегося тела, приблизительно в 4/3
больше, чем масса-энергия, связанная с плотностью энергии электромагнитного
поля этого тела. В [14] было показано, что проблема 4/3 точно
также существует и для гравитационного поля движущегося тела, причём для поля
как внутри, так и снаружи тела. Для вычисления интегралов (45-47) удобно ввести новые координаты следующим образом:
![]() ,
, ![]() ,
, ![]() . (48)
. (48)
Элемент
объёма определяется формулой ![]() , где
, где ![]() есть определитель
матрицы якобиана:
есть определитель
матрицы якобиана:
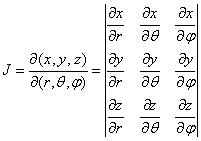 .
.
После вычисления этого определителя
видно, что ![]() .
.
За счёт лоренцевского сокращения при движении вдоль оси ![]() сфера должна
представляться движущимся эллипсоидом Хевисайда, уравнение поверхности которого
следующее:
сфера должна
представляться движущимся эллипсоидом Хевисайда, уравнение поверхности которого
следующее:
![]() . (49)
. (49)
Из (48-49) следует, что пределы
интегрирования по объёму в новых координатах следующие: радиус
![]() должен меняться от
должен меняться от ![]() до
до ![]() , а углы
, а углы ![]() и
и ![]() меняются так же, как и
в сферических координатах (от 0 до
меняются так же, как и
в сферических координатах (от 0 до ![]() для угла
для угла ![]() , и от 0 до
, и от 0 до ![]() для угла
для угла ![]() ).
).
Подставляя (48) и ![]() в (45-46), находим:
в (45-46), находим:
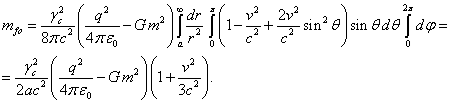 (50)
(50)
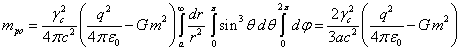 . (51)
. (51)
Если в (50) пренебречь множителем ![]() , то сравнивая с (51), получается хорошо известное
соотношение 4/3 для масс-энергий внешних полей:
, то сравнивая с (51), получается хорошо известное
соотношение 4/3 для масс-энергий внешних полей: ![]() . Таким образом, мы приходим к необходимости объяснения
неравенства масс-энергий поля за пределами движущегося тела в том случае, когда
эти массы-энергии извлекаются либо из плотности потока энергии поля, либо из плотности
энергии поля. Как видно, неравенство масс-энергий осуществляется по
отдельности, как для электромагнитного, так и соответственно для гравитационного
поля.
. Таким образом, мы приходим к необходимости объяснения
неравенства масс-энергий поля за пределами движущегося тела в том случае, когда
эти массы-энергии извлекаются либо из плотности потока энергии поля, либо из плотности
энергии поля. Как видно, неравенство масс-энергий осуществляется по
отдельности, как для электромагнитного, так и соответственно для гравитационного
поля.
Чтобы понять проблему 4/3, обратим
внимание на следующие обстоятельства. В тензоре энергии-импульса
электромагнитного поля (7) компоненты, входящие в соотношение (40) для теоремы
Пойнтинга за пределами тела, с учётом (21-22) равны:
![]() ,
, ![]() , (52)
, (52)
![]() ,
, ![]() .
.
Аналогично, в тензоре энергии-импульса
гравитационного поля (9) компоненты, входящие в соотношение (40), имеют вид:
![]() ,
, ![]() , (53)
, (53)
![]() ,
, ![]() .
.
Если бы компоненты тензора энергии-импульса
электромагнитного
поля (52) образовывали бы 4-вектор следующего вида: ![]() , то после интегрирования по объёму этих компонент мы могли
бы рассчитывать на то, что извлечённая из них масса-энергия была бы одной и той
же как для энергии поля, так и для импульса поля. Примером здесь является
4-импульс тела, содержащий энергию и релятивистский импульс, причём и в энергии
и в импульсе присутствует одна и та же инвариантная масса тела.
, то после интегрирования по объёму этих компонент мы могли
бы рассчитывать на то, что извлечённая из них масса-энергия была бы одной и той
же как для энергии поля, так и для импульса поля. Примером здесь является
4-импульс тела, содержащий энергию и релятивистский импульс, причём и в энергии
и в импульсе присутствует одна и та же инвариантная масса тела.
Однако компоненты (52) не образуют 4-вектор, а являются
компонентами 4-тензора. То же самое справедливо и для компонент (53) в
отношении гравитационного поля. Отсюда следует, что мы не должны ожидать
равенства масс-энергий вида ![]() , так как вычисляем эти массы-энергии не из компонент
4-векторов, а из компонент 4-тензоров. Вместо равенства масс-энергий расчёты
приводят к соотношению
, так как вычисляем эти массы-энергии не из компонент
4-векторов, а из компонент 4-тензоров. Вместо равенства масс-энергий расчёты
приводят к соотношению ![]() .
.
Различие масс-энергий ![]() и
и ![]() вытекает из различных
зависимостей массы-энергии в (50) и в (51). Но именно это различие зависимостей
энергии и импульса электромагнитного и гравитационного полей требуется для
того, чтобы эти поля за пределами тела удовлетворяли обобщённой теореме
Пойнтинга (40). При этом теорема Пойнтинга является следствием уравнения
движения в ковариантной форме (1-2). В то же время предполагаемое равенство
масс-энергий вида
вытекает из различных
зависимостей массы-энергии в (50) и в (51). Но именно это различие зависимостей
энергии и импульса электромагнитного и гравитационного полей требуется для
того, чтобы эти поля за пределами тела удовлетворяли обобщённой теореме
Пойнтинга (40). При этом теорема Пойнтинга является следствием уравнения
движения в ковариантной форме (1-2). В то же время предполагаемое равенство
масс-энергий вида ![]() ничем не обосновано.
Оно могло бы ожидаться для случая 4-векторов, но не в случае 4-тензоров,
описывающих поля. Проблема 4/3 в таком случае должна рассматриваться как
неожиданный, но закономерный парадокс, возникающий при переходе от 4-векторов к
4-тензорам для описания поля. Это также означает, что 4-тензор энергии-импульса
какого-либо поля нельзя представлять, как соединение некоторого 4-вектора,
составленного из временных компонент этого тензора, и трёхмерного тензора
натяжений, составленного из пространственных компонент тензора. Такая аналогия
возможна для 4-вектора, состоящего из скалярной и векторной компонент, но
становится неточной в случае тензоров как более сложных математических
объектов. Коэффициент 4/3 выступает в данном случае как мера такой неточности.
ничем не обосновано.
Оно могло бы ожидаться для случая 4-векторов, но не в случае 4-тензоров,
описывающих поля. Проблема 4/3 в таком случае должна рассматриваться как
неожиданный, но закономерный парадокс, возникающий при переходе от 4-векторов к
4-тензорам для описания поля. Это также означает, что 4-тензор энергии-импульса
какого-либо поля нельзя представлять, как соединение некоторого 4-вектора,
составленного из временных компонент этого тензора, и трёхмерного тензора
натяжений, составленного из пространственных компонент тензора. Такая аналогия
возможна для 4-вектора, состоящего из скалярной и векторной компонент, но
становится неточной в случае тензоров как более сложных математических
объектов. Коэффициент 4/3 выступает в данном случае как мера такой неточности.
Обратим внимание на то, что если взять какое-то одно поле,
например, электромагнитное или гравитационное, то для него внутри тела также
возникает проблема 4/3. Однако если мы одновременно рассматриваем все имеющиеся
внутри тела поля, включая поле давления и поле ускорений, как компоненты общего
поля, то получается равенство масс-энергий: ![]() , и в этом случае проблема 4/3 исчезает. Это происходит
потому, что все поля компенсируют друг друга так, что инвариантная масса-энергия
общего поля обращается в нуль. При этом компенсация полей оказывается следствие
обобщённой теоремы Пойнтинга. Мы видим, что в равновесной системе возможна
компенсация движений частиц вещества и поля, благодаря обмену энергией и
импульсом между веществом и полем. Там же, где нет вещества и есть только
фундаментальные электромагнитное и гравитационное поля, компенсации нет и
обнаруживается неравенство масс-энергий, известное как проблема 4/3.
, и в этом случае проблема 4/3 исчезает. Это происходит
потому, что все поля компенсируют друг друга так, что инвариантная масса-энергия
общего поля обращается в нуль. При этом компенсация полей оказывается следствие
обобщённой теоремы Пойнтинга. Мы видим, что в равновесной системе возможна
компенсация движений частиц вещества и поля, благодаря обмену энергией и
импульсом между веществом и полем. Там же, где нет вещества и есть только
фундаментальные электромагнитное и гравитационное поля, компенсации нет и
обнаруживается неравенство масс-энергий, известное как проблема 4/3.
6. Релятивистская
энергия
В [11] в рамках ковариантной теории гравитации была вычислена
релятивистская энергия рассматриваемой нами физической системы в виде
неподвижной сферы с частицами с учётом четырёх полей, включая электромагнитное
и гравитационное поле, поле давления и поле ускорений. Энергия первых двух
полей бралась в расчёт не только внутри, но и снаружи сферы, так как электромагнитное
и гравитационное поля тела простираются на бесконечность. Для энергии системы
было получено следующее выражение:
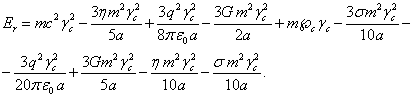
При вычислении энергии частиц, находящихся в гравитационном
потенциале ![]() внутри сферы и имеющих
фактор Лоренца
внутри сферы и имеющих
фактор Лоренца ![]() , в [11] использовалась формула:
, в [11] использовалась формула:
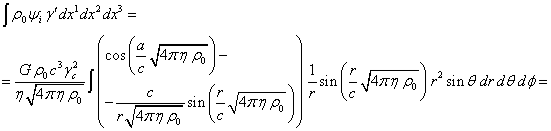
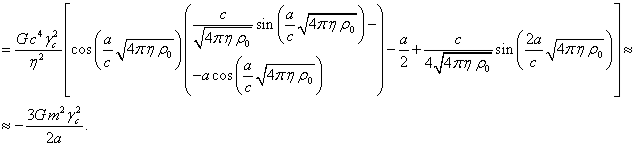
Значение энергии ![]() было получено исходя
из того, что периодические функции типа
было получено исходя
из того, что периодические функции типа ![]() и
и ![]() в квадратной скобке
раскладывались до членов второго порядка. Теперь мы хотим увеличить точность
расчётов и раскладывать периодические функции до членов третьего и даже
четвёртого порядка. В частности, это даёт:
в квадратной скобке
раскладывались до членов второго порядка. Теперь мы хотим увеличить точность
расчётов и раскладывать периодические функции до членов третьего и даже
четвёртого порядка. В частности, это даёт:
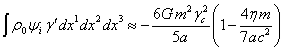 .
.
То же самое получается и для энергии заряженных частиц,
находящихся в электрическом потенциале ![]() внутри сферы –
суммарная энергия этих частиц от значения
внутри сферы –
суммарная энергия этих частиц от значения ![]() уменьшается до
уменьшается до 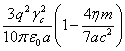 . Это означает, что энергия системы изменяется и становится
равной следующему выражению:
. Это означает, что энергия системы изменяется и становится
равной следующему выражению:
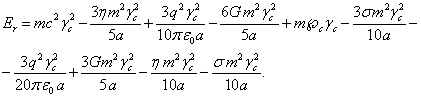 (54)
(54)
В (54) масса ![]() есть произведение
плотности массы
есть произведение
плотности массы ![]() на объём сферы с частицами, а заряд
на объём сферы с частицами, а заряд ![]() определяется
аналогично как произведение плотности заряда
определяется
аналогично как произведение плотности заряда ![]() на объём сферы. Однако
за пределами сферы потенциалы электромагнитного и гравитационного поля
определяются с помощью гравитационной массы
на объём сферы. Однако
за пределами сферы потенциалы электромагнитного и гравитационного поля
определяются с помощью гравитационной массы ![]() и электрического
заряда
и электрического
заряда ![]() . Для этих масс получается
[11]:
. Для этих масс получается
[11]:
![]() ,
, ![]() . (55)
. (55)
Фактор Лоренца для частиц в центре сферы, и скалярный
потенциал поля давления в центре сферы выражаются через соответствующие
величины на поверхности сферы:
![]() ,
, ![]() . (56)
. (56)
Подставляя сумму ![]() из (32) в (54) с
учётом (55) и (56), находим для энергии и инвариантной (инерциальной) массы
системы
из (32) в (54) с
учётом (55) и (56), находим для энергии и инвариантной (инерциальной) массы
системы ![]() следующее:
следующее:
![]() . (57)
. (57)
Для большинства космических тел можно положить, что для
поверхности тела фактор Лоренца ![]() , а также скалярный потенциал поля давления
, а также скалярный потенциал поля давления ![]() .
.
Формула для энергии (57) отличается от формулы для энергии системы в [11], имеющей
вид:
![]() .
.
Различие формул для энергии, кроме уточнения энергии частиц в
потенциалах гравитационного и электромагнитного полей в (54), связано ещё с
тем, что в [11] применялись соотношения для коэффициентов полей
согласно формуле: ![]() . В свою очередь, эти соотношения были определены в [12]
в результате интегрирования уравнения движения (1) по бесконечному четырёхмерному
объёму. Последующее применение четырёхмерной теоремы дивергенции с переходом от
интегрирования дивергенции суммы тензоров энергии-импульса четырёх полей по
четырёхмерному объёму к интегрированию суммы этих тензоров по трёхмерному
объёму даёт интегральный 4-вектор:
. В свою очередь, эти соотношения были определены в [12]
в результате интегрирования уравнения движения (1) по бесконечному четырёхмерному
объёму. Последующее применение четырёхмерной теоремы дивергенции с переходом от
интегрирования дивергенции суммы тензоров энергии-импульса четырёх полей по
четырёхмерному объёму к интегрированию суммы этих тензоров по трёхмерному
объёму даёт интегральный 4-вектор:
![]() . (58)
. (58)
Для того, чтобы 4-вектор ![]() всегда сохранялся, он
был приравнен нулю. Как следствие, для коэффициентов полей получалась формула:
всегда сохранялся, он
был приравнен нулю. Как следствие, для коэффициентов полей получалась формула: ![]() . Теперь мы видим, что эта формула является
лишь первым приближением к действительности. В самом деле, при интегрировании в
(58) учитывался вклад электромагнитного и гравитационного полей одновременно и
внутри, и снаружи движущейся сферы. Однако обобщённая теорема Пойнтинга
рассматривает энергию и потоки полей локальным образом, в любом малом объёме
пространства. Внутри тела действуют по крайней мере четыре поля, а за пределами
тела – только два поля, так как здесь нет поля давления и поля ускорений частиц
вещества. Соответственно, содержание полей в локальных объёмах внутри и снаружи
тела неодинаково, и 4-вектор
. Теперь мы видим, что эта формула является
лишь первым приближением к действительности. В самом деле, при интегрировании в
(58) учитывался вклад электромагнитного и гравитационного полей одновременно и
внутри, и снаружи движущейся сферы. Однако обобщённая теорема Пойнтинга
рассматривает энергию и потоки полей локальным образом, в любом малом объёме
пространства. Внутри тела действуют по крайней мере четыре поля, а за пределами
тела – только два поля, так как здесь нет поля давления и поля ускорений частиц
вещества. Соответственно, содержание полей в локальных объёмах внутри и снаружи
тела неодинаково, и 4-вектор
![]() должен вычисляться
отдельно для внутреннего объёма тела и отдельно для объёма за пределами тела.
должен вычисляться
отдельно для внутреннего объёма тела и отдельно для объёма за пределами тела.
С другой стороны, в (58) содержатся
временные компоненты тензоров энергии-импульса, и мы показали в предыдущем разделе,
что эти компоненты не составляют какой-либо 4-вектор. Это приводит к тому, что ![]() равно нулю только
внутри тела, как это следует из обобщённой теоремы Пойнтинга в разделе 3.1. Что
касается пространства за пределами тела, то здесь
равно нулю только
внутри тела, как это следует из обобщённой теоремы Пойнтинга в разделе 3.1. Что
касается пространства за пределами тела, то здесь ![]() нулю не равно. Таким
образом, концепция интегрального 4-вектора в виде (58) пригодна лишь внутри
космических тел либо для бесконечно больших систем из вещества и полей, когда
фундаментальные поля за пределами системы не вносят заметного вклада в расчёты
энергии и импульса.
нулю не равно. Таким
образом, концепция интегрального 4-вектора в виде (58) пригодна лишь внутри
космических тел либо для бесконечно больших систем из вещества и полей, когда
фундаментальные поля за пределами системы не вносят заметного вклада в расчёты
энергии и импульса.
Кроме этого, (58) не является полным выражением, так как при получении (58) в [12] не учитывались потоки энергии полей на границах бесконечного объёма.
Более точное применение теоремы
дивергенции к (1) даёт для четырёх полей в декартовых координатах лоренцевой
системы отсчёта, в которой символы Кристоффеля ![]() равны
нулю, следующее выражение:
равны
нулю, следующее выражение:
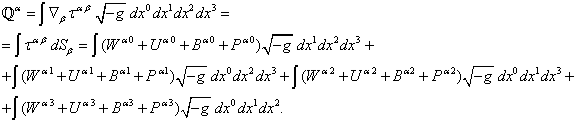
В данном выражении ![]() , а
, а ![]() представляет собой
4-вектор, составленный из соответствующих произведений дифференциалов координат;
этот 4-вектор дуален трёхмерной гиперповерхности, окружающей четырёхмерный
объём. При вычислении
представляет собой
4-вектор, составленный из соответствующих произведений дифференциалов координат;
этот 4-вектор дуален трёхмерной гиперповерхности, окружающей четырёхмерный
объём. При вычислении ![]() требуется вычислить
четыре интеграла, в каждом из которых подынтегральные функции с помощью
уравнения гиперповерхности должны быть выражены через те координаты, по которым
происходит интегрирование. В таком виде
требуется вычислить
четыре интеграла, в каждом из которых подынтегральные функции с помощью
уравнения гиперповерхности должны быть выражены через те координаты, по которым
происходит интегрирование. В таком виде ![]() сохраняется как
некоторая четырёхмерная величина, поскольку выражение для такого
сохраняется как
некоторая четырёхмерная величина, поскольку выражение для такого ![]() представляет собой
интегральное выражение обобщённой теоремы Пойнтинга (сравни с (19-20)).
представляет собой
интегральное выражение обобщённой теоремы Пойнтинга (сравни с (19-20)).
Сохранение ![]() в каждой замкнутой
физической системе означает, что такая физическая система не только имеет
некоторый постоянный 4-импульс, но и неизменное распределение энергий полей и
их потоков. Однако существование проблемы 4/3 означает, что величина
в каждой замкнутой
физической системе означает, что такая физическая система не только имеет
некоторый постоянный 4-импульс, но и неизменное распределение энергий полей и
их потоков. Однако существование проблемы 4/3 означает, что величина ![]() не является 4-вектором
и тем более не задаёт 4-импульс системы, как это предполагается в общей теории
относительности. Различие 4-импульса и
не является 4-вектором
и тем более не задаёт 4-импульс системы, как это предполагается в общей теории
относительности. Различие 4-импульса и ![]() вытекает из того, что
первое относится к суммарной энергии и импульсу всех частиц вещества системы, а
второе относится к энергии и потокам энергии (потокам импульса) всех полей
системы.
вытекает из того, что
первое относится к суммарной энергии и импульсу всех частиц вещества системы, а
второе относится к энергии и потокам энергии (потокам импульса) всех полей
системы.
7. Заключение
Анализ уравнений поля для не вращающейся в целом физической
системы из частиц и полей в виде сферы показывает, что с помощью обобщённой
теоремы Пойнтинга в рамках ковариантной теории гравитации становится возможным понять
некоторые закономерности, не имеющие простого объяснения в стандартном подходе.
Все поля, действующие в системе, составляют в совокупности общее поле. Мы
выделяем две основные компоненты общего поля: зарядовая компонента общего поля представлена электромагнитным полем, а
массовая компонента общего поля
состоит из гравитационного поля, поля
ускорений, поля давления, поля диссипации, макроскопических полей сильного и
слабого взаимодействий. Ограничившись только четырьмя основным полями, в
(15) мы выражаем коэффициент ![]() массовой компоненты общего поля
через коэффициент поля ускорений
массовой компоненты общего поля
через коэффициент поля ускорений ![]() , коэффициент поля давления
, коэффициент поля давления ![]() и гравитационную
постоянную
и гравитационную
постоянную ![]() . Далее мы показываем, что если в стационарной системе считать
все поля независимыми друг от друга, то внутри тела тензор энергии-импульса
массовой компоненты общего поля равен сумме тензоров энергии-импульса всех
полей, кроме электромагнитного поля.
. Далее мы показываем, что если в стационарной системе считать
все поля независимыми друг от друга, то внутри тела тензор энергии-импульса
массовой компоненты общего поля равен сумме тензоров энергии-импульса всех
полей, кроме электромагнитного поля.
В (32) мы находим между коэффициентами полей ![]() ,
, ![]() ,
, ![]() и электрической
постоянной
и электрической
постоянной ![]() связь, имеющуюся
внутри тел в состоянии равновесия. Это позволяет нам разрешить проблему 4/3,
долгое время не находящую точного решения. Во-первых, проблема 4/3 имеет место
для каждого из полей, причём как внутри, так и снаружи тела. Однако внутри тела
комбинация полей такова, что они компенсируют друг друга и для общего поля в
целом проблема 4/3 исчезает. Во-вторых, объяснение проблемы 4/3 за пределами
тела для электромагнитного и гравитационного полей заключается в том, что
плотность энергии поля и вектор потока энергии поля, входящие во временные
компоненты тензора энергии-импульса, не составляют 4-вектор. Это не позволяет
этим компонентам иметь одинаковые массы-энергии для движущегося тела, что и
выражается как проблема 4/3.
связь, имеющуюся
внутри тел в состоянии равновесия. Это позволяет нам разрешить проблему 4/3,
долгое время не находящую точного решения. Во-первых, проблема 4/3 имеет место
для каждого из полей, причём как внутри, так и снаружи тела. Однако внутри тела
комбинация полей такова, что они компенсируют друг друга и для общего поля в
целом проблема 4/3 исчезает. Во-вторых, объяснение проблемы 4/3 за пределами
тела для электромагнитного и гравитационного полей заключается в том, что
плотность энергии поля и вектор потока энергии поля, входящие во временные
компоненты тензора энергии-импульса, не составляют 4-вектор. Это не позволяет
этим компонентам иметь одинаковые массы-энергии для движущегося тела, что и
выражается как проблема 4/3.
В (54) мы представляем релятивистскую энергию рассматриваемой
системы из частиц и полей. Энергия складывается из двух частей – первая из них
есть сумма энергий частиц, находящихся под воздействием полей. Вторая часть
связана с суммой энергий полей как таковых. Если в [11] вторая часть
энергии, связанная с полями, приравнивалась к нулю, то в (54) это уже не так.
Это явилось следствием более точной связи коэффициентов полей в (32),
отличающейся от того, что использовалось в [11]. В (57) мы
выражаем релятивистскую энергию через массу ![]() и заряд системы
и заряд системы ![]() .
.
Обобщённая теорема Пойнтинга для четырёх полей представлена в (20). Если взять интеграл по объёму от всех членов в (20) и заменить интеграл по объёму от дивергенции суммы векторов на интеграл от этой суммы векторов по замкнутой поверхности, окружающей объём, получится следующее:
![]() ,
,
где ![]() обозначает вектор
нормали к поверхности.
обозначает вектор
нормали к поверхности.
В данном соотношении скорость изменения энергии полей в произвольном объёме точно компенсируется потоками энергии полей внутрь данного объёма через его поверхность. С точки зрения теории информации, вся информация, описывающая потоки частиц и квантов полей через поверхность, не исчезает и суммируется в информации, описывающей частицы и кванты поля внутри объёма. Это напоминает голографический принцип в теории струн, который предполагает, что квантовая информация, связанная с попавшими в чёрную дыру частицами и полями, находит своё отражение в колебаниях видимого гравитационного горизонта. Но в отличие от голографического принципа, обобщённая теорема Пойнтинга более фундаментальна, так как обосновывается всем аппаратом теории поля.
Особенностью нашего подхода является ещё то, что вещество полностью описывается в концепции поля, так что вместо тензора энергии-импульса вещества используется бесследовой симметричный тензор энергии-импульса поля ускорений. Тензоры энергии-импульса электромагнитного и гравитационного полей, поля давления и других полей, находимые по стандартной процедуре [6], также являются бесследовыми. Это свойство полей оказывается важным как при записи уравнения для метрики в ковариантной теории гравитации, так и при калибровке релятивистской энергии системы. В результате это приводит к единообразию зависимостей потенциалов и напряжённостей полей внутри тела [17] и к возможности использования обобщённой теоремы Пойнтинга для простого описания свойств систем из частиц и полей.
Соотношение для коэффициентов полей
(32) было выведено нами из уравнения движения (4) отдельно для временной и
пространственных компонент тензоров. В первом случае это привело к обобщённой
теореме Пойнтинга для плотностей и потоков энергии, а во втором – к уравнению
движения частиц под действием сил. При этом для вывода (32) нам понадобилось
учесть конкретную форму тензоров полей. Покажем теперь, что соотношение (32)
для релятивистской однородной системы может быть получено даже без вычисления
тензоров полей. Умножим (8) на отношение плотностей ![]() , считая это отношение постоянным, и затем сложим с (12-14),
с учётом того, что
, считая это отношение постоянным, и затем сложим с (12-14),
с учётом того, что ![]() ,
, ![]() :
:
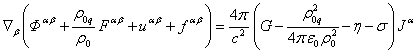 . (59)
. (59)
Уравнение (4) можно записать так:
![]() , (60)
, (60)
Используем теперь уравнение для метрики в ковариантной теории гравитации и соотношения непрерывности, вытекающие из уравнений полей [5]:
![]() ,
, ![]() ,
(62)
,
(62)
![]() ,
, ![]() .
.
Тензор гравитационного поля определяется через 4-потенциал ![]() так:
так: ![]() . Отсюда следует, что
. Отсюда следует, что ![]() , и то же самое должно быть для тензоров других полей.
Умножим теперь по очереди тензор каждого поля на обе стороны уравнения (61),
причём для электромагнитного поля умножим (61) на
, и то же самое должно быть для тензоров других полей.
Умножим теперь по очереди тензор каждого поля на обе стороны уравнения (61),
причём для электромагнитного поля умножим (61) на ![]() , а затем всё сложим:
, а затем всё сложим:
![]()
Учтём соотношения (62) в левой части этого уравнения:
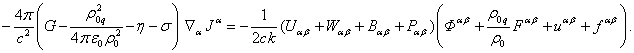
(63)
Тензоры полей в уравнении движения (60) возникают от вкладов
всех частиц системы и действуют на 4-ток ![]() , являющийся локальной величиной. Следовательно, сумма
тензоров полей в (60) не зависит от
, являющийся локальной величиной. Следовательно, сумма
тензоров полей в (60) не зависит от ![]() и
должна быть равна нулю:
и
должна быть равна нулю:
![]() . (64)
. (64)
Тогда из (59) и (63) следует равенство для коэффициентов
полей (32). С другой стороны, можно взять ковариантную производную ![]() в (59) и результат подставить в (63):
в (59) и результат подставить в (63):
![]()
Простейшим решением данного уравнения для тензоров полей
является соотношение (64). Кроме этого можно заметить, что в рассматриваемой
системе с однородной плотностью массы и заряда обнуляется и сумма тензоров
энергии-импульса всех полей внутри тела. Для временных компонент тензоров это
видно из (31) и (32). Тензоры энергии-импульса всех полей в (7), (9-11) имеют
один и тот же вид. Если справедливо (17) и (32), то сумма тензоров
энергии-импульса всех полей обнуляется
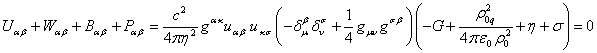 .
.
а уравнение для метрики (61) внутри тела приобретает очень
простой вид:
![]() .
.
Список использованных источников
1.
Poynting J. H. On
the Transfer of Energy in the Electromagnetic Field. Philosophical Transactions of the Royal Society of
London, 1884, Vol. 175, pp. 343-361. doi:10.1098/rstl.1884.0016.
2. Richter, E.; Florian, M.; Henneberger, K.
(2008). Poynting's theorem and energy conservation in the propagation of light
in bounded media. Europhysics Letters 81 (6): 67005. doi:10.1209%2F0295-5075%2F81%2F67005.
3.
Fedosin S.G. The
Concept of the General Force Vector Field.
OALib Journal, Vol. 3, pp. 1-15 (2016), e2459. http://dx.doi.org/10.4236/oalib.1102459;
Концепция общего силового векторного поля.
4. Fedosin S.G. Two components of the
macroscopic general field. Reports in Advances of Physical Sciences, Vol.
1,
No. 2,
1750002, 9 pages (2017). http://dx.doi.org/10.1142/S2424942417500025; Две компоненты макроскопического общего поля.
5.
Fedosin S.G. About the cosmological constant, acceleration field,
pressure field and energy. Jordan Journal of Physics, Vol. 9, No. 1, pp. 1-30 (2016).
http://dx.doi.org/10.5281/zenodo.889304; О
космологической постоянной, поле ускорения, поле давления и об энергии.
6. Fedosin S.G. The procedure of finding the stress-energy tensor and vector field
equations of any form. Advanced Studies in Theoretical Physics, 2014, Vol. 8,
pp. 771-779. doi:10.12988/astp.2014.47101; Процедура для
нахождения тензора энергии-импульса и уравнений векторного поля любого вида.
7. Jefimenko O. Causality, Electromagnetic Induction
and Gravitation. Star City, Electret Scientific Company, 2000.
8. Fock V. A. (1964). The Theory of Space, Time and Gravitation. Macmillan. Фок В.А.
Теория пространства, времени и гравитации. 2-е издание. – М.: Физматгиз, 1961. –568
с.
9. Fedosin S.G. Four-Dimensional Equation of Motion for Viscous
Compressible and Charged Fluid with Regard to the Acceleration Field, Pressure
Field and Dissipation Field. International
Journal of Thermodynamics. Vol. 18 (No. 1), pp. 13-24 (2015). doi:10.5541/ijot.5000034003; Четырёхмерное уравнение движения
вязкого сжимаемого вещества с
учётом поля
ускорений, поля
давления и
поля диссипации.
10.
Федосин С.Г. Физика и философия
подобия от преонов до метагалактик. Пермь: Стиль-МГ, 1999, 544 стр., Табл.66,
Ил.93, Библ. 377 назв. ISBN 5-8131-0012-1.
11.
Fedosin S.G. Relativistic Energy and Mass in the Weak Field Limit. Jordan Journal of Physics,
2015, Vol.
8, No.
1, pp.
1-16. http://dx.doi.org/10.5281/zenodo.889210;
Релятивистская энергия и масса в
пределе слабого поля.
12.
Fedosin S.G. The Integral Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based
on the Pressure Field and Acceleration Field. American Journal of Modern Physics, 2014, Vol.
3, No. 4, pp.
152-167. doi:10.11648/j.ajmp.20140304.12;
Интегральный 4-вектор энергии-импульса и анализ проблемы 4/3
на основе поля давления и поля ускорений.
13. Fedosin S.G. The
virial theorem and the kinetic energy of particles of a macroscopic system in
the general field concept. Continuum Mechanics and Thermodynamics, Vol. 29, Issue 2, pp. 361-371 (2017). https://dx.doi.org/10.1007/s00161-016-0536-8; Теорема вириала и
кинетическая
энергия
частиц
макроскопической
системы
в
концепции
общего
поля.
14. Fedosin S.G.
4/3 Problem for
the Gravitational Field. Advances in Physics Theories and
Applications, 2013, Vol. 23, pp. 19-25. http://dx.doi.org/10.5281/zenodo.889383;
Проблема 4/3 для гравитационного поля.
15. Heaviside, Oliver (1888/1894), Electromagnetic waves, the propagation of potential, and the
electromagnetic effects of a moving charge, Electrical
papers, 2, pp. 490–499. doi:10.1017/CBO9780511983139.017.
16. Searle G.F.C. On the steady motion of an
electrified ellipsoid. The
Philosophical Magazine Series 5, 44 (269), pp. 329-341 (1897). doi:10.1088/1478-7814/15/1/323.
17.
Fedosin S.G. Estimation of the physical
parameters of planets and stars in the gravitational equilibrium model.
Canadian
Journal of Physics, Vol.
94, No. 4, pp.
370-379 (2016). http://dx.doi.org/10.1139/cjp-2015-0593; Оценка
физических параметров планет и звёзд в модели гравитационного равновесия.
Источник:
http://sergf.ru/gpt.htm