International Frontier Science Letters,
Vol. 14, pp. 19-40 (2019). https://doi.org/10.18052/www.scipress.com/IFSL.14.19
The generalized Poynting theorem
for the general field and solution of the 4/3 problem
Sergey G. Fedosin
PO box 614088, Sviazeva str.
22-79, Perm, Perm Krai, Russia
The generalized Poynting
theorem is applied to the equilibrium system of particles, both inside and
outside the system. The particles are bound to each other by means of the
electromagnetic and gravitational fields, acceleration field and pressure
field. As a result, the correlation is found between the acceleration field
coefficient, the pressure field coefficient, the gravitational constant and the
vacuum permittivity. This correlation also depends on the ratio of the charge
density to the mass density of the particles inside the sphere. Due to the
correlation between the given field coefficients the 4/3 problem is solved and
the expression for the relativistic energy of the system is refined.
Keywords: Poynting theorem; acceleration field;
pressure field; 4/3 problem; system’s energy.
PACS: 03.50.De; 03.50.Kk; 04.50.+h; 14.80.-j.
1. Introduction
The Poynting theorem is most
widely used in electrodynamics, which describes the relation between the rate
of change of the energy density of the electromagnetic field inside a certain
volume and the electromagnetic energy flux through the surface of this volume,
as well as the capacity of work done by the field to move the charges
calculated per volume unit [1]. In the full physical system all fields acting
in it are taken into account and the stress-energy tensor of matter is
introduced into consideration. As a result, the generalized Poynting theorem
(or the Umov-Poynting theorem) becomes valid. In particular, the work done by
the fields to move the masses and charges per volume unit is equated to the
change in the energy density and energy flux in the stress-energy tensor of
matter. This leads to the fact that the Poynting theorem for the full physical
system in an arbitrary volume can be expressed only in terms of the rate of change
of the energy density of all the fields and the energy of matter in this
volume, as well as in terms of the energy fluxes of the fields and the energy
of matter through the surface surrounding this volume [2]. Thus, the
generalized Poynting theorem is transformed into the energy balance equation
for the fields and matter.
In the general field concept [3],
all the macroscopic particular fields can be included in one of the two
components, depending on which four-current is their source [4]. The mass four-current
generates such vector fields, as the
gravitational field, acceleration field, pressure field, dissipation field,
macroscopic fields of strong and weak interactions. All these fields are
included in the mass component of the general field. The charge component of
the general field is represented by the electromagnetic field and its source is
the charge four-current 
.
In contrast to the standard
approach, in the general field concept the stress-energy tensor of matter is
not used at all. The stress-energy tensor of the acceleration field is used
instead [5, 6]. This means that the description of the kinetic matter energy and the
flux of this energy ceases to be the phenomenological description, requiring
adjustment to the results of experiments, but is carried out as in a covariant
way using the terms of the velocity field and the corresponding acceleration
field.
The concept of the
acceleration field is intended for a more accurate description of the
accelerated motion of particles in a physical system. In the first
approximation, we can assume that the typical particles of the system behave
like non-rotating solid bodies during interaction. This corresponds to the fact
that only the scalar potential of the acceleration field is used, and the
proper vector potential of each particle is not taken into account. However,
even in case of parallel transport of a solid particle along a curved line, we
can see that where the instantaneous radius of rotation is larger, the matter
moves at a higher velocity than the velocity of the particle’s center of mass.
In case of the particle’s rotation, its energy would differ from the rest
energy of a stationary and non-rotating particle. The analysis of such cases is
significantly simplified when taking into account the vector potential of the
acceleration field as a new degree of freedom in the description of motion.
Since the scalar and vector potentials form the four-potential, the
acceleration field becomes a vector field. The four-potential of the acceleration field of a rectilinearly
moving solid particle coincides with its four-velocity. However, in the general
case, the four-potential is found by solving the wave equation of the
acceleration field in a way similar to that for other vector fields.
The same situation takes place
for the pressure field. As a rule, the pressure field is considered either as a
purely scalar field or as a certain effective vector field, in which the proper
vector potential of the pressure field of a typical particle is always equal to
zero. In the latter case, the role of the four-potential of the pressure field
in the system’s Lagrangian is played by the product of the pressure by the
particle’s four-velocity, divided by the square of the speed of light. Instead,
we consider an actual vector pressure field, when its four-potential is
determined by means of the corresponding four-dimensional wave equation. This
means that for the continuously distributed matter and a large number of interacting
particles, the global four-potentials of the acceleration field and the
pressure field are determined at the same time by all the particles of the
system and no longer depend on the four-velocity of the particle under
consideration.
Next, we will analyze the
generalized Poynting theorem for both components of the general field. This
will lead us to the relations that link the coefficients of the general field,
acceleration field and pressure field. In addition, we will provide the
solution of 4/3 problem and a more precise expression for the relativistic
energy of the system.
Note that
we consider the gravitational field as a vector field in the framework of the
covariant theory of gravitation, similar to the approach developed in [7].
In order to obtain exact
results without loss of generality, in analyzing the generalized Poynting
theorem we will rely on the relativistic uniform model [5]. This model
describes a stable physical system, the particles of which are in equilibrium
motion under the action of the global fields of the system. In such a system,
we can quite easily calculate the potentials and field strengths, find the
field tensors and the corresponding stress-energy tensors, which are necessary
for verifying the generalized Poynting theorem and solving the 4/3 problem.
2. The covariant form of the
generalized Poynting theorem
The equation of motion of
matter in two-component general field is written as follows [4]:
, (1)
where 
is the
electromagnetic tensor, 
is the tensor of the mass
component of the general field, 
is the
stress-energy tensor of the electromagnetic field, 
is the
stress-energy tensor of the mass component of the general field, 
is the
total stress-energy tensor of the physical system of matter and all the fields
acting in the system.
The generalized Poynting theorem follows from (1), provided that in the equation of motion the index value 
is selected:
. (2)
Tensor-differential equation
(2) describes the rate of change of the total energy of fields in an arbitrary
volume, depending on the fluxes of these fields directed inside this volume. If
in (1) we select the index 
, this leads to the equation
of motion of matter in the general field in the curved spacetime. As it is
shown in [4], the left side of the equation of motion will contain the product
of the mass density by the four-acceleration and the right side will contain
the sum of densities of the four-forces from the fields acting on the matter.
In the standard approach, the expression
is used for the generalized Poynting theorem,
while the tensor includes the stress-energy tensor of matter.
In the general theory of relativity the tensor takes on an additional meaning, because in
this theory not only the equation 
is considered as an equation of motion, but
also the equation for the metric, containing the tensor , determines the metric, which
is equivalent to the gravitational field in a tensor form [8].
The problem of this approach
is the fact that the form of the stress-energy tensor of matter is not
commonly-accepted and uniquely determined, and it depends on whether it
includes the contributions of pressure, internal matter energy and other
factors that are not clearly defined. The form of this tensor also depends
considerably on the form (scalar, vector, tensor), in which these factors are
taken into account in the Lagrangian.
In our approach, we avoid such
uncertainty, because instead of the stress-energy tensor of matter we use the
uniquely determined stress-energy tensor of the acceleration field, and the
contribution of pressure is taken into account with the help of a separate,
covariantly determined stress-energy tensor of the pressure field. The
contributions from the dissipation field [9], as well as other fields can be
taken into account in a similar way. It was thanks to the acceleration field
and the vector pressure field in [9] that for the first time it was possible to
accurately reproduce in the curved spacetime the phenomenological Navier-Stokes
equation in a covariant way.
The tensor of the mass component of the general field is
expressed in terms of the tensors of particular fields. For brevity, we will
further limit ourselves to the electromagnetic field and three more basic
fields, such as the gravitational field, acceleration field and pressure field.
The corresponding sum of tensors of these three fields gives the tensor :
.
(3)
Substituting (3) into (1)
yields the following:
, (4)
while the stress-energy tensor
of the mass component of the general field
depends on the tensor 
and the general field coefficient 
:
(5)
In turn, the tensor of the
mass component of the general field can be found from the field equations:
, 
. (6)
The stress-energy tensor and the electromagnetic field equations have
the standard form:
(7)
, 
. (8)
In these expressions: 
is the vacuum permittivity, 
is the speed of light, 
is the metric tensor, 
is the Kronecker symbol, 
is the Levi-Civita symbol.
Equation (4) can be analyzed
by two methods. In the first of them, we solve equations (6) and (8), find the
tensors 
and 
and then the tensors 
and in (5) and (7), which then we substitute into
(4) to calculate the divergence of the sum of these tensors. The second method
does not require finding the tensors and , in this case we use the
left-hand side of (4).
The stress-energy tensor of
the gravitational field according to [10] and the stress-energy tensors of the
acceleration field and pressure field according to [5] have the following form:
(9)
(10)
(11)
If we assume that all these
fields exist independently of each other and their contribution into the
Lagrangian is made independently, then the following wave equations hold true
for the tensors of these fields:
, 
. (12)
, 
. (13)
, 
. (14)
In (9-14) 
is the gravitational constant, 
is the acceleration field coefficient, 
is the pressure field coefficient.
Summing up the first equations
in (12-14), which contain the divergences of the field tensors, taking into
account (3) and comparing the result with the divergence of the mass component
of the general field 
in (6), we arrive at the following:
,
.
(15)
We will now transform the
composition of tensors 
with the help of (3):
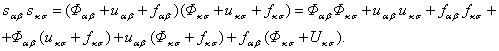
We can substitute this
equation into (5) and then take into account the expression for the tensors
(9-11):
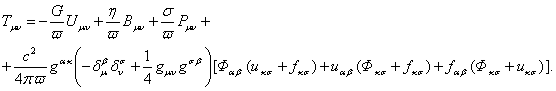
(16)
Field equations (12-14) were
solved in [11, 12] for a
massive charged spherical body, wherein it was found that field tensors have
similar components. In particular, we can write the following:
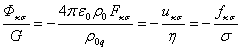. (17)
Substituting (17) into (16),
in view of (15) we find:
. (18)
Thus, if we consider all the
fields independent of each other, then inside the body the stress-energy tensor
of the mass component of the general field is equal to the sum of the
stress-energy tensors of all the fields, except for the electromagnetic field,
and the general field coefficient 
is expressed in terms of the coefficients of
the other fields, according to (15).
3. The generalized Poynting theorem in the weak field
limit
3.1 The analysis of equations inside the body
Let us substitute (18) into
the right side of (4) with the index 
:
. (19)
We will consider equation (19)
in the weak field limit, when the covariant derivative is transformed into the
four-gradient and the curvature of spacetime can be neglected. This case
corresponds to the Minkowski space of the special theory of relativity. From (19) it follows:
. (20)
In
(20) the Poynting vector of the electromagnetic field, the Heaviside vector of the gravitational field, the vectors of the energy flux density of the acceleration field and pressure fields, respectively, are defined by the following formulas:
, 
, 
, 
. (21)
Energy densities of the fields
have the form:
, 
,
, 
. (22)
In (21-22) the vectors of the
energy flux density and the energy densities are expressed in terms of the
corresponding field strengths and solenoidal vectors of the field.
Suppose there is a body of
spherical shape, which is in equilibrium under the action of its own
gravitational and electromagnetic fields, acceleration field and pressure
field. This body in general is not rotating and is motionless relative to the
reference frame 
, while the center of the
coordinate system is located in the center of the sphere. The body under
consideration consists of a number of small randomly moving particles with the
mass density 
and charge density 
in the reference frames associated with the
particles. If the space between the particles is small, as in liquids, we can
assume that the matter inside the body is distributed continuously. We studied
such a physical system in [12, 13]. Due to the randomness of
particles’ motion, in the vector field potentials and, accordingly,
the solenoidal vectors: 
(magnetic induction), 
(torsion field), 
and 
are equal to zero.
In addition, we found
expressions for the electric field strength 
, gravitational field strength
, and acceleration field
strength 
and pressure field strength 
inside the body as a function of the current
radius. After that, in [12] we made Lorentz transformation of coordinates from
the reference frame into the laboratory reference frame 
, relative to which the body
is moving at the velocity 
along the axis 
.
The vectors and are part of the components of the
electromagnetic tensor 
, therefore in Lorentz
transformations they are transformed in a special way - as tensor components. It is enough to know the vectors and in 
in order to find their form in the laboratory
reference frame .
Another way to find the
vectors and in is as follows: first we need to transform the
four-potential of the electromagnetic field 
from into with the help of Lorentz transformations, and
then to calculate the electromagnetic tensor components in by the formula: 
. In both cases, for the
electromagnetic field inside the moving sphere, after simplifying the
expression for the scalar field potential, we obtain the following:
, 
, 
,
, 
, 
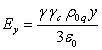. (23)
In (23) the Lorentz factor 
arises from the motion of the sphere at the
constant velocity 
in the reference frame , and 
is the
Lorentz factor for the velocities 
of the particles in the center of the sphere
in the reference frame . At the time point 
the sphere’s center is located at the origin
of the reference frame .
The gravitational field
strength and the torsion field inside the moving sphere under the same
conditions will be as follows:
, 
, 
,
, 
, 
. (24)
The components of the
acceleration field and the pressure field have similar expressions:
, 
, 
,
, 
, 
. (25)
, 
, 
,
, 
, 
. (26)
As we can see, in the physical
system under consideration the field strengths and their solenoidal vectors in
(24-26), included in the tensor components 
, 
and 
, satisfy relation (17).
With the help of (23-26) we
can calculate the components of the field energy flux vectors (21) and their
divergences. For the electromagnetic field:
, 
,
, 
. (27)
For the gravitational field:
, 
,
, 
. (28)
For the acceleration field:
, 
,
, 
. (29)
For the pressure field:
, 
, 
. (30)
Expression (28) for the
components of the energy flux vector of the gravitational field inside the
sphere is the same as in [14], where the gravitational field momentum is
calculated.
With the help of (23-26) we
find the energy densities of the fields (22) inside the moving sphere:
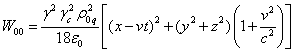. (31)
.
.
.
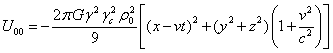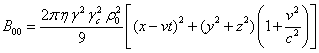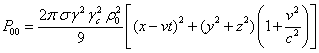Let us substitute (27-31) into
expression (20) for the Poynting theorem, taking into account all the four
existing fields. This gives the following:
. (32)
In (32) we found a
relationship between the acceleration field coefficient , the pressure field
coefficient , the gravitational constant and the vacuum permittivity . This relationship also
depends on the ratio of the charge density to the mass density of the particles inside the sphere, measured
in the reference frames associated with these particles. It is assumed that the
ratio 
is a constant. An ideal case is possible, when
the particles inside the sphere are not charged and the entire electric charge
is located in the sphere’s shell. Then for the particles inside the sphere 
, and the contribution from
the electromagnetic field in (32) vanishes. If we substitute (32) into (15),
then the coefficient of the general field inside the sphere depends only on the
electromagnetic component:
.
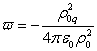(33)
In case, when the matter
inside the sphere is neutral and , the coefficient tends to zero.
Relation (32) is a manifestation
of the fact that at each point of the physical system under consideration the
sum of the energy densities of all the fields inside the body, included in the
time components of the tensors in (20), is equal to zero. The sum of the energy
flux vectors of all the fields inside the body is also equal to zero.
3.2 The analysis of equations outside the body
Let us now pass on to the
fields outside the body, where there is no matter and only the electromagnetic
and gravitational fields are left. In the reference frame the strengths of both fields look as if the
entire charge and mass are concentrated at the center of the fixed sphere. This
is due to the fact that the field strengths are inversely proportional to the
square of the distance from the sphere’s center to the point where the
strengths are determined. The electromagnetic field strength turns out to be
directly proportional to the total charge 
of the sphere filled with particles, and the
gravitational field strength is proportional to the mass 
of the sphere. With the help of Lorentz
transformations we can turn from the reference frame to the laboratory reference frame 
, in which the sphere with the
particles is moving at the velocity 
along the axis . Conversion of the components
of the electromagnetic and gravitational fields into the reference frame 
has been done in [12]. Outside the moving sphere these components are as follows:
, 
,
, 
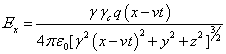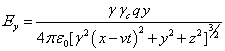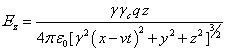, (34)
, 
.
, 
,
, 
,
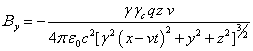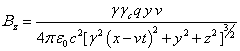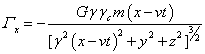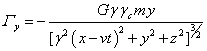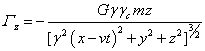(35)
, 
.
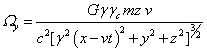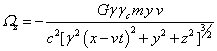Using (34-35), we calculate
the components of the field energy flux vectors (21) and their divergences. For the electromagnetic field:
, 
,
,
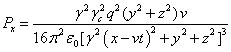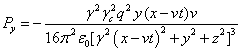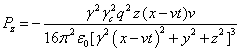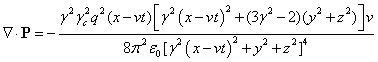. (36)
For the gravitational field:
, 
,
,
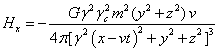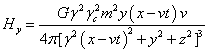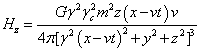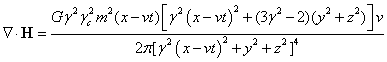. (37)
The energy densities of the
fields (22) outside the sphere and their partial derivatives with respect to
time for the field components (34-35) will be equal to:
.
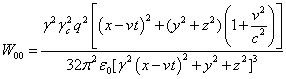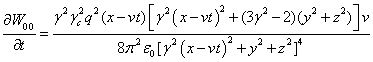. (38)
.
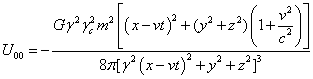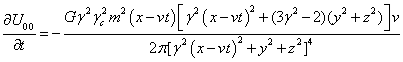. (39)
The generalized Poynting
theorem (20) outside the body can be written as follows:
. (40)
After substituting (36-39) in
(40) we see that the Poynting theorem outside the body is satisfied separately
for each field, while the electromagnetic and gravitational fields do not
depend on each other. In each spatial volume variation in time of the energy
density of a particular field is exactly compensated by the divergence of the
energy flux of this field.
4. The equation of motion of matter
Let us consider the left-hand
side of equation of motion (4) with respect to the four fields:
.
In the framework of the special theory of relativity, this equation for the spatial tensor components with the index value 
represents the equation of motion of the matter particles and can be expressed in terms of the field strengths and solenoidal vector of the fields:
. (41)
In
the derivation of (41) we used the expressions for the mass four-current 
and the charge four-current 
,
as well as the fact that the field tensors consist of the components of field
strengths and solenoidal vectors. Let us substitute in (41) the field
components from (23-26) inside the moving sphere, given that the vector of the
sphere’s velocity is directed along the axis 
,
with the components of the form 
. After reducing the nonzero multiplier we obtain the following:
.
This
obtained relation coincides with (32), which was derived for the time
components of the tensor equation (4) inside the moving body. This confirms the
self-consistency of the found field components with the equations of motion.
5. Solution of the 4/3 problem
Let us calculate the total
mass-energy of the four fields inside a spherical body moving at a constant
velocity, for which we take integral of the sum of the fields’ energy densities
over the volume of the moving body and divide it by the speed of light squared
and the Lorentz factor. For this we will use expressions (31):
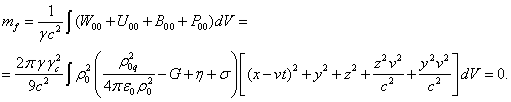(42)
The equality 
in (42) follows from expression (32), obtained from the generalized Poynting
theorem for the fields inside the body, as well as from the multiplier included
in the integral in (42).
Let us now calculate the total
mass-energy 
of all the four fields inside the body, moving
at a constant velocity, which is associated with the total momentum of these
fields. To do this, we need to take the integral over the volume of the moving
body of the sum of the fields’ momentum densities, while the momentum density
of each field is equal to the energy flux density of this field divided by the
square of the speed of light. The total momentum of the fields inside the body,
obtained by integration, must be equal to the product of the mass-energy 
by the Lorentz factor 
and the velocity of the body’s motion 
in the reference frame 
. For the case when the body’s
velocity is directed exactly along the axis of the reference frame 
, we can use the expressions
for the components of the energy flux densities of the fields in (27-30):
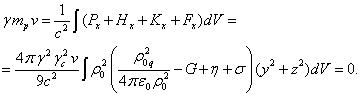(43)
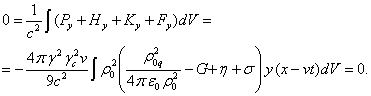(44)
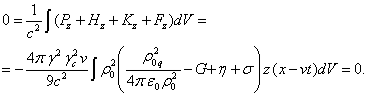
In (43), the mass is equal to zero due to relation (32), which is
found in (43)
as a separate multiplier within the integral. Zero on the left-hand side of (44) follows from the fact that the
total momentum of the fields cannot be directed along the axes 
and 
of the reference frame . Zero on the right-hand side
of (44)
is associated both with relation (32) and with the sphere’s symmetry with
respect to the limits of integration, as well as with the form of the
expression under the integral sign. From (42-44)
it follows that 
. This means that the total
mass-energies of the fields, found from the energy densities and energy flux
densities inside the body, are equal to each other, because they are equal to
zero.
Let us now consider the
situation outside of the moving body, where there are only electromagnetic and
gravitational fields. Using (38-39), similarly to (42), we find the total mass-energy of the external fields with the help of
the integral of the energy densities:
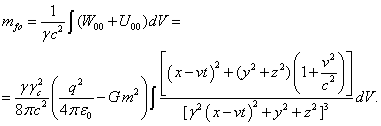(45)
Due to the motion of the body,
the mass-energy of the external fields emerges, which is associated with the
motion of these fields together with the body, that is, with the momenta of the
fields. Similarly to (43-44),
taking into account (36-37), for the body’s motion along the axis 
we obtain the following:
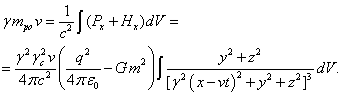(46)
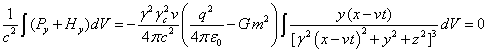. (47)
.
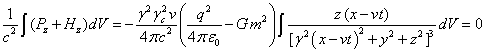The integrals of the form (45-47) have been calculated many times in the works, devoted to 4/3 problem,
for example in [15, 16]. Initially, the crux of the problem lay in the fact that the
mass-energy, associated with the momentum density of the electromagnetic field
of the moving body, was about 4/3 times greater than the mass-energy,
associated with the energy density of the electromagnetic field of this body.
In [14] it was shown that the 4/3 problem also exists for the gravitational
field of the moving body, specifically for the field both inside and outside
the body. To calculate the integrals (45-47)
it is convenient to introduce new coordinates as follows:
, 
, 
. (48)
The volume element is given by
the formula 
, where 
is the determinant of the Jacobian matrix:
.
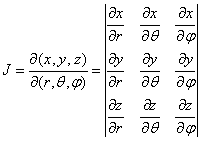After
calculating this determinant we can see that 
.
Due
to the Lorentz contraction during the motion along the axis 
, the sphere should take the form of a moving
Heaviside ellipsoid, which has the following surface equation:
.
(49)
From (48-49) it follows that the limits of integration over the volume in the new
coordinates are as follows: the radius 
must vary from 
to 
, and the angles 
and 
vary in the same way as in spherical
coordinates (from 0 up to 
for the angle
and from 0
up to 
for the angle 
) .
Substituting (48) and 
in (45-46), we find:
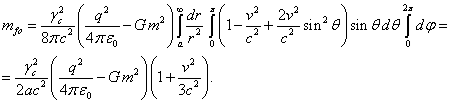(50)
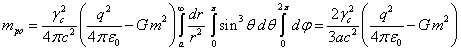. (51)
If in (50) we neglect the factor 
, then comparing it with (51) we obtain the well-known 4/3
relation for the mass-energies of the external fields: 
. Thus, there is a necessity
to explain the inequality of the field’s mass-energies outside the moving body
in case when these mass-energies are derived either from the field’s energy
flux density or from the field’s energy density. As we can see, the inequality
of mass energies holds separately both for the electromagnetic and
gravitational fields, respectively.
In order to understand the 4/3
problem we should pay attention to the following facts. In the stress-energy
tensor of the electromagnetic field (7), the components included in equation
(40) for the Poynting theorem outside the body, taking into account (21-22),
equal:
, 
, (52)
, 
.
Similarly, in the
stress-energy tensor of the gravitational field (9), the components included in
equation (40) have the form:
, 
, (53)
, 
.
If the components of the
stress-energy tensor of the electromagnetic field (52) formed a four-vector of the following form: 
, then after integration over
the volume of these components we could reckon that the mass-energy derived
from them would be the same both for the field energy and for the field
momentum. An example is the four-momentum of the body, which contains the
energy and the relativistic momentum, while both the energy and the momentum
include the same invariant body mass.
However, the components (52) do not form a four-vector but are
the components of the four-tensor. The same is true for the components (53) with respect to the gravitational
field. Hence, it follows that we should not expect the equality of
mass-energies of the form 
, as we do not calculate these
mass-energies from the components of four-vectors but from the components of
four-tensors. Instead of the equality of mass-energies the calculations lead to
the relation 
.
The difference between the
mass-energies 
and 
follows from different mass-energy
dependences in (50)
and (51).
But this very difference of the energy and momentum dependences of the
electromagnetic and gravitational fields is required so that these fields
outside the body would meet the generalized
Poynting theorem (40). Besides, the Poynting theorem is the consequence of the
equation of motion in a covariant form (1-2). At the same time, the expected
mass-energy equality of the form is ungrounded. It could be expected for the
case of the four-vectors, but not for the case of the four-tensors describing
the fields. The 4/3 problem in this case should be considered as an unexpected
but logical paradox arising from the transition from four-vectors to
four-tensors for describing the field. It also means that the stress-energy
four-tensor of any field cannot be represented as a combination of a certain
four-vector, composed of the time components of this tensor, and a
three-dimensional stress tensor, composed of the space components of this
tensor. This analogy is possible for the four-vector, consisting of the scalar
and vector components, but it becomes inaccurate in case of tensors as more
complex mathematical objects. The 4/3 coefficient in this case serves as a
measure of this inaccuracy.
We should note that if we take
a single field, for example, an electromagnetic or gravitational field, then
the 4/3 problem would take place for this field inside the body. However, if we
simultaneously consider all the fields inside the body, including the pressure
field and the acceleration field, as the general field components, then we
would obtain the equality of mass-energies: 
, and in this case, the 4/3
problem would disappear. This happens because all the fields compensate each
other so that the invariant mass-energy of the general field vanishes. Besides,
this compensation of fields is a consequence of the generalized Poynting
theorem. We see that in an equilibrium system the compensation of motion of the
particles of matter and field is possible due to the energy and momentum
exchange between the matter and the field. However, where there is no matter,
but there are only fundamental electromagnetic and gravitational fields, there
is no compensation and we discover inequality of mass-energies, known as the
4/3 problem.
6. Relativistic energy
In [11] in the framework of
the covariant theory of gravitation the relativistic energy of the physical
system under consideration in the form of a fixed sphere with particles was
calculated, taking into account the four fields, including the electromagnetic
and gravitational fields, pressure field and acceleration field. The energy of
the first two fields was taken into account not only inside, but also outside
the sphere, since the electromagnetic and gravitational fields of the body
extend to infinity. For the energy of the system we obtained the following
expression:
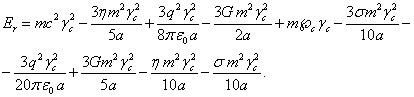
When calculating the energy of the particles, that are in the gravitational potential 
inside the sphere and have the Lorentz factor 
, in [11] we used the formula:
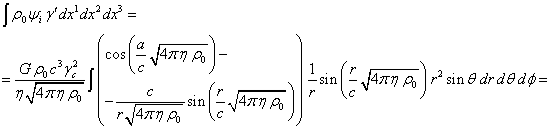
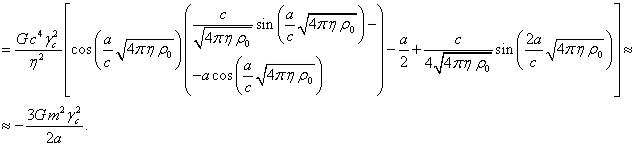
The energy value 
was obtained based on the fact that the
periodic functions such as 
and 
in the square brackets had been expanded into
the second-order terms. Now we wish to increase the accuracy of calculations
and to expand the periodic functions into the third-order or even fourth-order
terms. In particular, it gives the following:
.
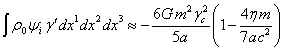The same is obtained for the energy
of the charged particles in the electrical potential 
inside the sphere – the total energy of these
particles decreases from the value 
to the value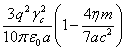 
. This means that the energy
of the system changes and becomes equal to the following expression:
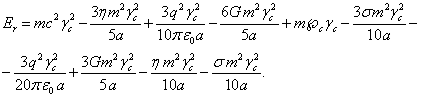(54)
In (54) the mass 
is the product of the mass density 
by the volume of the sphere with the
particles, and the charge 
is defined similarly as the product of the
charge density 
by the volume of the sphere. However, outside
the sphere the potentials of the electromagnetic and gravitational fields are
determined with the help of the gravitational mass 
and the electric charge 
. For these masses we obtain the following
[11]:
, 
. (55)
The Lorentz factor for the
particles in the center of the sphere and the scalar potential of the pressure
field in the center of the sphere are expressed in terms of the corresponding
quantities on the surface of the sphere:
, 
. (56)
Substituting the sum 
from (32) into (54), taking into account (55)
and (56), for the energy and the invariant (inertial) mass of the system 
we find the following:
. (57)
For the majority of cosmic
bodies we can assume that for the body’s surface the Lorentz factor is 
and the scalar potential of the pressure field
is 
.
The formula for the energy
(57) differs from the formula for the energy of the system in [11], which has
the following form:
.
The difference between the
formulas for the energy, excluding specification of the energy of particles in
the potentials of the gravitational and electromagnetic fields in (54), also
arises from the fact that in [11] we used the relations for the fields’
coefficients in accordance with the formula: 
. In turn, these relations
have been determined in [12] as a result of integrating the equation of motion
(1) with respect to the infinite four-dimensional volume. The subsequent
application of the four-dimensional divergence theorem with transition from
integrating the divergence of the sum of the stress-energy tensors of the four
fields with respect to the four-dimensional volume to integrating the sum of
these tensors with respect to the three-dimensional volume gives the integral
four-vector:
. (58)
In
order to always reserve the four-vector 
it was equated to zero. As a result, for the
field coefficients we obtained the formula: 
.
Now we see that this formula is only a first approximation to the truth. In
fact, during integration in (58) we took into account the contribution of the
electromagnetic and gravitational fields both inside and outside the moving
sphere. However, the generalized Poynting theorem considers the energy and
fluxes of the fields locally, in any small volume of space. There are at least
four fields inside the body, and outside the body there are only two fields,
because here there are no pressure field and acceleration field of the matter
particles. Consequently, the fields’ content in local volumes inside and
outside the body is different, and the four-vector 
must be calculated separately for the internal
body volume and for the volume outside the body.
On
the other hand, (58) contains the time components of the stress-energy tensors,
and we have shown in the previous section that these components do not form any
four-vector. This leads to the fact that 
is equal to zero only inside the body, as it
follows from the generalized Poynting theorem in section 3.1. As for the space
outside the body, here is not equal to zero. Thus, the concept
of the integral four-vector in the form of (58) is applicable only inside the
cosmic bodies or for infinitely large systems of matter and fields, when the
fundamental fields outside the system do not make a significant contribution
into the calculations of energy and momentum.
In
addition, (58) is not a complete expression, since during derivation of (58) in
[12] we did not take into account the field energy fluxes at the boundaries of
the infinite volume.
More
precise application of the divergence theorem to (1) results for the Cartesian
coordinates of the Lorentzian reference frame, in which the Christoffel symbols
are equal to zero, in the following expression
for the four fields:
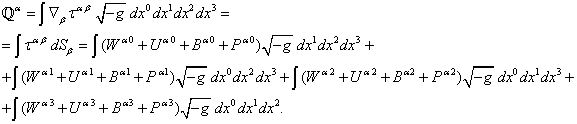
In this expression 
, and 
is a four-vector, composed of the
corresponding products of the coordinate differentials; this four-vector is
dual to the three-dimensional hypersurface, which surrounds the
four-dimensional volume. In the calculation of we need to calculate four integrals, in each
of which the integrands must be expressed with the help of the hypersurface
equation in terms of those coordinates, by which the integration is performed. In
this form is reserved as some four-dimensional quantity,
since the expression for such represents an integral expression of the
generalized Poynting theorem (compare with (19-20)).
Conservation of in each closed physical system means that such
a physical system has not only some constant four-momentum, but also has
unchanged distribution of the energies of the fields and their fluxes. However,
the existence of the 4/3 problem means that the quantity 
is not a four-vector and does not determine
the four-momentum of the system, as it is assumed in the general theory of
relativity. The difference between the four-momentum and follows from the fact that the first refers to
the total energy and momentum of all the particles of the system’s matter, and
the second refers to the energy and energy fluxes (momentum fluxes) of all the
system’s fields.
7. Conclusion
The analysis of the field
equations for a generally non-rotating physical system of particles and fields
in the form of a sphere shows that with the help of the generalized Poynting
theorem in the framework of the covariant theory of gravitation it is possible
to understand some regularities that have no simple explanation in the standard
approach. All the fields acting in the system collectively form the general
field. We distinguish two main components of the general field: the charge
component of the general field is represented by the electromagnetic field, and
the mass component of the general field consists of the gravitational field,
acceleration field, pressure field, dissipation field and the macroscopic
fields of strong and weak interactions. Being limited only by the four basic
fields, in (15) we express the coefficient 
of the mass component of the general field in
terms of the acceleration field coefficient 
, the pressure field
coefficient 
and the gravitational constant 
. Next we show that if in the
stationary system we consider all the fields independent of each other, then
inside the body the stress-energy tensor of the general field’s mass component
is equal to the sum of the stress-energy tensors of all the fields, except for
the electromagnetic field.
In (32) we find correlation
between the fields’ coefficients 
, 
, 
and the vacuum permittivity 
, which exists inside the
bodies in equilibrium state. This allows us to solve the 4/3 problem, which has
not had exact solution for a long time. Firstly, the 4/3 problem exists for
each field, both inside and outside the body. However, inside the body the
combination of fields is such that they compensate each other and for the
general field the 4/3 problem disappears. Secondly, the explanation of the 4/3
problem outside of the body for the electromagnetic and gravitational fields
consists in the fact that the field energy density and the field energy flux
vector, which are part of the time components of the stress-energy tensor, do
not form a four-vector. This does not allow these components to have the same
mass-energies for the moving body, which represents the 4/3 problem.
In (54) we represent the relativistic
energy of the system of particles and fields under consideration. The energy
consists of two parts, the first of which is the sum of the energies of
particles under the influence of the fields. The second part is associated with
the sum of the field energies as such. If in [11] the second part of the
energy, associated with the fields, was equated to zero, then in (54) it was no longer the case. This was
due to the more precise correlation between the field coefficients in (32),
which differed from what was used in [11]. In (57) we express the relativistic energy in terms of the mass 
and the charge of the system .
The
generalized Poynting theorem for the four fields is presented in (20). If we
take the integral over the volume of all the terms in (20) and replace the
volume integral of the divergence of the sum of vectors by the integral of this
sum of vectors over a closed surface, surrounding the volume, we obtain the
following:
,
where
denotes the normal vector to
the surface.
In
this relation the rate of change in the energy of the fields in an arbitrary
volume is exactly compensated by the fluxes of the fields’ energy inside this
volume through its surface. From the standpoint of the information theory, the
entire information describing the fluxes of particles and field quanta moving
through the surface, does not disappear and is summed up in the information
describing the particles and field quanta inside the volume. This reminds of
the holographic principle in the string theory, which suggests that the quantum
information, associated with the particles and fields that got into the black
hole, is reflected in the fluctuations of the visible gravitational horizon.
But in contrast to the holographic principle, the generalized Poynting theorem
is more fundamental, as it is substantiated by the entire apparatus of the
field theory.
A
peculiarity of our approach is the fact that the matter is fully described in
the concept of field, so that instead of the stress-energy tensor of matter we
use the traceless symmetric stress-energy tensor of the acceleration field. The
stress-energy tensors of the electromagnetic and gravitational fields, the
pressure field and other fields, found by a standard procedure [6], are also
traceless. This property of fields is important both in writing the equation
for the metric in the covariant theory of gravitation and in gauge of the
relativistic energy of the system. As a result, it leads to uniformity of
dependences of potentials and field strengths inside the body [17] and to the
possibility of using the generalized Poynting theorem for simple description of
the properties of systems of particles and fields.
The
relation for the field coefficients (32) was derived from the equation of
motion (4) separately for the time and space components of the tensors. In the
first case, this led to the generalized Poynting theorem for densities and
energy fluxes, and in the second case this led to the equation of the
particles’ motion under the action of forces. Besides, in order to derive (32)
we needed to take into account the particular form of the field tensors. We
will now show that relation (32) for the relativistic uniform system can be
obtained even without calculating the field tensors. Let us multiply (8) by the
ratio of densities 
,
assuming this ratio to be constant, and then add up with (12-14), taking into
account that 
, 
:
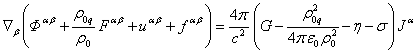. (59)
Equation
(4) can be written as follows:
, (60)
We
will now use the equation for the metric in the covariant theory of gravitation
and the continuity relations arising from the field equations [5]:
, (61)
, 
, (62)
, 
.
The gravitational field tensor
is determined using the four-potential 
as follows: 
. Hence it follows that 
, and the same should hold for
the tensors of other fields. Let us now multiply one after another the tensors
of each field by the both sides of equation (61), while for the electromagnetic
field we should multiply (61) by 
, and then sum up everything:
Let us take into account
relations (62) on the left-hand side of this equation:
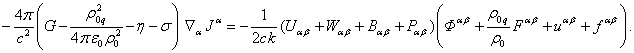
(63)
The field tensors in the
equation of motion (60) arise from the contributions of all the system’s
particles and act on the four-current 
, which is a local quantity.
Consequently, the sum of the field tensors in (60) does not depend on and must be equal to zero:
. (64)
Then the equality for the
field coefficients (32) follows from (59) and (63). On the other hand, we can
take the covariant derivative 
in (59) and substitute the result into (63):
The simplest solution of this
equation for the field tensors is relation (64). In addition, it can be noted
that in the system under consideration with the uniform mass and charge
density, the sum of the stress-energy tensors of all the fields inside the body
also becomes equal to zero. For the time components of the tensors, this can be
seen from (31) and (32). The stress-energy tensors of all the fields in (7),
(9-11) have the same form. If (17) and (32) are valid, then the sum of the
stress-energy tensors of all the fields becomes equal to zero
.
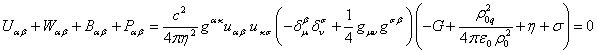and the equation for the
metric (61) inside the body acquires a very simple form:
.
References
1.
Poynting J. H. On
the Transfer of Energy in the Electromagnetic Field. Philosophical Transactions of the Royal Society of
London, Vol. 175, pp. 343-361 (1884). doi:10.1098/rstl.1884.0016.
2. Richter, E.; Florian, M.; Henneberger, K.
Poynting's theorem and energy conservation in the propagation of light in
bounded media. Europhysics Letters, Vol. 81 (6),
pp. 67005
(2008). doi:10.1209%2F0295-5075%2F81%2F67005.
3. Fedosin S.G. The
Concept of the General Force Vector Field.
OALib Journal, Vol. 3, pp. 1-15 (2016), e2459. doi:10.4236/oalib.1102459.
4. Fedosin S.G. Two components of the
macroscopic general field. Reports in Advances of Physical Sciences, Vol. 1, No. 2, 1750002, 9 pages (2017). doi:10.1142/S2424942417500025.
5. Fedosin S.G. About the cosmological constant, acceleration field,
pressure field and energy. Jordan Journal of Physics, Vol. 9, No. 1, pp. 1-30 (2016). doi:10.5281/zenodo.889304.
6. Fedosin S.G. The procedure of finding the stress-energy tensor
and vector field equations of any form. Advanced Studies in Theoretical Physics, Vol.
8, pp. 771-779 (2014). doi:10.12988/astp.2014.47101.
7. Jefimenko O. (2000). Causality, Electromagnetic
Induction and Gravitation. Star City, Electret Scientific Company.
8. Fock V. A. (1964). The Theory of Space, Time and Gravitation. Macmillan.
9. Fedosin S.G. Four-Dimensional Equation of Motion for Viscous
Compressible and Charged Fluid with Regard to the Acceleration Field, Pressure
Field and Dissipation Field. International
Journal of Thermodynamics, Vol. 18, pp. 13-24 (2015). doi:10.5541/ijot.5000034003.
10.
Fedosin S. G.
Fizika i filosofiia podobiia ot preonov do metagalaktik. (Perm, 1999). ISBN
5-8131-0012-1.
11. Fedosin S.G. Relativistic
Energy and Mass in the Weak Field Limit. Jordan Journal of Physics, Vol. 8, No. 1, pp. 1-16 (2015). doi:10.5281/zenodo.889210.
12. Fedosin S.G. The Integral Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based
on the Pressure Field and Acceleration Field. American Journal of Modern Physics, Vol. 3, No. 4, pp. 152-167 (2014). doi:10.11648/j.ajmp.20140304.12.
13. Fedosin S.G. The
virial theorem and the kinetic energy of particles of a macroscopic system in
the general field concept. Continuum Mechanics and Thermodynamics, Vol. 29, Issue 2, pp. 361-371 (2017). doi:10.1007/s00161-016-0536-8.
14. Fedosin S.G.
4/3 Problem for
the Gravitational Field. Advances in Physics Theories and
Applications, Vol. 23, pp. 19-25 (2013). doi:10.5281/zenodo.889383.
15. Heaviside, Oliver. Electromagnetic waves, the propagation of potential, and the
electromagnetic effects of a moving charge. Electrical
papers, 2, pp. 490–499 (1888/1894). doi:10.1017/CBO9780511983139.017.
16. Searle G.F.C. On the steady motion of an
electrified ellipsoid. The
Philosophical Magazine Series 5, Vol. 44 (269), pp. 329-341(1897). doi:10.1088/1478-7814/15/1/323.
17. Fedosin S.G.
Estimation of the physical parameters of planets and stars in the gravitational
equilibrium model. Canadian Journal of Physics, Vol. 94, No. 4, pp. 370-379 (2016). doi:10.1139/cjp-2015-0593.
Source: http://sergf.ru/gpten.htm