In English

 

 

Physica Scripta, Vol. 99, No. 5, 055034 (2024). https://doi.org/10.1088/1402-4896/ad3b45

 

 

Что мы должны понимать под 4-импульсом физической системы?

 

Федосин Сергей Григорьевич

ул. Свиязева 22-79, город Пермь, 614088, Пермский край, Россия

e-mail: fedosin@hotmail.com

 

Показывается, что в общем случае в искривлённом пространстве-времени ни одно известное определение 4-импульса не соответствует определению, в котором вклад в 4-импульс в явном виде дают все частицы и поля системы, включая поля за пределами вещества. Данный недостаток может быть устранён в предположении, что первичным представлением 4-импульса является сумма двух нелокальных 4-векторов интегрального типа с ковариантными индексами. Первым из этих 4-векторов является находимый через лагранжиан обобщённый 4-импульс, временная компонента которого в теории векторных полей пропорциональна энергии частиц в скалярных потенциалах полей, а пространственная компонента связана с векторными потенциалами полей. Второй 4-вектор представляет собой 4-импульс самих полей, и его временная компонента связана с энергией, задаваемой тензорными инвариантами. В результате 4-импульс системы определяется как 4-вектор с ковариантным индексом. Стандартный подход даёт возможность найти 4-импульс в ковариантном виде лишь для свободной точечной частицы. В отличие от этого, полученные формулы для вычисления компонент 4-импульса применяются к покоящейся и к движущейся релятивистской однородной системе, состоящей из множества частиц. При этом в учёт берутся основные собственные поля рассматриваемой системы, в том числе электромагнитное и гравитационное поля, поле ускорений и поле давления. Все эти поля рассматриваются как векторные поля, что позволяет однозначно определить уравнения движения самих полей и уравнения движения вещества в этих полях. Используемый формализм включает в себя принцип наименьшего действия, заряженные и нейтральные 4-токи, соответствующие 4-потенциалы и тензоры полей, что обеспечивает унификацию и возможность объединения полей в единое взаимодействие. В рамках специальной теории относительности показывается, что за счёт движения 4-импульс системы увеличивается пропорционально фактору Лоренца центра импульсов системы, при этом в веществе системы сумма энергий всех полей равна нулю. Вычисление компонент интегрального вектора в релятивистской однородной системе показывает, что так называемый интегральный вектор не равен 4-импульсу и вообще не является 4-вектором, хотя сохраняется в замкнутой системе. Таким образом, в теории релятивистских векторных полей 4-импульс не может быть найден через интегральный вектор и компоненты тензора энергии-импульса системы, в противоположность тому, как это предполагается в общей теории относительности.

Ключевые слова: обобщённый 4-импульс; 4-импульс поля; релятивистская однородная система; интегральный вектор.

 

What should we understand by the four-momentum of physical system?

 

Sergey G. Fedosin

PO box 614088, Sviazeva str. 22-79, Perm, Perm Krai, Russia

E-mail: fedosin@hotmail.com

 

It is shown that, in general, in curved spacetime, none of the known definitions of four-momentum correspond to the definition, in which all the system’s particles and fields, including fields outside matter, make an explicit contribution to the four-momentum. This drawback can be eliminated under the assumption that the primary representation of four-momentum is the sum of two nonlocal four-vectors of the integral type with covariant indices. The first of these four-vectors is the generalized four-momentum, found with the help of Lagrangian density. The time component of the generalized four-momentum, in theory of vector fields, is proportional to the particles’ energy in scalar field potentials, and the space component is related to vector field potentials. The second four-vector is the four-momentum of fields themselves, and its time component is related to the energy given by tensor invariants. As a result, the system’s four-momentum is defined as a four-vector with a covariant index. The standard approach makes it possible to find the four-momentum in covariant form only for a free point particle. In contrast, the obtained formulas for calculating the four-momentum components are applied to a stationary and moving relativistic uniform system, consisting of many particles. In this case, the main fields of the system under consideration are taken into account, including the electromagnetic and gravitational fields, the acceleration field and the pressure field. All these fields are considered vector fields, which makes it possible to unambiguously determine the equations of motion of the fields themselves and the equations of motion of matter in these fields. The formalism used includes the principle of least action, charged and neutral four-currents, corresponding four-potentials and field tensors, which ensures unification and the possibility of combining fields into a single interaction. Within the framework of the special theory of relativity, it is shown that due to motion, the four-momentum of the system increases in proportion to the Lorentz factor of the system’s center of momentum, while in the matter of the system the sum of the energies of all fields is equal to zero. The calculation of the integral vector’s components in the relativistic uniform system shows that the so-called integral vector is not equal to four-momentum and is not a four-vector at all, although it is conserved in a closed system. Thus, in the theory of relativistic vector fields, the four-momentum cannot be found with the help of an integral vector and components of the system’s stress-energy tensor, in contrast to how it is assumed in the general theory of relativity.

Keywords: generalized four-momentum; four-momentum of field; relativistic uniform system; integral vector.

 

1. Введение

По стандартному определению, принятому в теории относительности, 4-импульс физической системы есть 4-вектор следующего вида:

 

,                                                             (1)

 

где  есть энергия,  – скорость света,  – трёхмерный релятивистский импульс системы.

 

Определение (1) широко используется в механике в уравнении движения, где производная 4-импульса по собственному времени задаёт 4-силу, действующую на систему. Как , так и  являются аддитивными величинами, так что энергия получается путём суммирования энергий, содержащихся во всех элементах объёма системы. Что касается импульса системы, то он должен определяться путём векторного суммирования импульсов всех элементов объёма, включая и те, где нет вещества и имеется только поле.

Энергия и импульс системы, содержащей   частиц или отдельных элементов непрерывно распределённого вещества, могут быть выведены с помощью лагранжева формализма [1], для чего используется функция Лагранжа (Lagrangian)  как интеграл по бесконечному движущемуся объёму:

 

,                                                    (2)

 

,                                                     (3)

 

,                                                       (4)

 

здесь  – лагранжиан (Lagrangian density) как объёмная плотность функции Лагранжа,  есть произведение дифференциалов пространственных координат, величина  представляет собой детерминант метрического тензора ,  есть скорость движения частицы вещества с текущим номером ,  представляет собой трёхмерный импульс одного элемента объёма системы.

 

Подстановка (3) и (4) в (1) позволяет найти . Однако подобное определение 4-импульса является неудовлетворительным в том смысле, что оно не является прямым следствием лагранжева четырёхмерного формализма для 4-векторов и 4-тензоров. Насколько нам известно,  как 4-вектор не выражается в ковариантном виде ни с помощью функции Лагранжа , ни с помощью лагранжиана  , 4-импульс  просто конструируется вручную по формуле (1). Вместо этого в [2] можно найти ковариантное выражение 4-импульса, но лишь для одной свободной частицы, на которую не действуют внешние силы. При этом используется определение функции действии  с переменным верхним пределом интегрирования:

 

.                                                         (5)

 

.                                            (6)

 

Особенностью (5) является то, что верхний предел в интеграле по времени для функции действия не зафиксирован, в отличие от нижнего предела. Кроме этого, частица должна двигаться с нулевым 4-ускорением по некоторой истинной траектории согласно своему уравнению движения. При таких условиях вариация местоположения частицы в начальный момент времени равна нулю,, однако вариация в момент времени  нулю не равна. Согласно (6), 4-импульс  одной частицы оказывается 4-вектором с ковариантным индексом, в отличие от (1), где 4-импульс  системы частиц представляется как 4-вектор с контравариантным индексом.

В плоском пространстве-времени Минковского различие между 4-вектором с ковариантным индексом и тем же самым 4-вектором с контравариантным индексом заключается лишь в том, что их пространственные компоненты имеют противоположные знаки. В искривлённом пространстве-времени различие более существенно, так как для перехода к контравариантной форме 4-вектор с ковариантным индексом следует умножить на метрический тензор. В этом случае уравнения для частицы удобнее записывать через  (6), а не через , поскольку тогда метрический тензор не требуется. Это может существенно упростить решение уравнения движения, так как заранее метрический тензор может быть не известен.

В системе, состоящей из множества тесно взаимодействующих частиц, действуют различные силы и частицы приобретают некоторое 4-ускорение. Это нарушает условия, при которых действительно определение (6), так что суммирование 4-импульсов отдельных частиц может не дать суммарный 4-импульс  системы. Таким образом, для непрерывно распределённого вещества требуется другое ковариантное выражение как для 4-импульса отдельной частицы, так и для 4-импульса всей системы.

Согласно [3], ковариантное четырёхмерное уравнение Эйлера-Лагранжа должно иметь следующий вид:

 

,                                                      (7)

 

где  – 4-скорость,  – собственное время частицы,  – 4-радиус, задающий положение частицы.

 

Соотношение (7) является результатом вариации функции Лагранжа  в принципе наименьшего действия и представляет собой уравнение движения частицы. Для применения (7) необходимо знать зависимость  от значений  и  каждой индивидуальной частицы системы, что при большом количестве частиц оказывается затруднительно.

Величину  в (7) можно трактовать как 4-импульс произвольной частицы физической системы, величину  можно рассматривать как 4-силу, действующую на частицу, а полный 4-импульс должен получаться путём суммирования  отдельных  по всем частицам системы. Однако здесь возникает трудность с вкладом в 4-импульс от полей, выходящих за пределы вещества, и характеризующихся в функции Лагранжа с помощью интегралов по объёму от тензорных инвариантов. Дело в том, что выражение интегралов от тензорных инвариантов через 4-скорость частиц само по себе является достаточно сложной и нетривиальной задачей.

Существует совершенно другой подход к проблеме определения 4-импульса системы, связанный с общей теорией относительности. Так, в [2] можно найти следующее выражение:

 

,                                       (8)

 

где через  обозначены временные компоненты тензора энергии-импульса вещества и негравитационных полей, а через  обозначены временные компоненты псевдотензора гравитационного поля.

 

Утверждается, что величина  есть не что иное, как 4-импульс  физической системы с учётом вклада от гравитационного поля, причём в замкнутой системе  сохраняется. В связи с этим заметим, что для получения  необходимо исходить из уравнения движения в виде . Затем в это уравнение вводят такой псевдотензор гравитационного поля , чтобы от ковариантной производной перейти к частной производной. Уравнение движения приобретает вид , после чего оно интегрируется по объёму, приводя к (8).

Недостатком такого подхода является отсутствие доказательства того, что  действительно является 4-импульсом системы. Из (8) не следуют автоматически выражения (3) и (4) для энергии и импульса, и трудно понять, связано ли (8) с (6) или с  в (7). Более того, согласно [4] существует множество различных псевдотензоров гравитационного поля, дающих различные выражения для соответствующего , так что нет никакой гарантии, что хотя бы в одном случае выполняется равенство . Кроме этого, в [5] указывается, что в общей теории относительности не выполняется принцип соответствия, и инертная масса в общем случае в пределе слабого поля и малых скоростей не переходит в соответствующее выражение в теории Ньютона. Согласно [6], то же самое получается и для энергии, импульса и момента импульса системы.

В [7] было произведено сравнение вектора  с интегральным вектором, получаемым по формуле:

 

.                                                       (9)

 

Выражение (9) для интегрального вектора  справедливо для случая слабых полей и малых скоростей, когда в уравнении движения  ковариантную производную можно с небольшой погрешностью заменить на частную производную . Величина  со смешанными индексами в (9) задаёт временные компоненты тензора энергии-импульса системы, причём гравитационное поле рассматривается как векторное поле в рамках ковариантной теории гравитации [8]. Анализ вектора  показывает, что его временная компонента связана с суммой энергий всех полей системы, а пространственная компонента – с векторной суммой векторов потоков энергии полей. Если 4-импульс  задаёт энергию и импульс частиц и полей системы, то вектор  задаёт только энергии и потоки энергии полей.

По способу своего построения интегральный вектор  не является 4-вектором и может считаться четырёхмерным псевдовектором. Что касается вектора  в (8), то этот вектор обладает тем свойством, что нельзя одновременно выполнить два условия для замкнутой системы [9]: 1) Сохранение во времени суммы всех видов энергии, включая гравитационную энергию, задаваемую псевдотензором; 2) Независимость суммы всех видов энергии в данный момент времени от выбора системы отсчёта. В результате в [10] векторы типа  в общей теории относительности рассматриваются не как 4-векторы, а скорее как некоторые псевдовекторы, которые не могут задавать 4-импульс .

В связи с этим, целью данной работы является выведение ковариантной формулы для 4-импульса системы, действительной для искривлённого пространства-времени и для непрерывно распределённого вещества. Учёт последнего обстоятельства приводит к тому, что в расчётах вместо функции Лагранжа  на первое место выходит лагранжиан . В наш анализ будут включены четыре наиболее часто встречающиеся поля, такие как электромагнитное и гравитационное поля, поле ускорений [11] и поле давления [12], которые рассматриваются как векторные поля. Используемый нами лагранжев формализм позволяет рассматривать все эти поля как компоненты единого общего поля [13-15], при этом действующие в системе силы от каждого поля имеют один и тот же вид, подобный силе Лоренца.

Как мы покажем далее, выведенная формула для 4-импульса будет отличаться от известных стандартных определений. Кроме того, путём прямого расчёта интегрального вектора  будет показано его отличие от 4-импульса движущейся физической системы.

В Приложении A кратко описаны два способа представления 4-импульса  физической системы. В первом из этих способов необходимо вычислять энергию и импульс системы, а во втором способе 4-импульс  представляется суммой двух нелокальных интегральных векторов в виде . В Приложении B даются детали расчётов в соотношениях (119-122). В Приложении C представлен список используемых обозначений.

 

2. Методы

Прежде, чем рассматривать 4-импульс физической системы, необходимо определить обобщённый 4-импульс, являющийся основной частью 4-импульса.

При расчёте обобщённого 4-импульса будем исходить из лагранжева формализма для непрерывно распределённого вещества в четырёхмерной форме. В общем случае лагранжиан зависит от координатного времени , от 4-токов  и , от 4-потенциалов и тензоров полей в каждой точке поля, в том числе внутри частиц, а также от метрического тензора  и от скалярной кривизны :

 

,     (10)

 

где  задаёт точку наблюдения, в которой в данный момент времени находится типичная частица с номером ,   есть 4-скорость типичной частицы в этой точке.

 

Величины  в (10) обозначают 4-потенциалы электромагнитного и гравитационного полей, поля ускорений и поля давления, соответственно, а величины  представляют собой тензоры этих полей. С учётом (2) функция действия на интервале времени  с фиксированными пределами интегрирования равна:

 

.                                       (11)

 

После подстановки (10) в (11) можно произвести варьирование функции действия и получить уравнения для каждого поля, уравнение для метрики и уравнение движения частиц вещества [11], [16]. Кроме этого, для каждой типичной частицы получается четырёхмерное уравнение Эйлера-Лагранжа [17]:

 

.                                                  (12)

 

Величина  в (12) представляет ту часть лагранжиана , которая содержит массовый 4-ток  и зарядовый 4-ток , так как только 4-токи могут зависеть прямо от 4-радиуса  и от 4-скорости  частиц. Все остальные величины в лагранжиане, включая 4-потенциалы, тензоры полей и метрический тензор, становятся функциями от  и от  только после решения соответствующих уравнений и потому не дифференцируются в (12), ведя себя как постоянные.

Действительно, уравнение какого-либо поля получается лишь после варьировании лагранжиана в принципе наименьшего действия по 4-потенциалу соответствующего поля. Это уравнение даёт связь 4-тока, генерирующего поле, с тензором поля. Учитывая выражение тензора поля через 4-потенциал, уравнение поля можно представить также как связь 4-тока и 4-потенциала. При варьировании предполагается, что тензор поля прямо зависит только от 4-потенциала и от его производных. В качестве примера можно рассмотреть уравнения Максвелла для электромагнитного поля, решения которых дают либо электромагнитный тензор , либо 4-потенциал  как функции от 4-тока  с известной зависимостью  от времени, координат и скоростей.

С другой стороны, в (10) все величины в большой скобке предполагаются независимыми друг от друга с точки зрения процедуры варьирования этих величин. При этом  и  появляются в лагранжиане не прямо, а косвенно, поскольку от них зависят 4-токи  и . В итоге вариации 4-токов в лагранжиане сводятся к вариациям от  [8], [11], [18].

Особенностью (12) является то, что оно справедливо для малого интервала  , когда временные компоненты  4-скоростей частиц можно полагать неизменными. Если же интервал   нельзя считать малым, его следует разделить на малые временные промежутки и на каждом таком промежутке проводить синхронное варьирование функции действия и задавать усреднённые постоянные временные компоненты  4-скоростей частиц. С другой стороны, уравнение (12) можно понимать как уравнение для типичных частиц системы, в этом случае постоянство  для каждой из частиц получается автоматически как следствие усреднения параметров частиц в каждой точке системы.

В отличие от уравнения движения (7), в котором появляется 4-сила , уравнение движения (12) записано для скорости изменения плотности 4-импульса и для плотности 4-силы , действующей в единичном элементе объёма, в котором находится типичная частица.

 

3. Результаты

3.1. Обобщённый 4-импульс

С помощью (12) в [17] был определён обобщённый 4-импульс:

 

.              (13)

 

В (13)  есть объёмная плотность обобщённого 4-импульса, присутствующая в (12),  задаёт временную компоненту 4-скорости частиц в каждой точке интегрирования по объёму , занимаемому веществом. Кроме этого, используется соотношение из [2]:

 

,                               (14)

 

где  есть дифференциал собственного объёма любой из частиц непрерывно распределённого вещества, вычисляемый в сопутствующей частице системе отсчёта.

 

В замкнутой системе 4-вектор  сохраняется и представляет собой обобщённый 4-импульс всех частиц системы.

Кроме  в (13), может быть определена следующая четырёхмерная величина:

 

.                                      (15)

 

Величина  не является 4-вектором, но при условии постоянства  выражение (15) переходит в выражение (13) для . Как показывается в [17], для чисто векторных полей часть лагранжиана  такова, что пространственные компоненты  и  совпадают друг с другом и с точностью до знака дают релятивистский импульс  частиц, являющийся частью (4). Для вычисления  необходимо вместо всей функции Лагранжа  подставить в (4) её часть , связанную с 4-токами.

 

3.2. Энергия поля в веществе

Разрешив уравнения для полей и для метрики внутри вещества, мы можем выразить 4-потенциалы, тензоры полей, метрический тензор и скалярную кривизну через 4-радиусы  и 4-скорости  частиц системы. В этом случае внутри вещества лагранжиан (10) принимает вид . Учитывая это в (2) и используя (14), находим:

 

.           (16)

 

Кроме этого, можно записать:

 

.                                      (17)

 

Выражение (17) представляет собой производную функции Лагранжа  по координатному времени . Эта производная записана как производная от сложной функции в предположении, что  и  являются функциями от времени .

Изохронная вариация  функции Лагранжа  с учётом стандартного равенства нулю вариации координатного времени  выражается через вариации  и :

 

.                                           (18)

 

Так как , , то будет:

                (19)

 

 

В (19) было использовано варьирование произведения двух функций в виде

 

.

 

Подстановка  из (19) в (18) даёт следующее:

 

       (20)

 

Подставим  в (11) вместо , найдём вариацию действия и с учётом (20) приравняем её к нулю:

 

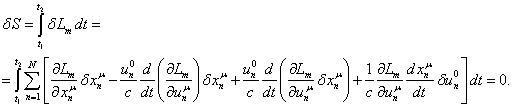
(21)

 

Действуя как в [17], будем считать, что в объёме каждой частицы временные компоненты  4-скорости частиц постоянны во время варьирования действия, так что  и последний член в (21) будет равен нулю. Для предпоследнего члена в (21) можно тогда записать:

 

       (22))

 

Равенство нулю в (22) следует из того, что вариации  в моменты времени  и  обращаются в нуль по условию варьирования. В (21) остаются первые два члена, разность которых должна быть равна нулю, как следствие  в принципе наименьшего действия. Это даёт следующее:

 

.                                                  (23)

 

Равенство (23) соответствует (7) с тем отличием, что вместо  используется функция Лагранжа  внутри вещества.

Выразим из (23)  и подставим в (17) с учётом соотношения :

 

                    (24)

 

Соотношение (24) можно записать так: , где

 

.                                                   (25)

 

Если лагранжиан  внутри вещества не зависит от времени, то  и тогда будет , , то есть величина  будет постоянна во времени и не зависеть от координат.

От суммы по частицам в (25) можно перейти к интегралу по объёму непрерывно распределённого вещества, выражая функцию Лагранжа  через лагранжиан  с помощью (16):

 

 

 

 

 

 

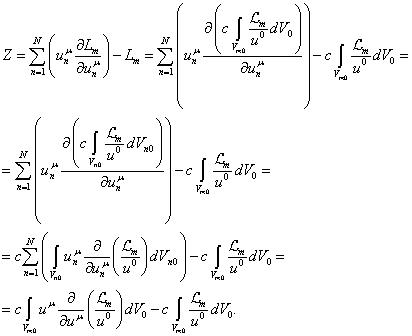
В представленном выше соотношении сумма  была заменена на сумму , в которой интеграл  берётся только по объёму одной частицы с номером . Это возможно потому, что производная  берётся только по 4-скорости  частицы с номером . Поэтому интеграл по объёму всех остальных частиц системы не зависит от 4-скорости частицы  с номером  и производная  для всех остальных частиц становится равной нулю.

После этого 4-скорость  вносится под знак интеграла  по инвариантному объёму  одной частицы, с учётом того, что  является постоянной в пределах объёма этой частицы. В интеграле  элемент объёма  не зависит от 4-скорости , поэтому производная  также вносится внутрь интеграла и действует там на .

Далее сумма  в выражении для  преобразуется в интеграл  по объёму всех частиц. Последующее использование выражение (14) для элемента объёма даёт:

 

                      (26)

 

 

 

 

 

В (21) мы предполагали, что временные компоненты  4-скорости частиц постоянны во время варьирования действия, В связи с этим временная компонента  4-скорости в (26) также рассматривается как постоянная величина при вычислении  производной  .

Из сравнения (25) и (3) видно, что величина  имеет размерность энергии. Чтобы лучше понять смысл , воспользуемся выражением лагранжиана для четырёх векторных полей [11], [19], состоящего из двух частей:

 

,                .                     (27)

 

(28)

 

где  – 4-потенциал электромагнитного поля, задаваемый с помощью скалярного потенциала  и векторного потенциала  этого поля,

 – зарядовый 4-ток,

– плотность заряда в сопутствующей частице системе отсчёта,

 – 4-скорость точечной частицы,

 – 4-потенциал гравитационного поля, описываемый через скалярный потенциал  и векторный потенциал  этого поля в рамках ковариантной теории гравитации,

 – массовый 4-ток,

 – плотность массы в сопутствующей частице системе отсчёта,

 – 4-потенциал поля ускорений, где  и  обозначают скалярный и векторный потенциалы, соответственно,

 – 4-потенциал поля давления, состоящий из скалярного потенциала  и векторного потенциала ;

 – магнитная постоянная,

 – электромагнитный тензор,

 – гравитационная постоянная,

 – гравитационный тензор,

 – коэффициент поля ускорений,

 – тензор ускорений, вычисляемый как 4-ротор от 4-потенциала поля ускорений,

 – коэффициент поля давления,

 – тензор поля давления,

, где  – некоторый коэффициент порядка единицы, подлежащий определению,

 

 

 – скалярная кривизна,

 – космологическая постоянная.

 

Компоненты  и  лагранжиана  в (27-28) обладают той замечательной особенностью, что все поля, будь то электромагнитное поле или поле давления, выражаются в одной и той же форме, то есть через свои собственные 4-потенциалы и через соответствующие тензоры. Хорошо известно, что электромагнитное поле в таком виде полностью описывает электромагнитные явления, в том числе все явления в искривлённом пространстве-времени с известной метрикой, а с учётом квантования описывает явления в микромире в рамках квантовой электродинамики с очень высокой точностью. То же самое следует ожидать и для других полей в (27-28).

Для примера, в [19] было показано, что ковариантное уравнение движения частиц в электромагнитном и гравитационном полях, в поле ускорений, в поле давления и в поле диссипации, после упрощения в рамках специальной теории относительности, точно переходит в феноменологическое уравнение Навье-Стокса в гидродинамике.

В качестве другого примера возьмём поле давления, которое до сих пор, даже в моделях звёзд при больших давлениях, трактуется как скалярное поле. Однако рассмотрение поля давления как векторного поля существенно увеличивает точность получаемых результатов, поскольку при этом появляется новая степень свободы в виде векторного потенциала поля давления, отвечающая за векторные эффекты, зависящие от скорости частиц. Таким образом, мы можем считать вполне оправданным наш выбор лагранжиана в (27-28).

За пределами вещества часть лагранжиана  обнуляется, так как здесь 4-токи  и  равны нулю, а в  обнуляются тензоры поля ускорений и поля давления, присутствующие только в веществе. При вычислении энергии и импульса в веществе мы можем не учитывать два последних члена в  по двум причинам. Во первых, скалярная кривизна  является функцией метрического тензора и его производных, и не содержит прямо 4-скорость, так что . Во-вторых, мы используем такую калибровку энергии и уравнения для метрики, что разность  в (28) обращается в нуль [11], [20].

Лагранжиан  есть лагранжиан  в (27), но вычисляемый только внутри вещества. Учтём, что 4-скорость  присутствует лишь в  (27), где она входит в состав 4-токов. Следовательно,

 

.                                 (29)

 

С учётом (27-29) найдём величину  в (26):

 

.  (30)

 

В (30) интегрирование осуществляется по объёму, занимаемому веществом. Отсюда видно, что энергия  выражается исключительно через тензоры полей и сохраняется, если лагранжиан внутри вещества прямо не зависит от времени. Последнее условие выполняется для лагранжиана (27), так что в замкнутой системе должна сохраняться энергия поля, связанная с тензорными инвариантами.

 

3.3. Энергия и импульс системы

В (27-28) лагранжиан был представлен в виде , где  зависит от 4-потенциалов и 4-токов, а  содержит тензорные инварианты полей. Также и функция Лагранжа  разбивается на две части, одна из которых  связана с частицами, а другая часть  связана с полями.

С учётом (2) можно записать: . Чтобы вычислить в выражении для энергии (3) производную , следует выразить часть функции Лагранжа  через интеграл по инвариантным объёмам частиц. С учётом (14) находим:

 

,               ,

 

 

 

 

 

 

 

В представленной выше сумме интеграл  по объёму всех частиц был заменён на интеграл  по объёму той частицы, по которой берётся частная производная , результат от этого не меняется. После этого  и  вносятся под знак интеграла , затем сумма интегралов по всем частицам превращается в интеграл по объёму всех частиц, давая . С учётом этого из (3) находим:

 

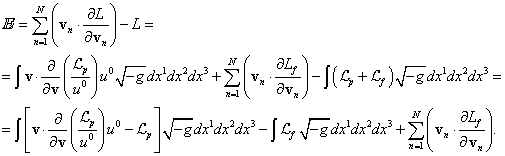
(31)

 

 

 

 

 

С учётом соотношений  и  зарядовый 4-ток  и массовый 4-ток  выразим в следующем виде:

 

.

 

.                                               (32)

 

Произведения электромагнитного 4-потенциала на зарядовый 4-ток  и гравитационного 4-потенциала на массовый 4-ток  с учётом (32) можно представить так:

 

,           .        (33)

 

Аналогично можно записать для поля ускорений и для поля давления:

 

,             .          (34)

 

С помощью (33-34)  в (27) выражается через скорость  движения элемента вещества или типичной частицы:

 

.       (35)

 

Подставим  из (35) и  из (28) в (31), и получим выражение для энергии системы:

 

(36)

 

 

 

 

 

В (36) предполагается, что в общем случае усреднённые потенциалы полей в объёме частиц, а также плотность массы  и плотность заряда  частиц могут зависеть от скорости  этих частиц. При подстановке  было использовано условие калибровки энергии, согласно которому разность  в (28) принимается равной нулю [11], [20].

Для импульса (4) с учётом (2), (35) и соотношения  можно записать:

 

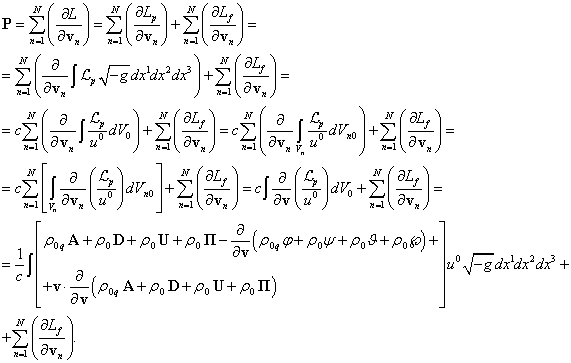
(37)

 

В (37) производная  от интеграла  по объёму всех частиц была заменена на производную  от интеграла  по собственному объёму частицы с номером , которая имеет скорость . После этого производная  была внесена под знак этого интеграла и индексы  внутри интеграла были убраны.

 

3.4. Компоненты 4-импульса с ковариантным индексом

Для объёма системы, занимаемой веществом, мы нашли энергию  в (26) и в (30), связанную с полями. Кроме этого, в данном объёме присутствует энергия, связанная с обобщённым 4-импульсом  в (13). Обе эти энергии сохраняются в замкнутой стационарной физической системе. Добавляя к этим энергиям энергию полей за пределами вещества, получаем релятивистскую энергию, которая в замкнутой системе также сохраняется. Это означает сохранение каждой компоненты энергии по отдельности, как следствие неизменности распределения энергии в равновесной системе.

Используем часть лагранжиана  из (27) и выразим с её помощью временную и пространственную компоненты  в (13). Если представить обобщённый 4-импульс в виде   и учесть выражения для 4-потенциалов полей, получится следующее:

 

.                      (38)

 

.                        (39)

 

.                          (40)

 

Временная компонента  обобщённого 4-импульса зависит от скалярных потенциалов полей в веществе, а суммарный обобщённый импульс  частиц вещества зависит от векторных потенциалов полей.

Далее кроме обобщённого 4-импульса  с ковариантным индексом нам понадобится другая его форма с контравариантным индексом:

 

.                      (41)

 

Чтобы получить (41), необходимо в (38) для каждого элемента вещества умножить 4-потенциалы полей на метрический тензор в этом элементе вещества, чтобы 4-потенциалы записать с контравариантным индексом. Имея интегральную форму, обобщённые 4-импульсы  и  отличаются от стандартных 4-векторов своей не локальностью. В результате выражения типа  для обобщённых 4-импульсов в искривлённом пространстве-времени недействительны.

В самом деле, когда события происходят локально, в малом объёме, как в точечной частице, мы вполне можем допустить выражение для 4-скорости частицы в виде , в котором ковариантные компоненты  4-скорости связаны с контравариантными компонентами  посредством метрического тензора . Однако объём  интегрирования в интегралах (38-41) включает в себя весь тот объём, в котором находятся все типичные частицы системы, и этот объём намного превышает объём одной частицы. Поэтому в пределах объёма  значения метрического тензора  могут существенно изменяться. Выражение (38) можно записать так:

 

.                   (42)

 

Если бы метрический тензор в (42) можно было вынести за знак интеграла, то с учётом выражения (41) получилось бы соотношение . Но это возможно лишь в том случае, когда , то есть в рамках специальной теории относительности, но не в искривлённом пространстве-времени.

Временные компоненты обобщённого 4-импульса в (41-42) могут быть записаны так:

 

.                      (43)

 

                  (44)

 

 

 

 

 

 

Сравнение (43) и (44) показывает, что в общем случае в искривлённом пространстве-времени контравариантная временная компонента  обобщённого 4-импульса не совпадает с ковариантной временной компонентой . В то же время видно, что произведение  из (39) содержится в (36) как одна из компонент энергии, а обобщённый импульс  (40) является частью импульса системы  в (37). Поскольку  и  являются компонентами обобщённого 4-импульса  в (38), то получается, что и 4-импульс системы, содержащий в своих компонентах энергию  и импульс , должен быть 4-вектором с ковариантным индексом. Таким образом получается, что первичным становится обобщённый 4-импульс в виде , а не в виде , и это же касается 4-импульса системы.

В связи с этим определим компоненты с ковариантным индексом 4-импульса системы аналогично (6) так:

 

,                                            (45)

 

где  есть трёхмерный релятивистский импульс системы, который в декартовых координатах имеет компоненты .

 

В (45) мы полагаем, что энергия  (36) входит во временную компоненту , то есть , в противоположность стандартному определению (1) для , где подразумевается, что .

Компоненты 4-импульса  могут быть связаны с соответствующими компонентами обобщённых 4-импульсов частиц и полей. Для выражения  через эти компоненты необходимо:

1) взять из (13) или из (38) обобщённый 4-импульс и записать его по компонентам с ковариантным индексом в произвольных координатах так: . В декартовых координатах получается , так что , , , где  есть суммарный обобщённый импульс частиц вещества (40).

2) добавить к  ещё один 4-вектор с ковариантным индексом .  В декартовых координатах будет , где  есть трёхмерный импульс, связанный с полями, действующими в системе.

 

В результате получается следующее:

 

,              ,             .                  (46)

 

С учётом (36) и (39) для  в (46) можно тогда записать:

 

(47)

 

 

 

 

 

Для определения вектора  необходимо учесть (37), (40) и (46):

 

.

(48)

 

В частном случае, когда справедлива специальная теория относительности, выражению 4-импульса  (45) можно придать более наглядный смысл. В этом случае импульс системы  будет направлен вдоль скорости  движения центра импульсов системы, а 4-импульс  направлен вдоль 4-скорости  движения центра импульсов системы:

 

.                                (49)

 

В (49)  обозначает энергию системы, вычисленную с помощью (36) в системе центра импульсов ;  есть временная компонента 4-скорости  центра импульсов в системе отсчёта , взятая с ковариантным индексом. Представление в виде (49) возможно потому, что по определению в системе отсчёта  импульс физической системы обнуляется, 4-импульс имеет вид , а лоренцевское преобразование 4-импульса  в произвольную систему отсчёта  приводит к (49).

В (49) были использованы следующие определения 4-радиуса и 4-скорости с ковариантными индексами, справедливые в специальной теории относительности:

 

,        .         (50)

 

Аналогичные выражения с контравариантным индексом имеют следующий вид:

 

,

 

.

(51)

 

В (51) скорость  движения центра импульсов выражена через контравариантные компоненты в виде . Заметим, что выражения (51) рассматриваются как первичные в том смысле, что они справедливы даже в искривлённом пространстве-времени.

Преобразуем 4-скорость (51) центра импульсов системы в выражение с ковариантным индексом с помощью метрического тензора в центре импульсов:

 

.                      (52)

 

Компоненты 4-скорости (52) имеют следующий вид:

 

.

 

.

 

.

 

.

(53)

 

Из (52-53) видно, что даже в случае, когда  и центр импульсов неподвижен в системе отсчёта , пространственные компоненты ,  и  4-скорости  могут быть не равны нулю. Сравнение компонент 4-скорости  (52-53) с компонентами  (51) показывает, что пространственные компоненты  в общем случае изменяются несимметрично по отношению к пространственным компонентам . Это означает, что релятивистский импульс системы  в (45) может быть не направлен вдоль скорости , и тогда равенство в правой части (49) не выполняется.

Из изложенного следует, что 4-импульс  представляется суммой двух интегральных векторов,  (38) с компонентами (39-40), и  (46) с компонентами в (47-48).

 

3.5. Компоненты 4-импульса с контравариантным индексом

Обобщённый 4-импульс с контравариантным индексом можно представить через компоненты так: . Тогда из (41) следуют выражения для  и :

 

              (54)

 

               (55)

 

 

 

 

В (55) индекс  задаёт пространственные компоненты обобщённого 4-импульса с контравариантным индексом. Мы можем подставить в (54) временные компоненты 4-потенциалов полей  ,  ,  и . При этом видно, что лишь в пространстве-времени Минковского, где метрический тензор  имеет постоянные диагональные компоненты  и равные нулю остальные компоненты, временная компонента  (54) становится равной временной компоненте  (39). В этом случае получается, что временная компонента  с точностью до множителя в виде скорости света может входить в энергию  (36), задавая там энергию частиц в скалярных потенциалах полей. В связи с этим и с целью упрощения результатов все последующие рассуждения будут относиться только к пространству-времени Минковского.

Определим 4-вектор с контравариантным индексом . По аналогии с (46), должно быть

 

,              ,             ,                  (56)

 

где индекс .

 

Величина  в (56) совпадает с  (47) как следствие того, что сейчас мы записываем формулы в пространстве-времени Минковского.

Аналогично (1), 4-импульс системы с контравариантным индексом записывается так:

 

.                                          (57)

 

В пространстве-времени Минковского центр импульсов физической системы движется с некоторой постоянной скоростью , входящей в 4-скорость (51). Как в (49) мы снова будем считать, что компоненты импульса системы  в (57) направлены вдоль компонент скорости  движения центра импульсов системы, а 4-импульс  направлен вдоль 4-скорости  движения центра импульсов системы:

 

.                                  (58)

 

В (58)  обозначает энергию системы, вычисленную с помощью (36) в системе центра импульсов ;  есть временная компонента 4-скорости центра импульсов, взятая с контравариантным индексом.

Из (49) и (58) видно , что различные выражения для одной и той же энергии  в виде  и  возможны потому, что только в специальной теории относительности для временных компонент 4-скорости с ковариантным и контравариантным индексами справедливо соотношение: , где  есть фактор Лоренца центра импульсов. При этом 4-импульсы (49) и (58) связываются между собой по формуле: , где  есть метрический тензор пространства-времени Минковского.

Для движущейся материальной точки стандартным выражением для 4-импульса является , где метрический тензор  берётся в месте расположения материальной точки. Очевидно, что для системы с множеством частиц такое локальное выражение 4-импульса  через метрический тензор  в какой-то одной точке оказывается неприемлемым. Для системы частиц вместо  следует использовать выражение  в (56), справедливое в специальной теории относительности. В искривлённом пространстве-времени для определения 4-импульса  с контравариантным индексом требуются дополнительные предположения.

 

3.6. Покоящаяся релятивистская однородная система

Применим полученные выше формулы для вычисления 4-импульса физической системы, являющейся релятивистской однородной системой. С целью упрощения будем производить расчёты в пространстве-времени Минковского, то есть в рамках специальной теории относительности.

Релятивистская однородная система исследовалась в ряде работ [11], [21-22] и достаточно хорошо изучена. Она представляет собой физическую систему сферической формы из заряженных частиц и полей, удерживаемую в равновесии собственным гравитационным полем, которому противостоит действие электромагнитного поля, поля ускорений и поля давления. Все указанные поля рассматриваются как векторные поля, в том числе гравитация представлена в рамках ковариантной теории гравитации [8], [23-25]. Предполагается, что частицы движутся хаотично и глобальные векторные потенциалы , , ,  всех полей в системе центра импульсов  равны нулю. В результате в покоящейся сфере равны нулю и все соленоидальные векторы, такие как магнитное поле и поле кручения (которое называется гравитомагнитное поле в теории гравитоэлектромагнетизма).

Так как векторные потенциалы в  равны нулю, то согласно (40) будет . Что касается временной компоненты обобщённого 4-импульса (39), то в  она была вычислена в [17] в следующем виде:

 

,          (59)

 

где  – фактор Лоренца частиц в центре сферы,  – коэффициент поля ускорений,  – коэффициент поля давления,  – радиус сферы, плотно наполненной частицами,  есть скалярный потенциал поля давления в центре сферы. Масса  есть сумма собственных масс всех частиц системы. Эта масса равна гравитационной массе  системы и находится через фактор Лоренца  частиц, зависящий от текущего радиуса. Масса  определяется по формуле:

 

.

(60)

 

Аналогично вычисляется и полный заряд сферы как сумма собственных зарядов всех частиц, находимых в сопутствующих частицам системах отсчёта:

 

.

(61)

 

Для вычисления в системе центра импульсов  энергии полей , воспользуемся результатами в [24], [26]. Для объёма, занимаемого веществом, получается следующее:

 

 

 

 

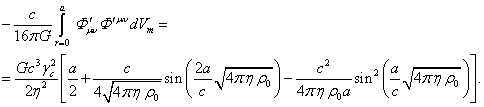
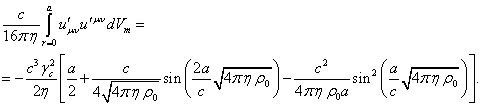
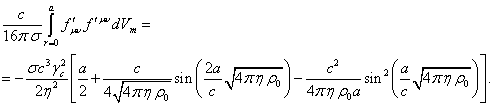
(62)

 

 

 

 

Согласно [15], [21], в рассматриваемой системе выполняется соотношение между коэффициентами полей, вытекающее из уравнения движения частиц:

 

,                                                  (63)

 

где  есть электрическая постоянная.

 

Если просуммировать интегралы от всех тензорных инвариантов в (62) и учесть (63), получится нуль:

 

.

(64)

 

Соотношение (64) соответствует тому, что энергия  в (30) становится равной нулю. Поэтому в рассматриваемой системе поля внутри вещества не будут давать вклад в компоненту  согласно (47).

За пределами вещества имеются только электромагнитное и гравитационное поля, для которых вместо (62) с учётом (61) и (60) можно записать:

 

(65)

 

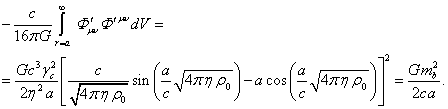
(66)

 

 

 

 

Сумма (64), (65) и (66) даёт интеграл от суммы тензорных инвариантов в (47), с учётом полей внутри и за пределами вещества:

 

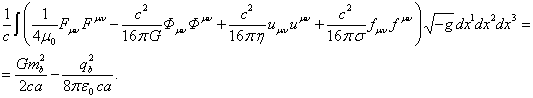
(67)

 

С учётом (67) из (47) находим:

 

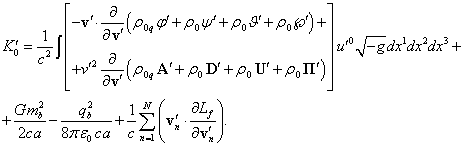
(68)

 

 

 

 

 

 

Все штрихованные величины означают, что данные величины вычисляются в системе центра импульсов , связанной с центром сферы.

В рамках специальной теории относительности глобальные скалярные и векторные потенциалы полей внутри сферы с хаотически движущимися частицами подчиняются уравнениям [16]:

 

,                     ,

 

,              ,

 

,                  ,

 

,                    .                          (69)

 

В неподвижной и не вращающейся сфере в условии равновесия плотность зарядового тока  и плотность массового тока  равны нулю, так как предполагается, что все физические величины не зависят от времени, а направленные потоки заряда и массы, необходимые для возникновения  и , отсутствуют. Как следствие, векторные потенциалы , ,  и  полей в (69) равны нулю. Скалярные потенциалы , ,  и  полей в (69) зависят от квадрата скорости  типичных частиц в точке наблюдения, так как  входит в фактор Лоренца .

 

 

 

В результате в  в пределе непрерывной среды глобальные скалярные потенциалы полей внутри сферы с хаотически движущимися частицами зависят от скорости типичных частиц  с точностью до членов, содержащих в знаменателе квадрат скорости света .

Согласно (28), лагранжиан  зависит от тензоров полей, каждый из которых находится путём вычисления 4-ротора от соответствующего 4-потенциала, содержащего скалярный и векторный потенциалы. Поэтому в системе отсчёта  часть лагранжиана  и соответствующая часть функции Лагранжа  имеют некоторую слабую зависимость от скорости . В (68) требуется найти производные  по скоростям частиц от потенциалов полей, и при вычислении суммы  необходимо найти производные  по скоростям типичных частиц . Это приводит к тому, что временная компонента  (68) приобретает небольшие добавочные члены, содержащие в знаменателе квадрат скорости света. С целью упрощения расчётов, мы не будем рассматривать такие члены, оставляя лишь основные члены.

В результате временная компонента  (68) в  будет приблизительно равна:

 

.                                                   (70)

 

В  должно выполняться соотношение (46) для энергий: . Отсюда с учётом (59) и (70) энергия покоящейся сферы будет равна:

 

.           (71)

 

В соответствии с (71) релятивистская энергия  покоящейся системы выражается через суммарную энергию частиц в потенциалах полей за вычетом энергии гравитационного и электромагнитного полей за пределами вещества.

Поскольку в  равны нулю как полный импульс, , так и обобщённый импульс, , то согласно (46) будет равен нулю и импульс полей: .

Для неподвижной сферы , фактор Лоренца , компонента 4-скорости сферы , и 4-импульс (49) в  запишется так:

 

.                                                (72)

 

3.7. Движущаяся релятивистская однородная система

В [17] было осуществлено преобразование 4-скорости произвольной частицы из  в инерциальную систему отсчёта  с помощью преобразований Лоренца для случая, когда сфера с частицами движется с постоянной скоростью  вдоль оси :

 

          (73)

 

,    ,    ,    .

(74)

 

Величина  обозначает здесь фактор Лоренца частицы в ; ,  и  есть компоненты скорости частицы в ;  есть фактор Лоренца центра импульсов, движущегося вместе с физической системой со скоростью ;  представляет собой фактор Лоренца частицы в системе центра импульсов ; ,  и  являются компонентами скорости частицы в .

В (73) временная компонента 4-скорости частицы равна . Используя это в (38-40), после преобразования из системы отсчёта  в  4-потенциалов полей и последующего усреднения по скоростям  хаотически и разнонаправленно движущихся частиц, в [17] было найдено следующее:

 

.        (75)

 

По сравнению с (59) компонента  (75) увеличилась в  раз за счёт движения физической системы как целое со скоростью . Одновременно с этим выполняется соотношение . Таким образом в  находятся все компоненты обобщённого 4-импульса для сферы с частицами, движущейся с постоянной скоростью  вдоль оси :  .

Теперь нам необходимо вычислить компоненты 4-вектора, связанного с энергией и импульсом полей, как в веществе, так и за его пределами. Согласно (47) временная компонента  находится через потенциалы и тензоры полей, причём для вычисления тензоров полей требуются напряжённости и соленоидальные векторы в .

Имеются два эквивалентных способа определения напряжённостей и соленоидальных векторов в . В первом из них можно взять эти величины в  и затем применить преобразование компонент тензоров из  в . Другой способ подразумевает вначале преобразование 4-потенциалов полей из  в  с помощью преобразований Лоренца, а затем вычисление напряжённостей и соленоидальных векторов в  через эти 4-потенциалы с помощью 4-ротора.

Для наглядности воспользуемся первым способом и найдём компоненты электромагнитного тензора в .

В декартовых координатах даже в искривлённом пространстве-времени для компонент напряжённости электрического поля , индукции магнитного поля  и тензора электромагнитного поля с ковариантными индексами  справедливы соотношения:

 

,                            .                              (76)

 

.                                           (77)

 

 

 

 

 

Тензор электромагнитного поля с контравариантными индексами можно найти, зная компоненты  в (77) и метрический тензор , по формуле:

 

.                                                      (78)

 

В специальной теории относительности метрический тензор  становится равным тензору  следующего вида:

 

.                                                 (79)

 

Подстановка (77) и (79) в (78) даёт выражение тензора :

 

.                                           (80)

 

 

 

 

 

Рассмотрим соотношения (76) в системе отсчёта . Так как в  глобальные векторные потенциалы , ,  и  полей равны нулю, как это следует из (69), вектор напряжённости электрического поля  внутри покоящейся сферы выражается в (76) через скалярный электрический потенциал , найденный в [26], по стандартной формуле для электростатики:

 

(81)

 

В (81)  есть текущий радиус внутри сферы, индекс  означает, что напряжённость  и  скалярный потенциал  относятся к внутреннему полю сферы. Поскольку , то согласно (76) в  магнитное поле везде равно нулю, .

Компоненты антисимметричного электромагнитного тензора  в  в специальной теории относительности выражаются согласно (80) через компоненты векторов  и  следующим образом:

 

.                                       (82)

 

 

 

 

 

,   ,   ,   ,   ,   .

(83)

 

Лоренцевское преобразование компонент тензора из  в  осуществляется по стандартным формулам (§ 24. Преобразование Лоренца для поля, в [2]):

 

,     ,     ,

 

,     ,     .              (84)

 

Подстановка (83) в (84) с учётом соотношений , ,  даёт:

 

,        ,        ,

 

,            ,           .                (85)

 

Согласно (85), за счёт движения сферы с внутренним электрическим полем в ней в системе отсчёта  возникает магнитное поле, хотя в системе отсчёта , связанной со сферой, магнитного поля нет. Это является следствием принципа относительности в отношении компонент электромагнитного поля, когда собственное электрическое поле движущегося объекта порождает дополнительное магнитное поле в другой системе отсчёта, а собственное магнитное поле движущегося объекта порождает дополнительное электрическое поле в другой системе отсчёта. При этом дополнительные поля оказываются пропорциональными скорости  движения объекта.

Вклад в  (47) от тензорного инварианта электромагнитного поля в системе отсчёта  будет таков:

 

.                               (86)

 

В (86) были учтены выражения  (77) и  (80), для которых получается . Индекс  в  и в  в (86) указывает на то, что напряжённость электрического поля  и индукция магнитного поля  берутся внутри движущейся сферы. Магнитная постоянная  и электрическая постоянная  связаны друг с другом и с квадратом скорости света соотношением .

Вычислим величины  и  с помощью компонент  и  (85), и подставим  и  в (86), с учётом выражения для фактора Лоренца :

 

.              (87)

 

В отличие от (62), в (87) интегрирование осуществляется по движущемуся объёму сферы. Как известно, движущаяся сфера в специальной теории относительности рассматривается как эллипсоид Хевисайда. Аналогично [27-28], введём в  новые координаты , связанные с декартовыми координатами:

 

,       ,       .                  (88)

 

Элемент объёма в данных координатах определяется формулой . Уравнение поверхности эллипсоида Хевисайда с учётом (88) будет следующее:

 

,                           .                                 (89)

 

Таким образом, пределы интегрирования по объёму сферы в новых координатах будут следующие: радиус  должен меняться от 0 до , а углы  и  меняются так же, как и в сферических координатах (от 0 до  для угла , и от 0 до  для угла ).

Если в  текущий радиус обозначить через , выразить координаты  через координаты  в  с помощью преобразований Лоренца и использовать (88), получится следующее:

 

.                                              (90)

 

Согласно (90) мы можем вместо  использовать в (81) координату , после чего вектор  можно подставить в (87). Учитывая ещё соотношение  , получим:

 

         (91)

 

 

 

 

 

Подобно этому, можно повторить аналогичные шаги для остальных полей. В напряжённость гравитационного поля внутри сферы, напряжённости поля ускорений и поля давления выражаются через скалярные потенциалы, найденные в [24], [26], [29]:

 

 

 

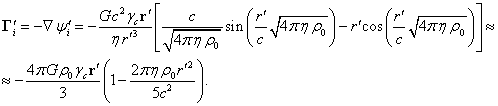
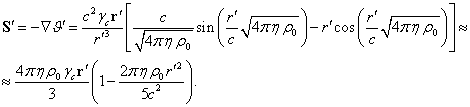
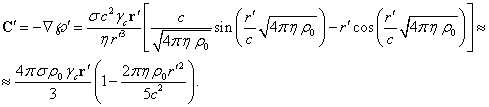
(92)

 

Аналогично (84-85), напряжённости и соленоидальные векторы полей в системе отсчёта  будут равны:

 

,        ,        ,

 

,            ,           .

 

,        ,        ,

 

,            ,           .

 

,        ,        ,

 

,            ,           .

(93)

 

Учитывая (86-91), а также (92-93), результаты интегрирования тензорных инвариантов по движущемуся объёму сферы для трёх оставшихся полей будут таковы:

 

 

 

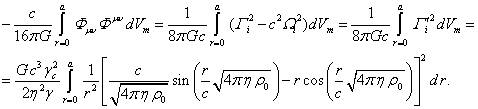
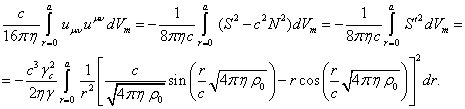
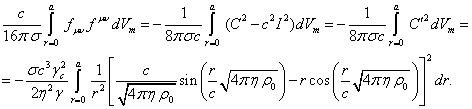
(94)

 

 

 

 

 

Просуммируем члены в (91) и (94), и учтём (63):

 

(95)

 

 

 

 

 

Сумма (95) входит как составная часть в  (47). Таким образом, в веществе внутри движущейся сферы сумма вкладов в  от всех полей обнуляется, как и в случае покоящейся сферы при суммировании интегралов от всех тензорных инвариантов в (64).

Теперь необходимо учесть в  электромагнитное и гравитационное поля за пределами сферы. В системе центра импульсов  имеется как напряжённость внешнего электрического поля, так и напряжённость внешнего гравитационного поля:

 

 

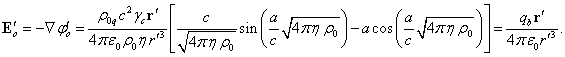
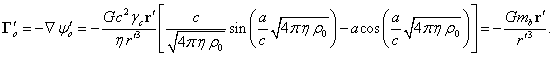
(96)

 

В (96) индекс  показывает, что величина относится к пространству за пределами вещества. В системе отсчёта , в которой сфера движется с постоянной скоростью  вдоль оси , аналогично (85) и (93) появляется магнитное поле , а также поле кручения :

 

,        ,        ,

 

,            ,           .

 

,          ,          ,

 

,             ,            .                 (97)

 

Учитывая соотношения (87-90), а также (97) и соотношение , для интегралов тензорных инвариантов внешних полей движущейся сферы находим:

 

 

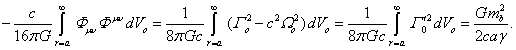
(98)

 

Подставляя (98) в (47) и учитывая (95) для полей внутри сферы, для временной компоненты  в  находим:

 

              (99)

 

 

 

 

 

В рассматриваемой системе , , и применяется приближение непрерывной среды, при этом в системе центра импульсов  в соответствии с (69) векторные потенциалы считаются равными нулю. В то же время скалярные потенциалы полей в месте расположения какой-либо частицы слабо зависят от скорости  этой частицы, и определяются с точностью до членов, содержащих в знаменателе квадрат скорости света. Ситуация не изменяется и в системе отсчёта  – хотя потенциалы приобретают зависимость от скорости  движения сферы, но они по-прежнему слабо зависят от компонент скорости  частиц, представленной в (74). Пренебрегая малыми членами, находим приблизительное выражение для  (99):

 

.                                  (100)

 

Представим  в виде . Внутри сферы с учётом (2) и (28) и условия калибровки энергии и метрики [11], [20] в виде  будет:

 

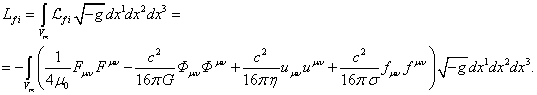
(101)

 

Если учесть (95), то внутри движущейся сферы получается , так  что в этом случае  (101) не делает вклада в  в (100). С учётом (98) найдём  в пространстве за пределами сферы, где имеются только электромагнитное и гравитационное поля:

 

.          (102)

 

В (102) присутствует фактор Лоренца ,

 

 

являющийся функцией скорости  движения сферы вдоль оси  системы отсчёта . Согласно (74), скорость частиц в  равна:

 

.                  (103)

 

Если усреднить скорости  соседних частиц, направленные по всем направлениям, в (103) получится . Это можно пояснить следующими выкладками:

 

            (104)

 

 

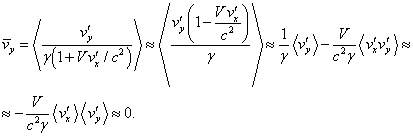
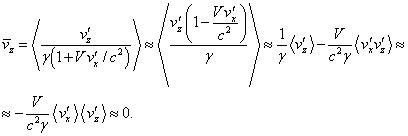
(105)

 

В (104) предполагается, что после усреднения по всем направлениям , и что малым членом  можно пренебречь. В (105) аналогично предполагается, что средние значения  и , и можно пренебречь малыми членами, содержащими в знаменателе квадрат скорости света.

Так как , , в (100) необходимо вычислить сумму , в том числе производную  по скоростям частиц . Однако  является результатом усреднения по скоростям отдельных частиц, и в первом приближении зависит только от . Поля за пределами сферы выглядят так, как будто они создаются одним телом без внутреннего движения частиц, причём это тело движется со скоростью  и имеет массу и заряд, равные сумме масс и зарядов отдельных частиц системы. Это позволяет заменить данную сумму на её среднее значение с заменой  на :

 

.                                  (106)

 

Чтобы лучше понять (106), можно рассмотреть электромагнитное поле за пределами движущейся сферы с радиусом , равномерно и симметрично заполненной большим количеством  заряженных частиц, каждая из которых имеет заряд . Ввиду симметрии с учётом теоремы Гаусса, поле за пределами сферы будет таким же, как если бы все заряды сферы были бы помещены в центр сферы и там был бы заряд . Так сфера с множеством  зарядов в отношении поля за пределами сферы становится эквивалентной одному заряду , который имеет радиус точечный частицы, много меньший, чем радиус , В этом случае можно считать, что сумма в (106) содержит только один член для одной частицы с зарядом , причём  является функцией Лагранжа для точечной заряженной частицы, движущейся со скоростью . Поле такой частицы с зарядом  эквивалентно полю движущейся сферы, что позволяет в (106) заменить сумму членов на один член.

Подставляя в (106)  из (102), с учётом выражения фактора Лоренца  находим:

 

.

 

.                  (107)

 

Сумма (107) присутствует в (100), что позволяет уточнить вид :

 

.                                               (108)

 

С учётом (75) и (108), которые надо подставить в (46), энергия движущейся сферы будет равна:

 

(109)

 

Из сравнения (109) с (71) для случая покоящейся сферы видно, что у движущейся сферы энергия увеличивается в  раз.

Используем теперь (48) для вычисления вектора , снова считая, что в рассматриваемой системе плотность заряда, плотность массы и потенциалы полей внутри движущейся сферы в первом приближении не зависят от скоростей отдельных частиц в точке интегрирования. Тогда в (48) интеграл обнуляется и остаётся следующее:

 

.                                                       (110)

 

В (110) , причём из (95) следует, что внутри сферы  в (101) равна нулю. Рассматривая среднее значение от суммы (110), учитывая выражение для скорости  и значение  (102) с учётом выражения  , находим:

 

,

 

,           ,           .                    (111)

 

Сравнение (108) и (111) даёт соотношения:

 

,       .          (112)

 

В (75) была представлена компонента  , позволяющая определить компоненту  для обобщённого 4-импульса  движущейся сферы:

 

,       .          (113)

 

Соотношения (112) для  имеют тот же вид, что и соотношения для  в (113).

Складывая векторы  и , согласно (46) находим импульс системы:

 

.   (114)

 

Согласно способу своего вычисления в (13), обобщённый 4-импульс  (113) представляет собой не локальный 4-вектор интегрального типа с ковариантным индексом, связанный с взаимодействием частиц друг с другом и с полями. Не локальность  является следствием его определения через интеграл по объёму, занимаемом всеми типичными частицами системы. Такими же свойствами обладает и 4-вектор  (112), задающим 4-импульс полей системы. Сумма 4-векторов  и  в (46) даёт полный 4-импульс физической системы  с ковариантным индексом.

 

3.8. Интегральный вектор внутри движущейся сферы

В [7] мы вычисляли интегральный вектор  (9) для неподвижной сферы в рамках специальной теории относительности. Определим теперь этот вектор для случая движения сферы с частицами с постоянной скоростью  вдоль оси  в системе отсчёта . Тензор энергии-импульса физической системы состоит из суммы тензоров энергии-импульса электромагнитного и гравитационного полей, поля ускорений и поля давления. С учётом используемой нами сигнатуры метрики  можно записать:

 

.                                            (115)

 

,

 

,

 

,

 

.                              (116)

 

Выражение тензора энергии-импульса физической системы  (115) следует из принципа наименьшего действия [11], при этом тензор  входит в уравнение для вычисления метрического тензора . В (116) , ,  и  есть соответственно тензоры энергии-импульса электромагнитного и гравитационного полей, поля ускорений и поля давления. При этом  выражается через тензор электромагнитного поля , тензор  выражается через тензор гравитационного поля , тензор  выражается через тензор поля ускорений , а тензор  выражается через тензор поля давления . В (116)  есть скорость света,  есть электрическая постоянная,  есть гравитационная постоянная,  и  есть постоянные поля ускорений и поля давления, соответственно.

Рассмотрим ситуацию вначале внутри сферы, то есть в её непрерывно распределённом веществе. Вычислим компоненты , ,  и  тензоров энергии-импульса полей, и учтём, что в пространстве-времени Минковского метрический тензор  переходит в метрический тензор  (79), который не зависит от времени и координат.

В декартовых координатах временные компоненты тензора энергии-импульса электромагнитного поля в (116) могут быть записаны через напряжённость электрического поля  и индукцию магнитного поля :

 

,                      ,

 

,                     .                      (117)

 

В (117) вектор  представляет собой векторное произведение векторов  и ;  обозначает проекцию вектора  на ось  декартовой системы координат. Аналогично этому,  есть проекция вектора  на ось , а  есть проекция вектора  на ось  декартовой системы координат.

Если учесть определение вектора Пойнтинга в виде  и соотношение , то (117) можно представить в стандартном виде так:

 

,        ,        ,        .

(118)

 

Подстановка компонент  и  (85) в (117) с учётом (81) и соотношения  даёт внутри движущейся сферы:

 

 

 

 

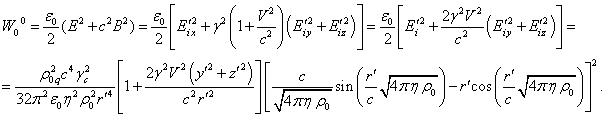
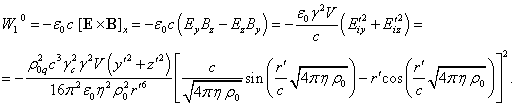
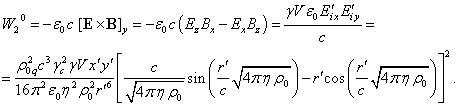
          (119)

 

 

 

 

 

Аналогично (117), временные компоненты тензоров энергии-импульса гравитационного поля, поля ускорений и поля давления в (116) могут быть записаны через напряжённости и соленоидальные векторы соответствующего поля [11]:

 

,                      ,

 

,                     .

 

,                      ,

 

,                     .

 

,                      ,

 

,                     .                       (120)

 

В (120)  и  есть напряжённость и поле кручения гравитационного поля;  и  есть напряжённость и соленоидальный вектор поля ускорений;  и  есть напряжённость и соленоидальный вектор поля давления.

Подставим (93) в (120) и учтём (92):

 

 

 

 

 

 

 

 

 

 

 

 

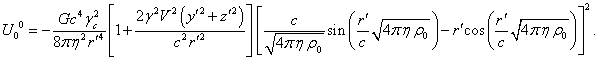
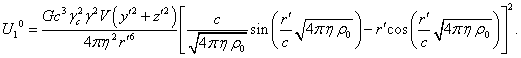
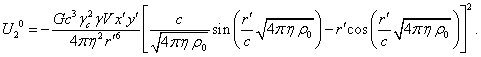
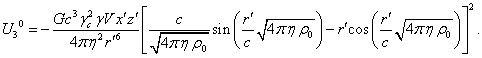
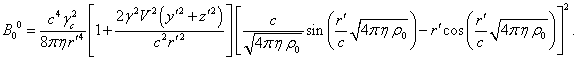
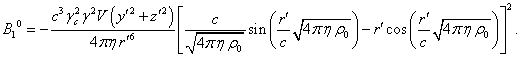
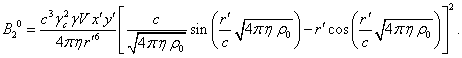
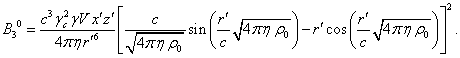
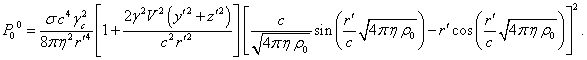
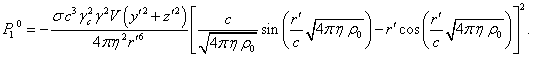
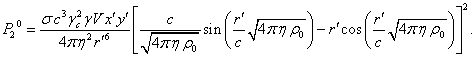
        (121)

 

Если подставить (119) и (121) в (115) и найти временные компоненты суммарного тензора энергии-импульса , то путём интегрирования  по объёму движущейся сферы согласно (9) можно найти компоненты интегрального вектора  внутри сферы:

 

 

 

 

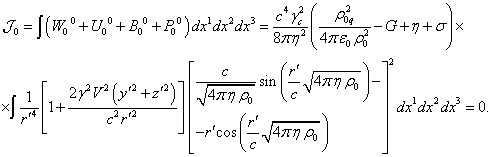
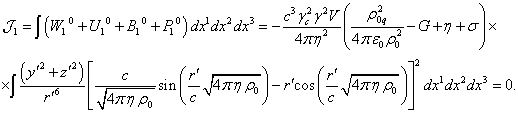
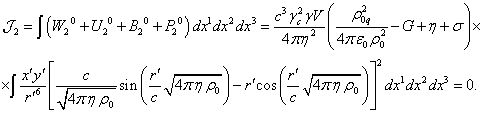
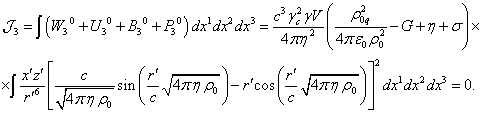
(122)

 

 

 

 

 

Перед каждым интегралом в (122) в соответствующей скобке находится сумма, которая согласно (63) равна нулю: . Это равенство, содержащее коэффициенты полей, было найдено в [15], [21], как следствие баланса сил от всех полей, действующих на типичные частицы.

Таким образом, внутри движущейся сферы интегральный вектор обнуляется, .

 

3.9. Интегральный вектор за пределами движущейся сферы

Для вычисления полного интегрального вектора  необходимо интегрировать  по всему объёму, как внутри, так и снаружи сферы. Поскольку поле ускорений и поле давления присутствуют только в веществе, за пределами сферы остаются только электромагнитное и гравитационное поля. Найдём временные компоненты тензоров энергии-импульса этих полей, учитывая (117), (120), (96-97):

 

 

 

.

 

.

 

,            ,

 

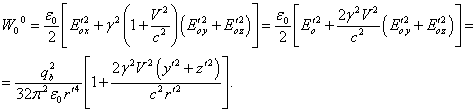
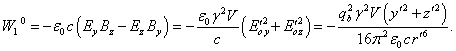
,                    .                        (123)

 

Подставим в (115)  и  из (123), найдём , а затем компоненту  в (9):

 

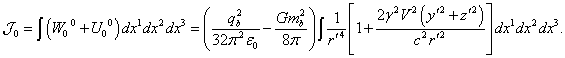
(124)

 

Интеграл в (124) берётся по объёму за пределами движущейся сферы, причём сфера рассматривается как эллипсоид Хевисайда. Согласно (90) мы считаем, что , где  есть текущий радиус в системе отсчёта , связанной с центром сферы, а  является радиальной координатой в (88). Из преобразований Лоренца при движении сферы с постоянной скоростью  вдоль оси  в системе отсчёта  следует, что , , . Тогда с учётом (88) имеем:

 

,    ,    ,    .        (125)

 

Как и в (91) элемент объёма будет равен . Используя всё это в (124), находим:

 

            (126)

 

 

 

 

Для пространственных компонент интегрального вектора  в (9) с помощью (123) и (125) аналогичным путём находим:

 

 

 

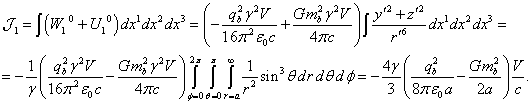
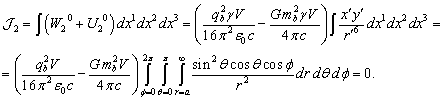
              (127)

 

 

 

 

 

4. Обсуждение результатов

В (122) мы нашли, что в веществе внутри сферы все компоненты интегрального вектора  обнуляются. Поэтому нам достаточно рассмотреть только компоненты интегрального вектора за пределами вещества.

Согласно (111-112) и (127) имеем:

 

.                                (128)

 

Сравнение (108) и (126) даёт:

 

.                                                 (129)

 

Из (128) следует, что пространственная компонента  интегрального вектора  пропорциональна пространственной компоненте  4-вектора , определяющего вклад полей в энергию-импульс рассматриваемой системы. Согласно (112), для компонент 4-вектора  выполняется соотношение . Однако для компонент интегрального вектора согласно (126-127) получается другое соотношение:

 

.                                         (130)

 

Из (130) следует, что компонента  сложным образом зависит от скорости  движения сферы. Даже в пределе малых скоростей в (130) получается не равный единице коэффициент , в отличие от соотношения для компонент 4-вектора  , где аналогичный коэффициент равен 1. Таким образом, интегральный вектор  не является 4-вектором, и значит, интегральный вектор не может задавать ни 4-импульс системы, ни 4-импульс полей.

Это же самое можно сказать другими словами. Согласно (9) интегральный вектор получается интегрированием по объёму временных компонент  суммарного тензора энергии-импульса системы. Значит, знания тензора энергии-импульса системы оказывается недостаточно для вычисления 4-импульса.

С другой стороны, коэффициент 4/3 в (130) связан с так называемой проблемой 4/3, согласно которой масса-энергия, содержащаяся в , оказывается приблизительно в 4/3 больше массы-энергии, содержащейся в компоненте . Очевидно, что такое поведение массы-энергий не согласуется с ролью массы в 4-импульсе одиночной точечной частицы, где масса в одинаковой степени входит и в энергию, и в импульс.

В таком случае, что же представляет собой интегральный вектор ? По своему смыслу он является интегралом по объёму от уравнения движения, и в [15] было показано, что компоненты тензора энергии-импульса  соответствуют обобщённой теореме Пойнтинга, согласно которой изменение энергии полей в любом заданном объёме точно компенсируется потоком энергии полей через поверхность, окружающую данный объём. Если же пытаться найти с помощью  интегральный вектор , то он оказывается не равным ни 4-импульсу системы , ни 4-вектору.

Тем не менее, в замкнутой системе, движущейся с постоянной скоростью, интегральный вектор  сохраняется. Это видно из (129-130), так как сохраняется величина  (108), пропорциональная той энергии полей, которая вычисляется с помощью тензорных инвариантов.

 

5. Заключение

Вместо 4-импульса  с контравариантным индексом (1) мы исходим из определения 4-импульса  с ковариантным индексом в (45). Переход между этими формами 4-импульса в виде ,  с участием метрического тензора  оказывается возможным лишь в специальной теории относительности. В более общем случае, в искривлённом пространстве-времени, для определения  требуются дополнительные предположения.

Основной причиной первичного определения 4-импульса  как 4-вектора с ковариантным индексом является необходимость учёта в  вклада от частиц в виде обобщённого 4-импульса , а также вклада от полей, имеющихся в системе, посредством 4-вектора . В результате получается соотношение , где  выражается ковариантным образом через лагранжиан в (13) и (38).

Для лагранжиана (27), в котором представлены четыре векторных поля, в (36) и в (37) определяются энергия и импульс системы, а компоненты  задаются в (47) и в (48). Как следствие, наш 4-импульс  (46) не совпадает ни с одним из выражений (1-9), представленных в литературе для характеристики 4-импульса.

При четырёхмерном варьировании функции действия мы получили в (25-26) ковариантное выражение для функции , которая в замкнутой системе сохраняется и для лагранжиана (27) задаёт энергию (30) полей в веществе, связанную с тензорными инвариантами. Из (62-64) следует, что энергия  в объёме, занятом веществом, становится равной нулю, и это же получается из (95) в веществе внутри движущейся сферы. Согласно (30) и (101), , где  обозначает ту часть функции Лагранжа, которая связана с тензорными инвариантами в веществе.

Из сравнения (38) и (41) вытекает, что обобщённые 4-импульсы  и , имеющие интегральную форму, отличаются от стандартных 4-векторов своей не локальностью и для них выражения типа  будут неверны. Это же справедливо и для 4-векторов  и . В специальной теории относительности 4-импульс  выражается согласно (49) через 4-скорость  центра импульсов системы. Именно благодаря использованию четырёхмерного лагранжева формализма и не локальности  становится видно, что 4-импульс должен задаваться как ковариантный 4-вектор .

С целью применения полученных формул для 4-векторов компоненты этих 4-векторов были вычислены для релятивистской однородной системы в виде сферы с частицами и полями в рамках специальной теории относительности. Для неподвижной сферы трёхмерный релятивистский импульс равен нулю, а энергия системы задаётся в (71). При этом энергия полей внутри вещества обнуляется, и энергия системы состоит из энергии частиц в скалярных потенциалах полей с учётом вклада от энергии полей за пределами вещества.

Для движущейся сферы из сравнения (59) и (75) следует, что за счёт движения временная компонента  обобщённого 4-импульса увеличивается в  раз,  где  обозначает фактор Лоренца центра импульсов движущейся сферы. Согласно (70) и (108), то же самое получается для временной компоненты , связанной с энергией от тензорных инвариантов полей. Указанные изменения в  и  хорошо видны в формуле для энергии системы (109), которую можно сравнить с (71) для неподвижной сферы.

Кроме 4-векторов ,  и , мы вычислили также компоненты интегрального вектора  (9). Согласно (122), внутри движущейся сферы интегральный вектор обнуляется, так что в рассматриваемом случае достаточно вычислить его компоненты за пределами сферы. Если сравнивать соотношения для  в (112) и для  в (113) с соотношением для  в (130), то видно, что  не является настоящим 4-вектором.

Полученные результаты можно подытожить следующим образом: для непрерывно распределённого вещества с целью уникального определения 4-импульса его следует определять как сумму двух не локальных 4-векторов интегрального типа, то есть как 4-вектор с ковариантным индексом в виде , с учётом вкладов энергии и импульса всех частиц и полей системы.

Что касается интегрального вектора , получаемого путём интегрирования по объёму временных компонент тензора энергии-импульса системы, то такой вектор не является 4-вектором и 4-импульсом, хотя и сохраняется в замкнутой системе.

Другой вывод, вытекающий из лагранжева формализма для векторных полей, касается того, что наиболее естественным представлением некоторых физически значащих 4-векторов является их форма с ковариантным индексом. К таким 4-векторам мы относим обобщённый 4-импульс (four-momentum) , релятивистский 4-импульс , 4-импульс  полей, 4-силу (four-force) , 4-потенциалы  электромагнитного и гравитационного полей, поля ускорений и поля давления, соответственно.

Следствием того, что 4-потенциалы полей определяются как 4-векторы с ковариантным индексом, является то, что и тензоры полей выражаются наиболее просто как тензоры с ковариантными индексами. Примером здесь является тензор электромагнитного поля , вычисляемый с помощью четырёхмерного ротора от 4-потенциала  по формуле: .

То, что 4-импульс  физической системы удаётся определить в ковариантном виде через сумму двух нелокальных 4-векторов  и , существенно изменяет наше понимание энергии и импульса системы. В отличие от случаев одной точечной частицы или множества невзаимодействующих точечных частиц, в системах с непрерывным распределением вещества происходит активный обмен энергией и импульсом у всех взаимодействующих частиц и полей. Кроме этого, даже в стационарных системах метрический тензор, присутствующий в формулах, является функцией времени и координат. Всё это и приводит к нелокальности 4-векторов  и . В дополнение к обобщённому 4-импульсу , связанному с частицами системы, при определении  необходимо учесть ещё 4-импульс , связанный с полями системы.

Другой особенностью рассмотренного подхода является то, что при учёте метрики необходимой является процедура калибровки энергии [11], [20], благодаря чему выражения для энергии и импульса системы перестают зависеть от космологической постоянной  и становятся однозначно определёнными в ковариантном виде.

С практической точки зрения, выведенные формулы для релятивистского 4-импульса  позволяют находить энергию и импульс любой физической системы. Особенно это актуально в системах, в которых значительна роль полей, действующих на частицы, либо когда необходимо изучить эффекты, связанные с энергией и импульсом самих полей.

Полученные результаты показывают также, что ни интегральный вектор  (9), компоненты которого были вычислены в (126-127), ни интегральный вектор  (8), предлагаемый в общей теории относительности [2], не могут рассматриваться как 4-импульс физической системы. Действительно, для вычисления  и  требуется знать временные компоненты тензора энергии-импульса с учётом всех полей системы, включая гравитационное поле. Однако временные компоненты тензора энергии-импульса системы по определению включают в себя плотности энергии всех полей и потоки энергии этих полей. После интегрирования временных компонент тензора энергии-импульса по движущемуся объёму появляются соответствующие компоненты интегральных векторов  и , которые пропорциональны энергии и импульсу полей.

Хотя в замкнутой системе компоненты  и  сохранятся, они имеют отношение не к 4-ипульсу физической системы, а к четырёхмерной теореме Пойнтинга, как это было показано в [15] в отношении . Согласно теореме Пойнтинга, в каждом объёме системы убыль энергии связывается с соответствующим потоком энергии из этого объёма. Компоненты  точно удовлетворяют теореме Пойнтинга, но не образуют 4-вектор. Вместо этого в соответствии с (130) для компонент  возникает так называемая проблема 4/3, так что в каждом даже малом объёме системы масса-энергия в этом объёме приблизительно в 4/3 раз отличается от массы энергии, содержащейся в импульсе поля в этом объёме.

Из изложенного следует, что для вычисления 4-импульса физической системы требуется знать не тензор энергии -импульса системы, а 4-потенциалы и тензоры всех полей, действующих в системе.

 

Приложение A.

Вопрос.1. Является ли в представленном подходе 4-импульс физической системы достаточно общим, чтобы описать 4-импульс для тороидальной геометрической топологии (или другой топологии) четырехмерного пространства)?

В ответе на этот вопрос мы используем двойную нумерацию формул, в которой последние цифры обозначают номер формулы в тексте статьи.

 

Релятивистский 4-импульс некоторой физической системы, расположенной в четырехмерном пространстве-времени с произвольной геометрией и топологией, может быть определен в ковариантной форме по формуле

 

.                      (1-45)

 

где энергия  системы выражается формулой

 

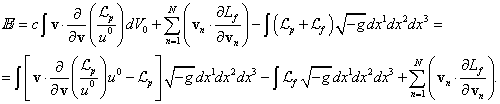
(2-31)

 

В (2-31) энергия  определяется по формуле, в которой лагранжиан  системы определяется суммой двух слагаемых, причем слагаемое  напрямую зависит от 4-токов  и , а значит, зависит от скорости частицы .

Используя для компонент лагранжиана выражения, соответствующие векторным полям, в виде

 

,                                            (3-27)

 

(4-28)

 

можно упростить выражение (2-31) для энергии системы:

 

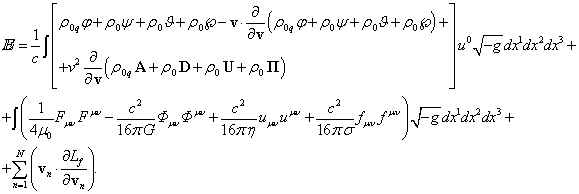
(5-36)

 

 

 

 

 

Импульс  системы в (1-45) выражается формулой

 

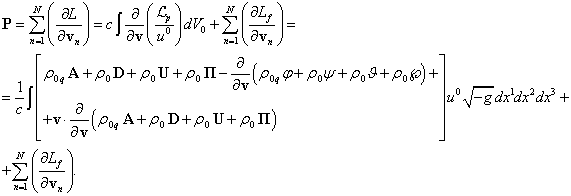
(6-37)

 

 

 

 

При этом в (6-37) учитываются выражения (3-27) и (4-28).

Второй метод расчета релятивистского 4-импульса произвольной физической системы предполагает расщепление  на два нелокальных 4-вектора:

 

.                                                      (7-46)

 

Для вычисления обобщенного 4-импульса  в (7-46) необходимо при заданных начальных условиях определить зависимость метрического тензора  и его определителя  от времени и координат, а также найти временную компоненту  4-скорости  частиц системы. Кроме того, необходимо знать выражение лагранжиана  системы, чтобы можно было вычислить производные , а затем определить  путём интегрирования по движущемуся объему системы:

 

.              (8-13)

 

Используя  (3-27), для  и его компонент имеем:

 

.                      (9-38)

 

.                        (10-39)

 

.                          (11-40)

 

Компоненты 4-вектора

 

 

в (7-46) с использованием (3-27) и (4-28) выражаются формулами:

 

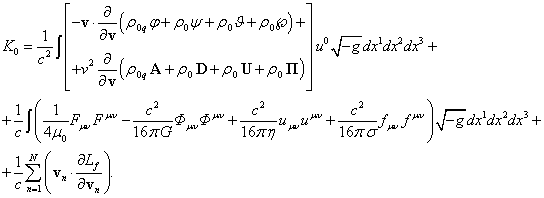
(12-47)

 

.       (13-48)

 

 

 

 

 

Оба из представленных выше методов определения релятивистского 4-импульса  предполагают, что сначала решаются уравнения для каждого поля, действующего в системе, а также находятся решения уравнения для метрики и уравнения движения частиц материи. После этого становится возможным определить компоненты 4-токов, метрического тензора, 4-потенциалов и тензоров поля, необходимые для нахождения .

 

Приложение B. Соотношения (119-122)

Далее мы используем двойную нумерацию формул, в которой последние цифры обозначают номер формулы в тексте статьи.

 

Рассмотрим тензор энергии-импульса электромагнитного поля со смешанными индексами:

 

.                        (1-116)

 

Временные компоненты тензора  (1-116) выражаются через напряжённость электрического поля  и индукцию магнитного поля  в декартовых координатах следующим образом:

 

,                      ,

 

,                     .                      (2-117)

 

Внутри движущейся сферы в системе отсчёта  компоненты  и  определяются выражениями

 

,        ,        ,

 

,            ,           .                (3-85)

 

В системе отсчёта , связанной с центром сферы, внутри сферы имеется напряжённость электрического поля , а магнитное поле  равно нулю ввиду отсутствия внутренних токов.  Выражения (3-85) получаются путём преобразования тензора электромагнитного поля, содержащего компоненты  и , из системы отсчёта  в систему отсчёта  с помощью преобразований Лоренца.

Электрическое поле  внутри сферы с заряженными частицами, являющейся релятивистской однородной системой, выражается формулой:

 

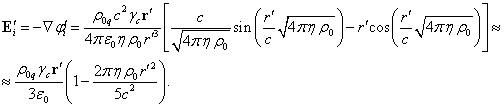
(4-81)

 

Подстановка компонент  из (4-81) в (3-85) с учётом того, что в (4-81) радиус-вектор есть , даёт следующее:

 

.

 

.

 

.

 

,       .

 

.              (5)

 

Учитывая компоненты полей (5), находим:

 

 

 

 

 

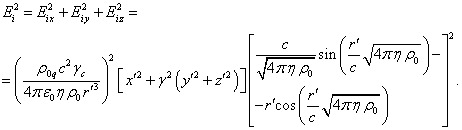
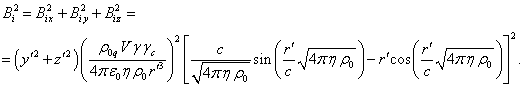
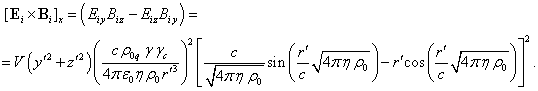
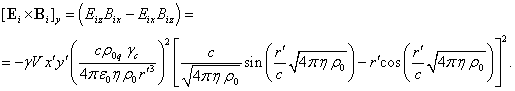
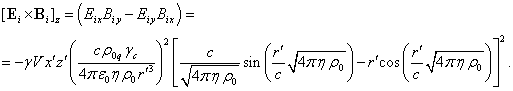
(6)

 

Подставляя в (2-117)  вместо  и  вместо , с учётом (6) и соотношения , находим:

 

 

,

 

.

 

.

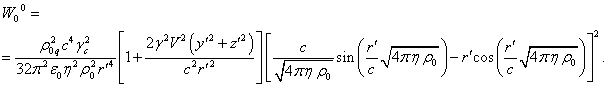
(7-119)

 

Из принципа наименьшего действия следуют уравнения электромагнитного и гравитационного полей, поля ускорений и поля давления. Все эти уравнения имеют одну и ту же форму, аналогичную уравнениям Максвелла. Это является следствием того, что данные поля являются векторными и имеют одинаковое представление через 4-потенциалы и тензоры этих полей, В результате выражения для тензоров полей, а также для тензоров энергии-импульса для электромагнитного поля , для гравитационного поля , поля ускорений  и поля давления  оказываются подобными друг другу и имеют одинаковую зависимость от времени и координат. Чтобы получить временные компоненты тензора энергии-импульса гравитационного поля , достаточно в (7-119) сделать замену плотности заряда  на плотность массы , а электрическую постоянную  заменить на , как это видно в (116):

 

 

,

 

.

 

.

 

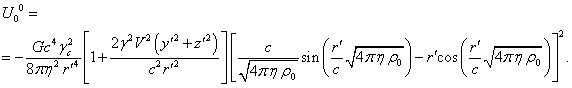
(8)

 

Точно также можно найти временные компоненты тензоров энергии-импульса поля ускорений  и поля давления , путём замены в (7-119) плотности заряда  на плотность массы , и замены электрической постоянной  соответственно на  и на :

 

 

,

 

.

 

.

 

 

,

 

.

 

.

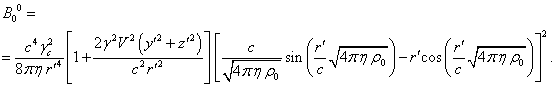
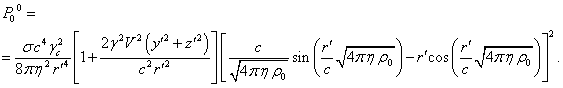
(9)

 

Тензоры энергии-импульса в (8-9) соответствуют выражениям тензоров энергии-импульса в (121).

Тензор энергии-импульса физической системы получается суммированием тензоров энергии-импульса всех полей:

 

.                                      (10-115)

 

Подстановка (7-119), (8) и (9) в (10-115) даёт возможность найти временные компоненты тензора энергии-импульса :

 

 

 

 

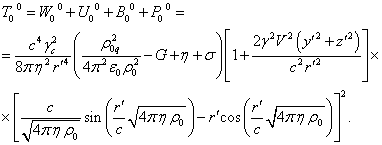
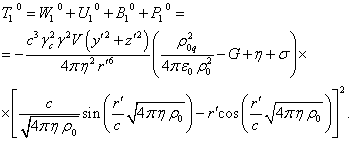
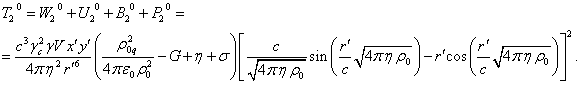
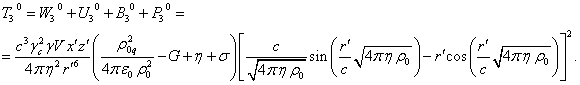
(11)

 

Уравнение движения частиц вещества под действием полей получается из принципа наименьшего действия. В случае релятивистской однородной системы из уравнения движения следует соотношение для коэффициентов полей:

 

.                                             (12-63)

 

Если подставить (12-63) в (11), становится видно, что в веществе движущейся сферы, представляющей собой релятивистскую однородную систему, временные компоненты , ,  и  тензора энергии-импульса рассматриваемой системы оказываются равными нулю.

Интегральный вектор определяется выражением:

 

,                                                       (13-9)

 

где индекс .

 

Поскольку все временные компоненты  в веществе внутри сферы равны нулю согласно (11) и (12-63), то и компоненты интегрального вектора  в (13-9) обращаются в нуль.

 

Приложение C. Список обозначений

  –  4-потенциал электромагнитного поля

  –   векторный потенциал электромагнитного поля

  –  радиус сферы

  –  индукция магнитного поля

  –  тензор энергии импульса поля ускорений со смешанными индексами

  –  напряжённость поля давления

  –  скорость света

  –  элемент объёма в виде произведения дифференциалов пространственных координат

  –  4-потенциал гравитационного поля в рамках ковариантной теории гравитации

  –  векторный потенциал гравитационного поля

  –  напряжённость электрического поля

  –  энергия системы

  –  энергия системы в системе отсчёта

  –  электрическая константа

  –  4-сила

  –  плотность -4-силы, действующей на единичный элемент объёма, в котором находится типичная частица с номером

  –  тензор электромагнитного поля

  –  тензор гравитационного поля

  –  тенор поля давления

  –  скалярный потенциал электромагнитного поля

  –  одна из угловых координат сферической системы координат

  –  гравитационная константа

 или   –  метрический тензор

  –  детерминант метрического тензора

  –  метрический тензор пространства-времени Минковского

  – постоянная поля ускорений

  –  напряжённость гравитационного поля

  обозначает фактор Лоренца центра импульсов движущейся сферы

  –  фактор Лоренца частиц в системе отсчёта

  –  фактор Лоренца частиц в центре сферы в системе отсчёта

 обозначает фактор Лоренца частиц в системе отсчёта

  –  соленоидальный вектор поля давления

  –  интегральный вектор в общей теории относительности

  –  интегральный вектор в ковариантной теории гравитации

  –  вспомогательная четырёхмерная величина

  –  зарядовый 4-ток

  –  массовый 4-ток

  –  плотность массового тока в системе отсчёта

  –  плотность зарядового тока в системе отсчёта

 или   –  4-импульс полей

  –  временная компонента 4-импульса поля , связанная с энергией в тензорных инвариантах полей

  –  импульс полей

  –  функция Лагранжа

 есть часть функции Лагранжа , связанная с тензорными инвариантами

 обозначает ту часть функции Лагранжа, которая связана с тензорными инвариантами в веществе

 обозначает ту часть функции Лагранжа, которая связана с тензорными инвариантами за пределами вещества

 есть часть функции Лагранжа , которая содержит массовый 4-ток  и зарядовый 4-ток

  –  функция Лагранжа в веществе

  –  Лагранжиан

 есть часть Лагранжиана , которая содержит тензорные инварианты

 есть часть Лагранжиана , которая массовый 4-ток  и зарядовый 4-ток

  –  Лагранжиан в веществе

  –  космологическая постоянная

  –  суммарная масса частиц релятивистской однородной системы

  –  гравитационная масса релятивистской однородной системы

  –  магнитная постоянная

  –  число частиц физической системы

  –  соленоидальный вектор поля ускорений

  –  текущий номер частицы или элемента объёма

  –  система отсчёта координатного наблюдателя

  –  система отсчёта, связанная с центром моментов движущейся сферы

  –  вектор поля кручения гравитационного поля

  –  трёхмерный релятивистский импульс системы

  –  трёхмерный импульс одной частицы или элемента объёма

  –  релятивистский импульс частиц

 or   –  4-импульс системы

  –  тензор энергии импульса поля давления со смешанными индексами

  –  4-потенциал поля давления

  –  плотность обобщённого 4-импульса

 или   –  обобщённый 4-импульс

  –  временная компонента обобщённого 4-импульса

  –  обобщённый импульс

  –  векторный потенциал поля давления

  –  заряд частицы

  –  суммарный заряд релятивистской однородной системы

  –  заряд движущейся сферы с частицами

  –  одна из угловых координат сферической системы координат

  –  скалярный потенциал поля ускорений

  –  скалярная кривизна

  –  трёхмерный вектор положения

  –  радиальная координата сферической системы координат

  –  текущий радиус внутри сферы

  –  инвариантная плотность массы частицы

  –  инвариантная плотность заряда частицы

  –  скалярный потенциал поля давления

  –  скалярный потенциал поля давления в центре сферы в системе отсчёта

  –  функция действия

  –  напряжённость поля ускорений

  –  вектор Пойнтинга

  –  постоянная поля давления

  –  coordinate time

  –  proper time

  –  тензор энергии импульса

  –   псевдотензор гравитационного поля

  – временная компонента тензора энергии-импульса

  –  временная компонента псевдотензора гравитационного поля

  –  векторный потенциал поля ускорений

  –  4-потенциал поля ускорений

  –  тензор энергии импульса гравитационного поля со смешанными индексами

 или   –   4-скорость

  – временная компонента 4-скорости частицы с номером

  –  тензор поля ускорений

  –  дифференциал элемента объёма в сопутствующей системе отсчёта

  –  объём, занимаемый веществом

  –  скорость движения центра импульсов системы

  –  скорость частицы или элемента вещества в системе отсчёта

  –  скорость частицы вещества с текущим номером

  –  скорость типичной частицы в системе отсчёта

  –  тензор энергии импульса электромагнитного поля со смешанными индексами

 или   –  4-положение

  –  скалярный потенциал гравитационного поля

  –  суммарная энергия поля в веществе, связанная с тензорными инвариантами

  –  декартовые координаты в системе отсчёта

  –  декартовые координаты в системе отсчёта

 

Список использованных источников

1.      Ландау Л.Д., Лифшиц Е.М. Механика. Издание 4-е, исправленное. М.: Наука, 1988. 215 с. («Теоретическая физика», том I). ISBN 5-02-013850-9. Landau L.D., Lifshitz E.M. (1976). Mechanics. Vol. 1 (3rd ed.). Butterworth-Heinemann. ISBN 978-0-7506-2896-9.

2.      Landau L.D., Lifshitz E.M. The Classical Theory of Fields, (1951). Pergamon Press. ISBN 7-5062-4256-7.

3.      Goldstein H., Poole C.P. and Safko J.L. Classical Mechanics (3rd ed.). Addison-Wesley. p. 680. ISBN 9780201657029. (2001).

4.      M. Sharif, Tasnim Fatima. Energy-Momentum Distribution: A Crucial Problem in General Relativity. Int. J. Mod. Phys. A, Vol. 20, p. 4309 (2005). https://doi.org/10.1142/S0217751X05020793.

5.      Денисов, В. И.; Логунов А. А. Инертная масса, определенная в общей теории относительности, не имеет физического смысла. ТМФ, 1982, том 51, номер 2, 163-170; Denisov V. I., Logunov A. A. The inertial mass defined in the general theory of relativity has no physical meaning. Theoretical and Mathematical Physics, Volume 51, Issue 2, pp. 421-426 (1982). http://dx.doi.org/10.1007/BF01036205.

6.      Денисов, В. И.; Логунов А. А. Имеет ли общая теория относительности классический ньютоновский предел? ТМФ, 1980, том 45, номер 3, 291-301; Denisov V. I., Logunov A. A. Does the general theory of relativity have a classical Newtonian limit? Theoretical and Mathematical Physics, Volume 45, Issue 3, pp. 1035-1041 (1980). https://doi.org/10.1007%2FBF01016702.

7.      Fedosin S.G. The covariant additive integrals of motion in the theory of relativistic vector fields. Bulletin of Pure and Applied Sciences, Vol. 37 D (Physics), No. 2, pp. 64-87 (2018). http://dx.doi.org/10.5958/2320-3218.2018.00013.1; Ковариантные аддитивные интегралы движения в теории релятивистских векторных полей.

8.      Fedosin S.G. The Principle of Least Action in Covariant Theory of Gravitation. Hadronic Journal, Vol. 35, No. 1, pp. 35-70 (2012). http://dx.doi.org/10.5281/zenodo.889804; Принцип наименьшего действия в ковариантной теории гравитации.

9.      Дирак П.А.М. Общая теория относительности: Пер. с англ./ Под. ред. Д. И. Блохинцева. – Пер. изд.: США, 1975. – М.: Атомиздат, 1978. – 64 с. Dirac P.A.M. General Theory of Relativity (1975), John Wiley & Sons Inc, quick presentation of the bare essentials of GTR. ISBN 978-0471215752.

10.  Khrapko, R.I.  The Truth about the Energy-Momentum Tensor  and  Pseudotensor. ISSN 0202-2893, Gravitation and Cosmology, Vol. 20, No. 4, pp. 264-273 (2014). Pleiades Publishing, Ltd., 2014. http://dx.doi.org/10.1134/S0202289314040082;  Храпко Р.И. Правда о тензоре и псевдотензоре энергии-импульса.

11.  Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy. Jordan Journal of Physics, Vol. 9, No. 1, pp. 1-30 (2016). http://dx.doi.org/10.5281/zenodo.889304;  О космологической постоянной, поле ускорения, поле давления и об энергии.

12.  Fedosin S.G. The Procedure of Finding the Stress-Energy Tensor and Equations of Vector Field of Any Form. Advanced Studies in Theoretical Physics, Vol. 8, No. 18, pp. 771-779 (2014). http://dx.doi.org/10.12988/astp.2014.47101. // Процедура для нахождения тензора энергии-импульса и уравнений векторного поля любого вида.

13.  Fedosin S.G. The concept of the general force vector field. OALib Journal, Vol. 3, pp. 1-15 (2016). http://dx.doi.org/10.4236/oalib.1102459. // Концепция общего силового векторного поля.

14.  Fedosin S.G. Two components of the macroscopic general field. Reports in Advances of Physical Sciences, Vol. 1, No. 2, 1750002, 9 pages (2017). http://dx.doi.org/10.1142/S2424942417500025. // Две компоненты макроскопического общего поля.

15.  Fedosin S.G. The generalized Poynting theorem for the general field and solution of the 4/3 problem. International Frontier Science Letters, Vol. 14, pp. 19-40 (2019). https://doi.org/10.18052/www.scipress.com/IFSL.14.19; Обобщённая теорема Пойнтинга для общего поля и решение проблемы 4/3.

16.  Fedosin S.G. Equations of Motion in the Theory of Relativistic Vector Fields. International Letters of Chemistry, Physics and Astronomy, Vol. 83, pp. 12-30 (2019). https://doi.org/10.18052/www.scipress.com/ILCPA.83.12. // Уравнения движения в теории релятивистских векторных полей.

17.  Fedosin S.G. Generalized Four-momentum for Continuously Distributed Materials. Gazi University Journal of Science, (2024). https://doi.org/10.35378/gujs.1231793. // Обобщённый 4-импульс для непрерывно распределённого вещества.

18.  Фок В.А. Теория пространства, времени и гравитации. 2-е издание. М.: Физматгиз, 1961. 568 с. Fock V.A. The Theory of Space, Time and Gravitation. Pergamon Press, London. (1959).

19.  Fedosin S.G. Four-Dimensional Equation of Motion for Viscous Compressible and Charged Fluid with Regard to the Acceleration Field, Pressure Field and Dissipation Field. International Journal of Thermodynamics, Vol. 18, No. 1, pp. 13-24 (2015). doi: 10.5541/ijot.5000034003; Четырёхмерное уравнение движения вязкого сжимаемого вещества с учётом поля ускорений, поля давления и поля диссипации.

20.  Fedosin S.G. Energy and metric gauging in the covariant theory of gravitation. Aksaray University Journal of Science and Engineering, Vol. 2, Issue 2, pp. 127-143 (2018). http://dx.doi.org/10.29002/asujse.433947. // Калибровка энергии и метрики в ковариантной теории гравитации.

21.  Fedosin S.G. Estimation of the physical parameters of planets and stars in the gravitational equilibrium model. Canadian Journal of Physics, Vol. 94, No. 4, pp. 370-379 (2016). http://dx.doi.org/10.1139/cjp-2015-0593; Оценка физических параметров планет и звёзд в модели гравитационного равновесия.

22.  Fedosin S.G. The virial theorem and the kinetic energy of particles of a macroscopic system in the general field concept. Continuum Mechanics and Thermodynamics, Vol. 29, Issue 2, pp. 361-371 (2016). https://dx.doi.org/10.1007/s00161-016-0536-8; Теорема вириала и кинетическая энергия частиц макроскопической системы в концепции общего поля.

23.  Fedosin S.G. The Hamiltonian in Covariant Theory of Gravitation. Advances in Natural Science, Vol. 5, No. 4, pp. 55-75 (2012). http://dx.doi.org/10.3968%2Fj.ans.1715787020120504.2023; Гамильтониан в ковариантной теории гравитации.

24.  Fedosin S.G. The Gravitational Field in the Relativistic Uniform Model within the Framework of the Covariant Theory of Gravitation. International Letters of Chemistry, Physics and Astronomy, Vol. 78, pp. 39-50 (2018). http://dx.doi.org/10.18052/www.scipress.com/ILCPA.78.39.

25.  Fedosin S.G. The Pioneer Anomaly in Covariant Theory of Gravitation. Canadian Journal of Physics, Vol. 93, No. 11, pp. 1335-1342 (2015). http://dx.doi.org/10.1139/cjp-2015-0134. // Эффект "Пионера" в ковариантной теории гравитации.

26.  Fedosin S.G. Relativistic Energy and Mass in the Weak Field Limit. Jordan Journal of Physics. Vol. 8, No. 1, pp. 1-16 (2015). http://dx.doi.org/10.5281/zenodo.889210; Релятивистская энергия и масса в пределе слабого поля.

27.  Searle G.F.C. On the steady motion of an electrified ellipsoid. The Philosophical Magazine Series 5, 44 (269), 329-341 (1897). doi:10.1088/1478-7814/15/1/323.

28.  Fedosin S.G. 4/3 Problem for the Gravitational Field. Advances in Physics Theories and Applications, Vol. 23, pp. 19-25 (2013). http://dx.doi.org/10.5281/zenodo.889383. // Проблема 4/3 для гравитационного поля.

29.  Fedosin S.G. The Integral Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based on the Pressure Field and Acceleration Field. American Journal of Modern Physics. Vol. 3, No. 4, pp. 152-167 (2014). http://dx.doi.org/10.11648/j.ajmp.20140304.12. // Интегральный 4-вектор энергии-импульса и анализ проблемы 4/3 на основе поля давления и поля ускорений.

 

Источник: http://sergf.ru/ws.htm

На научный сайт