Обобщённый 4-импульс для непрерывно распределённого вещества

Gazi University Journal of Science, Vol. 37, Issue 3, pp. 1509-1538 (2024). https://doi.org/10.35378/gujs.1231793.

Обобщённый 4-импульс для непрерывно распределённого вещества

Федосин Сергей Григорьевич

ул. Свиязева 22-79, город Пермь, 614088, Пермский край, Россия

На основе принципа наименьшего действия выводится дифференциальное четырёхмерное уравнение Эйлера-Лагранжа для непрерывно распределённого вещества, причём вместо функции Лагранжа данное уравнение содержит лагранжиан. Это позволяет определить в ковариантном виде плотность обобщённого 4-импульса как взятую с обратным знаком производную лагранжиана по 4-скорости типичных частиц системы, а затем вычислить сам обобщённый 4-импульс. Показывается, что обобщённый 4-импульс всех типичных частиц системы является интегральным 4-вектором и потому должен рассматриваться как особый вид 4-вектора. В частности, интегральные 4-векторы получаются путём интегрирования по объёму, являются нелокальными объектами и потому не могут трансформироваться из контравариантной в ковариантную форму и наоборот простым умножением на метрический тензор. Для такой трансформации необходимо ввести метрический тензор внутрь интеграла, описывающего обобщённый 4-импульс. Релятивистский импульс типичных частиц системы с точностью до знака оказывается пространственной компонентой обобщённого 4-импульса. Представленное выражение для обобщённого 4-импульса точно соответствует преобразованию Лежандра, которое связывает функции Лагранжа и Гамильтона. Полученные формулы используются для вычисления обобщённого 4-импульса покоящейся и движущейся релятивистской однородной системы для лагранжиана с частицами и векторными полями, включая электромагнитное и гравитационное поля, поле ускорений и поле давления. Показывается, что обобщённый 4-импульс движущейся системы зависит от суммарной массы частиц, от фактора Лоренца и от скорости движения центра импульсов системы. Кроме этого, дополнительный вклад вносят скалярные потенциалы поля ускорений и поля давления в центре системы. Направление обобщённого 4-импульса совпадает с направлением 4-скорости рассматриваемой системы, при этом обобщённый 4-импульс является частью релятивистского 4-импульса системы. Последнее связано с тем, что обобщённый 4-импульс связан с частицами системы, а релятивистский 4-импульс включает в себя ещё вклад от энергии и импульса самих полей.

Ключевые слова: уравнение Эйлера-Лагранжа; обобщённый 4-импульс; релятивистская однородная система; векторное поле; поле ускорений; поле давления.

Generalized four-momentum for continuously distributed matter

Sergey G. Fedosin

PO box 614088, Sviazeva str. 22-79, Perm, Perm Krai, Russia

E-mail: fedosin@hotmail.com

A four-dimensional differential Euler-Lagrange equation for continuously distributed materials is derived based on the principle of least action, and instead of Lagrangian, this equation contains the Lagrangian density. This makes it possible to determine the density of generalized four-momentum in covariant form as derivative of the Lagrangian density with respect to four-velocity of typical particles of a system taken with opposite sign, and then calculate the generalized four-momentum itself. It is shown that the generalized four-momentum of typical particles of a system is an integral four-vector and therefore should be considered as a special type of four-vectors. In particular, the integral four-vectors which are obtained by integration over volume, are nonlocal objects and therefore cannot be transformed from contravariant to covariant form and vice versa by simple multiplication by the metric tensor. For such a transformation, it is necessary to introduce the metric tensor inside the integral describing the generalized four-momentum. The relativistic momentum of the system’s typical particles turns out to be up to a sign equal to space component of the generalized four-momentum. The presented expression for generalized four-momentum exactly corresponds to the Legendre transformation connecting the Lagrangian and Hamiltonian. The obtained formulas are used to calculate generalized four-momentum of stationary and moving relativistic uniform systems for the Lagrangian with particles and vector fields, including electromagnetic and gravitational fields, acceleration field and pressure field. It turns out that the generalized four-momentum of a moving system depends on the total mass of particles, on the Lorentz factor and on the velocity of the system’s center of momentum. Besides, an additional contribution is made by the scalar potentials of the acceleration field and the pressure field at the center of system. The direction of the generalized four-momentum coincides with the direction of four-velocity of the system under consideration, while the generalized four-momentum is part of the relativistic four-momentum of the system. The latter is due to the fact that the generalized four-momentum is associated with particles of the system, and the relativistic four-momentum also includes contribution from the energy and momentum of the fields themselves.

Keywords: Euler-Lagrange equation; generalized four-momentum; relativistic uniform system; vector field; acceleration field; pressure field.

1. Введение

Трёхмерный обобщённый импульс является важной величиной любой системы, в которой берутся в учёт какие-либо поля, поскольку в этом случае обобщённый импульс содержит в себе векторные потенциалы полей и заменяет собой импульс классической механики. С точки зрения лагранжева формализма, обобщённый импульс одной частицы вычисляется как частная производная от функции Лагранжа по скорости этой частицы, а обобщённый импульс системы равен сумме обобщённых импульсов всех частиц системы [1].

В плоском пространстве Минковского и в искривлённом пространстве-времени основное значение имеют четырёхмерные величины, что требует введения концепции обобщённого 4-импульса. К сожалению, литература в отношении этой величины крайне малочисленна. Например, в [2] рассматривается возможный вид обобщённого 4-импульса для одной заряженной частицы во внешнем электромагнитном поле. Ситуация с определением обобщённого 4-импульса, который должен описывать непрерывно распределённое вещество, ещё хуже, вероятно, из-за трудностей, появляющихся от интегрирования физических величин по объёму. Так, четырёхмерный формализм для механики непрерывной среды используется в [3] для определения релятивистского тензора энергии-импульса и соответствующего уравнения Эйлера-Лагранжа в идеальной жидкости. При этом законы сохранения получаются приблизительно, в виде разложения по степеням отношения скорости частиц к скорости света.

В [4] предполагается, что ковариантное четырёхмерное уравнение Эйлера-Лагранжа, которое необходимо для вывода обобщённого 4-импульса, должно иметь следующий вид:

где есть функция Лагранжа; – 4-скорость; – 4-радиус, задающий положение частицы; ; – скорость света; – интервал. Время представляет собой метрическое собственное время частицы, которое не совпадает с физическим собственным временем . Для дифференциала времени имеется формула [1]: , где есть временная компонента метрического тензора, , и есть координатное время.

Представленное выше уравнение должно иметь другой вид для случая непрерывной среды, поскольку вместо функции Лагранжа необходимо применить лагранжиан , интеграл по объёму от которого даёт . Действительно, чтобы можно было найти величины и , должна зависеть от и каждой из всего множества частиц, входящих в систему.

Фактически же в непрерывной среде с множеством частиц функция Лагранжа зависит скорее от выбора точки наблюдения и от 4-скорости типичных частиц в этой точке, чем от параметров каких-либо конкретных частиц, проследить за которыми невозможно из-за их большого числа. По определению, типичные частицы полностью характеризуют физическую систему и являются идеальными, статистически усреднёнными частицами. Поэтому в случае непрерывной среды все физические величины, входящие в уравнения, вычисляются для типичных частиц, и это должно относиться и к плотности обобщённого 4-импульса.

Однако мы нигде не нашли такой формулы, в которой плотность обобщённого 4-импульса определялась бы непосредственно через какую-то четырёхмерную производную от для типичных частиц системы. Поэтому одной из наших задач будет нахождение соответствующего уравнения Эйлера-Лагранжа для лагранжиана и ковариантного выражения для плотности обобщённого 4-импульса, справедливого и в искривлённом пространстве-времени.

Другой нашей задачей будет вывод обобщённого 4-импульса в явном виде, позволяющем учесть все собственные поля системы. При этом будут рассмотрены четыре наиболее часто встречающиеся поля, такие как электромагнитное и гравитационное поля, поле ускорений [5] и векторное поле давления [6]. Все эти поля представляются как векторные поля и компоненты единого общего поля [7], причём гравитационное поле описывается в рамках ковариантной теории гравитации (КТГ) [8-9].

Используемый подход позволяет избежать те трудности, которые возникают в общей теории относительности (ОТО) при описании движения [10]. В ОТО метрика и гравитационное поле слиты воедино, так что в любом случае необходимо вначале решать уравнение для метрики, чтобы оценить вклад гравитации в физические величины, характеризующие движение. В КТГ гравитационное поле существует независимо от метрики, поэтому в плоском пространстве Минковского вклад гравитации в импульс вещества и в действующую силу учитывается точно без решения уравнения для метрики.

Основное наше внимание будет уделено изучению возможной формы обобщённого 4-импульса, вытекающей из лагранжева формализма. Далее мы выведем формулы для обобщённого 4-импульса, а также для релятивистского импульса типичных частиц системы, и покажем их взаимосвязь в случае векторных полей.

Указанные формулы будут применены для вычисления обобщённого 4-импульса покоящейся и движущейся релятивистской однородной системы в пределе непрерывной среды. Выбор такой физической системы не случаен, поскольку для неё путём решения волновых уравнений уже найдены 4-потенциалы полей, необходимые для вычисления обобщённого 4-импульса. В частности, выражения для скалярных потенциалов полей (32) и соответствующие ссылки на литературу представлены далее в разделе 6. Изучение свойств релятивистской однородной системы является важным потому, что такая физическая система с успехом используется для внедрения результатов теории поля в механику сплошных сред [11-12].

2. Структура лагранжиана и его вариация

По определению, функция действия есть интеграл от функции Лагранжа по координатному времени . В свою очередь, функция Лагранжа для непрерывно распределённого вещества в искривлённом пространстве-времени есть интеграл лагранжиана по движущемуся объёму:

, (1)

где есть произведение дифференциалов пространственных координат, величина представляет собой детерминант метрического тензора , обозначает объём системы.

Лагранжиан представляет собой сумму скалярных членов, каждый из которых имеет размерность объёмной плотности энергии и задаёт вклад в лагранжиан через определённую энергетическую функцию, связанную с соответствующим полем или с 4-током.

С учётом (1) функцию действия можно представить так:

. (2)

Предположим, что лагранжиан зависит от координатного времени , от 4-радиуса и от 4-скорости каждой из частиц системы с текущим номером , от 4-потенциалов и тензоров полей в каждой точке поля, а также от метрического тензора:

. (3)

В (3) величины являются 4-потенциалами электромагнитного и гравитационного полей, поля ускорений и поля давления, соответственно, а величины представляют собой тензоры этих полей. Выражение означает, что лагранжиан зависит ещё от скалярной кривизны , являющейся функцией метрического тензора и его частных производных. В общем случае можно считать, что инвариантная плотность массы и инвариантная плотность заряда некоторой частицы с текущим номером являются функциями от времени и от 4-радиуса этой частицы. Это приводит к тому, что массовый 4-ток , а также зарядовый 4-ток данной частицы становятся функциями от времени , от 4-радиуса и от 4-скорости . В окончательной записи скалярные члены в лагранжиане (3) появляются, как правило, в виде тензорных инвариантов вида , , а также, где есть тензор Риччи, являющийся функцией от метрического тензора и его производных.

Заметим, что в (3) не включена зависимость лагранжиана от ковариантных производных метрического тензора, так как .

Вариация функции действия (2) запишется так:

. (4)

Определитель метрического тензора является функцией компонент метрического тензора. В результате согласно [13] справедливо соотношение:

. (5)

Запишем вариацию лагранжиана (3) с учётом стандартного равенства нулю вариации координатного времени :

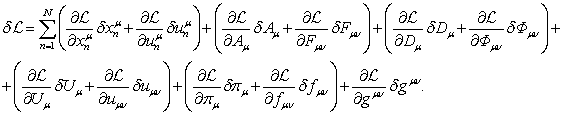
(6)

Вариацию в (6) мы записали не через ковариантные, а через частные производные, пользуясь тем, что лагранжиан является скалярным инвариантом, а не 4-тензором или 4-вектором.

В круглых скобках в (6) находятся члены, содержащие связанные друг с другом вариации. Например, вариация 4-радиуса частицы с номером связана с вариацией 4-скорости этой частицы, а вариация 4-потенциала электромагнитного поля в произвольной точке системы связана с вариацией тензора электромагнитного поля. Подставим (5) и (6) в (4):

(7)

Каждый из интегралов в (7) должен обращаться в нуль, поскольку переменные, от которых зависит лагранжиан (3), полагаются не зависимыми друг от друга. В частности, последний интеграл обращается в нуль при следующем условии:

. (8)

Величина представляет собой производную лагранжиана по метрическому тензору,

а уравнение (8) является уравнением для определения метрического тензора как в веществе, так и за его пределами.

В общем случае лагранжиан (3) мог бы зависеть ещё от первых и даже вторых частных производных метрического тензора по координатам и времени, и эти производные должны были бы присутствовать в (6), (7) и (8). Все эти производные как правило находятся только в одном члене лагранжиана для искривлённого пространства-времени, а именно в члене , где есть скорость света, – постоянная, – скалярная кривизна, – тензор Риччи. Однако скалярная кривизна обладает таким свойством, что вариация функции действия, связанной с кривизной, равна [8], [14]:

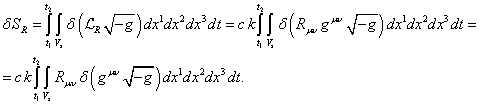
Из данного соотношения видно, что тензор Риччи при варьировании функции действия по метрическому тензору и его первым и вторым производным ведёт себя так, как будто он равен константе, а вариация зависит только от вариации по метрическому тензору. Это оправдывает вид (6), (7) и (8), и тогда получается, что , причём есть один из членов, входящих в лагранжиан в (8).

Для электромагнитного поля из (7) вытекает следующее условие:

Вариацию следует выразить через вариацию и после некоторых преобразований вынести за круглую скобку. То, что останется внутри скобки, необходимо приравнять к нулю. Это приводит к стандартному уравнению электромагнитного поля в искривлённом пространстве-времени, позволяющему вычислять компоненты тензора поля как в веществе, так и за его пределами. Аналогично из (7) получаются уравнения поля для остальных трёх полей.

Поскольку в лагранжиане (3) метрический тензор не должен прямо зависеть от 4-радиусов частиц, следует считать, что зависит от косвенно, через другие физические величины, например через точки наблюдения. Различие между и здесь в том, что метрический тензор можно вычислять и в таких точках , где отсутствуют частицы и потому не применимо.

Согласно предположению в [13], в этом случае 4-потенциалы, а также произведения и , где и обозначают зарядовый и массовый 4-токи, соответственно, не зависят прямо от метрического тензора. Тогда в уравнении для метрики (8) члены, содержащие произведения 4-потенциалов на 4-токи и обычно входящие в выражение для , исчезают.

Если же в лагранжиане (3) метрический тензор прямо зависит от 4-радиусов частиц, то вариация в (7) должна быть выражена через вариации частиц. Затем следует преобразовать последний интеграл в (7), выделить в нём отдельно и присоединить этот интеграл к первому интегралу в (7) для нахождения уравнения движения.

Другой эквивалентный подход предполагает [5], что лагранжиан (3) вместо 4-радиусов и 4-скоростей отдельных частиц прямо зависит от 4-токов и в следующем виде:

, (9)

где задаёт точку наблюдения, есть 4-скорость типичной частицы в этой точке.

Это приводит к тому, что вместо уравнения движения с обобщённым импульсом появляется уравнение движения частиц с тензорами полей и 4-токами, при этом остаются в силе уравнение для метрики (8) и уравнения для определения тензоров полей. Отсюда следует, что уравнение для метрики (8) должно выполняться независимо от того, как именно метрический тензор зависит от физических переменных, включая зависимости от и отдельных частиц либо зависимость от точки наблюдения.

3. Четырёхмерное уравнение Эйлера-Лагранжа

Мы можем считать, что все рассуждения в предыдущем разделе относятся к типичным частицам, множество которых непрерывно заполняет некоторый объём и представляет вещество физической системы. В этом случае различие между точкой наблюдения, задаваемой 4-вектором , и 4-радиусом типичной частицы в этой точке исчезает, причём 4-скорость типичной частицы в точке наблюдения равна . Согласно выражению лагранжиана (9), лишь зарядовые и массовые 4-токи и , присутствующие в каждом лагранжиане для непрерывной среды, могут быть прямыми функциями от точки наблюдения и от 4-скорости типичной частицы вещества в этой точке. Что касается 4-потенциалов и тензоров полей, а также метрического тензора, они становятся функциями от и от лишь после решения соответствующих полевых уравнений. Обозначим сумму членов в лагранжиане, содержащих 4-токи, через . Первый интеграл в (7) должен равняться нулю независимо от других интегралов, и в него следует подставить как часть лагранжиана, содержащую зависимость от и от типичных частиц:

(10)

здесь присутствует элемент ковариантного 4-объёма с текущим номером , , есть скорость света, представляет собой собственное время типичной частицы с номером , есть собственный объём такой частицы.

В (10) сумма должна интегрироваться по всему объёму системы, при этом каждый член суммы связан только с одной частицей. Это означает, что в (10) от интеграла по всему объёму можно перейти к сумме интегралов по объёмам отдельных типичных частиц, оставляя при этом подынтегральное выражение неизменным. Мы отразили это через два последних члена в (10).

Собственное время какой-либо частицы в (10) не равно собственному времени любой другой частицы системы. На основании этого считается, что вывести уравнение Эйлера-Лагранжа в ковариантном виде можно лишь для одной частицы, а для системы частиц это невозможно. Вероятно, с этим и связано отсутствие в литературе ковариантно определённого 4-вектора плотности обобщённого импульса для непрерывной среды. Таким образом, мы приходим к тому, что следует изменить процедуру варьирования и приспособить её к рассматриваемому случаю. Сделаем это следующим образом.

Вариации можно рассматривать как малые допустимые отклонения от истинной траектории рассматриваемой частицы, движущейся в пространстве и времени между двумя заданными точками. Учтём определение 4-скорости и определим её вариацию так: .

Несмотря на то, что собственное время в каждой частице течёт с разной скоростью, будем предполагать далее синхронность варьирования в отношении собственного времени для всех частиц. Для этого достаточно синхронизировать начало отсчёта собственного времени частиц и в этот момент произвести варьирование. Весь интервал времени , в пределах которого осуществляется интегрирование по времени в (10), соответствует некоторому интервалу времени для частицы с текущим номером , причём интервал будет различным у разных частиц. Интервал при интегрировании в (10) разбивается на множество дифференциалов времени , аналогично, для каждой частицы соответствующий интервал разбивается на множество дифференциалов времени . Так как 4-скорость каждой частицы всё время меняется, на каждом дифференциале в момент времени частица будет иметь различную 4-скорость и различную временную компоненту 4-скорости . Таким образом, чтобы достаточно точно покрыть все траектории движения частиц системы при варьировании действия по собственному времени, необходимо производить синхронизацию начала отсчёта собственного времени всех частиц множество раз, на каждом из соответствующих дифференциалов времени .

С другой стороны, с учётом соотношения можно записать:

Если здесь положить , то вариация 4-скорости сведётся к величине , приведённой выше.

Таким образом мы будем предполагать, что на каждом временном дифференциале длительностью не варьируется не только время , но и временная компонента 4-скорости, ведя себя как постоянная величина на этом дифференциале. При этом компонента на разных дифференциалах , то есть в разные моменты времени, может отличаться по величине, скачком изменяя своё значение при переходе к новому дифференциалу времени.

С учётом этого преобразуем последнее выражение в (10) по частям для каждой частицы:

(11)

Преобразуем теперь последний член в (11):

В данном равенстве внутри интеграла по объёму частицы с номером вариации в начальные моменты времени и , и вариации в конечные моменты времени и , равны нулю по условию варьирования. В результате последний член в (11) обращается в нуль и остаётся следующее:

В общем случае вариации различаются для разных частиц и не зависят друг от друга, являются произвольными и не равными нулю. Для того, чтобы выполнялось приведённое выше соотношение, должна равняться нулю квадратная скобка под знаком суммы. Отсюда следует четырёхмерное уравнение Эйлера-Лагранжа для каждой из частиц:

. (12)

С другой стороны, в пределах объёма одной частицы и в течение дифференциала времени временная компонента 4-скорости частицы остаётся постоянной согласно принятому нами условию варьирования,

и её можно внести под знак производной . Умножим и одновременно разделим на выражение внутри интеграла для :

Поскольку в данном выражении величины и в общем случае являются произвольными и не равными нулю, то в первом приближении должно выполняться следующее соотношение:

Обозначим через объёмную плотность обобщённого 4-импульса.

С учётом этого, убирая номер частицы, приходим к соотношению, которое по своей форме соответствует дифференциальному уравнению движения типичной частицы:

. (13)

Уравнение Эйлера-Лагранжа (12) было получено при условии постоянства временной компоненты ,

что соответствует движению частиц с постоянной амплитудой скорости, величина которой зависит от выбранного дифференциала времени на интервале времени . В пределе непрерывно распределённого вещества частицы не могут так двигаться из-за непрерывных взаимодействий друг с другом, поэтому вместо (12) мы используем (13), как более подходящее выражение в этом случае.

Особенностью уравнений (12) и (13) является то, что они выражены через производные от лагранжиана , а не через производные от функции Лагранжа . Следует отметить, что уравнения (12) и (13) справедливы в одинаковой мере, так как в них было использовано одно и то же условие постоянства временной компоненты типичных частиц при вариации лагранжиана. Чем меньше разности и в (10), тем лучше выполняется условие при варьировании, и тем точнее можно утверждать, что уравнения (12) и (13) справедливы, в том числе в искривлённом пространстве-времени.

Структура уравнений (12) и (13) такова, что они представляют собой одну из возможных форм четырёхмерных уравнений движения типичных частиц. При этом в левой части (13) присутствует полная скорость изменения во времени плотности обобщённого 4-импульса, соответственно в правой части находится объёмная плотность обобщённой 4-силы .

Уравнение движения может быть записано по крайней мере ещё в трёх эквивалентных формах, например, через тензоры полей, через 4-потенциалы полей и через тензоры энергии-импульса полей [5]. Так, в [11] ковариантное уравнение движения, действительное в искривлённом пространстве-времени, было выведено из принципа наименьшего действия с учётом векторного поля диссипации, поля давления, поля ускорений, гравитационного и электромагнитного полей. Данное уравнение, выраженное через тензоры полей и через 4-токи, в пределе слабого поля точно воспроизводит уравнение Навье-Стокса.

4. Обобщённый 4-импульс

Предположим теперь, что все частицы системы одновременно сдвигаются на некоторый постоянный 4-вектор , являющийся вариацией 4-радиуса . Так как

то при условиях , , , , будет . В этом случае вариация приводит в (10) к вариации функции действия следующего вида:

(14)

Для преобразования суммы в (14) было использовано (12) и выражение . Предполагается также, что при интегрировании по собственному времени и по объёму одной частицы величина является постоянной и в среднем не зависящей от времени, как в равновесной системе, так что можно внести под знак производной по времени. В пределе непрерывной среды от суммы интегралов по объёму отдельных частиц можно перейти к одному интегралу по всему объёму системы, для чего в правой части (14) можно заменить произведение дифференциалов на аналогично (10) и убрать номер частиц:

. (15)

Введём в рассмотрение обобщённый 4-импульс частиц системы:

. (16)

В (16) было использовано определение плотности обобщённого 4-импульса из (13) и соотношение из [1]:

, (17)

где есть дифференциал собственного объёма любой из частиц, вычисляемый в сопутствующей частице системе отсчёта.

Заметим, что по способу своего построения является 4-вектором, так же как и .

При этом предполагается, что в момент вычисления обоих 4-векторов временные компоненты 4-скоростей всех частиц не изменяются либо усредняются по времени. То, что плотность обобщённого 4-импульса есть 4-вектор, видно из ковариантного определения .

В пределе непрерывно распределённого вещества можно считать, что типичные частицы практически полностью заполняют весь объём вещества. Тогда обобщённый 4-импульс в (16) получается равным интегральной сумме произведений отдельных частиц на инвариантные объёмы этих частиц. Так как произведение скаляра на 4-вектор даёт 4-вектор, а сумма 4-векторов есть 4-вектор, то обобщённый 4-импульс в (16) есть 4-вектор.

Из (15) и (16) следует соотношение для обобщённого 4-импульса:

. (18)

Согласно (18), если перенос всех частиц системы на постоянный 4-вектор не изменяет физических свойств системы, то отсюда следует сохранение обобщённого 4-импульса . Замкнутая система не зависит от окружения и от полей от внешних источников, и для неё выполняется условие неизменности системы при переносе частиц. Поэтому для замкнутой системы будет справедливо соотношение .

Заметим, что указанный перенос на постоянный 4-вектор следует рассматривать как часть процесса вариации переменных, а не как реальный процесс перемещения частиц, в котором неизбежны периоды ускорения и излучения заряженных частиц, что приводит к изменению баланса энергии и импульса, изменяет физические свойства системы и нарушает условия варьирования.

В (14) мы предположили, что является постоянной величиной при интегрировании по объёму каждой типичной частицы, и в среднем не зависит от времени. Но именно это характерно для равновесной системы, описываемой с помощью типичных частиц и процедуры усреднения физических величин, и это вполне оправдывает наш подход. В таком случае мы можем пойти дальше и внести под знак производной в (14), учитывая соотношение , заменяя далее произведение дифференциалов на аналогично (10) и переходя к приближению непрерывной среды:

(19)

Определим новую четырёхмерную величину:

. (20)

Из (19) и (20) следует соотношение , то есть для равновесной замкнутой системы.

В общем случае не является 4-вектором, но становится им при условии, что для каждой частицы не меняется в момент вычисления . Действительно, в этом случае будет выполняться соотношение , и тогда становится равным обобщённому 4-импульсу в (16).

Значимость в (20) заключается в том, что его пространственная компонента с точностью до знака равняется релятивистскому импульсу частиц системы. Чтобы увидеть это, учтём следующие соотношения: , , . Если обозначить , то для из (20) тогда следует:

. (21)

В [1] трёхмерный обобщённый импульс системы, который учитывает все действующие поля и фактически представляет собой полный релятивистский импульс частиц системы, определяется следующим образом:

Мы снова должны учесть наши рассуждения в разделе 3 по поводу зависимости лагранжиана от времени, координат и скоростей частиц. Лишь часть лагранжиана, которую мы обозначили и которая содержит 4-токи, может прямо зависеть от скоростей частиц. С учётом этого, а также соотношений (1) и (17), находим:

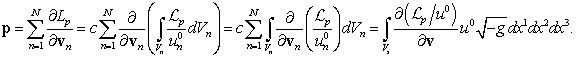
(22)

Полученное выражение совпадает с в (21), так что . Если обозначить обобщённый 4-импульс в виде и учесть совпадение и при условии, что для каждой частицы не меняется в момент вычисления импульса, то будет одновременно и суммарным релятивистским импульсом частиц системы в (22), и суммарным обобщённым импульсом частиц, входящим в в (16).

В отношении процедуры получения и физического смысла 4-векторов и следует добавить несколько замечаний. Во-первых, сдвиг всех без исключения частиц системы на некоторый постоянный 4-вектор в одну сторону, оставляющий физическую систему неизменной и представленный в (14), тесно связан с теоремой Нётер. Лишь при таком сдвиге система гарантированно сохраняет форму, взаимное расположение частиц и их скоростей, а также величины полей, что и приводит к сохранению импульса. В симметричных системах допустимы другие сдвиги, например, инверсия координат всех частиц (преобразование чётности, parity transformation) или замена противоположных частиц друг на друга. Согласно теореме Нётер, каждой непрерывной симметрии соответствует своё преобразование координат частиц и свой собственный закон сохранения той или иной физической величины.

Во-вторых, в приближении непрерывной среды, в уравнениях удобно вместо функции Лагранжа использовать её объёмную плотность, то есть лагранжиан , что позволяет отказаться от интегрирования в (1). В-третьих, благодаря большому количеству взаимодействующих частиц, 4-потенциалы и тензоры действующих в веществе полей перестают зависеть от координат и скоростей отдельных частиц, определяются лишь свойствами системы в целом и в системе центра импульсов зависят в основном от координат точки наблюдения.

Что касается зарядового (электромагнитного) и массового 4-токов, также входящих в лагранжиан, то полагают, что эти 4-токи связаны с движением так называемых типичных частиц системы. Характеристикой типичных частиц является то, что они задают основные черты физической системы и позволяют описывать её наиболее полным образом. Независимость функций поля от координат отдельных частиц и появление типичных частиц возникают в ходе усреднения движений отдельных частиц и калибровки свойств этих частиц. Как результат такого усреднения, мы можем считать, что в определённой точке неподвижной равновесной системы типичные частицы движутся с некоторой усреднённой 4-скоростью , зависящей от координат точки наблюдения. Усреднённой можно считать и временную компоненту 4-скорости типичных частиц, причём в неподвижной в целом системе будет постоянной, хотя и различаться по величине в разных частях системы. Именно такое постоянство типичных частиц следует подразумевать при выводе уравнений (12) и (13) и рассматривать (12) и (13) как уравнения для усреднённых физических величин. Другой способ представить себе постоянство , необходимое для вывода плотности обобщённого 4-импульса в (13), это полагать, что вычисляется как мгновенная величина за малое время, в течение которого скорости типичных частиц не успевают существенно измениться. Таким образом мы можем считать наш подход справедливым по крайней мере для систем, находящихся в равновесии и состоящих из непрерывно распределённого вещества. В разделе 8 мы также покажем, что представленная нами концепция обобщённого 4-импульса согласуется и с Гамильтоновой механикой, и с Лагранжевой механикой.

Особенностью обобщённого 4-импульса в (16) является необычность его определения через интеграл по объёму. Действительно, стандартные 4-векторы задаются локально или в области точечных размеров, что позволяет делать переходы от формы с ковариантным индексом к форме с контравариантным индексом с помощью метрического тензора в данной точке, например , . Однако задаёт обобщённый 4-импульс для всех частиц и вычисляется как интеграл по достаточно большому объёму. Такие 4-векторы не локальны и их следует называть интегральными 4-векторами. Для таких 4-векторов равенство типа в общем случае будет неверным, так как метрический тензор может иметь различные значения в каждой точке системы. Чтобы получить контравариантную форму , следует обратиться к самому определению интегрального 4-вектора в (16):

5. Лагранжиан для векторных полей

Для вычисления обобщённого 4-импульса мы будем использовать лагранжиан для четырёх векторных полей в искривлённом пространстве-времени согласно [5], [11]:

(23)

где – 4-потенциал электромагнитного поля, задаваемый с помощью скалярного потенциала и векторного потенциала этого поля,

– зарядовый 4-ток,

– плотность заряда в сопутствующей частице системе отсчёта,

– 4-скорость точечной частицы,

– 4-потенциал гравитационного поля, описываемый через скалярный потенциал и векторный потенциал этого поля в рамках ковариантной теории гравитации,

– массовый 4-ток,

– плотность массы в сопутствующей частице системе отсчёта,

– 4-потенциал поля ускорений, где и обозначают скалярный и векторный потенциалы, соответственно,

– 4-потенциал поля давления, состоящий из скалярного потенциала и векторного потенциала ; в случае, если внутри частицы векторный потенциал поля давления равен нулю, то , где – давление в сопутствующей частице системе отсчёта,

– магнитная постоянная,

– электромагнитный тензор,

– гравитационная постоянная,

– гравитационный тензор,

– коэффициент поля ускорений,

– тензор ускорений, вычисляемый как 4-ротор от 4-потенциала поля ускорений,

– коэффициент поля давления,

– тензор поля давления,

, где – некоторый коэффициент порядка единицы, подлежащий определению,

– скалярная кривизна,

– космологическая постоянная.

Плотность заряда и плотность массы , входящие в соответствующие 4-токи, не являются константами и определяются как ковариантные скалярные функции от 4-радиусов и 4-импульсов типичных частиц системы. Это означает, что при варьировании лагранжиана (23) в принципе наименьшего действия, и подлежат варьированию также, как например, скалярная кривизна .

Согласно [5], с целью калибровки релятивистской энергии системы космологическая постоянная задаётся таким образом, что возникает условие . В этом случае энергия не будет зависеть от и и становится однозначно определённой. Это же относится и к обобщённому 4-импульсу. Поэтому при его вычислении мы будем считать, что в (23) . Тогда из (23) следует выражение для как той части лагранжиана, которая содержит 4-токи как функции от 4-радиуса и от 4-скорости произвольной частицы вещества:

. (24)

В простейшем случае, когда глобальные 4-потенциалы и тензоры полей не зависят от 4-скоростей отдельных частиц системы, плотность обобщённого 4-импульса для (24) будет равна:

. (25)

Из (16) следует выражение для обобщённого 4-импульса в этом случае:

. (26)

Так как , для обобщённого импульса находим:

. (27)

Для из (21) с учётом (24) получается следующее:

(28)

Из сравнения (27) и (28) следует, что трёхмерная величина равна обобщённому импульсу: . Это же равенство было найдено в конце предыдущего раздела с помощью функции Лагранжа в (22). Таким образом, лагранжиан (23) и его часть (24) позволяют вычислить обобщённый импульс частиц , совпадающий с релятивистским импульсом частиц.

Из (26) при находим временную компоненту обобщённого 4-импульса:

. (29)

Из изложенного видно, что 4-векторы и характеризуют соответственно объёмную плотность и полный обобщённый 4-импульс всех частиц, то есть вычисляются по всему веществу системы. Вклад в эти 4-векторы делают все поля, действующие в системе. Однако поля имеются не только в веществе, но некоторые их них действуют и за пределами вещества. Типичным примером являются электромагнитное и гравитационное поля. Если система движется как целое, то выходящие за пределы системы поля приобретают дополнительный 4-импульс, который должен быть добавлен к обобщённому 4-импульсу , если мы хотим найти полный 4-импульс системы из частиц и полей. Таким образом, обобщённый 4-импульс является лишь частью полного 4-импульса системы, причём временная компонента задаёт энергию частиц и полей в веществе системы, а пространственная компонента при индексе задаёт релятивистский (обобщённый) импульс этих частиц и полей.

Согласно (18), в равновесной и замкнутой системе сохраняется, и то же самое можно сказать о 4-импульсе электромагнитного и гравитационное полей системы за пределами вещества, а также и о полном 4-импульсе системы. Причиной сохранения полного 4-импульса замкнутой системы является невозможность изменения 4-импульса вследствие отсутствия взаимодействия с окружением, при этом предполагается, что внутренние взаимодействия не способны изменить 4-импульс системы. Условие равновесной системы означает, что пропорции в энергии и импульсе для частиц и полей остаются всё время неизменными, что даёт сохранение как обобщённого 4-импульса , так и 4-импульса полей, выходящих за пределы вещества.

6. Покоящаяся релятивистская однородная система

Рассмотрим в рамках специальной теории относительности (СТО) релятивистскую однородную систему, тесно заполненную множеством частиц и удерживаемую в равновесии четырьмя векторными полями. Для макроскопических тел основной действующей силой является гравитационная сила, придающая телам сферическую форму.

Предположим, что все частицы системы движутся хаотично и независимо друг от друга, и в системе нет общего вращения и отсутствуют направленные потоки вещества. Будем считать также, что в сопутствующих частицам системах отсчёта обнуляются как собственные векторные потенциалы полей, так и соленоидальные векторы частиц. Тогда в покоящейся системе потенциалы и тензоры полей не будут зависеть от 4-скоростей отдельных частиц и будут применимы формулы (26-29).

Для электромагнитного поля это означает, например, что заряженные частицы не имеют собственного магнитного момента в сопутствующих им системах отсчёта. Что касается поля ускорений, то частицы должны иметь близкое к нулю собственное вращение. При таких предположениях нетрудно показать, что как следствие решения волновых уравнений для отдельных частиц и большого количества хаотически движущихся частиц в рассматриваемой системе, глобальные векторные потенциалы , , , , а также соленоидальные векторы полей в системе стремятся к нулю. Это приводит к тому, что становятся равными нулю в (27) и в (28), и нам достаточно определить лишь временную компоненту в (29). В рамках СТО в (29) , элемент объёма сферы и с учётом временной компоненты из (25) можно записать:

. (30)

. (31)

Скалярные потенциалы полей внутри сферы в случае и были определены в [15-17]:

, .

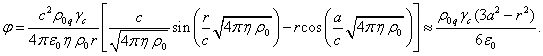
(32)

В (32) – электрическая постоянная, – фактор Лоренца частиц в центре сферы, – радиус сферы, есть скалярный потенциал поля давления в центре сферы. Для зарядового 4-тока имеем: , при этом 4-скорость частиц , , где есть фактор Лоренца для частиц, есть среднеквадратичная скорость частиц.

Появление синусов и косинусов в (32) связано с учётом фактора Лоренца собственного хаотического движения частиц. Если же пренебречь внутренним движением частиц, то потенциалы полей станут равными потенциалам внутри идеальной твёрдой сферы. Такие потенциалы указаны как приблизительные выражения в правых частях в (32).

В [12] при анализе уравнения движения вещества было показано, что в рассматриваемой системе выполняется следующее соотношение между коэффициентами полей:

. (33)

Подставим потенциалы (32) в (30) и учтём (33):

. (34)

Мы можем записать плотность обобщённого 4-импульса через компоненты так: , где есть плотность трёхмерного обобщённого импульса и пространственная компонента 4-вектора. В рассматриваемом случае у нас получается, что , и согласно (34), во всём объёме сферы. Таким образом, оказывается постоянным 4-вектором.

Подставим из (34) в (31) и проинтегрируем по объёму сферы. Так как , где задаётся в (32), получается следующее:

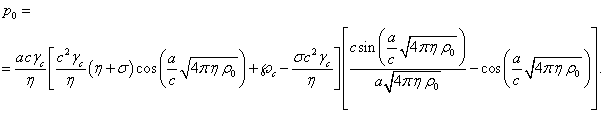
(35)

Если в (35) выполняется неравенство , то синусы и косинусы можно разложить до членов второго порядка. Это даёт:

где есть величина с размерностью массы, равная произведению плотности массы на объём сферы.

С другой стороны, в [15] было показано, что суммарная масса частиц внутри сферы определяется величиной , отличающейся от . Различие масс возникает от движения частиц, поскольку эффективная плотность движущейся частицы равна . Суммарная масса частиц внутри сферы определяется интегралом по объёму сферы:

(36)

При этом оказывается, что масса равна гравитационной массе , задающей скалярный потенциал и напряжённость гравитационного поля за пределами сферы. Для заряда системы аналогично (36) находим:

Подставим (36) в (35):

. (37)

Отсюда видно, что временная компонента обобщённого 4-импульса системы превышает значение приблизительно на величину . Запишем 4-вектор через временную и пространственную компоненты: , где есть трёхмерный обобщённый импульс. 4-вектор можно считать постоянным 4-вектором, так как в соответствии с (37) до тех пор, пока являются неизменными фактор Лоренца и скалярный потенциал в центре сферы, что справедливо для равновесной системы. Кроме этого, согласно (16) и (26) как следствие того, что в определении .

Поскольку 4-векторы и для покоящейся сферы оказываются постоянными, то выполняется соотношение (18), а из (13) вытекает следующее:

. (38)

Проверим соотношение (38) для случая покоящейся сферы в рамках СТО. Для этого необходимо выразить отношение через компоненты 4-радиуса . Рассмотрим сумму произведений 4-потенциалов полей на 4-токи в (24), и выразим эту сумму через компоненты. Так, для электромагнитного поля и других полей внутри сферы будет:

, , .

, . (39)

Поскольку векторные потенциалы полей , , , в данном случае равны нулю, то можно записать:

Подставим сюда (30) и учтём, что :

. (40)

Согласно (34) , так что с учётом (40) соотношение (38) удовлетворяется:

7. Движущаяся релятивистская однородная система

Рассмотрим сферу с частицами, движущуюся с постоянной скоростью вдоль оси , причём в начальный момент времени центр сферы находился в начале неподвижной системы отсчёта . В системе отсчёта , связанной с центром сферы, скалярные потенциалы полей выражаются формулами (32), а векторные потенциалы полей в среднем равны нулю.

Мы можем определить потенциалы полей с точки зрения системы отсчёта , учитывая тот факт, что потенциалы полей входят в соответствующие 4-потенциалы, которые преобразуются из в как 4-векторы. В рамках СТО 4-потенциалы преобразуются так же, как время и координаты при преобразованиях Лоренца. Например, если 4-потенциал электромагнитного поля в есть , то в для компонент 4-потенциала можно записать:

(41)

Здесь есть фактор Лоренца движения центра сферы в .

В (41) учтено, что в , где сфера неподвижна, все три компоненты векторного потенциала равны нулю. Для 4-потенциалов остальных полей можно записать аналогично:

. (42)

В скорость произвольной частицы внутри сферы равна , при этом фактор Лоренца . Обозначим полную скорость частицы в через , а фактор Лоренца частицы через . Преобразование 4-скорости частицы из в с помощью преобразований Лоренца даёт следующее:

(43)

Подставим (41) и (42) в (25) и найдём в временную и пространственную компоненты плотности обобщённого 4-импульса , где :

. (44)

В (44) скалярные потенциалы полей , , и в системе отсчёта являются скалярными потенциалами, которые представлены в (32). С учётом этого мы можем воспользоваться выражениями (30), (33), (34) для , и для системы отсчёта находим:

, . (45)

Согласно (45), в временная компонента плотности обобщённого 4-импульса увеличивается в раз по сравнению с . Кроме этого, появляется составляющая плотности трёхмерного обобщённого импульса вдоль оси , пропорциональная скорости движения сферы в .

С целью упрощения расчётов будем считать, что скорость движения сферы существенно превышает скорости движения частиц , и , и последними можно пренебречь. Если в (43) , то временная компонента . Беря из (45) компоненты в , с помощью (16), (26-27) при можно определить компоненты обобщённого 4-импульса , где :

, .

(46)

Если в (46) вычислить временную компоненту обобщённого 4-импульса, то тем самым определится и компонента трёхмерного обобщённого импульса.

В СТО движущаяся сфера с частицами представляется в как эллипсоид Хэвисайда, независимо от внутреннего движения частиц в . В [18] исследовались энергия и импульс электромагнитного поля движущейся заряженной сферы и была обнаружена проблема 4/3. То же самое было найдено в [19] в отношении гравитационного поля. Далее будем действовать аналогично [18-19], и введём в новые координаты , связанные с декартовыми координатами:

, , . (47)

В данных координатах элемент объёма в (46) определяется формулой . Согласно (32), в системе отсчёта фактор Лоренца движущихся внутри сферы частиц выражается через текущий радиус, который мы обозначим здесь через :

Если учесть преобразования Лоренца, то координаты в внутри эллипсоида Хэвисайда, присутствующие в (47), совпадают со сферическими координатами в внутри сферы, так что .

Всё это позволяет вычислить интеграл для в (46):

Подставим сюда из (45) и из (36):

. (48)

По сравнению с (37) компонента увеличилась в раз за счёт движения физической системы как целое со скоростью .

Для компоненты обобщённого импульса из (46) находим:

, (49)

где компонента вычислена в (48).

Пока сфера с частицами движется с постоянной скоростью вдоль оси , можно считать, что в (48) компонента . Это же будет справедливо и для в (49), причём . Отсюда следует, что обобщённый 4-импульс , где , является постоянным 4-вектором и потому выполняется условие сохранения (18).

Согласно определению 4-потенциала поля давления в [6], для скалярного потенциала в центре сферы можно записать: , где есть собственное давление внутри типичной частицы, движущейся в центре сферы.

С учётом этого из (48) и (49) следует выражение для импульса частиц системы:

Как видно, учёт собственного давления и собственной плотности частиц увеличивает значение суммарного импульса частиц системы независимо от вклада в импульс факторов Лоренца и .

Согласно (48) и (49) обобщённый 4-импульс можно записать так:

, (50)

где есть 4-скорость движения центра сферы. Таким образом, обобщённый 4-импульс направлен вдоль 4-скорости рассматриваемой системы.

Из (48-50) следует, что

так что в первом приближении суммарный импульс частиц пропорционален фактору Лоренца , скорости движения центра импульсов и суммарной массе частиц системы, определённой в (36). Кроме этого, чем больше скалярный потенциал поля ускорений и скалярный потенциал поля давления в центре сферы, тем больше импульс. Так как есть фактор Лоренца частиц в центре сферы, то видно, что за счёт движения частиц внутри сферы увеличивается эффективная масса, входящая в импульс частиц системы. Это означает, что вместо массы , типичной для покоящейся релятивистской однородной системы, эффективной суммарной массой частиц движущейся системы становится величина .

Нам осталось проверить ещё уравнение (13). Из (45) следует, что , , . Это означает, что плотность обобщённого 4-импульса , где , является постоянным 4-вектором и тогда левая часть уравнения (13) обнуляется, . Рассмотрим правую часть (13), где содержится величина . Используя выражение в (24), находим:

(51)

Согласно (43), фактор Лоренца и компоненты полной скорости произвольной частицы при движении сферы с частицами в равны:

, ,

, . (52)

Если в (52) пренебречь компонентами , , собственной скорости частицы внутри сферы, измеряемыми в , то будет . Тогда для электромагнитного поля , и подобные выражения будут для других полей с учётом (41) и (42). Подставим это в (51) и учтём ещё выражения для скалярных потенциалов вида из (41) и (42), а также из (44):

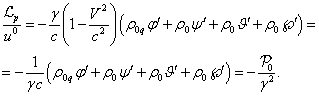
Так как согласно (45) , то получается и величина . Следовательно, правая часть (13) будет равна нулю, то есть , и уравнение (13) удовлетворяется.

8. Дополнительные замечания

При вычислении в системе отсчёта обобщённого 4-импульса движущейся однородной релятивистской системы, вместо временной компоненты 4-скорости произвольной частицы в (43) мы использовали приблизительное значение . Это привело к тому, что временная компонента в (48) увеличивается в раз за счёт движения физической системы как целое со скоростью , по сравнению со статическим случаем. Изменится ли что-нибудь, если принять ещё во внимание компоненту скорости в выражении ? В равновесной неподвижной в целом системе частиц их суммарный импульс как правило равен нулю. При хаотическом движении частиц их импульсы вычитаются друг из друга ввиду разнонаправленности скоростей частиц, то же самое следует для свободно вращающихся систем. Кроме этого, в системе центра импульсов суммарный импульс всегда равен нулю. Компонента скорости входит в как добавка в первой, нечётной степени, и затем интегрируется по объёму при вычислении в (46). Данная добавка ведёт себя как некоторая антисимметричная функция, меняющая свой знак, интеграл от которой по объёму становится равным нулю. Поэтому полученные в (48) и (49) оценки и остаются неизменными.

В [5] в искривлённом пространстве-времени была найдена релятивистская энергия для системы из частиц и векторных полей. Если система стационарна и в ней нет диссипации энергии за счёт не потенциальных сил, то гамильтониан системы становится равным энергии:

(53)

Подставим из (23) в (1), используем условие калибровки энергии в виде согласно [5], [20], сложим результат с (53) и учтём (25):

Здесь индекс задаёт пространственные компоненты 4-векторов и . Учтём теперь, что , а 4-скорость :

Перейдём с помощью (17) от движущихся объёмов частиц к их собственным объёмам и заменим интеграл по объёму на сумму интегралов по объёмам отдельных частиц:

Так как , то с учётом (16) находим:

Данное выражение представляет собой стандартное преобразование Лежандра, связывающее функцию Лагранжа , гамильтониан , скорости и обобщённые трёхмерные импульсы всех частиц системы. Таким образом, представленная нами концепция обобщённого 4-импульса согласуется и с Гамильтоновой механикой, и с Лагранжевой механикой [21].

Из (53) при условии калибровки энергии в виде и из (29) следует:

. (54)

Это означает, что временная компонента обобщённого 4-импульса системы задаёт ту часть энергии-импульса, которая связана с частицами, на которые действуют поля системы. Что касается вклада самих полей в энергию системы, то он определяется интегралом в (54) согласно [15], [16], [22]. Мы можем считать, что разделение энергии в (54) на энергию частиц и энергию полей возникает из самой структуры лагранжиана (23). В данном лагранжиане имеется часть (24), содержащая 4-потенциалы полей и 4-токи частиц, и ещё имеется часть, содержащая тензорные инварианты, появляющиеся в интеграле в (54).

Рассмотрим ещё подход к рассматриваемой проблеме в общей теории относительности (ОТО). В соответствии с [13], [21] лагранжиан ОТО для релятивистского флюида может быть представлен так:

(55)

Функция в (55) есть потенциальная энергия упругого сжатия флюида в расчёте на единицу массы,

а представляет собой давление. Первые три члена в (55) прямо зависят от 4-скорости и можно считать, что они составляют ту часть лагранжиана , с помощью которого вычисляется плотность обобщённого импульса в (13). Отсюда находим:

. (56)

Выражение (56) для плотности обобщённого импульса в ОТО показывает существенное различие по сравнению с выражением (25), найденным для векторных полей. В (56) первый член соответствует члену в (25). Однако 4-потенциал поля ускорений равен 4-скорости лишь для точечной частицы, а в общем случае для флюида как для системы тесно взаимодействующих частиц справедливо неравенство [23]. Второй член в (56), связанный с энергией давления, соответствует члену в (25). Но член всегда направлен вдоль 4-скорости , как для свободной точечной частицы, тогда как фактически частицы флюида взаимодействуют между собой так, что 4-потенциал поля давления не может не отличаться от величины . Наконец, если член для электромагнитного поля одинаково представлен и в (25) и в (56), то для гравитационного поля опять возникает различие. В (25) вклад в плотность обобщённого импульса делает , где есть гравитационный 4-потенциал. Но в (56) в выражении для отсутствует какой-либо член, задающий гравитационное поле. Это является очевидным следствием аксиоматики ОТО, в которой роль гравитационного поля играет метрика пространства-времени. Тем не менее, уравнения типа (12) и (13), в которые следует подставлять усреднённые по типичным частицам физические величины, должны оставаться в силе и в ОТО. Это возможно, поскольку обобщённая 4-сила в (13) зависит от метрики, а значит и от гравитационного поля в ОТО.

С другой стороны, согласно (16) обобщённый 4-импульс системы частиц есть интеграл по объёму от . Тогда получается, что в ОТО не содержит вклад от гравитационного поля, и потому пространственная компонента не может задавать релятивистский импульс частиц системы в отличие от того, что мы нашли для векторных полей в разделе 4. Ситуация в ОТО усугубляется ещё и тем, что попытка определить 4-импульс и релятивистский импульс физической системы другим способом, через интеграл по объёму от временных компонент тензора энергии-импульса, даже с учётом псевдотензора гравитационного поля, оказывается неудачной (смотри [21] и имеющиеся там ссылки). Вместо 4-импульса таким способом получается так называемый интегральный четырёхмерный вектор, который характеризует распределение энергии и потоков энергии полей в системе, сохраняется в замкнутой системе, но не является стандартным локально определённым 4-вектором.

9. Заключение

Анализ лагранжиана и его вариации в принципе наименьшего действия привёл нас к четырёхмерному уравнению Эйлера-Лагранжа (12) и к его варианту (13) для непрерывно распределённого вещества. В (16) мы определяем обобщённый 4-импульс , в (20) вспомогательную четырёхмерную величину , в (21) вектор и в (22) суммарный релятивистский импульс частиц системы, находимый через функцию Лагранжа. В силу своего определения, обобщённый 4-импульс оказывается интегральным 4-вектором, относящимся к особому классу нелокальных 4-векторов. Как показано в конце раздела 4, для таких 4-векторов требуется иной порядок преобразования между формой с ковариантным индексом и формой с контравариантным индексом.

В рамках принятых допущений, когда для каждой частицы не меняется в момент вычисления импульса, получается, что , причём оказывается ещё равным суммарному релятивистскому импульсу частиц системы.

Далее в качестве примера мы используем лагранжиан в (23), описывающий релятивистские векторные поля, и его часть в (24), содержащая 4-токи. Как следует из определения обобщённого 4-импульса, для его вычисления достаточно задать часть лагранжиана . Через вычисляются плотность обобщённого 4-импульса в (25), а также и члены уравнения (13). В результате оказывается, что для векторных полей обобщённый 4-импульс и четырёхмерная величина совпадают друг с другом, а уравнение (13) выполняется и при движении системы с постоянной скоростью.

Полученные результаты применяются для однородной релятивистской системы в виде сферы, исследованной ранее в [24]. Вначале компоненты и , входящие в состав обобщённого 4-импульса , вычисляются для покоящейся системы, а затем для такой же движущейся с постоянной скоростью системы. Из (37) и (48) следует, что компонента движущейся системы в раз превышает компоненту покоящейся системы, где есть фактор Лоренца движения центра сферы в лабораторной системе отсчёта . При этом движущаяся система приобретает релятивистский импульс (49). Особенностью компонент и является то, что в первом приближении они зависят от фактора Лоренца и от потенциала поля давления в центре сферы. Это видно в (50), где обобщённый 4-импульс выражается через 4-скорость сферы.

Анализ текущего положения в общей теории относительности (ОТО) показывает, что в связи с отсутствием ковариантного представления вклада гравитационного поля, полное описание релятивистского и обобщённого 4-импульсов с помощью ОТО в релятивистской гидродинамике отсутствует. Имеющиеся работы ограничиваются тем, что давление носит статический характер, так что в описании поля давления не используется ни его 4-потенциал, ни тензор поля давления в ковариантной формулировке. То же самое следует для поля ускорений, которое не только задаёт в лагранжиане плотность энергии частиц согласно формуле Эйнштейна, но ещё через свой 4-потенциал и тензор ускорений описывает вклад энергии собственного движения частиц внутри системы. Вместо этого используется обычно феноменологический термодинамический поход, когда потоки и энергии частиц вычисляются через температуру, давление, энтропию, химический потенциал и т.д. [25-34]. Однако подход на основе теории поля и Лагранжевой механики позволяет вывести более удобные и ковариантные выражения для обобщённого 4-импульса в (16) и плотности обобщённого 4-импульса в (25), действительные в искривлённом пространстве-времени. Полученные результаты становятся возможными благодаря использованию концепции типичных частиц для описания непрерывного вещества, что даёт возможность упростить процедуру варьирования и осуществить её полностью в четырёхмерном виде.

Список использованных источников

1. Landau L.D., Lifshitz E.M. The Classical Theory of Fields, (1951). Pergamon Press. ISBN 7-5062-4256-7.

2. Mekhitarian V.M. The invariant representation of generalized momentum. Journal of Contemporary Physics (Armenian Academy of Sciences), Vol. 47, Issue 6, pp. 249-256 (2012). doi: 10.3103/S1068337212060011.

3. Kienzler R., Herrmann G. On the four-dimensional formalism in continuum mechanics. Acta Mechanica, Vol. 161, pp. 103-125 (2003). https://doi.org/10.1007/s00707-002-0984-z.

4. Goldstein H., Poole C.P. and Safko J.L. Classical Mechanics (3rd ed.). Addison-Wesley. p. 680. ISBN 9780201657029. (2001).

5. Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy. Jordan Journal of Physics, Vol. 9, No. 1, pp. 1-30 (2016). http://dx.doi.org/10.5281/zenodo.889304; О космологической постоянной, поле ускорения, поле давления и об энергии.

6. Fedosin S.G. The Procedure of Finding the Stress-Energy Tensor and Equations of Vector Field of Any Form. Advanced Studies in Theoretical Physics, Vol. 8, No. 18, pp. 771-779 (2014). http://dx.doi.org/10.12988/astp.2014.47101. // Процедура для нахождения тензора энергии-импульса и уравнений векторного поля любого вида.

7. Fedosin S.G. Two components of the macroscopic general field. Reports in Advances of Physical Sciences, Vol. 1, No. 2, 1750002, 9 pages (2017). http://dx.doi.org/10.1142/S2424942417500025. // Две компоненты макроскопического общего поля.

8. Fedosin S.G. The Principle of Least Action in Covariant Theory of Gravitation. Hadronic Journal, Vol. 35, No. 1, pp. 35-70 (2012). http://dx.doi.org/10.5281/zenodo.889804; Принцип наименьшего действия в ковариантной теории гравитации.

9. Sergey Fedosin, The physical theories and infinite hierarchical nesting of matter, Volume 2, LAP LAMBERT Academic Publishing, pages: 420, ISBN-13: 978-3-659-71511-2. (2015).

10. Einstein A., Infeld L. and Hoffmann B. The Gravitational Equations and the Problem of Motion. Annals of Mathematics, Second Series, Vol. 39, No. 1, pp. 65-100 (1938). http://dx.doi.org/10.2307/1968714.

11. Fedosin S.G. Four-Dimensional Equation of Motion for Viscous Compressible and Charged Fluid with Regard to the Acceleration Field, Pressure Field and Dissipation Field. International Journal of Thermodynamics, Vol. 18, No. 1, pp. 13-24 (2015). doi: 10.5541/ijot.5000034003; Четырёхмерное уравнение движения вязкого сжимаемого вещества с учётом поля ускорений, поля давления и поля диссипации.

12. Fedosin S.G. Estimation of the physical parameters of planets and stars in the gravitational equilibrium model. Canadian Journal of Physics, Vol. 94, No. 4, pp. 370-379 (2016). http://dx.doi.org/10.1139/cjp-2015-0593; Оценка физических параметров планет и звёзд в модели гравитационного равновесия.

13. Фок В.А. Теория пространства, времени и гравитации. 2-е издание. М.: Физматгиз, 1961. 568 с. Fock V.A. The Theory of Space, Time and Gravitation. Pergamon Press, London. (1959).

14. Дирак П. А. М. Общая теория относительности: Пер. с англ./ Под. ред. Д. И. Блохинцева. – Пер. изд.: США, 1975. – М.: Атомиздат, 1978. – 64 с. Dirac P.A.M. General theory of relativity. Florida State University. John Wiley & Sons, Inc., New York - London - Sydney - Toronto, 1975.

15. Fedosin S.G. Relativistic Energy and Mass in the Weak Field Limit. Jordan Journal of Physics. Vol. 8, No. 1, pp. 1-16 (2015). http://dx.doi.org/10.5281/zenodo.889210; Релятивистская энергия и масса в пределе слабого поля.

16. Fedosin S.G. The Gravitational Field in the Relativistic Uniform Model within the Framework of the Covariant Theory of Gravitation. International Letters of Chemistry, Physics and Astronomy, Vol. 78, pp. 39-50 (2018). http://dx.doi.org/10.18052/www.scipress.com/ILCPA.78.39. // Гравитационное поле в релятивистской однородной модели в рамках ковариантной теории гравитации.

17. Fedosin S.G. The Integral Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based on the Pressure Field and Acceleration Field. American Journal of Modern Physics, Vol. 3, No. 4, pp. 152-167 (2014). doi: 10.11648/j.ajmp.20140304.12; Интегральный 4-вектор энергии-импульса и анализ проблемы 4/3 на основе поля давления и поля ускорений.

18. Searle G.F.C. On the steady motion of an electrified ellipsoid. The Philosophical Magazine Series 5, 44 (269), 329-341 (1897). doi:10.1088/1478-7814/15/1/323.

19. Fedosin S.G. 4/3 Problem for the Gravitational Field. Advances in Physics Theories and Applications, Vol. 23, pp. 19-25 (2013). http://dx.doi.org/10.5281/zenodo.889383. // Проблема 4/3 для гравитационного поля.

20. Fedosin S.G. Energy and metric gauging in the covariant theory of gravitation. Aksaray University Journal of Science and Engineering, Vol. 2, Issue 2, pp. 127-143 (2018). http://dx.doi.org/10.29002/asujse.433947. // Калибровка энергии и метрики в ковариантной теории гравитации .

21. Fedosin S.G. The covariant additive integrals of motion in the theory of relativistic vector fields. Bulletin of Pure and Applied Sciences, Vol. 37 D (Physics), No. 2, pp. 64-87 (2018). http://dx.doi.org/10.5958/2320-3218.2018.00013.1. // Ковариантные аддитивные интегралы движения в теории релятивистских векторных полей.

22. Fedosin S.G. The electromagnetic field in the relativistic uniform model. International Journal of Pure and Applied Sciences, Vol. 4, Issue. 2, pp. 110-116 (2018). http://dx.doi.org/10.29132/ijpas.430614. // Электромагнитное поле в релятивистской однородной модели.

23. Fedosin S.G. Equations of Motion in the Theory of Relativistic Vector Fields. International Letters of Chemistry, Physics and Astronomy, Vol. 83, pp. 12-30 (2019). https://doi.org/10.18052/www.scipress.com/ILCPA.83.12.

24. Fedosin S.G. The potentials of the acceleration field and pressure field in rotating relativistic uniform system. Continuum Mechanics and Thermodynamics, Vol. 33, Issue 3, pp. 817-834 (2021). https://doi.org/10.1007/s00161-020-00960-7. // Потенциалы поля ускорений и поля давления во вращающейся релятивистской однородной системе.

25. Luciano Rezzolla and Olindo Zanotti: Relativistic hydrodynamics. Oxford University Press, Oxford, pp. 752 (2013). ISBN: 978-0-19-852890-2.

26. Giulini D. Luciano Rezzolla and Olindo Zanotti: Relativistic hydrodynamics. General Relativity and Gravitation, Vol. 47, Article number: 3 (2015). https://doi.org/10.1007/s10714-014-1839-3.

27. Ehlers J. Contributions to the relativistic mechanics of continuous media. General Relativity and Gravitation, Vol. 25, no. 12, pp. 1225-1266 (1993). https://doi.org/10.1007/BF00759031.

28. Grot R.A. and Eringen A.C. Relativistic continuum mechanics: Part II – electromagnetic interactions with matter. International Journal of Engineering Science, Vol. 4(6), pp. 638-670 (1966). https://doi.org/10.1016/0020-7225(66)90009-7.

29. Salazar J.F. and Zannias T. On extended thermodynamics: From classical to the relativistic regime. International Journal of Modern Physics D, Vol. 29(15), p.2030010 (2020). https://doi.org/10.1142/S0218271820300104.

30. Israel W. and Stewart J.M. Transient relativistic thermodynamics and kinetic theory. Annals of Physics, Vol.118, no. 2, pp. 341-372 (1979). https://doi.org/10.1016/0003-4916(79)90130-1.

31. Ruggeri T. and Masaru S. Classical and Relativistic Rational Extended Thermodynamics of Gases. Heidelberg: Springer, 2021.

32. Souriau J.M. Thermodynamique Relativiste des Fluides. Rendiconti del Seminario Matematico; Università Politecnico di Torino: Torino, Italy, Vol. 35, pp. 21-34 (1978).

33. Géry de Saxcé, Claude Vallee. Bargmann group, momentum tensor and Galilean invariance of Clausius-Duhem inequality. International Journal of Engineering Science, Vol. 50 (1), pp.216-232 (2011). https://dx.doi.org/10.1016/j.ijengsci.2011.08.001.

34. Sedov L.I. A course in continuum mechanics. Volumes. I-IV. Wolters-Noordhoff Publishing, Netherlands, 1971. Седов Л.И., Цыпкин А.Г. Основы макроскопических теорий гравитации и электромагнетизма. М.: Наука (1989). 272 с. ISBN 5-02-013805-3.

Источник: http://sergf.ru/gfm.htm

На научный сайт