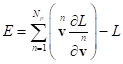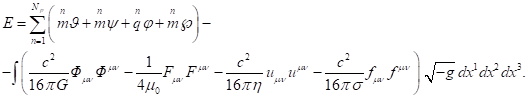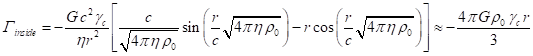Bulletin of Pure and Applied Sciences, Vol. 37 D (Physics), No. 2, pp. 64-87 (2018). http://dx.doi.org/10.5958/2320-3218.2018.00013.1.
Ковариантные аддитивные интегралы
движения в теории релятивистских векторных полей
Федосин Сергей Григорьевич
ул. Свиязева 22-79,
город Пермь, 614088, Пермский край, Россия
e-mail: fedosin@hotmail.com
Выводятся ковариантные выражения для энергии,
импульса и момента импульса произвольной физической системы из частиц и
действующих на них векторных полей. Указанные выражения основываются на функции
Лагранжа системы, являются аддитивными интегралами движения и в замкнутых
системах сохраняются во времени. В ковариантной форме определяются псевдотензор
момента импульса и радиус-вектор центра импульсов системы. Путём интегрирования
по объёму уравнения движения вычисляется интегральный вектор и доказывается
невозможность трактовки интегрального вектора как 4-импульса системы в
противоположность тому, как это делается в общей теории относительности. В
отличие от 4-импульса системы, совокупно характеризующего движение частиц
системы в окружающих их полях, физический смысл интегрального вектора оказывается
в учёте всех энергий и потоков энергии полей, генерируемых частицами. Различие
4-импульса и интегрального вектора связано не только с дуальностью частиц и
полей, но и с разными трансформационными законами для 4-векторов и 4-тензоров
второго ранга. В результате интегральный вектор оказывается псевдовектором
особого рода.
Ключевые слова: интеграл движения; векторное поле; ковариантная теория гравитации; псевдотензор момента импульса; интегральный
вектор; релятивистская однородная система.
The covariant additive integrals of motion in
the theory of relativistic vector fields
Sergey G. Fedosin
22 Sviazeva str., apt. 79, Perm, Perm Krai, 614088, Russia
E-mail: fedosin@hotmail.com
The covariant expressions
are derived for the energy, momentum, and angular momentum of an arbitrary
physical system of particles and vector fields acting on them. These
expressions are based on the Lagrange function of the system, are the additive
integrals of motion, and are conserved over time in closed systems. The angular
momentum pseudotensor and the radius-vector of the system’s center of momentum
are determined in a covariant form. By integrating the motion equation over the
volume the integral vector is calculated and the
impossibility of treatment of the integral vector as the system’s four-momentum
is proved as opposed to how it is done in the general theory of relativity. In
contrast to the system’s four-momentum, which collectively characterizes the
motion of the system’s particles in the surrounding fields, the physical
meaning of the integral vector consists in the taking account of all the
energies and energy fluxes of the fields generated by the particles. The
difference between the four-momentum and the integral vector is associated not
only with the duality of particles and fields, but also with different
transformation laws for four-vectors and four-tensors of second order. As a
result, the integral vector turns out to be a pseudovector of a special kind.
Keywords: integral of motion; vector
field; covariant theory of gravitation; angular momentum pseudotensor; integral
vector; relativistic uniform system.
1. Введение
При рассмотрении физических явлений в искривлённом
пространстве-времени такие аддитивные физические величины, как энергия, импульс
и момент импульса системы из частиц и полей, в ряде случаев могут сохраняться
во времени и тем самым однозначно характеризовать систему. Это обуславливает
важность этих величин, являющихся интегралами движения, как в механике, так и в
других областях физики. В общем случае при вычислении указанных величин
применяется функция Лагранжа, зависящая от метрики пространства-времени и от
полей, связанных с частицами системы [1].
Дальнейшее изложение будет посвящено в
основном векторным полям, используемым для описания явлений в макроскопических системах
с достаточно большим количеством частиц. Эффекты гравитации мы будем
рассматривать в рамках ковариантной теории гравитации [2]. Кроме
электромагнитного поля, являющегося векторным по своей природе, будут учтены
ещё векторное поле ускорений и поле давления [3]. Поле ускорений призвано
ковариантным образом описывать движение частиц, аналогично векторное поле
давления задаёт упругие свойства вещества. При необходимости мы могли бы точно
также учесть ещё поле диссипации [4] и
поля сильного и слабого взаимодействий [5], как соответствующие
макроскопические векторные поля.
Выбор векторных полей связан с тем, что
в них всегда имеется 4-потенциал, тензор поля и тензор энергии-импульса поля.
Это позволяет, в частности, однозначно находить энергию любой части системы,
что затруднительно, например, в общей теории относительности [6, 7], являющейся
тензорной теорией в отношении гравитационного поля.
Мы будем везде использовать сигнатуру
метрики вида (+,–,–,–). Исходной точкой наших
рассуждений является функция Лагранжа для системы частиц и четырёх основных
векторных полей [8, 9]:
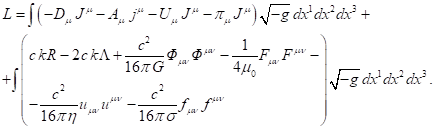(1)
–
массовый 4-ток,
– плотность массы в
сопутствующей частице системе отсчёта,
– 4-скорость точечной
частицы, 
есть 4-смещение, а 
– интервал,
– скорость света, как
мера скорости распространения электромагнитного и гравитационного
взаимодействий,
– зарядовый 4-ток,
– плотность заряда в сопутствующей частице системе отсчёта,
– 4-потенциал поля
ускорений, где 
и 
обозначают скалярный и
векторный потенциалы, соответственно,
– 4-потенциал поля
давления, состоящий из скалярного потенциала 
и векторного
потенциала 
, 
– давление в
сопутствующей частице системе отсчёта, отношение 
задаёт уравнение
состояния вещества,
, где 
– некоторый
коэффициент порядка единицы, подлежащий определению,
– гравитационная
постоянная,
– скалярная кривизна,
– космологическая
постоянная,
есть гравитационный
тензор (тензор напряжённостей гравитационного поля),
– определение
гравитационного тензора с контравариантными индексами с помощью метрического
тензора 
,
– магнитная
постоянная,
– электромагнитный
тензор (тензор напряжённостей электромагнитного поля),
– коэффициент поля
ускорений,
– тензор ускорений,
вычисляемый как 4-ротор от 4-потенциала поля ускорений,
– тензор поля
давления,
– инвариантный
координатный 3-объём, выражаемый через произведение 
дифференциалов
пространственных координат, и через квадратный корень 
из детерминанта 
метрического тензора,
взятого с отрицательным знаком.
Функцию Лагранжа (1) можно представить
в виде 
, то есть как функцию от радиус-векторов 
и скоростей 
каждой из множества
частиц, составляющих рассматриваемую систему. С учётом этого релятивистскую
энергию системы, содержащую 
частиц, можно
определить по формуле [1]:
, (2)
причём суммирование идёт не только по всем частицам, но также по всем трём компонентам скорости каждой частицы, как это требуется при операциях с векторными функциями, включая дифференцирование по вектору и скалярное произведение векторов.
Индекс 
задаёт в (2) номер той
или иной частицы. Мы поместили этот индекс над векторами, описывающими частицы,
чтобы не путать с обычными индексами векторов, выражающими компоненты этих
векторов.
После подстановки (1) в (2) и
калибровки энергии в [9] было представлено выражение для энергии, как для
системы из отдельных частиц, так и в случае непрерывно распределённого
вещества:
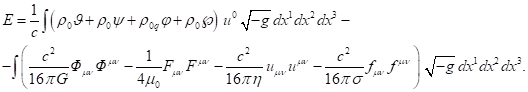(4)
В (3) скалярные потенциалы 
, 
, 
и 
являются усреднёнными
по объёму частиц величинами, которые умножаются на массы этих частиц,
результаты потом суммируются по всем частицам. Поскольку поля могут действовать
вдалеке от своих источников, скалярные потенциалы включают в себя не только собственные
усреднённые потенциалы рассматриваемой частицы, но и усреднённые потенциалы
полей от всего множества других частиц в месте расположения данной частицы.
Величина 
в (4) представляет
собой временную компоненту 4-скорости типичной частицы вещества в той точке,
где осуществляется интегрирование по объёму.
Нашей целью является ковариантное
выражение релятивистского импульса и момента импульса рассматриваемой системы
из частиц и четырёх векторных полей. Основываясь на функции Лагранжа и законах
сохранения, мы представим соответствующие выражения в следующих разделах. Затем
мы опишем псевдотензор момента импульса, содержащий в себе момент импульса
системы и вектор, задающий уравнение движения центра импульсов системы.
Кроме этого, мы рассмотрим определения
интегрального вектора в общей теории относительности и в ковариантной теории
гравитации. Это даст нам возможность понять сущность интегрального вектора и
его кардинальное отличие от 4-импульса системы.
2. Импульс системы
Стандартный подход требует, чтобы в
силу однородности пространства свойства физической системы не менялись при
любом параллельном переносе этой системы как целого. Напомним вкратце вывод
закона сохранения импульса согласно [1]. Пусть радиус-векторы всех частиц
одновременно изменяются от 
до 
, где 
–
некоторый постоянный бесконечно малый вектор. Это приводит к вариации функции
Лагранжа следующего вида:
.
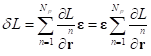Интеграл движения получается из произвольности
выбора и условия равенства нулю
вариации функции Лагранжа, а значит и из условия равенства нулю вариации
действия, как интеграла по координатному времени от функции Лагранжа. Это
приводит к выражению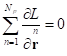 
. Далее применяются уравнения Лагранжа, которые в наших
обозначениях записываются так:
.
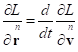(5)
Замена производных по радиус-векторам на производные по скоростям с помощью (5) даёт:
.
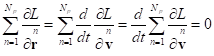В результате в замкнутой системе сохраняется сумма производных от функции Лагранжа по скоростям, рассматриваемая как импульс системы:
.
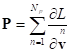(6)
Учтём теперь, что функция Лагранжа (1) согласно [9] может быть представлена как сумма по всем типичным частицам системы так:
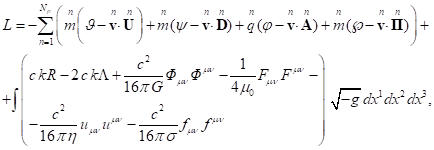(7)
Используя (7) в (6), находим:
. (8)
Импульс (8) согласно определению (6)
представляет собой обобщённый импульс системы и выражается через усреднённые по
объёму частиц векторные потенциалы полей, действующих на частицы системы с
массами 
и зарядами 
. Так как за пределами частиц нет ни массы, ни заряда,
векторные потенциалы гравитационного и электромагнитного полей за пределами
частиц не вносят вклада в импульс системы. Величина 
представляет в сумме
(8) импульс одной частицы с текущим номером 
. В плоском пространстве-времени Минковского векторный
потенциал поля ускорений отдельной точечной частицы равен 
, где 
обозначает фактор
Лоренца, 
есть скорость частицы
[3]. Отсюда видно, что величина 
в (8) действительно
есть релятивистский импульс, вклад в который делают векторные потенциалы всех
полей системы.
Для случая непрерывно распределённого
вещества массы и заряды частиц следует выразить соответственно через плотность
массы и плотность заряда. Учтём вначале выражение для временной компоненты
4-скорости частицы: 
. Тогда для вычисления массы частицы достаточно взять
интеграл по её объёму в системе отсчёта, связанной с частицей:
.
Если же частица движется, элемент её объёма изменяется вследствие движения. Поэтому при интегрировании по движущемуся объёму внутри интеграла появляется добавочный множитель. Это для массы и заряда частицы даёт следующее:
.
(9)
Подставляя (9) в (8) и переходя от суммирования к интегрированию, для релятивистского импульса системы находим:
.
(10)
Если действующие в системе поля не могут удержать частицы в равновесии друг относительно друга, скорости частиц могут отличаться настолько, что форма системы начнёт меняться. Несмотря на это, энергия и импульс замкнутой системы сохраняются. Данные величины входят в 4-импульс системы:
С другой стороны, 4-импульс
определяется как произведение инвариантной инертной массы системы 
на 4-скорость 
точки, называемой
центром импульсов системы:
, (12)
где 
и 
задают соответственно
радиус-вектор и скорость движения центра импульсов, 
есть дифференциал
координатного времени, 
обозначает
дифференциал собственного времени в точке центра импульсов.
Из сравнения (11) и (12) можно
определить скорость центра импульсов и произведение инертной массы системы на 
:
,
. (13)
Значение 
для центра импульсов
следует искать после определения метрики в системе, поскольку 
, где 
есть интервал, 
есть метрический
тензор. После этого из (13) при известной энергии 
определяется и масса
системы 
. Таким образом, энергия (4) и импульс (10) системы с помощью
(13) позволяют свести движение системы к движению центра импульсов.
С помощью преобразования времени и
координат можно перейти от системы отсчёта
, в которой рассматривается движение физической системы, к
системе отсчёта 
, в которой импульс системы 
обращается в нуль.
Такая система отсчёта называется система центра импульсов (center-of-momentum frame).
Как правило, в энергия системы 
имеет минимальное
значение, а 4-импульс записывается так: 
. При этом согласно (13) будет 
.
В центр импульсов
неподвижен, и потому возможное различие координатного времени 
и собственного времени
в центре импульсов
обусловлено лишь действием полей. Так, под действием гравитационного поля
собственное время часов замедлено по отношению к ходу времени часов за
пределами поля.
В пределе слабого поля и малых
скоростей метрика переходит в метрику плоского пространства-времени
Минковского, в которой 
зависит только от
скорости. В этом случае с помощью (13) можно оценить как Лоренц-фактор 
движения центра
импульсов, так и массу системы, выраженные через её энергию и импульс:
, 
.
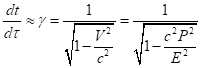3. Момент импульса системы
Для замкнутой системы, не
взаимодействующей с окружением, изотропия пространства должна проявляться в
том, что некоторое свойство физической системы остаётся неизменным при
произвольном повороте системы как целого в пространстве. Аналогично [1],
обозначим через 
вектор бесконечно
малого угла поворота системы относительно произвольной оси 
. Модуль этого вектора будет равен 
, и если смотреть на систему со стороны стрелки оси 
и при этом увеличивать
угол 
по мере вращения системы
против часовой стрелки, то вектор по определению будет
направлен вдоль оси .
Для отыскания интеграла движения
необходимо повернуть систему на произвольный угол и потребовать, чтобы
вариация функции Лагранжа 
при этом обращалась в
нуль. Поворот системы влечёт за собой соответствующие приращения радиус-векторов
и скоростей частиц, выражаемые через векторные произведения:
, 
.
Здесь второе равенство получается из
первого путём дифференцирования по координатному времени с учётом того, что 
ведёт себя при этом
как константа. Кроме этого считается, что дифференциал 
и вариация 
не зависят друг друга,
так что последовательность операций 
эквивалентна
последовательности операций 
. Радиус-векторы частиц 
отсчитываются от
начала системы отсчёта, зафиксированного на оси вращения, соответственно
скорости частиц 
определяются в этой же
системе отсчёта.
Для вариации функции Лагранжа после перестановки векторов в смешанных произведениях получается:
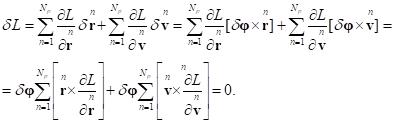
Учтём теперь (5):
.
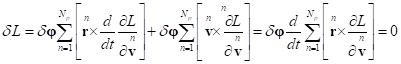Ввиду произвольности вектора отсюда следует,
что в замкнутой системе сохраняется вектор момента импульса:
.
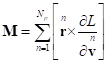(14)
Подставим в (14) функцию Лагранжа (7):
.
(15)
Согласно (15), вклад в суммарный момент
импульса 
вносят векторные
потенциалы всех полей, усреднённые по объёму каждой из частиц системы. При этом
момент импульса отдельной частицы есть 
, где 
есть релятивистский
импульс этой частицы, так что момент импульса 
получается как сумма
моментов импульса отдельных частиц.
Для непрерывно распределённого вещества массы и заряды частиц в (15) следует заменить через интегралы по объёму частиц с помощью (9), а от сумм перейти к интегралам. Это для момента импульса даёт следующее:
. (16)
Момент импульса (16) вычисляется относительно
начала координат выбранной системы отсчёта. При
сдвиге начала координат изменяются радиус-векторы 
, так что величина момента импульса зависит от выбора начала
системы отсчёта, в отличие от энергии и импульса. Вследствие этого вектор
момента импульса отличается от обычных
3-векторов и называется аксиальный вектор, ведя себя как псевдовектор.
4. Псевдотензор момента импульса
В четырёхмерном пространстве-времени
3-векторы заменяются на 4-векторы, а векторному произведению 3-векторов соответствует
операция антисимметричного векторного произведения 4-векторов. Псевдотензор
момента импульса для одной частицы с номером 
как правило
определяется следующим образом:
.
(17)
Для системы частиц следует просуммировать (17) по всем частицам:
. (18)
Четырёхмерный радиус-вектор мгновенного
положения частицы с декартовыми пространственными координатами имеет вид 
и в общем случае не является
4-вектором. Вместо этого 4-вектором является дифференциал 
. В результате 
в (18) является не
тензором, а псевдотензором, зависящим от выбора системы отсчёта.
Сравнение компонент псевдотензора в (18) и компонент 3-вектора момента импульса (15) даёт следующее:
,
, 
.
Это означает, что компоненты момента
импульса системы частиц
являются пространственными компонентами псевдотензора момента импульса . Что касается временных компонент псевдотензора 
, 
и 
, то они оказываются соответствующими компонентами некоторого
3-вектора 
. С учётом (8) и (18) имеем:
. (19)
В данном выражении величина 
представляет собой
временную компоненту 4-импульса частицы с номером 
, 
есть импульс
системы. Введём радиус-вектор центра
импульсов рассматриваемой системы:
.
(20)
Здесь энергия системы 
определена в (3) через
скалярные потенциалы полей и тензоры полей.
Заметим, что для (20) существует предел
слабых полей и малых скоростей движения частиц системы. Если частицы нейтральны
и слабо взаимодействуют друг с другом посредством полей, то в (3) можно
пренебречь вторым членом в виде интеграла для энергии полей, а в первом члене
учесть только скалярный потенциал поля ускорений 
. Тогда энергия одной частицы будет 
, и для радиус-вектора центра импульсов можно записать:
.
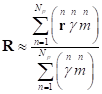Если пойти дальше и пренебречь ещё
факторами Лоренца 
частиц, то центр
импульсов превращается в так называемый центр масс, радиус-вектор 
которого будет равен:
.
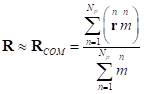Учитывая в (19) соотношение (20) и
заменяя импульс с помощью (13),
находим:
.
(21)
Вектор 
часто называется
время-зависимым динамическим массовым моментом (time-varying dynamic mass moment).
В замкнутой системе псевдотензор 
в (18) должен
сохраняться, и его компоненты должны быть некоторыми константами. Для
пространственных компонент псевдотензора это даёт сохранение момента импульса: 
. Из равенства временных компонент псевдотензора и компонент
вектора (21) тогда следует,
что должно быть 
. Это можно записать как
, где постоянный вектор 
задаёт положение
центра импульсов системы при 
. Так в данной системе отсчёта получается уравнение движения
центра импульсов с постоянной скоростью 
. При этом физическая система имеет сохраняющиеся энергию , импульс , момент импульса 
и псевдотензор момента
импульса . Постоянство скорости следует из постоянства
энергии и импульса согласно (13).
Обратим ещё внимание на выражение для
вектора в (19) и
определение радиус-вектора 
центра импульсов (20).
Они содержат такую величину, как , задающую временную компоненту 4-импульса одной частицы с
произвольным номером 
. Тем самым предполагается, что для каждой частицы
полностью известен её 4-импульс 
. На самом же деле легче всего определяется лишь
пространственная компонента 4-импульса в виде импульса
частицы 
, так как векторные потенциалы полей могут быть найдены из
решения уравнений для полей. Что касается энергии частицы 
, то здесь имеется проблема, связанная с энергией поля,
которая должна быть учтена в . Действительно, из формулы для энергии системы (3) следует,
что вклад в энергию системы посредством интеграла делают ещё поля как внутри
системы, так и за её пределами, вплоть до бесконечности. По всей видимости
энергия полей должна быть каким-то образом включена в энергию каждой из частиц системы,
но сделать это не просто, так как энергия полей в (3) имеет интегральный вид и
не может быть точно разделена на вклады от отдельных частиц.
В связи с этим на первый взгляд
кажется, что определение радиус-вектора центра импульсов (20) имеет формальный
характер. Тем не менее с его помощью можно удовлетворительно оценивать 
в том случае, когда
энергия полей мала по сравнению с энергией частиц в действующих на них
скалярных потенциалах полей. Если известны скорости частиц, можно
воспользоваться первым соотношением в (13) и приблизительно найти энергии
частиц при известных импульсах. Точно также, если известны массы и величины 
для каждой из частиц,
то с помощью второго соотношения в (13) можно оценить энергии отдельных частиц,
а затем подставить их в (20). Всё это для радиус-вектора центра импульсов даёт
следующее:
,
.
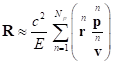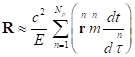(22)
Для случая непрерывно распределённого
вещества все суммы, входящие в определение псевдотензора момента импульса,
заменяются на интегралы, поскольку вместо масс и зарядов частиц используются
произведения плотности массы и плотности заряда на объём типичных частиц. При
этом пространственными компонентами псевдотензора будут компоненты момента
импульса системы частиц согласно
(16). Временные компоненты псевдотензора представлены компонентами вектора 
и согласно (21) они
остаются неизменными. Это следует из определений:
, 
, (23)
где 
обозначает
дифференциал, взятый от интеграла по объёму, 
есть 4-импульс системы
(11).
Для завершения картины выразим
временную и пространственную компоненты 
в (23) с помощью
выражений для энергии (4) и импульса (10) системы:
.
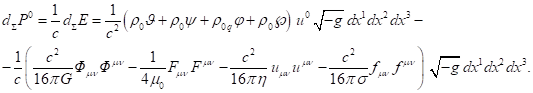
Здесь индекс 
задаёт
пространственные компоненты 4-импульса системы, являющиеся соответственно тремя
компонентами 3-вектора импульса . В частности, для декартовой координатной системы 
, 
, 
.
Для определения радиус-вектора центра
импульсов в случае непрерывного распределения вещества в первом приближении
может быть использовано второе соотношение в (22). Учитывая, что 
, где 
есть временная
компонента 4-скорости частицы с номером , и переходя от суммирования к интегрированию, находим:
. (24)
Здесь энергия 
системы задаётся
соотношением (4). При выводе (22) мы указывали на то, что вклад в энергию
отдельных частиц должны вносить также поля, присутствующие в системе. Это
относится и к (24). Проблема здесь в том, что взаимодействующие друг с другом
частицы не являются сами по себе замкнутыми системами, а погружены в общие
силовые поля, действующие на эти частицы на расстоянии и изменяющие их энергии
и импульсы. Для незамкнутой системы во внешнем поле в виде одной частицы внутри
рассматриваемой системы частиц и полей, применение (4) для интегрирования по
объёму этой частицы даёт энергию части общей системы частиц и полей в этом
объёме, но не энергию частицы как таковой.
В связи с этим нам следует обратиться к
исходной формуле (20) для оценки радиус-вектора центра импульсов. Для упрощения
ситуации будем считать, что рассматриваемая замкнутая система имеет
осесимметричную конфигурацию в отношении распределения энергий частиц и полей.
Тогда видно, что результирующие вклады полей, выходящих из системы за её
пределы, в величину и направление вектора 
обнуляются ввиду
симметрии конфигурации системы. Как бы энергии внешних полей не изменяли
энергии частиц в (20) по сравнению с
энергиями свободных частиц при тех же движениях частиц, величина 
останется прежней. Следовательно,
в (20) достаточно будет учесть энергии частиц в скалярных потенциалах полей и
энергии полей в объёме типичных частиц. Переходя от суммирования к
интегрированию по объёму и используя (4), находим:
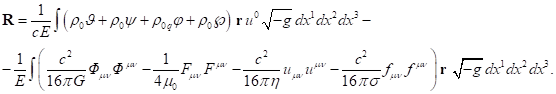(25)
Согласно вышеприведённым рассуждениям, для осесимметричных конфигураций в (25) можно не интегрировать по пространству за пределами системы, где вещество отсутствует.
С другой стороны, мы можем представить
физические системы, в которых основную роль играют энергии полей, а не энергии
частиц вещества. Например, система может состоять из множества заряженных
конденсаторов, в каждом из которых существует сильное электрическое поле.
Каждая энергия обладает инерцией и соответствующей массой, так что при движении
системы с конденсаторами появляется импульс системы, а при вращении системы
возникает и момент импульса. В таком случае основное значение в (25)
приобретает второй интеграл с энергиями полей. Следовательно, единичные
пространственные объёмы, содержащие поля, как внутри, так и за пределами
системы вплоть до бесконечности, можно рассматривать как частицы особого рода,
вносящие свой собственный вклад в определение радиус-вектора центра импульсов 
системы. Это означает,
что (25) должно быть справедливым не
только для осесимметричных систем, но и для систем любой формы. Поэтому в общем
случае интегрирование во втором интеграле в (25) следует осуществлять по всему
бесконечному объёму.
Указанные рассуждения можно
распространить на выражения для энергии 
в (4), для импульса 
в (10) и для момента
импульса 
в (16), в случае
непрерывного распределения вещества. В таком случае эти выражения действительно
становятся аддитивными интегралами движения, так как в них каждая малая часть
пространства содержит либо вещество и поля, либо только поля, и делает свой
собственный вклад в интегралы движения системы.
5. Ситуация в общей теории
относительности
Являясь тензорной теорией, общая теория относительности (ОТО) существенно отличается от векторной ковариантной теории гравитации (КТГ). Во-первых, гравитационное поле в ОТО не имеет ни собственного 4-потенциала, ни тензора поля, вместо этого все гравитационные эффекты выражаются через метрический тензор и его производные. Во-вторых, поле ускорений в ОТО представлено не как векторное, а как более простое, скалярное поле, и также не имеет своего тензора. Это видно из функции Лагранжа, применяемой в ОТО [10]. В наших обозначениях эта функция запишется так:
. (26)
Здесь 
, где ϰ есть гравитационная постоянная Эйнштейна.
В (26) последний член 
задаёт вклад в
функцию Лагранжа от упругой энергии вещества, и если эта энергия связана с
полем давления, то как правило такое поле рассматривается в ОТО не как
векторное, а как простое скалярное поле.
По определению 4-скорость калибруется
таким образом, что 
, так что отсюда вытекает определение для квадрата интервала
в виде 
. В связи с этим скалярная инвариантная величина 
в (26) может быть
записана также как 
[11, 12], а в [8] и [13] для этого используется
произведение 
, где 
есть массовый 4-ток. В отличие от этого, вместо величины мы применяем в (1) в
рамках КТГ инвариант поля ускорений в виде 
, при этом векторный характер поля ускорений
подчёркивается дополнительным инвариантом 
, содержащим тензор ускорений 
.
Рассмотрим теперь, как в ОТО
вычисляются релятивистская энергия, импульс и момент импульса системы из частиц
и связанных с ними полей. Тщательный анализ показывает, что в ОТО отсутствуют
формулы, точным и ковариантным способом определяющие данные величины в
искривлённом пространстве-времени. Мы уже ссылались на статьи [6, 7],
доказывающие невозможность однозначного вычисления в ОТО энергии и массы любой
произвольно выбранной малой части системы. Это связано в первую очередь с тем,
что в ОТО гравитационное поле представлено в функции Лагранжа не прямо, а
косвенно, через скалярную кривизну 
, выражаемую через метрический тензор и его производные.
Для оценки вклада энергии и потока энергии гравитационного поля в обобщённой
теореме Пойнтинга для рассматриваемой системы следовало бы использовать
соответствующий тензор энергии-импульса. Однако вместо него получается найти
лишь псевдотензор энергии-импульса гравитационного поля, обычно для случая,
когда равна нулю космологическая постоянная 
. При этом сам вид этого псевдотензора однозначно не
определён. Известен, например, псевдотензор Эйнштейна 
, который согласно [14] в сумме с тензором энергии-импульса 
вещества и
негравитационных полей должен давать закон сохранения следующего вида:
.
(27)
Предполагается,
что интегрирование по бесконечному трёхмерному объёму временных компонент
тензоров в (27) приводит к 4-импульсу системы с учётом вклада энергии и импульса
гравитационного поля:
. (28)
Индекс 
в 
показывает, что интегральный вектор 
вычисляется с
помощью псевдотензора
Эйнштейна.
Как
указывается в [13], в общем случае с помощью величины нельзя одновременно выполнить два условия для
замкнутой системы: 1) Сохранение во времени суммы всех видов энергии, включая
гравитационную энергию, задаваемую псевдотензором 
; 2) Независимость суммы всех видов энергии в данный момент
времени от выбора системы отсчёта.
Кроме этого,
в отличие от тензора псевдотензор 
несимметричен и потому интегральный
вектор нельзя применять для вычисления
релятивистского момента импульса системы. Для решения этой проблемы Ландау и
Лифшиц изобрели [15] симметричный псевдотензор гравитационного поля 
, так что
выполняется соотношение:
.
(29)
Интеграл по бесконечному объёму даёт:
. (30)
Предполагается, что интегральный вектор
также является
4-импульсом системы. Для обоснования этого вывода необходимо устремить в (30)
псевдотензор 
к нулю, тогда 
стремится к 4-импульсу
системы без учёта вклада гравитационного поля. В таком случае кажется, что 
должен давать
4-импульс с учётом вклада гравитационного поля.
Момент импульса системы Ландау и Лифшиц также находят через интеграл
по бесконечному объёму. Для этого они определяют четырёхмерный псевдотензор
момента импульса как интеграл по объёму от векторного произведения текущего
четырёхмерного радиуса-вектора на дифференциал интегрального вектора , относящегося к заданной точке в пространстве:
.
(31)
Необходимость интегрировать в (28),
(30) и (31) по бесконечному объёму связана с тем, что псевдотензор
гравитационного поля не задаёт однозначное распределение гравитационной энергии
и импульса в рассматриваемой физической системе, не зависящее от выбора системы
отсчёта. Предполагается, что интегрирование по всему объёму позволяет
минимизировать возможные неточности, возникающие в связи с этим
обстоятельством. При этом путём выбора соответствующей системы отсчёта
требуется добиться того, чтобы на бесконечности метрика физической системы
переходила в метрику плоского пространства-времени. В этом случае псевдотензор на бесконечности
обращается в нуль, как это должно быть для гравитационного взаимодействия.
В случае, если в (26) учитывается
космологическая постоянная 
, в (29) псевдотензор
гравитационного поля следует заменить на 
, и сделать соответствующие добавки в (30) и (31).
Аналогично, согласно [16] псевдотензор
в (27) должен быть
заменён на 
, а в (28) вместо 
необходимо
подставить 
.
Указанные выше псевдотензоры гравитационного
поля содержат лишь метрический тензор и его первые производные. Теоретически
возможно существование множества других псевдотензоров гравитационного поля,
которые в сумме с тензором энергии-импульса 
могли бы давать законы
сохранения типа (27) или (29). Мы не будем входить в историю этого вопроса и
описывать другие известные псевдотензоры, поскольку нашей целью была
иллюстрация самого факта неоднозначности выбора псевдотензора для закона
сохранения в ОТО. Ссылки на другие псевдотензоры и связанные с ними проблемы
можно найти, например, в [17].
По мнению авторов в [18], проанализировавших закон сохранения
(27), при выполнении необходимых условий (интегрирование по бесконечному
объёму, «погружённость» системы в пространство Минковского на бесконечности) величина в (28) должна быть
тождественно равна нулю и потому не может быть 4-импульсом и определять
инертную массу системы. Они также обращают внимание на разные трансформационные
законы для тензора материи и псевдотензора
гравитационного поля . Это должно приводить к разным значениям в разных системах
отсчёта, что противоречит условию независимости инертной массы физической
системы от выбора системы отсчёта. В связи с этим в [7] величины типа в (28) и 
в (30) рассматриваются
не как 4-векторы, а как псевдовекторы. В [6] подчёркивается, что ОТО не удовлетворяет принципу соответствия в том
смысле, что выражение для инертной массы в общем случае в пределе слабого поля
и малых скоростей не переходит в соответствующее выражение в теории Ньютона.
Согласно [19], принцип соответствия в ОТО не выполняется для всех аддитивных
интегралов движения, включая энергию, импульс и момент импульса.
Представленные выше соображения вызывают сомнения в том, что в общей теории относительности можно однозначно определить энергию, импульс, инертную массу и момент импульса рассматриваемой физической системы. По крайней мере это точно невозможно в том случае, когда необходимо вычислить эти величины для отдельной, произвольно выбранной внутренней части системы. Мы вернёмся к обсуждению этого вопроса в заключении данной работы, после представления интегрального вектора с точки зрения теории векторных полей.
6. Интегральный вектор
Уравнение для нахождения компонент
метрического тензора в ковариантной теории гравитации для тензоров со
смешанными индексами выглядит следующим образом [9]:
. (32)
Здесь 
– тензор Риччи со смешанными индексами; 
– единичный тензор или символ
Кронекера;
, 
, 
и 
– тензоры энергии-импульса гравитационного и
электромагнитного полей, поля ускорений и поля давления, соответственно.
С помощью ковариантной производной 
можно найти
4-дивергенцию обеих частей (32). Дивергенция левой части равна нулю в силу
равенства нулю дивергенции тензора Эйнштейна, 
, а также как следствие того, что за пределами тела
скалярная кривизна обращается в нуль, 
, а внутри тела она постоянна. Последнее вытекает из
условия калибровки энергии замкнутой системы. Дивергенция правой части (32)
также равна нулю:
. (33)
Тензор 
со смешанными
индексами представляет собой сумму тензоров энергии-импульса всех полей,
действующих в системе. Выражение (33) для пространственных компонент тензоров
есть не что-иное, как записанное в ковариантной форме дифференциальное
уравнение движения вещества под действием сил, генерируемых полями. Что
касается временных компонент тензоров, то для них (33) есть выражение
обобщённой теоремы Пойнтинга для всех полей.
Если (33) было бы возможно проинтегрировать по четырёхмерному объёму, то в результате можно было бы получить аддитивный интеграл движения. При этом надо учесть, что ситуации внутри непрерывно распределённого вещества и за его пределами существенно отличаются друг от друга, то же самое можно сказать о положении дел внутри частиц и за их пределами. Действительно, в пространстве, где нет вещества, есть только электромагнитное и гравитационное поля. В веществе же дополнительно действуют ещё поля ускорений и давления. Поэтому интегрирование по объёму в (33) следует разделить на две части, одно интегрирование по объёму для частиц вещества (либо для типичных частиц непрерывно распределённого вещества), а второе для пространства за пределами вещества.
Поскольку является симметричным
тензором, для его ковариантной производной справедливо следующее представление:
. (34)
Так как гравитация в ковариантной
теории гравитации рассматривается как самостоятельная сущность, не требующая
своего обоснования через метрику, то гравитационные эффекты не исчезают даже в
плоском пространстве-времени Минковского. То же самое справедливо и для
электромагнитного поля и его эффектов. В пространстве-времени Минковского
метрический тензор 
не зависит от
координат и времени и 
, а также 
. Следовательно, (34) упрощается и в слабом поле и при малых
скоростях движения частиц можно записать:
.
Данное выражение можно проинтегрировать
по 4-объёму с учётом теоремы Гаусса:
,
где 
означает элемент
некоторой трёхмерной гиперповерхности, окружающей рассматриваемый 4-объём.
В
замкнутой системе интегральный вектор 
должен быть
постоянным. Для того, чтобы получить представление о
векторе , достаточно определить его мгновенное значение при 
. Например, если 
, можно взять начальный момент
времени 
. В стандартной калибровке начала отсчёта времени и начала
отсчёта пространственных координат в начальный момент времени центр импульсов
замкнутой физической системы, движущийся со скоростью , пересекает начало системы отсчёта наблюдателя. Тогда для
интегрального вектора можно записать:
. (35)
Рассмотрим
теперь самую простую макроскопическую физическую систему в виде сферы,
заполненной хаотически движущимися заряженными типичными частицами настолько
плотно, что применимо приближение сплошной среды. Данные частицы удерживаются
внутри сферы гравитационным полем. Используем далее решения, известные для
такой системы в рамках релятивистской однородной модели, учитывающей векторные
гравитационное и электромагнитное поля, а также поле ускорений и поле давления.
Пусть начало системы отсчёта находится в центре сферы, так что мы будем искать 
в системе
отсчёта, где сфера неподвижна.
Если
учесть хаотичность движения типичных частиц в каждом достаточно большом
элементе объёма, то видно, что глобальные векторные потенциалы всех полей
внутри и снаружи сферы в среднем равны нулю. Это приводит к тому, что равны
нулю и все глобальные соленоидальные векторы, в том числе в среднем равны нулю
как магнитное поле, так и поле гравитационного кручения согласно ковариантной
теории гравитации. Следовательно, в данной физической системе, неподвижной
относительно выбранной системы отсчёта, отсутствуют какие-либо потоки энергии
(потоки импульса) полей, вычисляемые с помощью векторных произведений
напряжённостей полей на соответствующие соленоидальные векторы.
С учётом
(33), 
, причём при значениях индекса 
компоненты 
пропорциональны суммам
потоков энергии отдельных полей. В рассматриваемом случае потоки энергий полей,
типа вектора Пойнтинга или аналогичного вектора Хевисайда для гравитационного
поля, отсутствуют, и в (35) остаётся лишь одна ненулевая, временная компонента
интегрального вектора при значении индекса 
:
. (36)
Учтём теперь явные выражения тензоров
энергии-импульса гравитационного поля [2], [8], электромагнитного поля, поля
ускорений и поля давления [3], [9], выведенные из принципа наименьшего
действия:
,
,
,
. (37)
Как видно из (36) и (37),
для получения 
необходимо проинтегрировать
по объёму сумму временных компонент тензоров энергии-импульса всех полей, то
есть сумму плотностей энергии этих полей. В плоском пространстве-времени
Минковского и при равных нулю соленоидальных векторах плотности энергии полей
зависят только от напряжённостей полей, входящих в тензоры соответствующих
полей. Например, при равном нуле магнитном поле электромагнитный тензор 
зависит лишь от напряжённости
электрического поля 
, и для плотности энергии электромагнитного поля
получается выражение: 
.
Аналогично этому, для плотностей энергии гравитационного поля, поля ускорений и поля давления при равных нулю соленоидальных векторах получается [9], [20]:
, 
, 
,
(38)
где 
, 
и 
обозначают
напряжённости гравитационного поля, поля ускорений и поля давления
соответственно. При этом выражения для напряжённостей полей внутри сферы в
сферических координатах зависят только от текущего радиуса 
, и радиальные
компоненты напряжённостей полей имеют подобный друг другу вид [21]:
,
,
,
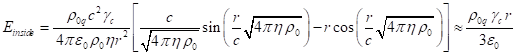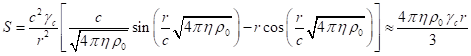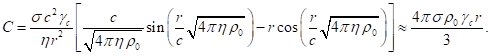
(39)
В (39) 
есть фактор Лоренца
типичных частиц, находящихся в движении в центре сферы. Подставляя (39) в (38),
а результаты в (36), находим внутри сферы путём интегрирования по объёму в
сферических координатах:
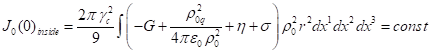. (40)
Как было найдено в [22], в силу уравнения движения типичных частиц внутри сферы в рассматриваемом случае выполняется соотношение:
.
Если учесть данное выражение в (40), то
видно, что временная компонента интегрального вектора внутри сферы обращается в
нуль: 
.
Радиальные компоненты напряжённостей
гравитационного и электромагнитного полей за пределами сферы радиуса 
равны [20]:
,
,
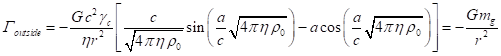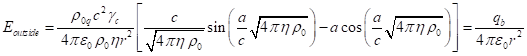(41)
где 
есть гравитационная
масса системы, 
есть полный заряд
системы. При этом инертная масса 
системы в (13)
отличается от гравитационной массы 
. Это связано с тем, что инертная масса 
вычисляется через релятивистскую
энергию системы (4) по формуле (13) и учитывает вклады от всех частиц и полей
системы, тогда как гравитационная масса 
равна суммарной
массе 
частиц, из которых
образовалась система. Аналогично, заряд есть суммарный заряд
частиц, из которых образовалась система.
С помощью (41) можно вычислить
выражения для
и 
в (38). Подставляя эти компоненты тензоров в (36), для временной компоненты интегрального вектора за
пределами сферы находим:
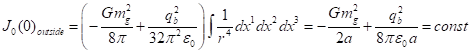. (42)
Складывая (40) и (42), для временной компоненты интегрального вектора имеем:
. (43)
Теперь мы можем понять сущность
интегрального вектора в (35). Данный вектор,
являющийся интегралом по 4-объёму в начальный момент времени от уравнения
движения, записанного в виде (33), показывает распределение в замкнутой системе
энергии и потоков энергии. При движении системы как целого относительно
внешнего наблюдателя вектор 
является функцией
координат и времени, это же касается потенциалов и напряжённостей всех полей.
Если же начало системы отсчёта движется синхронно с центром импульсов, то в
такой системе отсчёта интегральный вектор 
зависит только от
внутреннего движения частиц и полей физической системы. Наиболее простой
вид 
приобретает в том
случае, когда центр импульсов всё время совпадает с началом системы отсчёта, то
есть в системе центра импульсов.
Согласно (43), в неподвижной в среднем
физической системе, когда в веществе нет глобальных массовых и зарядовых токов,
не равна нулю лишь временная компонента 
интегрального вектора.
При этом в рамках релятивистской однородной модели 
равна сумме энергий
гравитационного и электрического полей за пределами вещества. Что касается
объёма внутри вещества системы, здесь сумма вкладов энергий всех полей
обращается в нуль. Для появления ненулевых пространственных компонент 
интегрального вектора
в (35) при значениях индекса 
, необходимо какое-либо стационарное движение вещества и
полей, например, общее вращение, пульсации объёма или перемешивание вещества. В
этом случае в системе появляются соленоидальные векторы и потоки энергии полей.
Очевидно, что в долговременной
перспективе интегральный вектор не будет сохраняться
со временем даже в замкнутой системе, если в нём не будет учтён ещё вклад
векторного поля диссипации, как это было сделано, например, в [4]. В реальных
системах всегда имеется диссипация энергии и превращение энергии движения
потоков частиц в тепловую энергию. Это приводит к изменению состояния имеющихся
в системе потоков вещества до тех пор, пока не наступит состояние равновесия,
когда градиенты скоростей частиц вещества в соседних потоках достигают
минимума. Одновременно с этим происходит и изменение потоков энергии полей, а
значит и компонент интегрального вектора.
Исходной
точкой наших рассуждений при определении аддитивных интегралов движения были
выражения функции Лагранжа (1) для непрерывного распределения вещества, и
функции Лагранжа (7) для случая, когда веществе состоит из отдельных частиц. С
помощью этих выражений по стандартной процедуре мы находим формулы (3) и (4)
для определения релятивистской энергии 
системы для случая
отдельных частиц и непрерывного распределения вещества соответственно, формулы
(8) и (10) для определения релятивистского импульса 
, формулы (15) и (16) для определения релятивистского момента
импульса 
. С помощью энергии 
и импульса 
становится возможным
определить в (11) 4-импульс системы 
.
Поскольку
момент импульса зависит от выбора
системы отсчёта, он является трёхмерным псевдовектором. Аналогично, тензор
момента импульса 
в (18) и в (23) является фактически четырёхмерным
псевдотензором, поскольку содержит в себе как компоненты псевдовектора 
, так и компоненты вектора 
в (21). Вектор задаёт уравнение
движения центра импульсов замкнутой системы с некоторой постоянной скоростью,
при этом радиус-вектор 
центра импульсов
определён нами в ковариантном виде в (25).
В разделе (5) мы кратко описываем, каким способом в общей теории относительности (ОТО) определяются интегралы движения. Анализ ситуации показывает, что в ОТО энергия системы зависит от псевдотензора энергии-импульса гравитационного поля, значения которого в каждой точке зависят от выбора системы отсчёта. Более того, существование множества различных форм псевдотензора энергии-импульса гравитационного поля говорит о том, что в ОТО невозможно однозначно вычислить энергию в любом наперёд заданном небольшом объёме внутри системы. Тем не менее утверждается, что полученные путём интегрирования по бесконечному объёму интегральные векторы типа (28) или (30) дают энергию и импульс системы. К сожалению, такой эвристический вывод не следует из стандартных процедур и физико-математической логики теории поля.
Действительно, для того, чтобы показать, что интегральный вектор в пределе слабого поля стремится к 4-импульсу системы, необходимо устремить к нулю псевдотензор гравитационного поля, а метрику искривлённого пространства-времени устремить к метрике пространства-времени Минковского. В таком предельном случае согласно ОТО гравитационные эффекты должны исчезать полностью, а все физические системы должны вести себя как инерциальные системы отсчёта. Таким образом, идеальные инерциальные системы в ОТО должны быть безмассовыми и не нести заряд, иначе они будут порождать гравитационные и электромагнитные поля, а значит изменится и метрический тензор.
Теперь можно поставить вопрос: можно ли в принципе устремить к нулю в какой-либо системе псевдотензор гравитационного поля? По видимому, сделать это возможно лишь в том случае, если одновременно убирать из системы вещество, несущее массу и заряд. Но тогда при обнулении псевдотензора в системе не останется ни массы, ни заряда, и 4-импульс системы станет равным нулю. Но это единственное состояние системы, в котором можно быть уверенным точно. Если же в системе есть и масса и псевдотензор гравитационного поля, то нет никаких гарантий, что интегральный вектор в ОТО определяет именно 4-импульс системы.
Кроме
этого, в ОТО поле давления используется не как векторное, а как скалярное поле,
то же самое относится к полю ускорений. В результате в интегральном векторе ОТО
не учитываются в полной мере энергии и потоки энергии этих полей. Между тем в
равновесном состоянии гравитационное и электромагнитные поля, поле ускорений и
поле давления в веществе внутри неподвижной в целом системы таковы, что
полностью уравновешивают друг друга. Это означает равенство нулю всех сил, приложенных
в среднем к каждой типичной частице вещества. Более того, наш подход с учётом
ковариантной теории гравитации и четырёх действующих полей показывает, что в
веществе обнуляется как сумма энергий всех полей, так и временная компонента
интегрального вектора 
согласно (40). Лишь
энергия полей (43), выходящих из системы за пределы вещества, вносит свой вклад
в интегральный вектор такой системы. В результате интегральный
вектор связан с энергиями и потоками энергии в системе, но не с 4-импульсом
системы. То же самое должно быть справедливо и для интегрального вектора в ОТО,
поскольку он также получается интегрированием по 4-объёму дивергенции, взятой
от тензора энергии-импульса вещества и
негравитационных полей с добавкой псевдотензора гравитационного поля. В связи с
этим трактовка интегрального вектора как 4-импульса в
ОТО на наш взгляд является ошибочной. Другие проблемы трактовки интегрального
вектора в ОТО как 4-импульса, с соответствующими ссылками, описаны выше в
разделе 5.
Разница
между нашим интегральным вектором 
и 4-импульсом существенна и
заключается в том, что в системе центра импульсов импульс системы , как пространственная векторная компонента 
, равен нулю и отражает движение частиц вещества в векторных
потенциалах полей. Это следует из определения в (8) и в (10), где
присутствуют либо масса и заряд, либо плотности массы и заряда частиц. Что
касается пространственной векторной компоненты интегрального вектора 
, то она связана с движением не частиц, а полей, то есть с
потоками энергии полей, содержащихся в тензорах энергии-импульса полей. То же
самое можно сказать про временные компоненты – если в временная
компонента связана с релятивистской энергией частиц в скалярных потенциалах
с добавкой от энергии полей, то в временная компонента
вычисляется через плотности энергии, содержащиеся в тензорах энергии-импульса
полей. Как видно, способы вычисления и кардинально отличаются
друг от друга, для нахождения требуются 4-потенциалы
полей, а для определения в (35) обязательно
нужны тензоры энергии-импульса всех полей. Получается, что различие и 
связано с
фундаментальным различием частиц и полей, одни не сводятся к другим, хотя и
взаимосвязаны друг с другом.
Другой
особенностью является то, что в произвольной системе
отсчёта импульс системы , как пространственная векторная компонента , уже не равен нулю и отражает свойство инерции как
сопротивление силе, изменяющей импульс 
. А какой смысл имеет пространственная векторная компонента
интегрального вектора 
в произвольной системе
отсчёта? Поскольку есть интегральный вектор
, взятый в начальный момент времени, он отражает лишь
конфигурацию энергии и потоков энергии полей системы в этот момент времени, и
соответствующий импульс полей. Для примера можно взять вращающееся тело,
которое при движении как целое имеет не только 4-импульс , но и за счёт появляющихся от вращения и линейного
движения потоков энергии полей имеет интегральный вектор с ненулевыми пространственными
компонентами. При этом в замкнутой системе в состоянии равновесия становятся
замкнутыми и потоки энергии полей в веществе и за его пределами.
Наконец,
следует упомянуть и то, что интегральный вектор не может в принципе являться
4-вектором и 4-импульсом системы. Это следует из того, что 4-импульс согласно
(12) может быть определён как произведение инертной массы системы на 4-скорость
системы: 
. Это определение действительно в любой системе отсчёта.
Однако подобное определение для интегрального вектора невозможно. Основой
доказательства здесь является так называемая проблема 4/3. Суть её для
электромагнитного поля в том, что масса-энергия поля движущегося заряженного
тела, вычисленная в начальный момент времени путём интегрирования по объёму
компоненты 
тензора
энергии-импульса электромагнитного поля, приблизительно в 4/3 раз меньше, чем
масса-энергия поля, вычисленная в начальный момент времени путём интегрирования
по объёму пространственных компонент 
тензора энергии-импульса.
Наличие
проблемы 4/3, то есть несовпадение указанных выше масс-энергий, вытекает из
того, что четыре временные компоненты тензора энергии-импульса
электромагнитного поля не составляют в совокупности какой-либо 4-вектор, и
преобразуются из одной системы отсчёта в другую не по векторному, а по
тензорному закону. То же самое справедливо и для гравитационного поля в
ковариантной теории гравитации [23], и вообще для любых векторных полей,
имеющих 4-потенциал. Так как интегральный вектор является интегралом по объёму
от суммы временных компонент тензоров энергии-импульса полей, то интегральный
вектор также не является 4-вектором. В этом можно убедиться непосредственно,
для чего достаточно пересчитать временную компоненту в (43), но уже для
движущейся системы в начальный момент времени. Данная компонента интегрального вектора
увеличится за счёт движения системы со скоростью 
приблизительно в 
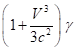раз, где 
есть фактор Лоренца. В
то же время энергия системы, входящая во временную компоненту 4-импульса 
, при тех же условиях увеличится только в 
раз.
Следовательно,
интегральный вектор 
в (35) является
четырёхмерным псевдовектором, но не 4-импульсом системы. Действительно,
интеграл по объёму от дифференциалов 4-импульса может дать 4-импульс системы,
но этого невозможно ожидать от интеграла по объёму от временных компонент
4-тензора энергии-импульса системы, ввиду различия трансформационных законов
4-векторов и 4-тензоров второго ранга.
То,
что интегральный вектор является четырёхмерным
псевдовектором, сближает его по смыслу с другим аддитивным интегралом движения
системы и трёхмерным псевдовектором, а именно с моментом импульса 
. При желании, с помощью мы могли бы подобно
Ландау и Лифшицу аналогично (31) ввести псевдотензор момента интегрального
вектора. Однако в соответствии с вышеизложенным такой псевдотензор был бы не
равен псевдотензору момента импульса 
системы в (18) и в (23), а характеризовал бы лишь момент
импульса потоков энергии полей.
Список использованных источников
1. Ландау, Л.Д., Лифшиц, Е.М.
Механика. Издание 4-е, исправленное. М.: Наука, 1988. 215 с. («Теоретическая физика»,
том I). ISBN 5-02-013850-9. Landau L.D.,
Lifshitz E.M. (1976). Mechanics. Vol. 1 (3rd ed.).
Butterworth-Heinemann. ISBN 978-0-7506-2896-9.
2.
Федосин С.Г. Физические теории и
бесконечная вложенность материи. Пермь, 2009, 844 стр., Табл. 21, Ил.41, Библ. 289 назв.
ISBN 978-5-9901951-1-0.
3.
Fedosin S.G. The procedure of
finding the stress-energy tensor and vector field equations of any form. Advanced
Studies in Theoretical Physics, Vol. 8, pp. 771-779 (2014). doi:10.12988/astp.2014.47101; Процедура для нахождения тензора
энергии-импульса и уравнений векторного поля любого вида.
4.
Fedosin S.G. Four-Dimensional Equation of
Motion for Viscous Compressible and Charged Fluid with Regard to the
Acceleration Field, Pressure Field and Dissipation Field. International
Journal of Thermodynamics, Vol. 18, No. 1, pp. 13-24, (2015). doi: 10.5541/ijot.5000034003; Четырёхмерное
уравнение движения вязкого сжимаемого вещества с
учётом поля ускорений, поля давления и поля диссипации.
5. Fedosin S.G. The Concept of the General Force Vector Field. OALib Journal, Vol. 3, pp. 1-15 (2016), e2459. http://dx.doi.org/10.4236/oalib.1102459 ; Концепция общего силового векторного поля.
6. Денисов
В.И.; Логунов А.А. Инертная
масса, определенная в общей теории относительности, не имеет физического смысла.
ТМФ, 1982, том 51, номер 2, 163-170; Denisov V. I., Logunov A. A. The inertial mass defined in the general theory of relativity has no physical meaning. Theoretical and Mathematical
Physics, Volume 51, Issue 2, pp. 421-426 (1982). http://dx.doi.org/10.1007/BF01036205.
7.
Khrapko R.I. The Truth about the Energy-Momentum Tensor and
Pseudotensor. ISSN 0202-2893, Gravitation and Cosmology, Vol. 20, No. 4, pp. 264-273
(2014). Pleiades Publishing, Ltd., 2014. http://dx.doi.org/10.1134/S0202289314040082; Храпко Р.И. Правда
о тензоре и псевдотензоре энергии-импульса.
8.
Fedosin S.G. The Principle of Least Action in
Covariant Theory of Gravitation. Hadronic
Journal, Vol. 35, No. 1, pp. 35-70 (2012). http://dx.doi.org/10.5281/zenodo.889804.
// Принцип наименьшего действия в
ковариантной теории гравитации.
9. Fedosin S.G. About the
cosmological constant, acceleration field, pressure field and energy. Jordan Journal of Physics, Vol. 9, No. 1, pp. 1-30 (2016}. http://dx.doi.org/10.5281/zenodo.889304;
О космологической постоянной, поле ускорения, поле
давления и об энергии.
10. Фок
В.А. Теория пространства, времени и гравитации. 2-е издание. М.: Физматгиз,
1961. 568 с. Fock V. A. The Theory of Space, Time and Gravitation. (Pergamon Press, London, 1959).
11. Hilbert D. Die
Grundlagen der Physik. (Erste Mitteilung), Göttinger Nachrichten, math.-phys.
Kl., 1915, pp. 395-407.
12.
Weyl H. Raum.
Zeit. Materie. Berlin, J. Springer. 1919.
13. Дирак
П.А.М. Общая теория относительности: Пер. с англ./ Под. ред. Д. И. Блохинцева. – Пер. изд.: США, 1975. – М.: Атомиздат, 1978. – 64 с. Dirac P. A. M. General Theory of Relativity
(1975), Princeton University Press, quick presentation of the bare essentials
of GTR. ISBN 0-691-01146-X.
14. Einstein A. Das hamiltonisches Prinzip und allgemeine Relativitätstheorie (The
Hamiltonian principle and general relativity). Sitzungsber.
preuss. Acad. Wiss. Vol. 2, 1111-1116 (1916).
15. Landau L.D., Lifshitz E.M. The Classical Theory of Fields, (1951). Pergamon Press. ISBN 7-5062-4256-7, chapter 11, section #96.
16. Паули
В. Теория относительности. Пер. с англ. – 2-е изд. / Под
ред. В.Л. Гинзбурга и В.П. Фролова. М.: Наука, 1983. 336 с. Pauli W. Theory of Relativity (Dover
Publications, New York, 1981).
17. M. Sharif, Tasnim Fatima. Energy-Momentum Distribution: A Crucial Problem
in General Relativity. Int. J. Mod. Phys. A, Vol. 20, p. 4309 (2005). https://doi.org/10.1142/S0217751X05020793.
18. Денисов
В.И.; Логунов А.А. Ещё
раз о неравенстве инертной и гравитационной масс в ОТО. ТМФ, 1990, том 85, номер 1, 16-24; Denisov V. I., Logunov A. A. Further remarks on the inequlity of
the inertial and gravitational masses in general relativity. Theoretical and Mathematical Physics, Volume 85, Issue 1, pp. 1022-1028 (1990). https://doi.org/10.1007/BF01017242.
19. Денисов
В.И.; Логунов А.А. Имеет
ли общая теория относительности классический ньютоновский предел? ТМФ,
1980, том 45, номер 3, 291-301; Denisov
V. I., Logunov A. A. Does the general theory of relativity have a classical Newtonian limit?
Theoretical and Mathematical
Physics, Volume 45, Issue 3, pp. 1035-1041 (1980). https://doi.org/10.1007%2FBF01016702.
20.
Fedosin S.G. The Integral Energy-Momentum
4-Vector and Analysis of 4/3 Problem Based on the Pressure Field and
Acceleration Field.
American Journal of Modern Physics. Vol. 3, No. 4, pp. 152-167 (2014). http://dx.doi.org/10.11648/j.ajmp.20140304.12.
// Интегральный 4-вектор энергии-импульса и
анализ проблемы 4/3 на основе поля давления и поля ускорений.
21.
Fedosin S.G. Relativistic Energy and Mass in the
Weak Field Limit. Jordan Journal of Physics. Vol. 8, No. 1, pp. 1-16 (2015). http://dx.doi.org/10.5281/zenodo.889210; Релятивистская
энергия и масса в пределе слабого поля.
22.
Fedosin S.G.
Estimation of the physical parameters of planets and stars in the gravitational
equilibrium model. Canadian Journal of Physics, Vol. 94, No. 4, pp. 370-379 (2016). http://dx.doi.org/10.1139/cjp-2015-0593; Оценка физических параметров планет и звёзд в модели гравитационного
равновесия.
23. Fedosin S.G. 4/3 Problem for the Gravitational Field. Advances in Physics Theories and
Applications, Vol.
23, pp. 19-25 (2013). http://dx.doi.org/10.5281/zenodo.889383. // Проблема 4/3 для гравитационного поля.
Источник: http://sergf.ru/ca.htm