Теорема энергии поля

Теорема энергии поля

Теорема энергии поля, называемая также интегральная теорема энергии поля или теорема Федосина, задаёт в ковариантном четырёхмерном виде в искривлённом пространстве-времени связь между компонентами энергии любого векторного поля, имеющего соответствующий 4-потенциал и тензор данного поля. Согласно данной теореме, интегральный тензорный инвариант энергии поля в произвольном объёме системы может быть определён через энергию частиц в 4-потенциале поля в данном объёме, через производную по времени от интеграла по объёму от произведения 4-потенциала и тензора поля, и через интеграл по поверхности данного объёма от произведения 4-потенциала и тензора поля.

Для электромагнитного (гравитационного) поля с помощью теоремы становится возможным ввести понятия кинетической и потенциальной энергий поля и связать их друг с другом в случае стационарной системы простым численным коэффициентом. В отличие от теоремы вириала, где кинетическая энергия частиц системы по абсолютной величине в два раза меньше потенциальной энергии системы, согласно теореме энергии поля кинетическая энергия электромагнитного (гравитационного) поля по абсолютной величине в два раза превышает всю потенциальную энергию поля. Это позволяет объяснить, почему электростатическая энергия системы заряженных частиц может быть найдена двумя на первый взгляд никак не связанными между собой путями – либо с использованием скалярного потенциала поля, либо с помощью интеграла по всему объёму от тензорного инварианта, являющегося частью тензора энергии-импульса электромагнитного поля.

Теорема энергии поля была доказана Федосиным в 2018 г. и опубликована в 2019 г. ^[1] Теорема может быть применена к таким векторным полям, как поле ускорений, поле давления, гравитационное поле, электромагнитное поле, поле диссипации, общее поле. и т.д. Как правило, в реальных системах одновременно присутствует сразу несколько полей. В предположении, что действует условие суперпозиции полей и независимость полей друг от друга, теорема может применяться к каждому векторному полю по отдельности. Проверка теоремы для идеальной релятивистской однородной системы, содержащей не вращающиеся и хаотически движущиеся частицы, показывает полное совпадение во всех значащих членах для каждого поля.

Содержание

1 Электромагнитное поле
2 Гравитационное поле
3 Поле ускорений и поле давления
4 Значение теоремы
5 Ссылки
6 См. также
7 Внешние ссылки

Электромагнитное поле

Интегральная теорема поля имеет следующий вид:

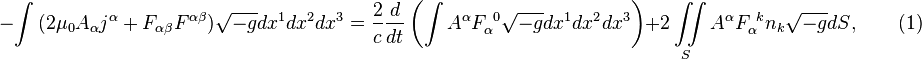
$~-\int {(2\mu _{0}A_{\alpha }j^{\alpha }+F_{{\alpha \beta }}F^{{\alpha \beta }}){\sqrt {-g}}dx^{1}dx^{2}dx^{3}}={\frac {2}{c}}{\frac {d}{dt}}\left(\int {A^{\alpha }F_{\alpha }^{{\ 0}}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}\right)+2\iint \limits _{S}{A^{\alpha }F_{\alpha }^{{\ k}}n_{k}{\sqrt {-g}}dS},\qquad (1)$

где $~\mu _{0}$ есть магнитная постоянная; $~A_{\alpha }$ – электромагнитный 4-потенциал; $~j^{\alpha }$ – электромагнитный 4-ток; $~F_{{\alpha \beta }}$ – тензор электромагнитного поля; $~{\sqrt {-g}}dx^{1}dx^{2}dx^{3}$ – элемент инвариантного объёма, выражаемый через произведение $~dx^{1}dx^{2}dx^{3}$ дифференциалов пространственных координат, и через квадратный корень $~{\sqrt {-g}}$ из детерминанта метрического тензора, взятого с отрицательным знаком; – скорость света; последний интеграл в правой части есть поверхностный интеграл второго рода по двумерной поверхности , окружающей рассматриваемый объём; $~n_{k}$ – трёхмерный вектор нормали к поверхности , направленный наружу.

Равенство (1) существенно упрощается в том случае, когда электромагнитное поле рассматривается не просто в ограниченном объёме, а сразу во всём бесконечном объёме, выходящем за пределы замкнутой физической системы. Тогда последний интеграл в правой части (1) обнуляется несмотря на бесконечную величину окружающей поверхности , так как вдали от зарядов системы, на бесконечности, равны нулю и 4-потенциал $~A^{\alpha }$ , и тензор поля $~F_{\alpha }^{{\ k}}$ .

Как правило, в электростатике, а также в релятивистской однородной системе, произведение $~A^{\alpha }F_{\alpha }^{{\ 0}}$ равно нулю, так что обнуляется и первый интеграл в правой части (1). В этом случае в (1) остаётся следующее:

$~\int {(2\mu _{0}A_{\alpha }j^{\alpha }+F_{{\alpha \beta }}F^{{\alpha \beta }}){\sqrt {-g}}dx^{1}dx^{2}dx^{3}}=0.\qquad (2)$

Если обозначить

$~E_{{kf}}=\int {A_{\alpha }j^{\alpha }{\sqrt {-g}}dx^{1}dx^{2}dx^{3}},$

$~W_{f}={\frac {1}{4\mu _{0}}}\int {F_{{\alpha \beta }}F^{{\alpha \beta }}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}},$

то (2) переписывается так:

$~E_{{kf}}+2W_{f}=0.\qquad (3)$

Здесь энергию $~E_{{kf}}$ можно считать кинетической энергией поля, связанной с 4-током $~j^{\alpha }$ . При этом энергию $~W_{f}$ следует рассматривать как потенциальную энергию поля, находимую через компоненты электромагнитного тензора, то есть через напряжённость электрического поля и индукцию магнитного поля.

Можно заметить, что (3) с точностью до численного коэффициента напоминает теорему вириала в виде

$~E_{k}+{\frac {1}{2}}W\approx 0,$

где $~E_{k}$ есть кинетическая энергия частиц системы, обозначает потенциальную энергию системы.

В теории векторных полей вклад зарядов и электромагнитного поля в релятивистскую энергию физической системы задаётся выражением: ^[2]

$~E_{{el}}={\frac {1}{c}}\int {\rho _{{0q}}\varphi u^{0}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}+{\frac {1}{4\mu _{0}}}\int {F_{{\mu \nu }}F^{{\mu \nu }}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}},$

где $~\rho _{{0q}}$ есть плотность заряда элемента вещества в сопутствующей ему системе отсчёта, $~\varphi$ – скалярный потенциал в месте нахождения элемента заряженного вещества, $~u^{0}$ – временная компонента 4-скорости элемента вещества.

Пусть для физической системы выполняется соотношение (2), причём глобальный векторный потенциал электромагнитного поля везде в веществе равен нулю либо таков, что не делает вклада в энергию $~E_{{kf}}$ . Тогда с учётом (3) будет:

$~E_{{el}}=E_{{kf}}+W_{f}=-W_{f}={\frac {1}{2}}E_{{kf}}.\qquad (4)$

В данном случае видно, что суммарная электромагнитная энергия частиц и поля может быть найдена двумя различными путями – либо через энергию $~W_{f}$ , либо через энергию $~E_{{kf}}$ . В электростатике энергия $~W_{f}$ выражается через напряжённость электрического поля и определяется временной компонентой тензора энергии-импульса электромагнитного поля, а энергия $~E_{{kf}}$ зависит лишь от распределения скалярного потенциала поля и 4-тока.

Гравитационное поле

Интегральная теорема для гравитационного поля записывается так:

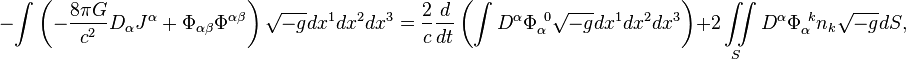
$~-\int {\left(-{\frac {8\pi G}{c^{2}}}D_{\alpha }J^{\alpha }+\Phi _{{\alpha \beta }}\Phi ^{{\alpha \beta }}\right){\sqrt {-g}}dx^{1}dx^{2}dx^{3}}={\frac {2}{c}}{\frac {d}{dt}}\left(\int {D^{\alpha }\Phi _{\alpha }^{{\ 0}}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}\right)+2\iint \limits _{S}{D^{\alpha }\Phi _{\alpha }^{{\ k}}n_{k}{\sqrt {-g}}dS},$

где есть гравитационная постоянная; $~D_{\alpha }$ – гравитационный 4-потенциал; $~J^{\alpha }$ – массовый 4-ток; $~\Phi _{{\alpha \beta }}$ – тензор гравитационного поля.

Все выводы, сделанные в отношении электромагнитного поля, остаются в силе и для гравитационного поля. Например, в системе с неподвижными массами и в релятивистской однородной системе будет справедливо соотношение:

$~\int {\left(-{\frac {8\pi G}{c^{2}}}D_{\alpha }J^{\alpha }+\Phi _{{\alpha \beta }}\Phi ^{{\alpha \beta }}\right){\sqrt {-g}}dx^{1}dx^{2}dx^{3}}=0.$

Выражения для кинетической и потенциальной энергии гравитационного поля:

$~E_{{kf}}=\int {D_{\alpha }J^{\alpha }{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}.$

$~W_{f}=-{\frac {c^{2}}{16\pi G}}\int {F_{{\alpha \beta }}F^{{\alpha \beta }}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}.$

Вклад частиц и гравитационного поля в энергию физической системы имеет вид:

$~E_{{gr}}={\frac {1}{c}}\int {\rho _{0}\psi u^{0}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}-{\frac {c^{2}}{16\pi G}}\int {\Phi _{{\mu \nu }}\Phi ^{{\mu \nu }}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}},$

где $~\rho _{0}$ есть плотность массы элемента вещества в сопутствующей ему системе отсчёта, $~\psi$ – гравитационный скалярный потенциал в месте нахождения элемента вещества.

Если векторный потенциал гравитационного поля не вносит свой вклад в энергию системы, то снова выполняется равенство типа (4), уже в отношении энергии $~E_{{gr}}$ гравитационного поля.

Поле ускорений и поле давления

Для поля ускорений и поля давления интегральная теорема энергии полей записывается следующим образом:

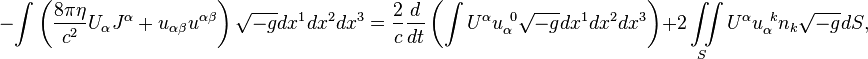
$~-\int {\left({\frac {8\pi \eta }{c^{2}}}U_{\alpha }J^{\alpha }+u_{{\alpha \beta }}u^{{\alpha \beta }}\right){\sqrt {-g}}dx^{1}dx^{2}dx^{3}}={\frac {2}{c}}{\frac {d}{dt}}\left(\int {U^{\alpha }u_{\alpha }^{{\ 0}}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}\right)+2\iint \limits _{S}{U^{\alpha }u_{\alpha }^{{\ k}}n_{k}{\sqrt {-g}}dS},$

$~-\int {\left({\frac {8\pi \sigma }{c^{2}}}\pi _{\alpha }J^{\alpha }+f_{{\alpha \beta }}f^{{\alpha \beta }}\right){\sqrt {-g}}dx^{1}dx^{2}dx^{3}}={\frac {2}{c}}{\frac {d}{dt}}\left(\int {\pi ^{\alpha }f_{\alpha }^{{\ 0}}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}\right)+2\iint \limits _{S}{\pi ^{\alpha }f_{\alpha }^{{\ k}}n_{k}{\sqrt {-g}}dS},$

где $~\eta$ есть постоянная поля ускорений; $~U_{\alpha }$ – 4-потенциал поля ускорений; $~u_{{\alpha \beta }}$ – тензор ускорений; $~\sigma$ – постоянная поля давления; $~\pi _{\alpha }$ – 4-потенциал поля давления; $~f_{{\alpha \beta }}$ – тензор поля давления.

Особенностью поля ускорений и поля давления является то, что эти поля действуют только в пределах вещества системы. Поэтому поверхностные интегралы в правой части выражений для энергии поля берутся по внешней поверхности того объёма, в котором присутствует вещество.

Значение теоремы

Значение теоремы заключается в том, что она позволяет во многих случаях существенно облегчить вычисление релятивистской энергии системы. По своему смыслу теорема энергии поля описывает связи между компонентами энергии полей и тем самым отличается от теоремы вириала, связанной с компонентами энергии частиц.

Теорема даёт возможность дополнительно связать между собой и разграничить роль 4-потенциалов, тензоров полей и тензоров энергии-импульса в теории векторных полей. Известно например, что уравнение движения частиц системы может быть записано через любые из этих величин, ^[3] причём временная компонента уравнения движения представляет собой обобщённую теорему Пойнтинга. ^[4]

Уравнение для метрики при соответствующей калибровке может быть выражено лишь через тензоры энергии-импульса полей, ^[5] так же как и четырёхмерный интегральный вектор, описывающий энергию полей системы и задающий вектор потока этой энергии. Однако интегральный вектор не является настоящим 4-вектором, и хотя он сохраняется в замкнутых системах, он не может заменить собой 4-импульс физической системы. ^[6]

С другой стороны, тензоры энергии-импульса полей полностью отсутствуют в лагранжиане, в гамильтониане, в энергии, в импульсе, в 4-импульсе и в обобщённом 4-импульсе системы. ^[7] Это означает, что плотности энергии полей и трёхмерные векторы потоков энергии полей типа вектора Пойнтинга, содержащиеся в тензорах энергии-импульса, не позволяют вычислить ни обобщённый 4-импульс, ни 4-импульс системы. Для этого необходимо использовать 4-потенциалы и тензоры полей. ^[8]

Ссылки

1. Fedosin S.G. The Integral Theorem of the Field Energy. Gazi University Journal of Science. Vol. 32, No. 2, pp. 686-703 (2019). http://dx.doi.org/10.5281/zenodo.3252783. // Интегральная теорема энергии поля.

2. Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy. Jordan Journal of Physics. Vol. 9, No. 1, pp. 1-30 (2016). http://dx.doi.org/10.5281/zenodo.889304; статья на русском языке: О космологической постоянной, поле ускорения, поле давления и об энергии.

3. Fedosin S.G. Equations of Motion in the Theory of Relativistic Vector Fields. International Letters of Chemistry, Physics and Astronomy, Vol. 83, pp. 12-30 (2019). https://doi.org/10.18052/www.scipress.com/ILCPA.83.12. // Уравнения движения в теории релятивистских векторных полей.

4. Fedosin S.G. The generalized Poynting theorem for the general field and solution of the 4/3 problem. International Frontier Science Letters, Vol. 14, pp. 19-40 (2019). https://doi.org/10.18052/www.scipress.com/IFSL.14.19. // Обобщённая теорема Пойнтинга для общего поля и решение проблемы 4/3.

5. Fedosin S.G. Energy and metric gauging in the covariant theory of gravitation. Aksaray University Journal of Science and Engineering, Vol. 2, Issue 2, pp. 127-143 (2018). http://dx.doi.org/10.29002/asujse.433947. // Калибровка энергии и метрики в ковариантной теории гравитации.

6. Fedosin S.G. The covariant additive integrals of motion in the theory of relativistic vector fields. Bulletin of Pure and Applied Sciences, Vol. 37 D (Physics), No. 2, pp. 64-87 (2018). http://dx.doi.org/10.5958/2320-3218.2018.00013.1. // Ковариантные аддитивные интегралы движения в теории релятивистских векторных полей.

7. Fedosin S.G. Generalized four-momentum for continuously distributed matter. Preprint, 2018.

8. Fedosin S.G. Что мы должны понимать под 4-импульсом физической системы? Preprint, 2018.

См. также

Теорема вириала
Теорема о равнораспределении
Уравнение векторного поля
Релятивистская однородная система
Электромагнитное поле

Внешние ссылки

Field_energy_theorem

Источник: http://sergf.ru/tp.htm

На список страниц