Field energy theorem

Field energy theorem

Field energy theorem, also called the integral theorem of field energy or Fedosin’s theorem, defines in a covariant four-dimensional form in a curved spacetime the relation between components of the energy of any vector field, which has the corresponding four-potential and the tensor of this field. According to this theorem, the integral tensor invariant of the field energy in an arbitrary volume of a system can be determined in terms of the particles’ energy in the field’s four-potential in the given volume, in terms of the time derivative of the volume integral of the product of the four-potential by the field tensor, and in terms of the integral over the surface of the given volume taken of the product of the four-potential by the field tensor.

For the electromagnetic (gravitational) field, with the help of the theorem we can introduce the concepts of the kinetic and potential energies of the field and relate them to each other with a simple numerical coefficient in the case of a stationary system. In contrast to the virial theorem, where the kinetic energy of the system’s particles is half as large in the absolute value as the system’s potential energy, according to the field energy theorem the kinetic energy of the electromagnetic (gravitational) field is twice as large in the absolute value as the entire potential energy of the field. This allows us to explain why the electrostatic energy of a system of charged particles can be found by two seemingly unrelated ways – using either the scalar field potential or the integral over the entire volume of the tensor invariant, which is part of the stress-energy tensor of the electromagnetic field.

The field energy theorem was proved by Fedosin in 2018 and was published in 2019. ^[1] The theorem can be applied to such vector fields as the acceleration field, pressure field, gravitational field, electromagnetic field, dissipation field, and general field, etc. As a rule, in real systems there are several fields at the same time. Under the assumption that the conditions of the fields’ superposition and independence of the fields from each other hold true, the theorem can be applied to each vector field separately. The verification of the theorem for an ideal relativistic uniform system containing non-rotating and randomly moving particles shows complete coincidence in all significant terms for each field.

Contents

1 Electromagnetic field
2 Gravitational field
3 Acceleration field and pressure field
4 Significance of the theorem
5 References
6 See also
7 External links

Electromagnetic field

The field energy theorem has the following form:

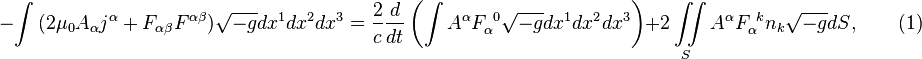
$~-\int {(2\mu _{0}A_{\alpha }j^{\alpha }+F_{{\alpha \beta }}F^{{\alpha \beta }}){\sqrt {-g}}dx^{1}dx^{2}dx^{3}}={\frac {2}{c}}{\frac {d}{dt}}\left(\int {A^{\alpha }F_{\alpha }^{{\ 0}}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}\right)+2\iint \limits _{S}{A^{\alpha }F_{\alpha }^{{\ k}}n_{k}{\sqrt {-g}}dS},\qquad (1)$

where $~\mu _{0}$ is the magnetic constant; $~A_{\alpha }$ is the electromagnetic four-potential; $~j^{\alpha }$ is the electromagnetic four-current; $~F_{{\alpha \beta }}$ is the electromagnetic field tensor; $~{\sqrt {-g}}dx^{1}dx^{2}dx^{3}$ is the element of the invariant volume, expressed in terms of the product $~dx^{1}dx^{2}dx^{3}$ of the differentials of space coordinates and in terms of the square root $~{\sqrt {-g}}$ of the determinant of the metric tensor taken with a negative sign; is the speed of light; the last integral on the right-hand side is the surface integral of the second kind taken over the two-dimensional surface surrounding the volume under consideration; $~n_{k}$ is the outward-directed three-dimensional normal vector to the surface .

Equation (1) is significantly simplified in case when the electromagnetic field is considered not just in a limited volume, but in the entire infinite volume that goes beyond the limits of a closed physical system. Then the last integral on the right-hand side of (1) vanishes despite the infinite size of the surrounding surface , since far from the system’s charges, at infinity, both the four-potential $~A^{\alpha }$ and the field tensor $~F_{\alpha }^{{\ k}}$ are equal to zero.

As a rule, in electrostatics, as well as in the relativistic uniform system, the product $~A^{\alpha }F_{\alpha }^{{\ 0}}$ is equal to zero, so the first integral on the right-hand side of (1) also vanishes. In this case, the following remains in (1):

$~\int {(2\mu _{0}A_{\alpha }j^{\alpha }+F_{{\alpha \beta }}F^{{\alpha \beta }}){\sqrt {-g}}dx^{1}dx^{2}dx^{3}}=0.\qquad (2)$

If we denote

$~E_{{kf}}=\int {A_{\alpha }j^{\alpha }{\sqrt {-g}}dx^{1}dx^{2}dx^{3}},$

$~W_{f}={\frac {1}{4\mu _{0}}}\int {F_{{\alpha \beta }}F^{{\alpha \beta }}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}},$

then (2) is rewritten as follows:

$~E_{{kf}}+2W_{f}=0.\qquad (3)$

Here, the energy $~E_{{kf}}$ can be considered as the field’s kinetic energy associated with the four-current $~j^{\alpha }$ . In this case, the energy $~W_{f}$ should be considered as the field’s potential energy, found in terms of the components of the electromagnetic tensor, that is, in terms of the electric field strength and the magnetic field induction.

It can be noted that (3), with an accuracy up to a numerical coefficient, resembles the virial theorem in the following form:

$~E_{k}+{\frac {1}{2}}W\approx 0,$

where $~E_{k}$ is the kinetic energy of the system’s particles, denotes the potential energy of the system.

In the theory of vector fields, the contribution of the charges and the electromagnetic field to the relativistic energy of a physical system is given by the expression: ^[2]

$~E_{{el}}={\frac {1}{c}}\int {\rho _{{0q}}\varphi u^{0}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}+{\frac {1}{4\mu _{0}}}\int {F_{{\mu \nu }}F^{{\mu \nu }}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}},$

where $~\rho _{{0q}}$ is the charge density of the matter element in the comoving reference frame, $~\varphi$ is the scalar potential at the location of the element of charged matter, $~u^{0}$ is the time component of the four-velocity of the matter element.

Suppose relation (2) holds for a physical system, while the global vector potential of the electromagnetic field is zero everywhere in the matter or such that it does not make a contribution to the energy $~E_{{kf}}$ . Then taking into account (3) we will obtain:

$~E_{{el}}=E_{{kf}}+W_{f}=-W_{f}={\frac {1}{2}}E_{{kf}}.\qquad (4)$

In this case, we can see that the total electromagnetic energy of the particles and the field can be found by two different ways – either in terms of the energy $~W_{f}$ or in terms of the energy $~E_{{kf}}$ . In electrostatics, the energy $~W_{f}$ is expressed in terms of the electric field strength and is defined by the time component of the stress-energy tensor of the electromagnetic field, and the energy $~E_{{kf}}$ depends only on the distribution of the scalar field potential and the four-current.

Gravitational field

The field energy theorem for the gravitational field is written as follows:

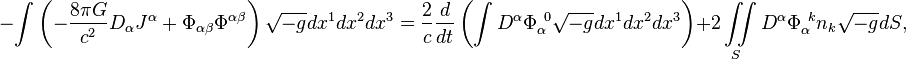
$~-\int {\left(-{\frac {8\pi G}{c^{2}}}D_{\alpha }J^{\alpha }+\Phi _{{\alpha \beta }}\Phi ^{{\alpha \beta }}\right){\sqrt {-g}}dx^{1}dx^{2}dx^{3}}={\frac {2}{c}}{\frac {d}{dt}}\left(\int {D^{\alpha }\Phi _{\alpha }^{{\ 0}}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}\right)+2\iint \limits _{S}{D^{\alpha }\Phi _{\alpha }^{{\ k}}n_{k}{\sqrt {-g}}dS},$

where is the gravitational constant; $~D_{\alpha }$ is the gravitational four-potential; $~J^{\alpha }$ is the mass four-current; $~\Phi _{{\alpha \beta }}$ is the gravitational tensor.

All the conclusions made with respect to the electromagnetic field hold true for the gravitational field. For example, in the system with fixed masses and in the relativistic uniform system, the following relation will be valid:

$~\int {\left(-{\frac {8\pi G}{c^{2}}}D_{\alpha }J^{\alpha }+\Phi _{{\alpha \beta }}\Phi ^{{\alpha \beta }}\right){\sqrt {-g}}dx^{1}dx^{2}dx^{3}}=0.$

The expressions for the kinetic and potential energy of the gravitational field are as follows:

$~E_{{kf}}=\int {D_{\alpha }J^{\alpha }{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}.$

$~W_{f}=-{\frac {c^{2}}{16\pi G}}\int {F_{{\alpha \beta }}F^{{\alpha \beta }}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}.$

The contribution of the particles and the gravitational field to the energy of the physical system has the form:

$~E_{{gr}}={\frac {1}{c}}\int {\rho _{0}\psi u^{0}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}-{\frac {c^{2}}{16\pi G}}\int {\Phi _{{\mu \nu }}\Phi ^{{\mu \nu }}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}},$

where $~\rho _{0}$ is the mass density of the matter element in the comoving reference frame, $~\psi$ is the gravitational scalar potential at the location of the matter element.

If the vector potential of the gravitational field does not make a contribution to the system’s energy, then the equation of type (4) is again satisfied, but now with respect to the energy $~E_{{gr}}$ of the gravitational field.

Acceleration field and pressure field

For the acceleration field and the pressure field, the integral theorem of field energy is written as follows:

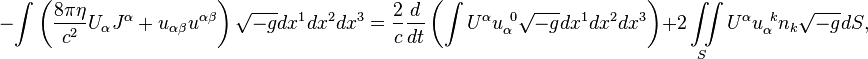
$~-\int {\left({\frac {8\pi \eta }{c^{2}}}U_{\alpha }J^{\alpha }+u_{{\alpha \beta }}u^{{\alpha \beta }}\right){\sqrt {-g}}dx^{1}dx^{2}dx^{3}}={\frac {2}{c}}{\frac {d}{dt}}\left(\int {U^{\alpha }u_{\alpha }^{{\ 0}}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}\right)+2\iint \limits _{S}{U^{\alpha }u_{\alpha }^{{\ k}}n_{k}{\sqrt {-g}}dS},$

$~-\int {\left({\frac {8\pi \sigma }{c^{2}}}\pi _{\alpha }J^{\alpha }+f_{{\alpha \beta }}f^{{\alpha \beta }}\right){\sqrt {-g}}dx^{1}dx^{2}dx^{3}}={\frac {2}{c}}{\frac {d}{dt}}\left(\int {\pi ^{\alpha }f_{\alpha }^{{\ 0}}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}\right)+2\iint \limits _{S}{\pi ^{\alpha }f_{\alpha }^{{\ k}}n_{k}{\sqrt {-g}}dS},$

where $~\eta$ is the acceleration field constant; $~U_{\alpha }$ is the four-potential of the acceleration field; $~u_{{\alpha \beta }}$ is the acceleration tensor; $~\sigma$ is the pressure field constant; $~\pi _{\alpha }$ is the four-potential of the pressure field; $~f_{{\alpha \beta }}$ is the pressure field tensor.

The characteristic feature of the acceleration field and the pressure field is that these fields act only within the limits of the system’s matter. Therefore, the surface integrals on the right-hand side of the expressions for the field energy are taken over the outer surface of the volume, in which the matter is present.

Significance of the theorem

The significance of the theorem lies in the fact that in many cases it allows us to simplify much the calculation of the system’s relativistic energy. According to its meaning, the field energy theorem describes the relations between the components of the fields’ energy and thus it differs from the virial theorem related to the components of the particles’ energy. The theorem additionally allows us to interrelate and differentiate the role of the four-potentials, field tensors and stress-energy tensors within the framework of the theory of vector fields. For example, it is known that the equation of motion of the system’s particles can be written in terms of any of these quantities, ^[3] while the time component of the equation of motion represents the generalized Pointing theorem. ^[4]

The equation for the metric with appropriate gauging can only be expressed in terms of the stress-energy tensors of the fields, ^[5] just as the four-dimensional integral vector describing the energy of the system’s fields and defining the vector of the flux of this energy. However, the integral vector is not a real four-vector, and although it is conserved in closed systems, it cannot replace the four-momentum of a physical system. ^[6]

On the other hand, the stress-energy tensors of the fields are completely absent in the Lagrangian, in the Hamiltonian, in the energy, in the momentum, in the four-momentum and in the generalized four-momentum of the system. ^[7] This means that the fields’ energy densities and the three-dimensional vectors of the fields’ energy fluxes, such as the Poynting vector, that are contained in the stress-energy tensors do not allow us to calculate either the generalized four-momentum or the system’s four-momentum. For this purpose, it is necessary to use the four-potentials and the field tensors. ^[8]

References

1. Fedosin S.G. The Integral Theorem of the Field Energy. Gazi University Journal of Science. Vol. 32, No. 2, pp. 686-703 (2019). http://dx.doi.org/10.5281/zenodo.3252783.

2. Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy. Jordan Journal of Physics. Vol. 9, No. 1, pp. 1-30 (2016). http://dx.doi.org/10.5281/zenodo.889304.

3. Fedosin S.G. Equations of Motion in the Theory of Relativistic Vector Fields. International Letters of Chemistry, Physics and Astronomy, Vol. 83, pp. 12-30 (2019). https://doi.org/10.18052/www.scipress.com/ILCPA.83.12.

4. Fedosin S.G. The generalized Poynting theorem for the general field and solution of the 4/3 problem. International Frontier Science Letters, Vol. 14, pp. 19-40 (2019). https://doi.org/10.18052/www.scipress.com/IFSL.14.19.

5. Fedosin S.G. Energy and metric gauging in the covariant theory of gravitation. Aksaray University Journal of Science and Engineering, Vol. 2, Issue 2, pp. 127-143 (2018). http://dx.doi.org/10.29002/asujse.433947.

6. Fedosin S.G. The covariant additive integrals of motion in the theory of relativistic vector fields. Bulletin of Pure and Applied Sciences, Vol. 37 D (Physics), No. 2, pp. 64-87 (2018). http://dx.doi.org/10.5958/2320-3218.2018.00013.1.

7. Fedosin S.G. Generalized four-momentum for continuously distributed matter. Preprint, 2018.

8. Fedosin S.G. Что мы должны понимать под 4-импульсом физической системы? Preprint, 2018.

See also

External links

Field energy theorem in Russian

Source: http://sergf.ru/tpen.htm

On the list of pages