Pressure field

Pressure field is a two-component vector force field, which describes in a covariant way the dynamic pressure of individual particles and the pressure emerging in systems with a number of closely interacting particles. The pressure field is a general field component, which is represented in the Lagrangian and Hamiltonian of an arbitrary physical system including the term with the energy of particles in the pressure field and the term with the field energy. ^[1] ^[2]

The pressure field is included in the equation of motion by means of the pressure field tensor and in the equation for the metric – by means the pressure stress-energy tensor. Any forces acting on the matter particles and causing a change in their interaction with each other make a contribution to the pressure field, its energy and momentum. The pressure field is generally considered as a macroscopic field, describing the averaged interaction of particles in an arbitrary small volume of a system. The cause of the pressure field emerging at the microlevel is different interactions. For example, electromagnetic forces and strong gravitation hold electrons and nucleons in atoms together. The action of the external forces causes the matter compression and change in the volume occupied by atoms and electrons in the matter atoms. This leads to a change in the system’s energy, which can be represented as a change in the pressure field energy.

1 The scalar pressure field
2 The vector pressure field

2.1 Mathematical description
2.2 Action, Lagrangian and energy
2.3 Equations
2.4 Stress–energy tensor
2.5 Application in certain problems

3 See also
4 References
5 External links

The scalar pressure field

In equilibrium states of matter and in the absence of mass forces, atoms and molecules usually move chaotically and their total directed motion can be neglected. Under these conditions, the characteristic of internal motion is the average velocity of particles $~ \bar {v}$ . In the molecular kinetic theory there is a formula for the pressure: $p= \frac{1}{3}m_0 n \bar {v}^2 ,$ where is the average mass of one particle of thermodynamic system, is the particle concentration.

As a macroscopic thermodynamic variable, the pressure is part of the equation of state, which relates various thermodynamic variables. In particular, the pressure as a physical variable is included in the ideal gas law:

$p\cdot V= \frac{m}{M}R\cdot T,$

where is the gas volume, is the gas mass, is the molar mass, is the universal gas constant, is the temperature, $k = \frac{R}{N_A}$ is the Boltzmann constant, is the Avogadro constant.

Pressure is part of the Bernoulli's principle for a stationary flux of ideal (i.e., without internal friction) incompressible liquid, which is the consequence of the conservation of energy:

$\tfrac{\rho v^2}{2} + \rho g h + p = \mathrm{const}$

where $~\rho$ is the liquid mass density, is the flux velocity, is the height at which this liquid unit is located, is the pressure at the point in space, where the center of mass of the liquid unit under consideration is located, is the free fall acceleration. The first term of the equation is the dynamic pressure, the second term gives the pressure from the mass forces (in this case from gravitation), the third term is the static pressure and the constant in the right side is called the total pressure.

The scalar pressure characterizes the continuous medium state, and in case of the equilibrium state in the liquid the pressure becomes hydrostatic. In this case the pressure is the diagonal component of the symmetric three-dimensional Cauchy stress tensor:

$~\sigma_{ij} = -p \delta_{ij} ,$

where $~\delta_{ij}$ is the Kronecker symbol.

In the general relativity, the pressure stress-energy tensor is used for the ideal liquid, which is a generalization of the formulas of classical mechanics: ^[3]

$~ P^{\mu \nu } = \frac {p}{c^2}u^\mu u^\nu - g^{\mu \nu } p,$

where $~ g^{\mu \nu }$ is the metric tensor, $~u^\mu$ is the four-velocity, is the speed of light.

In the concept of a scalar field, under the pressure field energy the work is meant, which is done by the pressure to change the system’s volume from the initial state with zero pressure to the current state, taking into account the contribution of the particles’ kinetic energy from the mass-energy change due to the pressure field.

The vector pressure field

The drawback of the scalar pressure field concept is the inaccurate method of taking into account the energy and momentum of the pressure field in accelerated reference frames with a number of the field sources, where the effects of field self-action and addition of individual pressure waves at a limited propagation velocity of the field are manifested. In the vector fields an additional degree of freedom appears in the form of a vector potential. As a result, the energy of one field component can go into the energy of another component, the field strength becomes a function of the scalar and vector potentials, and the force is determined by the field strength, motion velocity and solenoidal vector. The examples of the field self-action are the electromagnetic induction and gravitational induction.

The pressure as a two-component vector field was presented by Sergey Fedosin within the framework of the metric theory of relativity and the covariant theory of gravitation, and the equations of this field were developed as a consequence of the principle of least action. ^[4] ^[5]

Mathematical description

The four-potential of the pressure field is expressed in terms of the scalar $~\wp$ and vector $~ \boldsymbol {\Pi }$ potentials:

$~\pi_\mu = \left(\frac {\wp }{c},- \boldsymbol {\Pi } \right) .$

The antisymmetric pressure field tensor is calculated with the four-curl of the four-potential:

$f_{\mu \nu} = \nabla_\mu \pi_\nu - \nabla_\nu \pi_\mu = \frac{\partial \pi_\nu}{\partial x^\mu} - \frac{\partial \pi_\mu}{\partial x^\nu}.$

The pressure tensor components are the vector components of the pressure field strength $~\mathbf {C}$ and the solenoidal pressure vector $~\mathbf { I }$ :

$~ f_{\mu \nu}= \begin{vmatrix} 0 & \frac { C_x}{ c} & \frac { C_y}{ c} & \frac { C_z}{ c} \\ -\frac { C_x}{ c} & 0 & - I_{z} & I_{y} \\ -\frac { C_y}{ c} & I_{z} & 0 & - I_{x} \\ -\frac { C_z}{ c}& - I_{y} & I_{x} & 0 \end{vmatrix}.$

From here we obtain the following:

$~\mathbf{C}= -\nabla \wp - \frac{\partial \mathbf{\Pi }} {\partial t}, \qquad\qquad \mathbf{I }= \nabla \times \mathbf{\Pi }. \qquad\qquad (1)$

Action, Lagrangian and energy

In the covariant theory of gravitation, the four-potential $~ \pi_\mu$ of the pressure field is part of the four-potential of the general field $~ s_\mu$ , which is the sum of the four-potentials of particular fields, such as electromagnetic and gravitational fields, acceleration field, pressure field, dissipation field, strong interaction field, weak interaction field and other vector fields, acting on the matter and its particles. All these fields in one way or another are represented in the matter, so that the four-potential $~ s_\mu$ cannot consist solely of the four-potential $~ \pi_\mu$ . The energy density of interaction of the general field with the matter is given by the product of the four-potential of the general field and the mass four-current: $~ s_\mu J^\mu$ . From the four-potential of the general field we obtain the general field tensor by applying the four-curl:

$~ s_{\mu \nu} =\nabla_\mu s_\nu - \nabla_\nu s_\mu.$

The tensor invariant in the form of $~ s_{\mu \nu} s^{\mu \nu}$ is up to a constant factor proportional to the energy density of the general field. As a result, the action function that contains the scalar curvature and the cosmological constant $~ \Lambda$ is given by the expression: ^[1]

$~S =\int {L dt}=\int (kR-2k \Lambda - \frac {1}{c}s_\mu J^\mu - \frac {c}{16 \pi \varpi} s_{\mu\nu}s^{\mu\nu} ) \sqrt {-g}d\Sigma,$

where is the Lagrange function or Lagrangian, is the time differential of the coordinate reference frame, and $~ \varpi$ are the constants to be determined, is the speed of light, as a measure of the propagation velocity of electromagnetic and gravitational interactions, $~\sqrt {-g}d\Sigma= \sqrt {-g} c dt dx^1 dx^2 dx^3$ is the invariant four-volume, expressed in terms of the differential of the time coordinate , the product of differentials of the space coordinates and the square root $~\sqrt {-g}$ of the determinant of the metric tensor, taken with a negative sign.

Variation of the action function gives the general field equations, the four-dimensional equation of motion and the equation for determining the metric. Since the pressure field is a component of the general field, then the corresponding pressure field equations can be derived from the general field equations.

Given the gauge conditions of the cosmological constant are met in the following form:

$~ c k \Lambda = - s_\mu J^\mu ,$

the system’s energy does not depend on the term with the scalar curvature and it becomes uniquely determined: ^[5]

$~E = \int {( s_0 J^0 + \frac {c^2 }{16 \pi \varpi } s_{ \mu\nu} s^{ \mu\nu} ) \sqrt {-g} dx^1 dx^2 dx^3},$

where and denote the time components of the four-vectors $~ s_{\mu }$ and $~ J^{\mu }$ .

The four-momentum of the system is given by the formula:

$~p^\mu = \left( \frac {E}{c}{,} \mathbf {p}\right) = \left( \frac {E}{c}{,} \frac {E}{c^2}\mathbf {v} \right) ,$

where $~ \mathbf {p}$ and $~ \mathbf {v}$ denote the system’s momentum and the velocity of the system’s center of mass.

Equations

Main article: Equation of vector field

The four-dimensional equations of the pressure field are similar by their form to Maxwell equations and have the following form:

$\nabla_\sigma f_{\mu \nu}+\nabla_\mu f_{\nu \sigma}+\nabla_\nu f_{\sigma \mu}=\frac{\partial f_{\mu \nu}}{\partial x^\sigma} + \frac{\partial f_{\nu \sigma}}{\partial x^\mu} + \frac{\partial f_{\sigma \mu}}{\partial x^\nu} = 0.$

$~ \nabla_\nu f^{\mu \nu} = - \frac{4 \pi \sigma }{c^2} J^\mu,$

where $~J^\mu = \rho_{0} u^\mu$ is the mass four-current, $~\rho_{0}$ is the mass density in the co-moving reference frame, $~u^\mu$ is the four-velocity of the matter unit, $~ \sigma$ is a constant determined in each problem, and it is assumed that there is a balance between all the fields in the physical system under consideration.

The gauge condition for the four-potential of the field of pressure:

$~ \nabla^\mu \pi_\mu = 0 .$

In Minkowski space of the special theory of relativity, the form of the pressure field equations is simplified and they can be expressed in terms of the field strength $~\mathbf {C}$ and the solenoidal vector $~\mathbf { I }$ :

$~ \nabla \cdot \mathbf{C} = 4 \pi \sigma \gamma \rho_0, \qquad\qquad \nabla \times \mathbf{ I } = \frac{1}{c^2} \left( 4 \pi \sigma \mathbf{J} + \frac{\partial \mathbf{C}} {\partial t} \right),$

$~ \nabla \times \mathbf{C} = - \frac{\partial \mathbf{ I } } {\partial t} , \qquad\qquad \nabla \cdot \mathbf{ I } = 0 .$

where $~ \gamma = \frac {1}{\sqrt{1 - {v^2 \over c^2}}}$ is the Lorentz factor, $~ \mathbf{J}= \gamma \rho_0 \mathbf{v }$ is the mass current density , $~ \mathbf{v }$ is the matter unit velocity.

If we also use the gauge condition in the form of $~ \partial^\mu \pi_\mu = \frac {1}{c^2} \frac{\partial \wp }{\partial t}+\nabla \cdot \boldsymbol {\Pi }=0$ and relation (1), we can obtain the wave equations for the pressure field potentials from the field equations:

$~ \frac {1}{c^2}\frac{\partial^2 \wp }{\partial t^2 } -\Delta \wp = 4 \pi \sigma \gamma \rho_0, \qquad\qquad (2)$

$~ \frac {1}{c^2}\frac{\partial^2 \boldsymbol {\Pi } }{\partial t^2 } -\Delta \boldsymbol {\Pi }= \frac {4 \pi \sigma}{c^2} \mathbf{J}.$

The equation of motion of the matter unit in the general field is given by the formula:

$~ s_{\mu \nu} J^\nu =0$ .

Since $~ J^\nu = \rho_0 u^\nu$ , and the general field tensor is expressed in terms of tensors of particular fields, then the equation of motion can be represented using these tensors:^[6]

$~-u_{{\mu \nu }}J^{\nu }=F_{{\mu \nu }}j^{\nu }+\Phi _{{\mu \nu }}J^{\nu }+f_{{\mu \nu }}J^{\nu }+h_{{\mu \nu }}J^{\nu }+\gamma _{{\mu \nu }}J^{\nu }+w_{{\mu \nu }}J^{\nu }.\qquad \qquad (3)$

Here $~ u_{\mu \nu}$ is the acceleration tensor, $~ F_{\mu \nu}$ is the electromagnetic tensor, $~ j^\nu$ is the charge four-current, $~ \Phi_{\mu \nu}$ is the gravitational tensor, $~ h_{\mu \nu}$ is the dissipation field tensor, $~ \gamma_{\mu \nu}$ is the strong interaction field tensor, $~ w_{\mu \nu}$ is the weak interaction field tensor.

Stress–energy tensor

The pressure stress-energy tensor is calculated with the help of the pressure tensor:

$~ P^{ik} = \frac{c^2} {4 \pi \sigma }\left( -g^{im} f_{n m} f^{n k}+ \frac{1} {4} g^{ik} f_{m r} f^{m r}\right)$ .

The tensor $~ P^{ik}$ includes the three-vector of energy-momentum flux $~\mathbf {F}$ , which is similar in its meaning to the Poynting vector and the Heaviside vector. The vector $~\mathbf {F}$ can be represented through the vector product of the field strength $~ \mathbf {C}$ and the solenoidal vector $~ \mathbf { I }$ :

$~ \mathbf {F}=c P^{0i} = \frac {c^2}{4 \pi \sigma }[\mathbf {C}\times \mathbf { I }],$

here the index is

The covariant derivative of the stress-energy tensor of the pressure field determines the density of the pressure four-force:

$~f^{\alpha }=-\nabla _{\beta }P^{{\alpha \beta }}={f^{\alpha }}_{{k}}J^{k}\qquad \qquad (4)$

The stress-energy tensor of the pressure field is part of the stress-energy tensor of the general field $~ T^{ik}$ , but in the general case the tensor $~ T^{ik}$ also contains the cross-terms with the products of strengths and solenoidal vectors of particular fields:

$~ T^{ik}= k_1W^{ik}+ k_2U^{ik}+ k_3B^{ik}+ k_4P^{ik} + k_5Q^{ik}+ k_6 L^{ik}+ k_7A^{ik}+ cross \quad terms,$

where $~ k_1{,} k_2{,} k_3{,} k_4{,} k_5{,} k_6{,} k_7$ are some coefficients, $~ W^{ik}$ is the electromagnetic stress-energy tensor, $~ U^{ik}$ is the gravitational stress-energy tensor, $~ B^{ik}$ is the acceleration stress-energy tensor, $~ Q^{ik}$ is the dissipation stress-energy tensor, $~ L^{ik}$ is the strong interaction stress-energy tensor, $~ A^{ik}$ is the weak interaction stress-energy tensor.

By means of the tensor $~ T^{ik}$ , the stress-energy tensor of the pressure field becomes part of the equation for the metric:

$~ R^{ik} - \frac{1} {4 }g^{ik}R = \frac{8 \pi G \beta }{ c^4} T^{ik},$

where $~ R^{ik}$ is the Ricci tensor, is the gravitational constant, $~ \beta$ is a certain constant, and the gauge condition for the cosmological constant is used.

Application in certain problems

In the case when a certain vector potential of a particle is equal to zero in the rest frame of the particle, the four-potential of this vector field in an arbitrary frame of reference can be represented as follows: ^[4]

$~ L_\mu = \frac {k_f \varepsilon_p }{\rho_0 c^2} u_\mu ,$

where $~ k_f = \frac {\rho_0}{\rho_{0q}}$ for electromagnetic field and for other fields, $~ \rho_{0}$ and $~\rho_{0q}$ are the mass density and accordingly charge density in comoving reference frame, $~ \varepsilon_p$ is the energy density of the particle in the given field, $~ u_\mu$ is the covariant four-velocity.

For the pressure field $~ \varepsilon_p = p_0$ , , and according to the definition, for the four-potential of the pressure field of one particle we have the following:

$~\pi_\mu = \left(\frac {\wp }{c},- \boldsymbol {\Pi } \right) = \frac {p_0 }{\rho_0 c^2} u_\mu ,$

where is the scalar pressure. For an arbitrary particle, the components of the four-potential in the framework of the special relativity (STR) take the form: $~ \wp = \frac { \gamma p_0 }{\rho_0 },$ $~ \boldsymbol {\Pi }= \frac { \gamma p_0 }{\rho_0 c^2}\mathbf{v},$

and hence, the vector potential is directed along the particle’s velocity. If the vector potential components are the functions of time and do not directly depend on the space coordinates, then for such motion according to (1) the solenoidal vector $~ \mathbf { I }$ vanishes.

Due to the interaction of a set of particles with each other by means of various fields, including interaction at a distance without direct contact, the pressure field in the matter changes and is different from the pressure field of a single particle at the observation point. The pressure field in the system of particles is specified by the field strength and solenoid vector, which represent the typical averaged characteristics of the matter’s motion. For example, in a gravitationally-bound system a radial gradient of the vector $~ \mathbf { C }$ appears, and if some part of the particles is moving synchronously or rotating, then the vector $~ \mathbf { I }$ appears. From (3) and (4) we derive a general expression for the four-force density with a covariant index, which arises from the pressure field:

$~(f_{\mu })_{p}=f_{{\mu \nu }}J^{\nu }=\rho _{0}{\frac {cdt}{ds}}\left({\frac {1}{c}}{\mathbf {C}}\cdot {\mathbf {v}}{,}\qquad -{\mathbf {C}}-[{\mathbf {v}}\times {\mathbf {I}}]\right),$

where denotes the four-dimensional space-time interval.

For a stationary case, when the pressure field potentials do not depend on time, the wave equation (2) for the scalar potential in STR is transformed into the equation:

$~ \Delta \wp = - 4 \pi \sigma \gamma \rho_0.$

The solution of this equation for a fixed sphere with randomly moving particles in it has the following form: ^[7]

$~ \wp = \wp_c - \frac {\sigma \gamma_c c^2 }{\eta } + \frac {\sigma \gamma_c c^3 }{r \eta \sqrt {4 \pi \eta \rho_0} } \sin \left(\frac {r}{c}\sqrt {4 \pi \eta \rho_0} \right) \approx \wp_c - \frac {2 \pi \sigma \rho_0 r^2 \gamma_c }{3}.$

$~ p_0 \approx p_{0c} - \frac {2 \pi \sigma \rho^2_0 r^2 \gamma_c }{3}.$

$~ p_{0c} \approx \frac {3 \sigma M^2 }{8 \pi R^4}.$

Here $~ \eta$ is a coefficient of the acceleration field, $~ \wp_c$ represents the scalar potential of the pressure field in the center of the sphere, $~ \gamma_c = \frac {1}{\sqrt{1 - {v^2_c \over c^2}}}$ is the Lorentz factor for the velocities of the particles in the center of the sphere, and in view of the argument’s smallness the sine is expanded to the second-order terms. It follows from the formula that the pressure potential and the scalar pressure reach the maximum at the center and decrease, when approaching the surface of the sphere with the radius and the total mass .

The obtained dependence for the pressure at the center $~ p_{0c}$ holds true for a variety of space objects, including gas clouds, Bok globules, Earth, and neutron stars. In the center of the main sequence stars, including the Sun, the main contribution to the total pressure is made by thermonuclear reactions instead of gravitation. This contribution was taken into account in the article, ^[1] where the following relation was obtained for the pressure at the center of the Solar core:

$~ p_{0s} \approx \frac {3 \aleph M^2_c }{8 \pi R^4_c},$

where and denote the radius and mass of the Solar core, $~ \aleph$ is the constant in the stress-energy tensor of the strong interaction field, and $~ \aleph \approx \sigma$ .

In the system under consideration, the scalar potential $~ \wp$ becomes the function of the radius, and the vector potential $~ \boldsymbol {\Pi }$ and solenoidal vector $~ \mathbf { I }$ are equal to zero. The pressure field strength $~\mathbf {C}$ is found from (1). Next, we can calculate all the functions of the pressure field, including the four-acceleration of the pressure field, the energy of the particles in this field and the energy of the pressure field itself. ^[8] For cosmic bodies without additional sources of energy, the main contribution to the four-acceleration in the matter is made by the gravitational force and the pressure field. In this case we can automatically derive the relativistic rest energy of the system, taking into account the motion of particles inside the sphere. For a system of particles with the acceleration field, pressure field, gravitational and electromagnetic fields, this approach allowed us to solve the 4/3 problem and showed, where and in what form the system’s energy is contained. The following relation was found in this problem for the constant of the pressure field:

$~\sigma = 3G- \frac {3q^2}{4 \pi \varepsilon_0 m^2 },$

where $~ \varepsilon_0$ is the electric constant, and are the total charge and mass of the system.

In articles ^[9] ^[10] the ratio of the field’s coefficients for the fields was specified as follows:

$~\eta +\sigma =G-{\frac {\rho _{{0q}}^{2}}{4\pi \varepsilon _{0}\rho _{{0}}^{2}}}.$

If we introduce the parameter $~\mu$ as the number of nucleons per ionized gas particle, then the pressure field constant is expressed as follows:

$~\sigma ={\frac {2G}{2+3\gamma _{c}\mu }}.$

For the pressure inside the cosmic bodies in the gravitational equilibrium model we find the dependence on the current radius:

$~p_{0}=p_{{0c}}-{\frac {2\pi \sigma \rho _{0}\rho _{{0c}}\gamma _{c}r^{2}}{3}}+{\frac {\pi \sigma A\rho _{0}\gamma _{c}r^{3}}{3}}+{\frac {\pi \sigma B\rho _{0}\gamma _{c}r^{4}}{5}},$

where the coefficients and are included into the dependence of the mass density on the radius in the relation $~\rho _{0}=\rho _{{0c}}-Ar-Br^{2}.$

Under the assumption that the system’s typical particles have the mass $~{\stackrel {-}{m}}=\mu m_{u}$ , where $~m_{u}$ is the mass of one gas particle, for which the unified atomic mass unit is taken, and that it is typical particles that define the temperature and pressure, for the pressure field constant we obtain the following: ^[11]

$~\sigma ={\frac {2}{5}}\left(G-{\frac {\rho _{{0q}}^{2}}{4\pi \varepsilon _{0}\rho _{0}^{2}}}\right).$

The scalar potential at the center of the sphere is approximately equal to: ^[12]

$~\wp _{c}\approx {\frac {3\sigma m}{10a}}\left(1+{\frac {9}{2{\sqrt {14}}}}\right).$

The relativistic equation of motion of the viscous compressible fluid, with regard to the four-potential of the pressure field, pressure field tensor and stress-energy tensor of the pressure field, was presented within the limits of low curvature of spacetime in the form of the Navier-Stokes equations in hydrodynamics in the framework of STR. ^[13]

Taking into account the vector pressure field, within the framework of the relativistic uniform system, it is possible to refine the virial theorem, which in the relativistic form is written as follows: ^[14]

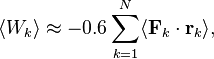
$~\langle W_{k}\rangle \approx -0.6\sum _{{k=1}}^{N}\langle {\mathbf {F}}_{k}\cdot {\mathbf {r}}_{k}\rangle ,$

where the value $~W_{k}\approx \gamma _{c}T$ exceeds the kinetic energy of the particles by a factor equal to the Lorentz factor $~\gamma _{c}$ of the particles at the center of the system. Under normal conditions we can assume that $~\gamma _{c}\approx 1$ , then we can see that in the virial theorem the kinetic energy is related to the potential energy not by the coefficient 0.5, but rather by the coefficient close to 0.6. The difference from the classical case arises due to considering the pressure field and the acceleration field of particles inside the system, while the derivative of the virial scalar $~G_{v}$ is not equal to zero and should be considered as the material derivative.

An analysis of the integral theorem of generalized virial makes it possible to find, on the basis of field theory, a formula for the root-mean-square speed of typical particles of a system without using the notion of temperature: ^[15]

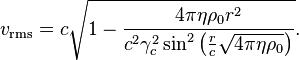
$v_{{\mathrm {rms}}}=c{\sqrt {1-{\frac {4\pi \eta \rho _{0}r^{2}}{c^{2}\gamma _{c}^{2}\sin ^{2}{\left({\frac {r}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)}}}}}.$

The integral field energy theorem for pressure field in a curved space-time is as follows: ^[16]

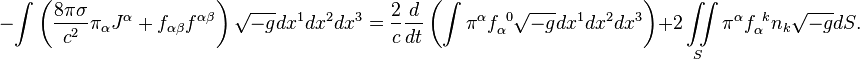
$~-\int {\left({\frac {8\pi \sigma }{c^{2}}}\pi _{\alpha }J^{\alpha }+f_{{\alpha \beta }}f^{{\alpha \beta }}\right){\sqrt {-g}}dx^{1}dx^{2}dx^{3}}={\frac {2}{c}}{\frac {d}{dt}}\left(\int {\pi ^{\alpha }f_{\alpha }^{{\ 0}}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}\right)+2\iint \limits _{S}{\pi ^{\alpha }f_{\alpha }^{{\ k}}n_{k}{\sqrt {-g}}dS}.$

In the relativistic uniform system, the scalar potential $~\wp$ of the pressure field is related to the scalar potential $~\vartheta$ of the acceleration field: ^[17]

$~\wp ={\frac {\sigma (\vartheta -c^{2})}{\eta }}={\frac {2(\vartheta -c^{2})}{3}}.$

The relativistic expression for pressure is as follows:

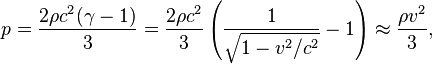
$p={\frac {2\rho c^{2}(\gamma -1)}{3}}={\frac {2\rho c^{2}}{3}}\left({\frac {1}{{\sqrt {1-v^{2}/c^{2}}}}}-1\right)\approx {\frac {\rho v^{2}}{3}},$

where $\rho$ is the mass density of moving matter, is the speed of light, $\gamma ={\frac {1}{{\sqrt {1-v^{2}/c^{2}}}}}$ is the Lorentz factor. In the limit of low velocities, this relationship turns into the standard formula of the kinetic theory of gases.

References

^1.0 ^1.1 ^1.2 Fedosin S.G. The Concept of the General Force Vector Field. OALib Journal, Vol. 3, pp. 1-15 (2016), e2459. http://dx.doi.org/10.4236/oalib.1102459.
Fedosin S.G. Two components of the macroscopic general field. Reports in Advances of Physical Sciences, Vol. 1, No. 2, 1750002, 9 pages (2017). http://dx.doi.org/10.1142/S2424942417500025.
C. W. Misner, K. S. Thorne, and J. A. Wheeler, Gravitation (W. H. Freeman, San Francisco, CA, 1973).
^4.0 ^4.1 Fedosin S.G. The procedure of finding the stress-energy tensor and vector field equations of any form. Advanced Studies in Theoretical Physics, Vol. 8, no. 18, pp. 771-779 (2014). http://dx.doi.org/10.12988/astp.2014.47101.
^5.0 ^5.1 Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy. Jordan Journal of Physics. Vol. 9, No. 1, pp. 1-30 (2016). http://dx.doi.org/10.5281/zenodo.889304.
Fedosin S.G. Equations of Motion in the Theory of Relativistic Vector Fields. International Letters of Chemistry, Physics and Astronomy, Vol. 83, pp. 12-30 (2019). https://doi.org/10.18052/www.scipress.com/ILCPA.83.12.
Fedosin S.G. The Integral Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based on the Pressure Field and Acceleration Field. American Journal of Modern Physics. Vol. 3, No. 4, pp. 152-167 (2014). https://dx.doi.org/10.11648/j.ajmp.20140304.12.
Fedosin S.G. Relativistic Energy and Mass in the Weak Field Limit. Jordan Journal of Physics. Vol. 8, No. 1, pp. 1-16 (2015). http://dx.doi.org/10.5281/zenodo.889210.
Fedosin S.G. Estimation of the physical parameters of planets and stars in the gravitational equilibrium model. Canadian Journal of Physics, Vol. 94, No. 4, pp. 370-379 (2016). http://dx.doi.org/10.1139/cjp-2015-0593.
Fedosin S.G. The generalized Poynting theorem for the general field and solution of the 4/3 problem. International Frontier Science Letters, Vol. 14, pp. 19-40 (2019). https://doi.org/10.18052/www.scipress.com/IFSL.14.19.
Fedosin S.G. The binding energy and the total energy of a macroscopic body in the relativistic uniform model. Middle East Journal of Science, Vol. 5, Issue 1, pp. 46-62 (2019). http://dx.doi.org/10.23884/mejs.2019.5.1.06.
Fedosin S.G. Energy and metric gauging in the covariant theory of gravitation. Aksaray University Journal of Science and Engineering, Vol. 2, Issue 2, pp. 127-143 (2018). http://dx.doi.org/10.29002/asujse.433947.
Fedosin S.G. Four-Dimensional Equation of Motion for Viscous Compressible and Charged Fluid with Regard to the Acceleration Field, Pressure Field and Dissipation Field. International Journal of Thermodynamics. Vol. 18, No. 1, pp. 13-24 (2015). http://dx.doi.org/10.5541/ijot.5000034003.
Fedosin S.G. The virial theorem and the kinetic energy of particles of a macroscopic system in the general field concept. Continuum Mechanics and Thermodynamics. (2017). https://dx.doi.org/10.1007/s00161-016-0536-8.
Fedosin S.G. The integral theorem of generalized virial in the relativistic uniform model. Continuum Mechanics and Thermodynamics, Vol. 31, Issue 3, pp. 627-638 (2019). https://dx.doi.org/10.1007/s00161-018-0715-x.
Fedosin S.G. The Integral Theorem of the Field Energy. Gazi University Journal of Science. Vol. 32, No. 2, pp. 686-703 (2019). http://dx.doi.org/10.5281/zenodo.3252783.
Fedosin S.G. The potentials of the acceleration field and pressure field in rotating relativistic uniform system Continuum Mechanics and Thermodynamics, Vol. 33, Issue 3, pp. 817-834 (2021). https://doi.org/10.1007/s00161-020-00960-7.

External links

Pressure field in Russian

Source: http://sergf.ru/fpen.htm

On the list of pages

На русском языке