Equation of vector field

Equation of vector field

Equation of vector field is a field equation that relates field’s four-potential or tensor with the field source in the form of the corresponding four-current or tensor. Due to the tensor representation the field equations are expressed in a covariant form and are valid in curved spacetime.

Vector fields include such fields as the electromagnetic field, acceleration field, pressure field, dissipation field, macroscopic field of strong interaction, macroscopic field of weak interaction. Within the framework of the covariant theory of gravitation, the gravitational field is also considered a vector field.

All these fields can be considered as the general field components represented in the Lagrangian and in the Hamiltonian of an arbitrary physical system by the corresponding term with the energy of the particles’ motion and by the term with the field energy. ^[1] ^[2] The relativistic uniform system is an example of a physical system, in which equations of vector field have a complete and exact solution for all vector fields.

Contents

1 Types of equations
2 Standard equations
3 Wave equations
4 Equation of motion
5 Generalized Poynting theorem
6 Equation for the metric
7 Field energy theorem
8 Integral equations
9 See also
10 References
11 External links

Types of equations

The standard field equation is a differential equation derived using the principle of least action. As a rule, such an equation contains the covariant derivative acting on the field tensor. The second covariant derivative turns the field equation into the wave equation for the field tensor. If the field tensor is expressed in terms of the four-potential, then the field equation can be transformed into the wave equation for the four-potential.

The equation of motion of matter particles can be considered such a type of field equations, in which the fields act on the field sources and cause them to move.

The generalized Poynting theorem defines the balance of energy and momentum at any point of the system, and is formulated as a tensor gauge condition in the form of equality to zero of the divergence of the total stress-energy tensor of all the fields acting in the system. Just in the same way, there is a continuity equation as a gauge condition for the four-currents, when equality to zero of the divergence of the mass and charge four-currents in the form $~\nabla _{\mu }J^{\mu }=0$ and $~\nabla _{\mu }j^{\mu }=0$ defines the local balance of the mass and charge at each point. This means that the mass (charge) density in a certain unit volume changes either when the mass (charge) flux from this volume arises, or when the metric in the given volume changes.

The equation for the metric is obtained by varying the action function with respect to the metric tensor and contains the Ricci tensor, scalar curvature, cosmological constant, and the fields’ stress-energy tensors. The result of the equation’s solution represents the metric tensor components as functions of time and coordinates.

The field energy theorem is expressed using the integral equation of field energy, generalizes the virial theorem with respect to the fields and presents it in the curved spacetime.

The integral field equations are obtained by integrating the standard field equations over the four-dimensional spacetime. This allows us to formulate several theorems with respect to the tensor components and the fields’ four-potentials, and to determine a number of new quantities that characterize the system as a whole.

Standard equations

Each vector field is described by two equations, one of which contains the field sources, and the other imposes restrictions on the type of the field, regardless of the field sources. ^[3] ^[4]

The electromagnetic field equations:

$~\nabla _{\nu }F^{{\mu \nu }}=-\mu _{0}j^{\mu },$

$\nabla _{\sigma }F_{{\mu \nu }}+\nabla _{\mu }F_{{\nu \sigma }}+\nabla _{\nu }F_{{\sigma \mu }}=0,$

where $F_{{\mu \nu }}$ is the electromagnetic tensor, $j^{\mu }=\rho _{{0q}}u^{\mu }$ is the charge four-current, $\rho _{{0q}}$ is the charge density in the comoving reference frame, $u^{\mu }$ is the four-velocity of the matter element, $~\mu _{0}$ is the magnetic constant (vacuum permeability), is the speed of light.

The latter equation can be written using the dual electromagnetic field tensor:

$~\nabla _{\beta }{\tilde {F}}^{{\alpha \beta }}=0,$

where $~{\tilde {F}}^{{\alpha \beta }}={\frac {1}{2}}\varepsilon ^{{\alpha \beta \gamma \delta }}F_{{\gamma \delta }},$ and the Levi-Civita symbol $~\varepsilon ^{{\alpha \beta \gamma \delta }}$ is used.

The gravitational field equations: ^[5]

$~\nabla _{\nu }\Phi ^{{\mu \nu }}={\frac {4\pi G}{c^{2}}}J^{\mu },$

$\nabla _{\sigma }\Phi _{{\mu \nu }}+\nabla _{\mu }\Phi _{{\nu \sigma }}+\nabla _{\nu }\Phi _{{\sigma \mu }}=0,$

where $\Phi _{{\mu \nu }}$ is the gravitational tensor, $J^{\mu }=\rho _{{0}}u^{\mu }$ is the mass four-current, $\rho _{{0}}$ is the mass density of the matter in the comoving reference frame, is the gravitational constant, is the speed of light as the speed of gravitation and the limiting propagation speed of the gravitational perturbation.

The acceleration field equations:

$~\nabla _{\nu }u^{{\mu \nu }}=-{\frac {4\pi \eta }{c^{2}}}J^{\mu },$

$\nabla _{\sigma }u_{{\mu \nu }}+\nabla _{\mu }u_{{\nu \sigma }}+\nabla _{\nu }u_{{\sigma \mu }}=0,$

where $u_{{\mu \nu }}$ is the acceleration tensor, $~\eta$ is the acceleration field constant determined in each problem.

The pressure field equations:

$~\nabla _{\nu }f^{{\mu \nu }}=-{\frac {4\pi \sigma }{c^{2}}}J^{\mu },$

$\nabla _{\sigma }f_{{\mu \nu }}+\nabla _{\mu }f_{{\nu \sigma }}+\nabla _{\nu }f_{{\sigma \mu }}=0,$

where $f_{{\mu \nu }}$ is the pressure field tensor, $~\sigma$ is the pressure field constant.

The dissipation field equations: ^[6]

$~\nabla _{\nu }h^{{\mu \nu }}=-{\frac {4\pi \tau }{c^{2}}}J^{\mu },$

$\nabla _{\sigma }h_{{\mu \nu }}+\nabla _{\mu }h_{{\nu \sigma }}+\nabla _{\nu }h_{{\sigma \mu }}=0,$

where $h_{{\mu \nu }}$ is the dissipation field tensor, $~\tau$ is the dissipation field constant.

Wave equations

In the wave equations the sources of fields are the mass and charge four-currents, so that in case of motion of the masses and charges, wave phenomena are observed in the propagation of the fields’ potentials and strengths in the spacetime. As a result, each wave equation contains the four-dimensional scalar d’Alembert operator $~\nabla ^{\nu }\nabla _{\nu }$ , which can act both on the four-potential and on the field tensor. In some cases, the solution of wave equations is simpler than the solution of field equations, allowing us to directly find the field potentials that are part of the four-potentials.

The wave equations for the four-potentials of the above-mentioned fields are as follows:

$~\nabla ^{\nu }\nabla _{\nu }A_{\mu }+R_{{\mu \nu }}A^{\nu }=\mu _{0}j_{\mu },$

$~\nabla ^{\nu }\nabla _{\nu }D_{\mu }+R_{{\mu \nu }}D^{\nu }=-{\frac {4\pi G}{c^{2}}}J_{\mu },$

$~\nabla ^{\nu }\nabla _{\nu }U_{\mu }+R_{{\mu \nu }}U^{\nu }={\frac {4\pi \eta }{c^{2}}}J_{\mu },$

$~\nabla ^{\nu }\nabla _{\nu }\pi _{\mu }+R_{{\mu \nu }}\pi ^{\nu }={\frac {4\pi \sigma }{c^{2}}}J_{\mu },$

$~\nabla ^{\nu }\nabla _{\nu }\lambda _{\mu }+R_{{\mu \nu }}\lambda ^{\nu }={\frac {4\pi \tau }{c^{2}}}J_{\mu },$

where $~A_{\mu }$ is the four-potential of the electromagnetic field, $~R_{{\mu \nu }}$ is the Ricci tensor, $~D_{\mu }$ is the gravitational four-potential, $~U_{\mu }$ is the four-potential of the acceleration field, $~\pi _{\mu }$ is the four-potential of the pressure field, $~\lambda _{\mu }$ is the four-potential of the dissipation field.

The components of the fields’ four-potentials are not arbitrary functions and must be gauged. In the Lorentz gauge the divergences of the four-potentials are equal to zero:

$~\nabla _{\mu }A^{\mu }=0,\qquad \nabla _{\mu }D^{\mu }=0,\qquad \nabla _{\mu }U^{\mu }=0,\qquad \nabla _{\mu }\pi ^{\mu }=0,\qquad \nabla _{\mu }\lambda ^{\mu }=0.$

If in the standard field equations we take the divergence of both sides of the equations and apply the Lorentz gauge, the gauge conditions would also arise for the field tenors:

$~R_{{\mu \nu }}F^{{\mu \nu }}=0,\qquad R_{{\mu \nu }}\Phi ^{{\mu \nu }}=0,\qquad R_{{\mu \nu }}u^{{\mu \nu }}=0,\qquad R_{{\mu \nu }}f^{{\mu \nu }}=0,\qquad R_{{\mu \nu }}h^{{\mu \nu }}=0.$

The wave equations for the field tensors: ^[7]

$~\nabla ^{\sigma }\nabla _{\sigma }F_{{\mu \nu }}=\mu _{0}\nabla _{\mu }j_{\nu }-\mu _{0}\nabla _{\nu }j_{\mu }+F_{{\nu \rho }}{R^{\rho }}_{\mu }-F_{{\mu \rho }}{R^{\rho }}_{\nu }+R_{{\mu \nu ,\lambda \eta }}F^{{\eta \lambda }},$

$~\nabla ^{\sigma }\nabla _{\sigma }\Phi _{{\mu \nu }}=-{\frac {4\pi G}{c^{2}}}\nabla _{\mu }J_{\nu }+{\frac {4\pi G}{c^{2}}}\nabla _{\nu }J_{\mu }+\Phi _{{\nu \rho }}{R^{\rho }}_{\mu }-\Phi _{{\mu \rho }}{R^{\rho }}_{\nu }+R_{{\mu \nu ,\lambda \eta }}\Phi ^{{\eta \lambda }},$

$~\nabla ^{\sigma }\nabla _{\sigma }u_{{\mu \nu }}={\frac {4\pi \eta }{c^{2}}}\nabla _{\mu }J_{\nu }-{\frac {4\pi \eta }{c^{2}}}\nabla _{\nu }J_{\mu }+u_{{\nu \rho }}{R^{\rho }}_{\mu }-u_{{\mu \rho }}{R^{\rho }}_{\nu }+R_{{\mu \nu ,\lambda \eta }}u^{{\eta \lambda }},$

$~\nabla ^{\sigma }\nabla _{\sigma }f_{{\mu \nu }}={\frac {4\pi \sigma }{c^{2}}}\nabla _{\mu }J_{\nu }-{\frac {4\pi \sigma }{c^{2}}}\nabla _{\nu }J_{\mu }+f_{{\nu \rho }}{R^{\rho }}_{\mu }-f_{{\mu \rho }}{R^{\rho }}_{\nu }+R_{{\mu \nu ,\lambda \eta }}f^{{\eta \lambda }},$

$~\nabla ^{\sigma }\nabla _{\sigma }h_{{\mu \nu }}={\frac {4\pi \tau }{c^{2}}}\nabla _{\mu }J_{\nu }-{\frac {4\pi \tau }{c^{2}}}\nabla _{\nu }J_{\mu }+h_{{\nu \rho }}{R^{\rho }}_{\mu }-h_{{\mu \rho }}{R^{\rho }}_{\nu }+R_{{\mu \nu ,\lambda \eta }}h^{{\eta \lambda }},$

where $~R_{{\mu \nu ,\lambda \eta }}$ is the curvature tensor.

Equation of motion

The equation of motion of matter particles can be expressed in terms of the field tensors: ^[7]

$~-u_{{\mu \nu }}J^{\nu }=\rho _{0}{\frac {dU_{\mu }}{d\tau }}-J^{\nu }\partial _{\mu }U_{\nu }=F_{{\mu \nu }}j^{\nu }+\Phi _{{\mu \nu }}J^{\nu }+f_{{\mu \nu }}J^{\nu }+h_{{\mu \nu }}J^{\nu }+\gamma _{{\mu \nu }}J^{\nu }+w_{{\mu \nu }}J^{\nu }.$

Here $~\gamma _{{\mu \nu }}$ is the strong interaction field tensor, $~w_{{\mu \nu }}$ is the weak interaction field tensor. The acceleration field tensor can be expressed in terms of the four-potential in the form $~u_{{\mu \nu }}=\nabla _{\mu }U_{\nu }-\nabla _{\nu }U_{\mu }=\partial _{\mu }U_{\nu }-\partial _{\nu }U_{\mu }.$ The subsequent application of the operator of proper-time-derivative allows us to put the left-hand side of the equation in a form similar to the equation of motion in classical mechanics.

The first term on the right-hand side defines the density of electromagnetic Lorentz force in the four-dimensional form, the second term is the gravitational force density expressed using the gravitational field tensor, the third term describes the pressure force density, the force densities from the remaining fields are also represented using the corresponding tensors and the mass four-current. The total sum on the right-hand side of the equation of motion is the density of the total four-force acting in the system.

In the equation of motion, the tensors of all the fields can be expressed in terms of the corresponding four-potentials. For the four fields acting in the system this gives the following:

$~{\frac {d(U_{\mu }+D_{\mu }+\pi _{\mu })}{d\tau }}+{\frac {\rho _{{0q}}}{\rho _{0}}}{\frac {dA_{\mu }}{d\tau }}=u^{\nu }\partial _{\mu }U_{\nu }+u^{\nu }\partial _{\mu }D_{\nu }+{\frac {\rho _{{0q}}}{\rho _{0}}}u^{\nu }\partial _{\mu }A_{\nu }+u^{\nu }\partial _{\mu }\pi _{\nu }.$

Generalized Poynting theorem

The stress-energy tensor $~T_{{ik}}$ of the system is the sum of the tensors of individual components of the general field:

$~T_{{ik}}=W_{{ik}}+U_{{ik}}+B_{{ik}}+P_{{ik}}+Q_{{ik}}+L_{{ik}}+A_{{ik}},$

where $~W_{{ik}}$ is the electromagnetic stress–energy tensor, $~U_{{ik}}$ is the gravitational stress-energy tensor, $~B_{{ik}}$ is the acceleration stress-energy tensor, $~P_{{ik}}$ is the pressure stress-energy tensor, $~Q_{{ik}}$ is the dissipation stress-energy tensor, $~L_{{ik}}$ is the stress-energy tensor of the strong interaction field, $~A_{{ik}}$ is the stress-energy tensor of the weak interaction field.

The generalized Poynting theorem is written as equality to zero of the divergence of the stress-energy tensor of the general field:

$~\nabla _{\beta }T^{{\alpha \beta }}={\frac {1}{{\sqrt {-g}}}}\partial _{\beta }\left({\sqrt {-g}}T^{{\alpha \beta }}\right)+\Gamma _{{\mu \nu }}^{{\alpha }}T^{{\mu \nu }}=0,$

where $~\Gamma _{{\mu \nu }}^{{\alpha }}$ is the Christoffel symbol.

The obtained expression for the space components of this equation in the system’s matter defines the balance of the fields’ energy and momentum, and is nothing but the differential equation of the matter’s motion under the action of the forces, generated by the fields, written in a covariant form. ^[7] Outside the matter’s limits the equality to zero of the space components of this equation means that changes in the fluxes of the electromagnetic and gravitational fields occur only in the presence of spatial gradients of the respective components of the stress-energy tensors of these fields. As for the time components of the equation, for them the generalized Poynting theorem defines the balance of the energy and energy fluxes of all the fields in any selected volume of the system. ^[8]

At the same time there is a difference between the total energy density of all the fields at a certain point and the relativistic energy density at this point, since the relativistic energy also takes into account the particles’ energy and is calculated in a different way, without the use of the stress-energy tensor $~T^{{\alpha \beta }}$ of the system. Consequently, the Poynting theorem applies to the local rates of change of the field energy over time and the rates of change of the energy fluxes in space, while the law of conservation of energy-momentum deals with the energy and momentum of the system’s fields and particles. The relativistic energy of the system in the center-of-momentum frame defines the invariant energy equal to the product of the inertial mass by the speed of light squared. Thus, conservation of the energy in a closed system leads to conservation of the inertial mass of the system. There is also the gravitational mass of the system, which is determined by the gravitational interaction with other bodies (for example, when weighting), and in the covariant theory of gravitation the gravitational mass turns out to be greater than the inertial mass. ^[9] The difference between the masses follows from the fact that the gravitational mass is determined not from the relativistic energy or momentum, but from the sum of the invariant masses of all the system’s particles. In a closed system there is no exchange of the matter’s particles, energy and information with the environment, and therefore the gravitational mass is also conserved.

The generalized Poynting theorem can be represented in an integral form. Integrating $~\nabla _{\beta }T^{{\alpha \beta }}$ over the covariant four-volume and taking into account the divergence theorem, we find:

$~\int {\partial _{\beta }\left({\sqrt {-g}}T^{{\alpha \beta }}\right)dx^{0}dx^{1}dx^{2}dx^{3}}=\int {T^{{\alpha \beta }}{\sqrt {-g}}dS_{\beta }}=\int \limits _{V}{T^{{\alpha 0}}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}+$

$~+c\int {\left(\int {T^{{\alpha 1}}{\sqrt {-g}}dx^{2}dx^{3}}\right)dt}+c\int {\left(\int {T^{{\alpha 2}}{\sqrt {-g}}dx^{1}dx^{3}}\right)dt}+c\int {\left(\int {T^{{\alpha 3}}{\sqrt {-g}}dx^{1}dx^{2}}\right)dt}.$

With this in mind, we obtain:

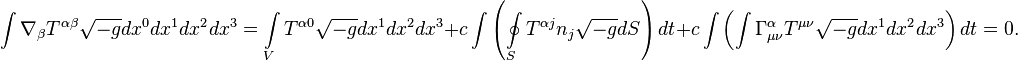
$~\int {\nabla _{\beta }T^{{\alpha \beta }}{\sqrt {-g}}dx^{0}dx^{1}dx^{2}dx^{3}}=\int \limits _{V}{T^{{\alpha 0}}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}+c\int {\left(\oint \limits _{S}{T^{{\alpha j}}n_{j}{\sqrt {-g}}dS}\right)dt}+c\int {\left(\int {\Gamma _{{\mu \nu }}^{{\alpha }}T^{{\mu \nu }}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}\right)dt}=0.$

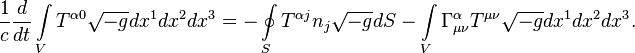
$~{\frac {1}{c}}{\frac {d}{dt}}\int \limits _{V}{T^{{\alpha 0}}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}=-\oint \limits _{S}{T^{{\alpha j}}n_{j}{\sqrt {-g}}dS}-\int \limits _{V}{\Gamma _{{\mu \nu }}^{{\alpha }}T^{{\mu \nu }}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}.$

Here and the vector $~n_{j}$ is a three-dimensional unit normal vector directed outward from the two-dimensional surface surrounding an arbitrarily selected volume in the system under consideration.

Equation for the metric

The equation for the metric is written in terms of the tensor $~T^{{ik}}$ : ^[10]

$~R^{{ik}}-{\frac {1}{4}}g^{{ik}}R={\frac {8\pi G\beta }{c^{4}}}T^{{ik}},$

where $~R^{{ik}}$ is the Ricci tensor, is the scalar curvature, $~g^{{ik}}$ is the metric tensor, $~\beta$ is a certain constant.

In the vector field theory, all four-vectors and tensors are gauged, including four-currents, four-potentials and field tensors. For example, the four-velocity gauging has the form: $~g_{{\mu \nu }}u^{\mu }u^{\nu }=u_{\nu }u^{\nu }=c^{2}.$ Applying here the operator of proper-time-derivative, we arrive at the four-acceleration gauging: $~a_{\mu }u^{\mu }=0,$ where the four-acceleration is $~a_{\mu }={\frac {Du_{\mu }}{D\tau }}.$ For the four-momentum gauging, we have: $~g_{{\mu \nu }}p^{\mu }p^{\nu }=p_{\nu }u^{\nu }=mc^{2}$ , where is the inertial mass of the system.

The four-displacement gauging: $~g_{{\mu \nu }}dx^{\mu }dx^{\nu }=dx_{\nu }dx^{\nu }=ds^{2},$ where is the four-dimensional spacetime interval. The metric tensor gauging: $~g^{{\mu \nu }}g_{{\nu \lambda }}=\delta _{\lambda }^{\mu }$ , $~g^{{\mu \nu }}g_{{\nu \mu }}=\delta _{\mu }^{\mu }=4,$ where $~\delta _{\lambda }^{\mu }$ is the Kronecker delta.

The curvature tensor is not an exception, from this tensor, using the contraction with the metric tensor, we first obtain the Ricci tensor, and then the scalar curvature. The gauge condition for the scalar curvature is as follows: $~\nabla _{\mu }R=0.$ The cosmological constant $~\Lambda$ is also gauged as follows: $~R=2\Lambda .$ This allows us to eliminate in the expression for the relativistic energy both the scalar curvature and the cosmological constant in the only possible way. ^[4]

Field energy theorem

The field energy theorem for the electromagnetic field has the following form: ^[11]

$~-\int {(2\mu _{0}A_{\alpha }j^{\alpha }+F_{{\alpha \beta }}F^{{\alpha \beta }}){\sqrt {-g}}dx^{1}dx^{2}dx^{3}}={\frac {2}{c}}{\frac {d}{dt}}\left(\int {A^{\alpha }F_{\alpha }^{{\ 0}}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}\right)+2\iint \limits _{S}{A^{\alpha }F_{\alpha }^{{\ k}}n_{k}{\sqrt {-g}}dS},$

where $~\mu _{0}$ is the magnetic constant; $~A_{\alpha }$ is the electromagnetic four-potential; $~j^{\alpha }$ is the electromagnetic four-current; $~F_{{\alpha \beta }}$ is the electromagnetic field tensor; $~{\sqrt {-g}}dx^{1}dx^{2}dx^{3}$ is the element of the invariant volume, expressed in terms of the product $~dx^{1}dx^{2}dx^{3}$ of the differentials of the space coordinates and in terms of the square root $~{\sqrt {-g}}$ of the determinant of the metric tensor, taken with a negative sign; is the speed of light; the last integral on the right-hand side is the surface integral of the second kind taken over the two-dimensional surface , surrounding the volume under consideration; $~n_{k}$ is the outward-directed three-dimensional normal vector to the surface .

Similarly, we obtain the following for the gravitational field, acceleration field and pressure field:

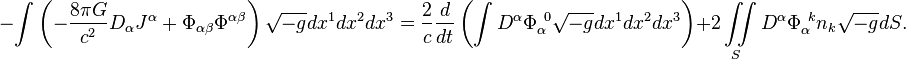
$~-\int {\left(-{\frac {8\pi G}{c^{2}}}D_{\alpha }J^{\alpha }+\Phi _{{\alpha \beta }}\Phi ^{{\alpha \beta }}\right){\sqrt {-g}}dx^{1}dx^{2}dx^{3}}={\frac {2}{c}}{\frac {d}{dt}}\left(\int {D^{\alpha }\Phi _{\alpha }^{{\ 0}}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}\right)+2\iint \limits _{S}{D^{\alpha }\Phi _{\alpha }^{{\ k}}n_{k}{\sqrt {-g}}dS}.$

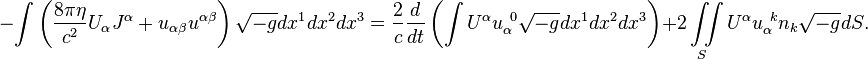
$~-\int {\left({\frac {8\pi \eta }{c^{2}}}U_{\alpha }J^{\alpha }+u_{{\alpha \beta }}u^{{\alpha \beta }}\right){\sqrt {-g}}dx^{1}dx^{2}dx^{3}}={\frac {2}{c}}{\frac {d}{dt}}\left(\int {U^{\alpha }u_{\alpha }^{{\ 0}}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}\right)+2\iint \limits _{S}{U^{\alpha }u_{\alpha }^{{\ k}}n_{k}{\sqrt {-g}}dS}.$

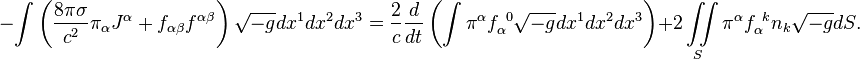
$~-\int {\left({\frac {8\pi \sigma }{c^{2}}}\pi _{\alpha }J^{\alpha }+f_{{\alpha \beta }}f^{{\alpha \beta }}\right){\sqrt {-g}}dx^{1}dx^{2}dx^{3}}={\frac {2}{c}}{\frac {d}{dt}}\left(\int {\pi ^{\alpha }f_{\alpha }^{{\ 0}}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}\right)+2\iint \limits _{S}{\pi ^{\alpha }f_{\alpha }^{{\ k}}n_{k}{\sqrt {-g}}dS}.$

The above expressions are the integral equations, relating the four-potentials, four-currents and tensors of the respective fields.

Integral equations

For the electromagnetic field, the integral equations in the curved spacetime have been considered in the article. ^[12]

Integrating the standard equation of the electromagnetic field over the four-dimensional volume and applying the divergence theorem gives the following equation:

$~{\frac {1}{c}}{\frac {d}{dt}}\int \limits _{V}{F^{{\alpha 0}}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}+\int {F^{{\alpha 1}}{\sqrt {-g}}dx^{2}dx^{3}}+\int {F^{{\alpha 2}}{\sqrt {-g}}dx^{3}dx^{1}}+\int {F^{{\alpha 3}}{\sqrt {-g}}dx^{1}dx^{2}}=-\mu _{0}\int \limits _{V}{j^{\alpha }{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}.\quad (1)$

For the index $~\alpha =0$ , taking into account the equality $~j^{0}=\rho _{0}u^{0}$ , we obtain from (1) the Gauss's law in the covariant notation:

$~\int \limits _{S}{F^{{0k}}{\sqrt {-g}}dS_{k}}=-{\frac {\Phi _{E}}{c}}=-\mu _{0}\int \limits _{V}{\rho _{0}u^{0}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}=-c\mu _{0}q,$

where $~dS_{k}=dS^{{ij}}=dx^{i}dx^{j}$ is an orthonormal element of the two-dimensional surface surrounding the charge ; $~\Phi _{E}=c\int \limits _{S}{F^{{k0}}{\sqrt {-g}}dS_{k}}$ represents the electric flux through the closed surface; cyclically repeated three-dimensional indices , which do not coincide with each other.

Now let us assume that in (1) the indices $~\alpha =i=1,2,3$ :

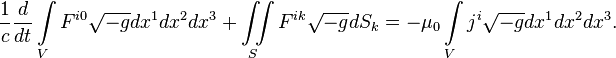
$~{\frac {1}{c}}{\frac {d}{dt}}\int \limits _{V}{F^{{i0}}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}+\iint \limits _{S}{F^{{ik}}{\sqrt {-g}}dS_{k}}=-\mu _{0}\int \limits _{V}{j^{i}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}.$

This equation is valid for any three-dimensional volume and the two-dimensional surface surrounding it. If we split the volume by a certain plane perpendicularly to the axis , then at the index we can pass on from integration over and to integration over the cross-section area and the contour of this cross-section:

$~{\frac {1}{c}}{\frac {d}{dt}}\int {F^{{10}}{\sqrt {-g}}dx^{2}dx^{3}}+\int {F^{{12}}{\sqrt {-g}}dx^{3}}-\int {F^{{13}}{\sqrt {-g}}dx^{2}}=-\mu _{0}\int {j^{1}{\sqrt {-g}}dx^{2}dx^{3}}.$

The obtained covariant expression represents the theorem on the magnetic field circulation (Ampère's circuital law), and $~\Phi _{E}=c\int {F^{{10}}{\sqrt {-g}}dx^{2}dx^{3}}$ can be considered here as the flux of the electric field through the cross-section surface in the direction of the axis . Hence it follows that the magnetic field circulation in the contour occurs not only due to changing over time of the flux of the electric field through the contour, but also occurs when the contour area changes with the constant electric field.

Integration of the electromagnetic field equation with the dual electromagnetic field tensor over the four-dimensional volume, taking into account the divergence theorem, leads to the following equation:

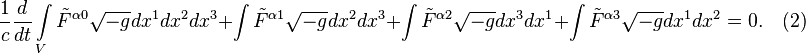
$~{\frac {1}{c}}{\frac {d}{dt}}\int \limits _{V}{{\tilde {F}}^{{\alpha 0}}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}+\int {{\tilde {F}}^{{\alpha 1}}{\sqrt {-g}}dx^{2}dx^{3}}+\int {{\tilde {F}}^{{\alpha 2}}{\sqrt {-g}}dx^{3}dx^{1}}+\int {{\tilde {F}}^{{\alpha 3}}{\sqrt {-g}}dx^{1}dx^{2}}=0.\quad (2)$

Hence, with the index $~\alpha =0$ , taking into account the dual tensor components, we obtain the Gauss's law for magnetism:

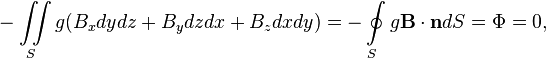
$~-\iint \limits _{S}{g(B_{x}dydz+B_{y}dzdx+B_{z}dxdy)}=-\oint \limits _{S}{g{\mathbf {B\cdot n}}dS}=\Phi =0,$

where the covariant quantity $~\Phi =-\oint \limits _{S}{g{\mathbf {B\cdot n}}dS}$ is the flux of the magnetic field through the closed surface.

If in equation (2) we assume that the index $~\alpha =1$ , then when the volume under consideration is split by a plane perpendicular to the axis , for the obtained cross-section and the contour surrounding it, we have the following equation:

$~-\oint \limits _{\ell }{g{\mathbf {E\cdot }}d{\mathbf r}}=\varepsilon ={\frac {d}{dt}}\iint \limits _{S}{g{\mathbf {B\cdot n}}dS}=-{\frac {d\Phi }{dt}}.$

This integral equation represents the theorem on the electric field circulation and the Faraday's law of induction in a covariant form, where the quantity $~\Phi =-\iint \limits _{S}{g{\mathbf {B\cdot n}}dS}$ is the magnetic flux through the surface bounded by the conductive contour $~\ell$ , and the quantity $~\varepsilon =-\oint \limits _{\ell }{g{\mathbf {E\cdot }}d{\mathbf r}}$ is the electromotive force.

If we write the four-potential of the electromagnetic field with a contravariant index in terms of the components in the form $~A^{\mu }=(A^{0},A^{1},A^{2},A^{3})$ and denote the flux of the vector potential over a closed two-dimensional surface as follows

$~\Phi _{A}=\int {A^{1}{\sqrt {-g}}dx^{2}dx^{3}}+\int {A^{2}{\sqrt {-g}}dx^{3}dx^{1}}+\int {A^{3}{\sqrt {-g}}dx^{1}dx^{2}},$

then the equation will hold true

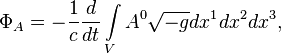
$~\Phi _{A}=-{\frac {1}{c}}{\frac {d}{dt}}\int \limits _{V}{A^{0}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}},$

which means that when the volume integral of scalar potential changes over time, the flux of the vector potential appears.

The integral equations, similar to those provided above for the electromagnetic field, must also be valid for other vector fields.

See also

References

1. Fedosin S.G. The Concept of the General Force Vector Field. OALib Journal, Vol. 3, pp. 1-15 (2016), e2459. http://dx.doi.org/10.4236/oalib.1102459.

2. Fedosin S.G. Two components of the macroscopic general field. Reports in Advances of Physical Sciences, Vol. 1, No. 2, 1750002, 9 pages (2017). http://dx.doi.org/10.1142/S2424942417500025.

3. Fedosin S.G. The procedure of finding the stress-energy tensor and vector field equations of any form. Advanced Studies in Theoretical Physics, Vol. 8, No. 18, pp. 771-779 (2014). http://dx.doi.org/10.12988/astp.2014.47101.

4. ^{4.0 4.1}Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy. Jordan Journal of Physics. Vol. 9, No. 1, pp. 1-30 (2016). http://dx.doi.org/10.5281/zenodo.889304.

5. Fedosin S.G. The Principle of Least Action in Covariant Theory of Gravitation. Hadronic Journal, Vol. 35, No. 1, pp. 35-70 (2012). http://dx.doi.org/10.5281/zenodo.889804.

6. Fedosin S.G. Four-Dimensional Equation of Motion for Viscous Compressible and Charged Fluid with Regard to the Acceleration Field, Pressure Field and Dissipation Field. International Journal of Thermodynamics. Vol. 18, No. 1, pp. 13-24 (2015). http://dx.doi.org/10.5541/ijot.5000034003.

7. ^{7.0 7.1 7.2}Fedosin S.G. Equations of Motion in the Theory of Relativistic Vector Fields. International Letters of Chemistry, Physics and Astronomy, Vol. 83, pp. 12-30 (2019). https://doi.org/10.18052/www.scipress.com/ILCPA.83.12.

8. Fedosin S.G. The generalized Poynting theorem for the general field and solution of the 4/3 problem. International Frontier Science Letters, Vol. 14, pp. 19-40 (2019). https://doi.org/10.18052/www.scipress.com/IFSL.14.19.

9. Fedosin S.G. The Mass Hierarchy in the Relativistic Uniform System. Bulletin of Pure and Applied Sciences, Vol.38 D (Physics), No. 2, pp. 73-80 (2019). http://dx.doi.org/10.5958/2320-3218.2019.00012.5.

10. Fedosin S.G. Energy and metric gauging in the covariant theory of gravitation. Aksaray University Journal of Science and Engineering, Vol. 2, Issue 2, pp. 127-143 (2018). http://dx.doi.org/10.29002/asujse.433947.

11. Fedosin S.G. The Integral Theorem of the Field Energy. Gazi University Journal of Science. Vol. 32, No. 2, pp. 686-703 (2019). http://dx.doi.org/10.5281/zenodo.3252783.

12. Fedosin S.G. On the Covariant Representation of Integral Equations of the Electromagnetic Field. Progress In Electromagnetics Research C, Vol. 96, pp. 109-122 (2019). https://doi.org/10.2528/PIERC19062902.

External links

Equation of vector field in Russian

Source: http://sergf.ru/uven.htm

On the list of pages