На русском языке

Acceleration field

Acceleration field is a two-component vector field, describing in a covariant way the four-acceleration of individual particles and the four-force that occurs in systems with multiple closely interacting particles. The acceleration field is a component of the general field, which is represented in the Lagrangian and Hamiltonian of an arbitrary physical system by the term with the energy of particles’ motion and the term with the field energy. [1]  [2]  The acceleration field is included in most equations of vector field. Moreover, the acceleration field enters into the equation of motion through the acceleration tensor and into the equation for the metric through the acceleration stress-energy tensor.

The acceleration field was presented by Sergey Fedosin within the framework of the metric theory of relativity and covariant theory of gravitation, and the equations of this field were obtained as a consequence of the principle of least action. [3] [4]

Contents

  • 1 Mathematical description
    • 1.1 Action, Lagrangian and energy
    • 1.2 Equations
    • 1.3 Stress-energy tensor
  • 2 Specific solutions for acceleration field functions
    • 2.1 Ideally solid particle
    • 2.2 Rotation of a particle
    • 2.3 System of particles
  • 3 Other approaches
  • 4 The use in general theory of relativity
  • 5 See also
  • 6 References
  • 7 External links

Mathematical description

The 4-potential of the acceleration field is expressed in terms of the scalar ~ \vartheta   and vector ~ \mathbf {U}   potentials:

~U_\mu = \left(\frac {\vartheta }{c},- \mathbf {U} \right) .

The antisymmetric acceleration tensor is calculated with the help of the 4-curl of the 4-potential:

~ u_{\mu \nu} = \nabla_\mu U_\nu - \nabla_\nu U_\mu = \partial_\mu U_\nu - \partial_\nu U_\mu .

The acceleration tensor components are the components of the field strength ~\mathbf {S}   and the components of the solenoidal vector ~\mathbf {N} :

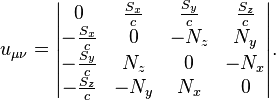
~ u_{\mu \nu}= \begin{vmatrix} 0 & \frac {S_x}{ c} & \frac {S_y}{ c} & \frac {S_z}{ c} \\ -\frac {S_x}{ c} & 0 & - N_{z} & N_{y} \\ -\frac {S_y}{ c} & N_{z} & 0 & -N_{x} \\ -\frac {S_z}{ c}& -N_{y} & N_{x} & 0 \end{vmatrix}.

We obtain the following:

~ \mathbf {S} = - \nabla \vartheta - \frac {\partial \mathbf {U}}{\partial t},\qquad\qquad \mathbf {N} = \nabla \times \mathbf {U}.\qquad\qquad (1)

 

In the general case the scalar and vector potentials are found by solving the wave equations for the acceleration field potentials.

 

Action, Lagrangian and energy

In the covariant theory of gravitation the 4-potential  ~U_\mu   of the acceleration field is part of the 4-potential of the general field  ~ s_\mu, which is the sum of the 4-potentials of particular fields, such as the electromagnetic and gravitational fields, acceleration field, pressure field, dissipation field, strong interaction field, weak interaction field and other vector fields, acting on the matter and its particles. All of these fields are somehow represented in the matter, so that the 4-potential ~ s_\mu  cannot consist of only one 4-potential  ~U_\mu  . The energy density of interaction of the general field and the matter is given by the product of the 4-potential of the general field and the mass 4-current: ~ s_\mu J^\mu . We obtain the general field tensor from the 4-potential of the general field, using the 4-curl:

~ s_{\mu \nu} =\nabla_\mu s_\nu - \nabla_\nu s_\mu.

The tensor invariant in the form ~ s_{\mu \nu} s^{\mu \nu}   is up to a constant factor proportional to the energy density of the general field. As a result, the action function, which contains the scalar curvature ~R  and the cosmological constant ~ \Lambda , is given by the expression: [1]

~S =\int {L dt}=\int (kR-2k \Lambda - \frac {1}{c}s_\mu J^\mu - \frac {c}{16 \pi \varpi} s_{\mu\nu}s^{\mu\nu} ) \sqrt {-g}d\Sigma,

where ~L   is the Lagrange function or Lagrangian; ~dt   is the time differential of the coordinate reference system; ~k   and ~ \varpi    are the constants to be determined; ~c   is the speed of light as a measure of the propagation speed of the electromagnetic and gravitational interactions; ~\sqrt {-g}d\Sigma= \sqrt {-g} c dt dx^1 dx^2 dx^3  is the invariant 4-volume expressed in terms of the differential of the time coordinate ~ dx^0=cdt , the product ~ dx^1 dx^2 dx^3   of differentials of the space coordinates and the square root  ~\sqrt {-g}   of the determinant ~g   of the metric tensor, taken with a negative sign.

The variation of the action function gives the general field equations, the four-dimensional equation of motion and the equation for the metric. Since the acceleration field is the general field component, then from the general field equations the corresponding equations of the acceleration field are derived.

Given the gauge condition of the cosmological constant in the form

~ c k \Lambda = - s_\mu J^\mu ,

is met, the system energy does not depend on the term with the scalar curvature and is uniquely determined: [4]

~E = \int {( s_0 J^0 + \frac {c^2 }{16 \pi \varpi } s_{ \mu\nu} s^{ \mu\nu} ) \sqrt {-g} dx^1 dx^2 dx^3},

where ~ s_0   and ~ J^0  denote the time components of the 4-vectors ~ s_{\mu }   and  ~ J^{\mu } .

In an arbitrary reference frame K, the 4-momentum of a system is determined by the formula: [5] [6]

~p_{\mu }=\left({\frac {E}{c}}{,}-{\mathbf {p}}\right)=Mu_{\mu }={\frac {E_{0}}{cu'_{0}}}u_{\mu },

where  ~E  and  ~{\mathbf {p}}  denote the energy and momentum of the physical system in K;  ~M  is the inertial mass;  ~u_{\mu }  is the 4-velocity of the center of momentum of the physical system in  K. If we place the origin of coordinates of the reference frame K' at the center of momentum and calculate in K' the energy of the system  ~E_{0}  and the time component  ~u'_{0}  of the 4-velocity of the center of momentum, then we can find the inertial mass  ~M={\frac {E_{0}}{cu'_{0}}}  of the system. Note that in the reference frame K' the three-dimensional momentum ~{\mathbf {p'}} of a physical system is by definition equal to zero.

Equations

The four-dimensional equations of the acceleration field are similar in their form to Maxwell equations and are as follows:

\nabla_\sigma u_{\mu \nu}+\nabla_\mu u_{\nu \sigma}+\nabla_\nu u_{\sigma \mu}=\frac{\partial u_{\mu \nu}}{\partial x^\sigma} + \frac{\partial u_{\nu \sigma}}{\partial x^\mu} + \frac{\partial u_{\sigma \mu}}{\partial x^\nu} = 0.

 

~ \nabla_\nu u^{\mu \nu} = - \frac{4 \pi \eta }{c^2} J^\mu,

where J^\mu = \rho_{0} u^\mu   is the mass 4-current, \rho_{0}  is the mass density in the co-moving reference frame, u^\mu   is the 4-velocity of the matter unit, ~ \eta   is a constant, which is determined in each problem, and it is supposed that there is an equilibrium between all fields in the observed physical system.

The gauge condition of the 4-potential of the acceleration field:

~ \nabla^\mu U_{\mu} =0 .

If the second equation with the field source is written with the covariant index in the following form:

~\nabla ^{\nu }u_{{\mu \nu }}=-{\frac {4\pi \eta }{c^{2}}}J_{\mu },

then after substituting here the expression for the acceleration tensor  u_{{\mu \nu }}  through the 4-potential  ~U_\mu   of the acceleration field  we obtain the wave equation for calculating the potentials of the acceleration field: [7]

~ \nabla^\nu \nabla_\nu U_\mu + R_{\mu \nu} U^\nu = \frac{4 \pi \eta }{c^2} J_\mu,

where  ~R_{{\mu \nu }}   is the Ricci tensor, found using the formula in the book. [8]  If the Ricci tensor is calculated using the formula in the book, [9]  the sign of the Ricci tensor in the wave equation should be reversed.

The continuity equation in curved space-time is:

~\nabla _{{\alpha }}J^{{\alpha }}=0.

In Minkowski space of the special theory of relativity, the Ricci tensor is set to zero, the form of the acceleration field equations is simplified and they can be expressed in terms of the field strength ~\mathbf {S}   and the solenoidal vector ~\mathbf {N} :

~ \nabla \cdot \mathbf{S} = 4 \pi \eta \gamma \rho_0, \qquad\qquad \nabla \times \mathbf{N} = \frac{1}{c^2} \left( 4 \pi \eta \mathbf{J} + \frac{\partial \mathbf{S}} {\partial t} \right),

 

~ \nabla \times \mathbf{S} = - \frac{\partial \mathbf{N} } {\partial t} , \qquad\qquad \nabla \cdot \mathbf{N} = 0 .

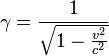where  ~ \gamma = \frac {1}{\sqrt{1 - {v^2 \over c^2}}}   is the Lorentz factor, ~ \mathbf{J}= \gamma \rho_0 \mathbf{v }  is the mass current density, ~ \mathbf{v }   is the velocity of the matter unit.

The wave equation is also simplified and can be written separately for the scalar and vector potentials:

 

~\partial ^{\nu }\partial _{\nu }\vartheta ={\frac {1}{c^{2}}}{\frac {\partial ^{2}\vartheta }{\partial t^{2}}}-\Delta \vartheta =4\pi \eta \gamma \rho _{0},\qquad \qquad (2)

 

 

~\partial ^{\nu }\partial _{\nu }{\mathbf {U}}={\frac {1}{c^{2}}}{\frac {\partial ^{2}{\mathbf {U}}}{\partial t^{2}}}-\Delta {\mathbf {U}}={\frac {4\pi \eta }{c^{2}}}{\mathbf {J}}.\qquad \qquad (3)

 

The equation of motion of the matter unit in the general field is given by the formula:

~ s_{\mu \nu} J^\nu =0 .

Since  ~ J^\nu = \rho_0 u^\nu , and the general field tensor is expressed in terms of the tensors of particular fields, then the equation of motion can be represented with the help of these tensors: [7] [10] 

~-u_{{\mu \nu }}J^{\nu }=F_{{\mu \nu }}j^{\nu }+\Phi _{{\mu \nu }}J^{\nu }+f_{{\mu \nu }}J^{\nu }+h_{{\mu \nu }}J^{\nu }+\gamma _{{\mu \nu }}J^{\nu }+w_{{\mu \nu }}J^{\nu }=\rho _{0}{\frac {Du_{\mu }}{D\tau }}=\rho _{0}A_{\mu }.\qquad (4)

Here ~ F_{\mu \nu}  is the electromagnetic tensor, ~ j^\nu   is the charge 4-current, ~ \Phi_{\mu \nu}  is the gravitational tensor, ~ f_{\mu \nu}  is the pressure field tensor, ~ h_{\mu \nu}  is the dissipation field tensor, ~ \gamma_{\mu \nu}  is the strong interaction field tensor, ~ w_{\mu \nu}  is the weak interaction field tensor. ~\rho _{0}  is invariant mass density,  ~u_{\mu }  and  ~A_{\mu }  are the 4-velocity and 4-acceleration of the matter unit.

Stress-energy tensor

The acceleration stress-energy tensor is calculated with the help of the acceleration tensor:

~ B^{ik} = \frac{c^2} {4 \pi \eta }\left( -g^{im} u_{n m} u^{n k}+ \frac{1} {4} g^{ik} u_{m r} u^{m r}\right) .

We find as part of the tensor ~ B^{ik} the 3-vector of energy flux density of acceleration field ~\mathbf {K} , which is similar in its meaning to the Poynting vector and the Heaviside vector. The vector ~\mathbf {K}   can be represented through the vector product of the field strength ~ \mathbf {S}   and the solenoidal vector ~ \mathbf {N} :

~ \mathbf {K}=c B^{0i} = \frac {c^2}{4 \pi \eta }[\mathbf {S}\times \mathbf {N}],

here the index is   ~ i=1,2,3.

The covariant derivative of the stress-energy tensor of the acceleration field with mixed indices specifies the 4-force density:

~f_{\alpha }=\nabla _{\beta }{B_{\alpha }}^{\beta }=-u_{{\alpha k}}J^{k}=-\rho _{0}u_{{\alpha k}}u^{k}=\rho _{0}{\frac {DU_{\alpha }}{D\tau }}-J^{k}\nabla _{\alpha }U_{k}=\rho _{0}{\frac {dU_{\alpha }}{d\tau }}-J^{k}\partial _{\alpha }U_{k},\qquad (5)

where ~ D \tau   denotes the proper time differential in the curved spacetime.

The stress-energy tensor of the acceleration field is part of the stress-energy tensor of the general field ~ T^{ik} :

~ T^{ik}= W^{ik}+ U^{ik}+ B^{ik}+ P^{ik} + Q^{ik}+ L^{ik}+ A^{ik},  

where  ~ W^{ik}   is the electromagnetic stress–energy tensor, ~ U^{ik}  is the gravitational stress-energy tensor, ~ P^{ik}  is the pressure stress-energy tensor, ~ Q^{ik}  is the dissipation stress-energy tensor, ~ L^{ik}  is the strong interaction stress-energy tensor, ~ A^{ik}   is the weak interaction stress-energy tensor.

Through the tensor ~ T^{ik}   the stress-energy tensor of the acceleration field enters into the equation for the metric:

~ R^{ik} - \frac{1} {4 }g^{ik}R = \frac{8 \pi G \beta }{ c^4} T^{ik},

where ~ R^{ik}   is the Ricci tensor, ~ G   is the gravitational constant, ~ \beta   is a certain constant, and the gauge condition of the cosmological constant is used.

Specific solutions for acceleration field functions

The four-potential of any vector field, the global vector potential of which is equal to zero in the proper reference frame K', that is, in the center-of-momentum frame, in case of rectilinear motion in the laboratory reference frame K, can be presented as follows: [3] [7]

~ L_{\mu L} = \frac { k_f \varepsilon }{\rho_0 c^2} u_{\mu L},

where   ~ k_f = \frac {\rho_0}{\rho_{0q}}   is for the electromagnetic field and  ~ k_f = 1  for the remaining fields; ~ \rho_{0}  and  ~\rho_{0q}  are the invariant mass density and the charge density in the comoving reference frame, respectively; ~ \varepsilon   is the invariant energy density of the interaction, calculated as product of the four-potential of the field and the corresponding four-current; ~ u_{\mu L}   is the covariant four-velocity that determines the motion of the center of momentum of the physical system in K.

In the special relativity (SR), in the center-of-momentum frame K'  the energy density is  ~ \varepsilon = \gamma' \rho_0 c^2 , where  ~ \gamma'   is the Lorentz factor, and for the acceleration field, while the physical system is moving in K, the four-potential of the acceleration field will equal  ~ U_{\mu L}= \gamma' u_{\mu L}.

In case when the physical system is stationary in K, we will have  ~ u_{\mu L} = (c,0,0,0)  , and consequently, the scalar potential will be  ~ \vartheta = \gamma' c^2 . If in the physical system, on the average, there are directed fluxes of matter or rotation of matter, the vector potential  ~ \mathbf {U}   of the acceleration field is no longer equal to zero.

If the four-potential  ~U'_{{\nu }}  of acceleration field in  K'  is known, then in the laboratory reference frame K the four-potential is determined using the matrix  ~M_{{\mu }}^{{\ \nu }}  connecting the coordinates and time of both frames: [11]

~U_{{\mu L}}=M_{{\mu }}^{{\ \nu }}U'_{{\nu }}.

In the special case of the system’s motion at the constant velocity  ~M_{{\mu }}^{{\ \nu }}  represents the Lorentz transformation matrix.

 

Ideally solid particle

In the approximation, when a particle is regarded as an ideally solid object, the matter inside the particle is motionless. It means that the Lorentz factor  ~ \gamma'   of this matter in the center-of-momentum frame  K'  is equal to unity, so that the four-potential of the acceleration field becomes equal to the four-velocity of motion of the center of momentum:

~ U_\mu = u_\mu.

In the SR, the expression for 4-velocity is simplified and we can write:

~U_\mu = \left( \frac {\vartheta }{c},- \mathbf {U} \right) = u_\mu = \left(\gamma c, - \gamma \mathbf {v} \right).

The acceleration tensor components according to (1) will equal:

~ \mathbf {S} = - c^2 \nabla \gamma - \frac {\partial (\gamma \mathbf { v })}{\partial t},\qquad\qquad \mathbf {N} = \nabla \times (\gamma \mathbf { v }).

Since in the solid-state motion equation for the four-acceleration with a covariant index ~ a_\mu   the relation holds

~ \rho_0 a_\mu = \rho_0 \frac {Du_\mu }{D \tau}= - u_{\mu \nu} J^\nu = - \rho_0 u_{\mu \nu} u^\nu,

 

then in SR we obtain the following:

~ \frac {Du_\mu }{D \tau}= \frac {du_\mu }{d \tau} =\gamma \frac {du_\mu }{dt}, \qquad\qquad u^\nu =\left(\gamma c, \gamma \mathbf {v} \right),

and the equations for the Lorentz factor ~ \gamma   and for the 3-acceleration   ~ a= \frac {d \mathbf { v }}{dt} :

~{\frac {d\gamma }{dt}}=-{\frac {1}{c^{2}}}{\mathbf {S}}\cdot {\mathbf {v}},\qquad (6)\qquad {\frac {d(\gamma {\mathbf {v}})}{dt}}=\gamma {\mathbf {a}}+{\frac {d\gamma }{dt}}{\mathbf {v}}=-{\mathbf {S}}-[{\mathbf {v}}\times {\mathbf {N}}].\qquad (7)

Multiplying equation (7) by the velocity  ~ \mathbf { v } , substituting the quantity  ~ \mathbf {S}\cdot \mathbf { v }   from equation (6) to (7), taking into account relation  ~\gamma^{-2}=1 - {v^2 \over c^2},  we find the well-known expression for the derivative of the Lorentz factor using the scalar product of the velocity and acceleration in SR:

~ \gamma^3 \mathbf {v}\cdot \mathbf { a }=c^2 \frac {d \gamma }{dt}.

We can prove the validity of equation (7) by substituting in its right-hand side expression for the strength  ~{\mathbf {S}}  and solenoidal vector  ~{\mathbf {N}} given above:

~{\frac {d(\gamma {\mathbf {v}})}{dt}}=c^{2}\nabla \gamma +{\frac {\partial (\gamma {\mathbf {v}})}{\partial t}}-{\mathbf {v}}\times [\nabla \times (\gamma {\mathbf {v}})].\qquad \qquad (8)

Indeed, the use of the material derivative  gives the following:

~ \frac {d (\gamma \mathbf { v })}{dt}= \frac {\partial (\gamma \mathbf { v })}{\partial t} + (\mathbf { v } \cdot \nabla) (\gamma \mathbf { v }) = \frac {\partial (\gamma \mathbf { v })}{\partial t}+\gamma (\mathbf { v } \cdot \nabla) \mathbf { v } + \mathbf { v } (\mathbf { v } \cdot \nabla\gamma) .

In addition

~ - \mathbf { v }\times [ \nabla \times (\gamma \mathbf { v }) ] = - \gamma \mathbf { v }\times [ \nabla \times \mathbf { v } ] - \mathbf { v }\times [ \nabla \gamma \times \mathbf { v }] = -\frac {\gamma }{2} \nabla v^2 + \gamma (\mathbf { v } \cdot \nabla) \mathbf { v } - v^2 \nabla \gamma + \mathbf { v } (\mathbf { v } \cdot \nabla\gamma) .

Substituting these relations in (8), taking into account the expression  ~ \gamma^{-2}=1 - {v^2 \over c^2},  we obtain the identity:

~ c^2 \nabla \gamma - \frac {\gamma }{2} \nabla v^2 - v^2 \nabla \gamma =0 .

If the components of the particle velocity are the functions of time and they do not directly depend on the space coordinates, then the solenoidal vector ~ \mathbf { N }  vanishes in such a motion.

In the SR  ~E=\gamma mc^{2}  is the relativistic energy, ~{\mathbf p}=\gamma m{\mathbf v}  is the 3-vector of relativistic momentum. If the mass  ~m  of a particle is constant, then multiplying (8) by the mass, we arrive to following equation for the force:

~{\mathbf F}={\frac {d{\mathbf p}}{dt}}=\nabla E+{\frac {\partial {\mathbf p}}{\partial t}}-{\mathbf {v}}\times [\nabla \times {\mathbf p}].

 

Rotation of a particle

For a small ideally solid particle, we can neglect the motion of the matter inside the particle and can assume that the four-potential of the acceleration field is equal to the four-velocity of the particle’s center of momentum. Let us assume that the particle rotates about the axis OZ of the coordinate system at the distance  ~\rho ={\sqrt {x^{2}+y^{2}}}  from the axis at the constant angular velocity  ~\omega  counterclockwise, as viewed from the side, in which the OZ axis is directed. Then we can assume that the linear velocity of the particle depends only on the coordinates  ~x  and  ~y, and for the velocity’s projections on the axes of the coordinate system we can write:  ~{\mathbf v}=(-\omega y,\omega x,0),  while the square of the velocity equals  ~v^{2}=\omega ^{2}(x^{2}+y^{2}). For the Lorentz factor in the SR we obtain the following:

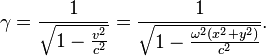
~\gamma ={\frac {1}{{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}={\frac {1}{{\sqrt {1-{\frac {\omega ^{2}(x^{2}+y^{2})}{c^{2}}}}}}}.

With this in mind, the potentials and field strengths of the acceleration field can be written as follows:

~\vartheta =\gamma c^{2},\qquad {\mathbf {U}}=\gamma {\mathbf {v}}.

 

~{\mathbf {S}}=-\nabla \vartheta -{\frac {\partial {\mathbf {U}}}{\partial t}}=\left(-\gamma ^{3}\omega ^{2}x,-\gamma ^{3}\omega ^{2}y,0\right).

 

~{\mathbf {N}}=\nabla \times {\mathbf {U}}=\left(0,0,\gamma \omega +\gamma ^{3}\omega \right).

 

If we substitute ~\gamma ,  ~{\mathbf v},  ~{\mathbf {S}}  and  ~{\mathbf {N}}  in (7), we can determine the acceleration components of the particle and the acceleration amplitude:

~{\mathbf {a}}=\left(-\omega ^{2}x,-\omega ^{2}y,0\right).

 

~a={\sqrt {a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}=\omega ^{2}{\sqrt {x^{2}+y^{2}}}=\omega ^{2}\rho =\omega v={\frac {v^{2}}{\rho }}.

 

The acceleration is directed towards the center of rotation and represents centripetal acceleration. Using now the classic vector description, we have also for the time and coordinates of reference frame at the center of rotation:

~{\vec \rho }=(x,y,0),\qquad {\vec \omega }={\frac {{\vec {d\varphi }}}{dt}}=(0,0,\omega ),

 

~{\mathbf {v}}=[{\vec \omega }\times {\vec \rho }],\qquad {\mathbf {a}}=[{\vec \omega }\times {\mathbf {v}}]=[{\vec \omega }\times [{\vec \omega }\times {\vec \rho }]]={\vec \omega }({\vec \omega }\cdot {\vec \rho })-{\vec \rho }({\vec \omega }\cdot {\vec \omega })=-\omega ^{2}{\vec \rho },

 

where  ~\rho   and  ~\varphi   are two coordinates of the cylindrical coordinate system, ~{\vec \rho }  is the vector from the center of rotation to the particle, ~{\vec {d\varphi }}  is the axial vector of the differential of the rotation angle directed along the axis OZ.

As we can see, in case of such a motion with acceleration the vector product   ~[{\mathbf {S}}\times {\mathbf {N}}]  is not equal to zero, just as the three-vector  ~{\mathbf {K}}  of energy flux density of the acceleration field inside the particle.

System of particles

Due to interaction of a number of particles with each other by means of various fields, including interaction at a distance without direct contact, the acceleration field in the matter changes and is different from the acceleration field of individual particles at the observation point. As a result, the density of the 4-force in the system of particles is given by the strength and the solenoidal vector, which represent the typical average characteristics of the matter motion. For example, in a gravitationally bound system there is a radial gradient of the vector ~ \mathbf { S },  and if the system is moving or rotating, there is a vector ~ \mathbf { N }.  From (5) there follows the general expression for the density of 4-force with covariant index:

~ f_\nu = \rho_0 \frac {cdt}{ds}\left(-\frac {1}{c} \mathbf{S} \cdot \mathbf{v}{,} \qquad \mathbf{S}+[\mathbf{v} \times \mathbf{N}] \right), 

where ~ ds   denotes a four-dimensional space-time interval. For a stationary case, when the potentials of the acceleration field are independent of time, under the assumption that  ~ \vartheta = \gamma c^2,   wave equation (2) for the scalar potential in the SR is transformed into the equation:

~ \Delta \gamma= - \frac {4 \pi \eta \gamma \rho_0}{c^2}.

The solution of this equation for a fixed sphere with the particles randomly moving in it has the form: [12]

~\gamma= \frac {c \gamma_c }{r \sqrt {4 \pi \eta \rho_0} } \sin \left(\frac {r}{c}\sqrt {4 \pi \eta \rho_0} \right) \approx \gamma_c - \frac {2 \pi \eta \rho_0 r^2 \gamma_c }{3 c^2}.

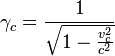where  ~ \gamma_c = \frac {1}{\sqrt{1 - {v^2_c \over c^2}}}   is the Lorentz factor for the velocities ~ v_c  of the particles in the center of the sphere, and due to the smallness of the argument the sine is expanded to the second order terms. From the formula it follows that the average velocities of the particles are maximal in the center and decrease when approaching the surface of the sphere.

In such a system, the scalar potential ~ \vartheta  becomes the function of the radius, and the vector potential ~ \mathbf {U}   and the solenoidal vector ~ \mathbf { N }  are equal to zero. The acceleration field strength ~\mathbf {S}   is found with the help of (1). Then we can calculate all the functions of the acceleration field, including the energy of particles in this field and the energy of the acceleration field itself. [13] For cosmic bodies the main contribution to the four-acceleration in the matter makes the gravitational force and the pressure field.

At the same time the relativistic rest energy of the system is automatically derived, taking into account the motion of particles inside the sphere. For the system of particles with the acceleration field, pressure field, gravitational and electromagnetic fields the given approach allowed solving the 4/3 problem and showed where and in what form the energy of the system is contained. The relation for the acceleration field constant in this problem was found:

~\eta = 3G- \frac {3q^2}{4 \pi \varepsilon_0 m^2 },

where ~ \varepsilon_0  is the electric constant, ~q   and ~m   are the total charge and mass of the system.

The solution of the wave equation for the acceleration field within the system results in temperature distribution according to the formula: [12]

~ T=T_c - \frac {\eta M_p M(r)}{3kr} ,

where ~ T_c   is the temperature in the center, ~ M_p   is the mass of the particle, for which the mass of the proton is taken (for systems which are based on hydrogen or nucleons in atomic nuclei), ~ M(r)   is the mass of the system within the current radius ~ r , ~ k  is the Boltzmann constant.

This dependence is well satisfied for a variety of space objects, including gas clouds and Bok globules, the Earth, the Sun and neutron stars.

In articles [14] [15] the ratio of the field’s coefficients for the fields was specified as follows:

~\eta +\sigma =G-{\frac {\rho _{{0q}}^{2}}{4\pi \varepsilon _{0}\rho _{{0}}^{2}}},

where ~\sigma   is the pressure field constant.

If we introduce the parameter ~\mu   as the number of nucleons per ionized gas particle, then the acceleration field constant is expressed as follows:

~\eta ={\frac {3\gamma _{c}\mu G}{2+3\gamma _{c}\mu }}.

For the temperature inside the cosmic bodies in the gravitational equilibrium model we find the dependence on the current radius:

~T=T_{c}-{\frac {4\pi \eta m_{u}\rho _{{0c}}\gamma _{c}r^{2}}{9k}}+{\frac {2\pi \eta Am_{u}\gamma _{c}r^{3}}{9k}}+{\frac {2\pi \eta Bm_{u}\gamma _{c}r^{4}}{15k}},

where ~m_{u}  is the mass of one gas particle, which is taken as the unified atomic mass unit, and the coefficients ~A  and  ~B  are included into the dependence of the mass density on the radius in the relation  ~\rho _{0}=\rho _{{0c}}-Ar-Br^{2}.

Under the assumption that the system’s typical particles have the mass  ~{\stackrel {-}{m}}=\mu m_{u} , and that it is typical particles that define the temperature and pressure, for the acceleration field constant we obtain the following: [16]

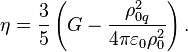
~\eta ={\frac {3}{5}}\left(G-{\frac {\rho _{{0q}}^{2}}{4\pi \varepsilon _{0}\rho _{0}^{2}}}\right).

The Lorentz factor of the particles in the center of the system is also determined: [17]

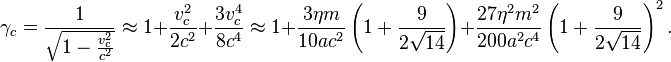
~\gamma _{c}={\frac {1}{{\sqrt {1-{\frac {v_{c}^{2}}{c^{2}}}}}}}\approx 1+{\frac {v_{c}^{2}}{2c^{2}}}+{\frac {3v_{c}^{4}}{8c^{4}}}\approx 1+{\frac {3\eta m}{10ac^{2}}}\left(1+{\frac {9}{2{\sqrt {14}}}}\right)+{\frac {27\eta ^{2}m^{2}}{200a^{2}c^{4}}}\left(1+{\frac {9}{2{\sqrt {14}}}}\right)^{2}.

 

The wave equation (3) for the vector potential of the acceleration field was used to represent the relativistic equation of the fluid’s motion in the form of the Navier–Stokes equations in hydrodynamics and to describe the motion of the viscous compressible and charged fluid. [10]

Taking into account the acceleration field and pressure field, within the framework of the relativistic uniform system, it is possible to refine the virial theorem, which in the relativistic form is written as follows: [18]

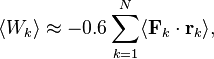
~\langle W_{k}\rangle \approx -0.6\sum _{{k=1}}^{N}\langle {\mathbf {F}}_{k}\cdot {\mathbf {r}}_{k}\rangle ,

 

where the value  ~W_{k}\approx \gamma _{c}T exceeds the kinetic energy of the particles  ~T by a factor equal to the Lorentz factor ~\gamma _{c}  of the particles at the center of the system. Under normal conditions we can assume that  ~\gamma _{c}\approx 1 , then we can see that in the virial theorem the kinetic energy is related to the potential energy not by the coefficient 0.5, but rather by the coefficient close to 0.6. The difference from the classical case arises due to considering the pressure field and the acceleration field of particles inside the system, while the derivative of the virial scalar function  ~G_{v}  is not equal to zero and should be considered as the material derivative.

An analysis of the integral theorem of generalized virial makes it possible to find, on the basis of field theory, a formula for the root-mean-square speed of typical particles of a system without using the notion of temperature: [19]

 

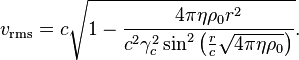
v_{{\mathrm {rms}}}=c{\sqrt {1-{\frac {4\pi \eta \rho _{0}r^{2}}{c^{2}\gamma _{c}^{2}\sin ^{2}{\left({\frac {r}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)}}}}}.

 

The integral field energy theorem for acceleration field in a curved space-time is as follows:[11]

 

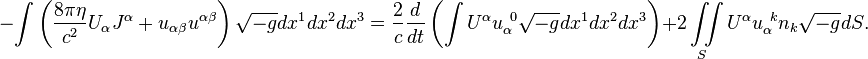
~-\int {\left({\frac {8\pi \eta }{c^{2}}}U_{\alpha }J^{\alpha }+u_{{\alpha \beta }}u^{{\alpha \beta }}\right){\sqrt {-g}}dx^{1}dx^{2}dx^{3}}={\frac {2}{c}}{\frac {d}{dt}}\left(\int {U^{\alpha }u_{\alpha }^{{\ 0}}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}\right)+2\iint \limits _{S}{U^{\alpha }u_{\alpha }^{{\ k}}n_{k}{\sqrt {-g}}dS}.

 

In the relativistic uniform system, the scalar potential ~\vartheta  of the acceleration field is related to the scalar potential ~\wp  of the pressure field: [20]

 

~\wp ={\frac {\sigma (\vartheta -c^{2})}{\eta }}={\frac {2(\vartheta -c^{2})}{3}}.

 

The relativistic expression for pressure is as follows:

 

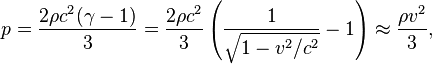
p={\frac {2\rho c^{2}(\gamma -1)}{3}}={\frac {2\rho c^{2}}{3}}\left({\frac {1}{{\sqrt {1-v^{2}/c^{2}}}}}-1\right)\approx {\frac {\rho v^{2}}{3}},

 

where \rho  is the mass density of moving matter, c is the speed of light,  \gamma ={\frac {1}{{\sqrt {1-v^{2}/c^{2}}}}}  is the Lorentz factor. In the limit of low velocities, this relationship turns into the standard formula of the kinetic theory of gases.

In [21] it is shown how the acceleration field contributes to the mass of a physical system. Similarly, the acceleration field contributes to the space-time metric, both in the matter of the physical system and beyond it. [22]

The concept of the acceleration field allows one to define in a covariant form in curved space-time the generalized four-momentum, [23] the energy, momentum and total four-momentum of a physical system taking into account particles and fields, [5]  and also the angular momentum pseudotensor. [6]

 

Other approaches

Studying the Lorentz covariance of the 4-force, Friedman and Scarr found incomplete covariance of the expression for the 4-force in the form ~ F^\mu = \frac {d p^\mu }{d \tau } .  [24]

This led them to conclude that the four-acceleration in special theory of relativity must be expressed with the help of a certain antisymmetric tensor  ~ {A^\mu}_\nu  :

~c \frac { d u^\mu }{d \tau } = {A^\mu}_\nu u^\nu .  

Based on the analysis of various types of motion, they estimated the required values of components of tensor ~{A^{\mu }}_{\nu } , thereby giving indirect definition to this tensor.

In contrast, according to (5) the density of the 4-force is equal to  ~f_{\mu }=-u_{{\mu \nu }}J^{\nu },  and in (4)   ~-u_{{\mu \nu }}J^{\nu }=\rho _{0}{\frac {Du_{\mu }}{D\tau }}=\rho _{0}A_{\mu }.  Thus, in a curved space-time, the 4-acceleration of an element of matter will be  ~A_{\mu }={\frac {Du_{\mu }}{D\tau }}=-u_{{\mu \nu }}u^{\nu }. Taking this into account, the tensor  ~{A^{\mu }}_{\nu } , up to a sign and a constant factor, has the same meaning as the acceleration field tensor ~u_{{\mu \nu }}.

Mashhoon and Muench considered transformation of inertial reference frames, co-moving with the accelerated reference frame, and obtained the relation: [25]

 

~c \frac { d \lambda_\alpha }{d \tau } = {\Phi_\alpha}^\beta \lambda_\beta.

The tensor  ~ {\Phi_\alpha}^\beta   has the same properties as the acceleration field tensor ~u_{{\mu \nu }} 

The use in general theory of relativity

The action function in the general relativity (GR) can be represented as the sum of the four terms, which are responsible, respectively, for the spacetime metric, the matter in the form of substance, the electromagnetic field and the pressure field:

~S=S_{m}+S_{{mat}}+S_{{em}}+S_{p}.

Additional terms can be included in the action function, if other fields must be taken into account. The first, second and third terms of the action have the standard form: [8]

~S_{m}=\int (kR-2k\Lambda ){\sqrt {-g}}d\Sigma .

~S_{{mat}}=\int (-c\rho _{0}){\sqrt {-g}}d\Sigma .

~S_{{em}}=\int (-{\frac {1}{c}}A_{\mu }j^{\mu }-{\frac {c\varepsilon _{0}}{4}}F_{{\mu \nu }}F^{{\mu \nu }}){\sqrt {-g}}d\Sigma ,

where A_{\mu }  is the electromagnetic four-potential.

The term  ~S_{p}, which is responsible for the contribution of pressure into the action function, is different in the works of different authors, depending on how the pressure is related to the elastic energy and whether the pressure field is considered to be a scalar field or a vector field. It should be noted that in the GR, the gravitational field is included in the action function not directly, but indirectly, by means of the metric tensor. In this case, as a rule, the pressure field is considered to be a scalar field.

In contrast, in covariant theory of gravitation (CTG), the term  ~S_{{ac}}  associated with the acceleration field is used instead of the term  ~S_{{mat}}, and the action function can be written as follows: [4]

~S=S_{m}+S_{{ac}}+S_{{em}}+S_{p}.

Here

~ S_{ac} = \int ( - \frac {1}{c } U_\mu J^\mu - \frac {c}{ 16 \pi \eta } u_{\mu\nu}u^{\mu\nu} ) \sqrt {-g}d\Sigma ,

 

~S_{p}=\int (-{\frac {1}{c}}\pi _{\mu }J^{\mu }-{\frac {c}{16\pi \sigma }}f_{{\mu \nu }}f^{{\mu \nu }}){\sqrt {-g}}d\Sigma ,

where ~\pi _{\mu }  is the four-potential of the pressure field, ~\sigma   is the coefficient of the pressure field, ~f_{{\mu \nu }}  is the pressure field tensor, J^{\mu }=\rho _{{0}}u^{\mu }.

In the case of rectilinear motion of a rigid body without rotation, the following relations will hold:  U_\mu = u_\mu  ,   ~ u_\mu u^\mu = c^2  , and in the term  ~ S_{ac}   the relation  ~ - \frac {1}{c } U_\mu J^\mu = - c \rho_0  is obtained. In this particular case it is clear that the term  ~ S_{ac}   differs from the term ~ S_{mat}   by an additional term associated with the energy of the acceleration field.

This is due to the fact that in the covariant theory of gravitation the acceleration field is considered to be a vector field, whereas as in the general relativity the acceleration field is actually used as a scalar field that does not depend on the particles’ velocities. In both theories, the acceleration field allows us to determine the contribution of the rest energy of the particles into the total energy of the system of particles and fields. However, the use of the acceleration field as a scalar field in the general relativity does not agree in its form with the vector nature of the electromagnetic field. Indeed, in the limiting case, when only the particles’ accelerations and electromagnetic forces are taken into account, the acceleration must be two-component, as is the case for the acceleration due to the action of the two-component Lorentz force. But this is only possible in the case where the acceleration field itself is a vector field. The situation can be improved if, in addition to the gravitational field function, we ascribe to the metric field  ~g_{{\mu \nu }}  in the general relativity the function of the vector component of the acceleration field, but this makes the equations of the theory even more complex and complicated.

It should be noted that in the general case of arbitrary motion of the matter the relation  ~ - \frac {1}{c } U_\mu J^\mu = - c \rho_0  is no longer satisfied and CTG does not coincide any more with GR in the method of describing the rest energy of a physical system. This means that in GR the motion of the matter is considered in a simplified way, as rectilinear motion of a solid body, whereas in CTG the use of the four-potential  U_\mu o  f the acceleration field allows us to take into account the internal motion of the matter in each selected volume element. For example, when a particle moves round a circle, the four-potential  U_\mu   of the particle’s matter will depend on the location of this matter with respect to the circle line, since the velocity of the particle’s matter depends on the radius of rotation.

See also

References

  1. 1.0 1.1 Fedosin S.G. The Concept of the General Force Vector Field. OALib Journal, Vol. 3, pp. 1-15 (2016), e2459. http://dx.doi.org/10.4236/oalib.1102459.
  2. Fedosin S.G. Two components of the macroscopic general field. Reports in Advances of Physical Sciences, Vol. 1, No. 2, 1750002, 9 pages (2017). http://dx.doi.org/10.1142/S2424942417500025.
  3. 3.0 3.1 Fedosin S.G. The procedure of finding the stress-energy tensor and vector field equations of any form. Advanced Studies in Theoretical Physics, Vol. 8, No. 18, pp. 771-779 (2014). http://dx.doi.org/10.12988/astp.2014.47101.
  4. 4.0 4.1 4.2 Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy. Jordan Journal of Physics. Vol. 9, No. 1, pp. 1-30 (2016). http://dx.doi.org/10.5281/zenodo.889304.
  5. 5.0 5.1 Fedosin S.G. What should we understand by the four-momentum of physical system? Physica Scripta, Vol. 99, No. 5, 055034 (2024). https://doi.org/10.1088/1402-4896/ad3b45.
  6. 6.0 6.1 Fedosin S.G. Lagrangian formalism in the theory of relativistic vector fields. International Journal of Modern Physics A, Vol. 40, No. 02, 2450163 (2025). https://doi.org/10.1142/S0217751X2450163X.
  7. 7,0 7,1 7,2 Fedosin S.G. Equations of Motion in the Theory of Relativistic Vector Fields. International Letters of Chemistry, Physics and Astronomy, Vol. 83, pp. 12-30 (2019). https://doi.org/10.18052/www.scipress.com/ILCPA.83.12.
  8. 8.0 8.1 Fock, V. A. (1964). "The Theory of Space, Time and Gravitation". Macmillan.
  9. Landau L.D., Lifshitz E.M. The Classical Theory of Fields, (1951). Pergamon Press. ISBN 7-5062-4256-7.
  10. 10.0 10.1 Fedosin S.G. Four-Dimensional Equation of Motion for Viscous Compressible and Charged Fluid with Regard to the Acceleration Field, Pressure Field and Dissipation Field. International Journal of Thermodynamics. Vol. 18, No. 1, pp. 13-24 (2015). http://dx.doi.org/10.5541/ijot.5000034003.
  11. 11.0 11.1 Fedosin S.G. The Integral Theorem of the Field Energy. Gazi University Journal of Science. Vol. 32, No. 2, pp. 686-703 (2019). http://dx.doi.org/10.5281/zenodo.3252783.
  12.  12,0 12,1 Fedosin S.G. The Integral Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based on the Pressure Field and Acceleration Field. American Journal of Modern Physics. Vol. 3, No. 4, pp. 152-167 (2014). http://dx.doi.org/10.11648/j.ajmp.20140304.12.
  13. Fedosin S.G. Relativistic Energy and Mass in the Weak Field Limit. Jordan Journal of Physics. Vol. 8, No. 1, pp. 1-16 (2015). http://dx.doi.org/10.5281/zenodo.889210.
  14. Fedosin S.G. Estimation of the physical parameters of planets and stars in the gravitational equilibrium model. Canadian Journal of Physics, Vol. 94, No. 4, pp. 370-379 (2016). http://dx.doi.org/10.1139/cjp-2015-0593.
  15. Fedosin S.G. The generalized Poynting theorem for the general field and solution of the 4/3 problem. International Frontier Science Letters, Vol. 14, pp. 19-40 (2019). https://doi.org/10.18052/www.scipress.com/IFSL.14.19.
  16. Fedosin S.G. The binding energy and the total energy of a macroscopic body in the relativistic uniform model. Middle East Journal of Science, Vol. 5, Issue 1, pp. 46-62 (2019). http://dx.doi.org/10.23884/mejs.2019.5.1.06.
  17. Fedosin S.G. Energy and metric gauging in the covariant theory of gravitation. Aksaray University Journal of Science and Engineering, Vol. 2, Issue 2, pp. 127-143 (2018). http://dx.doi.org/10.29002/asujse.433947.
  18. Fedosin S.G. The virial theorem and the kinetic energy of particles of a macroscopic system in the general field concept. Continuum Mechanics and Thermodynamics. Vol. 29, Issue 2, pp. 361-371 (2017). https://dx.doi.org/10.1007/s00161-016-0536-8.
  19. Fedosin S.G. The integral theorem of generalized virial in the relativistic uniform model. Continuum Mechanics and Thermodynamics, Vol. 31, Issue 3, pp. 627-638 (2019). https://dx.doi.org/10.1007/s00161-018-0715-x.
  20. Fedosin S.G. The potentials of the acceleration field and pressure field in rotating relativistic uniform system. Continuum Mechanics and Thermodynamics, Vol. 33, Issue 3, pp. 817-834 (2021). https://doi.org/10.1007/s00161-020-00960-7.
  21. Fedosin S.G. The Mass Hierarchy in the Relativistic Uniform System. Bulletin of Pure and Applied Sciences, Vol. 38 D (Physics), No. 2, pp. 73-80 (2019). http://dx.doi.org/10.5958/2320-3218.2019.00012.5.
  22. Fedosin S.G. The relativistic uniform model: the metric of the covariant theory of gravitation inside a body. St. Petersburg Polytechnical State University Journal. Physics and Mathematics, Vol. 14, No. 3, pp.168-184 (2021). http://dx.doi.org/10.18721/JPM.14313.
  23. Fedosin S.G. Generalized Four-momentum for Continuously Distributed Materials. Gazi University Journal of Science, Vol. 37, Issue 3, pp. 1509-1538 (2024). https://doi.org/10.35378/gujs.1231793.
  24. Yaakov Friedman and Tzvi Scarr. Covariant Uniform Acceleration. Journal of Physics: Conference Series Vol. 437 (2013) 012009 doi:10.1088/1742-6596/437/1/012009.
  25. Bahram Mashhoon and Uwe Muench. Length measurement in accelerated systems. Annalen der Physik. Vol. 11, Issue 7, P. 532–547, 2002.

 

External links

·         Acceleration field in Russian

 

Source: http://sergf.ru/afen.htm

On the list of pages