На русском языке

Four-acceleration

Four-acceleration (4-acceleration) is a four-vector, considered as relativistic generalization of the classical three-dimensional acceleration vector for the four-dimensional spacetime. Any physical system, whether a point material particle or a connected set of particles, has its own four-acceleration. Inside a body with continuous matter distribution, as a rule, there are gradients of velocities of motion of typical particles of this matter. As a result, the four-acceleration of typical particles inside bodies, averaged over the volume with the sizes of such particles, is a certain function of coordinates and time, leading to internal stresses in the matter.

Содержание

1 Definition
2 Single particle

2.1 Application
2.2 Four-momentum and four-force
2.3 Expression of four-acceleration in terms of acceleration field

3 System of closely interacting particles
4 See also
5 References
6 External links

Definition

In the general case, the four-acceleration of a particle is defined as the derivative of the four-velocity $~u^{\lambda }$ with respect to the particle’s proper time $~\tau$ :

$~A^{\lambda }:={\frac {Du^{\lambda }}{D\tau }}=u^{{\mu }}\nabla _{\mu }u^{\lambda }=u^{{\mu }}\partial _{\mu }u^{\lambda }+\Gamma _{{\mu \nu }}^{\lambda }u^{\mu }u^{\nu }={\frac {du^{\lambda }}{d\tau }}+\Gamma _{{\mu \nu }}^{\lambda }u^{\mu }u^{\nu }.$

In the above expression, the operator of proper-time-derivative $~{\frac {D}{D\tau }}=u^{\mu }\nabla _{\mu }$ is used, which generalizes the material derivative to the curved spacetime, ^[1] and the quantities $~\Gamma _{{\mu \nu }}^{\lambda }$ represent the Christoffel symbols.

The metric tensor $~g_{{\nu \lambda }}$ is needed to determine the four-acceleration with a covariant index:

$~A_{\nu }=g_{{\nu \lambda }}A^{\lambda }={\frac {Du_{\nu }}{D\tau }}=u^{{\mu }}\nabla _{\mu }u_{\nu }=u^{{\mu }}\partial _{\mu }u_{\nu }-\Gamma _{{\mu \nu }}^{\lambda }u^{\mu }u_{\lambda }={\frac {du_{\nu }}{d\tau }}-\Gamma _{{\mu \nu }}^{\lambda }u^{\mu }u_{\lambda }.$

Single particle

The motion of solid-state point physical particles, as well as of physical systems consisting of a set of particles, moving as a single whole, is described with the help of the four-velocity. In this case, the velocity of motion of a particle or the velocity of the momentum center of a system is directly included into the space component of the four-velocity.

Sometimes it is convenient to pass on from the particle’s proper time $~\tau$ to the coordinate time of the reference frame, in which the particle is moving. Let’s take into account that the four-velocity can be written in the following form:

$~u^{\lambda }:={\frac {dx^{\lambda }}{d\tau }}=\left(c{\frac {dt}{d\tau }},{\frac {d{\mathbf r}}{d\tau }}\right)={\frac {u^{0}}{c}}\left(c,{\mathbf v}\right),$

where $~x^{\lambda }=(ct,{\mathbf r})$ is the instantaneous four-position of the particle, is the speed of light, $~{\mathbf r}$ is the three-vector of the particle’s position, $~u^{0}=c{\frac {dt}{d\tau }}$ is the time component of the four-velocity, $~{\mathbf v}={\frac {d{\mathbf r}}{dt}}=(v^{1},v^{2},v^{3})=(v_{x},v_{y},v_{z})$ is the three-velocity of the particle with the corresponding components.

For the four-acceleration components the following is then obtained:

$~A^{0}={\frac {u^{0}}{c}}{\frac {du^{0}}{dt}}+\Gamma _{{\mu \nu }}^{0}u^{\mu }u^{\nu }.\qquad A^{1}={\frac {u^{0}}{c^{2}}}{\frac {d(u^{0}v^{1})}{dt}}+\Gamma _{{\mu \nu }}^{1}u^{\mu }u^{\nu }.$

$~A^{2}={\frac {u^{0}}{c^{2}}}{\frac {d(u^{0}v^{2})}{dt}}+\Gamma _{{\mu \nu }}^{2}u^{\mu }u^{\nu }.\qquad A^{3}={\frac {u^{0}}{c^{2}}}{\frac {d(u^{0}v^{3})}{dt}}+\Gamma _{{\mu \nu }}^{3}u^{\mu }u^{\nu }.$

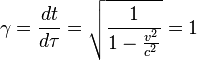In the inertial reference frame, instantaneously co-moving with the moving particle, the velocity $~{\mathbf v}=0$ , the Lorentz factor $~\gamma ={\frac {dt}{d\tau }}={\sqrt {{\frac {1}{1-{\frac {v^{2}}{c^{2}}}}}}}=1$ , the Christoffel symbols become equal to zero, $~u^{0}=\gamma c=c$ , and denoting in the given reference frame the proper three-acceleration as $~{\mathbf a}={\frac {d{\mathbf v}}{dt}}$ , we obtain for the four-acceleration the following: $~A^{\lambda }=(0,{\mathbf a})$ . Since in this reference frame the four-velocities with contravariant and covariant indices coincide, $~u^{\lambda }=(c,0)=u_{\lambda }$ , then the scalar product is $~u_{\lambda }A^{\lambda }=0$ . Since the scalar product of any four-vectors is an invariant, then from the equality of the scalar product to zero it follows that in any other reference frames the four-velocity and four-acceleration of a particle are always perpendicular to each other.

If we assume that the four-velocity is directed along the world line of the particle, then the four-acceleration at each point will be perpendicular to this line and directed in the same way as the curvature vector of the world line.

Application

In case when a certain force field acts on a particle, the acceleration of the particle will depend on both components of this field, that is, on the field strength and the corresponding solenoidal vector. Thus, the electric field strength, magnetic field, charge and velocity of the particle determine the value of Lorentz force, which accelerates the particle in electromagnetic field. The same situation takes place in the covariant theory of gravitation, where there are the gravitational field strength and the gravitational torsion field.

For the fields superposition principle holds, according to which scalar potential of a field at some point is arithmetic sum of scalar potentials of all the available field sources, and vector potential at this point is vector sum of vector potentials of the field sources. With the help of known field potentials it is easy to determine field strength and corresponding solenoidal field vector, and hence corresponding acceleration of the particle. For expression of the force in a more general, tensor form, the concept of four-force is used, which is proportional to the four-acceleration.

In general relativity, the gravitational force is reduced to curvature of spacetime and is found through the metric tensor. As a result, in the absence of other forces, the particle in the gravitational field moves along the geodesic line, while the four-acceleration $~A^{\lambda }$ of the particle and four-force are equal to zero. Hence we obtain the geodesic equation as equation of motion of a particle in a given metric:

$~A^{\lambda }={\frac {du^{\lambda }}{d\tau }}+\Gamma _{{\mu \nu }}^{\lambda }u^{\mu }u^{\nu }=0.$

Under similar conditions in covariant theory of gravitation, the gravitational four-acceleration of a particle is found either through gravitational tensor $~\Phi _{{\mu \nu }}$ or through gravitational stress-energy tensor $~U_{{\mu \nu }}$ . In this case the four-acceleration is not equal to zero, as long as there is a non-zero gravitational force. The equation of motion of a solid particle is the equality between the four-acceleration of a particle and four-acceleration from gravitational field:

$~A^{\lambda }=g^{{\lambda \mu }}\Phi _{{\mu \nu }}u^{\nu }=-{\frac {1}{\rho _{0}}}\nabla _{\mu }U^{{\lambda \mu }}.$

In the presence of other fields, acting on the particle, the above equations of motion change. For example, in the presence of charge of the particle with the mass , the equation of motion in general relativity will be as follows: ^[2]

$~A^{\lambda }={\frac {du^{\lambda }}{d\tau }}+\Gamma _{{\mu \nu }}^{\lambda }u^{\mu }u^{\nu }={\frac {q}{m}}g^{{\lambda \mu }}F_{{\mu \nu }}u^{\nu }=-{\frac {1}{\rho _{0}}}\nabla _{\mu }W^{{\lambda \mu }},$

where $~F_{{\mu \nu }}$ is electromagnetic tensor, $~W^{{\lambda \mu }}$ is electromagnetic stress-energy tensor, $~\rho _{{0}}$ is the average mass density of the particle in its proper reference frame.

In matter inside a body, several fields can act simultaneously on the particle, for example, gravitational and electromagnetic fields, pressure field, and dissipation field. In covariant theory of gravitation, gravitational field is considered as a vector field, just like an electromagnetic field. If we assume that other fields in macroscopic bodies are described by the vector fields and are the general field components, then equation of motion of a solid particle in the specified four fields has the form: ^[3]

$~A^{\lambda }=g^{{\lambda \mu }}\left(\Phi _{{\mu \nu }}u^{\nu }+{\frac {q}{m}}F_{{\mu \nu }}u^{\nu }+f_{{\mu \nu }}u^{\nu }+h_{{\mu \nu }}u^{\nu }\right)=-{\frac {1}{\rho _{0}}}\nabla _{\mu }(U^{{\lambda \mu }}+W^{{\lambda \mu }}+P^{{\lambda \mu }}+Q^{{\lambda \mu }}).\qquad (1)$

Here $~f_{{\mu \nu }}$ is pressure field tensor, $~h_{{\mu \nu }}$ is dissipation field tensor, $~P^{{\lambda \mu }}$ is pressure stress-energy tensor, and $~Q^{{\lambda \mu }}$ is dissipation stress-energy tensor.

Four-momentum and four-force

Four-momentum of a particle is determined as the product of the particle’s invariant inertial mass by the four-velocity:

$~p^{\lambda }:=mu^{\lambda }=\left({\frac {E}{c}},\quad {\mathbf p}\right),$

where $~E=mcu^{0}$ is relativistic energy, $~{\mathbf p}={\frac {mu^{0}{\mathbf v}}{c}}$ is three-vector of the relativistic momentum of the particle.

In order to calculate the four-force we need to apply the operator of proper-time-derivative to four-momentum:

$~F^{\lambda }:={\frac {Dp^{\lambda }}{D\tau }}={\frac {dp^{\lambda }}{d\tau }}+\Gamma _{{\mu \nu }}^{\lambda }p^{\mu }u^{\nu }.$

If the mass is constant, it can be taken out beyond the sign of the differential:

$~F^{\lambda }=m{\frac {Du^{\lambda }}{D\tau }}=mA^{\lambda }.$

In this case, the four-force is proportional to the mass and four-acceleration. If we determine that $~W={\frac {dE}{dt}}$ is the power as the rate of change of the particle’s energy, and $~{\mathbf F}={\frac {d{\mathbf p}}{dt}}=(F_{x},F_{y},F_{z})$ is the three-force, written also in Cartesian coordinates and acting on the particle, then the components of the four-force will be expressed in terms of the power, the three-force components and four-acceleration components as follows:

$~F^{0}={\frac {u^{0}W}{c^{2}}}+\Gamma _{{\mu \nu }}^{0}p^{\mu }u^{\nu }=mA^{0}.\qquad F^{1}={\frac {u^{0}F_{x}}{c}}+\Gamma _{{\mu \nu }}^{1}p^{\mu }u^{\nu }=mA^{1}.\qquad (2)$

$~F^{2}={\frac {u^{0}F_{y}}{c}}+\Gamma _{{\mu \nu }}^{2}p^{\mu }u^{\nu }=mA^{2}.\qquad F^{3}={\frac {u^{0}F_{z}}{c}}+\Gamma _{{\mu \nu }}^{3}p^{\mu }u^{\nu }=mA^{3}.$

Expression of four-acceleration in terms of acceleration field

The acceleration field is characterized by its own four-potential, the acceleration tensor $~u_{{\mu \nu }}$ and the acceleration stress-energy tensor $~B_{{\mu \nu }}$ . The acceleration tensor components are components of two three-vectors – the field strength $~{\mathbf S}$ and the solenoidal vector $~{\mathbf N}$ of acceleration field. For a solid particle, the four-acceleration with covariant index can be expressed in terms of the following quantities: ^[4]

$~A_{\mu }=-u_{{\mu \nu }}u^{{\nu }}={\frac {u^{0}}{c}}\left(-{\frac {1}{c}}{\mathbf S}\cdot {\mathbf v},\quad {\mathbf S}+[{\mathbf v}\times {\mathbf N}]\right)={\frac {1}{\rho _{0}}}g_{{\mu \beta }}\nabla _{\nu }B^{{\beta \nu }}.\qquad (3)$

The equality for the four-acceleration with the right-hand side (3), containing stress-energy tensor of acceleration field, follows from the principle of least action. The equality for the four-acceleration with the left-hand side (3) is proved as follows. For a point solid particle, the four-potential of acceleration field is four-velocity of the particle with covariant index $~u_{\nu }$ , and acceleration tensor will equal:

$~u_{{\mu \nu }}=\nabla _{\mu }u_{\nu }-\nabla _{\nu }u_{\mu }.$

Multiplying this equality by $~u^{\nu }$ gives the required relation:

$~u_{{\mu \nu }}u^{\nu }=u^{\nu }\nabla _{\mu }u_{\nu }-u^{\nu }\nabla _{\nu }u_{\mu }=-u^{\nu }\nabla _{\nu }u_{\mu }=-A_{\mu }.$

In this case, we took into account the equality $~u_{\nu }u^{\nu }=c^{2}$ and its covariant derivative:

$~\nabla _{\mu }(u_{\nu }u^{\nu })=u_{\nu }\nabla _{\mu }u^{\nu }+u^{\nu }\nabla _{\mu }u_{\nu }=2u^{\nu }\nabla _{\mu }u_{\nu }=\nabla _{\mu }c^{2}=0.$

With the help of the metric tensor we can pass on to the four-acceleration with a contravariant index:

$~A^{\lambda }=g^{{\lambda \mu }}A_{\mu }=-u_{\nu }^{\lambda }u^{{\nu }}={\frac {1}{\rho _{0}}}\nabla _{\nu }B^{{\lambda \nu }}.\qquad (4)$

After substituting (4) into the right-hand side of (2) we can see that there is a relationship between the power and the three-force $~{\mathbf F}$ on the one hand, and the scalar product $~{\mathbf S}\cdot {\mathbf v}$ and the sum $~{\mathbf S}+[{\mathbf v}\times {\mathbf N}]$ on the other hand.

In flat spacetime, the Christoffel symbols become equal to zero, $~u^{0}=c\gamma$ , and the metric tensor has only the diagonal components that are equal in the absolute value to 1. In this case we obtain the following:

$~W=-m{\mathbf S}\cdot {\mathbf v}={\mathbf F}\cdot {\mathbf v},\qquad {\mathbf F}=-m\left({\mathbf S}+[{\mathbf v}\times {\mathbf N}]\right).$

Thus, the power of work done by an arbitrary force and the force itself are expressed in terms of the velocity of motion $~{\mathbf v}$ , the strength $~{\mathbf S}$ and the solenoidal vector $~{\mathbf N}$ of acceleration field.

The expressions for the vectors $~{\mathbf S}$ and $~{\mathbf N}$ follow from definition of four-potential and acceleration tensor:

$~{\mathbf {S}}=-\nabla \vartheta -{\frac {\partial {\mathbf {U}}}{\partial t}},\qquad \qquad {\mathbf {N}}=\nabla \times {\mathbf {U}}.$

In the flat spacetime, the scalar potential of the particle’s acceleration field is $~\vartheta =\gamma c^{2}={\frac {E}{m}}$ , and the vector potential of acceleration field is $~{\mathbf {U}}=\gamma {\mathbf v}={\frac {{\mathbf p}}{m}}$ . Finding the vectors $~{\mathbf S}$ and $~{\mathbf N}$ with the help of these potentials, and substituting them into expressions for the power and force, we obtain the following:

$~W={\mathbf v}\cdot \nabla E+{\mathbf v}\cdot {\frac {\partial {\mathbf {p}}}{\partial t}}={\frac {dE}{dt}}={\mathbf v}\cdot {\frac {d{\mathbf p}}{dt}}.$

$~{\mathbf F}=\nabla E+{\frac {\partial {\mathbf {p}}}{\partial t}}-{\mathbf v}\times [\nabla \times {\mathbf p}]={\frac {d{\mathbf p}}{dt}}.$

The vectors $~{\mathbf S}$ and $~{\mathbf N}$ are expressed in terms of partial derivatives, characteristic of the four-vector algebra, and similarly we obtain the expressions for the power and force. In addition, there are two other expressions for the force, ^[2] ^[1] with the use of three-acceleration of the particle:

$~{\mathbf F}=m\gamma \left({\mathbf {a}}+\gamma ^{2}{\frac {({\mathbf {v}}\cdot {\mathbf {a}})}{c^{2}}}{\mathbf {v}}\right)=m\gamma ^{3}\left({\mathbf {a}}+{\frac {{\mathbf {v}}\times [{\mathbf {v}}\times {\mathbf {a}}]}{c^{2}}}\right).$

System of closely interacting particles

The four-acceleration concept for a sufficiently large system of particles differs significantly from the four-acceleration of a single point particle. Multiparticle interactions in the system result in a new quality, when not the motion of a particular physical particle becomes important, but the motion of certain typical particles, which characterize the system under consideration on the average. As a result of averaging of kinetic energies and momenta of individual particles, such macroscopic parameters emerge as temperature and pressure. A peculiarity of a typical particle is that its root mean square speed of motion becomes a function of location in the system. In simple physical systems consisting of particles of one phase or having sufficiently uniform composition, the pressure, temperature and velocity of typical particles at the center of the system usually reach the maximum value.

In order to describe the motion of a typical particle the same equations can be used, as for a physical particle, with the difference that these equations should be averaged. This requires averaging of the field strengths and solenoidal vectors of all the acting fields over the volume of a typical particle at its location. In fact, averaging is performed by using corresponding field equations, while approximation of continuous medium is often used.

In many cases, dependences of fields as well as of the mass and charge densities on coordinates and time are known in the system, but distribution of the particles’ four-velocity is unknown. Then, in the concept of general field and covariant theory of gravitation, for calculating basic parameters of the system, the expressions presented in the article equation of vector field may be required:^[5]

1) The equation for calculating the metric:

$~R^{{\lambda \mu }}-{\frac {1}{4}}g^{{\lambda \mu }}R={\frac {8\pi G\beta }{c^{4}}}(U^{{\lambda \mu }}+W^{{\lambda \mu }}+P^{{\lambda \mu }}+Q^{{\lambda \mu }}),$

where $~R^{{\lambda \mu }}$ is Ricci tensor, is scalar curvature, is gravitational constant, $~\beta$ is a certain constant, and gauge condition of cosmological constant is used.

2) The acceleration field equations for calculating the vectors $~{\mathbf S}$ and $~{\mathbf N}$ as components of acceleration tensor $~u_{{\mu \nu }}$ :

$\nabla _{\sigma }u_{{\mu \nu }}+\nabla _{\mu }u_{{\nu \sigma }}+\nabla _{\nu }u_{{\sigma \mu }}={\frac {\partial u_{{\mu \nu }}}{\partial x^{\sigma }}}+{\frac {\partial u_{{\nu \sigma }}}{\partial x^{\mu }}}+{\frac {\partial u_{{\sigma \mu }}}{\partial x^{\nu }}}=0.$

$~\nabla _{\nu }u^{{\mu \nu }}=-{\frac {4\pi \eta }{c^{2}}}J^{\mu },$

where $J^{\mu }=\rho _{{0}}u^{\mu }$ is mass four-current, $~\eta$ is acceleration field constant.

Sometimes it is easier to use first the wave equation to calculate the four-potential $~ U_\mu$ of acceleration field

$~ \nabla^\nu \nabla_\nu U_\mu + R_{\mu \nu} U^\nu = \frac{4 \pi \eta }{c^2} J_\mu,$

and then to apply four-curl to $~ U_\mu$ in order to determine $~u_{{\mu \nu }}$ .

3) The equation of motion (1), if typical particles of the system are considered as solid particles.

4) The gauge condition of four-potential of the acceleration field and continuity equation for the mass four-current, respectively:

$~ \nabla^\mu U_{\mu} = 0 .$

$~R_{{\mu \alpha }}u^{{\mu \alpha }}={\frac {4\pi \eta }{c^{2}}}\nabla _{{\alpha }}J^{{\alpha }}=0.$

The connection between metric and four-velocity is also contained in the invariant:

$~g^{{\mu \nu }}u_{{\mu }}u_{{\nu }}=u_{{\mu }}u^{{\mu }}=c^{2}.$

As it was said, all physical quantities in these equations should refer to typical particles and therefore should be averaged. This also applies to Ricci tensor $~R_{{\mu \alpha }}$ , scalar curvature, and cosmological constant inside the body. ^[6]

In items 1) and 2), the vectors $~{\mathbf S}$ and $~{\mathbf N}$ , necessary to calculate the four-acceleration in relation (3), are expressed in terms of metric and acceleration field coefficient $~\eta$ . With the help of item 3) the coefficient $~\eta$ is expressed in terms of the coefficients of other fields. In item 4) additional restrictions are imposed on the acceptable type of functions, including the particles’ velocities and their potentials. Due to complexity and interdependence of the equations, they often have to be solved simultaneously.

The situation becomes more complicated in the case when the system’s typical particles are not solid and have nonzero vector field potentials. For example, the particles can have the spin and magnetic moment, leading to the vector potential $~ \mathbf U$ of acceleration field and to the vector potential $~ \mathbf A$ of electromagnetic field. In this case, the four-potential of acceleration field $~ U_\mu = \left( \frac {\vartheta }{ c}, -\mathbf{U } \right)$ is no longer equal to the particle’s four-velocity $~ u_\mu$ . Instead of the four-acceleration, the covariant derivative of stress-energy tensor of accelerated field with mixed indices defines density of four-force: ^[7]

$~ f_\alpha = \nabla_\beta {B_\alpha}^\beta = - u_{\alpha k} J^k = - \rho_0 u_{\alpha k}u^k = \rho_0 \frac {DU_\alpha }{D \tau}- J^k \nabla_\alpha U_k = \rho_0 \frac {dU_\alpha }{d \tau}- J^k \partial_\alpha U_k . \qquad (5)$

From the foregoing we can see that if the four-velocity in matter is not initially specified, it should be found from the field equations and then be used to calculate four-acceleration by the formula:

$~ A^\lambda = \frac{D u^\lambda }{D\tau} .$

From comparison of (5) and (3) it follows that the four-acceleration in matter inside a typical particle can be estimated in the first approximation as follows:

$~ A_\alpha \approx \frac {1}{\rho_0 } f_\alpha = \frac {dU_\alpha }{d \tau}- u^k \partial_\alpha U_k .$

In this expression, the four-acceleration depends on four-velocity $~ u_\mu$ of matter’s motion inside the particle, on four-potential $~ U_\mu$ of acceleration field as a function of coordinates inside the particle and on the coordinates of the particle itself inside the system.

In case of using general relativity instead of covariant theory of gravitation, the described above order of calculating the four-acceleration in general remains the same. An exception is that in general relativity, gravitational force and its contribution into four-acceleration are included in metric, which changes both the equation for the metric and the equation of motion.

See also

Four-vector
4-velocity
Four-force
4-momentum
Acceleration field

References

^1.0 ^1.1 Fedosin S.G. Fizicheskie teorii i beskonechnaia vlozhennost’ materii. – Perm, 2009, 844 pages, Tabl. 21, Pic. 41, Ref. 289. ISBN 978-5-9901951-1-0. (in Russian).
^2.0 ^2.1 Ландау Л. Д., Лифшиц Е. М. Теория поля. – Издание 7-е, исправленное. – М.: Наука, 1988. – 512 с. – (Теоретическая физика, том II).
Fedosin S.G. Four-Dimensional Equation of Motion for Viscous Compressible and Charged Fluid with Regard to the Acceleration Field, Pressure Field and Dissipation Field. International Journal of Thermodynamics. Vol. 18, No. 1, pp. 13-24 (2015). http://dx.doi.org/10.5541/ijot.5000034003.
Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy. Jordan Journal of Physics. Vol. 9, No. 1, pp. 1-30 (2016). http://dx.doi.org/10.5281/zenodo.889304.
Fedosin S.G. Lagrangian formalism in the theory of relativistic vector fields. International Journal of Modern Physics A, Vol. 40, No. 02, 2450163 (2025). https://doi.org/10.1142/S0217751X2450163X.
Fedosin S.G. Energy and metric gauging in the covariant theory of gravitation. Aksaray University Journal of Science and Engineering, Vol. 2, Issue 2, pp. 127-143 (2018). http://dx.doi.org/10.29002/asujse.433947.
Fedosin S.G. Equations of Motion in the Theory of Relativistic Vector Fields. International Letters of Chemistry, Physics and Astronomy, Vol. 83, pp. 12-30 (2019). https://doi.org/10.18052/www.scipress.com/ILCPA.83.12.

External links

Four-acceleration in Russian

Source: http://sergf.ru/faen.htm

On the list of pages