Dissipation field

Dissipation field is a two-component vector force field, which describes in a covariant way friction force and energy dissipation emerging in systems with a number of closely interacting particles. The dissipation field is a general field component, which is represented in Lagrangian and Hamiltonian of an arbitrary physical system including term with energy of particles in dissipation field and term with field energy. ^[1] ^[2] The dissipation field is included in equation of motion by means of dissipation field tensor and in equation for metric – by means of dissipation stress-energy tensor.

By energy dissipation is meant conversion of energy of directed motion of particles into energy of random motion of these particles and particles of surrounding medium, as well as conversion into energy of intramolecular and atomic motion, while energy of motion of fast-moving fluxes of particles decreases due to friction with slower fluxes. Typical examples of dissipation of mechanical energy are damping of motion of a jet in a liquid and heating of falling meteorites during their motion in the Earth's atmosphere.

Dissipation field is generally considered as a macroscopic field with its energy and momentum, describing averaged interaction of particles in an arbitrary small volume of a system. The cause of dissipation field emerging at micro level is different interactions leading to effects of friction and deceleration of individual particles or their fluxes. At atomic level, electromagnetic forces and strong gravitation are prevailing, by which particles interact with each other and exchange their energy. Friction forces in a system of particles appear as a collective effect and are proportional not only to velocity, but also to its derivatives with respect to time and coordinates. Since the friction force is described by dissipation field tensor and corresponding stress-energy tensor, dissipation field in each small volume obtains its energy density and energy flux density. In dissipative processes, some change occurs in internal energy of system, mainly due to change in quantity of heat or in energy of phase transitions, which can be considered as a change in dissipation field energy. Internal energy also changes when pressure field energy and energy of particles’ acceleration field change, as well as due to change in energy of electromagnetic, gravitational and other fields. In turn, dissipation field energy flux makes its contribution into flux of internal energy and flux of relativistic energy of the system.

1 Classical mechanics
2 Relativistic hydrodynamics
3 Dissipation field as vector field

3.1 Mathematical description
3.2 Action, Lagrangian and energy
3.3 Equations
3.4 Stress–energy tensor
3.5 Application

4 See also
5 References
6 External links

Classical mechanics

Main processes that lead to energy dissipation are viscous friction of layers of liquid or gas against each other, friction during motion of solid bodies due to interaction with surrounding medium, thermal conductivity and diffusion in gases and liquids. All of these processes belong to transport phenomena: friction occurs during transfer of momentum, heat conductivity occurs during internal energy transfer, and diffusion is associated with transfer of mass (charge, electric and magnetic moment, etc.). Friction is the main source of energy dissipation. Thermal conductivity and diffusion also make some contribution, since in real processes all kinds of transfer are intertwined with each other.

In order to describe friction forces in Euler–Lagrange equation the friction forces are introduced: ^[3]

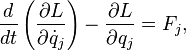
$\frac{d}{dt}\left(\frac{\partial L}{\partial \dot q_j}\right) - \frac{\partial L}{\partial q_j} = F_j,$

where is Lagrangian, are generalized coordinates. In addition, dissipation function is introduced into consideration, so that the following relation holds:

$~ F_j = - \frac{\partial D }{\partial \dot q_j }.$

Rayleigh dissipation function is given by expression:

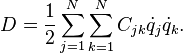
$D = \frac{1}{2} \sum_{j=1}^N \sum_{k=1}^N C_{jk} \dot q_j \dot q_k .$

If tensor $~ C_{jk}$ does not depend on velocities, corresponding friction force is equal to:

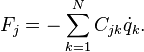
$~ F_j = - \sum_{k=1}^N C_{jk} \dot q_k.$

Dissipation function has dimension of power and the tensor $~ C_{jk}$ must have dimension kg/s. If the tensor is symmetrical, friction force appears to be directed oppositely to velocity of particle’s motion relative to surrounding medium.

This shows that dissipation function represents some form of a scalar potential, which depends on products of projections of relative velocities, and dissipation field is considered as corresponding scalar field. But unlike standard scalar potentials of fundamental fields, friction force is not in the form of a gradient of dissipative functions but in the form of a derivative with respect to motion velocity. This approach cannot be considered as a fully covariant description of friction processes, it can only serve as a first approximation, because it does not take into consideration friction in accelerated motion.

Newton's law of fluid friction describes internal friction force in liquid layer, moving relative to other parallel layers, in the form:

$~ dF = - \mu \frac {dv}{dr} dS,$

here $~ \mu$ is coefficient of internal friction or coefficient of dynamic viscosity, $~ \frac {dv}{dr}$ is gradient of velocity of layers’ motion in direction perpendicular to the layer surface, is surface area of the layer.

A more accurate description of motion in a viscous medium is given by the Navier–Stokes equations:

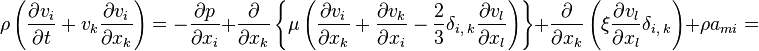
$\rho\left(\frac{\partial v_i}{\partial t}+v_k\frac{\partial v_i}{\partial x_k}\right)=-\frac{\partial p}{\partial x_i}+\frac{\partial}{\partial x_k}\left\{\mu\left(\frac{\partial v_i}{\partial x_k}+\frac{\partial v_k}{\partial x_i}-\frac{2}{3}\delta_{i,\;k}\frac{\partial v_l}{\partial x_l}\right)\right\}+\frac{\partial}{\partial x_k}\left(\xi \frac{\partial v_l}{\partial x_l}\delta_{i,\;k}\right) + \rho a_{mi}=$

$~= \nabla_k P^{ik} + \rho a_{mi} ,$

$\frac{\partial \rho}{\partial t} + \nabla\cdot (\rho \vec v)=0,$

where $~ \rho$ is mass density of matter, $~ \xi$ is "second viscosity", or volume viscosity, $~\delta_{i,\;k}$ is Kronecker delta, $~ P^{ik}$ is Cauchy stress tensor, $~ a_{mi}$ is acceleration due to the mass forces (including the gravitational and electromagnetic forces and force of inertia), while second equation is continuity equation.

Relativistic hydrodynamics

Instead of tensor $~ P^{ik}$ in relativistic case four-dimensional viscous stress tensor is used to describe equation of motion of viscous and heat-conducting media: ^[4]

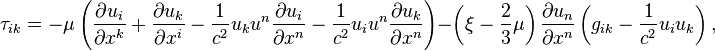
$~ \tau_{ik} = - \mu \left( \frac {\partial u_i} {\partial x^k}+ \frac {\partial u_k} {\partial x^i}- \frac{1} {c^2 }u_k u^n \frac {\partial u_i} {\partial x^n} - \frac{1} {c^2 }u_i u^n \frac {\partial u_k} {\partial x^n} \right) - \left( \xi- \frac {2}{3} \mu \right) \frac {\partial u_n} {\partial x^n} \left( g_{ik}- \frac{1} {c^2 }u_i u_k \right),$

where is four-velocity with a contravariant index, is four-velocity with a covariant index, $~ \xi$ is coefficient of second (volume) viscosity, $~ g_{ik}$ is metric tensor, is speed of light.

Density of four-force, arising from viscosity, is calculated using covariant derivative of tensor $~ \tau_{ik}$ and is present in right side of Navier-Stokes equations. By its meaning the tensor $~ \tau_{ik}$ is stress-energy tensor, but it cannot be derived from principle of least action.

Dissipation field as vector field

Dissipation field as a two-component vector field was presented by Sergey Fedosin within the framework of metric theory of relativity and covariant theory of gravitation. Equations of this field were developed as a consequence of principle of least action, ^[5] and a special procedure was used. ^[6]

Mathematical description

Four-potential of dissipation field is expressed in terms of scalar $~ \varepsilon$ and vector $~ \mathbf {\Theta }$ potentials:

$~ \lambda_\mu = \left( \frac {\varepsilon }{ c}, -\mathbf{\Theta } \right).$

Antisymmetric dissipation field tensor is calculated with four-curl of four-potential:

$h_{\mu \nu} = \nabla_\mu \lambda_\nu - \nabla_\nu \lambda_\mu = \frac{\partial \lambda_\nu}{\partial x^\mu} - \frac{\partial \lambda_\mu}{\partial x^\nu}.$

Dissipation field tensor components are vector components of dissipation field strength $~ \mathbf{X}$ and solenoidal vector $~\mathbf { Y }$ :

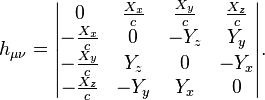
$~ h_{\mu \nu}= \begin{vmatrix} 0 & \frac { X_x}{ c} & \frac { X_y}{ c} & \frac { X_z}{ c} \\ -\frac { X_x}{ c} & 0 & - Y_{z} & Y_{y} \\ -\frac { X_y}{ c} & Y_{z} & 0 & - Y_{x} \\ -\frac { X_z}{ c}& - Y_{y} & Y_{x} & 0 \end{vmatrix}.$

This yields the following:

$~ \mathbf{X}= -\nabla \varepsilon - \frac{\partial \mathbf{\Theta}} {\partial t}, \qquad\qquad \mathbf{Y }= \nabla \times \mathbf{\Theta }. \qquad\qquad (1)$

Action, Lagrangian and energy

In covariant theory of gravitation, four-potential $~ \lambda_\mu$ of dissipation field is part of four-potential of general field $~ s_\mu$ , which is sum of the four-potentials of particular fields, such as electromagnetic and gravitational fields, acceleration field, pressure field, dissipation field, strong interaction field, weak interaction field and other vector fields, acting on matter and its particles. Energy density of interaction of general field with matter is given by product of four-potential of general field and mass four-current: $~ s_\mu J^\mu$ . From four-potential of general field we obtain general field tensor by applying four-curl:

$~ s_{\mu \nu} =\nabla_\mu s_\nu - \nabla_\nu s_\mu.$

Tensor invariant in the form of $~ s_{\mu \nu} s^{\mu \nu}$ is up to a constant factor proportional to energy density of general field. As a result, action function that contains scalar curvature and cosmological constant $~ \Lambda$ is given by expression: ^[1]

$~S =\int {L dt}=\int (kR-2k \Lambda - \frac {1}{c}s_\mu J^\mu - \frac {c}{16 \pi \varpi} s_{\mu\nu}s^{\mu\nu} ) \sqrt {-g}d\Sigma,$

where is Lagrange function or Lagrangian, is time differential, and $~ \varpi$ are constants to be determined, is speed of light, as a measure of the propagation velocity of electromagnetic and gravitational interactions, $~\sqrt {-g}d\Sigma= \sqrt {-g} c dt dx^1 dx^2 dx^3$ is invariant four-volume, expressed in terms of differential of time coordinate , product of differentials of space coordinates and square root $~\sqrt {-g}$ of determinant of metric tensor, taken with negative sign.

Variation of action function gives general field equations, four-dimensional equation of motion and equation for determining metric. Since dissipation field is a component of general field, then corresponding dissipation field equations can be derived from the general field equations.

Given gauge conditions of cosmological constant are met in the following form:

$~ c k \Lambda = - s_\mu J^\mu ,$

the system’s energy does not depend on the term with the scalar curvature and it becomes uniquely determined: ^[7]

$~E = \int {( s_0 J^0 + \frac {c^2 }{16 \pi \varpi } s_{ \mu\nu} s^{ \mu\nu} ) \sqrt {-g} dx^1 dx^2 dx^3},$

where and denote time components of four-vectors $~ s_{\mu }$ and $~ J^{\mu }$ .

Equations

Main article: Equation of vector field

Four-dimensional equations of dissipation field are similar by their form to Maxwell equations and have the following form:

$\nabla_\sigma h_{\mu \nu}+\nabla_\mu h_{\nu \sigma}+\nabla_\nu h_{\sigma \mu}=\frac{\partial h_{\mu \nu}}{\partial x^\sigma} + \frac{\partial h_{\nu \sigma}}{\partial x^\mu} + \frac{\partial h_{\sigma \mu}}{\partial x^\nu} = 0.$

$~ \nabla_\nu h^{\mu \nu} = - \frac{4 \pi \tau }{c^2} J^\mu,$

where $~J^\mu = \rho_{0} u^\mu$ is mass four-current, $~\rho_{0}$ is mass density in comoving reference frame, $~u^\mu$ is four-velocity of matter unit, $~ \tau$ is a constant determined in each problem, and it is assumed that there is a balance between all fields in the physical system.

Gauge condition for four-potential of dissipation field is:

$~ \nabla^\mu \lambda_\mu = 0 .$

In Minkowski space of special theory of relativity, the form of dissipation field equations is simplified and they can be expressed in terms of field strength $~\mathbf {X}$ and solenoidal vector $~\mathbf { Y }$ :

$~ \nabla \cdot \mathbf{X} = 4 \pi \tau \gamma \rho_0, \qquad\qquad \nabla \times \mathbf{ Y } = \frac{1}{c^2} \left( 4 \pi \tau \mathbf{J} + \frac{\partial \mathbf{X}} {\partial t} \right),$

$~ \nabla \times \mathbf{X} = - \frac{\partial \mathbf{ Y } } {\partial t} , \qquad \nabla \cdot \mathbf{ Y} = 0 .$

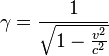where $~ \gamma = \frac {1}{\sqrt{1 - {v^2 \over c^2}}}$ is Lorentz factor, $~ \mathbf{J}= \gamma \rho_0 \mathbf{v }$ is the mass current density , $~ \mathbf{v }$ is matter unit velocity.

If we also use gauge condition in the form of $~ \partial^\mu \lambda_\mu = \frac {1}{c^2} \frac{\partial \varepsilon }{\partial t}+\nabla \cdot \mathbf {\Theta } = 0$ and relation (1), we can obtain wave equations for dissipation field potentials from field equations:

$~ \frac {1}{c^2}\frac{\partial^2 \varepsilon }{\partial t^2 } -\Delta \varepsilon = 4 \pi \tau \gamma \rho_0,$

$~ \frac {1}{c^2}\frac{\partial^2 \mathbf {\Theta } }{\partial t^2 } -\Delta \mathbf {\Theta }= \frac {4 \pi \tau }{c^2} \mathbf{J}.$

In curved space equation of motion of matter unit in general field is given by the formula:

$~ s_{\mu \nu} J^\nu =0$ .

Since $~ J^\nu = \rho_0 u^\nu$ , and general field tensor is expressed in terms of tensors of particular fields, then equation of motion can be represented using these tensors :^[8]

$~-u_{{\mu \nu }}J^{\nu }=F_{{\mu \nu }}j^{\nu }+\Phi _{{\mu \nu }}J^{\nu }+f_{{\mu \nu }}J^{\nu }+h_{{\mu \nu }}J^{\nu }+\gamma _{{\mu \nu }}J^{\nu }+w_{{\mu \nu }}J^{\nu }.\qquad (2)$

Here $~ u_{\mu \nu}$ is acceleration tensor, $~ F_{\mu \nu}$ is electromagnetic tensor, $~ j^\nu$ is charge four-current, $~ \Phi_{\mu \nu}$ is gravitational tensor, $~ f_{\mu \nu}$ is pressure field tensor, $~ \gamma_{\mu \nu}$ is strong interaction field tensor, $~ w_{\mu \nu}$ is weak interaction field tensor.

Stress-energy tensor

Dissipation stress-energy tensor is calculated with the help of dissipation field tensor:

$~ Q^{ik} = \frac{c^2} {4 \pi \tau } \left( - g^{im} h_{nm} h^{nk}+ \frac {1} {4} g^{ik}h_{mr}h^{mr}\right) .$

Tensor $~ Q^{ik}$ includes three-vector of energy-momentum flux $~\mathbf {Z}$ , which is similar in its meaning to Poynting vector and Heaviside vector. Vector $~\mathbf {Z}$ can be represented through vector product of field strength $~ \mathbf {X}$ and solenoidal vector $~ \mathbf { Y }$ :

$~ \mathbf {Z}=c Q^{0i} = \frac {c^2}{4 \pi \tau }[\mathbf {X}\times \mathbf { Y }],$

here index is

Covariant derivative of stress-energy tensor of dissipation field determines density of dissipation four-force:

$~f^{\alpha }=-\nabla _{\beta }Q^{{\alpha \beta }}={h^{\alpha }}_{{k}}J^{k}.\qquad \qquad (3)$

Stress-energy tensor of dissipation field is part of stress-energy tensor of general field $~ T^{ik}$ , but in general case the tensor $~ T^{ik}$ also contains cross-terms with products of strengths and solenoidal vectors of particular fields:

$~ T^{ik}= k_1W^{ik}+ k_2U^{ik}+ k_3B^{ik}+ k_4P^{ik} + k_5Q^{ik}+ k_6 L^{ik}+ k_7A^{ik}+ cross \quad terms,$

where $~ k_1{,} k_2{,} k_3{,} k_4{,} k_5{,} k_6{,} k_7$ are some coefficients, $~ W^{ik}$ is electromagnetic stress-energy tensor, $~ U^{ik}$ is gravitational stress-energy tensor, $~ B^{ik}$ is acceleration stress-energy tensor, $~ P^{ik}$ is pressure stress-energy tensor, $~ L^{ik}$ is strong interaction stress-energy tensor, $~ A^{ik}$ is weak interaction stress-energy tensor.

By means of tensor $~ T^{ik}$ , the stress-energy tensor of dissipation field becomes part of equation for metric:

$~ R^{ik} - \frac{1} {4 }g^{ik}R = \frac{8 \pi G \beta }{ c^4} T^{ik},$

where $~ R^{ik}$ is Ricci tensor, is gravitational constant, $~ \beta$ is a certain constant, and gauge condition for cosmological constant is used.

Application

In case when a certain vector potential of a particle is equal to zero in rest frame of the particle, four-potential of this vector field in an arbitrary frame of reference can be represented as follows: ^[6]

$~ L_\mu = \frac { k_f \varepsilon_p }{\rho_0 c^2} u_\mu ,$

where $~ k_f = \frac {\rho_0}{\rho_{0q}}$ for electromagnetic field and for other fields, $~ \rho_{0}$ and $~\rho_{0q}$ are mass density and accordingly charge density in comoving reference frame, $~ \varepsilon_p$ is energy density of particle in given field, $~ u_\mu$ is covariant four-velocity.

For dissipation field $~ \varepsilon_p = \alpha \rho_0$ and , and according to definition, for four-potential of dissipation field of one particle we have the following:

$~ \lambda_\mu = \left( \frac {\varepsilon }{ c}, - \mathbf{\Theta } \right) = \frac {\alpha }{c^2} u_\mu ,$

where $~ \alpha$ is dissipation function. For an arbitrary particle, components of e four-potential in framework of special relativity (STR) take the form: $~ \varepsilon = \gamma \alpha,$ $~ \mathbf{\Theta }= \frac { \gamma \alpha }{c^2}\mathbf{v},$

and hence, vector potential is directed along the particle’s velocity. If the vector potential components are functions of time and do not directly depend on space coordinates, then for such motion according to (1) solenoidal vector $~ \mathbf { Y }$ vanishes.

Due to interaction of a set of particles with each other by means of various fields, including interaction at a distance without direct contact, dissipation field in matter changes and is different from dissipation field of a single particle at observation point. Dissipation field in a system of particles is specified by field strength and solenoid vector, which represent typical averaged characteristics of matter’s motion. As a rule, in a gravitationally-bound system radial gradients of different field strengths appear, including dissipation field strength $~ \mathbf { X },$ and if some part of particles is moving synchronously or rotating, then vector $~ \mathbf { Y }$ appears. From (2) and (3) we derive a general expression for four-force density with a covariant index, which arises from the dissipation field:

$~(f_{\mu })_{d}=h_{{\mu \nu }}J^{\nu }=\rho _{0}{\frac {cdt}{ds}}\left({\frac {1}{c}}{\mathbf {X}}\cdot {\mathbf {v}}{,}\qquad -{\mathbf {X}}-[{\mathbf {v}}\times {\mathbf {Y}}]\right),$

where denotes four-dimensional space-time interval.

Relativistic equation of motion of viscous compressible matter, taking into account four-potential of dissipation field, dissipation field tensor and stress-energy tensor of dissipation field, within the limits of low curvature of spacetime can be represented as follows: ^[5]

$~ \frac {d}{dt}[\gamma \mathbf{v} (1+ \frac {p_0}{\rho_0 c^2}+\frac {\alpha }{c^2})] = \mathbf{a_m} - \frac {1}{\gamma }\nabla (\frac { p_0}{\rho_0 }) - \frac {\varsigma }{4 \pi \eta \gamma^2 c^2 \rho^2_0 } (\frac{\partial^2 (\gamma \mathbf{v}) }{\partial t^2 } - c^2 \Delta (\gamma \mathbf{v} ) ) + \frac {\omega }{\gamma \rho_0 }\nabla (\nabla \cdot \mathbf{v} ) ,$

where $~ \mathbf{a_m} = \mathbf{\Gamma} + \mathbf{v} \times \mathbf{\Omega} +\frac {\rho_{0q} }{\rho_0 }(\mathbf{E} + \mathbf{v} \times \mathbf{B})$ is acceleration of gravitational and electromagnetic mass forces, $~ \mathbf{\Gamma}$ is gravitational field strength, $~ \mathbf{\Omega }$ is gravitational torsion field, $~ \mathbf{E}$ is t electric field strength, $~ \mathbf{B}$ is magnetic field.

At low velocities, for Lorentz factor we can assume $~ \gamma=1$ . Under ordinary conditions, we can also neglect contribution of pressure and dissipation function $~ \alpha$ on the left side of equation. Determining dynamic viscosity by expression $~ \mu = \frac {\varsigma }{4 \pi \eta \gamma^2 \rho_0 }$ , where $~ \eta$ is acceleration field coefficient, and denoting $~ \omega = \xi + \frac {\mu }{3}$ , we obtain the following:

$~ \frac {d \mathbf{v}}{dt} =\frac{\partial \mathbf{v} }{\partial t}+ (\mathbf{v} \cdot\nabla ) \mathbf{v} = \mathbf{a_m} - \nabla (\frac { p_0}{\rho_0 }) + \frac {\mu }{ \rho_0 } \Delta \mathbf{v} - \frac {\mu }{ \rho_0 c^2} \frac{\partial^2 \mathbf{v} }{\partial t^2 } + \frac {1 }{ \rho_0 } (\xi + \frac {\mu }{3}) \nabla (\nabla \cdot \mathbf{v} ) .$

Main difference of this equation from Navier–Stokes equation is a small additional term, which contains second time derivative of flux velocity $~ \mathbf{v}$ and square of speed of light in denominator.

References

^1.0 ^1.1 Fedosin S.G. The Concept of the General Force Vector Field. OALib Journal, Vol. 3, pp. 1-15 (2016), e2459. http://dx.doi.org/10.4236/oalib.1102459.
Fedosin S.G. Two components of the macroscopic general field. Reports in Advances of Physical Sciences, Vol. 1, No. 2, 1750002, 9 pages (2017). http://dx.doi.org/10.1142/S2424942417500025.
Torby, Bruce (1984). "Energy Methods". Advanced Dynamics for Engineers. HRW Series in Mechanical Engineering. United States of America: CBS College Publishing. ISBN 0-03-063366-4. (p. 271).
Ландау Л. Д., Лифшиц Е. М. Гидродинамика. – Издание 7-е, исправленное. – М.: Наука, 1988. – 731 с. – (Теоретическая физика, том VI).
^5.0 ^5.1 Fedosin S.G. Four-Dimensional Equation of Motion for Viscous Compressible and Charged Fluid with Regard to the Acceleration Field, Pressure Field and Dissipation Field. International Journal of Thermodynamics. Vol. 18, No. 1, pp. 13-24 (2015). http://dx.doi.org/10.5541/ijot.5000034003.
^6.0 ^6.1 Fedosin S.G. The procedure of finding the stress-energy tensor and vector field equations of any form. Advanced Studies in Theoretical Physics, Vol. 8, no. 18, pp. 771-779 (2014). http://dx.doi.org/10.12988/astp.2014.47101.
Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy. Jordan Journal of Physics. Vol. 9, No. 1, pp. 1-30 (2016). http://dx.doi.org/10.5281/zenodo.889304.
Fedosin S.G. Equations of Motion in the Theory of Relativistic Vector Fields. International Letters of Chemistry, Physics and Astronomy, Vol. 83, pp. 12-30 (2019). https://doi.org/10.18052/www.scipress.com/ILCPA.83.12.

На русском языке