На русском языке
Covariant
theory of gravitation
Covariant theory
of gravitation
(CTG) is a theory of gravitation published by Sergey Fedosin in 2009. It
includes extended special theory of
relativity, Lorentz-invariant theory
of gravitation, metric theory of
relativity and Newtonian law of gravitation, and describes gravitation as a
physical force acting on the particles of matter. The matter, the gravitational
field, as well as other fields change such properties of wave quanta as their
propagation velocity and frequency of oscillations. Since the spacetime
measurements are carried out by means of waves, it follows that the observed
geometrical properties of spacetime depend on the sources of energy and energy flux in the form of matter and fields which
are present in the reference frame. This dependence is determined by the field equations for the metric, forming a system of partial
differential equations. In CTG gravitational field is a
component of the general field.
Just as the general theory of relativity (GTR) and some
other alternative theories of gravitation, CTG predicts change in the rate of
time, the observed geometry of space, the trajectories of falling bodies,
propagation of light. However, there is a difference between the predictions of
GTR and CTG in the description of such effects as gravitational time dilation,
gravitational redshift of the wavelength, signal delay in the gravitational
field. This difference conforms to correction containing the fourth degree of
speed of light, within the limits of which all the tests of GTR with respect to
wave signals give the same results as CTG. If gravitation in GTR is consequence
of curvature of spacetime by the sources of energy and energy flux, in CTG gravitation appears as the result of
influence of gravitons on matter within the framework of modernized Le Sage's
theory of gravitation. The fluxes of gravitons also affect propagation of waves
and hence effective spacetime metric near the sources of energy and energy flux, so in CTG geometry is secondary relative
to the physics of phenomena. In weak fields and at low velocities CTG turns
into LITG. Since equations of LITG are
similar to equations of Maxwell's electrodynamics (see Maxwell-like gravitational equations) which
are successfully quantized, it allows us to quantize the
equations of gravitational field of LITG in the framework of quantum
gravitation.
Among the astrophysical applications, CTG as well as GTR,
based on the effect of light deflection in gravitational field, predicts the
phenomenon of gravitational lensing, when there are multiple images of the same
remote astronomical object. CTG assumes gravitational radiation from particular accelerated massive bodies, and
it can have dipole character (whereas in GTR only quadrupole and multipole radiations are always considered). However, acceleration of one body always
implies the opposite acceleration of other bodies in a system, so that in the
total radiation of the system of bodies the dipole component disappears.
Contents
|
History
The first step in development of CTG was presenting by
Fedosin the complete Lorentz-invariant
theory of gravitation (LITG) in the book in 1999. [1]
LITG is valid for inertial reference frames and describes all the gravitational
effects associated with delay of gravitation propagation and with the gravitational torsion field.
In 2002 the second book by Fedosin appeared, which was
devoted to the development of the theory of relativity. [2]
In this book the axioms of extended special
theory of relativity (ESTR) were formulated. In ESTR it is proved that the
constancy of the speed of light in all inertial reference frames, assumed by
the special theory of relativity (STR), is the result of the procedure of
spacetime measurements, in which two-way propagation of light (electromagnetic
wave) is always used. This leads to the averaging of the wave velocity in all
directions, regardless of the true speed of light and the velocity of the
reference frame, making the effective speed of light constant for each observer.
According to ESTR we can consider such an isotropic reference frame in which
the fluxes of gravitons have the same intensity from all sides. This reference
frame can be considered fixed relative to the electrogravitational
vacuum as the medium consisting of the fluxes of gravitons. In ESTR it is
also shown that the theory of relativity as the theory, which allows us to
recalculate the results of measurements of the coordinates, time and physical
quantities from one frame to another, depends on the wave representation, that
is, on the type and the properties of the wave used for spacetime measurements.
This dependence is expressed in particular through the Lorentz factor of the
form ![]() containing the effective wave
velocity
containing the effective wave
velocity ![]() which depends on the properties of the medium
(e.g., the refractive index of the medium), and the velocity
which depends on the properties of the medium
(e.g., the refractive index of the medium), and the velocity ![]() of
the reference frame as its average velocity in the period of the wave.
of
the reference frame as its average velocity in the period of the wave.
In his article in 2007 [3]
Fedosin draws a deep analogy between the electromagnetic and gravitational fields,
considering the similarity of their equations and contribution that the field
as sources of energy
and energy flux must make in
the result of determining the spacetime metric through the Hilbert-Einstein
equations. Another article in 2008 [4] considers the
violation of the equivalence principle, which is the methodological basis of
GTR, as applied to the mass-energy of the gravitational field. The following
article deals with the phenomenon of gravitation in the concept of gravitons
(the Le Sage's theory of gravitation) in the framework of the Theory of Infinite Hierarchical Nesting of Matter. [5]
Based on the concepts of gravitation as the force
interaction which arises from the action of gravitons and conforms to the
condition of Lorentz invariance in the inertial reference frames; the
conventionality of the constancy of the speed of light, following from the
measurement procedure; the dependence of the results of spacetime measurements
on the type and the properties of the used wave; the assumption about the same
propagation speed of gravitational and electromagnetic waves, based on the
model of the electrogravitational vacuum and the assumed structure of the
corresponding photons, in his book in 2009 Fedosin develops CTG with the help
of postulated by him axioms of the metric
theory of relativity (MTR) and the covariant force equations of motion
suitable for all possible reference frames. [6]
The structure of CTG also includes the gravitational field equations of LITG,
which are generalized to any reference frames by means of replacing the metric
tensor of the flat Minkowski spacetime by the metric tensor of the curved
spacetime, and which use the operation of covariant differentiation.
Just as in GTR, in CTG the most difficult task is finding
exact solutions of equations to determine the components of the metric tensor.
The solution of these equations in CTG is much more complicated than in GTR,
since in CTG, in contrast to GTR, the proper gravitational field of the body is
taken into account, which changes the metric both inside and outside of the
body. One of the exact solutions, determining the metric tensor outside a
single spherical body, was found by Fedosin. [6]
[7] [8] Using this solution
he described in the framework of CTG the anomalous precession of the perihelion
of planets, including Mercury; the deflection of relativistic particles, radio
signals and the light of stars, passing close to the Sun's surface; the anomalous
acceleration of "Pioneers"; the gravitational redshift; the
gravitational time dilation; the effects associated with the spin, generating
gravitational torsion field.
Transition from classical physics to
CTG
The covariant theory of gravitation must be considered in
several aspects. On the one hand, CTG is a theory of gravitational field. On
the other hand, CTG describes interaction of gravitational field with matter,
and gravitational force according to Newton second law leads to acceleration of
bodies. Besides, the gravitational field and other sources of energy and energy flux influence the propagation of wave quanta,
change their velocity, energy and frequency. This leads to the effective
curvature of spacetime and to deviation of the form of the metric tensor from
its value in the flat Minkowski spacetime. In turn, the metric tensor and its
derivatives with respect to coordinates are involved in determining the
gravitational force and the quantities, characterizing the gravitational field
and the motion of bodies, from the perspective of the coordinate observer, in
whose reference frame the metric is calculated.
Newtonian gravitation
According to classical mechanics the motion of physical
bodies is described as the combination of free motion by inertia and some
deflection from it. The reasons for the deflection are various forces acting on
the body. According to Newton second law the force’s value is determined by the
product of the body mass and its acceleration. According to the Newtonian law
of gravitation between any two bodies the force of gravitational attraction
appears which is proportional to the masses of bodies and inversely proportional
to the square of the distance between them. Therefore, the trajectory of the
test particle near the massive body is deflected from a straight line and the
velocity changes due to the gravitational acceleration. Due to the
proportionality of the gravitational force to the gravitational mass of test
particles, the latter will move with the same acceleration near the massive
body. This means that the free-fall trajectories of the particles depend on the
initial position and the initial velocity, but not on the mass of the particles
or their physical or chemical composition. This property of gravitation is
defined as the principle of universality of free fall (in GTR it is called the
weak equivalence principle) and is associated with the principle of equivalence
of the passive gravitational and inertial masses.
The last principle can be explained as follows. Due to
the equality of the gravitational acceleration, the masses of the test
particles on the surface of the massive body (for example, in the laboratory on
the Earth) can be determined simply by weighing (the more is the gravitation,
the greater is the mass, in this case, the passive gravitational mass). Then
any non-gravitational forces, which give the test particles acceleration, equal
to the free fall acceleration on the Earth surface, can be equated by their
effect to the corresponding gravitational forces. Because in the Newton second
law for non-gravitational forces there is the so-called inertial mass, then
from the equality of gravitational and non-gravitational forces and
accelerations the equality follows of gravitational and inertial masses. In
other words, with the appropriate calibration of forces and accelerations both
masses can be equated to each other.
The Newtonian spacetime is characterized by Euclidean
geometry and the independence of the rate of time on the spatial coordinates
and the velocities of the bodies. Space and time depend neither on each other,
nor on the material bodies, nor on the motion of these bodies. Transformations
of the time and the coordinates from one frame to another are carried out by
means of the Galilean transformations, in which the measurements of time and
coordinates are carried out mechanically and not by means of electromagnetic
waves. To synchronize the clocks in each reference frame, they are transferred
from the origin of the reference frame to other points at infinitesimal
velocity. It is assumed that the speed of interaction transfer by means of the
force field is infinitely large.
Relativistic generalization
The emergence in the early 20th century of the special
theory of relativity (STR) changed significantly the classical mechanics and
the theory of gravitation as the part of it, giving them relativistic form. The
Galilean transformations of classical mechanics were replaced by the Lorentz
transformations. Previously independent of each other, the space and the time
were combined into a single continuum, called Minkowski space. Mathematically
this was expressed in the transformation of the time coordinate (multiplied by
the speed of light to save the dimension) and the three-dimensional position
vector of a point into the four-vector describing an event in the
four-dimensional Minkowski space. Scalar and 3-vector physical quantities were
combined in the 4-vectors and tensors, to obtain the value of which in
different inertial reference frames the Lorentz transformations should be used
(in general, in the presence of shifts and turns of reference frames Poincare
transformations should be used). Due to these innovations the mechanics became
consistent with electrodynamics and the concept of carrying out any spacetime
measurements by means of electromagnetic waves with finite velocity of
propagation. This allowed describing accurately the motion of particles even at
speeds, close to the speed of light, and the phenomena with the release of
energy, comparable to the rest energy.
In the theory of gravitation STR has led to the creation
of the Lorentz-invariant theory of
gravitation (LITG). In the inertial reference frames the force of
gravitation must be transformed in a Lorentz-covariant way as any other force.
If there is a physical system with a massive body and test particles, the
observer can make his inertial reference frame with the help of additional
forces, which balance the force of gravitation. For such observer the moving
body creates not only the gravitational field strength, but also the gravitational torsion field, influencing
additionally the moving test particles. The equations of LITG have relativistic
form and are similar to the Maxwell equations in electrodynamics. [9] The Newtonian law of gravitation is a
special case of LITG.
Clarification of the essence of SRT is done in the extended special theory of relativity, as
it was described above in the historic section.
General relativity
Main source: Metric theory of relativity
The transition from the inertial to arbitrary reference
frames means transition from special (partial) relativity of inertial reference
frames to general relativity of accelerated reference frames. In case if a
force is acting on the reference frame reference, the frame begins to
accelerate and can no longer be considered inertial. In the presence of acceleration the relation between the physical quantities in
different reference frames through the Lorentz transformation is inaccurate and
requires correction. The situation is more complicated when not only on the
reference frame but also to on all the matter in it the omnipresent force of
gravitation is acting. The example is the isolated massive body, near which the
trajectories of motion of test particles are deflected from the straight lines,
having a special name – the geodesic lines.
General relativity is contained in GTR in which
gravitational force and the difference of the geodesic lines from straight
lines are the consequence of the curvature of spacetime near the bodies.
Accordingly, the flat Minkowski space in the presence of gravitation looks like
pseudo-Riemannian curved spacetime. In the free fall of particles near a
massive body the velocity of the particles and the gravitational acceleration
acting on them increase. Despite this, in GTR it is assumed that in the freely
falling reference frame the same laws hold as in the inertial Lorentz reference
frame. In this particular case general relativity differs not much from special
relativity, as indicated by some experiments with the propagation of light,
such as gravitational redshift. The assumption that free-falling frames are
Minkowskian in GTR is called Einstein equivalence principle. It means that the
falling observer with the help of internal experiments may not know whether he
is falling in the uniform gravitational field, or is moving by inertia without
such a field. Obviously, this assumption is only an idealization and in reality can be not satisfied. For example, in the free fall
of a charged test body by changing the acceleration of the fall by the law of
inverse square of the distance between the attracting center and the body,
there is electromagnetic emission, proportional to the charge of the body,
which is absent in the Lorentz inertial frames.
The common property of the gravitational field can be
considered the slowdown of the rate of electromagnetic clock in comparison with
the same clock outside the gravitational field. This follows from the reduction
of the speed of light as it approaches the massive bodies. The visible sizes of
bodies are also reduced in the direction of the gradient of the gravitational
field. In contrast to STR, in the presence of gravitation the position vector
is not a real 4-vector, and the main role is played by 4-vectors of
displacement (position shift). This means the impossibility to use the integral
Lorentz transformations for physical quantities. In particular, not the time
and the coordinates of events are subject to transformations from one frame to
another, but also the differentials of time and coordinates near these events.
In the Newtonian theory is the principle of equivalence
of accelerations: if all bodies in the reference frame are given the same
acceleration, then it is mechanically equivalent to the action of some uniform
gravitational field, creating at all points in space the same gravitational
acceleration. Einstein extended this principle to non-mechanical phenomena.
Based on this principle Fedosin determined the metric inside a uniformly
accelerated reference frame. [6] It allowed
finding the relation between the coordinates and time in the accelerated and
stationary reference frames. In particular it turned out that in the
accelerated reference frame the transverse dimensions visually decrease, in the
direction of the body’s acceleration they get longer, and at different points
of the accelerated frame the time flows differently with respect to the origin
of coordinates.
The main characteristic that specifies the geometry of
curved spacetime is the metric tensor. It can be used to calculate the Riemann
curvature tensor, as well as the connection coefficients, which determine the
parallel translation of the 4-vector in curved spacetime. In general case the metric tensor is a function of
time and coordinates. Due to its properties the metric tensor is included in
the equations of motion of test particles and wave quanta, is taken into
account in calculations of spacetime parameters and in measurements in the
gravitational field, as well as in recalculation of physical quantities from
one reference frame to another.
The generalization of general relativity is the metric theory of relativity (MTR), the
purpose of which is the expression of general relativity of phenomena in
different reference frames with the help of the metric. In MTR it is emphasized
that the geometry of spacetime is not absolute, it depends on the properties of
test particles and wave quanta used for the spacetime measurements and fixing
the metric. The metric can depend on the velocity of test particles, and can be
different for particles and wave quanta. By definition in MTR, the square of
the interval is equal to zero if it is connected with two close events on the
world line of test particles (wave quanta), used for spacetime measurements. In
this case, the speed of test particles (wave quanta) is included in the
expression for the 4-vectors and tensors, so that physical quantities are
determined in the corresponding wave representation.
Theoretically, propagation speed of light and
gravitational perturbations can be different, which can give two different
representations – for electromagnetic and gravitational waves, respectively. Just as in GTR, the metric in MTR is
found using the corresponding equations for the metric and depends on all the
sources of energy and energy flux available in the reference frame. An important difference of MTR from GTR
is that gravitational field of massive body, like any other field, becomes the
source of energy and
energy flux and is involved
in determination of metric. If in GTR the dependence of metric on time and
coordinates as if gives rise to gravitation, then in MTR this means that
gravitation is not the consequence of curvature of spacetime, on the contrary,
gravitation itself leads to this dependence of metric. In this case, the metric
shows how under the influence of energy and energy flux sources the difference of phenomena occurs from their form in Minkowski
space, in particular due to changing of velocity and frequency of
electromagnetic waves and their deflection near massive bodies, changing of the
rate of time, etc. STR, ESTR and general relativity in GTR, are particular
cases of MTR.
Relations of CTG
The gravitational field in CTG is considered as a vector
field, and therefore, each equation of
vector field will be valid for it. [10]
CTG includes three components:
- The equations of the gravitational
field taken from LITG, and
written in a covariant way for all reference frames.
- Equation for the metric, designed to determine the
components of the metric tensor through the known sources of energy and energy flux.
- The equations of motion of particles
and wave quanta under action of the given field strengths or sources of energy and energy flux.
The covariant gravitational field equations have the
form:
![]()
![]()
where ![]() is
the gravitational tensor;
is
the gravitational tensor; ![]() is the mass 4-current (mass current
density), which generates the gravitational field;
is the mass 4-current (mass current
density), which generates the gravitational field; ![]() is the 4-velocity of the matter element in the curved spacetime;
is the 4-velocity of the matter element in the curved spacetime; ![]() is the 4-vector of displacement;
is the 4-vector of displacement; ![]() is
the differential of proper time;
is
the differential of proper time; ![]() is the mass density in the frame at rest relative to the matter;
is the mass density in the frame at rest relative to the matter; ![]() is the gravitational
constant;
is the gravitational
constant; ![]() is
the speed of light.
is
the speed of light.
In contrast
to Newtonian gravitational theory, where the source of gravitational force is
assumed to be the mass of bodies, in relativistic mechanics mass density is
part of stress-energy tensor, taking into account the energies of motion and
pressure in matter. This tensor is used in GTR to determine the metric inside
matter. In CTG, the gravitational stress-energy tensor is
additionally used. which is not equal to zero even outside
matter. As a result, the equation for the metric can be written as follows: [11]
![]()
where ![]() is the Ricci tensor, which is
the trace of the Riemann curvature tensor,
is the Ricci tensor, which is
the trace of the Riemann curvature tensor, ![]() is the scalar curvature,
is the scalar curvature, ![]() is the metric tensor,
is the metric tensor, ![]() is the coefficient subject to be determined,
is the coefficient subject to be determined, ![]() is the acceleration stress-energy tensor,
is the acceleration stress-energy tensor, ![]() is the pressure stress-energy tensor,
is the pressure stress-energy tensor, ![]() is the gravitational stress-energy tensor,
is the gravitational stress-energy tensor, ![]() is the stress-energy tensor of electromagnetic field.
is the stress-energy tensor of electromagnetic field.
Outside the
matter, in accordance with the procedure of energy and metric gauging, both the
cosmological constant and the scalar curvature, as well as tensors ![]() and
and ![]() become zero. [12] As a
result, the equation for the metric is simplified:
become zero. [12] As a
result, the equation for the metric is simplified:
![]()
The equation of motion for the particles
has the following form: [10] [13] [14] [15]
![]()
taking into account the expression for the
4-vector of force density ![]() (see the
4-force) through the covariant derivative of the
stress-energy tensor of the acceleration field and through the operator
of proper-time-derivative
of the 4-potential
(see the
4-force) through the covariant derivative of the
stress-energy tensor of the acceleration field and through the operator
of proper-time-derivative
of the 4-potential ![]() of
the acceleration field in the Riemannian space
of
the acceleration field in the Riemannian space
![]()
where ![]() — invariant mass density of an
element of matter,
— invariant mass density of an
element of matter, ![]() — 4-velocity,
— 4-velocity, ![]() — 4-acceleration of the matter
element,
— 4-acceleration of the matter
element, ![]() is the acceleration tensor,
is the acceleration tensor, ![]() is the proper dynamic time of the element in its
rest frame,
is the proper dynamic time of the element in its
rest frame, ![]() is the tensor of electromagnetic field
strengths,
is the tensor of electromagnetic field
strengths, ![]() is the pressure field tensor,
is the pressure field tensor, ![]() is the electromagnetic 4-current
,
is the electromagnetic 4-current
, ![]() is the density of the electric
charge of the matter element in its rest frame.
is the density of the electric
charge of the matter element in its rest frame.
In CTG it is considered that the ordinary
gravitational and electromagnetic forces are acting on the wave quanta in a
special way, the fields change mainly their velocity and frequency. This is due
to its proximity to zero of the rest mass and charge of the quanta, which leads
to nulling of the densities ![]() ,
, ![]() , and correspondingly of the
4-vectors
, and correspondingly of the
4-vectors ![]() and
and ![]() for quanta, and to reduction of the
action of forces on the quanta from the strengths of external fields.
for quanta, and to reduction of the
action of forces on the quanta from the strengths of external fields.
Therefore, the covariant derivatives of
stress-energy tensors of the gravitational and electromagnetic fields which
specify the corresponding forces for quanta will be small. On the other hand,
for the electromagnetic waves the interval is set to zero: ![]() , which reflects the fact that these waves
are used for spacetime measurements (see also the third axiom of the metric
theory of relativity).
, which reflects the fact that these waves
are used for spacetime measurements (see also the third axiom of the metric
theory of relativity).
Since for the square of the interval the
relation holds: ![]() , then
for the waves the differential of the proper time
, then
for the waves the differential of the proper time ![]() is also zero. If in the equation of
motion (2) we assume
is also zero. If in the equation of
motion (2) we assume ![]() to be exactly equal to zero, then
in the equation uncertainty arises. It is to avoid this uncertainty by
multiplying equation (2) by the squared differential
to be exactly equal to zero, then
in the equation uncertainty arises. It is to avoid this uncertainty by
multiplying equation (2) by the squared differential ![]() ,
and then dividing by the squared differential
,
and then dividing by the squared differential ![]() , where
, where ![]() is the time parameter which marks
the position of the wave quantum in its trajectory. The right side of equation
(2) vanishes because of the presence of zero multiplier in the form of the
differential of the proper time
is the time parameter which marks
the position of the wave quantum in its trajectory. The right side of equation
(2) vanishes because of the presence of zero multiplier in the form of the
differential of the proper time ![]() , and for the electromagnetic waves the
equation of motion takes the following form:
, and for the electromagnetic waves the
equation of motion takes the following form:
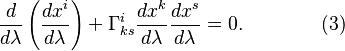
The
obtained equation of motion will have the same form as in GTR for the waves on
the zero geodesic line. In
deriving (3), it was taken into account that for solid-state point particles
and wave quanta, the 4-potential of the acceleration field and the 4-velocity
are equal to each other, ![]() . In addition,
since
. In addition,
since ![]() , the following equality holds:
, the following equality holds:
![]()
Essence of CTG
Basic definitions and properties
Just as GTR, CTG is the metric theory of gravitation. In
contrast to LITG, satisfying only the Lorentz transformations, the equations of
the gravitational field of CTG are written in covariant form and satisfy any
transformations possible for the reference frames. The equations of motion for
the particles and wave quanta are also covariant (covariance here means that
the equations are written in the tensor form suitable for any reference frames). Before finding the physical
quantities characterizing gravitational field or motion of test particles, it
is necessary to determine the metric tensor corresponding to distribution of
sources of energy and
energy flux in this reference
frame. For this
purpose, the appropriate equations for the metric are used.
According to the axioms of CTG the source of the
gravitational field is the mass 4-current ![]() , and the field itself is characterized by
the gravitational
four-potential
, and the field itself is characterized by
the gravitational
four-potential ![]() , where
, where ![]() is
the scalar potential and
is
the scalar potential and ![]() is the vector potential. Through the 4-vector
is the vector potential. Through the 4-vector ![]() the antisymmetric gravitational tensor is determined in a
covariant way:
the antisymmetric gravitational tensor is determined in a
covariant way:
![]() .
.
In turn, the tensor ![]() allows us to determine the gravitational stress-energy tensor:
allows us to determine the gravitational stress-energy tensor:
![]() .
.
In CTG gravitation is a real physical force which can be
explained in the framework of the Le Sage's theory of gravitation as the result
of the action of the fluxes of gravitons on the matter. Under the action of the
fluxes of gravitons near massive bodies the medium, in which the wave quanta
propagate, changes its properties so that the propagation velocity and the
frequency of the quanta become dependent on the gravitational potential.
The gravitational field equations of CTG are written in
the language of 4-vectors and tensors of second rank. Due to the correspondence
principle in the weak field, these equations turn into the equations of LITG,
which are valid in the special theory of relativity (STR). In turn, for the
fixed bodies and with the zero vector gravitational
potential, the equations of LITG can be represented as one equation for the
scalar gravitational potential, which turns into the Poisson equation for the
gravitational potential of classical physics.
After we could write in the explicit form the axioms of
the general theory of relativity (GTR), it became possible to compare them with
the systems of axioms of the metric theory
of relativity (MTR) and CTG. [16] [17] It turns out that the equations of motion
of GTR are a special case of the equations of motion of CTG.
The integral
field
energy theorem for gravitational field in a curved
space-time is as follows: [18]
![]()
The derivation of the generalized Poynting theorem and
the solution of the 4/3 problem in the presence of a gravitational field are
described in the article. [19]
Solution of equations
Comparison of equations of motion for
particles in CTG and GTR shows their essential difference. The equation of motion in GTR for particles in view of
electromagnetic field and its stress-energy
tensor ![]() has the form:
has the form:
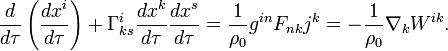
This equation of motion is not suitable
for description of reaction propulsion. Meanwhile, if in the equation (2) of
motion of CTG the mass density ![]() bring in the derivative, then with condition
bring in the derivative, then with condition ![]() for motion of
solid-state particle in the
equation will be the rate of change of momentum density of matter due to
changes in mass density.
for motion of
solid-state particle in the
equation will be the rate of change of momentum density of matter due to
changes in mass density.
If this density changes with time, its
derivative specifies the term for reactive force, analogous to the well-known Meshcherskiy formula in classical mechanics for bodies
of variable mass. [20] The equation of motion of CTG has
the meaning of the law of conservation of energy
and momentum of matter which is under action of forces
in electromagnetic, gravitational and other fields. In contrast to this, the
equation of motion of GTR reflects only equivalence principle (the acceleration
of the fall is equal to the acceleration originating from the curvature of
spacetime and from the non-gravitational
forces), and is not connected with the law of
conservation of energy and
momentum. Therefore, in GTR there is no definite
limiting transition to STR, i.e. to the case of weak fields, which would be
based on the correspondence
principle and the laws of conservation of physical
quantities such as energy, momentum and angular momentum. [21]
In the presence of moving matter and
propagating waves solution of equations of CTG becomes significantly more
complicated. Due to motion of the sources of energy
and energy flux and their
interaction with each other, the metric tensor in considered reference frame
becomes dependent on time. This leads to a change of motion of matter and
waves, and a change of the field strengths, including due to contribution of
changing metric tensor. As a result, the gravitational field equations, the
equations for metric and the equations of motion become coupled and must be
solved simultaneously. Since these equations contain partial derivatives up to
second order, the exact solution is possible only in some special cases.
For example, the metric near massive body,
taking into account the energy and
energy flux of its gravitational and electromagnetic
field, has been calculated by Fedosin. [6] [7] The contribution to metric and to
total gravitational field from test particles is considered negligible, so that
the motion of the particles is regulated only by the gravitation of massive
body. The standard expression for the square of interval between two close
points in all metric theories is the following:
![]()
Substituting in this expression of the metric
tensor components, found for the space outside the isolated massive body, in
the four-dimensional spherical coordinates ![]() gives:
gives:
![]()
where ![]() is the time component of the metric
tensor.
is the time component of the metric
tensor.
In article, [8] within
the framework of the relativistic uniform model, the components of the metric
inside a spherical body were calculated in the following form:
![]()
where ![]() is the gravitational constant;
is the gravitational constant; ![]() is the coefficient to be
determined;
is the coefficient to be
determined; ![]() is the radial coordinate;
is the radial coordinate; ![]() is the speed of light;
is the speed of light; ![]() is the invariant mass density of
matter particles, moving inside the body;
is the invariant mass density of
matter particles, moving inside the body; ![]() is the Lorentz factor of particles
moving at the center of body;
is the Lorentz factor of particles
moving at the center of body; ![]() is the gravitational potential at
the surface of sphere with radius
is the gravitational potential at
the surface of sphere with radius ![]() and gravitational mass
and gravitational mass ![]() ; quantities
; quantities ![]() and
and ![]() are
auxiliary values;
are
auxiliary values; ![]() is the invariant charge density of
matter particles, moving inside the body;
is the invariant charge density of
matter particles, moving inside the body; ![]() is the electric scalar potential at
the surface of sphere with total charge
is the electric scalar potential at
the surface of sphere with total charge ![]() ;
; ![]() is the potential of pressure field
at the center of body.
is the potential of pressure field
at the center of body.
On the surface of the body, with ![]() , the component
, the component ![]() of the metric tensor inside the body
must be equal to the component
of the metric tensor inside the body
must be equal to the component ![]() of the metric tensor outside the
body in (4). This allows us to refine the expression for the metric tensor
components outside the body by eliminating one unknown coefficient
of the metric tensor outside the
body in (4). This allows us to refine the expression for the metric tensor
components outside the body by eliminating one unknown coefficient ![]() :
:
![]()
where ![]() is the gravitational potential
outside the body;
is the gravitational potential
outside the body; ![]() is the electric potential outside
the body.
is the electric potential outside
the body.
The coefficient ![]() in (5) is equal to the
coefficient
in (5) is equal to the
coefficient ![]() in equation for the metric (1).
For
in equation for the metric (1).
For ![]() the metric tensor of CTG differs from
the metric tensor of GTR by small terms containing the fourth power of the
speed of light in the denominator.
the metric tensor of CTG differs from
the metric tensor of GTR by small terms containing the fourth power of the
speed of light in the denominator.
In the general case, for solutions of
equations it is necessary, as in GTR, to use the numerical methods, the method
of small perturbations, the parameterized post-Newtonian formalism (PPN
formalism) and other approximations. As a rule, the basic term of the given
approximations is determined by Newtonian gravitation, and the additions arise
from the general relativity of CTG (i.e., from the dependence of the results of
spacetime wave measurements on any sources of energy
and energy flux). The
feature of PPN formalism is that it allows us to compare the various
alternative theories of gravitation.
Principle of least action
The equations of motion of the matter, the
equations for determining the metric, the equations for the acceleration field and pressure field, gravitational and
electromagnetic fields can be derived from the principle of least action.
In the case of the matter, continuously
distributed throughout the space volume, the action function for the matter in
the gravitational and electromagnetic fields in the covariant theory of
gravitation is given by: [22] [11]
![]()
![]()
where ![]() is the Lagrange function or
Lagrangian,
is the Lagrange function or
Lagrangian, ![]() is the time differential of the
used reference frame,
is the time differential of the
used reference frame, ![]() is some coefficient,
is some coefficient, ![]() is the scalar curvature,
is the scalar curvature, ![]() is the cosmological constant, which
characterizes the energy density of the considered system as a whole, and
therefore is the function of the system,
is the cosmological constant, which
characterizes the energy density of the considered system as a whole, and
therefore is the function of the system, ![]() is the speed of light as the
measure of the propagation speed of the electromagnetic and gravitational
interactions,
is the speed of light as the
measure of the propagation speed of the electromagnetic and gravitational
interactions,
![]() is the electromagnetic 4-potential,
where
is the electromagnetic 4-potential,
where ![]() is the scalar potential and
is the scalar potential and ![]() is the vector potential,
is the vector potential, ![]() – electric four-current,
– electric four-current, ![]() is the electric constant,
is the electric constant, ![]() – electromagnetic tensor,
– electromagnetic tensor, ![]() and
and ![]() are the constants of
acceleration field and pressure field, respectively,
are the constants of
acceleration field and pressure field, respectively, ![]() – 4-potential of pressure
field,
– 4-potential of pressure
field,
![]() is the invariant 4-volume, expressed
through the differential of the time coordinate
is the invariant 4-volume, expressed
through the differential of the time coordinate ![]() ,
,
through the product ![]() of the differentials of the spatial
coordinates, and through the square root
of the differentials of the spatial
coordinates, and through the square root ![]() of the determinant
of the determinant ![]() of the metric tensor, taken with the
negative sign.
of the metric tensor, taken with the
negative sign.
Variations of the action function by the
metric tensor, by the coordinates, by the 4-potentials of the field give the
Euler-Lagrange equations as the equations of motion of the metric, matter and fields.
The action function contains
terms ![]() that
represent the density of the Lagrange function. With the help of these terms, a
vector theory of gravity was presented in the article, [23]
leading to the same results as the covariant theory of gravitation. Similar
terms are present in the Lagrangian in the article. [24]
that
represent the density of the Lagrange function. With the help of these terms, a
vector theory of gravity was presented in the article, [23]
leading to the same results as the covariant theory of gravitation. Similar
terms are present in the Lagrangian in the article. [24]
Gravitational
Aharonov-Bohm effect
Основная статья: Gravitational phase shift
The analysis
of the action function shows that it has the physical meaning of the function
describing the change of such intrinsic properties of bodies and reference
frames, as the rate of the proper time and the rate of increase of the phase
angle of periodic processes. For the gravitational and electromagnetic fields
difference of the clock in the weak field approximation is described by the
formulas: [25]
![]()
The clock 2,
which measures the time ![]() , is check one and the clock 1 measures the time
, is check one and the clock 1 measures the time ![]() and is under the influence of
additional 4-field potentials
and is under the influence of
additional 4-field potentials ![]() or
or ![]() . Time points 1 and 2 within the
integrals indicate the beginning and the end of the field action.
. Time points 1 and 2 within the
integrals indicate the beginning and the end of the field action.
The phase
shift for similar processes in the field and outside it, or occurring in
different states of motion is equal to:
![]()
The phase
shift, obtained due to the electromagnetic 4-potential ![]() , is proved by the Aharonov-Bohm effect. The phase shift in the
gravitational 4-potential is also confirmed in the papers. [26] [27]
[28]
, is proved by the Aharonov-Bohm effect. The phase shift in the
gravitational 4-potential is also confirmed in the papers. [26] [27]
[28]
From the
above formulas for fixed clocks, located in the field close to each other at
points 1 and 3, the next equations are following:
![]()
![]()
This shows
that the rates of the clocks at the points with different potentials of the
field do not match. In the case of the gravitational field
it gives gravitational time dilation.
Hamiltonian
With the help of the Legendre transformation we can proceed from the known Lagrangian to
the Hamiltonian in the four-dimensional form. In the covariant theory of gravitation the Hamiltonian is determined through the
4-velocity, the scalar potentials and the strengths of acceleration and
pressure fields, of gravitational and electromagnetic fields, taking into
account the metric, and for the continuously distributed matter it has the
following form: [11]
![]()
![]()
where ![]() and
and ![]() are the scalar potentials of
acceleration and pressure fields, respectively.
are the scalar potentials of
acceleration and pressure fields, respectively.
If we introduce the 4-vector of
generalized velocity with the covariant index:
![]()
then for the equation for the metric to
hold and to perform the calibration of the Hamiltonian, the following relation
is necessary:
![]()
Since
Hamiltonian specifies relativistic energy, it is included into time component
of 4-vector of the Hamiltonian. [25] In Minkowski space,
this 4-vector can be written in contravariant form: ![]() where
where ![]() is
velocity of center of momentum of the system.
is
velocity of center of momentum of the system.
Energy, momentum,
4-momentum and inertial mass
For
continuously distributed matter in curved space-time, expression for energy of
a physical system has the following form:[29]
![]()
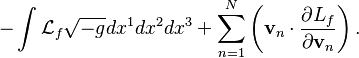
In this
expression, Lagrangian density of the system ![]() is presented as a sum of two
parts
is presented as a sum of two
parts ![]() , where
, where ![]() depends on 4-potentials and
4-currents, and
depends on 4-potentials and
4-currents, and ![]() contains tensor invariants of
fields. The quantity
contains tensor invariants of
fields. The quantity ![]() is that part of Lagrangian which is
obtained by integrating
is that part of Lagrangian which is
obtained by integrating ![]() over moving volume of physical system.
In matter of the system velocity of particles is
over moving volume of physical system.
In matter of the system velocity of particles is ![]() , the quantity
, the quantity ![]() is time component of 4-velocity of
these particles,
is time component of 4-velocity of
these particles, ![]() is determinant of metric tensor.
When calculating contribution of particle fields to energy of the system it is
necessary to divide matter into
is determinant of metric tensor.
When calculating contribution of particle fields to energy of the system it is
necessary to divide matter into ![]() particles or matter elements of
point sizes. Each such particle has a certain velocity
particles or matter elements of
point sizes. Each such particle has a certain velocity ![]() , while
, while ![]() and energy of the system
and energy of the system ![]() in general case depend on the
velocities
in general case depend on the
velocities ![]() .
.
Let four
vector fields act in the system under consideration, such as electromagnetic
and gravitational fields, acceleration field and pressure field. Then energy of
the system is expressed through scalar potentials of the fields ![]() , through vector potentials of the
fields
, through vector potentials of the
fields ![]() , and through tensors of the fields
, and through tensors of the fields ![]() :
:
![]()
![]()
![]()
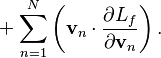
Momentum of
the system is determined by the formula:
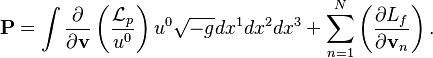
For vector
fields, the momentum is:
![]()
![~+{\mathbf v}\cdot {\frac {\partial }{\partial {\mathbf v}}}\left(\rho _{{0q}}{\mathbf A}+\rho _{0}{\mathbf D}+\rho _{0}{\mathbf U}+\rho _{0}{\mathbf \Pi }\right)\operatorname {{\big ]}}u^{0}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}+\sum _{{n=1}}^{N}\left({\frac {\partial L_{f}}{\partial {\mathbf v}_{n}}}\right).](ktgen.files/image141.gif)
The
4-momentum is defined as a 4-vector with covariant index of the form ![]() . The 4-momentum can be split into
two 4-vectors:
. The 4-momentum can be split into
two 4-vectors: ![]() . where
. where ![]() is generalized 4-momentum associated
with particles, and the 4-vector
is generalized 4-momentum associated
with particles, and the 4-vector ![]() is associated with the part of the
4-momentum to which the fields contribute.
is associated with the part of the
4-momentum to which the fields contribute.
In flat
space-time, inertial mass of a physical system is found by dividing by square
of speed of light the energy ![]() calculated in frame of reference
associated with center of momentum of the system:
calculated in frame of reference
associated with center of momentum of the system: ![]() . Indeed, in this reference frame momentum
of the system is always zero and 4-momentum depends only on the energy:
. Indeed, in this reference frame momentum
of the system is always zero and 4-momentum depends only on the energy: ![]() .
.
In curved
space-time and in an arbitrary reference frame, definition of inertial mass
involves calculating square root of square of 4-momentum: ![]() , where
, where ![]() is 4-momentum of the system with
contravariant index.
is 4-momentum of the system with
contravariant index.
Generalized 4-momentum
In CTG,
density of generalized 4-momentum is defined in covariant form as
follows: [30]
![]()
where ![]() is 4-velocity of matter particles.
is 4-velocity of matter particles.
Generalized
4-momentum of a system with a covariant index is calculated through integral
over invariant volume:
![]()
and can be
expressed through 4-potentials of fields:
![]()
To
calculate the generalized 4-momentum with contravariant index, the formula is
used:
![]()
Pseudotensor of angular
momentum
Pseudotensor
of angular momentum of a physical system in Cartesian coordinates has the
following form: : [10]
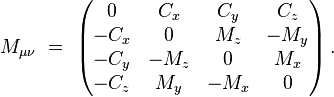
The
components of angular momentum pseudotensor are components of two
three-dimensional vectors. One of these vectors is angular momentum ![]() , the other vector is time-varying
dynamic mass moment
, the other vector is time-varying
dynamic mass moment ![]() . These vectors are defined by the
formulas
. These vectors are defined by the
formulas
![~{\mathbf M}=\int \left[{\mathbf r}\times {\frac {\partial }{\partial {\mathbf v}}}\left({\frac {{\mathcal {L}}_{p}}{u^{0}}}\right)\right]u^{0}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}+\sum _{{n=1}}^{N}\left({\mathbf r}_{n}\times {\frac {\partial L_{f}}{\partial {\mathbf v}_{n}}}\right).](ktgen.files/image159.gif)
![]()
![~-\sum _{{n=1}}^{N}\left[ct{\frac {\partial L_{f}}{\partial {\mathbf v}_{n}}}-{\frac {1}{c}}\left({\mathbf v}_{n}\cdot {\frac {\partial L_{f}}{\partial {\mathbf v}_{n}}}\right){\mathbf r}_{n}\right].](ktgen.files/image162.gif)
Radius
vector of center of momentum of the system is obtained in the following form:
![~{\mathbf R}={\frac {1}{E}}\left\{\int {\mathbf r}\left[{\mathbf v}\cdot {\frac {\partial }{\partial {\mathbf v}}}\left({\frac {{\mathcal {L}}_{p}}{u^{0}}}\right)u^{0}-{\mathcal {L}}_{p}-{\mathcal {L}}_{f}\right]{\sqrt {-g}}dx^{1}dx^{2}dx^{3}+\sum _{{n=1}}^{N}\left({\mathbf v}_{n}\cdot {\frac {\partial L_{f}}{\partial {\mathbf v}_{n}}}\right){\mathbf r}_{n}\right\}.](ktgen.files/image164.gif)
Taking into
account expressions for momentum ![]() , energy
, energy ![]() and radius vector of the center of
momentum
and radius vector of the center of
momentum ![]() , dynamic mass moment
, dynamic mass moment ![]() is expressed by the formula:
is expressed by the formula:
![]()
Consequences of theory
Effects associated with wave
propagation
These effects include gravitational time dilation,
gravitational redshift of the wavelength, the signal delay in the gravitational
field, the deflection of light beams in the gravitational field of the Sun, and
others.
Although the equation of motion of the CTG for wave
quanta (3) coincides with the corresponding equation of GTR, a small difference
arises in the value of the Christoffel symbol ![]() , which is a function of the metric
tensor and its derivatives. In this case, the difference between the time
component
, which is a function of the metric
tensor and its derivatives. In this case, the difference between the time
component ![]() in (5) in the CTG and the
corresponding value in GTR is estimated by a value of the order of
in (5) in the CTG and the
corresponding value in GTR is estimated by a value of the order of ![]() . With the same degree of accuracy, all CTG effects associated with wave
propagation give the same result as GTR.
. With the same degree of accuracy, all CTG effects associated with wave
propagation give the same result as GTR.
Gravitational waves
If we consider the electromagnetic field from the
moving charged particles, then it is characterized by the dipole, quadrupole,
and multipole radiation. As a rule, the intensity of quadrupole radiation and
of the subsequent multipoles is much less than the intensity of dipole
radiation. The similar situation for gravitational radiation takes place in
CTG, as the consequence of similarity of the equations of the electromagnetic
and gravitational fields and the vector character of the field sources. Meanwhile,
in GTR the dipole radiation as such is absent, and the quadrupole and multipole
gravitational radiations are associated with the tensor sources of the field
and the metric oscillations propagating at the speed of light.
From observations of parameters of orbits of binary
neutron stars and the speeds of their approaching the change of the total
energy of stars’ interaction due to the radiation of gravitational waves is
estimated. [31]
In such systems the radiation can be only quadrupole, as
the consequence of stars’ rotation relative to their common center of momentum.
This conclusion satisfies both CTG and GTR. Although the dipole and multipole
gravitational radiations can be calculated separately for each body, but in a
closed system the total dipole radiation of all the bodies of the system tends
to zero.
Orbital and spin effects
In some cases, in CTG the contributions from the effective
curvature of spacetime and from the forces arising from the ordinary
gravitational field and gravitational torsion field are combined. This leads to
different effects in the motion of test particles around massive bodies. Among
them, the precession of the perihelions of the orbits, the spin and orbital
Lense-Thirring effects, the geodetic precession, the effect of
"Pioneers", the approaching of the orbits of bodies due to the
emission of gravitational waves by them, etc.
Precession of perihelion of orbits
Calculation of finite motion of a test particle around
massive body in Kepler problem in CTG using the equation for the metric (1) in
the square of the interval (4) and with the solution (5) indicated above,
allows us to determine the the last unknown constant in the form ![]() when comparing the results of
calculations with the shift of perihelion of Mercury or other planets.
when comparing the results of
calculations with the shift of perihelion of Mercury or other planets.
Interaction of spins
During the rotation of the body there is the gravitational torsion field near it, the
main term of which is the dipole component of the torsion field proportional to
the spin (the proper angular momentum) of the body. In the formula for the
torsion field strength there is an inverse proportional dependence on the cube
of distance from the rotating body to the observation point, and on the square
of the velocity of the gravitation propagation. The latter indicates that the
torsion field is a relativistic effect and the consequence of the delay of the
change of the gravitational field during the motion of the bodies. Since these
effects are fully taken into account in STR, then to describe the interaction
of two fixed rotating bodies through the torsion field, in the first
approximation the formulas of LITG are sufficient, into which the formulas of
CTG turn in the weak field. [1] [6]
In particular, checking of the effect was carried out on
the Gravity Probe B satellite in 2004-2005 by measuring the angular velocity of
the precession of the gyroscope in the torsion field of the Earth ![]() . If the gyroscope would always be located
only over the North Pole of the Earth, where the spin of the Earth
. If the gyroscope would always be located
only over the North Pole of the Earth, where the spin of the Earth ![]() and the radius vector of the distance
and the radius vector of the distance ![]() from the center of the Earth to the satellite are parallel, the angular
velocity of the precession of the gyroscope would be equal to the maximum
value:
from the center of the Earth to the satellite are parallel, the angular
velocity of the precession of the gyroscope would be equal to the maximum
value:
![]()
For the Gravity Probe B the value ![]() should be approximately equal to 0,0409 arc
seconds per year, or 6.28•10–15 rad/s. The same formula for the
effect is obtained in GTR, but later is was averaged
over the entire orbit. [32] In GTR the effect of spin-spin interaction is called the Lense-Thirring
spin effect or the Schiff effect, and is assumed to be the consequence of
dragging of the spin inertial reference frames (frame-dragging). To describe
the torsion field in GTR the so-called gravitomagnetic field is often involved,
see gravitoelectromagnetism.
should be approximately equal to 0,0409 arc
seconds per year, or 6.28•10–15 rad/s. The same formula for the
effect is obtained in GTR, but later is was averaged
over the entire orbit. [32] In GTR the effect of spin-spin interaction is called the Lense-Thirring
spin effect or the Schiff effect, and is assumed to be the consequence of
dragging of the spin inertial reference frames (frame-dragging). To describe
the torsion field in GTR the so-called gravitomagnetic field is often involved,
see gravitoelectromagnetism.
Orbital Lense-Thirring effect
If we give a test particle of some velocity ![]() of
the motion in its orbit around the rotating massive body with the spin
of
the motion in its orbit around the rotating massive body with the spin ![]() ,
under the action of the torsion field
,
under the action of the torsion field ![]() from this spin the moment of force arises, changing the orbital angular
momentum of the particle:
from this spin the moment of force arises, changing the orbital angular
momentum of the particle:
![]()
where the force is equal: ![]() ,
, ![]() denotes the mass of the particle,
denotes the mass of the particle, ![]() is the gravitational field strength
(gravitational acceleration) from the massive body, the radius vector of the distance
is the gravitational field strength
(gravitational acceleration) from the massive body, the radius vector of the distance ![]() is measured from the center of the rotating body to the test particle, and
the orbital angular momentum of the particle equals
is measured from the center of the rotating body to the test particle, and
the orbital angular momentum of the particle equals ![]()
If we express the torsion field ![]() through the spin of the body
through the spin of the body ![]() , then for the case of circular motion we
obtain the formula for the angular velocity of precession of the orbital plane
of the particle relative to the direction of the body’s spin:
, then for the case of circular motion we
obtain the formula for the angular velocity of precession of the orbital plane
of the particle relative to the direction of the body’s spin:
![]()
This result, as it follows from GTR and the experiments,
should be doubled, because it does not take into account the spacetime metric
in the reference frame of the body. In this reference frame according to CTG
the gravitational field is rotating with the body and in the space
there is the torsion field, which makes its contribution to the metric as the
source of energy
and energy flux. As a result,
the metric near the rotating massive body differs from the metric of a
stationary body and by its form must resemble the Newman metric found in GTR
for the rotating and charged body. [33] In the Newman metric in comparison to the Reissner metric for a stationary
charged body, [34] there is an additional quantity
associated with the rotation of the body.
Therefore, in the CTG metric
near a rotating massive body, which takes into account energy and energy flux
of gravitational field of the rotating body, instead of coefficients of the
type ![]() and
and ![]() in
in ![]() in the metric (4), a new form of square of
interval and other coefficients appear in the metric. By choosing their values
in accordance with the equation of motion of test particle and the experiments
on measuring orbital precession, it is possible to specify the form of metric
around a rotating massive body from the perspective of CTG.
in the metric (4), a new form of square of
interval and other coefficients appear in the metric. By choosing their values
in accordance with the equation of motion of test particle and the experiments
on measuring orbital precession, it is possible to specify the form of metric
around a rotating massive body from the perspective of CTG.
Geodetic precession
This type of precession is sometimes called the de Sitter
effect or the Fokker precession. This precession occurs during the orbital
motion of the test particle with the spin around the body, which may or may not
rotate (the presence of rotation of the body is shown as the absolute effect
and is expressed in the emergence of centripetal acceleration). The spin of the
particle tends to maintain its direction in space in any motion of the
particle. The parallel transfer of the spin of the particle in the orbit in the
curved spacetime around the massive body leads to the fact that the spin is
affected by the effective moment of force which changes its direction in space
and leads to the precession with some angular velocity.
Geodetic precession also occurs in LITG, where the
curvature of spacetime is not taken into account. From the perspective of the
observer in the reference frame of the rotating particle, the body moves around
the particle in some orbit, creating the torsion field. This torsion field acts
on the spin of the particle, creating the moment of force and the corresponding
spin precession of the particle. Both effects, from the spacetime curvature and
from the spin-orbit interaction of torsion fields, depend on the same variables
and can be added. According to GTR and to the results of experiments, [35] the contribution from the curvature of spacetime is
two times greater than the contribution from the interaction of torsion fields.
This gives the formula for the angular velocity of the precession of gyroscope,
which equivalent to the rotating test particle:
![]()
where ![]() is
the velocity of the motion of the gyroscope in the orbit,
is
the velocity of the motion of the gyroscope in the orbit, ![]() is the gravitational acceleration acting on the
gyroscope from the massive body.
is the gravitational acceleration acting on the
gyroscope from the massive body.
For accurate calculation of geodetic precession in CTG we
should use the form of the metric near the rotating massive body and with the
help of it calculate the orbital motion of the rotating test particle. As in
the case of the orbital Lense-Thirring effect, the indefinite coefficients in
the metric are subject to redefining in comparison with the experimental
results.
Pioneer anomaly
The difference of the methods of including the
gravitational field into equations for the metric and the discrepancy between
the equations of motion in CTG and GTR lead to the fact that in CTG it becomes
possible to explain the Pioneer anomaly. [6]
[36] This effect consists in the fact that in measuring the
frequency of wave signals from the spacecrafts on the Earth there is difference
from the predictions of GTR. According to CTG it is the consequence of the
inaccuracy of the equations of GTR. CTG predicts the difference in the
velocities of the spacecrafts, moving with the engines turned off and
decelerated by the attraction of the Sun, is of the order of several cm/s as
compared with the results of GTR in the Solar system limits. This difference in
the velocities, probably also manifested as a flyby
anomaly, [37] apparently creates the Pioneer
anomaly.
Spacetime
The concept of space-time in CTG is consistent with
the idea of scale dimension which determines the
location of cosmic objects on the scale axis, and to the Theory of Infinite Hierarchical Nesting of Matter.
At each basic matter level we can consider its proper gravitation (the examples
are the strong gravitation at the level
of atoms and the ordinary gravitation at the stars), and its proper spacetime,
and the rate of time at the lowest levels of matter increases. Due to SPФ symmetry, the equations of physics
remain the same if in the transition from one matter level to another, we shall
make in them the corresponding transformations of such physical quantities, as
mass, size and velocity. From this the relativity of spacetime follows, not
only from the point of view of the method of determining its properties by
definite measuring procedures, but also as the consequence of the location of
the reference frame on the scale ladder of matter.
Astrophysical applications
Due to GTR in astrophysics such notions have become
familiar as gravitational lensing and microlensing, detectors of gravitational
waves, black holes, cosmological theories of the Universe. The phenomena
associated with waves in CTG almost exactly coincide with their description in
GTR. This concerns gravitational lensing, as the consequence of the deflection
of light beams from the distant source by some intermediate massive object
located in the way of the beams. However, the interpretation of black holes and
cosmological theories in CTG is different from the standard approach.
Black holes
Main source: Black
hole
The most complete picture of black holes has been
developed in GTR. In this theory the proper gravitational field of the body
usually is not involved in determining the metric, the metric as the object of
geometric form defines gravitation and the gravitational force is the result of
the spacetime geometry. However, the question – why and how does the massive
body change the spacetime away from it – can not be answered by GTR. It is
common for GTR and the Newtonian gravitational model – in the latter the cause
of gravitation is also unknown, although there is its description as the
formula for the force. As a result, in GTR neither the maximum possible degree
of spacetime curvature actually realized in the nature is known, nor, accordingly, the maximum gravitational force that would be capable of turning a
star into a black hole is known.
If we assume that the speed of light is the limiting
speed of propagation of interactions, then this speed corresponds to the rest
energy of each body, which is also proportional to body mass (see the
mass–energy equivalence). Theoretically, in the formation of a black hole the
mass-energy of its constituent matter should substantially decrease due to the
contribution of the negative mass-energy of the gravitational field of the
black hole. GTR predicts for black holes the so-called event horizon and the singularity
of spacetime. It is assumed that the matter or emission, which are under the
horizon of the black hole, can not get outside of the horizon and must somehow
move inside the hole at relativistic velocities. From outside the black hole
must look as an all-absorbing dark object with the strong gravitational field.
In
CTG the description of objects with the gravitational field is made based on
the modernized Le Sage's theory of gravitation, in
which gravitation is generated by the fluxes of gravitons, penetrating all
bodies. The calculations allow us to deduce Newton's gravitational formula and
to estimate the spatial energy density of the fluxes of gravitons and their
penetrating ability in the matter. [1] [5] It becomes possible to understand
the origin of mass and inertia of a body, since the mass can be expressed
through the power of the energy flux of gravitons, interacting with the matter
of the body. [38] [39] [40]
As gravitons the relativistic particles, photons and
neutrinos are assumed, generated by the matter at the lower scale levels of
matter. [41] This is consistent with the essence of the Theory
of Infinite Hierarchical Nesting of Matter
and electrogravitational vacuum,
according to which the objects similar to stars, white dwarfs and neutron
stars, create various relativistic particles and emissions at the same level of
matter, and these particles and emissions with sufficiently high density of
their energy lead to clustering and compression of the matter at a higher scale
level. Thus gravitons as the field quanta from the
scattered matter generate new compact objects, which in turn become the sources
of new, more powerful field quanta. In this process the density of gravitational
energy, achieved in material objects, decreases during the transition to more
massive objects. In the described picture there is no place for black holes in
the traditional sense. Here are some arguments against black holes:
- In models of neutron stars between
the nucleons (the main part of which is made up of neutrons) there are
short intervals, so that the nucleons remain to be independent particles
and behave almost the same as in atomic nuclei. However, the radii of
black holes of stellar masses must be several times smaller than the sizes
of neutron stars. In this case the nucleons must merge with each other,
and the binding energy of a black hole per one nucleon must be close to
the binding energy of a free nucleon (this follows from the approximate
equality of the gravitational energy of the black holes and the
mass-energy of its matter). For the transition of the matter into the
state of a black hole this transition must be quick enough, like a
supernova explosion in the formation of neutron stars, in order to
overcome the nuclear forces of repulsion between the nucleons of the
matter. However, the experiments with even the most energetic nucleon
beams do not lead to the formation of objects of the type of black holes,
only various elementary particles are formed. Consequently, for the
emergence of black holes it is necessary that the force of gravitation
must overcome the nuclear forces. In GTR the essence of gravitation is not
revealed, nor is the maximum gravitational force found, so the conclusion
of GTR about the black holes is hypothetical. From the point of view of
the Theory of Infinite Hierarchical Nesting of Matter, the analogues of
nucleons at the stellar level of matter are neutron stars, the collisions
of which, like the collisions of nucleons in accelerators, can not lead to
the formation of a black hole. This is the consequence of the significant
excess of the nuclear forces between the nucleons of the neutron star over
the forces of ordinary gravitation. In the gravitational
model of strong interaction
one of the components of the nuclear forces is strong gravitation, binding the
matter of elementary particles. [6] The
range of action of strong gravitation in the matter is small and at large
distances the ordinary gravitation dominates (due to the differences in
the properties of gravitons of strong gravitation and gravitons of
ordinary gravitation). Because of the excess energy density of the strong
gravitation over the energy density of ordinary gravitation the latter can
not transfer to the matter by means of the pressure from the fluxes of
gravitons enough energy for transition into the state of the black hole.
- If we assume that black holes are
the objects absorbing the matter and emission, and not releasing anything
out, then in the Theory of Infinite Hierarchical Nesting of Matter such
objects must exist at all scale levels. In Le Sage's theory, gravitons are various
relativistic particles and field quanta arising in the processes of
transformation of the matter of compact objects of the type of stars, and
in the interaction of these objects with each other and with the scattered
matter. Since the similar processes at lower scale levels take less time,
then black holes at these levels would long ago have absorbed all the
surrounding matter and emission. Then we would observe neither
relativistic particles nor gravitons, nor the phenomenon of gravitation as
such. Thus the existence of black holes at the
lower scale levels contradicts their formation at the higher scale levels
of matter.
- At each scale level of matter only
one the densest gravitationally bound object can exist which has the
highest energy density of the gravitational field. For elementary
particles such object is the proton, the stability of which, including the
mass is estimated by a period of not less than 1021 years. For
the level of stars such an object is assumed to be the neutron star
(magnetar). If the matter fell on such objects, part of its energy would
be emitted by the electromagnetic and gravitational waves, and the rest
part of the mass-energy and matter would be emitted after the fall while
hitting the surface and in thermonuclear flashes. This allows these objects to
maintain long-term constancy of their mass. If the proton were a black
hole, it would absorb mass and energy in case if the matter fell on it and
would not have constant mass. This fact speaks against the existence of
black holes.
- In GTR black holes as the
manifestation of spacetime singularities mean that they do not use the
field equations and the known laws of nature. If the theory admits the
existence of such objects and can not describe it, it shows either the
drawback of GTR as the complete physical theory, or its contradictoriness.
- There are a number of
observational data that do not conform to the idea of black holes. For
example, the progenitor of the neutron star CXO J164710.2-455216 is
assumed a very massive star with the mass of about 40 solar masses. [42] Previously it was assumed that such massive
stars obligatorily generate black holes at the end of their evolution. It
was expected that in the globular cluster Omega Centauri there is a black
hole with intermediate mass but after verification of the data its
presence became unnecessary. [43]
- There are more than a dozen
massive relativistic objects, X-ray sources, which are not identified as
neutron stars. The masses of these sources range from 2.5 solar masses for
the XN Per to 18 solar masses for Cyg X-1. [44]
According to one version, the relativistic objects in X-ray sources are
black holes. But there is another point of view, according to which in
these cases there are composite objects of neutron stars similar to atomic
nuclei. We can explain by clusters of neutron stars the phenomena in the
central parts of galaxies, attributed to black holes of large masses.
Cosmology
In the present time the main cosmological models are the models
arising from the equations for the metric in GTR. As a rule
it is considered that the Universe is expanding after the Big Bang which
happened in the past, and the galaxies scatter from each other. Cosmological
theories are meant to describe the known experimental facts, such as the
redshift of the spectra of distant galaxies, homogeneity, isotropy and almost
exact Euclidean character of cosmic space and of the distribution of matter on
large scales, the distribution of concentrations of chemical elements in cosmos
and the nucleosynthesis, the structure and the forms of large galactic systems,
the isotropic cosmic microwave background radiation, the existence of dark
matter, etc.
In CTG the cosmological theories on the basis of GTR are
treated critically. In view of the Theory of Infinite Hierarchical Nesting of
Matter and the Le Sage's theory of gravitation, the Universe can be assumed
consisting of hierarchically related scale levels of matter. The observed part
of the Universe, called the Metagalaxy, according to the similarity of matter levels and the SPФ symmetry is similar in size and mass
to one of the objects of the metagalactic level of matter. At different scale
levels of matter the gravitational quanta and gravitational fields can act
which are different in energy density, penetrability and range of action. In
this case, applying the conclusions of GTR with respect to ordinary gravitation
to the supposedly homogeneous and infinite Universe is wrongful. Outside the
Metagalaxy we can expect voids in the distribution of matter, stretching up to
other similar objects. As for the experimental observations such as the
redshift of the spectra of distant galaxies or the background microwave
radiation, for all of them there are other explanations. For example, the
redshift and the Hubble constant can be connected with the absorption of the
energy of photons during their propagation in cosmological space. [6] [45] It is known that in the Big Bang theory the initial state of the Universe
is assumed the singularity of spacetime. Then GTR must explain not only the
emergence of the hypothetical state of singularity, but the reason for its
explosive instability. For the complete and self-consistent explanation of this
problem in GTR quantum gravitation is considered necessary, which has not yet
been properly developed. In contrast to this in CTG neither black holes nor
singularities are required, which removes a number of problems in cosmology.
In the derivation of the equations of CTG from the
principle of least action we managed to show that the cosmological constant up
to a constant factor determines the mass-energy density of the matter in the
Universe, without taking into account the contribution of mass-energy of the
macroscopic gravitational and electromagnetic fields. This means that the
cosmological constant depends only on the fundamental microscopic fields acting
at the level of elementary particles. [22]
Problem of mass
According to the principle of equivalence of mass and energy, the inertial mass of an isolated object at rest can be found
through the energies of the matter and field associated with this object. To do
this in GTR it is necessary to sum all kinds of energy, including the rest
energy of matter, its internal energy and the energy of fields both inside and
outside the object. The sum of all the energies gives the relativistic energy,
which must be equal to the product of the object inertial mass and the squared speed of light. As
the mass density of the object increases due to reduction of the volume under
the influence of gravitation, the gravitational energy becomes more negative,
which according to GTR reduces both the relativistic energy and the mass of the
object, while the gravitational mass is
equal to inertial mass.
Thus, the star must be less massive than the sum of the masses of all the
particles of which it consists.
In contrast to GTR, in CTG
the other conclusions are made. This
follows from the fact that the gravitational energy must be part of the
relativistic energy with the negative sign due to the energy of matter in the
potentials of field, and with the positive sign in relation to the energy of
the field associated with field strengths. Are taken into account even the
energy of matter in the acceleration field,
in the pressure field and in the
electromagnetic field and the energies of these fields. [46]
As a result
there is a difference between the gravitational mass and the inertial mass of
the system, so that the gravitational mass exceeds the inertial mass.
Considering the
relativistic energy for the case of spherically symmetrical collapse leads to
four types of mass.
Gravitational mass ![]() is obtained equal to the mass
is obtained equal to the mass ![]() , calculated as volume integral of product of invariant
mass density and Lorentz factor. Inertial mass of the system taking into account the
particles and fields is
, calculated as volume integral of product of invariant
mass density and Lorentz factor. Inertial mass of the system taking into account the
particles and fields is ![]() , and the fourth mass
, and the fourth mass ![]() is found from the condition of the
absence in the matter of the energy of macroscopic fields, and is obtained, for
example, after sputtering of matter, and removing it to infinity. With this
mass ratio is:
is found from the condition of the
absence in the matter of the energy of macroscopic fields, and is obtained, for
example, after sputtering of matter, and removing it to infinity. With this
mass ratio is: ![]()
In GTR, the mass of the system on the
principle of equivalence is equal to the gravitational mass, and for the mass
ratio another expression obtained: ![]()
The article [47]
shows that in
CTG the relativistic uniform system with continuous matter
distribution is characterized by five types of mass: the gauge mass ![]() is related to the cosmological
constant and represents the mass-energy of matter’s particles in
four-potentials of the system’s fields; the inertial mass
is related to the cosmological
constant and represents the mass-energy of matter’s particles in
four-potentials of the system’s fields; the inertial mass ![]() ; the auxiliary mass
; the auxiliary mass ![]() is equal to the product of the
particles’ invariant mass density by the volume of the system. The relation for these masses
is as follows:
is equal to the product of the
particles’ invariant mass density by the volume of the system. The relation for these masses
is as follows:
![]()
At the same time, the energy of a physical
system, calculated at the center of the system's momenta, determines the
invariant inertial mass ![]() of the system. [29] ] The square of this mass, multiplied
by the square of the speed of light, is equal to the square of four-momentum of
the system.
of the system. [29] ] The square of this mass, multiplied
by the square of the speed of light, is equal to the square of four-momentum of
the system.
Relativistic uniform
system
Main source: Relativistic uniform system
In the gravitationally-bound uniform
system, in the framework of CTG, we managed to calculate precisely the kinetic
energy of particles and to find the difference from the classical virial
theorem, taking into account the vector pressure field,
acceleration
field and electromagnetic field. [48] In
particular, the ratio of the kinetic energy to the energy of the forces, acting
on the particles, turned out to be equal to 0.6 instead of 0.5 in the classical
case. Moreover, it was proved that in the equation of motion the material
derivative should be used, because the velocity of typical particles turned out to be the function of
spatial coordinates.
An analysis of the integral theorem of generalized virial allows us to find
formulas for the radial component of the velocity of typical particles of the
system and for their root-mean-square speed, without using the notion of
temperature. [49] The relation between the
theorem and the cosmological constant, characterizing the physical system under
consideration, is shown. The difference is explained between the kinetic energy
and the energy of motion, the value of which is equal to half the sum of the
Lagrangian and the Hamiltonian.
The model allows us to estimate the particles’
velocity ![]() at the center of the sphere, the
corresponding Lorentz factor
at the center of the sphere, the
corresponding Lorentz factor ![]() , the scalar potential
, the scalar potential ![]() of the pressure field; to find the
relationship between the field coefficients; to express the dependences of the
scalar curvature and the cosmological constant in the matter as functions of
the parameters of typical particles and field potentials. [12] Besides, comparison of the cosmological
constants inside a proton, a neutron star and in the observable Universe allows
us to explain the problem of the cosmological constant arising in the
Lambda-CDM model.
of the pressure field; to find the
relationship between the field coefficients; to express the dependences of the
scalar curvature and the cosmological constant in the matter as functions of
the parameters of typical particles and field potentials. [12] Besides, comparison of the cosmological
constants inside a proton, a neutron star and in the observable Universe allows
us to explain the problem of the cosmological constant arising in the
Lambda-CDM model.
In article, [50] covariant formulas are
derived for such additive integrals of system motion as momentum, energy,
four-momentum, angular momentum, pseudo-tensor of angular momentum, and also
for radius-vector of center of the system momentum. In a closed system, the
integrals of motion are preserved, and the center of momentum moves at a
constant speed. The difference between the four-momentum and the integral
vector, obtained by integrating equation of motion through the stress-energy tensors of fields, is shown. This difference is
associated with the difference of particles and fields as such.
With the help of the covariant theory of gravitation
the total energy, binding energy, energy of fields, pressure energy and the
potential energy of the system consisting of particles and four fields is
precisely calculated in the relativistic uniform model. [51] A noticeable difference is shown between the
obtained results and the relations for simple systems in classical mechanics,
in which the acceleration field and pressure field are not taken into account
or the pressure is considered to be a simple scalar quantity. In this case the
inertial mass of the massive system is less than the total inertial mass of the
system’s parts.
The proton, neutron star and observable Universe are very close in their
properties to the relativistic uniform system. At the same time, they are
extremal objects in the sense that their gravitational field significantly
deviates from the form prescribed by the classical uniform system. [52] For a neutron star, this allows us to find the Lorentz factor for the
motion of matter in the center of the star, equal to 1.04. Similarly, for the
proton, the Lorentz factor in the center is 1.9. Analysis of the formula for
the gravitational field allows us to explain the weakening of the field at the
boundaries of the Metagalaxy, which manifests itself in the large-scale
cellular structure of the Universe.
In a relativistic uniform system, the exact values of
the strengths and potentials of all active fields are known. [53] This allows us to check
the field energy theorem for such a
system and verify the theorem. [18] This
theorem explains, in particular, why electrostatic energy can be calculated
either through the field strength, included in the electromagnetic field
tensor, or in another way, through the field potential.
Model of gravitational
equilibrium
This model is used to describe the
internal parameters of such cosmic objects as planets and stars. In contrast to
the polytropic model, relating the pressure and density by means of a certain
assumed power law, the model of gravitational equilibrium is the consequence of
the equations of the gravitational field, pressure field, acceleration field,
electromagnetic field and other fields, acting in the matter. The approach
under consideration allows us to find the distribution of the internal
pressure, temperature, and other parameters. [54] The acceleration
field coefficient η and the
pressure field coefficient σ are
the functions of the state of matter, and their sum is close in magnitude to
the gravitational constant G. For
macroscopic objects the gravitational field is the main component of the general
field. [55] [15]
Navier-Stokes equation
The phenomenological Navier-Stokes equation describes the
motion of the viscous fluid with regard to the dissipation field.
The gravitational and electromagnetic fields are included in this equation,
providing the so-called mass terms in the expressions for the acting forces. It
is possible to derive the Navier-Stokes equation in a covariant way, taking
into account the acceleration field and
the equation of the matter’s motion in the CTG. [14]
The viscosity effect is described in
this approach by the 4-potential of the field of energy dissipation, dissipation
field tensor and dissipation stress-energy
tensor. A complete set of equations is presented, which
suffices to solve the problem of motion of viscous compressible and charged
fluid in the gravitational and electromagnetic fields.
Comparison of CTG with
general theory of relativity
Due to difference in representation of gravitational
field in the covariant theory of gravitation (CTG) and general theory of
relativity (GTR), the two theories treat gravitational force and gravitational
energy differently. In CTG, density of gravitational four-force is calculated either through the gravitational
tensor or the gravitational stress-energy tensor. These
tensors contribute to both the relativistic energy and inertial mass of a
physical system.
In contrast, in GTR, the gravitational four-force and gravitational four-acceleration are equal to zero, and gravitational effects are associated with the
metric tensor of spacetime and derivatives of this tensor's components with
respect to coordinates and time. As a result, the energy of gravitational field
cannot be calculated precisely in GTR; various types of pseudotensors are
proposed to estimate this energy.
The aim of the article [56] is to
analyze the foundations of general relativity, including derivation of
equations of GTR from the principle of least action. The article concludes that
GTR can be refined if vector fields, such as acceleration
field and pressure field, are used in it instead of
scalar fields. In addition, the article provides formulas with which one can
estimate the energy and momentum of a system in GTR, taking into account
contribution from the gravitational field.
References
- 1.0 1.1 1.2 Fedosin
S.G. Fizika i filosofiia podobiia ot preonov do metagalaktik, Perm, pages 544, 1999. ISBN 5-8131-0012-1.
- Fedosin S.G. Sovremennye problemy fiziki: v poiskakh novykh printsipov. Moskva:
Editorial URSS, 2002, 192 pages. ISBN 5-8360-0435-8.
- Fedosin S.G. Electromagnetic and Gravitational Pictures of the World. Apeiron, Vol. 14, No. 4, pp. 385-413 (2007). http://dx.doi.org/10.5281/zenodo.891124.
- Fedosin S.G. Mass, Momentum and Energy of Gravitational Field. Journal of Vectorial Relativity, Vol. 3, No. 3, pp.30-35
(2008). http://dx.doi.org/10.5281/zenodo.890899.
- :5.0 5.1 Fedosin
S.G. Model of Gravitational Interaction in the Concept of Gravitons. Journal of Vectorial Relativity, Vol. 4, No. 1, pp. 1-24
(2009). http://dx.doi.org/10.5281/zenodo.890886.
- 6.0 6.1 6.2 6.3 6.4 6.5 6.6 6.7 Fedosin
S.G. Fizicheskie teorii i beskonechnaia vlozhennost’ materii. – Perm, 2009, 844 pages, Tabl. 21, Pic. 41, Ref. 289. ISBN 978-5-9901951-1-0. (in Russian).
- 7.0 7.1 Fedosin
S.G. The Metric Outside a Fixed Charged Body in the Covariant Theory of
Gravitation. International Frontier Science Letters, Vol. 1, No. 1 , pp. 41-46 (2014). http://dx.doi.org/10.18052/www.scipress.com/ifsl.1.41.
- 8.0 8.1 Fedosin
S.G. The relativistic uniform model: the metric
of the covariant theory of gravitation inside a body, St. Petersburg Polytechnical State University Journal. Physics
and Mathematics, Vol. 14, No. 3, pp.168-184 (2021). http://dx.doi.org/10.18721/JPM.14313. arXiv 2110.00342. Bibcode 2021arXiv211000342F.
- Sergey Fedosin, The physical theories and
infinite hierarchical nesting of matter,
Volume 2, LAP LAMBERT Academic Publishing, pages: 420, ISBN-13:
978-3-659-71511-2. (2015).
- 10.0 10.1 10.2 Fedosin
S.G. Lagrangian formalism in the theory of relativistic vector fields.
International Journal of Modern Physics A, Vol. 40, No. 02, 2450163
(2025). https://doi.org/10.1142/S0217751X2450163X.
- 11.0 11.1 11.2 Fedosin
S.G. About the cosmological
constant, acceleration field, pressure field and energy. Jordan Journal of Physics. Vol. 9, No. 1, pp. 1-30,
(2016). http://dx.doi.org/10.5281/zenodo.889304.
- 12.0 12.1 Fedosin
S.G. Energy and metric gauging in the covariant theory of gravitation.
Aksaray University Journal of Science and Engineering, Vol. 2, Issue 2,
pp. 127-143 (2018). http://dx.doi.org/10.29002/asujse.433947.
- Fedosin S.G. Equations of Motion in the
Theory of Relativistic Vector Fields. International Letters of Chemistry,
Physics and Astronomy, Vol. 83, pp. 12-30 (2019). https://doi.org/10.18052/www.scipress.com/ILCPA.83.12.
- 14.0 14.1 Fedosin S.G. Four-Dimensional Equation
of Motion for Viscous Compressible and Charged Fluid with Regard to the
Acceleration Field, Pressure Field and Dissipation Field. International
Journal of Thermodynamics. Vol. 18, No. 1, pp. 13-24 (2015). http://dx.doi.org/10.5541/ijot.5000034003.
- 15.0 15.1 Fedosin
S.G. Two components of the macroscopic general field. Reports in Advances
of Physical Sciences, Vol. 1, No. 2, 1750002, 9 pages (2017). http://dx.doi.org/10.1142/S2424942417500025.
- Comments to the book: Fedosin S.G. Fizicheskie teorii i beskonechnaia vlozhennost’
materii. – Perm, 2009, 844 pages. ISBN 978-5-9901951-1-0. (in Russian).
- Fedosin S.G. The General Theory of Relativity, Metric Theory of Relativity and
Covariant Theory of Gravitation: Axiomatization and Critical Analysis. International Journal of Theoretical and Applied Physics
(IJTAP), Vol.4, No. I, pp. 9-26 (2014). http://dx.doi.org/10.5281/zenodo.890781.
- 18.0 18.1 Fedosin
S.G. The Integral Theorem of the Field Energy. Gazi University Journal of Science. Vol. 32, No. 2, pp.
686-703 (2019). http://dx.doi.org/10.5281/zenodo.3252783.
- Fedosin S.G. The generalized Poynting
theorem for the general field and solution of the 4/3 problem.
International Frontier Science Letters, Vol. 14, pp. 19-40 (2019). https://doi.org/10.18052/www.scipress.com/IFSL.14.19.
- I. V. Meshchersky ("Dynamics of a
point of variable mass," IV Meshchersky, St. Petersburg., 1897). Мещерский И.В. Соч.:
Работы по механике переменной массы, 2 изд., М., 1952.
- Gorelik, Gennady. The Problem of Conservation and
the Poincare Quasigroup in General Relativity.
- 22.0 22.1 Fedosin
S.G. The Principle of Least Action in Covariant Theory of Gravitation. Hadronic Journal, Vol. 35, No. 1, pp. 35-70 (2012). http://dx.doi.org/10.5281/zenodo.889804.
- Borodikhin V.N. Vector theory of gravity.
Gravit. Cosmol. Vol. 17, pp. 161-165 (2011). https://doi.org/10.1134/S0202289311020071.
- Behera H., Barik N. Attractive
Heaviside-Maxwellian (Vector) Gravity from Special Relativity and Quantum
Field Theory. arXiv: 1709.06876v2. (2017).
- Fedosin S.G. The Hamiltonian in Covariant Theory of Gravitation. Advances in Natural Science, Vol. 5, No. 4, pp. 55-75
(2012). http://dx.doi.org/10.3968%2Fj.ans.1715787020120504.2023.
- B. S. DeWitt, Superconductors and
gravitational drag. Phys. Rev. Lett., Vol. 24, 1092–3 (1966).
- G. Papini, Particle wave functions in weak
gravitational fields. Nuovo Cimento B, Vol.v52, 136–41 (1967).
- M.A. Hohensee, B. Estey, P. Hamilton, A.
Zeilinger, and H. M¨uller, Force-free gravitational redshift: Proposed
gravitational Aharonov-Bohm experiment, Phys. Rev. Lett. 108, 230404
(2012). doi: 10.1103/PhysRevLett.108.230404.
- 29.0 29.1 Fedosin
S.G. What should we understand by the four-momentum of physical system?
Physica Scripta, Vol. 99, No. 5, 055034 (2024). https://doi.org/10.1088/1402-4896/ad3b45.
- Fedosin S.G. Generalized Four-momentum for
Continuously Distributed Materials. Gazi University Journal of Science,
Vol. 37, Issue 3, pp. 1509-1538 (2024). https://doi.org/10.35378/gujs.1231793.
- Weisberg J., Taylor J. Relativistic Binary
Pulsar B1913+16: Thirty Years of Observation and Analysis. / Binary Radio
Pulsars. ASP Conference Series, Vol. TBD, 2004, Rasio F. A., Stairs I. H.
(eds.) // arXiv: astro-ph/0407149.
- Yi Mao , Max
Tegmark, Alan Guth, Serkan Cabi. Constraining Torsion with Gravity Probe B, arXiv:gr-qc/0608121v45, Phys. Rev. D. 76, 104029, 2007.
- Newman E.T., Couch E., Chinnapared K.,
Exton A., Prakash A., Torrence Д. // Journ. Math. Phys., 1965,
Vol. 6, P. 918.
- Reissner H. – Ann. d .
Phys., 1916, Bd 50, S. 106.
- Straumann N. General Relativity and
relativistic Astrophysics. – Springer-Verlag, Berlin, Heidelberg, New
York, 1991.
- Fedosin S.G. The Pioneer Anomaly in
Covariant Theory of Gravitation. Canadian
Journal of Physics, Vol. 93, no. 11, P. 1335-1342 (2015). http://dx.doi.org/10.1139/cjp-2015-0134.
- Anderson J.D., Campbell J.K. and Nieto M.M.
The Energy Transfer Process in Planetary Flybys // New Astronomy, 2007,
Vol. 12, P. 383–397. – arXiv:astro-ph/0608087.
- Fedosin S.G. The graviton field as the source of mass and gravitational force in
the modernized Le Sage’s model. Physical
Science International Journal, Vol. 8, Issue 4, pp. 1-18 (2015). http://dx.doi.org/10.9734/PSIJ/2015/22197.
- Fedosin S.G. The force vacuum field as an alternative
to the ether and quantum vacuum.
WSEAS Transactions on Applied and Theoretical Mechanics, Vol. 10, Art. #3,
pp. 31-38 (2015). http://dx.doi.org/10.5281/zenodo.888979.
- Fedosin S.G. The charged component of the
vacuum field as the source of electric force in the modernized Le Sage’s
model. Journal of Fundamental and
Applied Sciences, Vol. 8, No. 3, pp. 971-1020 (2016). http://dx.doi.org/10.4314/jfas.v8i3.18, https://dx.doi.org/10.5281/zenodo.845357.
- Fedosin S.G. On the structure of the force field in
electro gravitational vacuum.
Canadian Journal of Pure and Applied Sciences, Vol. 15, No. 1, pp.
5125-5131 (2021). http://doi.org/10.5281/zenodo.4515206.
- Muno M. P. at al. A Neutron Star with a Massive Progenitor
in Westerlund 1. – arXiv: astro-ph / 0509408
v3, 26 Jan 2006.
- Jay Anderson, Roeland P. van der Marel. New
Limits on an Intermediate Mass Black Hole in Omega Centauri: I. Hubble
Space Telescope Photometry and Proper Motions. - arxiv:0905.0627.
- Черепащук А.М. Чёрные дыры в двойных звёздных системах.
– в книге «Современное естествознание. Физика элементарных частиц.
Астрофизика». М.: Магистр-пресс, 2000, стр. 228–233.
- Fedosin S.G. Cosmic Red Shift, Microwave Background, and New Particles. Galilean Electrodynamics, Vol. 23, Special Issues No. 1, pp.
3-13 (2012). http://dx.doi.org/10.5281/zenodo.890806.
- Fedosin S.G. Relativistic Energy and Mass in
the Weak Field Limit. Jordan Journal of
Physics. Vol. 8, No. 1, pp. 1-16 (2015). http://dx.doi.org/10.5281/zenodo.889210.
- Fedosin S.G. The Mass Hierarchy in the
Relativistic Uniform System.
Bulletin of Pure and Applied Sciences, Vol. 38 D (Physics), No. 2, pp.
73-80 (2019). http://dx.doi.org/10.5958/2320-3218.2019.00012.5.
- Fedosin S.G. The virial theorem and the kinetic energy
of particles of a macroscopic system in the general field concept. Continuum Mechanics and Thermodynamics, Vol. 29, Issue 2, pp.
361-371 (2017). https://dx.doi.org/10.1007/s00161-016-0536-8.
- Fedosin S.G. The integral theorem of
generalized virial in the relativistic uniform model. Continuum Mechanics and Thermodynamics, Vol. 31, Issue 3, pp.
627-638 (2019). https://dx.doi.org/10.1007/s00161-018-0715-x.
- Fedosin S.G. The covariant additive
integrals of motion in the theory of relativistic vector fields. Bulletin of Pure and Applied Sciences, Vol. 37 D (Physics), No.
2, pp. 64-87 (2018). http://dx.doi.org/10.5958/2320-3218.2018.00013.1.
- Fedosin S.G. The binding energy and the
total energy of a macroscopic body in the relativistic uniform model.
Middle East Journal of Science, Vol. 5, Issue 1, pp. 46-62 (2019). http://dx.doi.org/10.23884/mejs.2019.5.1.06.
- Fedosin S.G. The Gravitational Field in the
Relativistic Uniform Model within the Framework of the Covariant Theory of
Gravitation. International Letters of Chemistry, Physics and Astronomy,
Vol. 78, pp. 39-50 (2018). http://dx.doi.org/10.18052/www.scipress.com/ILCPA.78.39.
- Fedosin S.G. The potentials of the acceleration field and pressure field in
rotating relativistic uniform system.
Continuum Mechanics and Thermodynamics, Vol. 33, Issue 3, pp. 817-834
(2021). https://doi.org/10.1007/s00161-020-00960-7.
- Fedosin S.G. Estimation of the physical
parameters of planets and stars in the gravitational equilibrium model.
Canadian Journal of Physics, Vol. 94, No. 4, pp. 370-379 (2016). http://dx.doi.org/10.1139/cjp-2015-0593.
- Fedosin S.G. The Concept of the General Force Vector
Field. OALib Journal, Vol. 3, pp.
1-15 (2016), e2459. http://dx.doi.org/10.4236/oalib.1102459.
- Fedosin S.G. Comparison of tensor and vector theories
of gravitation. Iranian Journal of Physics
Research, (2025). Articles in Press, Accepted Manuscript, Available Online
from 29 June 2025. https://ijpr.iut.ac.ir/article_3636_5f5bc9308ee52ff299b3b3a67df63b3f.pdf.
See also
External links
|
Theories of
gravitation |
|||||
|
|||||