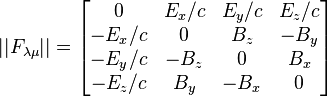Four-force

Four-force (4-force) is a four-vector, considered as a relativistic generalization of classical 3-vector of force to the four-dimensional spacetime. As in classical mechanics, the 4-force can be defined in two ways. The first one measures the change in energy and momentum of a particle per unit of proper time. The second method introduces force characteristics – strengths of field, and with their help in certain energy and momentum of the particle is calculated 4-force acting on the particle in the field. The equality of 4-forces produced by these methods, gives the equation of motion of the particle in given force field.

In special relativity 4-force is derivative of 4-momentum $~ p^\lambda$ with respect to the proper time $~ \tau$ of a particle: ^[1]

$~F^\lambda = \frac{dp^\lambda }{d\tau}. \qquad\qquad (1)$

For a particle with constant invariant mass m > 0, $~ p^\lambda = m u^\lambda$ , where $~ u^\lambda$ is 4-velocity. This allows connecting 4-force with four-acceleration $~ a^\lambda$ similarly to Newton's second law:

$~F^\lambda = m a^\lambda$ ,

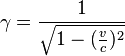Given $~ \mathbf{v}$ is the classic 3-vector of particle velocity; $~ \gamma = \frac{1}{\sqrt{1-(\frac{v}{c})^2}}$ is Lorentz factor;

$||F^\lambda ||=\left(\gamma \frac{\mathbf{F}\cdot \mathbf{v}}{c} , \gamma \mathbf{F} \right)$ ,

$~{\mathbf {F}}={d \over dt} \left(\gamma m {\mathbf {v}} \right)={d\mathbf{p} \over dt}= \gamma m\left(\mathbf{a} +\gamma^2 \frac{\left(\mathbf{v} \cdot \mathbf{a} \right)}{c^2}\mathbf{v}\right)= m \gamma^3 \left( \mathbf{a} + \frac {\mathbf{v} \times [ \mathbf{v} \times \mathbf {a}] } {c^2} \right)$

where $~{{\mathbf {F}}}$ is 3-vector of force, ^[2]

$~ \mathbf{p}$ is t 3-vector of relativistic momentum, $~ \mathbf{a}= \frac {d \mathbf{v}}{dt}$ is 3-acceleration,

$~\mathbf{F}\cdot\mathbf{v}={d \over dt} \left(\gamma m c^2 \right)={dE \over dt}$ ,

is relativistic energy.

In general relativity, the 4-force is determined by covariant derivative of 4-momentum with respect to the proper time: ^[3]

$F^\lambda := \frac{Dp^\lambda }{D\tau} = \frac{dp^\lambda }{d\tau } + \Gamma^\lambda {}_{\mu \nu}U^\mu p^\nu$ ,

where $~ \Gamma^\lambda {}_{\mu \nu}$ are the Christoffel symbols.

1 Examples
2 Density of 4-force
3 Four-force in CTG
3.1 Components of 4-force density
3.2 Relationship with four-acceleration
4 See also
5 References
6 External links

Examples

4-force acting in electromagnetic field on a particle with electric charge , is expressed as follows:

$~ F_\lambda = q u^\mu F_{\lambda \mu}$ ,

where $~F_{\lambda \mu}$ is electromagnetic tensor,

$||F_{\lambda \mu }|| = \begin{bmatrix} 0 & E_x/c & E_y/c & E_z/c \\ -E_x/c & 0 & B_z & -B_y \\ -E_y/c & -B_z & 0 & B_x \\ -E_z/c & B_y & -B_x & 0 \end{bmatrix}$

is 4-velocity.

Density of 4-force

To describe liquid and extended media, in which we must find forces in different points in space, instead of 4-vector of force 4-vector of force density is used, acting locally on a small volume unit of the medium:

$~f^\lambda := \frac{dJ^\lambda }{d\tau}, \qquad\qquad (2)$

where $~ J^{\lambda} = \rho_0 u^{\lambda}$ is the mass 4-current, $~ \rho_0$ is the mass density in the rest reference frame relative to the matter.

In the special theory of relativity, the relations hold:

$~ ||u^\lambda || = \left(\gamma c, \gamma {\mathbf {v}}\right)$ ,

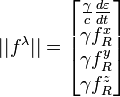$~||f^\lambda || = \begin{bmatrix} \frac{\gamma }{c} \frac{ d\varepsilon }{dt} \\ \gamma f_{R}^x \\ \gamma f_{R}^y \\ \gamma f_{R}^z \end{bmatrix}$ ,

where $~ \mathbf{ f } = {d \over dt} \left( \gamma \rho_0 \mathbf{ v } \right)={d \mathbf{J} \over dt}$ is 3-vector of force density, $~ \mathbf{J}$ is 3-vector of mass current, $~ \varepsilon = \gamma \rho_0 c^2$ is density of relativistic energy.

If we integrate (2) over the invariant volume of the matter unit, measured in the co-moving reference frame, we obtain the expression for 4-force (1):

$~\int {f^\lambda dV_0}= F^\lambda = \int {\frac{d(\rho_0 u^\lambda ) }{d\tau} dV_0} = \frac {d}{ d\tau } \int {\rho_0 u^\lambda dV_0} =\frac {d}{ d\tau } \int { u^\lambda d m } =\frac{dp^\lambda }{d\tau}.$

This formula and determination of the four-force density through the mass four-current $~J^{\lambda }$ when taking into account the fields acting in a system, require correction, since they do not contain an additional contribution from the four-momenta of the fields themselves. As was shown in the article, ^[4] instead of the four-force density (2) in a continuously distributed substance, one should consider the expression for generalized four-force density:

$~{\mathcal F}_{\mu }=-{\frac {\partial {\mathcal L}}{\partial x^{\mu }}}={\frac {d\wp _{\mu }}{d\tau }},$

where $~{\mathcal L}$ is Lagrangian, $~x^{\mu }$ are four-dimensional coordinates, $~\wp _{\mu }=-{\frac {\partial {\mathcal L}}{\partial u^{\mu }}}$ is density of generalized four-momentum.

If we take into account four vector fields in substance, such as electromagnetic and gravitational fields, acceleration field and pressure field, then the density of the generalized four-momentum will be equal to: ^[5]

$~\wp _{\mu }=\rho _{{0q}}A_{\mu }+\rho _{0}D_{\mu }+\rho _{0}U_{\mu }+\rho _{0}\pi _{\mu },$

where $~A_{\mu },D_{\mu },U_{\mu },\pi _{\mu }$ are 4-potentials of the electromagnetic and gravitational fields, acceleration field and pressure field, respectively.

Four-force in CTG

If s particle is in gravitational field, then according to the covariant theory of gravitation (CTG) gravitational 4-force equals:

$~ F^\nu = m \Phi^{\nu \mu} u_\mu = \Phi^{\nu \mu} p_\mu$ ,

where $~\Phi^{\nu \mu}$ is gravitational tensor, which is expressed through the gravitational field strength and gravitational torsion field, $~p_\mu$ is 4-momentum with lower (covariant) index, and particle mass includes contributions from mass-energy of fields associated with matter of the particle.

In CTG gravitational tensor with covariant indices $~ \Phi_ {rs}$ is determined directly, and for transition to the tensor with contravariant indices in the usual way the metric tensor is used which is in general a function of time and coordinates:

$~ \Phi^{\nu \mu}= g^{\nu r} g^{s \mu } \Phi_{rs} .$

Therefore the 4-force $~ F^\nu$ , which depends on the metric tensor through $~ \Phi^{\nu \mu}$ , also becomes a function of the metric. At the same time, definition of 4-force with covariant index does not require knowledge of the metric:

$~ F_\mu = m \Phi_{\mu \nu} u^\nu = \Phi_{\mu \nu} p^\nu.$

In covariant theory of gravitation 4-vector of force density is described with the help of acceleration field : ^[^6]^[7] ^[8]

$~ f_\alpha = \nabla_\beta {B_\alpha}^\beta = - u_{\alpha k} J^k = \rho_0 \frac {DU_\alpha }{D \tau}- J^k \nabla_\alpha U_k = \rho_0 \frac {dU_\alpha }{d \tau} - J^k \partial_\alpha U_k ,\qquad \qquad (3)$

where $~ {B_\alpha}^\beta$ is acceleration stress-energy tensor with mixed indices, $~ u_{\alpha k}$ is acceleration tensor, and the 4-potential of acceleration field is expressed in terms of the scalar potential $~ \vartheta$ and the vector potential $~ \mathbf {U}$ :

$~U_\alpha = \left(\frac {\vartheta }{c},- \mathbf {U} \right) .$

In expression (3) operator of proper-time-derivative $~\frac{ D } {d \tau }= U^\mu \nabla_\mu$ is used, which generalizes material derivative (substantial derivative) to curved spacetime. ^[2]

If there are only gravitational and electromagnetic forces and pressure force, then the following expression is valid:

$~f_\alpha = \Phi_{\alpha \mu } J^\mu + F_{\alpha \mu } j^\mu + f_{\alpha \mu } J^\mu = - \nabla_\mu \left( {U_\alpha }^\mu + {W_\alpha}^\mu + {P_\alpha}^\mu \right), \qquad \qquad (4)$

where $~ j^\mu = \rho_{0q} u^\mu$ is 4-vector of electromagnetic current density (4-current), $~\rho_{0q}$ is density of electric charge of matter unit in its rest reference frame, $~ f_{\alpha \mu }$ is pressure field tensor, $~ {U_\alpha }^\mu$ is gravitational stress-energy tensor, $~ {W_\alpha}^\mu$ is t electromagnetic stress-energy tensor, $~ {P_\alpha}^\mu$ is pressure stress-energy tensor.

In some cases, instead of the mass 4-current the quantity $~ h^\lambda = \rho u^\lambda$ is used, where $~\rho$ is density of moving matter in an arbitrary reference frame. The quantity $~h^{\lambda }$ is not a 4-vector, since the mass density is not an invariant quantity in coordinate transformations. After integrating over the moving volume of matter unit due to relations $~dm=\rho _{0}dV_{0}=\rho dV$ and $~dVdt=dV_{0}d\tau$ we obtain:

$~ \int {\frac {dh^\lambda}{ d\tau } dV}= \int {\frac{d(\rho u^\lambda ) }{d\tau} dV} = \frac {d}{ dt } \int {\rho u^\lambda dV_0}= \frac {d}{ dt } \int {\frac {dt}{ d\tau }u^\lambda dm}.$

For inertial reference systems in the last expression we can bring ${\frac {dt}{d\tau }}$ beyond the integral sign. This gives 4-force for these frames of reference:

$~ \frac {d}{ d\tau } \int {u^\lambda dm}= F^\lambda .$

However, in addition to the momentum of particles, moving matter also has momentum of field associated with matter, which requires a more general definition of four-momentum and four-force.

In general relativity, it is believed that stress-energy tensor of matter is determined by the expression $~ T^{\nu \lambda }= J^\nu u^\lambda$ , and for it $~ h^{\lambda} = \frac {T^{0 \lambda }}{c}$ , that is the quantity $~ h^\lambda = \rho u^\lambda$ consists of four timelike components of this tensor. The integral of these components over the moving volume gives respectively the energy (up to the constant, equal to ) and momentum of matter unit. However, such a solution is valid only in approximation of inertial motion, as shown above. In addition, according to findings in the article, ^[9] the integration of timelike components of stress-energy tensor for energy and momentum of a system in general is not true and leads to paradoxes such as the problem of 4/3 for gravitational and electromagnetic fields.

Instead of it, in covariant theory of gravitation 4-momentum containing the energy and momentum of a system is derived by variation of Lagrangian of the system and not from the stress-energy tensors.^[10]

Components of 4-force density

Expression (4) for 4-force density can be divided into two parts, one of which will describe the bulk density of energy capacity, and the other describe total force density of available fields.

In relation (4) we make a transformation:

$~ J^\mu = \rho_0 u^\mu = \rho_0 \frac {cdt}{ds} \frac {dx^\mu }{dt} = \rho \frac {dx^\mu }{dt} ,$

where denotes interval, is differential of coordinate time, $~ \rho= \rho_0 \frac {cdt}{ds}$ is mass density of moving matter, four-dimensional quantity $~ \frac {dx^\mu }{dt}=(c, \mathbf{v} )$ consists of the timelike component equal to the speed of light , and spatial component in the form of particle 3-velocity vector $~ \mathbf{v}$ .

Similarly, we write the charge 4-current through charge density of moving matter $~ \rho_{q}= \rho_{0q} \frac {cdt}{ds}$ :

$~ j^\mu = \rho_{0q} u^\mu = \rho_{0q} \frac {cdt}{ds} \frac {dx^\mu }{dt} = \rho_{q}\frac {dx^\mu }{dt}.$

In addition, we express the tensors through their components, that is, the corresponding 3-vectors of the field strengths. Then the timelike component of 4-force density with covariant index is:

$~ f_0 = \frac {1}{ c }( \rho \mathbf{\Gamma} \cdot \mathbf{v}+ \rho_{q} \mathbf{E} \cdot \mathbf{v}+\rho \mathbf{C} \cdot \mathbf{v} ) ,$

where $~ \mathbf{\Gamma}$ is gravitational field strength, $~ \mathbf{E}$ is electromagnetic field strength, $~ \mathbf{ C}$ is pressure field strength.

The spatial component of covariant 4-force is 3-vector $~ - \mathbf{f}$ , i.e. 4-force is

as $~ f_\lambda = (f_0{,} -f_x{,}-f_y{,}-f_z),$

wherein the 3-force density is:

$~ \mathbf{f}= \rho \mathbf{\Gamma}+ \rho [\mathbf{v} \times \mathbf{\Omega}] + \rho_{q}\mathbf{E}+ \rho_{q} [\mathbf{v} \times \mathbf{B}] + \rho \mathbf{C}+ \rho [\mathbf{v} \times \mathbf{I}],$

where $~ \mathbf{\Omega}$ is gravitational torsion field, $~ \mathbf{B}$ is magnetic field, $~ \mathbf{ I }$ is solenoidal vector of pressure field.

Expression for covariant density of 4-force can be written in terms of the components of acceleration tensor and covariant 4-acceleration. Similarly to (3) we have:

$~f_0 = - u_{0 k} J^k = - \frac {\rho }{ c } \mathbf{S} \cdot \mathbf{v},$

$~ \mathbf{f}= - \rho \mathbf{S} - \rho [\mathbf{v} \times \mathbf{N}] ,$

where $~ \mathbf{S}$ is acceleration field strength, $~ \mathbf{ N }$ is acceleration solenoidal vector.

Using expression for the 4-potential of accelerations field in terms of scalar potential and vector potential and definition of material derivative, from (3) and (4) for scalar and vector components of equation of motion, we obtain the following:

$~ \frac { d \vartheta }{dt} - \frac {dx^k }{dt} \frac {\partial U_k }{\partial t} = \mathbf{v}\cdot \nabla \vartheta + v_x \frac { \partial U_x}{\partial t} + v_y \frac { \partial U_y}{\partial t} + v_z \frac { \partial U_z}{\partial t} = - \mathbf{S} \cdot \mathbf{v}= \mathbf{\Gamma} \cdot \mathbf{v}+ \frac {\rho_{0q} }{\rho_0 } \mathbf{E} \cdot \mathbf{v}+ \mathbf{C} \cdot \mathbf{v} . \qquad (5)$

$~ \frac { d \mathbf {U} }{dt} + \nabla \vartheta - v_x \nabla U_x - v_y \nabla U_y - v_z \nabla U_z = - \mathbf{S} - [\mathbf{v} \times \mathbf{N}] = \mathbf{\Gamma }+ [\mathbf{v} \times \mathbf{\Omega}] + \frac {\rho_{0q} }{\rho_0 } (\mathbf{E}+ [\mathbf{v} \times \mathbf{B}] ) + \mathbf{C}+ [\mathbf{v} \times \mathbf{I}]. \qquad (6)$

Here are the components of vector potential $~ \mathbf {U}$ of acceleration field, are the components of velocity $~ \mathbf {v}$ of the element of matter or particle.

Equations of matter’s motion (5) and (6) are obtained in a covariant form and are valid in curved spacetime. On the left-hand side of these equations there are either potentials or strength and solenoidal vector of acceleration field. The right-hand side of the equations of motion is expressed in terms of strengths and solenoidal vectors of gravitational and electromagnetic fields, as well as pressure field inside the matter. Before solving these equations of motion, first it is convenient to find the potentials of all the fields with the help of corresponding wave equations. Next, taking four-curl of the fields’ four-potentials we can determine the strengths and the solenoidal vectors of all the fields. After substituting them in (5) and (6), it becomes possible to find relation between the field coefficients, express the acceleration field coefficient, and thus completely determine this field in matter.

Relationship with four-acceleration

Peculiarity of equations of motion (5) and (6) is that they do not have a direct relationship with the four-acceleration of matter particle under consideration. However, in some cases it is possible to determine e acceleration and velocity of motion, as well as dependence of distance traveled on time. The simplest example is rectilinear motion of a uniform solid particle in uniform external fields. In this case, the four-potential of acceleration field fully coincides with the four-velocity of the particle, so that the scalar potential $~ \vartheta = \gamma c^2$ , the vector potential $~ \mathbf {U}= \gamma \mathbf {v}$ , where $~ \gamma$ is Lorentz factor of the particle. Substituting the equality $~ U_\alpha = u_\alpha$ in (3) gives the following:

$~ \rho_0 \frac {dU_\alpha }{d \tau} = \rho_0 \frac {du_\alpha }{d \tau}= \rho_0 a_\alpha,$

$~ J^k \partial_\alpha U_k = \rho_0 u^k \partial_\alpha u_k =\frac {\rho_0 }{2} \partial_\alpha (u^k u_k) =\frac {\rho_0 }{2} \partial_\alpha c^2 =0,$

where $~ a_\alpha = \frac {du_\alpha }{d \tau}= u^\mu \partial_\mu u_\alpha$ is defined as the four-acceleration.

Then the equation for the four-acceleration of the particle follows from (3) and (4):

$~ a_\alpha = \Phi_{\alpha \mu } u^\mu + \frac {\rho_{0q} }{\rho_0 } F_{\alpha \mu } u^\mu + f_{\alpha \mu } u^\mu .$

After multiplying by the particle’s mass, this equation will correspond to equation (1) for the four-force.

In the considered case of motion of a solid particle, the four-acceleration with a covariant index can be expressed in terms of strength and solenoidal vector of acceleration field:

$~ a_\alpha = \frac {cdt}{ds}\left(-\frac {1}{c} \mathbf{S} \cdot \mathbf{v}{,} \qquad \mathbf{S}+[\mathbf{v} \times \mathbf{N}] \right).$

In special relativity 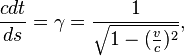$~ \frac {cdt}{ds}= \gamma = \frac{1}{\sqrt{1-(\frac{v}{c})^2}},$ and substituting the vectors $~ \mathbf{S}$ and $~ \mathbf{ N }$ for a particle, for the covariant 4-acceleration we obtain the standard expression:

$~ \mathbf {S} = - c^2 \nabla \gamma - \frac {\partial (\gamma \mathbf { v })}{\partial t},\qquad\qquad \mathbf {N} = \nabla \times (\gamma \mathbf { v }).$

$~ a_\alpha = \gamma \left( \frac {d(\gamma c)}{dt}{,} \qquad - \frac {d(\gamma \mathbf{v}) }{dt} \right).$

If the mass of the particle is constant, then for force acting on the particle, we can write:

$~ \mathbf F= \frac {d \mathbf p }{dt}= m \frac {d (\gamma \mathbf v )}{dt}= -m \left(\mathbf{S}+[\mathbf{v} \times \mathbf{N}] \right)= \nabla E + \frac {\partial \mathbf p }{\partial t} - \mathbf { v }\times [ \nabla \times \mathbf p ] ,$

where $~ E = \gamma m c^2$ is relativistic energy, $~ \mathbf p = \gamma m \mathbf v$ is 3-vector of relativistic momentum of the particle.

For a body with a continuous distribution of matter vectors $~ \mathbf{S}$ and $~ \mathbf{ N }$ are substantially different from the corresponding instantaneous vectors of specific particles in the vicinity of observation point. These vectors represent the averaged value of 4-acceleration inside the bodies. In particular, within the bodies there is a 4-acceleration generated by various forces in matter. The typical examples are relativistic uniform system and space bodies, where the major forces are the force of gravity and internal pressure generally oppositely directed. Upon rotation of the bodies the 4-force density, 4-acceleration, vectors $~ \mathbf{S}$ and $~ \mathbf{ N }$ are functions not only of radius, but the distance from the axis of rotation to the point of observation.

In the general case for extended bodies the four-acceleration at each point of a body becomes a certain function of coordinates and time. As a characteristic of physical system’s motion we can choose four-acceleration of the center of momentum, for evaluation of which it is necessary to integrate the force density over volume of entire matter and divide the total force by inertial mass of the system. Another method involves evaluation of four-acceleration through the strength and the solenoidal vector of acceleration field at the center of momentum in approximation of special theory of relativity, as was shown above.

References

Rindler, Wolfgang (1991). Introduction to Special Relativity (2nd). Oxford: Oxford University Press. ISBN 0-853971-853951-5.
^2.0 ^2.1 Fedosin S.G. Fizicheskie teorii i beskonechnaia vlozhennost’ materii. – Perm, 2009, 844 pages, Tabl. 21, Pic. 41, Ref. 289. ISBN 978-5-9901951-1-0. (in Russian).
Landau L.D., Lifshitz E.M. (1975). The Classical Theory of Fields. Vol. 2 (4th ed.). Butterworth-Heinemann. ISBN 978-0-750-62768-9.
Fedosin S.G. Generalized Four-momentum for Continuously Distributed Materials. Gazi University Journal of Science, Vol. 37, Issue 3, pp. 1509-1538 (2024). https://doi.org/10.35378/gujs.1231793.
Fedosin S.G. Lagrangian formalism in the theory of relativistic vector fields. International Journal of Modern Physics A, Vol. 40, No. 02, 2450163 (2025). https://doi.org/10.1142/S0217751X2450163X.
Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy. Jordan Journal of Physics. Vol. 9 (No. 1), pp. 1-30 (2016). http://dx.doi.org/10.5281/zenodo.889304.
Fedosin S.G. The procedure of finding the stress-energy tensor and vector field equations of any form. Advanced Studies in Theoretical Physics, Vol. 8, No. 18, pp. 771-779 (2014). http://dx.doi.org/10.12988/astp.2014.47101.
Fedosin S.G. Equations of Motion in the Theory of Relativistic Vector Fields. International Letters of Chemistry, Physics and Astronomy, Vol. 83, pp. 12-30 (2019). https://doi.org/10.18052/www.scipress.com/ILCPA.83.12.
Fedosin S.G. The generalized Poynting theorem for the general field and solution of the 4/3 problem. International Frontier Science Letters, Vol. 14, pp. 19-40 (2019). https://doi.org/10.18052/www.scipress.com/IFSL.14.19.
Fedosin S.G. What should we understand by the four-momentum of physical system? Physica Scripta, Vol. 99, No. 5, 055034 (2024). https://doi.org/10.1088/1402-4896/ad3b45.

External links

Four-force in Russian

Source: http://sergf.ru/ffen.htm

На русском языке