На русском языке

 

Relativistic uniform system

 

From Wikiversity

 

Relativistic uniform system is an ideal physical system, in which mass density (or any other physical quantity) depends on the Lorentz factor of the system’s particles, but is constant in the reference frames associated with the moving particles.

Содержание

Difference from classical uniform system

In classical physics, the ideal uniform body model is widely used, in which mass density is constant throughout the volume of the body or is given as the volume-averaged quantity. This model simplifies solution of physical problems and allows us to quickly estimate different physical quantities. For example, the body mass is calculated by simply multiplying the mass density by the body volume, which is easier than integrating the density over the volume in case of dependence of the density on coordinates. The disadvantage of the classical model is that the majority of real physical systems are far from this ideal uniformity.

The use of the concept of relativistic uniform system is based on the special theory of relativity (STR) and is the next step towards a more precise description of physical systems. In STR particular importance is given to invariant physical quantities, which can be calculated in each inertial reference frame and are equal to the values that these quantities have in the proper reference frame of the body. For example, multiplication of invariant mass by four-velocity gives the four-momentum of the body containing the invariant energy, and multiplication of corresponding invariant quantities by four-velocity allows us in the case of motion of solid point particles to find the four-potentials of any vector fields and to develop their complete theory. [1] Another example is that for determination of four-velocity or four-acceleration as a rule the operator of proper-time-derivative is used instead of time derivative. Therefore, the use of invariant mass density and charge density of moving particles that make up the system does not only conform to principles of STR but also significantly simplifies solution of relativistic equations of motion.

Field functions for bodies of spherical shape

Field equations are most easily solved in case of spherical symmetry in the absence of general rotation of particles. In this case all the physical quantities depend only on current radius, which starts at the center of the sphere. Below are presented solutions of equations for various fields within the framework of STR, including solutions for scalar potentials, field strengths and solenoidal vectors. Due to the random motion of the particles in the system, the vector field potentials become equal to zero. This leads to zeroing of solenoidal vectors of fields, including magnetic field and gravitational torsion field.

Acceleration field

The four-potential   Описание: ~U_{\mu }=\left({\frac {\vartheta }{c}},-{\mathbf U}\right)   of acceleration field includes the scalar potential  Описание: ~\vartheta  and the vector potential Описание: ~{\mathbf U}. Applying four-curl to the four-potential gives acceleration tensor  Описание: ~u_{{\mu \nu }}=\nabla _{\mu }U_{\nu }-\nabla _{\nu }U_{\mu } . In curved spacetime acceleration field equation with the field sources is derived from the principle of least action: [1] 

Описание: ~\nabla ^{\nu }u_{{\mu \nu }}=-{\frac {4\pi \eta }{c^{2}}}J_{\mu }.

This equation after expressing the acceleration tensor Описание: ~u_{{\mu \nu }}  in terms of four-potential turns into the wave equation for finding the four-potential of acceleration field:

Описание: ~\nabla ^{\nu }\nabla _{\mu }U_{\nu }-\nabla ^{\nu }\nabla _{\nu }U_{\mu }=-{\frac {4\pi \eta }{c^{2}}}J_{\mu },

 

which, taking into account the calibration condition of the four-potential Описание: ~\nabla ^{\mu }U_{\mu }=0  ,  can be transformed as follows:

Описание: ~\nabla ^{\nu }\nabla _{\nu }U_{\mu }+R_{{\mu \nu }}U^{\nu }={\frac {4\pi \eta }{c^{2}}}J_{\mu },

 

where Описание: ~c  is the speed of light, Описание: ~\eta   is acceleration field coefficient, Описание: ~J_{\mu }=g_{{\mu \nu }}J^{\nu }=g_{{\mu \nu }}\rho _{0}u^{\nu }  is mass four-current with the covariant index, Описание: ~g_{{\mu \nu }}  is metric tensor, Описание: ~R_{{\mu \nu }}  is Ricci tensor, Описание: ~u^{\nu }  is four-velocity, Описание: ~\rho _{0}  is invariant mass density of particles in comoving reference frames, which is the same for all the particles.

In Minkowski spacetime within the framework of STR, covariant derivatives of the form Описание: ~\nabla _{\mu }  turn into partial derivatives of the form Описание: ~\partial _{\mu }, while the result of action of the partial derivatives does not depend on the order of their action. As a consequence of calibration of the 4-potential, the equality holds: Описание: ~\partial ^{\nu }\partial _{\mu }U_{\nu }=\partial _{\mu }\partial ^{\nu }U_{\nu }=0.  As a result, the four-potential of acceleration field can be found from the wave equation:

Описание: ~\partial ^{\nu }\partial _{\nu }U_{\mu }={\frac {4\pi \eta }{c^{2}}}J_{\mu }. 

This equation can be divided into two equations – one for scalar potential and the other for vector potential of acceleration field. In the system under consideration the vector potential is equal to zero, and the scalar potential of acceleration field is given by:

Описание: ~\vartheta =cg_{{0\mu }}u^{\mu }=\gamma 'c^{2},

where Описание: ~g_{{0\mu }}  are time components of metric tensor, Описание: ~\gamma '  is Lorentz factor of particles in the reference frame K'  associated with the center of the sphere.

Since scalar potential of stationary system does not depend on time, the wave equation for the scalar potential turns into the Poisson equation: [2]

Описание: ~\triangle \vartheta =-4\pi \eta \rho _{0}\gamma '

and the following formula is obtained for the Lorentz factor of particles: [3]

Описание: ~\gamma '={\frac {c\gamma _{c}}{r{\sqrt {4\pi \eta \rho _{0}}}}}\sin \left({\frac {r}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\approx \gamma _{c}-{\frac {2\pi \eta \rho _{0}r^{2}\gamma _{c}}{3c^{2}}},\qquad \qquad (1)

where Описание: ~\gamma _{c}  is Lorentz factor of particles at the center of the sphere, Описание: ~r  is current radius.

The acceleration field strength and corresponding solenoidal vector are expressed by the formulas:

Описание: ~{\mathbf S}=-\nabla \vartheta -{\frac {\partial {\mathbf U}}{\partial t}}={\frac {c^{2}\gamma _{c}{\mathbf r}}{r^{3}}}\left[{\frac {c}{{\sqrt {4\pi \eta \rho _{0}}}}}\sin \left({\frac {r}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)-r\cos \left({\frac {r}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\right]\approx

Описание: ~\approx {\frac {4\pi \eta \rho _{0}\gamma _{c}{\mathbf r}}{3}}\left(1-{\frac {4\pi \eta \rho _{0}r^{2}}{10c^{2}}}\right).

 

Описание: ~{\mathbf N}=\nabla \times {\mathbf U}=0.

Pressure field

The four-potential  Описание: ~\pi _{\mu }=\left({\frac {\wp }{c}},-{\mathbf \Pi }\right) of the pressure field includes the scalar potential  Описание: ~\wp   and the vector potential  Описание: ~{\mathbf \Pi }, and obeys the calibration condition: Описание: ~\nabla ^{\mu }\pi _{\mu }=0 .

The pressure field equation with the field sources, pressure field tensor Описание: ~f_{{\mu \nu }}  and equation for finding the four-potential of pressure field have the form: [1]

Описание: ~\nabla ^{\nu }f_{{\mu \nu }}=-{\frac {4\pi \sigma }{c^{2}}}J_{\mu },\quad f_{{\mu \nu }}=\nabla _{\mu }\pi _{\nu }-\nabla _{\nu }\pi _{\mu },\quad \nabla ^{\nu }\nabla _{\nu }\pi _{\mu }+R_{{\mu \nu }}\pi ^{\nu }={\frac {4\pi \sigma }{c^{2}}}J_{\mu },

 

where  Описание: ~\sigma   is pressure field coefficient.

In STR the latter equation turns into the wave equation:

Описание: ~\partial ^{\nu }\partial _{\nu }\pi _{\mu }={\frac {4\pi \sigma }{c^{2}}}J_{\mu }.

In stationary case the potentials do not depend on time and time component of the wave equation turns into the Poisson equation for the scalar potential of the pressure field:

Описание: ~\triangle \wp =-4\pi \sigma \rho _{0}\gamma '.

Solution of this equation inside the sphere with particles is as follows: [3]

Описание: ~\wp =\wp _{c}-{\frac {\sigma c^{2}\gamma _{c}}{\eta }}+{\frac {\sigma c^{3}\gamma _{c}}{\eta r{\sqrt {4\pi \eta \rho _{0}}}}}\sin \left({\frac {r}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\approx \wp _{c}-{\frac {2\pi \sigma \rho _{0}r^{2}\gamma _{c}}{3}}.

where  Описание: ~\wp _{c}  is scalar potential at the center of the sphere. This potential is approximately equal to: [4]

~\wp _{c}\approx {\frac {3\sigma m}{10a}}\left(1+{\frac {9}{2{\sqrt {14}}}}\right),

where acceleration field constant  ~\eta  and pressure field constant  ~\sigma  are expressed by the formulas:

~\eta ={\frac {3}{5}}\left(G-{\frac {\rho _{{0q}}^{2}}{4\pi \varepsilon _{0}\rho _{0}^{2}}}\right),\qquad \qquad \sigma ={\frac {2}{5}}\left(G-{\frac {\rho _{{0q}}^{2}}{4\pi \varepsilon _{0}\rho _{0}^{2}}}\right).

 

The strength of pressure field and corresponding solenoidal vector are found as follows:

Описание: ~{\mathbf C}=-\nabla \wp -{\frac {\partial {\mathbf \Pi }}{\partial t}}={\frac {\sigma c^{2}\gamma _{c}{\mathbf r}}{\eta r^{3}}}\left[{\frac {c}{{\sqrt {4\pi \eta \rho _{0}}}}}\sin \left({\frac {r}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)-r\cos \left({\frac {r}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\right]\approx

Описание: ~\approx {\frac {4\pi \sigma \rho _{0}\gamma _{c}{\mathbf r}}{3}}\left(1-{\frac {4\pi \eta \rho _{0}r^{2}}{10c^{2}}}\right).

 

Описание: ~{\mathbf I}=\nabla \times {\mathbf \Pi }=0.

Gravitational field

The gravitational four-potential  Описание: ~D_{\mu }=\left({\frac {\psi }{c}},-{\mathbf D}\right)  of gravitational field is made up with the use of scalar Описание: ~\psi   and vector Описание: ~{\mathbf D}  potentials. Calibration condition of the four-potential is: Описание: ~\nabla ^{\mu }D_{\mu }=0 .

The gravitational field equation with field sources, the gravitational tensor  Описание: ~\Phi _{{\mu \nu }}  and the equation for finding the four-potential of gravitational field in covariant theory of gravitation have the form: [5] [6]

Описание: ~\nabla ^{\nu }\Phi _{{\mu \nu }}={\frac {4\pi G}{c^{2}}}J_{\mu },\quad \Phi _{{\mu \nu }}=\nabla _{\mu }D_{\nu }-\nabla _{\nu }D_{\mu },\quad \nabla ^{\nu }\nabla _{\nu }D_{\mu }+R_{{\mu \nu }}D^{\nu }=-{\frac {4\pi G}{c^{2}}}J_{\mu },

 

where Описание: ~G is gravitational constant.

In STR the latter equation is simplified and becomes the wave equation:

Описание: ~\partial ^{\nu }\partial _{\nu }D_{\mu }=-{\frac {4\pi G}{c^{2}}}J_{\mu }.

From the wave equation in stationary case, the Poisson equation follows for scalar potential inside the sphere with randomly moving particles in the framework of Lorentz-invariant theory of gravitation (LITG):

Описание: ~\triangle \psi _{i}=4\pi G\rho _{0}\gamma '.

The right-hand side of this equation contains Lorentz factor Описание: ~\gamma ', which depends on the radius according to (1). In addition, the internal scalar potential near the surface of the sphere must coincide with the scalar potential of external field of the system, in view of standard potential gauge, that is with equality of potential to zero at infinity.

As a result, dependence of scalar potential on the current radius differs from dependence in classical case of uniform sphere with the radius Описание: ~a and is equal to it only approximately: [3]

Описание: ~\psi _{i}=-{\frac {Gc^{2}\gamma _{c}}{\eta r}}\left[{\frac {c}{{\sqrt {4\pi \eta \rho _{0}}}}}\sin \left({\frac {r}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)-r\cos \left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\right]\approx -{\frac {2\pi G\rho _{0}\gamma _{c}(3a^{2}-r^{2})}{3}}.

For gravitational field strength and gravitational torsion field inside the sphere we obtain the following: [7]

Описание: ~{\mathbf \Gamma }_{i}=-\nabla \psi _{i}-{\frac {\partial {\mathbf D}_{i}}{\partial t}}=-{\frac {Gc^{2}\gamma _{c}{\mathbf r}}{\eta r^{3}}}\left[{\frac {c}{{\sqrt {4\pi \eta \rho _{0}}}}}\sin \left({\frac {r}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)-r\cos \left({\frac {r}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\right]\approx

Описание: ~\approx -{\frac {4\pi G\rho _{0}\gamma _{c}{\mathbf r}}{3}}\left(1-{\frac {4\pi \eta \rho _{0}r^{2}}{10c^{2}}}\right).

 

Описание: ~{\mathbf \Omega }_{i}=\nabla \times {\mathbf D}_{i}=0.

 

Solutions for external gravitational field potential and for field strength Описание: ~\Gamma _{o} according to LITG are as follows:

Описание: ~\psi _{o}=-{\frac {Gc^{2}\gamma _{c}}{\eta r}}\left[{\frac {c}{{\sqrt {4\pi \eta \rho _{0}}}}}\sin \left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)-a\cos \left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\right]\approx -{\frac {Gm\gamma _{c}}{r}}\left(1-{\frac {3\eta m}{10ac^{2}}}\right).

 

Описание: ~{\mathbf \Gamma }_{o}=-\nabla \psi _{o}-{\frac {\partial {\mathbf D}_{o}}{\partial t}}=-{\frac {Gc^{2}\gamma _{c}{\mathbf r}}{\eta r^{3}}}\left[{\frac {c}{{\sqrt {4\pi \eta \rho _{0}}}}}\sin \left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)-a\cos \left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\right]\approx

Описание: ~\approx -{\frac {Gm\gamma _{c}{\mathbf r}}{r^{3}}}\left(1-{\frac {3\eta m}{10ac^{2}}}\right).

Here, the auxiliary mass Описание: ~m  is equal to the product of mass density Описание: ~\rho _{0}  by volume of the sphere:  Описание: ~m={\frac {4\pi \rho _{0}a^{3}}{3}}. From expressions for potential and strength of external gravitational field we can see that the role of gravitational mass is played by the mass  Описание: ~m_{g}\approx m\gamma _{c}\left(1-{\frac {3\eta m}{10ac^{2}}}\right).  Since Описание: ~\gamma _{c}>1  then the relation  Описание: ~m_{g}>m  is satisfied.

To understand difference between these masses we should calculate total relativistic mass  Описание: ~m_{b}  of particles moving inside the sphere. For motion of particles there should be some voids between them. Both the average accelerations and average velocities of particles inside the sphere are functions of current radius. Dividing the particles’ velocities by their acceleration, we can find dependence of average period of oscillatory motion of particles on the radius. Finally, multiplying the velocity by the average period of motion, we can obtain an estimate of the size of voids between the particles.

In order to calculate volume of the sphere, it is necessary to sum up volumes of all typical particles moving inside the sphere, as well as volumes of the voids between them. Suppose now that the sizes of typical particles are much larger than the voids between the particles, and volume of the voids is substantially less than the total volume of particles. In this case, we can use approximation of continuous medium, so that unit of mass of matter inside the sphere will be given by approximate expression  Описание: ~dm\approx \rho _{0}\gamma 'dV, where  Описание: ~\rho _{0}  is mass density in reference frames associated with the particles, Описание: ~\gamma '  is Lorentz factor of the moving particles, the product  Описание: ~\rho _{0}\gamma '  gives mass density of the particles from viewpoint of an observer, who is stationary with respect to the sphere, and volume element  Описание: ~dV  inside the sphere corresponds to the volume of the particle from the viewpoint of this observer.

This leads to the fact that total volume of particles moving inside the sphere becomes approximately equal to the volume of the sphere. For the mass, in view of Lorentz factor (1), the following relation is obtained:

Описание: ~m_{b}=\int dm=\int \rho _{0}\gamma 'dV={\frac {c^{2}\gamma _{c}}{\eta }}\left[{\frac {c}{{\sqrt {4\pi \eta \rho _{0}}}}}\sin \left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)-a\cos \left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\right]\approx

Описание: ~\approx m\gamma _{c}\left(1-{\frac {3\eta m}{10ac^{2}}}\right).

This implies equality of gravitational mass Описание: ~m_{g}  and total relativistic mass Описание: ~m_{b}  of particles moving inside the sphere. The both masses are greater than the mass  Описание: ~m. By the method of its calculation, the mass Описание: ~m_{b}  is equal to the sum of invariant masses of particles that make up the system.

The external gravitational torsion field is equal to zero:

Описание: ~{\mathbf \Omega }_{o}=\nabla \times {\mathbf D}_{o}=0.

Electromagnetic field

The electromagnetic four-potential  Описание: ~A_{\mu }=\left({\frac {\varphi }{c}},-{\mathbf A}\right)  of electromagnetic field includes scalar potential  Описание: ~\varphi   and vector potential Описание: ~{\mathbf A}. The covariant Lorentz calibration for four-potential is:  Описание: ~\nabla ^{\mu }A_{\mu }=0  .  For a fixed uniformly charged spherical body with random motion of charges total electromagnetic field on the average is purely electric and the vector potential is equal to zero.

The electromagnetic field equation with the field sources, electromagnetic tensor Описание: ~F_{{\mu \nu }}  and equation for finding four-potential are expressed as follows:

Описание: ~\nabla ^{\nu }F_{{\mu \nu }}=-{\frac {1}{\varepsilon _{0}c^{2}}}j_{\mu },\quad F_{{\mu \nu }}=\nabla _{\mu }A_{\nu }-\nabla _{\nu }A_{\mu },\quad \nabla ^{\nu }\nabla _{\nu }A_{\mu }+R_{{\mu \nu }}A^{\nu }={\frac {1}{\varepsilon _{0}c^{2}}}j_{\mu },

 

where Описание: ~\varepsilon _{0}  is electric constant, Описание: ~j_{\mu }  is electromagnetic four-current.

The latter equation in STR turns into the wave equation:

Описание: ~\partial ^{\nu }\partial _{\nu }A_{\mu }={\frac {1}{\varepsilon _{0}c^{2}}}j_{\mu }.

Due to the absence of time-dependence in the case under consideration, the wave equation becomes the Poisson equation for scalar potential Описание: ~\varphi _{i}  inside the sphere:

Описание: ~\triangle \varphi _{i}=-{\frac {\rho _{{0q}}\gamma '}{\varepsilon _{0}}},

where Описание: ~\rho _{{0q}}  is charge density in the reference frames associated with the charges.

Dependence of scalar potential on current radius in general case differs from dependence in classical case of potential of a uniformly charged sphere with the radius Описание: ~a, coinciding with it only in the first approximation: [8]

 

Описание: ~\varphi _{i}={\frac {\rho _{{0q}}c^{2}\gamma _{c}}{4\pi \varepsilon _{0}\eta \rho _{0}r}}\left[{\frac {c}{{\sqrt {4\pi \eta \rho _{0}}}}}\sin \left({\frac {r}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)-r\cos \left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\right]\approx {\frac {\rho _{{0q}}\gamma _{c}(3a^{2}-r^{2})}{6\varepsilon _{0}}}.

 

Electric field strength and magnetic field inside the sphere have the form:

Описание: ~{\mathbf E}_{i}=-\nabla \varphi _{i}-{\frac {\partial {\mathbf A}_{i}}{\partial t}}={\frac {\rho _{{0q}}c^{2}\gamma _{c}{\mathbf r}}{4\pi \varepsilon _{0}\eta \rho _{0}r^{3}}}\left[{\frac {c}{{\sqrt {4\pi \eta \rho _{0}}}}}\sin \left({\frac {r}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)-r\cos \left({\frac {r}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\right]\approx

Описание: ~\approx {\frac {\rho _{{0q}}\gamma _{c}{\mathbf r}}{3\varepsilon _{0}}}\left(1-{\frac {4\pi \eta \rho _{0}r^{2}}{10c^{2}}}\right).

 

Описание: ~{\mathbf B}_{i}=\nabla \times {\mathbf A}_{i}=0.

 

Outside the system under consideration charge density is equal to zero and Poisson equation for scalar potential turns into Laplace equation:

Описание: ~\triangle \varphi _{o}=0.

Solution for external electric field potential, corresponding to potential gauge and Maxwell's equations for electric field strength Описание: ~E_{o}  is given by:

 

Описание: ~\varphi _{o}={\frac {\rho _{{0q}}c^{2}\gamma _{c}}{4\pi \varepsilon _{0}\eta \rho _{0}r}}\left[{\frac {c}{{\sqrt {4\pi \eta \rho _{0}}}}}\sin \left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)-a\cos \left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\right]\approx {\frac {q\gamma _{c}}{4\pi \varepsilon _{0}r}}\left(1-{\frac {3\eta m}{10ac^{2}}}\right).

 

Описание: ~{\mathbf E}_{o}=-\nabla \varphi _{o}-{\frac {\partial {\mathbf A}_{o}}{\partial t}}={\frac {\rho _{{0q}}c^{2}\gamma _{c}{\mathbf r}}{4\pi \varepsilon _{0}\eta \rho _{0}r^{3}}}\left[{\frac {c}{{\sqrt {4\pi \eta \rho _{0}}}}}\sin \left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)-a\cos \left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\right]\approx

Описание: ~\approx {\frac {q\gamma _{c}{\mathbf r}}{4\pi \varepsilon _{0}r^{3}}}\left(1-{\frac {3\eta m}{10ac^{2}}}\right).

 

External magnetic field is equal to zero:

Описание: ~{\mathbf B}_{o}=\nabla \times {\mathbf A}_{o}=0.

In these expressions, the charge Описание: ~q  is an auxiliary quantity equal to the product of charge density Описание: ~\rho _{{0q}}  by volume of the sphere:  Описание: ~q={\frac {4\pi \rho _{{0q}}a^{3}}{3}}.

In this case, the following quantity serves as total charge of the system:

Описание: ~q_{b}=\int \rho _{{0q}}\gamma 'dV={\frac {\rho _{{0q}}c^{2}\gamma _{c}}{\eta \rho _{0}}}\left[{\frac {c}{{\sqrt {4\pi \eta \rho _{0}}}}}\sin \left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)-a\cos \left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\right]\approx

Описание: ~\approx q\gamma _{c}\left(1-{\frac {3\eta m}{10ac^{2}}}\right),

 

while Описание: ~q_{b}>q.  The charge   Описание: ~q_{b}  is calculated in the same way as the mass Описание: ~m_{b}  and has the meaning of the sum of charges of all the system’s particles.

Tensor field invariants

The knowledge of field strengths and solenoidal components of fields allows us to find tensor components of corresponding fields with covariant indices. To pass on to the field tensors with contravariant indices we need to know metric tensor. In STR the metric tensor does not depend on coordinates and time, is uniquely defined, and in Cartesian coordinates consists of zeros and unities. As a result, it is easy to find the tensor field invariants  Описание: ~u_{{\mu \nu }}u^{{\mu \nu }},   Описание: ~f_{{\mu \nu }}f^{{\mu \nu }},     Описание: ~\Phi _{{\mu \nu }}\Phi ^{{\mu \nu }} and  Описание: ~F_{{\mu \nu }}F^{{\mu \nu }}, where  Описание: ~u_{{\mu \nu }},  Описание: ~f_{{\mu \nu }},   Описание: ~\Phi _{{\mu \nu }}  and   Описание: ~F_{{\mu \nu }}   are the acceleration tensor, the pressure field tensor, the gravitational tensor and the electromagnetic tensor, respectively.

The tensor field invariants are included in Lagrangian, Hamiltonian. action function and relativistic energy of the system, and they are located there inside integrals over space volume. In addition, they are included in corresponding stress-energy tensors of the fields. [2]  Since in the system under consideration the solenoidal vectors are zero, the tensor invariants depend only on the field strengths:

Описание: ~u_{{\mu \nu }}u^{{\mu \nu }}=-{\frac {2}{c^{2}}}(S^{2}-c^{2}N^{2})=-{\frac {2}{c^{2}}}S^{2}.

 

Описание: ~f_{{\mu \nu }}f^{{\mu \nu }}=-{\frac {2}{c^{2}}}(C^{2}-c^{2}I^{2})=-{\frac {2}{c^{2}}}C^{2}.

 

Описание: ~\Phi _{{\mu \nu }}\Phi ^{{\mu \nu }}=-{\frac {2}{c^{2}}}(\Gamma ^{2}-c^{2}\Omega ^{2})=-{\frac {2}{c^{2}}}\Gamma ^{2}.

 

Описание: ~F_{{\mu \nu }}F^{{\mu \nu }}=-{\frac {2}{c^{2}}}(E^{2}-c^{2}B^{2})=-{\frac {2}{c^{2}}}E^{2}.

 

The volume integrals of tensor invariants multiplied by corresponding factors were calculated in the article. [7]  For acceleration field and pressure field the integrals are taken only over volume of the sphere:

 

Описание: ~\int \limits _{{r=0}}^{{a}}{\frac {c^{2}}{16\pi \eta }}u_{{\mu \nu }}u^{{\mu \nu }}dV=-{\frac {c^{4}\gamma _{c}^{2}}{2\eta }}\left[{\frac {a}{2}}+{\frac {c}{4{\sqrt {4\pi \eta \rho _{0}}}}}\sin \left({\frac {2a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)-{\frac {c^{2}}{4\pi \eta \rho _{0}a}}\sin ^{2}\left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\right]\approx

Описание: ~\approx -{\frac {\eta m^{2}\gamma _{c}^{2}}{10a}}\left(1-{\frac {3\eta m}{7ac^{2}}}\right).

 

Описание: ~\int \limits _{{r=0}}^{{a}}{\frac {c^{2}}{16\pi \sigma }}f_{{\mu \nu }}f^{{\mu \nu }}dV=-{\frac {\sigma c^{4}\gamma _{c}^{2}}{2\eta ^{2}}}\left[{\frac {a}{2}}+{\frac {c}{4{\sqrt {4\pi \eta \rho _{0}}}}}\sin \left({\frac {2a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)-{\frac {c^{2}}{4\pi \eta \rho _{0}a}}\sin ^{2}\left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\right]\approx

Описание: ~\approx -{\frac {\sigma m^{2}\gamma _{c}^{2}}{10a}}\left(1-{\frac {3\eta m}{7ac^{2}}}\right).

 

The gravitational and electromagnetic fields of the system are present not only inside but also outside the sphere, where they extend to infinity, while field strengths of internal and external fields behave differently. The field strengths  Описание: ~{\mathbf \Gamma }_{i}  and  Описание: ~{\mathbf E}_{i}  are substituted respectively into integrals of tensor invariants of these fields taken over volume of the sphere, which gives the following:

 

Описание: ~-\int \limits _{{r=0}}^{{a}}{\frac {c^{2}}{16\pi G}}\Phi _{{\mu \nu }}\Phi ^{{\mu \nu }}dV=

Описание: ~={\frac {Gc^{4}\gamma _{c}^{2}}{2\eta ^{2}}}\left[{\frac {a}{2}}+{\frac {c}{4{\sqrt {4\pi \eta \rho _{0}}}}}\sin \left({\frac {2a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)-{\frac {c^{2}}{4\pi \eta \rho _{0}a}}\sin ^{2}\left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\right]\approx {\frac {Gm^{2}\gamma _{c}^{2}}{10a}}\left(1-{\frac {3\eta m}{7ac^{2}}}\right).

 

Описание: ~\int \limits _{{r=0}}^{{a}}{\frac {c^{2}\varepsilon _{0}}{4}}F_{{\mu \nu }}F^{{\mu \nu }}dV=

Описание: ~=-{\frac {\rho _{{0q}}^{2}c^{4}\gamma _{c}^{2}}{8\pi \varepsilon _{0}\eta ^{2}\rho _{0}^{2}}}\left[{\frac {a}{2}}+{\frac {c}{4{\sqrt {4\pi \eta \rho _{0}}}}}\sin \left({\frac {2a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)-{\frac {c^{2}}{4\pi \eta \rho _{0}a}}\sin ^{2}\left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\right]\approx

Описание: ~\approx -{\frac {q^{2}\gamma _{c}^{2}}{40\pi \varepsilon _{0}a}}\left(1-{\frac {3\eta m}{7ac^{2}}}\right).

 

Into volume integrals of tensor invariants of gravitational and electromagnetic fields of the system outside the sphere the field strengths  Описание: ~{\mathbf \Gamma }_{o}  and  Описание: ~{\mathbf E}_{o}  are substituted, respectively:

 

Описание: ~-\int \limits _{{r=a}}^{{\infty }}{\frac {c^{2}}{16\pi G}}\Phi _{{\mu \nu }}\Phi ^{{\mu \nu }}dV=

Описание: ~={\frac {Gc^{4}\gamma _{c}^{2}}{2\eta ^{2}a}}\left[{\frac {c}{{\sqrt {4\pi \eta \rho _{0}}}}}\sin \left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)-a\cos \left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\right]^{2}\approx {\frac {Gm^{2}\gamma _{c}^{2}}{2a}}\left(1-{\frac {3\eta m}{5ac^{2}}}\right).

 

Описание: ~\int \limits _{{r=a}}^{{\infty }}{\frac {c^{2}\varepsilon _{0}}{4}}F_{{\mu \nu }}F^{{\mu \nu }}dV=

Описание: ~=-{\frac {\rho _{{0q}}^{2}c^{4}\gamma _{c}^{2}}{8\pi \varepsilon _{0}\eta ^{2}\rho _{0}^{2}a}}\left[{\frac {c}{{\sqrt {4\pi \eta \rho _{0}}}}}\sin \left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)-a\cos \left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\right]^{2}\approx -{\frac {q^{2}\gamma _{c}^{2}}{8\pi \varepsilon _{0}a}}\left(1-{\frac {3\eta m}{5ac^{2}}}\right).

 

Energies of particles in field potentials

All the four fields act on particles inside the sphere, and therefore each particle of the system acquires corresponding energy in a particular field. The energy of a particle in a field is calculated as volume integral of product of effective mass density  Описание: ~\rho =\rho _{0}\gamma '  by corresponding scalar potential, and for electric field the energy is determined as volume integral of product of effective charge density  Описание: ~\rho _{q}=\rho _{{0q}}\gamma '   by scalar potential  Описание: ~\varphi , where Lorentz factor Описание: ~\gamma '  from (1) is used. In STR the energies of particles in acceleration field, pressure field, gravitational and electric fields in uniform relativistic spherical system, in view of expressions for the field potentials [7] and corrections to calculations, [8] [9] [10]  [11]  are, respectively:

 

Описание: ~\int \rho \vartheta dV=\rho _{0}c^{2}\int \gamma '^{2}dV={\frac {c^{4}\gamma _{c}^{2}}{\eta }}\left[{\frac {a}{2}}-{\frac {c}{4{\sqrt {4\pi \eta \rho _{0}}}}}\sin \left({\frac {2a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\right]\approx

Описание: ~\approx mc^{2}\gamma _{c}^{2}-{\frac {3\eta m^{2}\gamma _{c}^{2}}{5a}}\left(1-{\frac {2\eta m}{7ac^{2}}}\right).

 

Описание: ~\int \rho \wp dV=\rho _{0}\int \gamma '\wp dV={\frac {c^{2}\gamma _{c}}{\eta }}\left(\wp _{c}-{\frac {\sigma c^{2}\gamma _{c}}{\eta }}\right)\left[{\frac {c}{{\sqrt {4\pi \eta \rho _{0}}}}}\sin \left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)-a\cos \left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\right]+

Описание: ~+{\frac {\sigma c^{4}\gamma _{c}^{2}}{\eta ^{2}}}\left[{\frac {a}{2}}-{\frac {c}{4{\sqrt {4\pi \eta \rho _{0}}}}}\sin \left({\frac {2a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\right]\approx m\wp _{c}\gamma _{c}\left(1-{\frac {3\eta m}{10ac^{2}}}\right)-{\frac {3\sigma m^{2}\gamma _{c}^{2}}{10a}}\left(1-{\frac {13\eta m}{28ac^{2}}}\right).

 

Описание: ~\int \rho \psi _{i}dV=\rho _{0}\int \gamma '\psi _{i}dV=

Описание: ~={\frac {Gc^{4}\gamma _{c}^{2}}{\eta ^{2}}}\cos \left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\left[{\frac {c}{{\sqrt {4\pi \eta \rho _{0}}}}}\sin \left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)-a\cos \left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\right]-

 

Описание: ~-{\frac {Gc^{4}\gamma _{c}^{2}}{\eta ^{2}}}\left[{\frac {a}{2}}-{\frac {c}{4{\sqrt {4\pi \eta \rho _{0}}}}}\sin \left({\frac {2a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\right]\approx -{\frac {6Gm^{2}\gamma _{c}^{2}}{5a}}\left(1-{\frac {4\eta m}{7ac^{2}}}\right).

 

Описание: ~\int \rho _{q}\varphi _{i}dV=\rho _{{0q}}\int \gamma '\varphi _{i}dV=

Описание: ~=-{\frac {\rho _{{0q}}^{2}c^{4}\gamma _{c}^{2}}{4\pi \varepsilon _{0}\eta ^{2}\rho _{0}^{2}}}\cos \left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\left[{\frac {c}{{\sqrt {4\pi \eta \rho _{0}}}}}\sin \left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)-a\cos \left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\right]+

Описание: ~+{\frac {\rho _{{0q}}^{2}c^{4}\gamma _{c}^{2}}{4\pi \varepsilon _{0}\eta ^{2}\rho _{0}^{2}}}\left[{\frac {a}{2}}-{\frac {c}{4{\sqrt {4\pi \eta \rho _{0}}}}}\sin \left({\frac {2a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\right]\approx {\frac {3q^{2}\gamma _{c}^{2}}{10\pi \varepsilon _{0}a}}\left(1-{\frac {4\eta m}{7ac^{2}}}\right).

 

Note that all fields in which particles are located are not fields from external sources, but are generated by the particles themselves. As a result, the particles’ energies calculated above in scalar potentials of the fields are twice as large as potential energy of one or another interaction. For example, in order to calculate electrostatic energy of a system of two charges, it is sufficient to take potential of first charge at location of second charge and to multiply it by the value of the second charge. But if we use formula for energy in the form of an integral, then the electrostatic energy will be taken into account twice, because the term is added, which contains potential of second charge at location of first charge multiplied by the value of the first charge. On the other hand, the electrostatic energy must consist of two components that take into account both the energy of particles in each other’s fields and the energy of electric field itself.

Instead, in electrostatics, the electrostatic energy is calculated either through the scalar potential or through the field strength by integrating time component of stress-energy tensor over volume. Both methods provide the same result, but the connection between field energy and energy of particles in field potential is lost in this case, and it is not clear why these energies should coincide.

Relation between field coefficients

For the four fields under consideration equation of motion of matter in the concept of general field is as follows: [12] [13]

Описание: ~u_{{\mu \nu }}J^{\nu }+f_{{\mu \nu }}J^{\nu }+\Phi _{{\mu \nu }}J^{\nu }+F_{{\mu \nu }}j^{\nu }=0,

 

where Описание: ~J_{\mu }  is mass four-current, Описание: ~j^{\nu }  is electromagnetic four-current.

Components of field tensors are field strengths and corresponding solenoidal vectors, but in the physical system under consideration the latter are equal to zero. As a result, space component of the equation of motion is reduced to the relation:

Описание: ~{\mathbf S}+{\mathbf C}+{\mathbf \Gamma }_{i}+{\frac {\rho _{{0q}}}{\rho _{0}}}{\mathbf E}_{i}=0.

If we substitute here expression for field strengths inside the sphere, we obtain relation between field coefficients: [14]

Описание: ~\eta +\sigma =G-{\frac {\rho _{{0q}}^{2}}{4\pi \varepsilon _{0}\rho _{0}^{2}}}=G-{\frac {q^{2}}{4\pi \varepsilon _{0}m^{2}}}.\qquad \qquad (2)

The same is obtained for time component of equation of motion, which leads to generalized Poynting theorem. [9]

 

Relation between energies of internal and external fields

In article [15] it was found that energy of particles in gravitational field inside stationary sphere is up to a sign two times greater than total energy associated with tensor invariants of gravitational field inside and outside the sphere. A similar situation takes place in the system under consideration with random motion of particles and zero solenoidal vectors both for gravitational [10]  and electromagnetic fields. [8]  In particular, we can write the following:

 

Описание: ~\int \limits _{{r=0}}^{{a}}\rho \psi _{i}dV=2\int \limits _{{r=0}}^{{a}}{\frac {c^{2}}{16\pi G}}\Phi _{{\mu \nu }}\Phi ^{{\mu \nu }}dV+2\int \limits _{{r=a}}^{{\infty }}{\frac {c^{2}}{16\pi G}}\Phi _{{\mu \nu }}\Phi ^{{\mu \nu }}dV=2\int \limits _{{r=0}}^{{\infty }}{\frac {c^{2}}{16\pi G}}\Phi _{{\mu \nu }}\Phi ^{{\mu \nu }}dV.

 

Описание: ~\int \limits _{{r=0}}^{{a}}\rho _{q}\varphi _{i}dV=-2\int \limits _{{r=0}}^{{a}}{\frac {c^{2}\varepsilon _{0}}{4}}F_{{\mu \nu }}F^{{\mu \nu }}dV-2\int \limits _{{r=a}}^{{\infty }}{\frac {c^{2}\varepsilon _{0}}{4}}F_{{\mu \nu }}F^{{\mu \nu }}dV=-2\int \limits _{{r=0}}^{{\infty }}{\frac {c^{2}\varepsilon _{0}}{4}}F_{{\mu \nu }}F^{{\mu \nu }}dV.

 

These expressions relate the energy of particles in scalar field potentials with the energy found with the help of field strengths.

 

Relativistic energy

In curved spacetime the system’s energy for continuously distributed matter is given by the formula: [2] [4]

 

Описание: ~E_{r}={\frac {1}{c}}\int {(\rho _{0}\vartheta +\rho _{0}\wp +\rho _{0}\psi +\rho _{{0q}}\varphi )u^{0}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}+}

~+\int {\left({\frac {c^{2}}{16\pi \eta }}u_{{\mu \nu }}u^{{\mu \nu }}+{\frac {c^{2}}{16\pi \sigma }}f_{{\mu \nu }}f^{{\mu \nu }}-{\frac {c^{2}}{16\pi G}}\Phi _{{\mu \nu }}\Phi ^{{\mu \nu }}+{\frac {c^{2}\varepsilon _{0}}{4}}F_{{\mu \nu }}F^{{\mu \nu }}\right){\sqrt {-g}}dx^{1}dx^{2}dx^{3}}.\qquad \qquad (5)

 

This formula is valid in the case where it can be assumed that potentials and field strengths at each point in space do not have a direct dependence on the speeds of motion of individual particles of the system.

In STR the metric tensor determinant is Описание: ~g=-1, the time component of four-velocity is  Описание: ~u^{0}=c\gamma ', and in order to calculate the energy of spherical system with particles, taking into account the fields’ energies, we can use the above-mentioned energies of particles in field potentials and energies in the form of tensor invariants of the fields:

 

Описание: ~E_{r}\approx mc^{2}\gamma _{c}^{2}-{\frac {3\eta m^{2}\gamma _{c}^{2}}{5a}}\left(1-{\frac {2\eta m}{7ac^{2}}}\right)+m\wp _{c}\gamma _{c}\left(1-{\frac {3\eta m}{10ac^{2}}}\right)-{\frac {3\sigma m^{2}\gamma _{c}^{2}}{10a}}\left(1-{\frac {13\eta m}{28ac^{2}}}\right)-

Описание: ~-{\frac {6Gm^{2}\gamma _{c}^{2}}{5a}}\left(1-{\frac {4\eta m}{7ac^{2}}}\right)+{\frac {3q^{2}\gamma _{c}^{2}}{10\pi \varepsilon _{0}a}}\left(1-{\frac {4\eta m}{7ac^{2}}}\right)-{\frac {\eta m^{2}\gamma _{c}^{2}}{10a}}\left(1-{\frac {3\eta m}{7ac^{2}}}\right)-{\frac {\sigma m^{2}\gamma _{c}^{2}}{10a}}\left(1-{\frac {3\eta m}{7ac^{2}}}\right)+

Описание: ~+{\frac {Gm^{2}\gamma _{c}^{2}}{10a}}\left(1-{\frac {3\eta m}{7ac^{2}}}\right)-{\frac {q^{2}\gamma _{c}^{2}}{40\pi \varepsilon _{0}a}}\left(1-{\frac {3\eta m}{7ac^{2}}}\right)+{\frac {Gm^{2}\gamma _{c}^{2}}{2a}}\left(1-{\frac {3\eta m}{5ac^{2}}}\right)-{\frac {q^{2}\gamma _{c}^{2}}{8\pi \varepsilon _{0}a}}\left(1-{\frac {3\eta m}{5ac^{2}}}\right).

 

The expression for energy is simplified if we use the relation between field coefficients (2):

Описание: ~E_{r}\approx mc^{2}\gamma _{c}^{2}-{\frac {3\eta m^{2}\gamma _{c}^{2}}{5a}}\left(1-{\frac {2\eta m}{7ac^{2}}}\right)+m\wp _{c}\gamma _{c}\left(1-{\frac {3\eta m}{10ac^{2}}}\right)-{\frac {3\sigma m^{2}\gamma _{c}^{2}}{10a}}\left(1-{\frac {13\eta m}{28ac^{2}}}\right)-

Описание: ~-{\frac {6Gm^{2}\gamma _{c}^{2}}{5a}}\left(1-{\frac {4\eta m}{7ac^{2}}}\right)+{\frac {3q^{2}\gamma _{c}^{2}}{10\pi \varepsilon _{0}a}}\left(1-{\frac {4\eta m}{7ac^{2}}}\right)+{\frac {Gm^{2}\gamma _{c}^{2}}{2a}}\left(1-{\frac {3\eta m}{5ac^{2}}}\right)-{\frac {q^{2}\gamma _{c}^{2}}{8\pi \varepsilon _{0}a}}\left(1-{\frac {3\eta m}{5ac^{2}}}\right).

 

Taking into account relations between energies of internal and external fields also simplifies expression for the system’s energy:

 

Описание: ~E_{r}\approx mc^{2}\gamma _{c}^{2}-{\frac {3\eta m^{2}\gamma _{c}^{2}}{5a}}\left(1-{\frac {2\eta m}{7ac^{2}}}\right)+m\wp _{c}\gamma _{c}\left(1-{\frac {3\eta m}{10ac^{2}}}\right)-{\frac {3\sigma m^{2}\gamma _{c}^{2}}{10a}}\left(1-{\frac {13\eta m}{28ac^{2}}}\right)-

Relation between energy and cosmological constant

In the approach under consideration, relativistic energy of the system is not an absolute value and requires gauging. For this purpose the cosmological constant  Описание: ~\Lambda   is used. The gauge condition for the four main fields is related to sum of products of the fields’ four-potentials by corresponding four-currents and has the following form: [2] [4]

 

~-ck\Lambda =A_{\mu }j^{\mu }+(D_{\mu }+U_{\mu }+\pi _{\mu })J^{\mu },\qquad \qquad (6)

 

 

where for large cosmic systems  Описание: ~-ck={\frac {c^{4}}{16\pi G\beta }},  and  Описание: ~\beta   is a constant of order of unity.

Within the framework of STR gauge condition has the following form:

Описание: ~-ck\Lambda =\gamma \rho _{{0q}}(\varphi -{\mathbf A}\cdot {\mathbf v})+\gamma \rho _{{0}}(\psi -{\mathbf D}\cdot {\mathbf v}+\vartheta -{\mathbf U}\cdot {\mathbf v}+\wp -{\mathbf \Pi }\cdot {\mathbf v}).

 

If we divide the system’s particles and remove them to infinity and leave there at rest, the terms with products of vector field potentials by velocity of particles Описание: ~{\mathbf v}  would vanish, and Lorentz factor of an arbitrary particle would be  Описание: ~\gamma =1. On the right-hand side we will have only the sum of terms specifying energy density of particles located in potentials of their proper fields. Since  Описание: ~\vartheta \approx \gamma _{c}c^{2},  we see that the cosmological constant for each system’s particle is up to the multiplier Описание: ~-ck  equal to rest energy density of this particle with a certain addition from its proper fields. Then the integral over volume of all the particles gives a certain energy:

Описание: ~-ck\int \Lambda dV=m'c^{2},

where the gauge mass  Описание: ~m'  is related to gauge condition of the energy.

In the process of gravitational clustering the particles that were initially far from each other are united into closely bound systems, in which the field potentials increase manyfold. In the system under consideration Описание: ~\gamma =\gamma ',  solenoidal vectors of fields are considered equal to zero due to random motion of particles, which gives the following:

 

Описание: ~m'c^{2}=\int [\gamma '\rho _{{0q}}\varphi _{i}+\gamma '\rho _{{0}}(\psi _{i}+\vartheta +\wp )]dV.

 

Expression on the right-hand side is part of relativistic energy ~E_{r}  of the system, so that the energy can be written as follows:

Описание: ~E_{r}=Mc^{2}\approx m'c^{2}-{\frac {\eta m^{2}\gamma _{c}^{2}}{10a}}\left(1-{\frac {3\eta m}{7ac^{2}}}\right)-{\frac {\sigma m^{2}\gamma _{c}^{2}}{10a}}\left(1-{\frac {3\eta m}{7ac^{2}}}\right)+

Описание: ~+{\frac {Gm^{2}\gamma _{c}^{2}}{10a}}\left(1-{\frac {3\eta m}{7ac^{2}}}\right)-{\frac {q^{2}\gamma _{c}^{2}}{40\pi \varepsilon _{0}a}}\left(1-{\frac {3\eta m}{7ac^{2}}}\right)+{\frac {Gm^{2}\gamma _{c}^{2}}{2a}}\left(1-{\frac {3\eta m}{5ac^{2}}}\right)-{\frac {q^{2}\gamma _{c}^{2}}{8\pi \varepsilon _{0}a}}\left(1-{\frac {3\eta m}{5ac^{2}}}\right).

 

The mass Описание: ~M  is related to relativistic energy of generally stationary system and is the inertial mass of the system. In view of (2), the energy will be equal to:

Описание: ~E_{r}=Mc^{2}\approx m'c^{2}+{\frac {Gm^{2}\gamma _{c}^{2}}{2a}}\left(1-{\frac {3\eta m}{5ac^{2}}}\right)-{\frac {q^{2}\gamma _{c}^{2}}{8\pi \varepsilon _{0}a}}\left(1-{\frac {3\eta m}{5ac^{2}}}\right).

 

This shows that relativistic energy of this system is equal to gauge mass-energy  Описание: ~m'c^{2}, from which the gravitational and electromagnetic energy of fields outside the system should be subtracted.

Lagrange function and motion integrals

Lagrange function for a system of particles and four main vector fields has the following form:[1] [2]

 

~L=-\int {(U_{\mu }J^{\mu }+\pi _{\mu }J^{\mu }+D_{\mu }J^{\mu }+A_{\mu }j^{\mu }){\sqrt {-g}}dx^{1}dx^{2}dx^{3}+}

~+\int {\left(ckR-2ck\Lambda -{\frac {c^{2}}{16\pi \eta }}u_{{\mu \nu }}u^{{\mu \nu }}-{\frac {c^{2}}{16\pi \sigma }}f_{{\mu \nu }}f^{{\mu \nu }}+{\frac {c^{2}}{16\pi G}}\Phi _{{\mu \nu }}\Phi ^{{\mu \nu }}-{\frac {c^{2}\varepsilon _{0}}{4}}F_{{\mu \nu }}F^{{\mu \nu }}\right){\sqrt {-g}}dx^{1}dx^{2}dx^{3}}.

Here ~R  is scalar curvature. With the help of such Lagrange function, one can calculate the generalized momentum of the system:[16]

~{\mathbf p}={\frac {1}{c}}\int {(\rho _{0}{\mathbf U}+\rho _{0}{\mathbf \Pi }+\rho _{0}{\mathbf D}+\rho _{{0q}}{\mathbf A})u^{0}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}.

This vector depends on vector potentials of all four fields and is preserved in a closed physical system, that is, it is an integral of motion. Another integral of motion is relativistic energy of the system ~E_{r} , which is found by formula (5). Further, it is assumed that one can neglect the contributions from gravitational and electromagnetic fields outside the matter and take into account only the generalized momentum. Then we can assume that these values form a four-momentum of the system, written with a covariant index:

~p_{\mu }=\left({\frac {E_{r}}{c}},-{\mathbf p}\right).

The angular momentum of the system is also an integral of motion:

~{\mathbf M}={\frac {1}{c}}\int {(\rho _{0}[{\mathbf r}\times {\mathbf U}]+\rho _{0}[{\mathbf r}\times {\mathbf \Pi }]+\rho _{0}[{\mathbf r}\times {\mathbf D}]+\rho _{{0q}}[{\mathbf r}\times {\mathbf A}])u^{0}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}.

The antisymmetric angular momentum pseudotensor is determined through the four-radius  ~x_{\mu } , taken with a covariant index, and through the four-momentum  ~p_{\mu } :

~M_{{\mu \nu }}=\int {(x_{\mu }dp_{\nu }-x_{\nu }dp_{\mu })}.

The spatial components of the angular momentum pseudotensor ~M_{{\mu \nu }}  are the components of the angular momentum ~{\mathbf M}  of the system:

~M_{{12}}=-M_{{21}}=-M_{z},\qquad M_{{13}}=-M_{{31}}=M_{y},\qquad M_{{23}}=-M_{{32}}=-M_{x}.

The radius-vector of the center of momentum of a physical system is determined by the formula:

~{\mathbf R}_{m}={\frac {1}{cE_{r}}}\int {(\rho _{0}\vartheta +\rho _{0}\wp +\rho _{0}\psi +\rho _{{0q}}\varphi ){\mathbf r}u^{0}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}+}

~+{\frac {1}{E_{r}}}\int {\left({\frac {c^{2}}{16\pi \eta }}u_{{\mu \nu }}u^{{\mu \nu }}+{\frac {c^{2}}{16\pi \sigma }}f_{{\mu \nu }}f^{{\mu \nu }}-{\frac {c^{2}}{16\pi G}}\Phi _{{\mu \nu }}\Phi ^{{\mu \nu }}+{\frac {c^{2}\varepsilon _{0}}{4}}F_{{\mu \nu }}F^{{\mu \nu }}\right){\mathbf r}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}.

The time components of the pseudotensor  ~M_{{\mu \nu }}  are the components of the three-dimensional vector ~{\mathbf {{\mathbb C}}} , which is often called the time-varying dynamic mass moment:

~M_{{01}}=-M_{{10}}=-{\mathbb C}_{x},\qquad M_{{02}}=-M_{{20}}=-{\mathbb C}_{y},\qquad M_{{03}}=-M_{{30}}=-{\mathbb C}_{z}.

If we take into account definition of radius-vector of center of momentum and relationship between the momentum and velocity of the center of momentum in the form ~{\mathbf p}={\frac {E_{r}}{c^{2}}}{\mathbf V} , we get the relation:

~{\mathbf {{\mathbb C}}}={\frac {E_{r}}{c}}({\mathbf V}t-{\mathbf R}_{m}).

In a closed system the pseudotensor ~M_{{\mu \nu }}  must be conserved, and its components must be some constants. For space components of the pseudotensor this results in conservation of angular momentum: ~{\mathbf M}=const . From equality of the pseudotensor’s time components and components of the vector ~{\mathbf {{\mathbb C}}}  it follows that it should be  ~{\mathbf {{\mathbb C}}}=const. Given the expression for ~{\mathbf {{\mathbb C}}} , it can be written as  ~{\mathbf R}_{m}={\mathbf R}_{{m0}}+{\mathbf V}t , where the constant vector  ~{\mathbf R}_{{m0}} specifies position of the system’s center of momentum at  ~t=0. Thus, in this reference frame we obtain equation of motion of the center of momentum at constant velocity ~{\mathbf V}, as a property of motion of a closed system.

The component ~M_{z}  of angular momentum of a uniform ball, taking into account relativistic corrections, can be calculated by the formula: [17]

~M_{z}={\frac {3\pi \rho _{0}c^{4}a}{2\omega ^{3}}}-{\frac {\pi \rho _{0}c^{2}a^{3}}{2\omega }}-{\frac {3\pi \rho _{0}c^{5}\left(1-{\frac {\omega ^{2}a^{2}}{c^{2}}}\right)\left(1+{\frac {\omega ^{2}a^{2}}{3c^{2}}}\right)}{4\omega ^{4}}}\ln {\frac {1+{\frac {\omega a}{c}}}{1-{\frac {\omega a}{c}}}}.

Here ~\rho _{0}  is invariant mass density, ~\omega   is angular velocity of rotation of the ball having a radius ~a.

 

Integral vector

The equation used to find metric tensor components in covariant theory of gravitation for tensors with mixed indices has the following form:[2]

~R_{\alpha }^{{\ \beta }}-{\frac {1}{4}}R\delta _{\alpha }^{{\ \beta }}=-{\frac {1}{2ck}}\left(B_{\alpha }^{{\ \beta }}+P_{\alpha }^{{\ \beta }}+U_{\alpha }^{{\ \beta }}+W_{\alpha }^{{\ \beta }}\right).

here  ~R_{\alpha }^{{\ \beta }} is Ricci tensor with mixed indices; ~\delta _{\alpha }^{{\ \beta }}  is unit tensor or Kronecker delta; ~B_{\alpha }^{{\ \beta }} , ~P_{\alpha }^{{\ \beta }} , ~U_{\alpha }^{{\ \beta }} and  ~W_{\alpha }^{{\ \beta }} are stress-energy tensors of acceleration field and pressure field, gravitational and electromagnetic fields, respectively.

With the help of covariant derivative ~\nabla _{\beta }  we can find four-divergence of both sides of the above equation for metric. The divergence of the left-hand side is zero due to equality to zero of divergence of t Einstein tensor,  ~\nabla _{\beta }\left(R_{\alpha }^{{\ \beta }}-{\frac {1}{2}}R\delta _{\alpha }^{{\ \beta }}\right)=0  , and also as a consequence of the fact that outside the body the scalar curvature vanishes, ~R=0, and inside the body it is constant. The latter follows from the gauge condition of energy of closed system. The divergence of the right-hand side of equation for the metric is also zero:

~\nabla _{\beta }\left(B_{\alpha }^{{\ \beta }}+P_{\alpha }^{{\ \beta }}+U_{\alpha }^{{\ \beta }}+W_{\alpha }^{{\ \beta }}\right)=\nabla _{\beta }T_{\alpha }^{{\ \beta }}=0,

where the tensor  ~T_{\alpha }^{{\ \beta }} with mixed indices represents the sum of stress-energy tensors of all fields acting in the system.

The resulting expression for tensors’ space components is nothing but differential equation of matter’s motion under action of forces generated by fields, which is written in a covariant form. [13] As for the tensors’ time components, for them the expression is expression of generalized Poynting theorem for all the fields. [9]

In a weak field and at low velocities of motion of particles, the equation  ~\nabla _{\beta }T_{\alpha }^{{\ \beta }}\approx \partial _{\beta }T_{\alpha }^{{\ \beta }}=0  can be integrated over four-volume, taking into account the divergence theorem. As a result, at the initial moment of time for the system under consideration, the following relation will be valid:

~J_{\alpha }=\int {T_{\alpha }^{{\ 0}}dx^{1}dx^{2}dx^{3}}=const.

In a closed system, the four-dimensional integral vector  ~J_{\alpha }  must be constant. [16]  For a stationary sphere with randomly moving particles in continuous medium approximation, the energy fluxes of fields defining the components  ~T_{j}^{{\ 0}} , where  ~j=1,2,3 , are missing , so that the spatial components are zero,  ~J_{j}=0 . As for the time component  ~J_{0}  of integral vector, then for volume occupied by matter inside the sphere, it also vanishes due to relation (4) for field coefficients. However, outside the sphere, where there are only gravitational and electromagnetic fields, the time component of integral vector is not equal to zero. As a result, the contribution to this component is made by energies of external fields:

~J_{0}=-{\frac {Gm_{g}^{2}}{2a}}+{\frac {q_{b}^{2}}{8\pi \varepsilon _{0}a}}.

It follows from the above that integral vector shows distribution of energy and energy fluxes in the system under consideration.

For the nonzero space components  ~J_{j}  of integral vector to appear some stationary motion of matter and fields is required, for example, general rotation, volume pulsations or mixing of matter. In this case, solenoidal vectors and the fields’ energy fluxes appear in the system.

Since the integral vector  ~J_{\alpha }  is associated with energies and energy fluxes of fields in stress-energy tensors, it differs from the four-momentum  ~p_{\mu } , which includes invariant mass and proportional to its rest energy. It turns out that difference between ~J_{\alpha } and  ~p_{\mu }  is due to fundamental difference between particles and fields, they cannot be reduced to each other, although they are interrelated with each other.

Virial theorem and kinetic energy of particles

In article [18] kinetic energy of particles of the system under consideration is estimated by three methods: from virial theorem, from relativistic definition of energy and using generalized momenta and proper fields of the particles. In the limit of low velocities, all these methods give for kinetic energy the following:

Описание: ~E_{k}\approx {\frac {0.3608\eta m^{2}\gamma _{c}}{a}}.

The possibility to use generalized momenta to calculate the energy of particles’ motion is associated with the fact that despite zeroing of vector potentials and solenoidal vectors on the large scale, in volume of each randomly moving particle these potentials and vectors are not equal to zero. As a result, the energy of motion of the system’s particles can be found as the half-sum of scalar products of vector field potentials by the particles’ momentum, while for electromagnetic field we should take not the momentum, but the product of charge by velocity and Lorentz factor.

If we square the equation for Описание: ~\gamma '  in (1), we can obtain dependence of squared velocity of particles’ random motion on current radius:

Описание: ~{v'}^{2}\approx v_{c}^{2}-{\frac {4\pi \eta \rho _{0}r^{2}}{3}}.

On the other hand, we can assume that  Описание: ~{\mathbf v}'={\mathbf v}_{r}+{\mathbf v}_{\perp },   where Описание: ~{\mathbf v}_{r}  denotes averaged velocity component directed along the radius, and Описание: ~{\mathbf v}_{\perp }  is averaged velocity component perpendicular to the current radius. In addition, from statistical considerations, it follows that

Описание: ~{v'}^{2}=v_{r}^{2}+v_{\perp }^{2}=3v_{r}^{2}.

 

This implies dependence of radial velocity on the radius:

Описание: ~v_{r}\approx {\frac {v_{c}}{{\sqrt 3}}}\left(1-{\frac {2\pi \eta \rho _{0}r^{2}}{3v_{c}^{2}}}\right).

 

Next, from the virial theorem we find squared velocity of particles at the center of the sphere:

Описание: ~v_{c}^{2}\approx {\frac {3\eta m}{5a}}\left(1+{\frac {9}{{\sqrt {56}}}}\right)\approx {\frac {1.3216\eta m}{a}}.

 

This makes it possible to estimate the Lorentz factor at the center:

 

~\gamma _{c}={\frac {1}{{\sqrt {1-{\frac {v_{c}^{2}}{c^{2}}}}}}}\approx 1+{\frac {v_{c}^{2}}{2c^{2}}}+{\frac {3v_{c}^{4}}{8c^{4}}}\approx 1+{\frac {3\eta m}{10ac^{2}}}\left(1+{\frac {9}{2{\sqrt {14}}}}\right)+{\frac {27\eta ^{2}m^{2}}{200a^{2}c^{4}}}\left(1+{\frac {9}{2{\sqrt {14}}}}\right)^{2}.

 

In the ordinary interpretation of virial theorem the time-averaged kinetic energy of a system of particles must be two times less than averaged energy associated with the forces Описание: ~{\mathbf F}_{i}   holding the particles at the radius-vectors  Описание: ~{\mathbf r}_{i} :

Описание: ~\langle W_{k}\rangle _{m}=-0.5\langle \sum _{{i=1}}^{{N}}{\mathbf F}_{i}\cdot {\mathbf r}_{i}\rangle .

 

However, in relativistic uniform system this equation is changed:

Описание: ~\langle W_{k}\rangle \approx -0.6\langle \sum _{{i=1}}^{{N}}{\mathbf F}_{i}\cdot {\mathbf r}_{i}\rangle ,

 

while the quantity Описание: ~W_{k}  exceeds the kinetic energy of particles, Описание: ~W_{k}\approx \gamma _{c}E_{k},  and it becomes equal to it only in the limit of low velocities.

In contrast to classical case, total time derivative of virial in stationary system is other than zero due to the virial’s dependence on the radius:

Описание: ~{\frac {dG_{V}}{dt}}\approx {\mathbf v}\cdot \nabla {G_{V}}\approx {\frac {0.1216\eta m^{2}\gamma _{c}^{2}}{a}}.

 

An analysis of integral theorem of generalized virial makes it possible to find, on the basis of field theory, a formula for the root-mean-square speed of typical particles of a system without using the notion of temperature: [19]

 

v_{{\mathrm {rms}}}=c{\sqrt {1-{\frac {4\pi \eta \rho _{0}r^{2}}{c^{2}\gamma _{c}^{2}\sin ^{2}{\left({\frac {r}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)}}}}}.

 

Extreme objects

In formula (2) for gravitational field strength  Описание: {\displaystyle ~\mathbf {\Gamma } _{o}}  outside a body there is a quantity  Описание: {\displaystyle ~A=\sin \delta -\delta \cos \delta } , where  Описание: {\displaystyle ~\delta ={\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}} . As was shown in article, [11] at the value  Описание: {\displaystyle ~\delta =\delta _{0}=4.494}  radians the gravitational field strength  Описание: {\displaystyle ~\mathbf {\Gamma } _{o}}  vanishes and gravitational acceleration disappears. Therefore, in real physical objects the following condition must hold:  Описание: {\displaystyle ~\delta ={\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}<\delta _{0}} . If the angle  Описание: {\displaystyle ~\delta }  is increased, then the quantity  Описание: {\displaystyle ~A}  would first increase, and then would begin to decrease and even change its sign. So, at  Описание: {\displaystyle ~\delta ={\frac {\pi }{2}}}  we have  Описание: {\displaystyle ~A=1} , at  Описание: {\displaystyle ~\delta =\pi }  we have  Описание: {\displaystyle ~A=\pi } , at  Описание: {\displaystyle ~\delta ={\frac {3\pi }{2}}}  we have  Описание: {\displaystyle ~A=-1} .

Let us now consider the observable Universe, which on a scale 100 Mpc or more can be considered as a relativistic uniform system. The total mass-energy density of the Universe is close to the critical value  Описание: {\displaystyle ~\rho _{c}\approx 10^{-26}}  kg/m3 and the size of the Universe can be estimated as the Hubble length  Описание: {\displaystyle ~R_{H}=c/H_{0}\approx 10^{26}}  m, where  Описание: {\displaystyle ~H_{0}}  is Hubble parameter.

Using approximate equality  Описание: {\displaystyle ~\eta \approx {\frac {3}{5}}G}  according to, [14]  we find the value  Описание: {\displaystyle ~\delta _{U}={\frac {R_{H}}{c}}{\sqrt {4\pi \eta \rho _{c}}}\approx 1.7>{\frac {\pi }{2}}}  radians. Since the angle  Описание: {\displaystyle ~\delta _{U}}  is sufficiently large, then for modeling of gravitational field of the Universe it is necessary to use refined formulas with sines and cosines. For example, if we take the size of observable Universe equal to  Описание: {\displaystyle ~2.64R_{H}} , then we have  Описание: {\displaystyle ~\delta _{U}=\delta _{0}} , and gravitational field at t boundaries of the Universe will tend to zero. This is what we observe in the form of a large-scale cellular structure consisting of clusters of galaxies. The reason for the gravitation action weakening is assumed to be graviton scattering by the particles of space medium. [20]

Another extreme object is a proton, in which mass density in entire volume changes approximately by 1.5 times. As a result, in the first approximation a proton is a relativistic uniform system. The proton radius  Описание: {\displaystyle ~r_{p}}  is of the order of 0.873 fm, [21] and average density is of the order of  Описание: {\displaystyle ~\rho _{p}=6\cdot 10^{17}}  kg/m3. As a gravitational constant at the atomic level the strong gravitational constant  Описание: {\displaystyle ~G_{s}}  should be used. An estimate of the quantity  Описание: {\displaystyle ~\delta }  for a proton at  Описание: {\displaystyle ~\eta \approx {\frac {3}{5}}G_{s}}  gives:  Описание: {\displaystyle ~\delta _{p}={\frac {r_{p}}{c}}{\sqrt {4\pi \eta \rho _{p}}}\approx 2.4<\delta _{0}}  radians. This shows that a proton is an extreme object from the point of view of weakening of its gravitational field.

In article, [11] a method is provided for estimating Lorentz factor of matter’s motion at the center of a proton, which gives  Описание: {\displaystyle ~\gamma _{c}=1.9} . In addition, radius of action of strong gravitation in matter with the critical mass density  Описание: {\displaystyle ~\rho _{c}\approx 10^{-26}}  kg/m3 in observable Universe is estimated:  Описание: {\displaystyle ~r_{G}<1.3\cdot 10^{7}}  m. On a large scale in the Universe not the strong gravitation, but the ordinary gravitation is acting with the radius of action of the order of Hubble length.

Let us suppose that  Описание: {\displaystyle ~r_{G}}  corresponds to radius of a certain black hole for strong gravitation, calculated by the Schwarzschild formula:  Описание: {\displaystyle ~r_{G}={\frac {2G_{s}m}{c^{2}}}} . If the mass is  Описание: {\displaystyle ~m={\frac {4\pi \rho _{c}r_{G}^{3}}{3}}} , then for radius of a black hole with such mass we obtain Описание: {\displaystyle ~r_{G}=c{\sqrt {\frac {3}{8\pi G_{s}\rho _{c}}}}=2.7\cdot 10^{6}}  m, and mass is  Описание: {\displaystyle ~m=8\cdot 10^{-7}}  kg. The Schwarzschild formula admits a black hole for strong gravitation at small mass of the order of proton mass, large mass density and a radius smaller than the proton radius. In addition, substitution of the mass  Описание: {\displaystyle ~m}  and the radius  Описание: {\displaystyle ~r_{G}}  into Schwarzschild formula formally corresponds to a black hole with a large radius and low density  Описание: {\displaystyle ~\rho _{c}}. However, for an external observer, such a black hole would rather correspond not to a black hole, but to an object, containing strongly rarefied hydrogen gas of cosmic space. Similarly, the Metagalaxy with the radius of order of  Описание: {\displaystyle ~r_{H}}  and mass density  Описание: {\displaystyle ~\rho _{c}}  is not a black hole, although it corresponds to the Schwarzschild formula for ordinary gravitation.

Hence, in accordance with the theory of infinite nesting of matter, conclusion follows – at each level of matter corresponding gravitation forms only one type of the most compact and stable object. So, at the level of nucleons a proton appears under the action of strong gravitation, and at the level of stars the ordinary gravitation generates a neutron star. If we multiply the radius of a neutron star by coefficient of similarity in size  Описание: {\displaystyle ~P=1.4\cdot 10^{19}} , which is equal to the ratio of stellar radius to the proton radius, we obtain radius of the order of  Описание: {\displaystyle 1.7\cdot 10^{23}}  m. This radius must correspond to a compact object of a neutron star-type at the level of metagalaxies, which can emerge under the action of gravitation at this matter level. In the first approximation, the gravitational constant for metagalaxies is determined with the help of the similarity theory:  Описание: {\displaystyle ~G_{M}={\frac {GPS^{2}}{\Phi }}=3\cdot 10^{-50}}  m3•s–2•kg–1, where  Описание: {\displaystyle ~S=0.23}  is coefficient of similarity in velocities,  Описание: {\displaystyle ~\Phi =1.62\cdot 10^{57}}  is coefficient of similarity in mass.

By analogy with the case of a proton, a neutron star is also considered as a relativistic uniform system. For a star with the mass of 1.35 Solar masses, the radius  Описание: {\displaystyle ~R_{s}=12}  km and average density  Описание: {\displaystyle ~\rho _{s}\approx 3.7\cdot 10^{17}}  kg/m3, at  Описание: {\displaystyle ~\eta \approx {\frac {3}{5}}G}  we obtain the angle  Описание: {\displaystyle ~\delta _{s}={\frac {R_{s}}{c}}{\sqrt {4\pi \eta \rho _{s}}}\approx 0.546}  radians. With this in mind, if we substitute into (3) the stellar mass instead of Описание: {\displaystyle ~m_{b}}  and the stellar radius instead of  Описание: {\displaystyle ~a} , we can estimate Lorentz factor at the center of the star:  Описание: {\displaystyle ~\gamma _{cs}=1.04} . This allows us to estimate temperature at the center of the star:  Описание: {\displaystyle ~T_{s}\approx 2.8\cdot 10^{11}}  K, which is close enough to calculation of temperature at the center of a newly formed star. [14]

Thus, dependences of gravitational field inside and outside bodies in article [11] are in good agreement with conclusions of Le Sage’s theory of gravitation and the theory of Infinite Hierarchical Nesting of Matter, with strong gravitation at the level of nucleons and with the concept of a dynamic force field in electrogravitational vacuum.

Cosmological constant and scalar curvature

According to (6), outside a body, where the four-currents are equal to zero, cosmological constant  {\displaystyle ~\Lambda }  becomes equal to zero. In addition, scalar curvature {\displaystyle ~R}  also becomes equal to zero. [4]  Inside the body the relation  {\displaystyle ~R=2\Lambda }  holds true, so that in matter with higher density both the scalar curvature and the cosmological constant increase. These quantities can be calculated using (6) as averaged values for typical particles of physical system. For cosmic space we obtain approximately the following: {\displaystyle ~\Lambda _{0}\approx {\frac {16\pi G\rho _{0}}{c^{2}}}\approx 10^{-52}} m-2, where the average mass density is {\displaystyle ~\rho _{0}\approx 2.7\cdot 10^{-27}} kg/m3.

A similar formula for a proton gives the following: {\displaystyle ~\Lambda \approx {\frac {16\pi G\rho _{p}}{c^{2}}}\approx 2.2\cdot 10^{-8}} m-2. However, for a proton in the calculations we should use the strong gravitational constant  {\displaystyle ~G_{s}} . In this case, we find: {\displaystyle ~\Lambda _{p}\approx {\frac {16\pi G_{s}\rho _{p}}{c^{2}}}\approx 5.1\cdot 10^{31}} m-2. The obtained value is almost 84 orders of magnitude greater than the value of cosmological constant for cosmic space. The difference between cosmological constants for cosmic space and for a proton is associated with averaging procedure: the cosmological constant inside a proton is large, but in cosmic space matter containing protons, neutrons and electrons is very rarefied, the main place is occupied by void, so that cosmological constant averaged over entire space becomes a small value. Thus one of the paradoxes of general theory of relativity is solved, in which the cosmological constant is associated with zero vacuum energy and therefore it must be very large, but in fact the cosmological constant turns out to be a small value.

For relativistic uniform system with four fields acting in it, average value  {\displaystyle ~{\stackrel {-}{\Lambda }}}  of cosmological constant in matter is constant and can be written as follows:

 

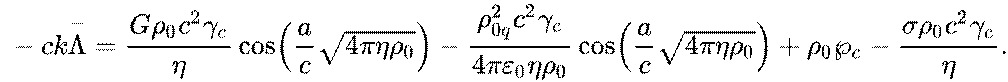
{\displaystyle ~-ck{\stackrel {-}{\Lambda }}={\frac {G\rho _{0}c^{2}\gamma _{c}}{\eta }}\cos \left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)-{\frac {\rho _{0q}^{2}c^{2}\gamma _{c}}{4\pi \varepsilon _{0}\eta \rho _{0}}}\cos \left({\frac {a}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)+\rho _{0}\wp _{c}-{\frac {\sigma \rho _{0}c^{2}\gamma _{c}}{\eta }}.}

This expression can be simplified by using scalar potential of gravitational field  {\displaystyle ~\psi _{a}=-{\frac {Gm_{g}}{a}}} and scalar potential of electric field  {\displaystyle ~\varphi _{a}={\frac {q_{b}}{4\pi \varepsilon _{0}a}}} on surface of body at  {\displaystyle ~r=a}  :

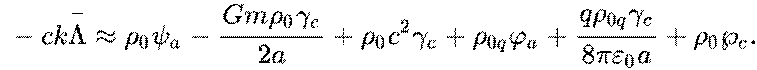
{\displaystyle ~-ck{\stackrel {-}{\Lambda }}\approx \rho _{0}\psi _{a}-{\frac {Gm\rho _{0}\gamma _{c}}{2a}}+\rho _{0}c^{2}\gamma _{c}+\rho _{0q}\varphi _{a}+{\frac {q\rho _{0q}\gamma _{c}}{8\pi \varepsilon _{0}a}}+\rho _{0}\wp _{c}.}

 

Field energy theorem

In a relativistic uniform system, the exact values of strengths and potentials of all active fields are known. This allows us to check the field energy theorem for such a system and verify the theorem.[22] This theorem explains, in particular, why electrostatic energy can be calculated either through the field strength, included in the electromagnetic field tensor, or in another way, through the field potential.

The kinetic energy and potential energy of electromagnetic field are defined as follows:

~E_{{kf}}=\int {A_{\alpha }j^{\alpha }{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}.

 

~W_{f}={\frac {1}{4\mu _{0}}}\int {F_{{\mu \nu }}F^{{\mu \nu }}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}.

If we take entire infinite volume both inside and outside matter of the system, then in the framework of special theory of relativity and in the absence of magnetic fields, these expressions are simplified:

 

~E_{{kf}}=\int \rho _{q}\varphi _{i}dV\approx {\frac {3q^{2}\gamma _{c}^{2}}{10\pi \varepsilon _{0}a}}\left(1-{\frac {4\eta m}{7ac^{2}}}\right).

 

~W_{{fi}}=\int \limits _{{r=0}}^{{a}}{\frac {c^{2}\varepsilon _{0}}{4}}F_{{\mu \nu }}F^{{\mu \nu }}dV\approx -{\frac {q^{2}\gamma _{c}^{2}}{40\pi \varepsilon _{0}a}}\left(1-{\frac {3\eta m}{7ac^{2}}}\right).

 

~W_{{fo}}=\int \limits _{{r=a}}^{{\infty }}{\frac {c^{2}\varepsilon _{0}}{4}}F_{{\mu \nu }}F^{{\mu \nu }}dV\approx -{\frac {q^{2}\gamma _{c}^{2}}{8\pi \varepsilon _{0}a}}\left(1-{\frac {3\eta m}{5ac^{2}}}\right).

 

~W_{f}=W_{{fi}}+W_{{fo}}\approx -{\frac {3q^{2}\gamma _{c}^{2}}{20\pi \varepsilon _{0}a}}\left(1-{\frac {4\eta m}{7ac^{2}}}\right).

By virtue of the field energy theorem, the following relation will be satisfied:

~E_{{kf}}+2W_{f}=0.

In general case, tensor invariant is expressed in terms of square of electric field strength and square of magnetic field induction: ~F_{{\mu \nu }}F^{{\mu \nu }}=-{\frac {2}{c^{2}}}(E^{2}-c^{2}B^{2}) . The field energy density is found through the time component of stress-energy tensor: ~W^{{00}}={\frac {1}{2}}(\varepsilon _{0}E^{2}+{\frac {1}{\mu _{0}}}B^{2}) .

In electrostatics, when there are no magnetic fields and ~B=0, volume integral of tensor invariant becomes proportional to volume integral of the component  ~W^{{00}} . As a result, electrostatic energy can be calculated in different ways:

~U_{e}=E_{{kf}}+W_{f}\approx {\frac {3q^{2}\gamma _{c}^{2}}{20\pi \varepsilon _{0}a}}\left(1-{\frac {4\eta m}{7ac^{2}}}\right).

Besides:

~U_{e}=-W_{f}={\frac {1}{2}}E_{{kf}}=\int W^{{00}}dV.

 

Binding energy

With the help of covariant theory of gravitation total energy, binding energy, energy of fields, pressure energy and potential energy of a system consisting of particles and four fields is precisely calculated in the relativistic uniform model. [23] A noticeable difference is shown between the obtained results and relations for simple systems in classical mechanics, in which the acceleration field and pressure field are not taken into account or the pressure is considered to be a simple scalar quantity. In this case the inertial mass of a massive system is less than the total inertial mass of the system’s parts.

 

System mass

The article [24] shows that relativistic uniform system with continuous matter distribution is characterized by five types of mass: the gauge mass ~m'  is related to cosmological constant and represents mass-energy of matter’s particles in four-potentials of the system’s fields; the inertial mass ~M; the auxiliary mass ~m is equal to product of the particles’ mass density by volume of the system; the mass ~m_{b}  is the sum of invariant masses (rest masses) of the system’s particles, which is equal in value to gravitational mass ~m_{g} . The relation for these masses is as follows:

~m'<M<m<m_{b}=m_{g}.

 

Solution of 4/3 problem

For the electromagnetic and gravitational fields, the 4/3 problem consists in inequality of mass-energy extracted from the energy of field of a body at rest, and mass-energy resulting from the field momentum of the moving body. If such a body is a relativistic uniform system of spherical shape, then mass-energy associated with electrostatic energy of the system is:

~m_{f}={\frac {E_{e}}{c^{2}}}\approx {\frac {3q^{2}\gamma _{c}^{2}}{20\pi \varepsilon _{0}ac^{2}}}.

The energy flux of electromagnetic field of a moving sphere is calculated using the Poynting vector. Let ~\gamma  be Lorentz factor, and ~v be velocity of the sphere. Having calculated energy fluxes of the field inside and outside the sphere, as well as total energy flux, we can find corresponding quantities with dimension of momentum associated with these energy fluxes: [9]

 

~g_{{pi}}\approx {\frac {\gamma q^{2}\gamma _{c}^{2}v}{30\pi \varepsilon _{0}ac^{2}}}.

 

~g_{{po}}\approx {\frac {\gamma q^{2}\gamma _{c}^{2}v}{6\pi \varepsilon _{0}ac^{2}}}.

 

~g_{p}=g_{{pi}}+g_{{po}}\approx {\frac {\gamma q^{2}\gamma _{c}^{2}v}{5\pi \varepsilon _{0}ac^{2}}}.

From here we find the mass-energy associated with the field energy fluxes:

~m_{p}={\frac {g_{p}}{\gamma v}}\approx {\frac {q^{2}\gamma _{c}^{2}}{5\pi \varepsilon _{0}ac^{2}}}.

For mass-energies, a ratio describing the 4/3 problem is obtained:

~m_{p}={\frac {4}{3}}m_{f}.

If we consider the energy and energy flux of electromagnetic field only inside the sphere, or only outside the sphere, similar correlations are obtained for corresponding mass-energies.

As indicated in the article, [9]  the mass-energy mismatch is a consequence of the fact that time components of electromagnetic stress-energy tensor and their integrals over volume do not together form any four-vector. In contrast, four-momentum of a system is a four-vector, so that the same inertial mass enters both the energy and momentum of the system. On the other hand, energy and momentum of electromagnetic field are included only as components in energy and momentum of entire system under consideration, and therefore they themselves do not have to form a four-vector.

To calculate a four-momentum of the system, it is necessary to add energy and momentum of other fields operating in the system to the energy and momentum of electromagnetic field. In addition to electromagnetic field, the minimum set of fields of the system includes acceleration field, pressure field and gravitational field, and therefore it is necessary to take into account their energy and momentum. In this case, inside the sphere, the sum of energies of all fields found through tensor invariants and through stress-energy tensors is zeroed out. The total energy flux and total momentum of fields inside the sphere are also zero, so that within the sphere, the 4/3 problem as applied to general field disappears. The equality to zero of sum of energies and sum of momenta of fields inside the sphere with randomly moving particles is a consequence of the fact that particles and fields have the opportunity to exchange energy and momentum with each other. As a result, contribution to relativistic energy of the system is made only by particle energies in scalar potentials of fields, and energies of electromagnetic and gravitational fields outside the sphere.

The 4/3 problem shows in particular why energy and momentum of an electron and any other body cannot be reduced only to action of its own electromagnetic field. Despite the fact that an electron has a maximum charge per unit mass and is extremely charged, there are other fields in the electron's matter, for example strong gravitation. These fields have their own energy and momentum, which contribute to four-momentum of the electron.

Relations between field potentials

In the article, [25] a connection was found between scalar potentials of acceleration field and pressure field in relativistic uniform system:

~\wp ={\frac {\sigma (\vartheta -c^{2})}{\eta }}={\frac {2(\vartheta -c^{2})}{3}}.

In addition, a relativistic expression for pressure was found:

p={\frac {2\rho c^{2}(\gamma -1)}{3}}={\frac {2\rho c^{2}}{3}}\left({\frac {1}{{\sqrt {1-v^{2}/c^{2}}}}}-1\right)\approx {\frac {\rho v^{2}}{3}},

where  \rho  is mass density of moving matter, c is speed of light,  \gamma ={\frac {1}{{\sqrt {1-v^{2}/c^{2}}}}}  is Lorentz factor.

In the limit of low velocities, this relationship turns into standard formula of kinetic theory of gases.

Metric inside and outside system

Standard expression for square of interval between two close points in metric theories is the following:

ds^{2}\ =\ g_{{\mu \nu }}(x)\ dx^{{\mu }}\ dx^{{\nu }}.

For static metric with spherical coordinates x^{0}=ct,  x^{1}=r, x^{2}=\theta , x^{3}=\phi , there are four nonzero components of the metric tensor: g_{{00}}, g_{{11}}, g_{{22}}, and g_{{33}}=g_{{22}}\sin ^{2}\theta . As a result, there is

ds^{2}\ =g_{{00}}c^{2}dt^{2}+g_{{11}}dr^{2}+g_{{22}}d\theta ^{2}+g_{{22}}\sin ^{2}\theta d\phi ^{2}.

As it was found for components of metric inside a spherical body within the framework of relativistic uniform model, [26]  g_{{22}}=-r^{2}, and

 

(g_{{00}})_{i}=-{\frac {1}{(g_{{11}})_{i}}}=1+{\frac {8\pi G\beta r^{2}}{3c^{4}}}\left(\rho _{0}c^{2}\gamma _{c}+\rho _{0}\psi _{a}-{\frac {Gm\rho _{0}\gamma _{c}}{2a}}+\rho _{{0q}}\varphi _{a}+{\frac {q\rho _{{0q}}\gamma _{c}}{8\pi \varepsilon _{0}a}}+\rho _{0}\wp _{c}\right),

 

where G is gravitational constant; \beta  is a coefficient to be determined; r is radial coordinate; c is the speed of light; \rho _{0}  is invariant mass density of matter particles; \gamma _{c} is Lorentz factor of particles moving at the center of body; \psi _{a}=-{\frac {Gm_{g}}{a}} is gravitational potential at the surface of sphere with radius a and gravitational mass m_{g} ; quantities m={\frac {4\pi a^{3}\rho _{0}}{3}}  and  q={\frac {4\pi a^{3}\rho _{{0q}}}{3}}  are auxiliary values; \rho _{{0q}} is invariant charge density of matter particles, moving inside the body; \varphi _{a}={\frac {q_{b}}{4\pi \varepsilon _{0}a}} is electric scalar potential at the surface of sphere with total charge q_{b}; \wp _{c} is potential of pressure field at the center of body.

On surface of the body, with r=a, the component (g_{{00}})_{i} of metric tensor inside the body must be equal to the component (g_{{00}})_{o} of metric tensor outside the body. This allows us to refine expression for metric tensor components outside the body:

(g_{{00}})_{o}=-{\frac {1}{(g_{{11}})_{o}}}=1+{\frac {2Gm\gamma _{c}\beta }{c^{2}r}}+{\frac {2G\beta }{c^{4}r}}\left(m\psi _{a}+{\frac {1}{2}}m_{g}(\psi -\psi _{a})-{\frac {Gm^{2}\gamma _{c}}{2a}}+q\varphi _{a}+{\frac {1}{2}}q_{b}(\varphi -\varphi _{a})+{\frac {q^{2}\gamma _{c}}{8\pi \varepsilon _{0}a}}+m\wp _{c}\right),

where \psi =-{\frac {Gm_{g}}{r}} is gravitational potential outside the body; \varphi ={\frac {q_{b}}{4\pi \varepsilon _{0}r}} is electric potential outside the body.

 

Generalized four-momentum and total four-momentum

In the paper, [27] formulas were found for calculating generalized four-momentum of a physical system in curved space-time taking into account contribution from particles and fields of the system. A differential four-dimensional Euler-Lagrange equation for continuously distributed matter was also obtained. Both the formulas for generalized four-momentum and Euler-Lagrange equation are satisfied in relativistic uniform system. In the paper, [28] covariant formulas for relativistic four-momentum of a physical system were derived, which were also verified in a relativistic uniform system. It was shown that four-momentum is expressed by the sum of two four-vectors of integral type with covariant indices, one of these four-vectors is generalized four-momentum of the system, and the other four-vector describes four-momentum of fields of the system. Additionally, the 4/3 problem and interpretation of integral vector found by integrating over volume of time components of stress-energy tensor of the system were considered. The fact that integral vector cannot be four-momentum of the system, as is assumed in general theory of relativity, is confirmed by direct calculation and follows from the fact that a four-vector cannot be obtained from tensor components. Similarly, volume integral of time components of stress-energy tensor of electromagnetic field does not yield four-momentum of electromagnetic field, but an integral vector that is not a four-vector. As a consequence, the mass-energies contained in components of integral vector are not equal to each other and are related in the proportion 4/3.

Covariant formulas for four-momentum were used to determine the components of angular momentum tensor of a physical system in the article. [29]

 

References

  1. 1.0 1.1 1.2 1.3 Fedosin S.G. The procedure of finding the stress-energy tensor and vector field equations of any form. Advanced Studies in Theoretical Physics, Vol. 8, no. 18, 771-779 (2014). http://dx.doi.org/10.12988/astp.2014.47101.
  2. 2.0 2.1 2.2 2.3 Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy. Jordan Journal of Physics. Vol. 9, No. 1, pp. 1-30 (2016). http://dx.doi.org/10.5281/zenodo.889304.
  3. 3.0 3.1 3.2 3.3 3.4 3.5 Fedosin S.G. The Integral Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based on the Pressure Field and Acceleration Field. American Journal of Modern Physics. Vol. 3, No. 4, pp. 152-167 (2014). http://dx.doi.org/10.11648/j.ajmp.20140304.12 .
  4. 4.0 4.1 4.2  4.3  Fedosin S.G. Energy and metric gauging in the covariant theory of gravitation. Aksaray University Journal of Science and Engineering, Vol. 2, Issue 2, pp. 127-143 (2018). http://dx.doi.org/10.29002/asujse.433947.
  5. Fedosin S.G. Fizicheskie teorii i beskonechnaia vlozhennost’ materii. – Perm, 2009, 844 pages, Tabl. 21, Pic. 41, Ref. 289. ISBN 978-5-9901951-1-0. (in Russian).
  6. Fedosin S.G. The Principle of Least Action in Covariant Theory of Gravitation. Hadronic Journal, Vol. 35, No. 1, pp. 35-70 (2012). http://dx.doi.org/10.5281/zenodo.889804.
  7. 7.0 7.1 7.2 Fedosin S.G. Relativistic Energy and Mass in the Weak Field Limit. Jordan Journal of Physics. Vol. 8, No. 1, pp. 1-16 (2015). http://dx.doi.org/10.5281/zenodo.889210.
  8. 8.0 8.1 8.2 Fedosin S.G. The electromagnetic field in the relativistic uniform model. International Journal of Pure and Applied Sciences, Vol. 4, Issue. 2, pp. 110-116 (2018). http://dx.doi.org/10.29132/ijpas.430614.
  9.  9.0 9.1 9.2 9.3 9.4  Fedosin S.G. The generalized Poynting theorem for the general field and solution of the 4/3 problem. International Frontier Science Letters, Vol. 14, pp. 19-40 (2019). https://doi.org/10.18052/www.scipress.com/IFSL.14.19.
  10. 10.0 10.1 Fedosin S.G. The gravitational field in the relativistic uniform model within the framework of the covariant theory of gravitation. 5th Ulyanovsk International School-Seminar “Problems of Theoretical and Observational Cosmology” (UISS 2016), Ulyanovsk, Russia, September 19-30, 2016, Abstracts, p. 23, ISBN 978-5-86045-872-7.
  11. 11.0 11.1 11.2 11.3 Fedosin S.G. The Gravitational Field in the Relativistic Uniform Model within the Framework of the Covariant Theory of Gravitation. International Letters of Chemistry, Physics and Astronomy, Vol. 78, pp. 39-50 (2018). http://dx.doi.org/10.18052/www.scipress.com/ILCPA.78.39.
  12. Fedosin S.G. The Concept of the General Force Vector Field. OALib Journal, Vol. 3, pp. 1-15 (2016), e2459. http://dx.doi.org/10.4236/oalib.1102459.
  13. 13.0 13.1 Fedosin S.G. Equations of Motion in the Theory of Relativistic Vector Fields. International Letters of Chemistry, Physics and Astronomy, Vol. 83, pp. 12-30 (2019). https://doi.org/10.18052/www.scipress.com/ILCPA.83.12.
  14. 14.0 14.1 14.2 Fedosin S.G. Estimation of the physical parameters of planets and stars in the gravitational equilibrium model. Canadian Journal of Physics, Vol. 94, No. 4, pp. 370-379 (2016). http://dx.doi.org/10.1139/cjp-2015-0593.
  15. Fedosin S.G. The Hamiltonian in Covariant Theory of Gravitation. Advances in Natural Science, Vol. 5, No. 4, pp. 55-75 (2012). http://dx.doi.org/10.3968%2Fj.ans.1715787020120504.2023.
  16. 16.0 16.1 Fedosin S.G. The covariant additive integrals of motion in the theory of relativistic vector fields. Bulletin of Pure and Applied Sciences, Vol. 37 D (Physics), No. 2, pp. 64-87 (2018). http://dx.doi.org/10.5958/2320-3218.2018.00013.1.
  17. Fedosin S.G. On the Dependence of the Relativistic Angular Momentum of a Uniform Ball on the Radius and Angular Velocity of Rotation. International Frontier Science Letters, Vol. 15, pp. 9-14 (2020). https://doi.org/10.18052/www.scipress.com/IFSL.15.9.
  18. Fedosin S.G. The virial theorem and the kinetic energy of particles of a macroscopic system in the general field concept. Continuum Mechanics and Thermodynamics, Vol. 29, Issue 2, pp. 361-371 (2017). https://dx.doi.org/10.1007/s00161-016-0536-8.
  19. Fedosin S.G. The integral theorem of generalized virial in the relativistic uniform model. Continuum Mechanics and Thermodynamics, Vol. 31, Issue 3, pp. 627-638 (2019). https://dx.doi.org/10.1007/s00161-018-0715-x.
  20. Fedosin S.G. Cosmic Red Shift, Microwave Background, and New Particles. Galilean Electrodynamics, Vol. 23, Special Issues No. 1, pp. 3-13 (2012). http://dx.doi.org/10.5281/zenodo.890806.
  21. Fedosin S.G. The radius of the proton in the self-consistent model. Hadronic Journal, Vol. 35, No. 4, pp. 349-363 (2012). http://dx.doi.org/10.5281/zenodo.889451.
  22. Fedosin S.G. The Integral Theorem of the Field Energy. Gazi University Journal of Science. Vol. 32, No. 2, pp. 686-703 (2019). http://dx.doi.org/10.5281/zenodo.3252783.
  23. Fedosin S.G. The binding energy and the total energy of a macroscopic body in the relativistic uniform model. Middle East Journal of Science, Vol. 5, Issue 1, pp. 46-62 (2019). http://dx.doi.org/10.23884/mejs.2019.5.1.06.
  24. Fedosin S.G. The Mass Hierarchy in the Relativistic Uniform System. Bulletin of Pure and Applied Sciences, Vol. 38 D (Physics), No. 2, pp. 73-80 (2019). http://dx.doi.org/10.5958/2320-3218.2019.00012.5.
  25. Fedosin S.G. The potentials of the acceleration field and pressure field in rotating relativistic uniform system. Continuum Mechanics and Thermodynamics, Vol. 33, Issue 3, pp. 817-834 (2021). https://doi.org/10.1007/s00161-020-00960-7.
  26. Fedosin S.G. The relativistic uniform model: the metric of the covariant theory of gravitation inside a body, St. Petersburg Polytechnical State University Journal. Physics and Mathematics (Научно-технические ведомости СПбГПУ. Физико-математические науки), Vol. 14, No. 3, pp.168-184 (2021). http://dx.doi.org/10.18721/JPM.14313. arXiv :2110.00342. Bibcode 2021arXiv211000342F. // О метрике ковариантной теории гравитации внутри тела в релятивистской однородной модели.
  27. Fedosin S.G. Generalized Four-momentum for Continuously Distributed Materials. Gazi University Journal of Science, Vol. 37, Issue 3, pp. 1509-1538 (2024). https://doi.org/10.35378/gujs.1231793. // Обобщённый 4-импульс для непрерывно распределённого вещества.
  28. Fedosin S.G. What should we understand by the four-momentum of physical system? Physica Scripta, Vol. 99, No. 5, 055034 (2024). https://doi.org/10.1088/1402-4896/ad3b45. // Что мы должны понимать под 4-импульсом физической системы?
  29. Fedosin S.G. Lagrangian formalism in the theory of relativistic vector fields. International Journal of Modern Physics A, Vol. 40, No. 02, 2450163 (2025). https://doi.org/10.1142/S0217751X2450163X. // Лагранжев формализм в теории релятивистских векторных полей.

 

See also

External links

 

Source: http://sergf.ru/roen.htm

On the list of pages