На русском языке

 

Operator of proper-time-derivative

Operator of proper-time-derivative is a differential operator and the relativistic generalization of material derivative (substantial derivative) in four-dimensional spacetime.

In coordinate notation, this operator is written as follows: [1]

~\frac{ D } {D \tau }= u^\mu \nabla_\mu,

where ~ D  – the symbol of differential in curved spacetime, ~ \tau  – proper time, which is measured by a clock moving with test particle, ~ u^\mu  – 4-velocity of test particle or local volume of matter, ~ \nabla_\mu  – covariant derivative.

In flat Minkowski spacetime operator of proper-time-derivative is simplified, since the covariant derivative transforms into 4-gradient (the operator of differentiation with partial derivatives with respect to coordinates):

~\frac{ d } {d \tau }= u^\mu \partial_\mu.

To prove this expression it can be applied to an arbitrary 4-vector ~ A^\nu :

~ u^\mu \partial_\mu A^\nu = \frac {c{} dt}{d\tau } \frac {\partial A^\nu }{c{}\partial t } + \frac {dx}{d\tau }\frac {\partial A^\nu }{\partial x } + \frac {dy}{d\tau }\frac {\partial A^\nu }{\partial y } + \frac {dz}{d\tau }\frac {\partial A^\nu }{\partial z }

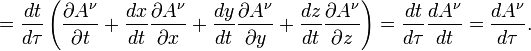
~=\frac {dt}{d\tau } \left( \frac {\partial A^\nu }{\partial t } + \frac {dx}{dt }\frac {\partial A^\nu }{\partial x }+ \frac {dy}{dt }\frac {\partial A^\nu }{\partial y }+ \frac {dz}{dt }\frac {\partial A^\nu }{\partial z }\right) =\frac {dt}{d\tau }\frac {dA^\nu }{dt }=\frac{ dA^\nu } {d \tau }.

Above was used material derivative in operator equation for an arbitrary function ~ F :

\frac {dF}{dt}= \frac {\partial F }{\partial t }+\mathbf{V}\cdot \nabla F,

where ~ \mathbf{V}  is the velocity of local volume of matter, ~ \nabla  – nabla operator.

In turn, the material derivative follows from the representation of differential function ~ F  of spatial coordinates and time:

~ dF(t,x,y,z) = \frac {\partial F}{\partial t}dt + \frac {\partial F}{\partial x}dx + \frac {\partial F}{\partial y}dy + \frac {\partial F}{\partial z}dz.

Contents

 

Applications

Operator of proper-time-derivative is applied to different four-dimensional objects – to scalar functions, 4-vectors and 4-tensors. One exception is 4-position (4-radius), which in four-Cartesian coordinates has the form  ~ x^\mu=(ct,x,y,z)=(ct, \mathbf{r} )  because 4-position is not a 4-vector in curved space-time, but its differential (displacement)  ~ dx^\mu=(c{}dt,dx,dy,dz)=(cdt, d\mathbf{r} )  is. Effect of the left side of operator of proper-time-derivative on the 4-position specifies the 4-velocity: ~ \frac{ D x^\mu } {D \tau }= u^\mu  , but the right side of the operator does not so: ~ u^\nu \nabla_\nu x^\mu \not = u^\mu .

In the covariant theory of gravitation operator of proper-time-derivative is used to determine the density of 4-force acting on a solid point particle in curved spacetime: [2]

~f^\nu = \frac{ DJ^\nu } {D \tau }= u^\mu \nabla_\mu J^\nu =\frac{ dJ^\nu } {d \tau }+ \Gamma^\nu _{\mu \lambda} u^\mu J^\lambda,

where  ~ J^\nu = \rho_0 u^\nu  is 4-vector momentum density of matter, ~ \rho_0  – density of matter in its rest system, ~ \Gamma^\nu _{\mu \lambda}  – Christoffel symbol.

However in the common case the 4-force is determined with the help of 4-potential of acceleration field: [3]

~f_{\alpha }=\nabla _{\beta }{B_{\alpha }}^{\beta }=-u_{{\alpha k}}J^{k}=\rho _{0}{\frac {DU_{\alpha }}{D\tau }}-J^{k}\nabla _{\alpha }U_{k}=\rho _{0}{\frac {dU_{\alpha }}{d\tau }}-J^{k}\partial _{\alpha }U_{k},

where  ~{B_{\alpha }}^{\beta }  is the acceleration stress-energy tensor with the mixed indices,  ~u_{{\alpha k}}  is the acceleration tensor,  and the 4-potential of acceleration field is expressed in terms of the scalar  ~\vartheta  and vector ~{\mathbf {U}}  potentials:

~U_{\alpha }=\left({\frac {\vartheta }{c}},-{\mathbf {U}}\right).

In general relativity freely falling body in a gravitational field moves along a geodesic, and four-acceleration of body in this case is equal to zero: [4]

~a^\nu = \frac{Du^\nu } {D \tau }= u^\mu \nabla_\mu u^\nu =\frac{ du^\nu } {d \tau }+ \Gamma^\nu_{\mu \lambda} u^\mu u^\lambda=0.

Since interval ~ds = c d\tau , then equation of motion of the body along a geodesic in general relativity can be rewritten in equivalent form:

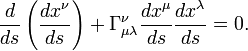
~ \frac{ d } {d s }\left(\frac{ dx^\nu } {d s } \right) + \Gamma^\nu_{\mu \lambda } \frac{ dx^\mu } {d s } \frac{ dx^\lambda } {d s } = 0.

If, instead of the proper time to use a parameter ~ p , and equation of a curve set by the expression ~ x^\mu (p) , then there is the operator of derivative on the parameter along the curve: [5]

~\frac{ D } {D p }= \frac {d x^\mu }{dp} \nabla_\mu .

 

See also

References

  1. Fedosin S.G. Fizicheskie teorii i beskonechnaia vlozhennost’ materii. – Perm, 2009-2011, 858 pages, Tabl. 21, Pic. 41, Ref. 293. ISBN 978-5-9901951-1-0. (in Russian).
  2. Fedosin S.G. The General Theory of Relativity, Metric Theory of Relativity and Covariant Theory of Gravitation: Axiomatization and Critical Analysis. International Journal of Theoretical and Applied Physics, Vol. 4, No. 1, pp. 9-26 (2014). http://dx.doi.org/10.5281/zenodo.890781.
  3. Fedosin S.G. Equations of Motion in the Theory of Relativistic Vector Fields. International Letters of Chemistry, Physics and Astronomy, Vol. 83, pp. 12-30 (2019). https://doi.org/10.18052/www.scipress.com/ILCPA.83.12.
  4. Fock, V. A. (1964). "The Theory of Space, Time and Gravitation". Macmillan.
  5. Carroll, Sean M. (2004), Spacetime and Geometry, Addison Wesley, ISBN 0-8053-8732-3

 

External links

 

Source: http://sergf.ru/oden.htm

On the list of pages