In English

Поле ускорений

Из проекта Викизнание

Поле ускорений — двухкомпонентное векторное поле, ковариантным образом описывающее 4-ускорение отдельных частиц и плотность 4-силы, возникающие в системах с множеством тесно взаимодействующих частиц. Поле ускорений является компонентой общего поля, представленной в лагранжиане и в гамильтониане произвольной физической системы членом с энергией движения частиц, и членом с энергией поля. [1] [2] Поле ускорений входит в большинство уравнений векторного поля. При этом в уравнение движения поле ускорений входит через тензор ускорений, а в уравнение для метрики – через тензор энергии-импульса поля ускорений.

Поле ускорений было представлено Сергеем Федосиным в рамках метрической теории относительности и ковариантной теории гравитации, а уравнения этого поля появились как следствие принципа наименьшего действия. [3] [4]

Содержание 

Математическое описание

4-потенциал поля ускорений выражается через скалярный ~\vartheta  и векторный ~{\mathbf {U}} потенциалы:

~U_{\mu }=\left({\frac {\vartheta }{c}},-{\mathbf {U}}\right).

Антисимметричный тензор ускорений вычисляется через 4-ротор от 4-потенциала:

~u_{{\mu \nu }}=\nabla _{\mu }U_{\nu }-\nabla _{\nu }U_{\mu }=\partial _{\mu }U_{\nu }-\partial _{\nu }U_{\mu }.

Компонентами тензора ускорений являются компоненты напряжённости поля ~{\mathbf {S}} и компоненты соленоидального вектора ~{\mathbf {N}}:

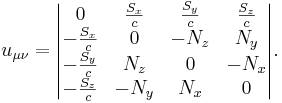
~u_{{\mu \nu }}={\begin{vmatrix}0&{\frac {S_{x}}{c}}&{\frac {S_{y}}{c}}&{\frac {S_{z}}{c}}\\-{\frac {S_{x}}{c}}&0&-N_{{z}}&N_{{y}}\\-{\frac {S_{y}}{c}}&N_{{z}}&0&-N_{{x}}\\-{\frac {S_{z}}{c}}&-N_{{y}}&N_{{x}}&0\end{vmatrix}}.

При этом получается следующее:

~{\mathbf {S}}=-\nabla \vartheta -{\frac {\partial {\mathbf {U}}}{\partial t}},\qquad \qquad {\mathbf {N}}=\nabla \times {\mathbf {U}}.\qquad \qquad (1)

В общем случае скалярный и векторный потенциалы находятся путём решения волновых уравнений для потенциалов поля ускорений.

Действие, Лагранжиан и энергия

В ковариантной теории гравитации 4-потенциал ~U_{\mu } поля ускорений является частью 4-потенциала общего поля ~s_{\mu }, который является суммой 4-потенциалов таких частных полей, как электромагнитное и гравитационное поля, поле ускорений, поле давления, поле диссипации, поле сильного взаимодействия, поле слабого взаимодействия, других векторных полей, действующих на вещество и его частицы. Все эти поля так или иначе представлены в веществе, так что 4-потенциал ~s_{\mu } не может состоять только из одного 4-потенциала ~U_{\mu }. Плотность энергии взаимодействия общего поля с веществом задаётся произведением 4-потенциала общего поля на массовый 4-ток: ~s_{\mu }J^{\mu }. Из 4-потенциала общего поля путём применения 4-ротора получается тензор общего поля:

~s_{{\mu \nu }}=\nabla _{\mu }s_{\nu }-\nabla _{\nu }s_{\mu }.

Тензорный инвариант, в виде ~s_{{\mu \nu }}s^{{\mu \nu }}, с точностью до постоянного коэффициента пропорционален плотности энергии общего поля. В результате функция действия, содержащая скалярную кривизну ~R и космологическую постоянную ~\Lambda , определяется выражением: [1]

~S=\int {Ldt}=\int (kR-2k\Lambda -{\frac {1}{c}}s_{\mu }J^{\mu }-{\frac {c}{16\pi \varpi }}s_{{\mu \nu }}s^{{\mu \nu }}){\sqrt {-g}}d\Sigma ,

где ~L – функция Лагранжа или лагранжиан, ~dt – дифференциал времени координатной системы отсчёта, ~k и ~\varpi  – постоянные, подлежащие определению, ~c – скорость света, как мера скорости распространения электромагнитного и гравитационного взаимодействий, ~{\sqrt {-g}}d\Sigma ={\sqrt {-g}}cdtdx^{1}dx^{2}dx^{3} – инвариантный 4-объём, выражаемый через дифференциал временной координаты ~dx^{0}=cdt, через произведение ~dx^{1}dx^{2}dx^{3} дифференциалов пространственных координат, и через квадратный корень ~{\sqrt {-g}} из детерминанта ~g метрического тензора, взятого с отрицательным знаком.

Варьирование функции действия даёт уравнения общего поля, четырёхмерное уравнение движения и уравнение для определения метрики. Так как поле ускорений является компонентой общего поля, то из уравнений общего поля вытекают соответствующие уравнения поля ускорений.

При выполнении условия калибровки космологической постоянной в виде

~ck\Lambda =-s_{\mu }J^{\mu },

энергия системы не зависит от члена со скалярной кривизной и становится однозначно определённой: [4]

~E=\int {(s_{0}J^{0}+{\frac {c^{2}}{16\pi \varpi }}s_{{\mu \nu }}s^{{\mu \nu }}){\sqrt {-g}}dx^{1}dx^{2}dx^{3}},

где ~s_{0} и ~J^{0} обозначают временные компоненты 4-векторов ~s_{{\mu }} и ~J^{{\mu }}.

В произвольной системе отсчёта K 4-импульс системы определяется формулой: [5] [6]

~p_{\mu }=\left({\frac {E}{c}}{,}-{\mathbf {p}}\right)=Mu_{\mu }={\frac {E_{0}}{cu'_{0}}}u_{\mu },

где  ~E  и  ~{\mathbf {p}}  обозначают энергию и импульс физической системы в K;  ~M  есть инерциальная масса;  ~u_{\mu }  есть 4-скорость движения центра импульсов физической системы в K. Если в центре импульсов поместить начало координат системы отсчёта K', и вычислить в K' энергию системы  ~E_{0}  и временную компоненту  ~u'_{0}  4-скорости центра импульсов, то можно найти инерциальную массу  ~M={\frac {E_{0}}{cu'_{0}}}  системы. Заметим, что в системе отсчёта K' трёхмерный импульс  ~{\mathbf {p'}}  физической системы по определению равен нулю.

Уравнения

Четырёхмерные уравнения поля ускорений по своей форме оказываются подобными уравнениям Максвелла и имеют следующий вид:

\nabla _{\sigma }u_{{\mu \nu }}+\nabla _{\mu }u_{{\nu \sigma }}+\nabla _{\nu }u_{{\sigma \mu }}={\frac {\partial u_{{\mu \nu }}}{\partial x^{\sigma }}}+{\frac {\partial u_{{\nu \sigma }}}{\partial x^{\mu }}}+{\frac {\partial u_{{\sigma \mu }}}{\partial x^{\nu }}}=0.

~\nabla _{\nu }u^{{\mu \nu }}=-{\frac {4\pi \eta }{c^{2}}}J^{\mu },

где J^{\mu }=\rho _{{0}}u^{\mu } есть массовый 4-ток, \rho _{{0}} – плотность массы в сопутствующей системе отсчёта, u^{\mu } – 4-скорость движения элемента вещества, ~\eta  – постоянная, определяемая в каждой задаче, и предполагается, что имеется равновесие между всеми полями в рассматриваемой физической системе.

Условие калибровки 4-потенциала поля ускорений:

~\nabla ^{\mu }U_{{\mu }}=0.

Если второе уравнение с источником поля записать с ковариантным индексом в следующем виде:

~\nabla ^{\nu }u_{{\mu \nu }}=-{\frac {4\pi \eta }{c^{2}}}J_{\mu },

то после подстановки сюда выражения тензора ускорений u_{{\mu \nu }} через 4-потенциал поля ускорений ~U_{\mu } получается волновое уравнение для вычисления потенциалов поля ускорения: [7]

 

~\nabla ^{\nu }\nabla _{\nu }U_{\mu }+R_{{\mu \nu }}U^{\nu }={\frac {4\pi \eta }{c^{2}}}J_{\mu },

где ~R_{{\mu \nu }} – тензор Риччи, находимый по формуле в книге.[8]  В случае, если тензор Риччи вычисляется по формуле в книге, [9]  в волновом уравнении перед тензором Риччи следует изменить знак на противоположный.

Уравнение непрерывности в искривлённом пространстве-времени:

~\nabla _{{\alpha }}J^{{\alpha }}=0.

В пространстве Минковского специальной теории относительности тензор Риччи обнуляется, вид уравнений поля ускорений упрощается и их можно выразить через напряжённость поля ~{\mathbf {S}} и соленоидальный вектор ~{\mathbf {N}}:

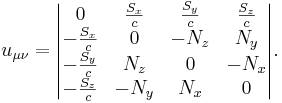
~\nabla \cdot {\mathbf {S}}=4\pi \eta \gamma \rho _{0},\qquad \qquad \nabla \times {\mathbf {N}}={\frac {1}{c^{2}}}\left(4\pi \eta {\mathbf {J}}+{\frac {\partial {\mathbf {S}}}{\partial t}}\right),

~\nabla \times {\mathbf {S}}=-{\frac {\partial {\mathbf {N}}}{\partial t}},\qquad \qquad \nabla \cdot {\mathbf {N}}=0.

где ~\gamma ={\frac {1}{{\sqrt {1-{v^{2} \over c^{2}}}}}} есть фактор Лоренца, ~{\mathbf {J}}=\gamma \rho _{0}{\mathbf {v}} – плотность тока массы, ~{\mathbf {v}} – скорость элемента вещества.

Упрощается и волновое уравнение, которое может быть записано отдельно для скалярного и векторного потенциалов:

~\partial ^{\nu }\partial _{\nu }\vartheta ={\frac {1}{c^{2}}}{\frac {\partial ^{2}\vartheta }{\partial t^{2}}}-\Delta \vartheta =4\pi \eta \gamma \rho _{0},\qquad \qquad (2)

~\partial ^{\nu }\partial _{\nu }{\mathbf {U}}={\frac {1}{c^{2}}}{\frac {\partial ^{2}{\mathbf {U}}}{\partial t^{2}}}-\Delta {\mathbf {U}}={\frac {4\pi \eta }{c^{2}}}{\mathbf {J}}.\qquad \qquad (3)

Уравнение движения элемента вещества в общем поле описывается формулой:

~s_{{\mu \nu }}J^{\nu }=0.

Так как ~J^{\nu }=\rho _{0}u^{\nu }, а тензор общего поля выражается через тензоры частных полей, то уравнение движения можно представить через эти тензоры: [7] [10] 

~-u_{{\mu \nu }}J^{\nu }=F_{{\mu \nu }}j^{\nu }+\Phi _{{\mu \nu }}J^{\nu }+f_{{\mu \nu }}J^{\nu }+h_{{\mu \nu }}J^{\nu }+\gamma _{{\mu \nu }}J^{\nu }+w_{{\mu \nu }}J^{\nu }=\rho _{0}{\frac {Du_{\mu }}{D\tau }}=\rho _{0}A_{\mu }.\qquad (4)

Здесь ~F_{{\mu \nu }} – тензор электромагнитного поля, ~j^{\nu } – зарядовый 4-ток, ~\Phi _{{\mu \nu }} – тензор гравитационного поля, ~f_{{\mu \nu }} – тензор поля давления, ~h_{{\mu \nu }} – тензор поля диссипации, ~\gamma _{{\mu \nu }} – тензор поля сильного взаимодействия, ~w_{{\mu \nu }} – тензор поля слабого взаимодействия, ~\rho _{0} — инвариантная плотность массы,  ~u_{\mu }  и  ~A_{\mu }  обозначают 4-скорость и 4-ускорение элемента вещества.

Тензор энергии-импульса

Тензор энергии-импульса поля ускорений вычисляется с помощью тензора ускорений:

~B^{{ik}}={\frac {c^{2}}{4\pi \eta }}\left(-g^{{im}}u_{{nm}}u^{{nk}}+{\frac {1}{4}}g^{{ik}}u_{{mr}}u^{{mr}}\right).

В составе тензора ~B^{{ik}} находится 3-вектор плотности потока энергии поля ускорений ~{\mathbf {K}}, подобный по смыслу вектору Пойнтинга и вектору Хевисайда. Вектор ~{\mathbf {K}} можно представить через векторное произведение вектора напряжённости поля ~{\mathbf {S}} и соленоидального вектора ~{\mathbf {N}}:

~{\mathbf {K}}=cB^{{0i}}={\frac {c^{2}}{4\pi \eta }}[{\mathbf {S}}\times {\mathbf {N}}],

здесь индекс ~i=1,2,3.

Ковариантная производная от тензора энергии-импульса поля ускорений со смешанными индексами задаёт плотность 4-силы:

~f_{\alpha }=\nabla _{\beta }{B_{\alpha }}^{\beta }=-u_{{\alpha k}}J^{k}=-\rho _{0}u_{{\alpha k}}u^{k}=\rho _{0}{\frac {DU_{\alpha }}{D\tau }}-J^{k}\nabla _{\alpha }U_{k}=\rho _{0}{\frac {dU_{\alpha }}{d\tau }}-J^{k}\partial _{\alpha }U_{k},\qquad (5)

где ~D\tau  обозначает дифференциал собственного времени в искривлённом пространстве-времени.

Тензор энергии-импульса поля ускорений входит в состав тензора энергии-импульса общего поля ~T^{{ik}}:

~T^{{ik}}=W^{{ik}}+U^{{ik}}+B^{{ik}}+P^{{ik}}+Q^{{ik}}+L^{{ik}}+A^{{ik}},

где ~W^{{ik}} – тензор энергии-импульса электромагнитного поля, ~U^{{ik}} – тензор энергии-импульса гравитационного поля, ~P^{{ik}} – тензор энергии-импульса поля давления, ~Q^{{ik}} – тензор энергии-импульса поля диссипации, ~L^{{ik}} – тензор энергии-импульса поля сильного взаимодействия, ~A^{{ik}} – тензор энергии-импульса поля слабого взаимодействия.

Через тензор ~T^{{ik}} тензор энергии-импульса поля ускорений входит в уравнение для метрики:

~R^{{ik}}-{\frac {1}{4}}g^{{ik}}R={\frac {8\pi G\beta }{c^{4}}}T^{{ik}},

где ~R^{{ik}} – тензор Риччи, ~G – гравитационная постоянная, ~\beta  – некоторая постоянная, и использовано условие калибровки космологической постоянной.

Частные решения для функций поля ускорений

4-потенциал любого векторного поля, глобальный векторный потенциал которого равен нулю в собственной системе отсчёта K', то есть в системе центра импульсов, при прямолинейном движении в лабораторной системе отсчёта K может быть представлен так: [3] [7]

~L_{{\mu L}}={\frac {k_{f}\varepsilon }{\rho _{0}c^{2}}}u_{{\mu L}},

где ~k_{f}={\frac {\rho _{0}}{\rho _{{0q}}}} для электромагнитного поля и ~k_{f}=1 для остальных полей; ~\rho _{{0}} и ~\rho _{{0q}} – инвариантная плотность массы и соответственно плотность заряда в сопутствующей системе отсчёта; ~\varepsilon  – инвариантная плотность энергии взаимодействия, вычисляемая как произведение 4-потенциала поля на соответствующий 4-ток; ~u_{{\mu L}} – ковариантная 4-скорость, задающая движение центра импульсов физической системы в K.

В специальной теории относительности (СТО), в системе центра импульсов K' плотность энергии ~\varepsilon =\gamma '\rho _{0}c^{2}, где ~\gamma ' есть фактор Лоренца, и для поля ускорений при движении физической системы в K 4-потенциал поля ускорений будет равен ~U_{{\mu L}}=\gamma 'u_{{\mu L}}.

В том случае, когда физическая система неподвижна в K, будет ~u_{{\mu L}}=(c,0,0,0), и следовательно, скалярный потенциал ~\vartheta =\gamma 'c^{2}. Если в физической системе в среднем имеются направленные потоки вещества или вращение вещества, векторный потенциал ~{\mathbf {U}} поля ускорений перестаёт быть равен нулю.

Если известен 4-потенциал ~U'_{{\nu }} поля ускорений в K', то в лабораторной системе отсчёта K 4-потенциал определяется с помощью матрицы ~M_{{\mu }}^{{\ \nu }}, связывающей координаты и время обеих систем отсчёта:[11]

~U_{{\mu L}}=M_{{\mu }}^{{\ \nu }}U'_{{\nu }}.

В частном случае движения системы с постоянной скоростью ~M_{{\mu }}^{{\ \nu }} представляет собой матрицу преобразований Лоренца.

Идеально твёрдая частица

В приближении, когда частица рассматривается как идеально твёрдый объект, вещество внутри частицы неподвижно. Это означает, что фактор Лоренца ~\gamma ' этого вещества в системе центра импульсов K' равен единице, так что 4-потенциал поля ускорений становится равным 4-скорости движения центра импульсов:

~U_{\mu }=u_{\mu }.

В СТО выражение для 4-скорости упрощается и можно записать:

~U_{\mu }=\left({\frac {\vartheta }{c}},-{\mathbf {U}}\right)=u_{\mu }=\left(\gamma c,-\gamma {\mathbf {v}}\right).

Компоненты тензора ускорений согласно (1) будут равны:

~{\mathbf {S}}=-c^{2}\nabla \gamma -{\frac {\partial (\gamma {\mathbf {v}})}{\partial t}},\qquad \qquad {\mathbf {N}}=\nabla \times (\gamma {\mathbf {v}}).

Так как в уравнении твердотельного движения для 4-ускорения с ковариантным индексом ~a_{\mu } справедливо соотношение

~\rho _{0}a_{\mu }=\rho _{0}{\frac {Du_{\mu }}{D\tau }}=-u_{{\mu \nu }}J^{\nu }=-\rho _{0}u_{{\mu \nu }}u^{\nu },

то в СТО получается следующее:

~{\frac {Du_{\mu }}{D\tau }}={\frac {du_{\mu }}{d\tau }}=\gamma {\frac {du_{\mu }}{dt}},\qquad \qquad u^{\nu }=\left(\gamma c,\gamma {\mathbf {v}}\right),

а также уравнения для лоренцевского фактора ~\gamma  и для 3-ускорения ~a={\frac {d{\mathbf {v}}}{dt}}:

~{\frac {d\gamma }{dt}}=-{\frac {1}{c^{2}}}{\mathbf {S}}\cdot {\mathbf {v}},\qquad (6)\qquad {\frac {d(\gamma {\mathbf {v}})}{dt}}=\gamma {\mathbf {a}}+{\frac {d\gamma }{dt}}{\mathbf {v}}=-{\mathbf {S}}-[{\mathbf {v}}\times {\mathbf {N}}].\qquad (7)

Умножая скалярно уравнение (7) на скорость ~{\mathbf {v}}, подставляя из уравнения (6) в (7) величину ~{\mathbf {S}}\cdot {\mathbf {v}}, учитывая соотношение ~\gamma ^{{-2}}=1-{v^{2} \over c^{2}}, находим известное выражение для производной фактора Лоренца через скалярное произведение скорости и ускорения в СТО:

~\gamma ^{3}{\mathbf {v}}\cdot {\mathbf {a}}=c^{2}{\frac {d\gamma }{dt}}.

В справедливости уравнения (7) можно убедиться, если подставить в его правую часть выражения для напряжённости  ~{\mathbf {S}}  и соленоидального вектора  ~{\mathbf {N}} , приведённые выше:

~{\frac {d(\gamma {\mathbf {v}})}{dt}}=c^{2}\nabla \gamma +{\frac {\partial (\gamma {\mathbf {v}})}{\partial t}}-{\mathbf {v}}\times [\nabla \times (\gamma {\mathbf {v}})].\qquad \qquad (8)

Действительно, применение производной Лагранжа даёт:

~{\frac {d(\gamma {\mathbf {v}})}{dt}}={\frac {\partial (\gamma {\mathbf {v}})}{\partial t}}+({\mathbf {v}}\cdot \nabla )(\gamma {\mathbf {v}})={\frac {\partial (\gamma {\mathbf {v}})}{\partial t}}+\gamma ({\mathbf {v}}\cdot \nabla ){\mathbf {v}}+{\mathbf {v}}({\mathbf {v}}\cdot \nabla \gamma ).

Кроме этого

~-{\mathbf {v}}\times [\nabla \times (\gamma {\mathbf {v}})]=-\gamma {\mathbf {v}}\times [\nabla \times {\mathbf {v}}]-{\mathbf {v}}\times [\nabla \gamma \times {\mathbf {v}}]=-{\frac {\gamma }{2}}\nabla v^{2}+\gamma ({\mathbf {v}}\cdot \nabla ){\mathbf {v}}-v^{2}\nabla \gamma +{\mathbf {v}}({\mathbf {v}}\cdot \nabla \gamma ).

Подставляя эти соотношения в (8), с учётом выражения ~\gamma ^{{-2}}=1-{v^{2} \over c^{2}}, приходим к тождеству:

~c^{2}\nabla \gamma -{\frac {\gamma }{2}}\nabla v^{2}-v^{2}\nabla \gamma =0.

Если компоненты скорости частицы являются функциями от времени и прямо не зависят от пространственных координат, то для такого движения соленоидальный вектор ~{\mathbf {N}} обращается в нуль.

В СТО ~E=\gamma mc^{2} – релятивистская энергия, ~{\mathbf p}=\gamma m{\mathbf v} – 3-вектор релятивистского импульса частицы. Если масса ~m частицы постоянна, то умножая (8) на массу частицы, приходим к следующему выражению для силы:

~{\mathbf F}={\frac {d{\mathbf p}}{dt}}=\nabla E+{\frac {\partial {\mathbf p}}{\partial t}}-{\mathbf {v}}\times [\nabla \times {\mathbf p}].

Вращение частицы

Для малой по размерам идеально твёрдой частицы можно пренебречь движением вещества внутри частицы и считать, что 4-потенциал поля ускорений равен 4-скорости центра импульсов частицы. Пусть частица вращается вокруг оси OZ системы координат на расстоянии ~\rho ={\sqrt {x^{2}+y^{2}}} от оси с постоянной угловой скоростью ~\omega  против часовой стрелки, если смотреть с той стороны, куда направлена ось OZ. Тогда можно считать, что линейная скорость частицы зависит только от координат ~x и ~y, и для проекций скорости на оси системы координат можно записать: ~{\mathbf v}=(-\omega y,\omega x,0), при этом квадрат скорости равен ~v^{2}=\omega ^{2}(x^{2}+y^{2}). Для фактора Лоренца в рамках СТО получается следующее:

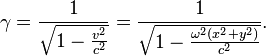
~\gamma ={\frac {1}{{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}={\frac {1}{{\sqrt {1-{\frac {\omega ^{2}(x^{2}+y^{2})}{c^{2}}}}}}}.

С учётом этого потенциалы и напряжённости поля ускорений запишутся так:

~\vartheta =\gamma c^{2},\qquad {\mathbf {U}}=\gamma {\mathbf {v}}.

~{\mathbf {S}}=-\nabla \vartheta -{\frac {\partial {\mathbf {U}}}{\partial t}}=\left(-\gamma ^{3}\omega ^{2}x,-\gamma ^{3}\omega ^{2}y,0\right).

~{\mathbf {N}}=\nabla \times {\mathbf {U}}=\left(0,0,\gamma \omega +\gamma ^{3}\omega \right).

Если подставить ~\gamma , ~{\mathbf v}, ~{\mathbf {S}} и ~{\mathbf {N}} в (7), можно определить компоненты ускорения частицы и амплитуду ускорения:

~{\mathbf {a}}=\left(-\omega ^{2}x,-\omega ^{2}y,0\right).

~a={\sqrt {a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}=\omega ^{2}{\sqrt {x^{2}+y^{2}}}=\omega ^{2}\rho =\omega v={\frac {v^{2}}{\rho }}.

Ускорение направлено к центру вращения и представляет собой центростремительное ускорение. Используя далее классическое векторное описание, в координатах и времени системы отсчёта в центре вращения находим:

~{\vec \rho }=(x,y,0),\qquad {\vec \omega }={\frac {{\vec {d\varphi }}}{dt}}=(0,0,\omega ),

~{\mathbf {v}}=[{\vec \omega }\times {\vec \rho }],\qquad {\mathbf {a}}=[{\vec \omega }\times {\mathbf {v}}]=[{\vec \omega }\times [{\vec \omega }\times {\vec \rho }]]={\vec \omega }({\vec \omega }\cdot {\vec \rho })-{\vec \rho }({\vec \omega }\cdot {\vec \omega })=-\omega ^{2}{\vec \rho },

где ~\rho  и ~\varphi  являются двумя координатами цилиндрической системы координат, ~{\vec \rho } есть вектор от центра вращения до частицы, ~{\vec {d\varphi }} обозначает аксиальный вектор дифференциала угла вращения, который направлен вдоль оси OZ.

Как видно, при таком движении с ускорением векторное произведение ~[{\mathbf {S}}\times {\mathbf {N}}] не равно нулю, так же как и 3-вектор ~{\mathbf {K}} плотности потока энергии поля ускорений внутри частицы.

Система частиц

Благодаря взаимодействию множества частиц друг с другом посредством различных полей, в том числе на расстоянии без непосредственного контакта, поле ускорений в веществе изменяется и отличается от поля ускорений отдельных частиц в точке наблюдения. В результате плотность 4-силы в системе частиц задаётся через напряжённость и соленоидальный вектор, характеризующие типичные усреднённые характеристики движения вещества. Например, в гравитационно-связанной системе возникает радиальный градиент вектора ~{\mathbf {S}}, а если система движется или имеет вращение, то возникает вектор ~{\mathbf {N}}. Из (5) следует общее выражение для плотности 4-силы с ковариантным индексом:

~f_{\nu }=\rho _{0}{\frac {cdt}{ds}}\left(-{\frac {1}{c}}{\mathbf {S}}\cdot {\mathbf {v}}{,}\qquad {\mathbf {S}}+[{\mathbf {v}}\times {\mathbf {N}}]\right),

где ~ds обозначает четырёхмерный пространственно-временной интервал.

Для стационарного случая, когда потенциалы поля ускорений не зависят от времени, в предположении, что ~\vartheta =\gamma c^{2}, волновое уравнение (2) для скалярного потенциала в СТО преобразуется в уравнение:

~\Delta \gamma =-{\frac {4\pi \eta \gamma \rho _{0}}{c^{2}}}.

Решение этого уравнения для неподвижной сферы с хаотически движущимися в ней частицами имеет вид: [12]

~\gamma ={\frac {c\gamma _{c}}{r{\sqrt {4\pi \eta \rho _{0}}}}}\sin \left({\frac {r}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)\approx \gamma _{c}-{\frac {2\pi \eta \rho _{0}r^{2}\gamma _{c}}{3c^{2}}}.

где ~\gamma _{c}={\frac {1}{{\sqrt {1-{v_{c}^{2} \over c^{2}}}}}} есть фактор Лоренца для скоростей ~v_{c} частиц в центре сферы, и ввиду малости аргумента синус разложен до членов второго порядка. Из формулы следует, что средние скорости частиц максимальны в центре и уменьшаются при приближении к поверхности сферы.

В такой системе скалярный потенциал ~\vartheta  становится функцией радиуса, а векторный потенциал ~{\mathbf {U}} и соленоидальный вектор ~{\mathbf {N}} равны нулю. Напряжённость поля ускорений ~{\mathbf {S}} находится с помощью (1). Далее могут быть вычислены все функции поля ускорений, включая 4-ускорение, энергию частиц в этом поле и энергию самого поля ускорений. [13] Для космических тел основной вклад в 4-ускорение в веществе вносит гравитационная сила тяжести и поле давления. При этом автоматически выводится релятивистская энергия покоя системы, с учётом движения частиц внутри сферы. Для системы частиц с полем ускорения, полем давления, гравитационным и электромагнитным полями указанный подход позволил решить проблему 4/3 и показал, где и в какой форме содержится энергия системы. При этом было найдено соотношение для постоянной поля ускорения в этой задаче:

~\eta =3G-{\frac {3q^{2}}{4\pi \varepsilon _{0}m^{2}}},

где ~\varepsilon _{0} – электрическая постоянная, ~q и ~m – полный заряд и масса системы.

Решение волнового уравнения для поля ускорений внутри системы приводит к распределению температуры по формуле: [12]

~T=T_{c}-{\frac {\eta M_{p}M(r)}{3kr}},

где ~T_{c} – температура в центре, ~M_{p} – масса частицы, в качестве которой принимается масса протона (для систем, основой которых является водород или нуклоны в атомных ядрах), ~M(r) – масса системы внутри текущего радиуса ~r, ~k – постоянная Больцмана.

Данная зависимость хорошо выполняются для самых разных космических объектов, включая газовые облака и глобулы Бока, Землю, Солнце и нейтронные звёзды.

В статьях [14] [15] соотношение для коэффициентов полей было уточнено следующим образом:

~\eta +\sigma =G-{\frac {\rho _{{0q}}^{2}}{4\pi \varepsilon _{0}\rho _{{0}}^{2}}},

где ~\sigma  есть постоянная поля давления.

Если ввести параметр ~\mu  как количество нуклонов на одну частицу ионизированного газа, то постоянная поля ускорения выразится так:

~\eta ={\frac {3\gamma _{c}\mu G}{2+3\gamma _{c}\mu }}.

Для температуры внутри космических тел в модели гравитационного равновесия находится зависимость от текущего радиуса:

~T=T_{c}-{\frac {4\pi \eta m_{u}\rho _{{0c}}\gamma _{c}r^{2}}{9k}}+{\frac {2\pi \eta Am_{u}\gamma _{c}r^{3}}{9k}}+{\frac {2\pi \eta Bm_{u}\gamma _{c}r^{4}}{15k}},

где ~m_{u} есть масса одной частицы газа, в качестве которой берётся атомная единица массы, коэффициенты ~A и ~B входят в зависимость плотности массы от радиуса в соотношении ~\rho _{0}=\rho _{{0c}}-Ar-Br^{2}.

В предположении, что типичные частицы системы имеют массу ~{\stackrel {-}{m}}=\mu m_{u} и именно типичные частицы задают температуру и давление, для постоянной поля ускорения получается следующее: [16]

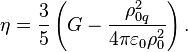
~\eta ={\frac {3}{5}}\left(G-{\frac {\rho _{{0q}}^{2}}{4\pi \varepsilon _{0}\rho _{0}^{2}}}\right).

Находится также фактор Лоренца частиц в центре системы: [17]

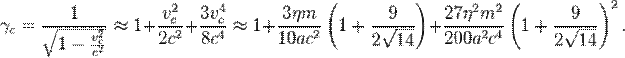
~\gamma _{c}={\frac {1}{{\sqrt {1-{\frac {v_{c}^{2}}{c^{2}}}}}}}\approx 1+{\frac {v_{c}^{2}}{2c^{2}}}+{\frac {3v_{c}^{4}}{8c^{4}}}\approx 1+{\frac {3\eta m}{10ac^{2}}}\left(1+{\frac {9}{2{\sqrt {14}}}}\right)+{\frac {27\eta ^{2}m^{2}}{200a^{2}c^{4}}}\left(1+{\frac {9}{2{\sqrt {14}}}}\right)^{2}.

Волновое уравнение (3) для векторного потенциала поля ускорений было использовано для того, чтобы релятивистское уравнение движения жидкости представить в виде уравнения Навье-Стокса в гидродинамике и описать движение вязкого сжимаемого вещества. [10]

Учёт поля ускорений и поля давления в релятивистской однородной системе позволил уточнить теорему вириала, которая в релятивистской форме записывается так: [18]

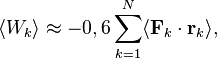
~\langle W_{k}\rangle \approx -0,6\sum _{{k=1}}^{N}\langle {\mathbf {F}}_{k}\cdot {\mathbf {r}}_{k}\rangle ,

причём величина ~W_{k}\approx \gamma _{c}T превышает кинетическую энергию частиц ~T на множитель, равный фактору Лоренца ~\gamma _{c} частиц в центре системы. В обычных условиях можно считать, что ~\gamma _{c}\approx 1, и тогда видно, что в теореме вириала кинетическая энергия связана с потенциальной энергией не коэффициентом 0,5, а скорее коэффициентом, близким к 0,6. Отличие от классического случая возникает за счёт учёта поля давления и поля ускорений частиц внутри системы, при этом производная от вириальной скалярной функции ~G_{v} не равна нулю и должна рассматриваться как производная Лагранжа.

Анализ интегральной теоремы обобщённого вириала позволяет найти на основе теории поля формулу для среднеквадратичной скорости типичных частиц системы, не используя понятия температуры: [19]

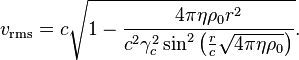
v_{{\mathrm {rms}}}=c{\sqrt {1-{\frac {4\pi \eta \rho _{0}r^{2}}{c^{2}\gamma _{c}^{2}\sin ^{2}{\left({\frac {r}{c}}{\sqrt {4\pi \eta \rho _{0}}}\right)}}}}}.

Интегральная теорема энергии поля для поля ускорений в искривлённом пространстве-времени выглядит следующим образом:[11]

~-\int {\left({\frac {8\pi \eta }{c^{2}}}U_{\alpha }J^{\alpha }+u_{{\alpha \beta }}u^{{\alpha \beta }}\right){\sqrt {-g}}dx^{1}dx^{2}dx^{3}}={\frac {2}{c}}{\frac {d}{dt}}\left(\int {U^{\alpha }u_{\alpha }^{{\ 0}}{\sqrt {-g}}dx^{1}dx^{2}dx^{3}}\right)+2\iint \limits _{S}{U^{\alpha }u_{\alpha }^{{\ k}}n_{k}{\sqrt {-g}}dS}.

В релятивистской однородной системе скалярный потенциал ~\vartheta  поля ускорений связан со скалярным потенциалом ~\wp  поля давления соотношением: [20]

~\wp ={\frac {\sigma (\vartheta -c^{2})}{\eta }}={\frac {2(\vartheta -c^{2})}{3}}.

При этом находится релятивистское выражение для давления:

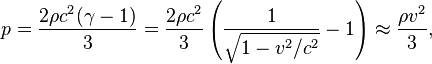
p={\frac {2\rho c^{2}(\gamma -1)}{3}}={\frac {2\rho c^{2}}{3}}\left({\frac {1}{{\sqrt {1-v^{2}/c^{2}}}}}-1\right)\approx {\frac {\rho v^{2}}{3}},

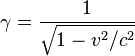где \rho  — плотность движущегося вещества, c — скорость света,  \gamma ={\frac {1}{{\sqrt {1-v^{2}/c^{2}}}}} — Лоренц-фактор. В пределе малых скоростей это соотношение переходит в стандартную формулу молекулярно-кинетической теории.

В [21] показывается, каким образом поле ускорений делает свой вклад в массу физической системы. Аналогично этому, поле ускорений делает свой вклад в метрику пространства-времени, и в веществе физической системы, и за его пределами. [22]

Концепция поля ускорений позволяет в ковариантном виде в искривлённом пространстве-времени определить обобщённый 4-импульс, [23] энергию, импульс и полный 4-импульс физической системы с учётом частиц и полей, [5] а также псевдотензор момента импульса. [6]

Другие подходы

Изучая лоренц-ковариантность 4-силы, Friedman и Scarr нашли не полную ковариантность выражения для 4-силы в виде ~F^{\mu }={\frac {dp^{\mu }}{d\tau }}. [24] Это привело их к выводу, что 4-ускорение в специальной теории относительности должно быть выражено с помощью некоторого антисимметричного тензора  ~{A^{\mu }}_{\nu }:

~c{\frac {du^{\mu }}{d\tau }}={A^{\mu }}_{\nu }u^{\nu }.

Исходя из анализа различных видов движения, они оценили требуемые для них значения компонент тензора  ~{A^{\mu }}_{\nu } , дав тем самым этому тензору косвенное определение.

В отличие от этого, согласно (5) плотность 4-силы равна  ~f_{\mu }=-u_{{\mu \nu }}J^{\nu },  а в (4)  ~-u_{{\mu \nu }}J^{\nu }=\rho _{0}{\frac {Du_{\mu }}{D\tau }}=\rho _{0}A_{\mu }.  Таким образом, в искривлённом пространстве-времени 4-ускорение элемента вещества будет  ~A_{\mu }={\frac {Du_{\mu }}{D\tau }}=-u_{{\mu \nu }}u^{\nu }. С учётом этого, тензор  ~{A^{\mu }}_{\nu }  с точностью до знака и постоянного множителя имеет тот же смысл, что и тензор поля ускорений  ~u_{{\mu \nu }}.

Mashhoon и Muench рассматривали преобразование инерциальных систем отсчёта, сопутствующих ускоренной системе отсчёта, и пришли к соотношению: [25]

~c{\frac {d\lambda _{\alpha }}{d\tau }}={\Phi _{\alpha }}^{\beta }\lambda _{\beta }.

Тензор  ~{\Phi _{\alpha }}^{\beta }  имеет те же свойства, что и тензор поля ускорений  ~u_{{\mu \nu }}

Использование в общей теории относительности

Функция действия в общей теории относительности (ОТО) может быть представлена как сумма четырёх членов, отвечающих соответственно за метрику пространства-времени, за материю в виде вещества, за электромагнитное поле и за поле давления:

~S=S_{m}+S_{{mat}}+S_{{em}}+S_{p}.

В функцию действия можно включать дополнительные члены, если требуется учесть другие поля. Первый, второй и третий члены действия имеют стандартный вид: [8]

~S_{m}=\int (kR-2k\Lambda ){\sqrt {-g}}d\Sigma .

~S_{{mat}}=\int (-c\rho _{0}){\sqrt {-g}}d\Sigma .

~S_{{em}}=\int (-{\frac {1}{c}}A_{\mu }j^{\mu }-{\frac {c\varepsilon _{0}}{4}}F_{{\mu \nu }}F^{{\mu \nu }}){\sqrt {-g}}d\Sigma ,

где A_{\mu } есть электромагнитный 4-потенциал.

Член ~S_{p}, отвечающий за вклад давления в функцию действия, оказывается различным у разных авторов, в зависимости от того, как давление связано с упругой энергией, и является ли поле давления скалярным или считается векторным полем. Заметим, что в ОТО гравитационное поле входит в функцию действия не прямо, а косвенно, через метрический тензор. При этом как правило поле давления считается скалярным полем.

В отличие от этого, в ковариантной теории гравитации (КТГ) вместо члена ~S_{{mat}} используется член ~S_{{ac}}, связанный с полем ускорений, и функция действия может быть записана так: [4]

~S=S_{m}+S_{{ac}}+S_{{em}}+S_{p}.

Здесь

~S_{{ac}}=\int (-{\frac {1}{c}}U_{\mu }J^{\mu }-{\frac {c}{16\pi \eta }}u_{{\mu \nu }}u^{{\mu \nu }}){\sqrt {-g}}d\Sigma ,

~S_{p}=\int (-{\frac {1}{c}}\pi _{\mu }J^{\mu }-{\frac {c}{16\pi \sigma }}f_{{\mu \nu }}f^{{\mu \nu }}){\sqrt {-g}}d\Sigma ,

где ~\pi _{\mu } – 4-потенциал поля давления, ~\sigma  – коэффициент поля давления, ~f_{{\mu \nu }} – тензор поля давления, J^{\mu }=\rho _{{0}}u^{\mu }.

В случае прямолинейного движения твёрдого тела без вращения будут выполняться соотношения: U_{\mu }=u_{\mu }, ~u_{\mu }u^{\mu }=c^{2}, и в члене ~S_{{ac}} получается соотношение ~-{\frac {1}{c}}U_{\mu }J^{\mu }=-c\rho _{0}. В этом частном случае видно, что член ~S_{{ac}} отличается от члена ~S_{{mat}} дополнительным слагаемым, связанным с энергией поля ускорений. Это является следствием того, что в КТГ поле ускорений представляет собой векторное поле, тогда как как в ОТО поле ускорений используется фактически как скалярное поле, не зависящее от скоростей частиц. В обеих теориях поле ускорений позволяет определить вклад энергии покоя частиц в общую энергию системы из частиц и полей. Однако применение поля ускорений в виде скалярного поля в ОТО по своей форме не согласуется с векторной природой электромагнитного поля. Действительно, в предельном случае, когда в учёт берутся только ускорения частиц и электромагнитные силы, ускорение должно быть двухкомпонентным, как это имеет место для ускорения от действия двухкомпонентной силы Лоренца. Но такое возможно лишь в случае, когда поле ускорений само является векторным полем. Улучшить ситуацию можно, если приписать метрическому полю ~g_{{\mu \nu }} в ОТО кроме функции гравитационного поля ещё и функцию векторной компоненты поля ускорений, однако это ещё более усложняет и запутывает уравнения теории.

Следует заметить, что в общем случае произвольного движения вещества соотношение ~-{\frac {1}{c}}U_{\mu }J^{\mu }=-c\rho _{0} уже не выполняется и КТГ перестаёт совпадать с ОТО в способе описания энергии покоя физической системы. Это означает, что в ОТО движение вещества рассматривается упрощённо, как прямолинейное движение твёрдого тела, тогда как в КТГ использование 4-потенциала поля ускорений U_{\mu } позволяет учесть внутреннее движение вещества в каждом выделенном элементе объёма. Например, при вращении частицы по окружности 4-потенциал U_{\mu } вещества частицы будет зависеть от местоположения этого вещества относительно линии окружности, так как скорость вещества частицы зависит от радиуса вращения.

См. также

Ссылки

  1. 1,0 1,1 Fedosin S.G. The Concept of the General Force Vector Field. OALib Journal, Vol. 3, pp. 1-15 (2016), e2459. http://dx.doi.org/10.4236/oalib.1102459; статья на русском языке: Концепция общего силового векторного поля.
  2.  Fedosin S.G. Two components of the macroscopic general field. Reports in Advances of Physical Sciences, Vol. 1, No. 2, 1750002, 9 pages (2017). http://dx.doi.org/10.1142/S2424942417500025; статья на русском языке: Две компоненты макроскопического общего поля.
  3. 3,0 3,1 Fedosin S.G. The procedure of finding the stress-energy tensor and vector field equations of any form. Advanced Studies in Theoretical Physics, Vol. 8, No. 18, pp. 771-779 (2014). http://dx.doi.org/10.12988/astp.2014.47101; статья на русском языке: Процедура для нахождения тензора энергии-импульса и уравнений векторного поля любого вида.
  4. 4,0 4,1 4,2 Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy. Jordan Journal of Physics. Vol. 9, No. 1, pp. 1-30 (2016). http://dx.doi.org/10.5281/zenodo.889304; статья на русском языке: О космологической постоянной, поле ускорения, поле давления и об энергии.
  5. 5.0 5.1 Fedosin S.G. What should we understand by the four-momentum of physical system? Physica Scripta, Vol. 99, No. 5, 055034 (2024). https://doi.org/10.1088/1402-4896/ad3b45. // Что мы должны понимать под 4-импульсом физической системы?
  6. 6.0 6.1 Fedosin S.G. Lagrangian formalism in the theory of relativistic vector fields. International Journal of Modern Physics A, Vol. 40, No. 02, 2450163 (2025). https://doi.org/10.1142/S0217751X2450163X. // Лагранжев формализм в теории релятивистских векторных полей.
  7. 7,0 7,1 7,2 Fedosin S.G. Equations of Motion in the Theory of Relativistic Vector Fields. International Letters of Chemistry, Physics and Astronomy, Vol. 83, pp. 12-30 (2019). https://doi.org/10.18052/www.scipress.com/ILCPA.83.12. // Уравнения движения в теории релятивистских векторных полей.
  8. 8.0 8.1 Фок В.А. Теория пространства, времени и гравитации. 2-е издание. – М.: Физматгиз, 1961. – 568 с.
  9. Ландау Л. Д., Лифшиц Е. М. Теория поля. – Издание 7-е, исправленное. – М.: Наука, 1988. – 512 с. – (Теоретическая физика, том II).
  10. 10.0 10.1 Fedosin S.G. Four-Dimensional Equation of Motion for Viscous Compressible and Charged Fluid with Regard to the Acceleration Field, Pressure Field and Dissipation Field. International Journal of Thermodynamics. Vol. 18, No. 1, pp. 13-24 (2015). http://dx.doi.org/10.5541/ijot.5000034003; статья на русском языке: Четырёхмерное уравнение движения вязкого сжимаемого вещества с учётом поля ускорений, поля давления и поля диссипации.
  11. 11.0 11.1 1 Fedosin S.G. The Integral Theorem of the Field Energy. Gazi University Journal of Science. Vol. 32, No. 2, pp. 686-703 (2019). http://dx.doi.org/10.5281/zenodo.3252783. // Интегральная теорема энергии поля.
  12.  12,0 12,1 Fedosin S.G. The Integral Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based on the Pressure Field and Acceleration Field. American Journal of Modern Physics. Vol. 3, No. 4, pp. 152-167 (2014). http://dx.doi.org/10.11648/j.ajmp.20140304.12 ; статья на русском языке: Интегральный 4-вектор энергии-импульса и анализ проблемы 4/3 на основе поля давления и поля ускорений.
  13. Fedosin S.G. Relativistic Energy and Mass in the Weak Field Limit. Jordan Journal of Physics. Vol. 8, No. 1, pp. 1-16 (2015). http://dx.doi.org/10.5281/zenodo.889210; статья на русском языке: Релятивистская энергия и масса в пределе слабого поля.
  14. Fedosin S.G. Estimation of the physical parameters of planets and stars in the gravitational equilibrium model. Canadian Journal of Physics, Vol. 94, No. 4, pp. 370-379 (2016). http://dx.doi.org/10.1139/cjp-2015-0593; статья на русском языке: Оценка физических параметров планет и звёзд в модели гравитационного равновесия.
  15. Fedosin S.G. The generalized Poynting theorem for the general field and solution of the 4/3 problem. International Frontier Science Letters, Vol. 14, pp. 19-40 (2019). https://doi.org/10.18052/www.scipress.com/IFSL.14.19. // Обобщённая теорема Пойнтинга для общего поля и решение проблемы 4/3.
  16. Fedosin S.G. The binding energy and the total energy of a macroscopic body in the relativistic uniform model. Middle East Journal of Science, Vol. 5, Issue 1, pp. 46-62 (2019). http://dx.doi.org/10.23884/mejs.2019.5.1.06. // Энергия связи и полная энергия макроскопического тела в релятивистской однородной модели.
  17. Fedosin S.G. Energy and metric gauging in the covariant theory of gravitation. Aksaray University Journal of Science and Engineering, Vol. 2, Issue 2, pp. 127-143 (2018). http://dx.doi.org/10.29002/asujse.433947. // Калибровка энергии и метрики в ковариантной теории гравитации.
  18. Fedosin S.G. The virial theorem and the kinetic energy of particles of a macroscopic system in the general field concept. Continuum Mechanics and Thermodynamics. Vol. 29, Issue 2, pp. 361-371 (2017). https://dx.doi.org/10.1007/s00161-016-0536-8; статья на русском языке: Теорема вириала и кинетическая энергия частиц макроскопической системы в концепции общего поля.
  19. Fedosin S.G. The integral theorem of generalized virial in the relativistic uniform model. Continuum Mechanics and Thermodynamics, Vol. 31, Issue 3, pp. 627-638 (2019). https://dx.doi.org/10.1007/s00161-018-0715-x. // Интегральная теорема обобщённого вириала в релятивистской однородной модели.
  20. Fedosin S.G. The potentials of the acceleration field and pressure field in rotating relativistic uniform system. Continuum Mechanics and Thermodynamics, Vol. 33, Issue 3, pp. 817-834 (2021). https://doi.org/10.1007/s00161-020-00960-7. // Потенциалы поля ускорений и поля давления во вращающейся релятивистской однородной системе.
  21. Fedosin S.G. The Mass Hierarchy in the Relativistic Uniform System. Bulletin of Pure and Applied Sciences, Vol. 38 D (Physics), No. 2, pp. 73-80 (2019). http://dx.doi.org/10.5958/2320-3218.2019.00012.5. // Иерархия масс в релятивистской однородной системе.
  22. Fedosin S.G. The relativistic uniform model: the metric of the covariant theory of gravitation inside a body. St. Petersburg Polytechnical State University Journal. Physics and Mathematics, Vol. 14, No. 3, pp.168-184 (2021). http://dx.doi.org/10.18721/JPM.14313. // О метрике ковариантной теории гравитации внутри тела в релятивистской однородной модели.
  23. Fedosin S.G. Generalized Four-momentum for Continuously Distributed Materials. Gazi University Journal of Science, Vol. 37, Issue 3, pp. 1509-1538 (2024). https://doi.org/10.35378/gujs.1231793. // Обобщённый 4-импульс для непрерывно распределённого вещества.
  24.  Yaakov Friedman and Tzvi Scarr. Covariant Uniform Acceleration. Journal of Physics: Conference Series Vol. 437 (2013) 012009 doi:10.1088/1742-6596/437/1/012009.
  25. Bahram Mashhoon and Uwe Muench. Length measurement in accelerated systems. Annalen der Physik. Vol. 11, Issue 7, P. 532–547, 2002. 

Внешние ссылки

 

Источник: http://sergf.ru/af.htm

На список страниц